I. Tìm GTLN và GTNN trên một khoảng, nữa khoảng
1. Phương pháp
– Để tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên tập $D$, ta thường lập bảng biến thiên của hàm số trên tập $D$ để kết luận.
– Ta quy ước rằng khi nói giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f(x)$ (mà không nói “trên tập $D$ “) thì ta hiểu đó là giá trị lớn nhất hay giá trị nhỏ nhất của $f(x)$ trên tập xác định của hàm số.
2. Các ví dụ
Ví dụ 1. Tìm GTLN và GTNN của hàm số $y = \frac{{3x – 2}}{{x – 1}}$ trên khoảng $\left( {1; + \infty } \right)$.
Lời giải
Ta có: $y’ = \frac{{3.( – 1) – ( – 2).1}}{{{{\left( {x – 1} \right)}^2}}} = \frac{{ – 1}}{{{{\left( {x – 1} \right)}^2}}} < 0,\,\forall x \in \left( {1; + \infty } \right)$.
Bảng biến thiên
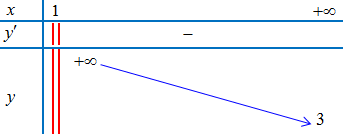
Vậy
– Không tồn tại giá trị lớn nhất trên $\left( {1; + \infty } \right)$.
– Không tồn tại giá trị nhỏ nhất trên $\left( {1; + \infty } \right)$.
Ví dụ 2. Tìm GTLN và GTNN của hàm số $y = \frac{{4x – 3}}{{x + 2}}$ trên nữa khoảng $\left( { – 2;7} \right]$.
Lời giải
Ta có: $y’ = \frac{{4.2 – ( – 3).1}}{{{{\left( {x + 2} \right)}^2}}} = \frac{{11}}{{{{\left( {x + 2} \right)}^2}}} > 0,\,\forall x \in \left( { – 2;7} \right]$.
Bảng biến thiên
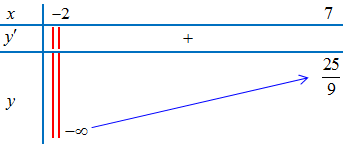
Vậy
– $\mathop {max}\limits_{\left( { – 2;7} \right]} = y\left( 7 \right) = \frac{{25}}{9}$.
– Không tồn tại giá trị nhỏ nhất trên $\left( { – 2;7} \right]$.
Ví dụ 3. Tìm GTLN và GTNN của hàm số $y = \frac{{{x^2} – 2x + 16}}{{x – 2}}$ trên khoảng $\left( {2; + \infty } \right)$.
Lời giải
Ta có: $y’ = \frac{{{{\left( {{x^2} – 2x + 16} \right)}^\prime }\left( {x – 2} \right) – \left( {{x^2} – 2x + 16} \right){{\left( {x – 2} \right)}^\prime }}}{{{{\left( {x – 2} \right)}^2}}}$
$ = \frac{{\left( {2x – 2} \right)\left( {x – 2} \right) – \left( {{x^2} – 2x + 16} \right).1}}{{{{\left( {x – 2} \right)}^2}}}$
$ = \frac{{2{x^2} – 4x – 2x + 4 – {x^2} + 2x – 16}}{{{{\left( {x – 2} \right)}^2}}}$$ = \frac{{{x^2} – 4x – 12}}{{{{\left( {x – 2} \right)}^2}}}$.
$y’ = 0 \Leftrightarrow \frac{{{x^2} – 4x – 12}}{{{{\left( {x – 2} \right)}^2}}} = 0$
$ \Rightarrow {x^2} – 4x – 12 = 0 \Leftrightarrow \left[ \begin{gathered}
x = 6\,\,(nhận) \hfill \\
x = – 2\,\,(loại) \hfill \\
\end{gathered} \right.$
Bảng biến thiên
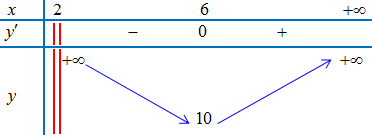
Vậy
– $\mathop {\min }\limits_{\left( {2; + \infty } \right)} y = y(6) = 10$
– Không tồn tại giá trị lớn nhất trên $\left( {2; + \infty } \right)$.
Ví dụ 4. Tìm GTLN và GTNN của hàm số $y = \frac{{4{x^2} + 4x + 9}}{{x + 1}}$ trên khoảng $\left( { – \infty ; – 1} \right)$.
Lời giải
Ta có: $y’ = \frac{{{{\left( {4{x^2} + 4x + 9} \right)}^\prime }\left( {x + 1} \right) – \left( {4{x^2} + 4x + 9} \right){{\left( {x + 1} \right)}^\prime }}}{{{{\left( {x + 1} \right)}^2}}}$
$ = \frac{{\left( {8x + 4} \right)\left( {x + 1} \right) – \left( {4{x^2} + 4x + 9} \right).1}}{{{{\left( {x + 1} \right)}^2}}}$
$ = \frac{{8{x^2} + 8x + 4x + 4 – 4{x^2} – 4x – 9}}{{{{\left( {x + 1} \right)}^2}}}$$ = \frac{{4{x^2} + 8x – 5}}{{{{\left( {x + 1} \right)}^2}}}$
$y’ = 0 \Leftrightarrow \frac{{4{x^2} + 8x – 5}}{{{{\left( {x + 1} \right)}^2}}} = 0$
$ \Rightarrow 4{x^2} + 8x – 5 = 0 \Leftrightarrow \left[ \begin{gathered}
x = \frac{1}{2}\,\,(loại) \hfill \\
x = – \frac{5}{2}\,\,(nhận) \hfill \\
\end{gathered} \right.$
Bảng biến thiên
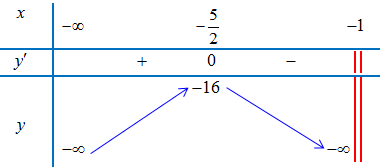
Vậy
– $\mathop {max}\limits_{\left( { – \infty ; – 1} \right)} = y\left( { – \frac{5}{2}} \right) = – 16$
– Không tồn tại giá trị nhỏ nhất trên $\left( { – \infty ; – 1} \right)$.
Ví dụ 5. Tìm GTLN và GTNN của hàm số $y = \frac{{2{x^2} – 3}}{{{x^2} + 2}}$.
Lời giải
Tập xác định: $D = \mathbb{R}$
Ta có: $y’ = \frac{{{{\left( {2{x^2} – 3} \right)}^\prime }\left( {{x^2} + 2} \right) – \left( {2{x^2} – 3} \right){{\left( {{x^2} + 2} \right)}^\prime }}}{{{{\left( {{x^2} + 2} \right)}^2}}}$
$ = \frac{{4x.\left( {{x^2} + 2} \right) – \left( {2{x^2} – 3} \right).2x}}{{{{\left( {{x^2} + 2} \right)}^2}}}$
$ = \frac{{4{x^3} + 8x – 4{x^3} + 6x}}{{{{\left( {{x^2} + 2} \right)}^2}}}$$ = \frac{{14x}}{{{{\left( {{x^2} + 2} \right)}^2}}}$
$y’ = 0 \Leftrightarrow \frac{{14x}}{{{{\left( {{x^2} + 2} \right)}^2}}} = 0$
$ \Leftrightarrow 14x = 0 \Leftrightarrow x = 0$
Bảng biến thiên
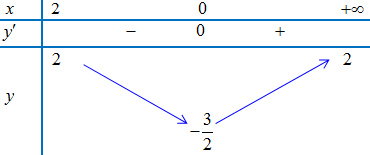
Vậy
– $\mathop {\min }\limits_\mathbb{R} y = y(0) = – \frac{3}{2}$.
– Không tồn tại giá trị lớn nhất trên $\mathbb{R}$.
Ví dụ 6. Tìm GTLN và GTNN của hàm số $y = \sqrt {{x^2} – 25} $.
Lời giải
Tập xác định: $D = \left( { – \infty ; – 5} \right] \cup \left[ {5; + \infty } \right)$
Ta có: $y’ = \frac{{{{\left( {{x^2} – 25} \right)}^\prime }}}{{2\sqrt {{x^2} – 25} }} = \frac{{2x}}{{2\sqrt {{x^2} – 25} }} = \frac{x}{{\sqrt {{x^2} – 25} }}$
$y’ = 0 \Rightarrow x = 0\,(loại)$.
Bảng biến thiên
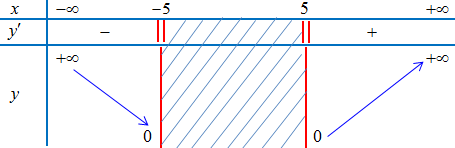
Vậy
– $\mathop {\min }\limits_D y = y\left( { – 5} \right) = y\left( 5 \right) = 0$.
– Không tồn tại giá trị lớn nhất trên $D$.
2. Tìm GTLN và GTNN trên một đoạn
1. Phương pháp
Các bước tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f(x)$ trên đoạn $[a ; b]$:
1. Tìm các điểm $x_1, x_2, \ldots, x_n \in(a ; b)$, tại đó $f'(x)$ bằng 0 hoặc không tồn tại.
2. Tính $f\left(x_1\right), f\left(x_2\right), \ldots, f\left(x_n\right), f(a)$ và $f(b)$.
3. Tìm số lớn nhất $M$ và số nhỏ nhất $m$ trong các số trên.
Ta có: $M = \mathop {max}\limits_{\left[ {a;b} \right]} f(x)$; $m = \mathop {\min }\limits_{\left[ {a;b} \right]} f(x)$.
2. Các ví dụ
Ví dụ 7. Tìm GTLN và GTNN của hàm số $y = {x^3} – 3{x^2} + 5$ trên đoạn $\left[ {1;4} \right]$.
Lời giải
Trên đoạn $\left[ {0;4} \right]$, ta có: $y’ = 3{x^2} – 6x$.
$y’ = 0 \Leftrightarrow 3{x^2} – 6x = 0 \Leftrightarrow \left[ \begin{gathered}
x = 2 \hfill \\
x = 0\,(loại) \hfill \\
\end{gathered} \right.$
$y(1) = 3$; $y\left( 4 \right) = 21$; $y\left( 2 \right) = 1$.
Vậy
– $\mathop {max}\limits_{\left[ {1;4} \right]} = y\left( 4 \right) = 21$
– $\mathop {\min }\limits_{\left[ {1;4} \right]} y = y(2) = 1$.
Ví dụ 8. Tìm GTLN và GTNN của hàm số $y = – {x^4} + 8{x^2} + 4$ trên đoạn $\left[ { – \sqrt 5 ;2} \right]$.
Lời giải
Trên đoạn$\left[ { – \sqrt 5 ;2} \right]$, ta có: $y’ = – 4{x^3} + 16x$.
$y’ = 0 \Leftrightarrow – 4{x^3} + 16x = 0 \Leftrightarrow \left[ \begin{gathered}
x = 2\,(nhận) \hfill \\
x = 0\,(nhận)\, \hfill \\
x = – 2\,\,(nhận) \hfill \\
\end{gathered} \right.$
$y\left( { – \sqrt 5 } \right) = 19$; $y\left( 2 \right) = 20$; $y\left( 0 \right) = 4$; $y\left( { – 2} \right) = 20$ .
Vậy
– $\mathop {max}\limits_{\left[ { – \sqrt 5 ;2} \right]} = y\left( { – 2} \right) = y\left( 2 \right) = 20$
– $\mathop {\min }\limits_{\left[ { – \sqrt 5 ;2} \right]} y = y(0) = 4$.
Ví dụ 9. Tìm GTLN và GTNN của hàm số $y = \frac{{ – 3x + 5}}{{x – 7}}$ trên đoạn $\left[ { – 3;0} \right]$.
Lời giải
Trên đoạn $\left[ { – 3;0} \right]$, ta có: $y’ = \frac{{16}}{{{{\left( {x – 7} \right)}^2}}} > 0,\,\forall x \in \left[ { – 3;0} \right]$.
$y\left( { – 3} \right) = – \frac{7}{5}$; $y\left( 0 \right) = – \frac{5}{7}$.
Vậy
– $\mathop {max}\limits_{\left[ { – 3;0} \right]} = y\left( 0 \right) = – \frac{5}{7}$
– $\mathop {\min }\limits_{\left[ { – 3;0} \right]} y = y( – 3) = – \frac{7}{5}$
Ví dụ 10. Tìm GTLN và GTNN của hàm số $y = \sqrt {27 – 3{x^2}} $.
Lời giải
Tập xác định: $D = \left[ { – 3;3} \right]$
Ta có: $y’ = \frac{{{{\left( {27 – 3{x^2}} \right)}^\prime }}}{{2\sqrt {27 – 3{x^2}} }} = \frac{{ – 6x}}{{2\sqrt {27 – 3{x^2}} }} = \frac{{ – 3x}}{{\sqrt {27 – 3{x^2}} }}$
$y’ = 0 \Rightarrow – 3x = 0 \Leftrightarrow x = 0\,(nhận)$.
$y\left( { – 3} \right) = 0$; $y\left( 3 \right) = 0$; $y\left( 0 \right) = 3\sqrt 3 $.
Vậy
– $\mathop {max}\limits_{\left[ { – 3;3} \right]} = y\left( 0 \right) = 3\sqrt 3 $
– $\mathop {\min }\limits_{\left[ { – 3;3} \right]} y = y( – 3) = y(3) = 0$
Ví dụ 11. Tìm GTLN và GTNN của hàm số $y = \sqrt { – {x^2} + 8x – 7} $.
Lời giải
Tập xác định: $D = \left[ {1;7} \right]$
Ta có: $y’ = \frac{{{{\left( { – {x^2} + 8x – 7} \right)}^\prime }}}{{2\sqrt { – {x^2} + 8x – 7} }} = \frac{{ – 2x + 8}}{{2\sqrt { – {x^2} + 8x – 7} }}$ $ = \frac{{ – x + 4}}{{\sqrt { – {x^2} + 8x – 7} }}$
$y’ = 0 \Rightarrow – x + 4 = 0$ $ \Leftrightarrow x = 4\,(nhận)$.
$y\left( 1 \right) = 0$; $y\left( 7 \right) = 0$; $y\left( 4 \right) = 3$.
Vậy
– $\mathop {max}\limits_{\left[ {1;7} \right]} = y\left( 4 \right) = 3$
– $\mathop {\min }\limits_{\left[ { – 3;3} \right]} y = y(1) = y(7) = 0$
Ví dụ 12: (ĐỀ THI TỐT NGHIỆP THPT NĂM 2024) Giá trị lớn nhất của hàm số $f\left( x \right) = – 6{x^3} + 27{x^2} – 16x + 1$ trên đoạn $\left[ {1;5} \right]$ bằng
A. 6 .
B. $\frac{{329}}{9}$.
C. $ – \frac{{14}}{9}$.
D. -154 .
Lời giải
Ta có: $f’\left( x \right) = – 18{x^2} + 54x – 16$
$f’\left( x \right) = 0 \Leftrightarrow – 18{x^2} + 54x – 16 = 0$$ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = \frac{8}{3}\,(nhận)} \\
{x = \frac{1}{3}\,(loại)}
\end{array}} \right.$
Khi đó, $f\left( 1 \right) = 6,f\left( 5 \right) = – 154,f\left( {\frac{8}{3}} \right) = \frac{{329}}{9}$
Suy ra, $\mathop {max}\limits_{\left[ {1;5} \right]} f(x) = f\left( {\frac{8}{3}} \right) = \frac{{329}}{9}$.
Chọn B





