Chuyên Đề Cực Trị Của Hàm Số Ôn Thi Tốt Nghiệp THPT

Chuyên đề Cực trị của hàm số ôn thi tốt nghiệp THPT file word và PDF gồm 25 trang. Các bạn xem và tải về ở dưới.

CHUYÊN ĐỀ: CỰC TRỊ CỦA HÀM SỐ

I. Hệ thống kiến thức liên quan

1. Khái niệm cực trị của hàm số

Cho $f:D \to \mathbb{R}$ và ${x_0} \in D$.

a) ${x_0}$ được gọi là một điểm cực đại của $f$ nếu tồn tại khoảng $\left( {a;b} \right)$ sao cho

$\left\{ \begin{gathered}
{x_0} \in \left( {a;b} \right) \subset D \hfill \\
f\left( x \right) < f\left( {{x_0}} \right)\;\forall x \in \left( {a;b} \right)\backslash \left\{ {{x_0}} \right\}. \hfill \\
\end{gathered} \right.$

b) ${x_0}$ được gọi là một điểm cực tiểu của $f$ nếu tồn tại khoảng $\left( {a;b} \right)$ sao cho

$\left\{ \begin{gathered}
{x_0} \in \left( {a;b} \right) \subset D \hfill \\
f\left( x \right) > f\left( {{x_0}} \right)\;\forall x \in \left( {a;b} \right)\backslash \left\{ {{x_0}} \right\}. \hfill \\
\end{gathered} \right.$

c) Điểm cực đại và điểm cực tiểu được gọi chung là điểm cực trị.

2. Điều kiện cần để hàm số đạt cực trị

Nếu hàm số $y = f(x)$ có đạo hàm trên khoảng $\left( {a;b} \right)$ và đạt cực trị tại ${x_0}$ thì $f’\left( {{x_0}} \right) = 0$.

3. Điều kiện đủ để hàm số đạt cực trị

a) Quy tắc 1

 Nếu $f’\left( x \right)$ đổi dấu từ dương sang âm khi $x$ đi qua ${x_0}$ thì $f(x)$ đạt cực đại tại ${x_0}$;

 Nếu $f’\left( x \right)$ đổi dấu từ âm sang dương khi $x$ đi qua ${x_0}$ thì $f(x)$ đạt cực tiểu tại ${x_0}$.

b) Quy tắc 2:

 $ \Rightarrow $ $f(x)$ đạt cực đại tại ${x_0}$;

 $ \Rightarrow $ $f$ đạt cực tiểu tại ${x_0}$.

II. Các dạng toán về cực trị của hàm số thường gặp

Dạng 1: Câu hỏi lí thuyết

Câu 1. Cho hàm số $y = f(x)$ xác định và có đạo hàm cấp một và cấp hai trên khoảng $\left( {a;b} \right)$và ${x_0}\, \in \left( {a;b} \right)$. Khẳng định nào sau đây sai?

A. $y'({x_0}) = 0$ và $y”({x_0}) \ne 0$ thì ${x_0}$ là điểm cực trị của hàm số.

B. $y'({x_0}) = 0$ và $y”({x_0}) > 0$ thì ${x_0}$ là điểm cực trị của hàm số.

C. Hàm số đạt cực đại tại ${x_0}$ thì $y'({x_0}) = 0$.

D. $y'({x_0}) = 0$ và $y”({x_0}) = 0$ thì ${x_0}$ không là điểm cực trị của hàm số.

Lời giải

Chọn D

Xét hàm số $y = {x^4}$ trên $\mathbb{R}$ thỏa mãn $y'(0) = 0$và $y”(0) = 0$ nhưng ${x_0} = 0$ vẫn là điểm cực tiểu của hàm số.

Vậy khẳng định D là sai.

Câu 2. Cho hàm số $y = f(x)$ có đạo hàm tại điểm ${x_0}$. Trong các mệnh đề sau, mệnh đề nào đúng?

A. Nếu $f'({x_0}) = 0$ thì hàm số đạt cực trị tại điểm ${x_0}$.

B. Nếu hàm số đạt cực trị tại điểm ${x_0}$ thì $f'({x_0}) = 0$.

C. Hàm số đạt cực trị tại ${x_0}$ thì $f(x)$đổi dấu khi qua ${x_0}$.

D. Nếu hàm số đạt cực trị tại điểm ${x_0}$ thì $f({x_0}) = 0$.

Lời giải

Chọn B

Nếu hàm số đạt cực trị tại điểm ${x_0}$ thì $f'({x_0}) = 0$.

Câu 3. Phát biểu nào sau đây đúng?

A. Hàm số $y = f(x)$ đạt cực trị tại điểm ${x_0}$ khi và chỉ khi$f'({x_0}) = 0$.

B. Nếu $f'({x_0}) = 0$ và $f”({x_0}) = 0$ thì ${x_0}$ không phải là cực trị của hàm số.

C. Nếu $f'({x_0})$đổi dấu khi $x$ qua điểm ${x_0}$ và $f(x)$liên tục tại ${x_0}$ thì hàm số $y = f(x)$ đạt cực trị tại điểm $x = {x_0}$.

D. Nếu $f'({x_0}) = 0$ và $f”({x_0}) > 0$ thì ${x_0}$ hàm số đạt cực đại tại $x = {x_0}$.

Lời giải

Chọn C

Nếu $f'({x_0})$đổi dấu khi $x$ qua điểm ${x_0}$ và $f(x)$liên tục tại ${x_0}$ thì hàm số $y = f(x)$ đạt cực trị tại điểm $x = {x_0}$.

Câu 4. Giả sử hàm số $(C):\,y = f(x)$ xác định trên tập ${\rm K}$ và ${x_0} \in {\rm K}$.

Cho các phát biểu sau:

(I). Nếu $f'({x_0}) \ne 0$ thì hàm số $y = f(x)$ không đạt cực trị tại ${x_0}$.

(II). Nếu $f'({x_0}) = 0$ thì hàm số $y = f(x)$ đạt cực trị tại ${x_0}$.

(III). Nếu ${x_0}$ là điểm cực trị của hàm số $y = f(x)$ thì điểm $\left( {{x_0};f({x_0})} \right)$ là điểm cực trị của đồ thị hàm số $(C)$.

(IV). Hàm số $y = f(x)$ có thể đạt cực trị tại ${x_0}$ mà không có đạo hàm tại ${x_0}$.

Số phát biểu đúng là

A. 1. B. 2. C. 3. D. 4.

Lời giải

Chọn C

(I) đúng ; (II) sai; (III) đúng ; (IV) đúng.

Vậy có 3 phát biểu đúng.

Câu 5. Giả sử hàm số $(C):\,y = f(x)$ có đạo hàm trên khoảng K. Xét các phát biểu sau:

(I). Nếu hàm số $y = f(x)$đạt cực tiểu trên khoảng K thì cũng sẽ đạt cực đại trên khoảng đó.

(II). Nếu hàm số $y = f(x)$có hai điểm cực tiểu thì phải có một điểm cực đại.

(II). Số nghiệm của phương trình $f'(x) = 0$ bằng số điểm cực trị của hàm số đã cho.

(IV). Hàm số có thể đạt cực trị tại một điểm mà tại đó hàm số không có đạo hàm.

Số phát biểu đúng là

A. 1. B. 2. C. 0. D. 3.

Lời giải

Chọn A

(I) ; (II) sai vì hàm số có thể có điểm cực đại mà không có điểm cực tiểu và ngược lại. Chẳng hạn, hàm số$y = {x^4}$ có điểm cực tiểu mà không có điểm cực đại.

(III) sai. Vì $f'(x) = 0$ chỉ là điều kiện cần để hàm số đạt cực trị. Nói cách khác $f'({x_0}) = 0$ thì chưa thể nói rằng ${x_0}$ là điểm cực trị.

(IV) đúng.

Vậy có 1 phát biểu đúng.

Dạng 2. Tìm cực trị của hàm số khi biết y, y’

Bước 1. Tìm tập xác định của hàm số. Tính $y’\left( {{x_0}} \right)$.

Bước 2. Giải phương trình $y’\left( x \right) = 0.$

Bước 3. Lập bảng biến thiên và kết luận về cực trị hàm số.

Câu 1: Hàm số $y = \frac{{2x + 3}}{{x + 1}}$ có bao nhiêu điểm cực trị?

A. $3.$ B. $0.$ C. $2$. D. $1$.

Lời giải

Chọn B

Có $y’ = \frac{{ – 1}}{{{{\left( {x + 1} \right)}^2}}} > 0,\forall x \ne – 1$ nên hàm số không có cực trị.

Câu 2: Giá trị cực đại ${y_{{\text{CĐ}}}}$ của hàm số $y = {x^3} – 3x + 2$ là

A. ${y_{{\text{CĐ}}}} = 4$. B. ${y_{{\text{CĐ}}}} = 1$. C. ${y_{{\text{CĐ}}}} = 0$. D. ${y_{{\text{C\S}}}} = – 1$.

Lời giải

Chọn A

Ta có $y’ = 3{x^2} – 3$.

$y’ = 0$$ \Leftrightarrow 3{x^2} – 3 = 0$$ \Leftrightarrow \left[ \begin{gathered}
x = 1{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \Rightarrow y\left( 1 \right) = 0 \hfill \\
x = – 1{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \Rightarrow y\left( { – 1} \right) = 4. \hfill \\
\end{gathered} \right.$

$\mathop {\lim }\limits_{x \to – \infty } {\mkern 1mu} \left( {{x^3} – 3x + 2} \right)$$ = \mathop {\lim }\limits_{x \to – \infty } {\mkern 1mu} {x^3}\left( {1 – \frac{3}{{{x^2}}} + \frac{2}{{{x^3}}}} \right) = – \infty ,{\mkern 1mu} $

${\mkern 1mu} \mathop {\lim }\limits_{x \to + \infty } {\mkern 1mu} \left( {{x^3} – 3x + 2} \right)$$ = \mathop {\lim }\limits_{x \to + \infty } {\mkern 1mu} {x^3}\left( {1 – \frac{3}{{{x^2}}} + \frac{2}{{{x^3}}}} \right) = + \infty $.

Bảng biến thiên

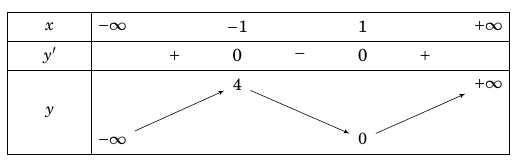
Từ bảng biến thiên, ta thấy giá trị cực đại của hàm số bằng $4$.

Câu 3. Hàm số nào dưới đây không có cực trị?

A. $y = \frac{{{x^2} + 1}}{x}$. B. $y = \frac{{2x – 2}}{{x + 1}}$. C. $y = {x^2} – 2x + 1$. D. $y = – {x^3} + x + 1$.

Lời giải

Chọn B

Xét hàm số $y = \frac{{2x – 2}}{{x + 1}}$.

Tập xác định $D = \mathbb{R}\backslash \left\{ { – 1} \right\}$, $y’ = \frac{4}{{{{\left( {x + 1} \right)}^2}}} > 0,\,\forall x \in D$.

Nên hàm số luôn đồng biến trên từng khoảng xác định.

Do đó hàm số $y = \frac{{2x – 2}}{{x + 1}}$ không có cực trị.

Câu 4. Cho hàm số $f\left( x \right)$ có đạo hàm $f’\left( x \right) = x{\left( {x + 1} \right)^2},\forall x \in \mathbb{R}$. Số điểm cực trị của hàm số đã cho là

A. $0$. B. $1$. C. $2$. D. $3$.

Lời giải

Chọn B

Ta có $f’\left( x \right) = x{\left( {x + 1} \right)^2}$chỉ đổi dấu đúng một lần khi qua nghiệm$x = 0$.

Suy ra, hàm số có đúng một điểm cực trị là $x = 0$.

Câu 5. Cho hàm số $f\left( x \right)$ có đạo hàm $f’\left( x \right) = x\left( {x – 1} \right){\left( {x + 2} \right)^3},\forall x \in \mathbb{R}$. Số điểm cực trị của hàm số đã cho là

A. 3. B. 2. C. 5. D. 1.

Lời giải

Chọn A

Ta có

$f’\left( x \right) = 0 \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
x = 1 \hfill \\
x = – 2. \hfill \\
\end{gathered} \right.$

Bảng dấu $f’\left( x \right)$

Từ bảng dấu suy ra hàm số đã cho có 3 điểm cực trị.

Câu 6. Hàm số $y = {x^3} – 3{x^2} – 9x + 4$ đạt cực trị tại ${x_1}$ và ${x_2}$ thì tích các giá trị cực trị bằng

A. $25.$ B. $ – 82.$ C. $ – 207.$ D. $ – 302.$

Lời giải

Chọn C

Ta có $y’ = 3{x^2} – 6x – 9$ .

$y’ = 0 \Leftrightarrow \left[ \begin{gathered}
x = – 1 \hfill \\
x = 3. \hfill \\
\end{gathered} \right.$

Từ đó ${y_1} = y( – 1) = 9,\,\,{y_2} = y(3) = – 23.$

Vậy ${y_1}.{y_2} = – 207$.

Câu 7. Hàm số $y = {x^3} – 3{x^2} + 2$ có đồ thị $(C)$. Gọi $A,\,\,B$ là các điểm cực trị của $(C)$. Độ dài đoạn $AB$ bằng

A. $2\sqrt 5 $ B. $5$. C. $4$. D. $5\sqrt 2 $

Lời giải

Chọn A

Ta có $y’ = 3{x^2} – 6x$ .

$y’ = 0 \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
x = 2. \hfill \\
\end{gathered} \right.$

Đồ thị hàm số có hai điểm cực trị là $A(0;\,2)$ và $B(2;\, – 2)$.

Độ dài AB bằng $\sqrt {{{(2 – 0)}^2} + {{( – 2 – 2)}^2}} = 2\sqrt 5 $.

Dạng 3. Tìm cực trị của hàm số dựa vào bảng biến thiên, đồ thị của hàm số y, y’

Câu 1. Cho hàm số có đồ thị như hình vẽ.

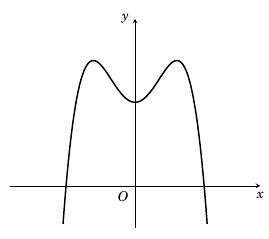
Số điểm cực trị của hàm số đã cho là

A. $3$. B. $1$. C. $2$. D. $0$.

Lời giải

Chọn A

Hàm số có ba điểm cực trị.

Câu 2. Cho hàm số $y = f(x)$ xác định, liên tục trên $\mathbb{R}$ và có đồ thị là đường cong trong hình vẽ.

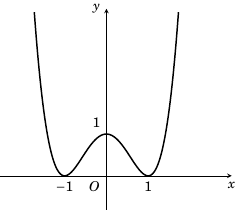
Hàm số $f(x)$ đạt cực đại tại

A. $x = 0$. B. $x = – 1$. C. $y = 0$. D. $x = 1$.

Lời giải

Chọn A

Hàm số $y = f(x)$ đạt cực đại tại $x = 0$.

Câu 3. Cho hàm số $f(x)$ có bảng biến thiên như sau:

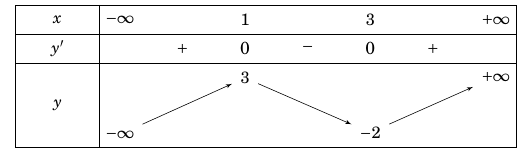
Hàm số đạt cực đại tại

A. $x = – 2$. B. $x = 3$. C. $x = 1$. $x = 2$.

Lời giải

Chọn C

Hàm số $f\left( x \right)$ xác định tại $x = 1$, $f'(1) = 0$ và đạo hàm đổi dấu từ $( + )$ sang $( – )$.

Câu 4. Cho hàm $f\left( x \right)$ có bảng biến thiên như sau:

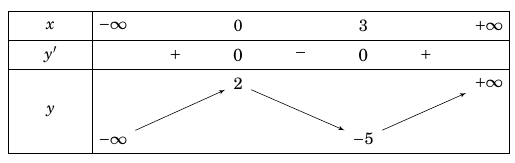
Giá trị cực tiểu của hàm số đã cho bằng

A. $3$. B. $ – 5$. C. $0$. D. $2$.

Lời giải

Chọn B.

Từ bảng biến thiên ta có hàm số đạt giá trị cực tiểu $f\left( 3 \right) = – 5$ tại $x = 3$

Câu 5. Cho hàm số $y = f\left( x \right)$ có bảng xét dấu của đạo hàm như sau:

Số điểm cực trị của hàm số đã cho là

A. $3$. B. $4$. C. $2$. D. $5$.

Lời giải

Chọn B.

Đạo hàm của hàm số đã cho đổi dấu $4$lần qua các điểm $ – 2,\,\, – 1,\,\,2,\,\,4$. Nên hàm số đã cho có $4$ cực trị.

Câu 6. Cho hàm số $y = f\left( x \right)$ có bảng xét dấu của đạo hàm như sau:

Số điểm cực trị của hàm số đã cho là

A. $3$. B. $4$. C. $2$. D. $1$.

Lời giải

Chọn B

Dựa vào bảng xét dấu đạo hàm ta thấy đạo hàm đổi dấu qua các điểm $ – 2,\,2$.

Vậy hàm số có 2 điểm cực trị.

Câu 7. Cho hàm số $y = f\left( x \right)$ xác định và có đạo hàm $f'(x)$. Đồ thị hàm số $y = f'(x)$ như hình vẽ

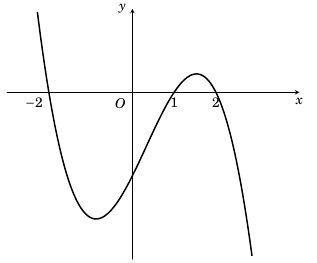
Khẳng định nào sau đây đúng?

A. Hàm số $y = f\left( x \right)$ có 2 cực trị.

B. Hàm $y = f\left( x \right)$đã cho có 2 cực tiểu và 1 cực đại.

C. Hàm số $y = f\left( x \right)$ đạt cực tiểu tại $x = 2$.

D. Hàm số $y = f\left( x \right)$ đạt cực đại tại $x = 2$.

Lời giải

Chọn D

Đồ thị hàm số $y = f’\left( x \right)$ cắt trục $Ox$ tại ba điểm -2, 1, 2. Nên hàm số $y = f\left( x \right)$ có 3 cực trị.

Mà $f’\left( x \right)$ đổi dấu từ dương sang âm khi qua $x = 2$.

Vậy hàm số $y = f\left( x \right)$đạt cực đại tại $x = 2$.
Dạng 4. Tìm m để hàm số đạt cực trị tại ${x_0}$ cho trước
Bước 1. Tính $y’\left( {{x_0}} \right),y”\left( {{x_0}} \right)$

Bước 2. Giải phương trình $y’\left( {{x_0}} \right) = 0 \Rightarrow m?$

Bước 3. Thế $m$ vào $y”\left( {{x_0}} \right)$ nếu giá trị $\left[ \begin{gathered}
y” > 0 \to {x_0} = CT \hfill \\
y” < 0 \to {x_0} = CD \hfill \\
\end{gathered} \right.$

Câu 1. Tìm giá trị thực của tham số $m$ để hàm số $y = \frac{1}{3}{x^3} – m{x^2} + \left( {{m^2} – 4} \right)x + 3$ đạt cực đại tại $x = 3$.

A. $m = – 1$. B. $m = – 7$. C. $m = 5$. D. $m = 1$.

Lời giải

Chọn C

Ta có $y’ = {x^2} – 2mx + \left( {{m^2} – 4} \right)$; $y” = 2x – 2m$.

Hàm số $y = \frac{1}{3}{x^3} – m{x^2} + \left( {{m^2} – 4} \right)x + 3$ đạt cực đại tại $x = 3$

$ \Leftrightarrow \left\{ \begin{gathered}
y’\left( 3 \right) = 0 \hfill \\
y”\left( 3 \right) < 0 \hfill \\
\end{gathered} \right.$$ \Leftrightarrow \left\{ \begin{gathered}
9 – 6m + {m^2} – 4 = 0 \hfill \\
6 – 2m < 0 \hfill \\
\end{gathered} \right.$

$ \Leftrightarrow \left\{ \begin{gathered}
{m^2} – 6m + 5 = 0 \hfill \\
m > 3 \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
\left[ \begin{gathered}
m = 1\left( L \right) \hfill \\
m = 5\left( {TM} \right) \hfill \\
\end{gathered} \right. \hfill \\
m > 3. \hfill \\
\end{gathered} \right.$

Vậy $m = 5$ là giá trị cần tìm.

Câu 2. Tìm các giá trị thực của tham số $m$ để hàm số $y = {x^3} – 2m{x^2} + mx + 1$ đạt cực tiểu tại $x = 1$.

A. $m = – 1$. B. $m = \pm 1$. C. $m = 1$. D. $m \in \left\{ {1;2} \right\}$.

Lời giải

Để $x = 1$ là điểm cực tiểu của hàm số

$ \Leftrightarrow \left\{ \begin{gathered}
y’\left( 1 \right) = 0 \hfill \\
y”\left( 1 \right) > 0 \hfill \\
\end{gathered} \right.$
$ \Leftrightarrow \left\{ \begin{gathered}
3 – 4m + m = 0 \hfill \\
6 – 4m > 0 \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
m = 1 \hfill \\
m < \frac{3}{2} \hfill \\
\end{gathered} \right. \Leftrightarrow m = 1.$

Thử lại với $m = 1,$ hàm số đã cho trở thành $y = {x^3} – 2{x^2} + x + 1$.

Ta có $y’ = 3{x^2} – 4x + 10 \Leftrightarrow \left[ \begin{gathered}
x = 1 \hfill \\
x = \frac{1}{3}. \hfill \\
\end{gathered} \right.$

Bảng biến thiên

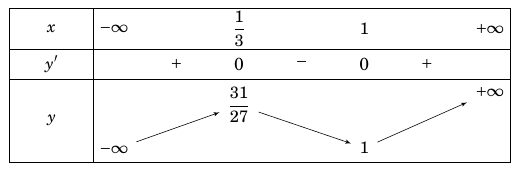
Quan sát bảng biến thiên ta thấy $m = 1$ thỏa yêu cầu bài toán.

Câu 3. Tìm các giá trị của tham số $m$ để hàm số $y = {x^3} – 3{x^2} + mx + 1$ đạt cực tiểu tại $x = 2$.

A. $m = 0$. B. $m > 4$. C. $0 \leqslant m < 4$. D. $0 < m \leqslant 4$.

Lời giải

Chọn A

$y’ = 3{x^2} – 6x + m$; $y” = 6x – 6$.

Hàm số đạt cực tiểu tại $x = 2 \Leftrightarrow \left\{ \begin{gathered}
y’\left( 2 \right) = 0 \hfill \\
y”\left( 2 \right) > 0 \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
m = 0 \hfill \\
6 > 0 \hfill \\
\end{gathered} \right. \Leftrightarrow m = 0$.

Vậy $m = 0$ thỏa mãn yêu cầu đề bài.

Câu 4. Có bao nhiêu số thực $m$ để hàm số $y = \frac{1}{3}{x^3} – m{x^2} + \left( {{m^2} – m + 1} \right)x + 1$ đạt cực đại tại $x = 1$.

A. $0$ B. $2$ C. $1$ D. $3$

Lời giải

Chọn C

$y’ = {x^2} – 2mx + {m^2} – m + 1$

$y” = 2x – 2m$

Hàm số đạt cực đại tại $x = 1$ nên ta có $\left\{ \begin{gathered}
y’\left( 1 \right) = 0 \hfill \\
y”\left( 1 \right) < 0 \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
{m^2} – 3m + 2 = 0 \hfill \\
2 – 2m < 0 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} \left[ \begin{gathered} m = 1 \hfill \\ m = 2 \hfill \\ \end{gathered} \right. \hfill \\ m > 1 \hfill \\
\end{gathered} \right. \Leftrightarrow m = 2$.
Vậy $m = 1$ thỏa mãn yêu cầu đề bài.

Dạng 5. Cực trị của hàm bậc ba $y = a{x^3} + b{x^2} + cx + d$

Xét hàm số bậc ba $y = a{x^3} + b{x^2} + cx + d$
Hàm số có hai điểm cực trị khi $\left\{ \begin{gathered}
a \ne 0 \hfill \\
\Delta ‘ = {b^2} – 3ac > 0. \hfill \\
\end{gathered} \right.$
Hàm số không có cực trị khi $y’ = 0$ vô nghiệm hoặc có nghiệm kép.

Gọi ${x_1},{\text{ }}{x_2}$ là 2 nghiệm của phương trình $y’ = 0.$
Theo Viét, ta có $\left\{ \begin{gathered}
S = {x_1} + {x_2} = – \frac{b}{a} \hfill \\
P = {x_1}{x_2} = \frac{c}{a}. \hfill \\
\end{gathered} \right.$

Câu 1. Tìm tất cả các giá trị của tham số thực $m$ để hàm số $y = m{x^3} – 2m{x^2} + (m – 2)x + 1$ không có cực trị.

A. $m \in ( – \infty ;6) \cup (0; + \infty )$. B. $m \in \left( { – 6;0} \right)$. C. $m \in \left[ { – 6;0} \right)$. D. $m \in \left[ { – 6;0} \right]$

Lời giải

Chọn D

Ta có $y’ = 3m{x^2} – 4mx + (m – 2)$.

TH1: $m = 0$

$ \Rightarrow {\text{ }}y’ = – 2 < 0{\text{ (}}\forall x \in \mathbb{R})$. Nên hàm số không có cực trị.

Do đó $m = 0$(TM) (1).

TH2: $m \ne 0$

Hàm số không có cực trị $ \Leftrightarrow y’$ không đổi dấu

$ \Leftrightarrow \Delta ‘ \leqslant 0 \Leftrightarrow 4{m^2} – 3m(m – 2) \leqslant 0 \Leftrightarrow {m^2} + 6m \leqslant 0 \Rightarrow – 6 \leqslant m < 0$ (do $m \ne 0$) (2).

Kết hợp (1) và (2) ta được $ – 6 \leqslant m \leqslant 0$.

Câu 2. Với giá trị nào của tham số $m$ để đồ thị hàm số $y = {x^3} – 3{x^2} + m$ có hai điểm cực trị $A,\,B$ thỏa mãn $OA = OB$ ($O$ là gốc tọa độ)?

A. $m = \frac{3}{2}$. B. $m = 3$. C. $m = \frac{1}{2}$. D. $m = \frac{5}{2}$.

Lời giải

Chọn D

Tập xác định $D = \mathbb{R}$.

Ta có $y’ = 3{x^2} – 6x$.

$y’ = 0 \Leftrightarrow 3{x^2} – 6x = 0 \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
x = 2. \hfill \\
\end{gathered} \right.$

Đồ thị hàm số có hai điểm cực trị là $A\left( {0;m} \right)$ và $B\left( {2; – 4 + m} \right)$.

Theo giả thiết

$OA = OB \Leftrightarrow \sqrt {{0^2} + {m^2}} = \sqrt {{2^2} + {{\left( {4 – m} \right)}^2}} $
$ \Leftrightarrow {m^2} = 4 + {\left( {4 – m} \right)^2}$
$ \Leftrightarrow 20 – 8m = 0 \Leftrightarrow m = \frac{5}{2}$.

Vậy $m = \frac{5}{2}$ thỏa mãn yêu cầu đề bài.

Câu 3. Có tất cả bao nhiêu giá trị thực của tham số $m$ để đồ thị hàm số $y = \frac{2}{3}{x^3} – m{x^2} – 2\left( {3{m^2} – 1} \right)x + \frac{2}{3}$ có hai điểm cực trị có hoành độ $x{}_1$, ${x_2}$ sao cho ${x_1}{x_2} + 2\left( {{x_1} + {x_2}} \right) = 1$.

A. $1$. B. $0$. C. $3$. D. $2$.

Lời giải

Chọn A

$y’ = 2{x^2} – 2mx – 2\left( {3{m^2} – 1} \right) = 0$

$ \Leftrightarrow g\left( x \right) = {x^2} – mx – 3{m^2} + 1 = 0$.

Đồ thị hàm số có hai điểm cực trị khi và chỉ khi $y’$ có hai nghiệm phân biệt

$ \Leftrightarrow $ $g\left( x \right)$ có hai nghiệm phân biệt

$ \Leftrightarrow $ $\Delta = 13{m^2} – 4 > 0$$ \Leftrightarrow $ $\left[ \begin{gathered}
m > \frac{{2\sqrt {13} }}{{13}} \hfill \\
m < – \frac{{2\sqrt {13} }}{{13}}. \hfill \\
\end{gathered} \right.$ (*)

${x_1}$, ${x_2}$ là các nghiệm của $g\left( x \right)$ nên theo định lý Vi-ét, ta có $\left\{ \begin{gathered}{x_1} + {x_2} = m \hfill \\{x_1}{x_2} = – 3{m^2} + 1. \hfill \\\end{gathered} \right.$

Do đó ${x_1}{x_2} + 2\left( {{x_1} + {x_2}} \right) = 1$ $ \Leftrightarrow $ $ – 3{m^2} + 2m + 1 = 1$ $ \Leftrightarrow $ $ – 3{m^2} + 2m = 0$ $ \Leftrightarrow $ $\left[ \begin{gathered}
m = 0 \hfill \\
m = \frac{2}{3}. \hfill \\
\end{gathered} \right.$

Đối chiếu với điều kiện (*), ta có $m = \frac{2}{3}$ thỏa mãn yêu cầu bài toán.

Vậy có $1$ giá trị của tham số $m$thỏa mãn yêu cầu bài toán.

Câu 4. Tìm tất cả cả các giá trị của tham số m để hàm số $y = {x^3} – 3{x^2} + mx – 1$ đạt cực trị tại ${x_1},{x_2}$ thỏa mãn $x_1^2 + x_2^2 = 6$.

A. $m = – 3$. B. $m = 3$. C. $m = – 1$. D. $m = 1$.

Lời giải

Chọn A

Ta có $y’ = 3{x^2} – 6x + m$.

Hàm số đạt cực trị tại ${x_1},{x_2}$

$ \Leftrightarrow $ Phương trình $y’ = 0$ có hai nghiệm phân biệt
$ \Leftrightarrow $$\Delta ‘ = 9 – 3m > 0\,\, \Leftrightarrow \,\,m < 3$.

Theo viet ta có $\left\{ \begin{gathered}
{x_1} + {x_2} = 2 \hfill \\
{x_1}.{x_2} = \frac{m}{3}. \hfill \\
\end{gathered} \right.$

Theo giả thiết $x_1^2 + x_2^2 = 6\, \Leftrightarrow \,{({x_1} + {x_2})^2} – 2{x_1}{x_2}\, = 6\,$

$ \Leftrightarrow \,4 – \frac{{2m}}{3} = 6\, \Leftrightarrow m = – 3$ (thỏa mãn).

Vậy $m = – 3$ thỏa mãn yêu cầu đề bài.

Câu 5. Tìm tất cả giá trị thực của tham số $m$ để đồ thị hàm số $y = {x^3} – 3m{x^2} + 2$ có hai điểm cực trị $A$ và $B$ sao cho các điểm $A$, $B$ và $M\left( {1;\, – 2} \right)$ thẳng hàng.

A. $m = \sqrt 2 $. B. $m = – \sqrt 2 $. C. $m = 2$. D. $m = – \sqrt 2 $; $m = \sqrt 2 $.

Lời giải

Ta có: $y’ = 3{x^2} – 6mx$ ; $y’ = 0$ $ \Leftrightarrow $ $3{x^2} – 6mx = 0$ $ \Leftrightarrow $ $x = 0$, $x = 2m$.

Đồ thị hàm số có hai điểm cực trị

$ \Leftrightarrow $$y’ = 0$ có hai nghiệm phân biệt $ \Leftrightarrow $ $2m \ne 0$ $ \Leftrightarrow $ $m \ne 0$.

Khi đó hai điểm cực trị là $A\left( {0;\,2} \right)$, $B\left( {2m;\,2 – 4{m^3}} \right)$.

Ta có $\overrightarrow {MA} = \left( { – 1;\,4} \right)$, $\overrightarrow {MB} = \left( {2m – 1;\,4 – 4{m^3}} \right)$.

Ba điểm $A$, $B$ và $M\left( {1;\, – 2} \right)$ thẳng hàng $ \Leftrightarrow $ $\overrightarrow {MA} $, $\overrightarrow {MB} $ cùng phương

$ \Leftrightarrow $ $\frac{{2m – 1}}{{ – 1}} = \frac{{4 – 4{m^3}}}{4}$ $ \Leftrightarrow $ $\frac{{2m – 1}}{{ – 1}} = \frac{{1 – {m^3}}}{1}$ $ \Leftrightarrow $ $2m – 1 = {m^3} – 1$ $ \Leftrightarrow $ ${m^3} = 2m$

$ \Leftrightarrow $ $\left[ \begin{gathered}
m = 0 \hfill \\
{m^2} = 2 \hfill \\
\end{gathered} \right.$ $ \Leftrightarrow $ $\left[ \begin{gathered}
m = 0\,\,\,\,(l) \hfill \\
m = \pm \sqrt 2 \,\,(TM). \hfill \\
\end{gathered} \right.$

Vậy $m = \pm \sqrt 2 $ thỏa mãn yêu cầu đề bài.
Dạng 6. Biện luận số cực trị của hàm bậc bốn $y = a{x^4} + b{x^2} + c\,\,\,(a \ne 0)$
Hàm số $y = a{x^4} + b{x^2} + c$có ba cực trị khi $ab < 0.$

Hàm số $y = a{x^4} + b{x^2} + c$có $1$ cực trị khi $ab \geqslant 0.$

Câu 1. Tìm tất cả các giá trị thực của tham số $m$ để hàm số $y = \left( {m – 1} \right){x^4} – 2\left( {m – 3} \right){x^2} + 1$ không có cực đại?

A. $1 < m \leqslant 3$ B. $m \leqslant 1$ C. $m \geqslant 1$ D. $1 \leqslant m \leqslant 3$

Lời giải

Chọn D

TH1: Nếu $m = 1 \Rightarrow y = 4{x^2} + 1$. Suy ra hàm số không có cực đại.

TH2: Nếu $m > 1$.

Để hàm số không có cực đại thì $ – 2\left( {m – 3} \right) \geqslant 0 \Leftrightarrow m \leqslant 3$. Suy ra $1 < m \leqslant 3$.

Vậy $1 \leqslant m \leqslant 3$.

Câu 2. Cho hàm số $f(x) = \frac{1}{3}{x^3} – m{x^2} + (4m – 3)x + 1$. Tìm $m$ để hàm số có hai cực trị.

A. $m < 1$ hoặc $m > 3$. B. $m \leqslant 13$. C. $m \geqslant 3$. D. $m \leqslant 1$ hoặc $m \geqslant 3$.

Lời giải

Chọn A

Tập xác định $D = \mathbb{R}$.

Ta có $y’ = {x^2} – 2mx + 4m – 3$.

Hàm số có hai điểm cực trị

$ \Leftrightarrow \,y’ = 0$ có hai nghiệm phân biệt và đổi dấu qua hai nghiệm ấy.

$ \Leftrightarrow \left\{ \begin{gathered}
a = 1 \ne 0 \hfill \\
\Delta ‘ = {m^2} – 4m + 3 > 0 \hfill \\
\end{gathered} \right. \Leftrightarrow \left[ \begin{gathered}
m > 3 \hfill \\
m < 1. \hfill \\
\end{gathered} \right.$

Vậy $m < 1$ hoặc $m > 3$.

Câu 3. Tất cả các giá trị thực của tham số $m$ để hàm số $y = – {x^4} – \left( {m – 3} \right){x^2} + m + 1$ có điểm cực đại mà không có điểm cực tiểu là

A. $m \geqslant 3$. B. $m > 3$. C. $m < 3.$ D. $m \leqslant 3$.

Lời giải

Chọn A

Cách 1:

Hàm số có điểm cực đại mà không có điểm cực tiểu $\left\{ \begin{gathered}
a.b \geqslant 0 \hfill \\
a < 0 \hfill \\
\end{gathered} \right.$ hoặc $\left\{ \begin{gathered}
a = 0 \hfill \\
b < 0 \hfill \\
\end{gathered} \right.$
$ \Leftrightarrow – 1.\left[ { – (m – 3)} \right] \geqslant 0 \Leftrightarrow m \geqslant 3$

Cách 2:

Tập xác định $D = \mathbb{R}$.
$y’ = 4{x^3} – 4mx = 4x\left( {{x^2} – m} \right)$.
$y’ = 0 \Leftrightarrow 4x\left( {{x^2} – m} \right) = 0 \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
{x^2} = m{\text{ }}\left( * \right). \hfill \\
\end{gathered} \right.$
Hàm số có $3$ cực trị $ \Leftrightarrow y’ = 0$ có $3$ nghiệm phân biệt
$ \Leftrightarrow $ phương trình $\left( * \right)$có $2$ nghiệm phân biệt $x \ne 0$$ \Leftrightarrow m > 0$.

Câu 4. Cho hàm số $y = {x^4} – 2m{x^2} + m$. Tìm tất cả các giá trị thực của $m$ để hàm số có $3$ cực trị.

A. $m > 0$. B. $m \geqslant 0$. C. $m < 0$. D. $m \leqslant 0$.

Lời giải

Chọn A

Cách 1:

Hàm số có 3 cực trị $ \Leftrightarrow a.b < 0 \Leftrightarrow 1.( – 2m) < 0 \Leftrightarrow m > 0$

Cách 2:

Tập xác định $D = \mathbb{R}$.

$y’ = 4{x^3} – 4mx = 4x\left( {{x^2} – m} \right)$.

$y’ = 0 \Leftrightarrow 4x\left( {{x^2} – m} \right) = 0 \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
{x^2} = m{\text{ }}\left( * \right). \hfill \\
\end{gathered} \right.$

Hàm số có $3$ cực trị $ \Leftrightarrow y’ = 0$ có $3$ nghiệm phân biệt

$ \Leftrightarrow $ phương trình $\left( * \right)$có $2$ nghiệm phân biệt $x \ne 0$$ \Leftrightarrow m > 0$.

Câu 5. Có bao nhiêu giá trị nguyên của tham số $m$ để hàm số $y = {m^2}{x^4} – \left( {{m^2} – 2019m} \right){x^2} – 1$ có đúng một cực trị?

A. $2019$. B. $2020$. C. $2018$. D. $2017$.

Lời giải

Chọn A

Trường hợp 1: $m = 0$ $ \Rightarrow y = – 1$ nên hàm số không có cực trị.

$ \Rightarrow m = 0$ (loại).

Trường hợp 2: $m \ne 0 \Rightarrow {m^2} > 0$.

Hàm số $y = {m^2}{x^4} – \left( {{m^2} – 2019m} \right){x^2} – 1$ có đúng một cực trị $ \Leftrightarrow a.b \geqslant 0 \Leftrightarrow – {m^2}.\,\left( {{m^2} – 2019m} \right) \geqslant 0 \Leftrightarrow {m^2} – 2019m \leqslant 0 \Leftrightarrow 0 \leqslant m \leqslant 2019$.

Vì $m \ne 0$$ \Rightarrow 0 < m \leqslant 2019$.

Do $m \in \mathbb{Z}$ nên có $2019$ giá trị nguyên của tham số $m$ thỏa mãn.
Dạng 7. Đường thẳng đi qua 2 điểm cực trị
Câu 1. Đồ thị hàm số $y = {x^3} – 3{x^2} – 9x + 1$ có hai cực trị $A$ và $B$. Điểm nào dưới đây thuộc đường thẳng $AB$?

A. $M\left( {0; – 1} \right)$. B. $N\left( {1; – 10} \right)$. C. $P\left( {1;0} \right)$. D. $Q\left( { – 1;10} \right)$.

Lời giải

Chọn B

Ta có: $y’ = 3{x^2} – 6x – 9 = 0\, \Leftrightarrow \,\left[ \begin{gathered}
x = – 1 \hfill \\
x = 3. \hfill \\
\end{gathered} \right.$

Đồ thị hàm số có hai điểm cực trị là $A(1; – 10)$ và $B\left( {3; – 26} \right)$.

Do đó, điểm $N\left( {1; – 10} \right)$ thuộc đường thẳng $AB$.

Câu 2. Tìm giá trị thực của tham số $m$ để đường thẳng $d:y = \left( {2m – 1} \right)x + 3 + m$ vuông góc với đường thẳng đi qua hai điểm cực trị của đồ thị hàm số $y = {x^3} – 3{x^2} + 1$.

A. $m = \frac{3}{2}$. B. $m = \frac{3}{4}$. C. $m = – \frac{1}{2}$. D. $m = \frac{1}{4}$.

Lời giải

Chọn B

Ta có $y’ = 3{x^2} – 6x = 0\, \Leftrightarrow \,\left[ \begin{gathered}
x = 0 \hfill \\
x = 2. \hfill \\
\end{gathered} \right.$

Đồ thị hàm số có hai điểm cực trị $A\left( {0;1} \right)$, $B\left( {2; – 3} \right)$.

Đường thẳng qua hai điểm cực trị có phương trình $y = ax + b$.

Ta có hệ $\left\{ \begin{gathered}
b = 1 \hfill \\
2a + b = – 3 \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
a = – 2 \hfill \\
b = 1. \hfill \\
\end{gathered} \right.$

Đường thẳng qua hai điểm cực trị có phương trình $y = – 2x + 1$.

Đường thẳng này vuông góc với đường thẳng $y = \left( {2m – 1} \right)x + 3 + m$ khi và chỉ khi $\left( {2m – 1} \right)\left( { – 2} \right) = – 1 \Leftrightarrow m = \frac{3}{4}$.

Câu 3. Tìm giá trị thực của tham số $m$ để đường thẳng $y = \left( {2m – 1} \right)x + m + 3$ song song với đường thẳng đi qua các điểm cực trị của đồ thị hàm số $y = {x^3} – 3{x^2} + 1$.

A. $m = \frac{3}{4}$. B. $m = \frac{1}{2}$. C. $m = – \frac{3}{4}$. D. $m = – \frac{1}{2}$.

Lời giải

Chọn D

Hàm số $y = {x^3} – 3{x^2} + 1$ có TXĐ: $\mathbb{R}$;

$y’ = 3{x^2} – 6x$; $y’ = 0 \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
x = 2. \hfill \\
\end{gathered} \right.$

Suy ra đồ thị hàm số có hai điểm cực trị là $A\left( {0;1} \right)$, $B\left( {2; – 3} \right) \Rightarrow \overrightarrow {AB} = \left( {2; – 4} \right)$.

Đường thẳng $d$ đi qua hai điểm $A$, $B$ có phương trình: $\frac{x}{2} = \frac{{y – 1}}{{ – 4}} \Leftrightarrow y = – 2x + 1$.

Đường thẳng $y = \left( {2m – 1} \right)x + m + 3$ song song với đường thẳng $d \Leftrightarrow \left\{ \begin{gathered}
2m – 1 = – 2 \hfill \\
m + 3 \ne 1 \hfill \\
\end{gathered} \right. \Leftrightarrow m = – \frac{1}{2}$.

Câu 4. Tìm giá trị thực của tham số $m$ để đường thẳng $d:y = \left( {3m + 1} \right)x + 3 + m$ vuông góc với đường thẳng đi qua hai điểm cực trị của đồ thị hàm số $y = {x^3} – 3{x^2} – 1$.

A. $\frac{1}{3}$. B. $ – \frac{1}{6}$. C. $m = \frac{1}{6}$. D. $ – \frac{1}{3}$.

Lời giải

Chọn B

Hàm số $y = {x^3} – 3{x^2} – 1$ có TXĐ: $\mathbb{R}$; $y’ = 3{x^2} – 6x$; $y’ = 0 \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
x = 2. \hfill \\
\end{gathered} \right.$

Suy ra đồ thị hàm số có hai điểm cực trị là $A\left( {0; – 1} \right)$, $B\left( {2; – 5} \right) \Rightarrow \overrightarrow {AB} = \left( {2; – 4} \right)$.

Đường thẳng $d$ đi qua hai điểm $A$, $B$ có phương trình: $\frac{x}{2} = \frac{{y + 1}}{{ – 4}} \Leftrightarrow y = – 2x – 1$.

Để $d$ vuông góc với $\Delta $ thì $\left( {3m + 1} \right).\left( { – 2} \right) = – 1$ $ \Leftrightarrow m = – \frac{1}{6}$.

Vậy giá trị cần tìm của $m$ là $m = – \frac{1}{6}$.

III. Những lỗi học sinh thường mắc

Sai lầm thứ nhất : Không phân biệt được các khái niệm liên quan đến cực trị

Ví dụ 1: Điểm cực tiểu của đồ thị hàm số $y = – {x^4} + 2{x^2} + 3$ là

A. $x = 1$. B. $\left( {1;4} \right)$. C. $\left( {0;3} \right)$. D. $x = 0$.

Trong ví dụ này, học sinh hay nhầm lẫn giữa phương án C và D.

Nếu ${x_0}$ là điểm cực trị của hàm số $y = f(x)$ thì điểm $\left( {{x_0};f({x_0})} \right)$ là điểm cực trị của đồ thị hàm số $(C)$. Phương án đúng C.

Ví dụ 2: Cho hàm số có bảng biến thiên như sau :

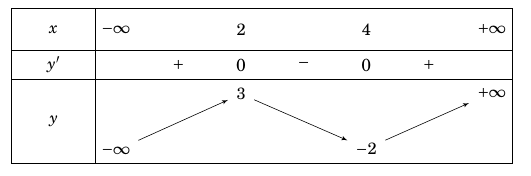
Khẳng định nào sau đây đúng ?

A. Hàm số đạt cực đại tại $x = 2$. B. Hàm số đạt cực đại tại $x = 3$.

C. Hàm số đạt cực đại tại $x = 4$. D. Hàm số đạt cực đại tại $x = – 2$.

Trong ví dụ này học sinh hay nhầm lẫn giữa A và C.

Phương án đúng C.

Cách khắc phục: Nắm vững các khái niệm sau

Cho hàm số $y = f(x)$ nếu ${x_0}$ là điểm cực trị của hàm số thì

Hàm số đạt cực trị tại ${x_0}$ (${x_0}$ là điểm cực trị của hàm số).

Cực tiểu (giá trị cực tiểu) của hàm số là $y = f({x_0})$.

Điểm cực trị của đồ thị hàm số là $\left( {{x_0};f({x_0})} \right)$.

Sai lầm thứ 2: Phương trình $f'(x) = 0$ vô nghiệm thì kết luận hàm số không có cực trị

Ví dụ 1 : Số cực trị của hàm số $y = \sqrt[3]{{{{(x – 2)}^2}}}$là

A. $0$. B. $2$. C. $1$. D. $3$.

Ta có $y’ = \frac{2}{{\sqrt[3]{{x – 2}}}}$.

Phương trình $y’ = 0$ vô nghiệm nên hàm số đã cho không có cực trị.

Lời giải như trên là sai.

Ta có bảng biến thiên của hàm số đã cho như sau

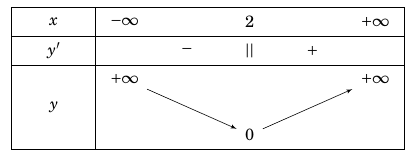
Vậy hàm số đã cho có $1$ cực trị.

Sai lầm thứ 3: Hàm số không có đạo hàm tại ${x_0}$ thì không đạt cực trị tại điểm đó

Ví dụ 1: Cho hàm số $y = f\left( x \right)$ xác định, liên tục trên $\mathbb{R}$ và có bảng biến thiên như sau :

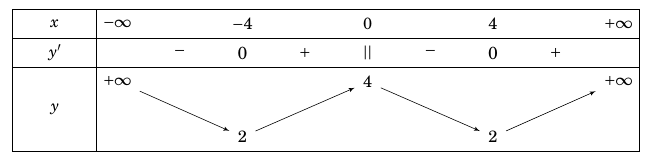
Số điểm cực trị của hàm số đã cho là

A. $0$. B. $2$. C. $1$. D. $3$.

Học sinh có thể mắc sai lầm chọn B vì hàm số không có đạo hàm tại $x = 0$.

Phương án đúng là D. Do $f'(x)$đổi dấu khi qua $ – 4,\,0,\,4$ nên hàm số đã cho có 3 cực trị.

Ví dụ 2: Cho hàm số $y = f\left( x \right)$ xác định, liên tục trên $\mathbb{R}$ và có bảng biến thiên như sau:

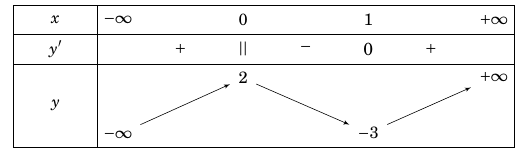
Khẳng định nào sau đây là khẳng định đúng?

A. Hàm số có đúng một cực trị.

B. Hàm số có giá trị cực tiểu bằng $2$.

C. Hàm số có giá trị lớn nhất bằng $2$ và giá trị nhỏ nhất bằng $ – 3$.

D. Hàm số đạt cực đại tại $x = 0$ và đạt cực tiểu tại $x = 1$.

Học sinh có thể chọn phương án A vì $f'(x)$ không xác định tại $x = 0$.

Học sinh cũng chọn phương án C vì đồng nhất giữa giá trị cực tiểu và giá trị nhỏ nhất, giá trị cực đại và giá trị lớn nhất.

Phương án đúng D.

Cách khắc phục: Lập bảng biến thiên của hàm số, $f'(x)$ đổi dấu thì hàm số có cực trị.

Sai lầm thứ 4: Nếu ${x_0}$ là nghiệm của phương trình $f'(x) = 0$ thì ${x_0}$ là điểm cực trị của hàm số

Ví dụ: Số cực trị của hàm số $y = {x^3} – 1$ là

A. $0$. B. $2$. C. $1$. D. $3$.

Học sinh dễ chọn C do tính được $y’ = 3{x^2}$ có một nghiệm $x = 0$.

Tuy nhiên do $x = 0$là nghiệm bội chẵn nên $f'(x)$ không đổi dấu khi đi qua $x = 0$ nên hàm số không đạt cực trị tại đó. Phương án đúng A.

Cách khắc phục: Lập bảng biến thiên của hàm số, $f'(x)$ đổi dấu thì hàm số có cực trị.

Sai lầm thứ 5: Nếu ${x_0}$ là điểm cực đại của hàm số $y = f(x)$thì $f”({x_0}) < 0$ (tương tự đối với cực tiểu)

Ví dụ : Tìm $m$để hàm số $y = {x^4} – m{x^2}$đạt cực tiểu tại $x = 0$.

A. $m \geqslant 0$. B. $m = 0$. C. $m \leqslant 0$. D. $m < 0$.

Lời giải sai

Ta có $y’ = 4{x^3} – 2mx,\,\,\,y” = 8x – 2m$.

Hàm số đạt cực tiểu tại $x = 0$ $ \Leftrightarrow \left\{ \begin{gathered}
y'(0) = 0 \hfill \\
y”(0) \geqslant 0 \hfill \\
\end{gathered} \right. \Leftrightarrow – 2m > 0 \Leftrightarrow m < 0$. Chọn D.

Sai lầm : Với $m = 0$ hàm số trở thành $y = {x^4}$. Hàm số đạt cực đại tại $x = 0$. Do đó , $m = 0$ thỏa mãn yêu cầu bài toán.

Lời giải đúng

Ta có $y’ = 4{x^3} – 2mx = 2x({x^2} – m)$.

Nếu $m \leqslant 0$ thì $y’ = 0$ có một nghiệm $x = 0$.

Ta có bảng biến thiên

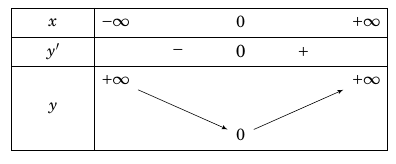
Hàm số đạt cực tiểu tại $x = 0$.

Nếu $m > 0$thì $y’ = 0$ có ba nghiệm.

Ta có bảng biến thiên

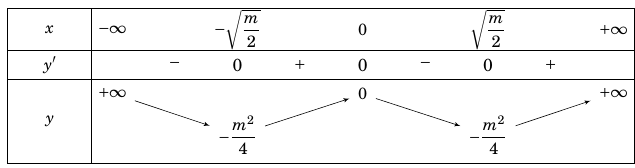
Hàm số đã cho đạt cực đại tại $x = 0$ (loại).

Vậy $m \leqslant 0$thỏa mãn yêu cầu đề bài. Chọn C

IV- Hệ thống câu hỏi ôn tập

Câu 1. Cho hàm số $y = {x^4} – 2{x^2} + 1$. Xét các mệnh đề sau đây :

1) Hàm số có 3 điểm cực trị.

2) Hàm số đồng biến trên các khoảng $\left( { – 1;0} \right)$; $\left( {1; + \infty } \right)$.

3) Hàm số có 1 điểm cực trị.

4) Hàm số nghịch biến trên các khoảng $\left( { – \infty ; – 1} \right)$; $\left( {0;1} \right)$.

Có bao nhiêu mệnh đề đúng trong bốn mệnh đề trên?

A. 2. B. 1. C. 4. D. 3.

Lời giải

Chọn D

$y’ = 4{x^3} – 4x \Rightarrow y’ = 0 \Leftrightarrow \left[ \begin{gathered}
x = 0\,\,\,\,\, \Rightarrow y = 1 \hfill \\
x = 1\,\,\,\,\,\, \Rightarrow y = 0 \hfill \\
x = – 1\,\,\, \Rightarrow y = 0. \hfill \\
\end{gathered} \right.$

Bảng biến thiên

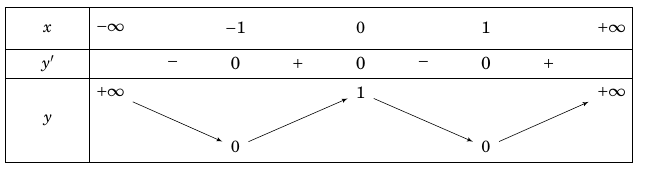
Hàm số có $3$ điểm cực trị, đồng biến trên khoảng $\left( { – 1;0} \right)$; $\left( {1; + \infty } \right)$ và nghịch biến trên khoảng $\left( { – \infty ; – 1} \right)$; $\left( {0;1} \right)$.

Vậy các mệnh đề $1$, $2$, $4$ đúng.

Câu 2. Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau:

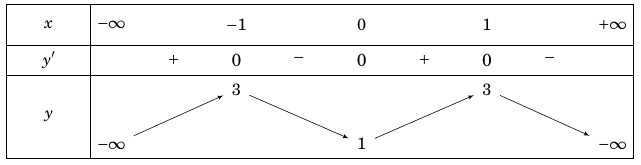
Giá trị cực tiểu của hàm số đã cho bằng

A. $0$. B. $3$. C. $1$. D. $ – 1$.

Lời giải

Chọn C

Nhìn vào bảng biến thiên ta thấy giá trị cực tiểu của hàm số đã cho bằng $1$.

Câu 3. Cho hàm số $y = a{x^4} + b{x^2} + c$ có đồ thị là đường cong như hình vẽ

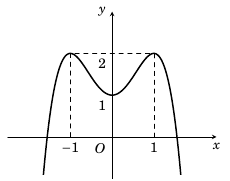
Điểm cực tiểu của đồ thị hàm số đã cho có tọa độ là

A. $( – 1;\,2)$. B. $(1;\,2)$. C. $(0;\,1)$. D. $(1;\,0)$.

Lời giải

Chọn C

Nhìn vào đồ thị ta thấy điểm cực tiểu của đồ thị hàm số là $(0;\,1)$.

Câu 4. Cho hàm số $y = f\left( x \right)$ liên tục trên đoạn $\left[ { – 2;3} \right],$ có bảng biến thiên như hình vẽ

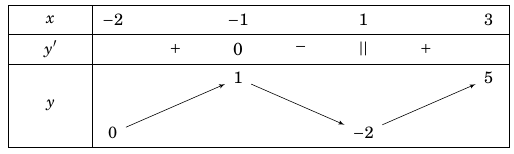
Khẳng định nào sau đây là khẳng định đúng ?

A. Giá trị cực tiểu của hàm số là $0$. B. Hàm số đạt cực đại tại điểm $x = 1$.

C. Hàm số đạt cực tiểu tại điểm $x = 1$. D. Giá trị cực đại của hàm số là $5$.

Lời giải

Chọn C

Dựa vào bảng biến thiên, hàm số đã cho đạt cực tiểu tại điểm $x = 1$.

Câu 5. Biết $M\left( {0;2} \right)$, $N\left( {2; – 2} \right)$ là các điểm cực trị của đồ thị hàm số $y = a{x^3} + b{x^2} + cx + d$. Tính giá trị của hàm số tại $x = – 2$.

A. $y\left( { – 2} \right) = 2$. B. $y\left( { – 2} \right) = 22$. C. $y\left( { – 2} \right) = 6$. D. $y\left( { – 2} \right) = – 18$.

Lời giải

Chọn D

Ta có $y’ = 3a{x^2} + 2bx + c$.

Vì $M\left( {0;2} \right)$,$N\left( {2; – 2} \right)$ là các điểm cực trị của đồ thị hàm số nên

$\left\{ \begin{gathered}
y’\left( 0 \right) = 0 \hfill \\
y’\left( 2 \right) = 0 \hfill \\
y\left( 0 \right) = 2 \hfill \\
y\left( 2 \right) = – 2 \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
c = 0 \hfill \\
12a + 4b + c = 0 \hfill \\
d = 2 \hfill \\
8a + 4b + 2c + d = – 2 \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
a = 1 \hfill \\
b = – 3 \hfill \\
c = 0 \hfill \\
d = 2. \hfill \\
\end{gathered} \right.$ $ \Rightarrow y = {x^3} – 3{x^2} + 2$.

Vậy $y\left( { – 2} \right) = – 18$.

Câu 6. Cho hàm số $f\left( x \right)$, bảng xét dấu của $f’\left( x \right)$ như sau:

Số điểm cực trị của hàm số đã cho là

A. $0$. B. $2$. C. $1$. D. $3$.

Lời giải

Chọn B

Ta có $f’\left( x \right) = 0 \Leftrightarrow \left[ \begin{gathered}
x = – 1 \hfill \\
x = 0 \hfill \\
x = 1. \hfill \\
\end{gathered} \right.$

Từ bảng biến thiên ta thấy $f’\left( x \right)$ đổi dấu khi $x$ qua nghiệm $ – 1$ và nghiệm $1$; không đổi dấu khi $x$ qua nghiệm $0$ nên hàm số có hai điểm cực trị.

Câu 7. Cho hàm số $f\left( x \right)$ có đạo hàm $f’\left( x \right) = {x^3}\left( {x – 1} \right)\left( {x – 2} \right),\forall x \in \mathbb{R}$. Số điểm cực trị của hàm số đã cho là

A. $1$. B. $3$. C. $5$. D. $2$.

Lời giải

Chọn B

Ta có: $f’\left( x \right) = 0 \Leftrightarrow {x^3}\left( {x – 1} \right)\left( {x – 2} \right) = 0 \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
x = 1 \hfill \\
x = 2. \hfill \\
\end{gathered} \right.$

Bảng xét dấu

Dựa vào bảng xét dấu nhận thấy hàm số $f\left( x \right)$ có $3$ điểm cực trị.

Câu 8. Cho hàm số $f\left( x \right)$ có đạo hàm $f’\left( x \right)$ trên khoảng ${\rm K}$. Đồ thị hàm số $y = f’\left( x \right)$như hình vẽ

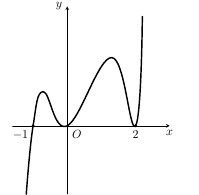
Số điểm cực trị của hàm số $f\left( x \right)$ là

A. $1$. B. $3$. C. $0$. D. $2$.

Lời giải

Chọn B

Dựa vào đồ thị ta thấy phương trình $f’\left( x \right) = 0$chỉ có một nghiệm đơn (và hai nghiệm kép) nên $f’\left( x \right)$chỉ đổi dấu khi qua nghiệm đơn này. Do đó suy ra hàm số $f\left( x \right)$có đúng một cực trị.

Câu 9. Tìm tất cả các giá trị của tham số $m$để hàm số $y = 2{x^4} – (m + 1){x^2} + 4$ có ba điểm cực trị?

A. $m \geqslant – 1$. B. $m \geqslant 0$. C. $m > – 1$. D. $m > 0$.

Lời giải

Chọn C

Ta có $y’ = 8{x^3} – 2(m + 1)x$.

$y’ = 0\, \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
{x^2} = \frac{{m + 1}}{4}\,\,\,\,(1). \hfill \\
\end{gathered} \right.$

Hàm số có ba điểm cực trị khi và chỉ khi $y’ = 0$có ba nghiệm phân biệt

$ \Leftrightarrow $ Phương trình một có hai nghiệm phân biệt khác $0$$ \Leftrightarrow $ $\frac{{m + 1}}{4} > 0\, \Leftrightarrow m > – 1$.

Vậy $m > – 1$ thỏa mãn yêu cầu bài toán.

Cách nhanh: Hàm số có ba điểm cực trị $ \Leftrightarrow ab < 0\, \Leftrightarrow – (m + 1) < 0 \Leftrightarrow m > – 1$.

Câu 10. Tìm tất cả các giá trị của tham số $m$để hàm số $y = 2{x^3} + 3(m – 1){x^2} + 6(m – 2)x$ đạt cực đại và cực tiểu .

A. Không có giá trị nào của $m$. B. Với mọi $m$. C. $m = 3$. D. $m \ne 3$.

Lời giải

Chọn D

Ta có $y’ = 6{x^2} + 6(m – 1)x + 6(m – 2)$.

Hàm số đạt cực đại và cực tiểu thì $y’ = 0$ có hai nghiệm phân biệt

$ \Leftrightarrow \Delta = {(m – 3)^2} > 0\, \Leftrightarrow m\, \ne 3$.

Vậy $m \ne 3$ thỏa mãn yêu cầu bài toán.

Câu 11. Cho hàm số $y = m{x^4} – (2m + 1){x^2} + 1$. Tìm tất cả các giá trị của $m$ để hàm số có một điểm cực đại?

A. $m \leqslant – \frac{1}{2}$. B. $ – \frac{1}{2} \leqslant m \leqslant 0$ C. $ – \frac{1}{2} \leqslant m < 0$. D. $m \geqslant – \frac{1}{2}$.

Lời giải

Chọn D

Với $m = 0$, hàm số trở thành $y = – {x^2} + 1$ . Đồ thị hàm số là một Parabol có một điểm cực đại. Từ đó $m = 0$ thỏa mãn.

Với $m \ne 0$

Hàm số đã cho có một điểm cực đại $ \Leftrightarrow \,\left[ \begin{gathered}
\left\{ \begin{gathered}
a < 0 \hfill \\
b \leqslant 0 \hfill \\
\end{gathered} \right. \hfill \\
\left\{ \begin{gathered}
a > 0 \hfill \\
b \leqslant 0 \hfill \\
\end{gathered} \right. \hfill \\
\end{gathered} \right.\, \Leftrightarrow \left[ \begin{gathered}
\left\{ \begin{gathered}
m < 0 \hfill \\
2m + 1 \geqslant 0 \hfill \\
\end{gathered} \right. \hfill \\
\left\{ \begin{gathered}
m > 0 \hfill \\
2m + 1 \geqslant 0 \hfill \\
\end{gathered} \right. \hfill \\
\end{gathered} \right.\, \Leftrightarrow \left[ \begin{gathered}
– \frac{1}{2} \leqslant m < 0 \hfill \\
m > 0. \hfill \\
\end{gathered} \right.$

Vậy $m \geqslant – \frac{1}{2}$ thỏa mãn yêu cầu đề bài.

Câu 12. Cho hàm số $y = {x^3} – 3m{x^2} + 3({m^2} – 1)x$. Tìm tất cả các giá trị của $m$ để hàm số đạt cực đại tại ${x_0} = 1$.

A. $m = 0$. B. $m = 0$ hoặc $m = 2$. C. $m \ne 0$ và $m \ne 2$. D. $m = 2$.

Lời giải

Chọn D

Ta có $y’ = 3{x^2} – 6mx + 3({m^2} – 1);\,\,y” = 6x – 6m$.

Hàm số đạt cực đại tại ${x_0} = 1$ $ \Leftrightarrow \left\{ \begin{gathered}
y'(1) = 0 \hfill \\
y”(1) < 0 \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
3{m^2} – 6m = 0 \hfill \\
m > 1 \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
\left[ \begin{gathered}
m = 0 \hfill \\
m = 2 \hfill \\
\end{gathered} \right. \hfill \\
m > 1. \hfill \\
\end{gathered} \right.$

Vậy $m = 2$ thỏa mãn yêu cầu bài toán.

Câu 13. Tìm tập hợp tất cả các giá trị của $m$ để hàm số $y = {x^3} + \left( {3m – 1} \right){x^2} + {m^2}x – 3$ đạt cực tiểu tại $x = – 1$.

A. $\left\{ {5;1} \right\}$. B. $\left\{ 5 \right\}$. C. $\emptyset $. D. $\left\{ 1 \right\}$.

Lời giải

Chọn B

Ta có $y’ = 3{x^2} + 2\left( {3m – 1} \right)x + {m^2} \Rightarrow y” = 6x + 6m – 2$.

Hàm số đạt cực tiểu tại $x = – 1$

$ \Leftrightarrow \left\{ \begin{gathered}
f’\left( { – 1} \right) = 0 \hfill \\
f”\left( { – 1} \right) > 0 \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
{m^2} – 6m + 5 = 0 \hfill \\
6m – 8 > 0 \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
\left[ \begin{gathered}
m = 1 \hfill \\
m = 5 \hfill \\
\end{gathered} \right. \hfill \\
m > \frac{4}{3} \hfill \\
\end{gathered} \right. \Leftrightarrow m = 5$.

Câu 14. Có tất cả bao nhiêu giá trị nguyên của $m$ trên miền $\left[ { – 10;10} \right]$ để hàm số$y = {x^4} – {\text{ }}2\left( {2m + 1} \right){x^2} + {\text{ }}7$ có ba điểm cực trị?

A. $20$ B. $10$ C. Vô số D. $11$

Lời giải

Chọn D

Cách 1:

Hàm số có ba điểm cực trị $a.b < 0 \Leftrightarrow 1.\left[ { – 2(2m + 1)} \right] < 0 \Leftrightarrow 2m + 1 > 0 \Leftrightarrow m > – \frac{1}{2}$

Cách 2:

Ta có $y’ = 4x\left[ {{x^2} – \left( {2m + 1} \right)} \right]$.

$y’ = 0 \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
{x^2} = 2m + 1{\text{ }}\left( * \right) \hfill \\
\end{gathered} \right.$

Hàm số đã cho có ba cực trị khi và chỉ khi $y’ = 0$ có ba nghiệm phân biệt, hay (*) có hai nghiệm phân biệt khác $0$$ \Leftrightarrow 2m + 1 > 0 \Leftrightarrow m > – \frac{1}{2}$.

Do $m \in \left[ { – 10;10} \right]$ nên có $11$ giá trị thỏa mãn.

Câu 15. Biết ${m_0}$ là giá trị của tham số $m$ để hàm số $y = {x^3} – 3{x^2} + mx – 1$ có hai điểm cực trị ${x_1},{x_2}$ sao cho ${x_1}^2 + {x_2}^2 – {x_1}{x_2} = 13$. Mệnh đề nào dưới đây đúng?

A. ${m_0} \in \left( { – 1;7} \right)$. B. ${m_0} \in \left( {7;10} \right)$. C. ${m_0} \in \left( { – 15; – 7} \right)$. D. ${m_0} \in \left( { – 7; – 1} \right)$.

Lời giải

Chọn C

TXĐ: $D = \mathbb{R}$

$y’ = 3{x^2} – 6x + m$.

Xét $y’ = 0 \Leftrightarrow 3{x^2} – 6x + m = 0$; $\Delta ‘ = 9 – 3m$.

Hàm số có hai điểm cực trị $ \Leftrightarrow \Delta ‘ > 0 \Leftrightarrow m < 3$.

Hai điểm cực trị ${x_1};{x_2}$ là nghiệm của $y’ = 0$ nên ${x_1} + {x_2} = 2;\,{x_1}.{x_2} = \frac{m}{3}$.

Để ${x_1}^2 + {x_2}^2 – {x_1}{x_2} = 13 \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} – 3{x_1}.{x_1} = 13$

$ \Leftrightarrow 4 – m = 13 \Leftrightarrow m = – 9$.

Vậy ${m_0} = – 9 \in \left( { – 15; – 7} \right)$.

Câu 16. Biết rằng đồ thị hàm số $f\left( x \right) = \frac{1}{3}{x^3} – \frac{1}{2}m{x^2} + x – 2$ có giá trị tuyệt đối của hoành độ hai điểm cực trị là độ dài hai cạnh của tam giác vuông có cạnh huyền là $\sqrt 7 $. Số giá trị của $m$là

A. $3$. B. $1$. C. Không có $m$. D. $2$.

Lời giải

Chọn D

Có $y’\left( x \right) = {x^2} – mx + 1$, $y’ = 0 \Leftrightarrow {x^2} – mx + 1 = 0$ $\left( 1 \right)$.

• Để hàm số có cực trị thì $\left( 1 \right)$ có hai nghiệm phân biệt

$ \Leftrightarrow \Delta > 0$ $ \Leftrightarrow {m^2} – 4 > 0$ $ \Leftrightarrow \left[ \begin{gathered}
m > 2 \hfill \\
m < – 2. \hfill \\
\end{gathered} \right.$

• Gọi hai nghiệm của $\left( 1 \right)$ là ${x_1}$, ${x_2}$. Khi đó, ta có $\left\{ \begin{gathered}
{x_1} + {x_2} = m \hfill \\
{x_1}.{x_2} = 1. \hfill \\
\end{gathered} \right.$

Độ dài hai cạnh của tam giác vuông đó là $\left| {{x_1}} \right|$, $\left| {{x_2}} \right|$.

Theo bài ra ta có phương trình

$x_1^2 + x_2^2 = 7$ $ \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} – 2{x_1}{x_2} = 7$ $ \Leftrightarrow {m^2} – 2 = 7$ $ \Leftrightarrow {m^2} = 9$ $ \Leftrightarrow m = \pm 3$ (thỏa mãn).

Vậy có $2$ giá trị $m$ thỏa mãn yêu cầu bài toán.