- Phương Pháp Tìm Cực Trị Của Hàm Số Cho Bởi Công Thức
- Phương Pháp Tìm Cực Trị Của Hàm Số Dựa Vào Bảng Biến Thiên Và Đồ Thị
- Phương Pháp Tìm m Để Hàm Số Đạt Cực Trị Tại Một Điểm
I. Phương pháp
Nếu $f’\left( x \right)$ đổi dấu khi qua ${x_0} \in D$ thì ${x_0}$ là cực trị.
+ Nếu $f’\left( x \right)$ đổi dấu từ + sang – thì ${x_0}$ là điểm cực đại.
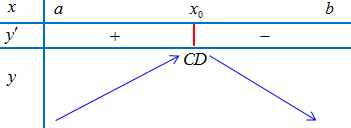
+ Nếu $f’\left( x \right)$ đổi dấu từ – sang + thì ${x_0}$ là điểm cực tiểu.
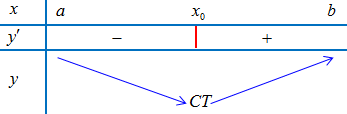
Chú ý 1:
• Hàm số đạt cực trị tại: $x = $
• Điểm cực trị của hàm số là: $x = $
• Giá trị cực trị của hàm số là: $y = $
• Cực trị của hàm số là: $y = $
• Điểm cực trị của đồ thị hàm số: $\left( {x;y} \right)$
Chú ý 2: Đối với đồ thị hàm số $y = f'(x)$
+ Nếu trên $(a;b)$ đồ thị hàm số $y = f'(x)$ nằm phía trên trục hoành thì $f'(x) > 0$ nên hàm số $y = f(x)$ đồng biến trên khoảng $(a;b)$.
+ Nếu trên $(a;b)$ đồ thị hàm số $y = f'(x)$ nằm phía dưới trục hoành thì $f'(x) < 0$ nên hàm số $y = f(x)$ nghịch biến trên khoảng $(a;b)$.
+ Nếu đồ thị hàm số $y = f'(x)$ cắt trục hoành tại điểm ${x_0}$ thì $f'({x_0}) = 0$.
II. Các ví dụ minh họa
Ví dụ 1. Cho hàm $f\left( x \right)$ có bảng biến thiên như sau:
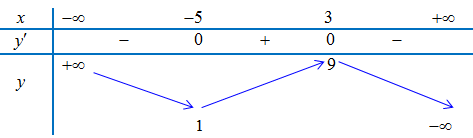
a) Tìm điểm cực đại và điểm cực tiểu của hàm số.
b) Tìm giá trị cực đại và giá trị cực tiểu của hàm số.
c) Tìm điểm cực đại và điểm cực tiểu của đồ thị hàm số.
Lời giải
a) Điểm cực đại của hàm số là $x = 3$.
Điểm cực tiểu của hàm số là $x = – 5$.
b) Giá trị cực đại của hàm số là ${y_{CĐ}} = 9$.
Giá trị cực tiểu của hàm số là ${y_{CT}} = 1$.
c) Điểm cực đại của đồ thị hàm số là $\left( {3;9} \right)$.
Điểm cực tiểu của đồ thị hàm số là $\left( { – 5;1} \right)$.
Ví dụ 2. Cho hàm $f\left( x \right)$ có bảng biến thiên như sau:
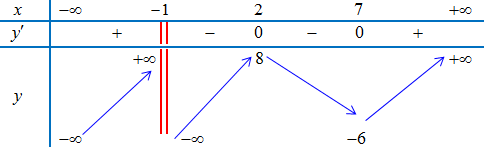
a) Tìm điểm cực đại và điểm cực tiểu của hàm số.
b) Tìm giá trị cực đại và giá trị cực tiểu của hàm số.
c) Tìm điểm cực đại và điểm cực tiểu của đồ thị hàm số.
Lời giải
a) Điểm cực đại của hàm số là $x = 2$.
Điểm cực tiểu của hàm số là $x = 7$.
b) Giá trị cực đại của hàm số là ${y_{CĐ}} = 8$.
Giá trị cực tiểu của hàm số là ${y_{CT}} = – 6$.
c) Điểm cực đại của đồ thị hàm số là $\left( {2;8} \right)$.
Điểm cực tiểu của đồ thị hàm số là $\left( {7; – 6} \right)$.
Ví dụ 3: Cho hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$ và có đồ thị như hình bên.
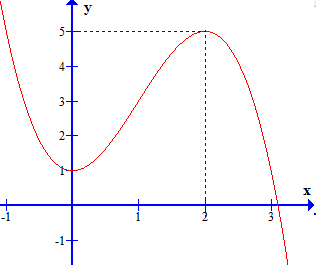
a) Tìm điểm cực đại và điểm cực tiểu của hàm số.
b) Tìm giá trị cực đại và giá trị cực tiểu của hàm số.
c) Tìm điểm cực đại và điểm cực tiểu của đồ thị hàm số.
Lời giải
a) Điểm cực đại của hàm số là $x = 2$.
Điểm cực tiểu của hàm số là $x = 0$.
b) Giá trị cực đại của hàm số là ${y_{CĐ}} = y\left( 1 \right) = 5$;
Giá trị cực tiểu của hàm số là ${y_{CT}} = y\left( 0 \right) = 1$.
c) Điểm cực đại của đồ thị hàm số là $\left( {2;5} \right)$.
Điểm cực tiểu của đồ thị hàm số là $\left( {0;1} \right)$.
Ví dụ 4: Cho hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$ và có đồ thị như hình bên.
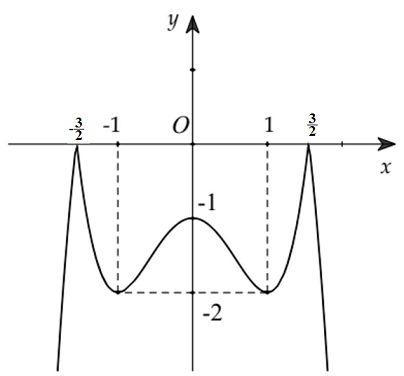
a) Tìm điểm cực đại và điểm cực tiểu của hàm số.
b) Tìm giá trị cực đại và giá trị cực tiểu của hàm số.
c) Tìm điểm cực đại và điểm cực tiểu của đồ thị hàm số.
Lời giải
a) Điểm cực đại của hàm số là $x = – \frac{3}{2};x = 0;x = \frac{3}{2}$.
Điểm cực tiểu của hàm số là $x = – 1;\,x = 1$.
b) Giá trị cực đại của hàm số là ${y_{CĐ}} = y\left( { \pm \frac{3}{2}} \right) = 0$; ${y_{CĐ}} = y\left( 0 \right) = – 1$
Giá trị cực tiểu của hàm số là ${y_{CT}} = y\left( { \pm 1} \right) = – 2$.
c) Điểm cực đại của đồ thị hàm số là $\left( { – \frac{3}{2};0} \right)$, $\left( {\frac{3}{2};0} \right)$, $\,\left( {0; – 1} \right)$.
Điểm cực tiểu của đồ thị hàm số là $\left( { – 1; – 2} \right)$, $\left( {1; – 2} \right)$.
Ví dụ 5: Cho hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$ và có đồ thị $y = f'(x)$ như hình dưới.
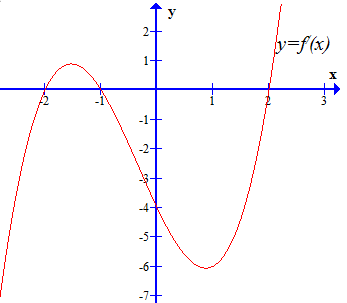
Tìm điểm cực đại và điểm cực tiểu của hàm số.
Lời giải
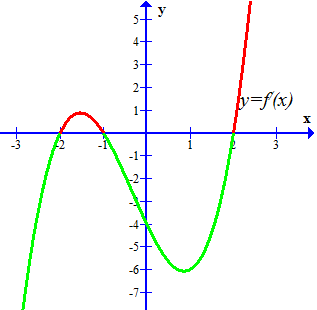
Nhìn đồ thị hàm số $y = f'(x)$ ta thấy
– Trên các khoảng $\left( { – 2; – 1} \right)$ và $\left( {2; + \infty } \right)$ (phần màu đỏ) đồ thị hàm số $y = f'(x)$ nằm phía trên trục hoành.
Do đó, $f'(x) > 0,\,\forall x \in \left( { – 2; – 1} \right) \cup \left( {2; + \infty } \right)$.
– Trên các khoảng $\left( { – \infty ; – 2} \right)$ và $\left( { – 1;2} \right)$ (phần màu xanh lá cây) đồ thị hàm số $y = f'(x)$ nằm phía dưới trục hoành.
Do đó, $f'(x) < 0,\,\forall x \in \left( { – \infty ; – 2} \right) \cup \left( { – 1;2} \right)$.
Do đó, ta có bảng biến thiên
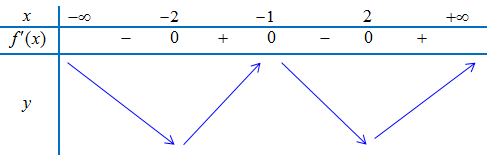
Vậy
– Điểm cực đại của hàm số là $x = – 1$.
– Điểm cực tiểu của hàm số là $x = – 2$; $x = 2$.
Ví dụ 6: Cho hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$ và có đồ thị $y = f'(x)$ như hình dưới.
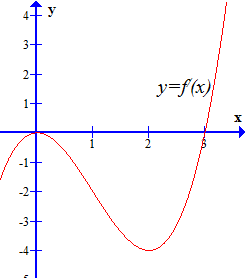
Tìm điểm cực đại và điểm cực tiểu của hàm số.
Lời giải
Từ đồ thị hàm số $y = f'(x)$ ta có bảng biến thiên
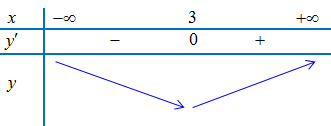
Vậy
– Hàm số không có điểm cực tiểu.
– Điểm cực đại của hàm số là $x = 3$.
Ví dụ 7: Cho hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$ và có đồ thị $y = f'(x)$ như hình dưới.
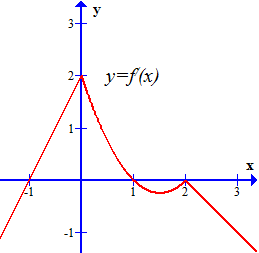
Tìm điểm cực đại và điểm cực tiểu của hàm số.
Lời giải
Từ đồ thị hàm số $y = f'(x)$ ta có bảng biến thiên
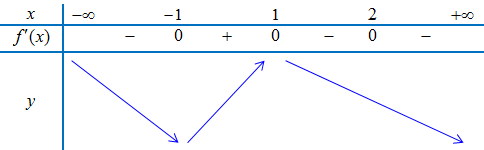
Vậy
– Điểm cực đại của hàm số là $x = 1$.
– Điểm cực tiểu của hàm số là $x = – 1$.
Ví dụ 8: Cho hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$ và có đạo hàm $f'(x) = (6 – x)(x + 4)$
Tìm điểm cực đại và điểm cực tiểu của hàm số.
Lời giải
Ta có:
$f'(x) = 0 \Leftrightarrow (6 – x)(x + 4) = 0$$ \Leftrightarrow \left[ \begin{gathered}
6 – x = 0 \hfill \\
x + 4 = 0 \hfill \\
\end{gathered} \right. \Leftrightarrow \left[ \begin{gathered}
x = 6 \hfill \\
x = – 4 \hfill \\
\end{gathered} \right.$
Bảng biến thiên
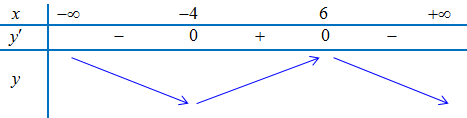
Vậy
– Điểm cực đại của hàm số là $x = 6$.
– Điểm cực tiểu của hàm số là $x = – 4$.
Ví dụ 9: Cho hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$ và có đạo hàm $f'(x) = (x – 2){(x + 5)^2}\left( {x – 7} \right)$
Tìm điểm cực đại và điểm cực tiểu của hàm số.
Lời giải
Ta có:
$f'(x) = 0 \Leftrightarrow (x – 2){(x + 5)^2}\left( {x – 7} \right) = 0$$ \Leftrightarrow \left[ \begin{gathered}
x – 2 = 0 \hfill \\
{\left( {x + 5} \right)^2} = 0 \hfill \\
x – 7 = 0 \hfill \\
\end{gathered} \right. \Leftrightarrow \left[ \begin{gathered}
x = 2 \hfill \\
x = – 5 \hfill \\
x = 7 \hfill \\
\end{gathered} \right.$
Bảng biến thiên
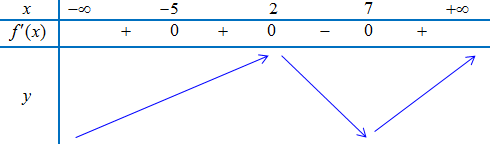
Vậy
– Điểm cực đại của hàm số là $x = 2$.
– Điểm cực tiểu của hàm số là $x = 7$.







