Các Dạng Câu Trả Lời Ngắn Biểu Thức Tọa Độ Các Phép Toán Vectơ Lớp 12

Các dạng câu trả lời ngắn biểu thức tọa độ các phép toán vectơ lớp 12 giải chi tiết được soạn dưới dạng file word và PDF gồm 4 trang. Các bạn xem và tải về ở dưới.

DẠNG 1: CÁC PHÉP TOÁN VECTƠ

Câu 1. Cho $\vec a = \left( {5;4; – 1} \right)$, $\vec b = \left( {2; – 5;3} \right)$. Biết vectơ $\vec x = \left( {m;n;p} \right)$ thỏa mãn $\vec a + 2\vec x = \vec b$. Tính $2m + 2n + p$.

Lời giải

+ Gọi vectơ $\vec x$ có tọa độ: $\vec x = \left( {x;y;z} \right) \Rightarrow 2\vec x = \left( {2x;2y;2z} \right)$

+ Ta có: $\left\{ \begin{gathered}
\vec a + 2\vec x = \left( {5 + 2x;4 + 2y; – 1 + 2z} \right) \hfill \\
\vec b = \left( {2; – 5;3} \right) \hfill \\
\end{gathered} \right.$

+ Vì $\vec a + 2\vec x = \vec b$ nên: $\left\{ \begin{gathered}
5 + 2x = 2 \hfill \\
4 + 2y = – 5 \hfill \\
– 1 + 2z = 3 \hfill \\
\end{gathered} \right.$

$ \Leftrightarrow \left\{ \begin{gathered}
x = \frac{3}{2} \hfill \\
y = – \frac{9}{2} \hfill \\
z = 2 \hfill \\
\end{gathered} \right. \Rightarrow \vec x = \left( {\frac{3}{2}; – \frac{9}{2};2} \right)$

Suy ra, $2m + 2n + p = 2.\frac{3}{2} + 2\left( { – \frac{9}{2}} \right) + 2 = – 4$.

Câu 2. Cho vectơ $\vec a = (1; – 1;0)$ cùng phương với vectơ $\overrightarrow u = (2;2k – 1;0)$. Biết $k = \frac{m}{n}$ với $\frac{m}{n}$ là phân số tối giản và $n > 0$. Tính $m + n$.

Lời giải

$\vec a$ cùng phương với $\overrightarrow u $$ \Leftrightarrow \frac{2}{1} = \frac{{2k – 1}}{{ – 1}} \Leftrightarrow 2k – 1 = – 2 \Leftrightarrow k = \frac{{ – 1}}{2}$.

Suy ra, $m + n = – 1 + 2 = 1$.

Câu 3. Cho ba vectơ $\vec a = \left( {1; – 7;9} \right),\,\,\vec b = \left( {3; – 6;1} \right),\,\,\vec c = \left( {2;1; – 7} \right)$. Biểu diễn vectơ $\vec u = ( – 4;13; – 6)$ theo các vectơ $\vec a,\,\,\vec b,\,\,\vec c$ ta được $\overrightarrow u = x\overrightarrow a + y\overrightarrow b + z\overrightarrow c $. Tính $x + y + z$.

Lời giải

Ta có: $\overrightarrow u = x\overrightarrow a + y\overrightarrow b + z\overrightarrow c $

$ \Leftrightarrow ( – 4;13; – 6) = \left( {x; – 7x;9x} \right) + \left( {3y; – 6y;y} \right) + \left( {2z;z; – 7z} \right)$

$ \Leftrightarrow ( – 4;13; – 6) = \left( {x + 3y + 2z; – 7x – 6y + z;9x + y – 7z} \right)$

$ \Leftrightarrow \left\{ \begin{gathered}
x + 3y + 2z = – 4 \hfill \\
– 7x – 6y + z = 13 \hfill \\
9x + y – 7z = – 6 \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
x = 3 \hfill \\
y = – 5 \hfill \\
z = 4 \hfill \\
\end{gathered} \right.$

Vậy $x + y + z = 3 – 5 + 4 = 2$.

Câu 4. Trong không gian tọa độ $Oxyz$ cho $ A\left( {2;\;5;\;3} \right), B\left( {3;7;\;4} \right), C\left( {x;y;\;6} \right)$. Biết ba điểm $A,B,C$ thẳng hàng. Tính $x + y$.

Lời giải

Ta có: $\overrightarrow {AB} = \left( {1;2;1} \right)$; $\overrightarrow {AC} = \left( {x – 2;y – 5;3} \right)$.

Ba điểm $A,B,C$thẳng hàng $ \Leftrightarrow \overrightarrow {AB} $ và $\overrightarrow {AC} $ cùng phương

$ \Leftrightarrow \frac{{x – 2}}{1} = \frac{{y – 5}}{2} = \frac{3}{1} \Leftrightarrow \left\{ \begin{gathered}
\frac{{x – 2}}{1} = \frac{3}{1} \hfill \\
\frac{{y – 5}}{2} = \frac{3}{1} \hfill \\
\end{gathered} \right.$

$ \Leftrightarrow \left\{ \begin{gathered}
x – 2 = 3 \hfill \\
y – 5 = 6 \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
x = 5 \hfill \\
y = 11 \hfill \\
\end{gathered} \right.$

Vậy $x + y = 5 + 11 = 16$.

DẠNG 2: TÍCH VÔ HƯỚNG HAI VECTƠ

Câu 5. Trong hệ tọa độ $Oxyz$ cho $\vec a = (1; – 2;\frac{1}{4})$, $\vec b = ( – 2;1;1)$. Biết $\cos (\overrightarrow a ,\overrightarrow b ) = – \frac{{m\sqrt n }}{p}$ với $\frac{m}{p}$ tối giản, $n$ nguyên tố và $p > 0$. Tính $m + n + p$.

Lời giải

Ta có: $\cos (\overrightarrow a ,\overrightarrow b ) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{1.( – 2) + ( – 2).1 + \frac{1}{4}.1}}{{\sqrt {{1^2} + {{\left( { – 2} \right)}^2} + {{\left( {\frac{1}{4}} \right)}^2}} .\sqrt {{{( – 2)}^2} + {1^2} + {1^2}} }} = – \frac{{5\sqrt 6 }}{{18}}$.

Vậy $m + n + p = 5 + 6 + 18 = 29$.

Câu 6. Trong hệ tọa độ $Oxyz$, cho vectơ $\vec a = \left( {2;5;4} \right)$, $\vec b = \left( {6;0; – 3} \right)$. Tính góc giữa 2 vectơ $\vec a$ và $\vec b$.

Lời giải

Ta có: $\cos (\overrightarrow a ,\overrightarrow b ) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{2.6 + 5.0 + 4.( – 3)}}{{\sqrt {{2^2} + {5^2} + {4^2}} .\sqrt {{6^2} + {0^2} + {{\left( { – 3} \right)}^2}} }} = 0$.

Vậy $(\overrightarrow a ,\overrightarrow b ) = {90^0}$

Câu 7. Trong hệ tọa độ $Oxyz$, cho 3 vectơ $\vec a = \left( {3;2;2\sqrt 3 } \right),\, \vec b = \left( {\sqrt 3 ;2\sqrt 3 ; – 1} \right)$. Biết $\cos (\overrightarrow a ,\overrightarrow b ) = \frac{{\sqrt m }}{n}$ với $\frac{m}{p}$ tối giản. Tính $m + n$.

Lời giải

Ta có: $\cos (\overrightarrow a ,\overrightarrow b ) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}}$

$ = \frac{{3.\sqrt 3 + 2.2\sqrt 3 + 2\sqrt 3 .( – 1)}}{{\sqrt {{3^2} + {2^2} + {{\left( {2\sqrt 3 } \right)}^2}} .\sqrt {{{\left( {\sqrt 3 } \right)}^2} + {{\left( {2\sqrt 3 } \right)}^2} + {{\left( { – 1} \right)}^2}} }}$

$ = \frac{{\sqrt 3 }}{4}$

Vậy $m + n = 3 + 4 = 7$.

Câu 8. Trong hệ tọa độ $Oxyz$ cho các vectơ $\vec a = (2;3; – 1)$,$\,\vec b = (1; – 2;3)$, $\vec c = (2; – 1;1)$, $\vec u = \left( {x;y;z} \right)$. Biết rằng: $\vec u \bot \vec a, \vec u \bot \vec b, \vec u.\vec c = – 6$. Tính $x + y + z$.

Lời giải

Ta có: $\vec u \bot \vec a, \vec u \bot \vec b, \vec u.\vec c = – 6$

$ \Leftrightarrow \left\{ \begin{gathered}
\vec u.\vec a = 0 \hfill \\
\vec u.\vec b = 0 \hfill \\
\vec u.\vec c = – 6 \hfill \\
\end{gathered} \right.$$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{2x + 3y – z = 0} \\
{x – 2y + 3z = 0} \\
{2x – y + z = – 6}
\end{array}} \right.$$ \Leftrightarrow \left\{ \begin{gathered}
x = – 3 \hfill \\
y = 3 \hfill \\
z = 3 \hfill \\
\end{gathered} \right.$

Suy ra, $x + y + z = – 3 + 3 + 3 = 3$

Câu 9. Trong không gian với hệ toạ độ $Oxyz$, cho 4 điểm $A(2;4; – 1)$,$B(1;4; – 1)$, $C(2;4;3)$ $D(2;2; – 1)$. Biết $M\left( {x;y;z} \right)$ là điểm sao cho $M{A^2} + M{B^2} + M{C^2} + M{D^2}$ đạt giá trị nhỏ nhất. Tính$x + y + z$.

Lời giải

Gọi $G$ là trọng tâm của $ABCD$ ta có: $G\left( {\frac{7}{3};\frac{{14}}{3};0} \right)$.

Ta có: $M{A^2} + M{B^2} + M{C^2} + M{D^2}$

$ = 4M{G^2} + G{A^2} + G{B^2} + G{C^2} + G{D^2}$≥ $G{A^2} + G{B^2} + G{C^2} + G{D^2}$.

Dấu bằng xảy ra khi $M \equiv $$G\left( {\frac{7}{3};\frac{{14}}{3};0} \right) \Rightarrow x + y + z = 7$.

Câu 10. Trong không gian với hệ trục tọa độ $Oxyz$, cho ba điểm $A\left( {1;1;1} \right)$,$B\left( { – 2;1;0} \right)$,$C\left( {2; – 3;1} \right)$. Điểm $S\left( {a;b;c} \right)$ sao cho $S{A^2} + 2S{B^2} + 3S{C^2}$ đạt giá trị nhỏ nhất. Biết $a + b + c = \frac{m}{n}$ với $\frac{m}{n}$ tối giản và $n > 0$. Tính $m + n$.

Lời giải

Gọi $G$ là điểm sao cho $\overrightarrow {GA} + 2\overrightarrow {GB} + 3\overrightarrow {GC} = \overrightarrow 0 $$ \Rightarrow G\left( {\frac{1}{2}; – 1;\frac{{ – 1}}{3}} \right)$

Ta có: $S{A^2} + 2S{B^2} + 3S{C^2} = {\overrightarrow {SA} ^2} + {\overrightarrow {2SB} ^2} + 3{\overrightarrow {SC} ^2}$

$ = {\left( {\overrightarrow {SG} + \overrightarrow {GA} } \right)^2} + 2{\left( {\overrightarrow {SG} + \overrightarrow {GB} } \right)^2} + 3{\left( {\overrightarrow {SG} + \overrightarrow {GC} } \right)^2}$

$ = 6S{G^2} + G{A^2} + 2G{B^2} + 3G{C^2}$

$S{A^2} + S{B^2} + S{C^2}$ nhỏ nhất khi $S \equiv G$ hay $S\left( {\frac{1}{2}; – 1;\frac{{ – 1}}{3}} \right)$.

Nên $T = a + b + c = – \frac{5}{6}$.

Vậy $m + n = – 5 + 6 = 1$.

Câu 11. Trong không gian tọa độ $Oxyz$ cho ba điểm $A\left( {2;5;1} \right),\,B\left( { – 2; – 6;2} \right),\,C\left( {1;2; – 1} \right)$ và điểm $M\left( {m;m;m} \right)$, để $M{A^2} – M{B^2} – M{C^2}$ đạt giá trị lớn nhất thì $m$ bằng bao nhiêu?

Lời giải

$\overrightarrow {MA} = \left( {2 – m;5 – m;1 – m} \right)$, $\,\overrightarrow {MB} = \left( { – 2 – m; – 6 – m;2 – m} \right)$, $\overrightarrow {MC} = \left( {1 – m;2 – m; – 1 – m} \right)$

$M{A^2} – M{B^2} – M{C^2}$

$ = – 3{m^2} – 24m – 20 = 28 – 3{\left( {m – 4} \right)^2} \leqslant 28$

Để $M{A^2} – M{B^2} – M{C^2}$đạt giá trị lớn nhất thì $m = 4$

Câu 12. Trong không gian tọa độ $Oxyz$cho ba điểm $A\left( {2;5;1} \right)$, $\,B\left( { – 2; – 6;2} \right)$, $C\left( {1;2; – 1} \right)$ và điểm $M\left( {m;m;m} \right)$, để $\left| {\overrightarrow {MB} – 2\overrightarrow {AC} } \right|$ đạt giá trị nhỏ nhất thì $m$ bằng bao nhiêu?

Lời giải

$\overrightarrow {AC} \left( { – 1; – 3; – 2} \right),\,\overrightarrow {MB} \left( { – 2 – m;\, – 6 – m;\,2 – m} \right)$

$\left| {\overrightarrow {MB} – 2\overrightarrow {AC} } \right| = \sqrt {{m^2} + {m^2} + {{\left( {m – 6} \right)}^2}} $

$ = \sqrt {3{m^2} – 12m + 36} = \sqrt {3{{\left( {m – 2} \right)}^2} + 24} $

Để $\left| {\overrightarrow {MB} – 2\overrightarrow {AC} } \right|$ nhỏ nhất thì $m = 2$

Câu 13. Trong không gian tọa độ $Oxyz$ cho điểm $A\left( {1;2;3} \right)$, $B\left( {2;2;1} \right)$, $M \in Ox$. Tìm điểm $M$ sao cho biểu thức $T = \left| {\overrightarrow {MA} + \overrightarrow {MB} } \right|$ đạt giá trị nhỏ nhất.

Lời giải

$M \in Ox$$ \Rightarrow M\left( {x;0;0} \right)$.

Gọi $I$ là trung điểm đoạn $AB$, ta có $I\left( {\frac{3}{2};2;2} \right)$ và $\overrightarrow {MI} = \left( {\frac{3}{2} – x;2;2} \right)$

$T = \left| {\overrightarrow {MA} + \overrightarrow {MB} } \right| = \left| {2\overrightarrow {MI} } \right| = 2\left| {\overrightarrow {MI} } \right|$

$ = 2\sqrt {{{\left( {\frac{3}{2} – x} \right)}^2} + {2^2} + {2^2}} = 2\sqrt {{{\left( {\frac{3}{2} – x} \right)}^2} + 8} \geqslant 2\sqrt {0 + 8} = 4\sqrt 2 $

Khi đó, $T$ nhỏ nhất $\frac{3}{2} – x = 0 \Leftrightarrow x = \frac{3}{2}$.

Vậy $M\left( {\frac{3}{2};0;0} \right)$.

Câu 14. Trong không gian tọa độ $Oxyz$ cho điểm $A\left( { – 1;2; – 3} \right),B\left( {0;2;1} \right),C\left( { – 1;2;1} \right),M \in Oy$. Tìm giá trị nhỏ nhất của biểu thức $T = \left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right|$ để $T$ đạt giá trị nhỏ nhất.

Lời giải

$M \in Oy$$ \Rightarrow M\left( {0;y;0} \right)$.

Gọi $G$ là trọng tâm tam giác $ABC$, ta có $G\left( { – \frac{2}{3};2; – \frac{1}{3}} \right)$ và $\overrightarrow {MG} = \left( { – \frac{2}{3};2 – y; – \frac{1}{3}} \right)$

$T = \left| {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right| = \left| {3\overrightarrow {MG} } \right| = 3\left| {\overrightarrow {MG} } \right|$

$ = 3\sqrt {{{\left( { – \frac{2}{3}} \right)}^2} + {{\left( {2 – y} \right)}^2} + {{\left( { – \frac{1}{3}} \right)}^2}} = 3\sqrt {{{\left( {2 – y} \right)}^2} + \frac{5}{9}} $

$ \geqslant 3\sqrt {0 + \frac{5}{9}} = \sqrt 5 $

Vậy ${T_{\min }} = \sqrt 5 $.

Câu 15. Trong không gian tọa độ $Oxyz$ cho điểm $A\left( {0;2;3} \right),B\left( {2;1;1} \right),C\left( {1;2;3} \right),M \in Oz$. Tìm điểm $M$ sao cho biểu thức $T = \left| {\overrightarrow {MA} – 2\overrightarrow {MB} + 3\overrightarrow {MC} } \right|$ đạt giá trị nhỏ nhất.

Lời giải

$M \in Oy$$ \Rightarrow M\left( {0;0;z} \right)$.

$T = \left| {\overrightarrow {MA} – 2\overrightarrow {MB} + 3\overrightarrow {MC} } \right| = \left| {\overrightarrow {MA} + \overrightarrow {MC} + 2\overrightarrow {MC} – 2\overrightarrow {MB} } \right|$

Gọi $I$ là trung điểm $BC$, ta có $I\left( {\frac{3}{2};\frac{3}{2};2} \right)$.

$\overrightarrow {MI} = \left( {\frac{3}{2};\frac{3}{2};2 – z} \right)$; $\overrightarrow {BC} = \left( { – 1;1;2} \right)$; $\overrightarrow {MI} + \overrightarrow {BC} = \left( {\frac{1}{2};\frac{5}{2};4 – z} \right)$.

Suy ra, $T = \left| {2\overrightarrow {MI} + 2\overrightarrow {BC} } \right| = 2\left| {\overrightarrow {MI} + \overrightarrow {BC} } \right|$

$ = 2\sqrt {{{\left( {\frac{1}{2}} \right)}^2} + {{\left( {\frac{5}{2}} \right)}^2} + {{\left( {4 – z} \right)}^2}} = 2\sqrt {\frac{{13}}{2} + {{\left( {4 – z} \right)}^2}} \geqslant 2\sqrt {\frac{{13}}{2}} $

Do đó, $T$ đạt giá trị nhỏ nhất $ \Leftrightarrow {\left( {4 – z} \right)^2} = 0 \Leftrightarrow z = 4$.

Vậy $M\left( {0;0;4} \right)$

Câu 16. Trong không gian với hệ tọa độ $Oxyz$, cho hai điểm $A\left( {2;2;0} \right),B\left( {2;0; – 2} \right)$ và điểm $M\left( {a,b,c} \right)$ với $a,b,c$ là các số thực thay đổi thỏa mãn $a + 2b – c – 1 = 0$. Biết $MA = MB$ và góc $\widehat {AMB}$ có số đo lớn nhất. Tính $S = a + 2b + 3c$.

Lời giải

Vì $MA = MB$ nên $M$ thuộc mặt phẳng trung trực $\left( P \right)$ của đoạn $AB$.

Ta có $\left( P \right):y + z = 0$ nên $\left\{ \begin{gathered}
b + c = 0 \hfill \\
a + 2b – c – 1 = 0 \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
c = – b \hfill \\
a = 1 – 3b \hfill \\
\end{gathered} \right.$.

$\overrightarrow {MA} = \left( {1 + 3b;2 – b;b} \right),\overrightarrow {MB} = \left( {1 + 3b; – b; – 2 + b} \right)$

$ \Rightarrow \cos \widehat {AMB} = \frac{{\overrightarrow {MA} .\overrightarrow {MB} }}{{\left| {\overrightarrow {MA} } \right|.\left| {\overrightarrow {MB} } \right|}}$

$ = \frac{{{{\left( {1 + 3b} \right)}^2} + 2b\left( {b – 2} \right)}}{{\sqrt {{{\left( {1 + 3b} \right)}^2} + {{\left( {b – 2} \right)}^2} + {b^2}} .\sqrt {{{\left( {1 + 3b} \right)}^2} + {{\left( {b – 2} \right)}^2} + {b^2}} }}$

$ = \frac{{9{b^2} + 6b + 1 + 2{b^2} – 4b}}{{9{b^2} + 6b + 1 + 2{b^2} – 4b + 4}} = \frac{{11{b^2} + 2b + 1}}{{11{b^2} + 2b + 5}}$

Xét $f\left( b \right) = \frac{{11{b^2} + 2b + 1}}{{11{b^2} + 2b + 5}}$ có $f’\left( b \right) = \frac{{4\left( {22b + 2} \right)}}{{11{b^2} + 2b + 5}} = 0 \Rightarrow b = \frac{{ – 1}}{{11}}$.

Nhận thấy $f\left( b \right)$ nhỏ nhất tại $b = – \frac{1}{{11}} \Rightarrow a = \frac{{14}}{{11}},c = \frac{1}{{11}}$

Nên $a + 2b + 3c = \frac{{14}}{{11}} – \frac{2}{{11}} + \frac{3}{{11}} = \frac{{15}}{{11}}$

DẠNG 3: ĐỘ DÀI ĐƯỜNG THẲNG-TÌM TỌA ĐỘ ĐIỂM

Câu 17. Trong hệ tọa độ $Oxyz$, cho $A\left( {2; – 3;14} \right)$, $B\left( {2; – 3;2} \right)$. Biết $I\left( {x;y;z} \right)$ là trung điểm của đoạn $AB$. Tính $x + y + z$.

Lời giải

Ta có: $I\left( {x;y;z} \right)$ là trung điểm của đoạn $AB$ nên $I\left( {\frac{{2 + 2}}{2};\frac{{ – 3 + ( – 3)}}{2};\frac{{14 + 2}}{2}} \right)$ hay $I\left( {2; – 3;8} \right)$.

Vậy $x + y + z = 2 + ( – 3) + 8 = 7$.

Câu 18. Trong hệ tọa độ $Oxyz$, cho $A\left( {4; – 1;8} \right)$, $B\left( {2; – 3;2} \right)$ và $I\left( {x;y;z} \right)$. Biết $A$ là trung điểm của đoạn $IB$. Tính $x + y + z$.

Lời giải

Ta có: $A$ là trung điểm của đoạn $IB$ nên $\left\{ \begin{gathered}
{x_A} = \frac{{{x_I} + {x_B}}}{2} \hfill \\
{y_A} = \frac{{{y_I} + {y_B}}}{2} \hfill \\
{z_A} = \frac{{{z_I} + {z_B}}}{2} \hfill \\
\end{gathered} \right.$$ \Leftrightarrow \left\{ \begin{gathered}
{x_I} = 2{x_A} – {x_B} \hfill \\
{y_I} = 2{y_A} – {y_B} \hfill \\
{z_I} = 2{z_A} – {z_B} \hfill \\
\end{gathered} \right.$

$ \Leftrightarrow \left\{ \begin{gathered}
{x_I} = 2.4 – 2 \hfill \\
{y_I} = 2.( – 1) – ( – 3) \hfill \\
{z_I} = 2.8 – 2 \hfill \\
\end{gathered} \right.$$ \Leftrightarrow \left\{ \begin{gathered}
{x_I} = 6 \hfill \\
{y_I} = 1 \hfill \\
{z_I} = 14 \hfill \\
\end{gathered} \right.$

Suy ra $I\left( {6;1;14} \right)$.

Vậy $x + y + z = 6 + 1 + 14 = 21$.

Câu 19. Trong hệ tọa độ $Oxyz$, cho tam giác $ABC$ có $A\left( {0; – 1;1} \right), B\left( {2; – 3;2} \right), C\left( {4; – 2;3} \right).$ Trọng tâm tam giác $ABC$ có tọa độ $\left( {x;y;z} \right)$. Tính $x + y + z$.

Lời giải

Ta có: $G\left( {x;y;z} \right)$ là trọng tâm tam giác $ABC$ nên $\left\{ \begin{gathered}
{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3} = \frac{{0 + 2 + 4}}{3} = 2 \hfill \\
{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3} = \frac{{ – 1 + ( – 3) + ( – 2)}}{3} = – 2 \hfill \\
{z_G} = \frac{{{z_A} + {z_B} + {z_C}}}{3} = \frac{{1 + 2 + 3}}{3} = 2 \hfill \\
\end{gathered} \right.$

Suy ra $G\left( {2; – 2;2} \right)$.

Vậy $x + y + z = 2 + ( – 2) + 2 = 2$.

Câu 20. Trong hệ tọa độ $Oxyz$, cho tam giác $ABC$ có $A\left( {0; – 1;1} \right), B\left( {2; – 3;2} \right), C\left( {4; – 2;3} \right)$. Gọi $K\left( {x;y;z} \right)$ là điểm sao cho $B$ là trọng tâm tam giác $ACK$. Tính $x + y + z$.

Lời giải

Ta có: $B$ là trọng tâm tam giác $ACK$ nên $\left\{ \begin{gathered}
{x_B} = \frac{{{x_A} + {x_C} + {x_K}}}{3} \hfill \\
{y_B} = \frac{{{y_A} + {y_C} + {y_K}}}{3} \hfill \\
{z_B} = \frac{{{z_A} + {z_C} + {z_K}}}{3} \hfill \\
\end{gathered} \right.$

$ \Rightarrow \left\{ \begin{gathered}
{x_K} = 3{x_B} – {x_A} – {x_C} \hfill \\
{y_K} = 3{y_B} – {y_A} – {y_C} \hfill \\
{z_K} = 3{z_B} – {z_A} – {z_C} \hfill \\
\end{gathered} \right.$$ \Rightarrow \left\{ \begin{gathered}
{x_K} = 3.2 – 0 – 4 = 2 \hfill \\
{y_K} = 3.( – 3) – ( – 1) – ( – 2) = 10 \hfill \\
{z_K} = 3.2 – 1 – 3 = 2 \hfill \\
\end{gathered} \right.$

Suy ra $K\left( {2;10;2} \right)$.

Vậy $x + y + z = 2 + 10 + 2 = 14$.

Câu 21. Trong hệ tọa độ $Oxyz$, cho $A\left( {1; – 1;1} \right)$, $B\left( {2; – 3;2} \right)$. Gọi $M\left( {x;y;z} \right)$ trên trục $Oy$ điểm cách đều hai điểm $AB$. Tính $x + 2y + z$.

Lời giải

Ta có: $M\left( {x;y;z} \right) \in Oy \Rightarrow M\left( {0;y;0} \right)$.

Khi đó, $M\left( {0;y;0} \right)$ cách đều hai điểm $AB$

$ \Leftrightarrow MA = MB \Leftrightarrow \sqrt {{1^2} + {{\left( { – 1 – y} \right)}^2} + {1^2}} = \sqrt {{2^2} + {{\left( { – 3 – y} \right)}^2} + {2^2}} $

$ \Leftrightarrow 1 + 1 + 2y + {y^2} + 1 = 4 + 9 + 6y + {y^2} + 4$

$ \Leftrightarrow – 4y = 14 \Leftrightarrow y = – \frac{7}{2}$

Vậy $x + 2y + z = – 7$.

Câu 22. Trong hệ tọa độ $Oxyz$ cho $A(4; – 1;2) ; B(7;3;2)$. Gọi $M\left( {a;b;c} \right)$ là điểm trên mặt phẳng $\left( {Oyz} \right)$ sao cho tam giác $ABM$ vuông cân tại $A$. Tính $a + b + c$.

Lời giải

Ta có: $M\left( {a;b;c} \right) \in \left( {Oyz} \right) \Rightarrow M\left( {0;b;c} \right)$.

Tam giác $ABM$ vuông cân tại $A$ nên $\left\{ \begin{gathered}
\overrightarrow {AM} \bot \overrightarrow {AB} \,\,\,(1) \hfill \\
AM = AB\,\,(2) \hfill \\
\end{gathered} \right.$

$\overrightarrow {AM} = \left( { – 4;b + 1;c – 2} \right)$; $\overrightarrow {AB} = \left( {3;4;0} \right)$

Ta có:

(1) $ \Leftrightarrow \overrightarrow {AM} .\overrightarrow {AB} = 0$$ \Leftrightarrow – 4.3 + \left( {b + 1} \right).4 + (c – 2).0 = 0$

$ \Leftrightarrow – 12 + 4b + 4 = 0 \Leftrightarrow b = 2$.

(2)$ \Leftrightarrow \sqrt {{{\left( { – 4} \right)}^2} + {{\left( {b + 1} \right)}^2} + {{\left( {c – 2} \right)}^2}} = \sqrt {{3^2} + {4^2} + {0^2}} $

$ \Leftrightarrow 16 + {b^2} + 2b + 1 + {c^2} – 4c + 4 = 25$

$ \Leftrightarrow {b^2} + 2b + {c^2} – 4c = 4$$ \Leftrightarrow {2^2} + 2.2 + {c^2} – 4c = 4$

$ \Leftrightarrow {c^2} – 4c + 4 = 0 \Leftrightarrow c = 2$

Suy ra $M\left( {0;2;2} \right)$

Vậy $a + b + c = 4$.

Câu 23. Trong không gian tọa độ $Oxyz$ cho ba điểm $A(3; – 4;7),\,B( – 5;3; – 2),\,C(1;2; – 3)$. Biết $\cos \widehat {ABC} = \frac{m}{{\sqrt n }}$ với $\frac{m}{n}$ tối giản. Tính $m + n$.

Lời giải

Ta có: $\overrightarrow {BA} = \left( {8; – 7;9} \right)$; $\overrightarrow {BC} = \left( {6; – 1; – 1} \right)$.

$cos\widehat {ABC} = cos\left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right) = \frac{{\overrightarrow {BA} .\overrightarrow {BC} }}{{\left| {\overrightarrow {BA} } \right|.\left| {\overrightarrow {BC} } \right|}}$

$ = \frac{{8.6 + ( – 7).( – 1) + 9.( – 1)}}{{\sqrt {{8^2} + {{\left( { – 7} \right)}^2} + {9^2}} .\sqrt {{6^2} + {{\left( { – 1} \right)}^2} + {{\left( { – 1} \right)}^2}} }}$

$ = \frac{{46}}{{\sqrt {194} .\sqrt {38} }} = \frac{{23}}{{\sqrt {1843} }}$

Vậy $m + n = 23 + 1843 = 1866$.

Câu 24. Cho hình hộp $ABCD.A’B’C’D’$ có $A\left( {1;2; – 1} \right)$, $B\left( { – 1;1;3} \right)$, $C\left( { – 1; – 1;2} \right)$, . Biết $A'(a;b;c)$. Tính $a + b + 10c$.

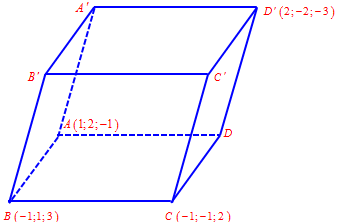
Lời giải

Gọi $D({x_D};{y_D};{z_D})$. Ta có: $\overrightarrow {DC} = \left( { – 1 – {x_D}; – 1 – {y_D};2 – {z_D}} \right)$; $\overrightarrow {AB} = \left( { – 2; – 1;4} \right)$

Do $ABCD$ là hình nên $\overrightarrow {DC} = \overrightarrow {AB} \Leftrightarrow \left\{ \begin{gathered}
– 1 – {x_D} = – 2 \hfill \\
– 1 – {y_D} = – 1 \hfill \\
2 – {z_D} = 4 \hfill \\
\end{gathered} \right.$

$ \Leftrightarrow \left\{ \begin{gathered}
{x_D} = 1 \hfill \\
{y_D} = 0 \hfill \\
{z_D} = – 2 \hfill \\
\end{gathered} \right.$

Suy ra, $D(1;0; – 2)$.

Ta có: $\overrightarrow {AA’} = \left( {a – 1;b – 2;c + 1} \right)$; $\overrightarrow {DD’} = \left( {1; – 2; – 1} \right)$

Do $A’ADD’$ là hình nên $\overrightarrow {AA’} = \overrightarrow {DD’} $

$ \Leftrightarrow \left\{ \begin{gathered}
a – 1 = 1 \hfill \\
b – 2 = – 2 \hfill \\
c + 1 = – 1 \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
a = 2 \hfill \\
b = 0 \hfill \\
c = – 2 \hfill \\
\end{gathered} \right.$

Suy ra, $A’\left( {2;0; – 2} \right)$

Vậy $a + b + 10c = – 18$.