Các Dạng Bài Tập Về Tích Phân Năm Học 2024-2025 Có Lời Giải Chi Tiết

Các dạng bài tập về tích phân có lời giải chi tiết được soạn dưới dạng file word và PDF gồm 3 trang. Các bạn xem và tải về ở dưới.

Dạng 1. Tích phân của hàm số lũy thừa:

Chú ý:

$\int {{x^\alpha }dx = \frac{{{x^{\alpha + 1}}}}{{\alpha + 1}}} + C$ với $\alpha \ne – 1$;

$\int {\frac{1}{x}dx = \ln \left| x \right|} + C$

Ví dụ 1. Tính các tích phân sau

a) $\int\limits_0^2 {{x^3}dx} $ b) $\int\limits_1^2 {\left( {2x – 3} \right)dx} $ c) $\int\limits_{ – 1}^1 {\left( {5{x^4} – 3{x^2}} \right)dx} $ d) $\int\limits_{ – 1}^2 {{{\left( {x – 2} \right)}^2}dx} $

Lời giải

a) $\int\limits_0^2 {{x^3}dx} = \left. {\frac{{{x^4}}}{4}} \right|_0^2 = \frac{1}{4}\left( {{2^4} – {0^4}} \right) = 4$

b) Cách 1: $\int\limits_1^2 {\left( {2x + 3} \right)dx} = \int\limits_1^2 {2xdx} + \int\limits_1^2 {3dx} = \left. {{x^2}} \right|_1^2 + \left. {3x} \right|_1^2$

$ = \left( {{2^2} – {1^2}} \right) + 3\left( {2 – 1} \right) = 6$

Cách 2: $\int\limits_1^2 {\left( {2x + 3} \right)dx} = \left. {\left( {{x^2} + 3x} \right)} \right|_1^2 = \left( {{2^2} + 3.2} \right) – \left( {{1^2} + 3.1} \right) = 6$

c) $\int\limits_{ – 1}^1 {\left( {5{x^4} – 3{x^2}} \right)dx} = \left. {\left( {{x^5} – {x^3}} \right)} \right|_{ – 1}^1 = \left( {{1^5} – {1^3}} \right) – \left( {{{( – 1)}^5} – {{( – 1)}^3}} \right) = 0$

d) $\int\limits_{ – 1}^2 {{{\left( {x – 2} \right)}^2}dx} = \int\limits_{ – 1}^2 {\left( {{x^2} – 4x + 4} \right)dx} = \left. {\left( {\frac{{{x^3}}}{3} – 2{x^2} + 4x} \right)} \right|_{ – 1}^2$

$ = \left( {\frac{{{2^3}}}{3} – {{2.2}^2} + 4.2} \right) – \left( {\frac{{{{( – 1)}^3}}}{3} – 2{{( – 1)}^2} + 4.( – 1)} \right) = 9$

Ví dụ 2. Tính các tích phân sau

a) $\int\limits_1^2 {\frac{1}{{{x^3}}}dx} $ b) $\int\limits_{ – 3}^{ – 1} {\frac{4}{{{x^2}}}dx} $ c) $\int\limits_1^2 {\left( {\frac{1}{{{x^4}}} – \frac{1}{{{x^5}}}} \right)dx} $

Lời giải

a) $\int\limits_1^2 {\frac{1}{{{x^3}}}dx} = \int\limits_1^2 {{x^{ – 3}}dx} = \left. { – \frac{1}{{2{x^2}}}} \right|_1^2 = – \frac{1}{2}\left( {\frac{1}{{{2^2}}} – \frac{1}{{{1^2}}}} \right) = \frac{1}{4}$

b) $\int\limits_{ – 3}^{ – 1} {\frac{4}{{{x^2}}}dx} = \int\limits_{ – 3}^{ – 1} {4{x^{ – 2}}dx} = \left. { – \frac{4}{x}} \right|_{ – 3}^{ – 1} = – 4\left( {\frac{1}{{ – 1}} – \frac{1}{{ – 3}}} \right) = \frac{8}{3}$

c) $\int\limits_1^2 {\left( {\frac{1}{{{x^4}}} – \frac{1}{{{x^5}}}} \right)dx} = \int\limits_1^2 {\left( {{x^{ – 4}} – {x^{ – 5}}} \right)dx} = \left. {\left( { – \frac{1}{{3{x^3}}} + \frac{1}{{4{x^4}}}} \right)} \right|_1^2$

$ = \left( { – \frac{1}{{{{3.2}^3}}} + \frac{1}{{{{4.2}^4}}}} \right) – \left( { – \frac{1}{{{{3.1}^3}}} + \frac{1}{{{{4.1}^4}}}} \right) = \frac{{11}}{{192}}$

Ví dụ 3. Tính các tích phân sau

a) $\int\limits_1^8 {\sqrt[3]{x}dx} $ b) $\int\limits_{ – 3}^{ – 1} {\frac{1}{x}dx} $ c) $\int\limits_e^{{e^3}} {\frac{6}{x}dx} $

Lời giải

a) $\int\limits_1^8 {\sqrt[3]{x}dx} = \int\limits_1^8 {{x^{\frac{1}{3}}}dx} = \left. {\frac{{{x^{\frac{4}{3}}}}}{{\frac{4}{3}}}} \right|_1^8 = \left. {\frac{3}{4}\sqrt[3]{{{x^4}}}} \right|_1^8$

$ = \frac{3}{4}\left( {\sqrt[3]{{{8^4}}} – \sqrt[3]{{{1^4}}}} \right) = \frac{3}{4}\left( {16 – 1} \right) = \frac{{45}}{4}$

b) $\int\limits_{ – 3}^{ – 1} {\frac{1}{x}dx} = \left. {\ln \left| x \right|} \right|_{ – 3}^{ – 1} = \ln \left| { – 1} \right| – \ln \left| { – 3} \right|$ $ = 0 – \ln 3 = – \ln 3$

c) $\int\limits_e^{{e^3}} {\frac{6}{x}dx} = 6\int\limits_e^{{e^3}} {\frac{1}{x}dx} = \left. {6\ln \left| x \right|} \right|_e^{{e^3}} = 6\left( {\ln \left| {{e^3}} \right| – \ln \left| e \right|} \right)$

$ = 6\left( {3 – 1} \right) = 12$

Ví dụ 4. Biết tích phân $I = \int\limits_1^2 {\left( {3{x^2} + \frac{2}{x}} \right)dx} = a + b\ln c$ với $a$, $b$, $c$ là số nguyên tố. Tính giá trị $a + b + c$.

Lời giải

$I = \int\limits_1^2 {\left( {3{x^2} + \frac{2}{x}} \right)dx} = \left. {\left( {{x^3} + 2\ln \left| x \right|} \right)} \right|_1^2$

$ = \left( {{2^3} + 2\ln \left| 2 \right|} \right) – \left( {{1^3} + 2\ln \left| 1 \right|} \right)$

$ = \left( {8 + 2\ln 2} \right) – \left( {1 + 0} \right) = 7 + 2\ln 2$

Vậy $a + b + c = 7 + 2 + 2 = 11$

Ví dụ 5. Biết tích phân $I = \int\limits_{ – 2}^{ – 1} {\frac{{{x^2} – 3x}}{x}dx} = a\ln b – \frac{c}{d}$ với $a$, $b$, $c$, $d$ là số nguyên tố. Tính giá trị $a + b + c + d$.

Lời giải

$I = \int\limits_{ – 2}^{ – 1} {\frac{{{x^2} – 3x}}{x}dx} = \int\limits_{ – 2}^{ – 1} {\left( {x – \frac{3}{x}} \right)dx} = \left. {\left( {\frac{{{x^2}}}{2} – 3\ln \left| x \right|} \right)} \right|_{ – 2}^{ – 1}$

$ = \left( {\frac{{{{( – 1)}^2}}}{2} – 3\ln \left| { – 1} \right|} \right) – \left( {\frac{{{{( – 2)}^2}}}{2} – 3\ln \left| { – 2} \right|} \right)$

$ = \frac{1}{2} – \left( {2 – 3\ln 2} \right) = 3\ln 2 – \frac{3}{2}$

Vậy $a + b + c + d = 3 + 2 + 3 + 2 = 10$

Dạng 2. Tích phân của hàm số lượng giác:

Chú ý:

$\int {cosxdx = \sin x} + C$; $\int {cos\left( {ax + b} \right)dx = \frac{1}{a}\sin \left( {ax + b} \right)} + C$;

$\int {\sin xdx = – cosx} + C$; $\int {\sin \left( {ax + b} \right)dx = – \frac{1}{a}cosx\left( {ax + b} \right)} + C$;

$\int {\frac{1}{{co{s^2}x}}dx = \tan x} + C$;

$\int {\frac{1}{{{{\sin }^2}x}}dx = – \cot x} + C$;

Ví dụ 6. Tính các tích phân sau

a) $\int\limits_{\frac{\pi }{4}}^{\frac{\pi }{2}} {cosxdx} $ b) $\int\limits_0^{\frac{\pi }{2}} {3\sin xdx} $ c) $\int\limits_{\frac{\pi }{4}}^{\frac{\pi }{3}} {\frac{7}{{co{s^2}x}}dx} $ d) $\int\limits_{\frac{\pi }{4}}^{\frac{\pi }{2}} {\left( {5cosx – \frac{4}{{{{\sin }^2}x}}} \right)dx} $

Lời giải

a) $\int\limits_{\frac{\pi }{4}}^{\frac{\pi }{2}} {cosxdx} = \left. {\sin x} \right|_{\frac{\pi }{4}}^{\frac{\pi }{2}} = \sin \frac{\pi }{2} – \sin \frac{\pi }{4} = 1 – \frac{{\sqrt 2 }}{2}$

b) $\int\limits_0^{\frac{\pi }{2}} {3\sin xdx} = \left. { – 3cosx} \right|_0^{\frac{\pi }{2}} = – 3\left( {cos\frac{\pi }{2} – cos0} \right) = – 3\left( {0 – 1} \right) = 3$

c) $\int\limits_{\frac{\pi }{4}}^{\frac{\pi }{3}} {\frac{7}{{co{s^2}x}}dx} = \left. {7\tan x} \right|_{\frac{\pi }{4}}^{\frac{\pi }{3}} = 7\left( {\tan \frac{\pi }{3} – \tan \frac{\pi }{4}} \right) = 7\left( {\sqrt 3 – 1} \right)$

d) $\int\limits_{\frac{\pi }{4}}^{\frac{\pi }{2}} {\left( {5cosx – \frac{4}{{{{\sin }^2}x}}} \right)dx} = \left. {\left( {5sinx + 4\cot x} \right)} \right|_{\frac{\pi }{4}}^{\frac{\pi }{2}}$

$ = \left( {5sin\frac{\pi }{2} + 4\cot \frac{\pi }{2}} \right) – \left( {5sin\frac{\pi }{4} + 4\cot \frac{\pi }{4}} \right)$

$ = \left( {5.1 + 4.0} \right) – \left( {5.\frac{{\sqrt 2 }}{2} + 4.1} \right) = 1 – \frac{{5\sqrt 2 }}{2}$

Ví dụ 7. Biết tích phân $I = \int\limits_0^{\frac{\pi }{4}} {\left( {\frac{9}{{co{s^2}x}} – 4\sin x} \right)dx}  = a\sqrt b  + c$ với $a$, $b$, $c$ là số nguyên tố. Tính giá trị $a + b + c$.

Lời giải

$I = \int\limits_0^{\frac{\pi }{4}} {\left( {\frac{9}{{co{s^2}x}} – 4\sin x} \right)dx} = \left. {\left( {9\tan x + 4cosx} \right)} \right|_0^{\frac{\pi }{4}}$

$ = \left( {9\tan \frac{\pi }{4} + 4cos\frac{\pi }{4}} \right) – \left( {9\tan 0 + 4cos0} \right)$

$ = \left( {9.1 + 4.\frac{{\sqrt 2 }}{2}} \right) – \left( {9.0 + 4.1} \right) = 2\sqrt 2 + 5$

Vậy $a + b + c = 2 + 2 + 5 = 9$

Ví dụ 8. Biết tích phân $I = \int\limits_0^{\frac{\pi }{3}} {\left[ {{{\left( {\sin \frac{x}{2} + cos\frac{x}{2}} \right)}^2} + 2} \right]dx} = a\pi + b$ với $a$, $b$, $c$ là số nguyên. Tính giá trị $3a + 4b$.

Lời giải

$I = \int\limits_0^{\frac{\pi }{3}} {\left[ {{{\left( {\sin \frac{x}{2} + cos\frac{x}{2}} \right)}^2} + 2} \right]dx} $

$ = \int\limits_0^{\frac{\pi }{3}} {\left[ {{{\sin }^2}\frac{x}{2} + 2\sin \frac{x}{2}cos\frac{x}{2} + co{s^2}\frac{x}{2} + 2} \right]dx} $

$ = \int\limits_0^{\frac{\pi }{3}} {\left[ {{{\sin }^2}\frac{x}{2} + co{s^2}\frac{x}{2} + 2\sin \frac{x}{2}cos\frac{x}{2} + 2} \right]dx} $

$ = \int\limits_0^{\frac{\pi }{3}} {\left[ {1 + 2\sin x + 2} \right]dx} = \int\limits_0^{\frac{\pi }{3}} {\left[ {3 + 2\sin x} \right]dx} $

$ = \left. {\left( {3x – 2cosx} \right)} \right|_0^{\frac{\pi }{3}} = \left( {3.\frac{\pi }{3} – 2cos\frac{\pi }{3}} \right) – \left( {3.0 – 2cos0} \right)$

$ = \left( {\pi – 1} \right) – \left( {0 – 2.1} \right) = \pi + 1$

Vậy $3a + 4b = 3.1 + 4.1 = 7$.

Dạng 3. Tích phân của hàm số mũ

Chú ý:

$\int {{e^x}dx = {e^x}} + C$; $\int {{e^{ax + b}}dx = \frac{1}{a}{e^{ax + b}}} + C$

$\int {{a^x}dx = \frac{{{a^x}}}{{\ln a}}} + C$

Ví dụ 9. Tính các tích phân sau

a) $\int\limits_0^{1} {6{e^x}dx} $ b) $\int\limits_{\ln 2}^{\ln 11} {{e^x}dx} $ c) $\int\limits_0^{{{\log }_5}19} {{5^x}dx} $ d) $\int\limits_{\frac{1}{4}}^{1} {{e^{4x}}dx} $.

Lời giải

a) $\int\limits_0^{1} {6{e^x}dx} = \left. {6{e^x}} \right|_0^1 = 6\left( {{e^1} – {e^0}} \right) = 6\left( {e – 1} \right)$

b) $\int\limits_{\ln 2}^{\ln 11} {{e^x}dx} = \left. {{e^x}} \right|_{\ln 2}^{\ln 11} = {e^{\ln 11}} – {e^{\ln 2}} = 11 – 2 = 9$

c) $\int\limits_0^{{{\log }_5}19} {{5^x}dx} = \left. {\frac{{{5^x}}}{{\ln 5}}} \right|_0^{{{\log }_5}19} = \frac{{{5^{{{\log }_5}19}}}}{{\ln 5}} – \frac{{{5^0}}}{{\ln 5}}$ $ = \frac{{19}}{{\ln 5}} – \frac{1}{{\ln 5}} = \frac{{18}}{{\ln 5}}$

d) $\int\limits_{\frac{1}{4}}^{1} {{e^{4x}}dx} = \left. {\frac{1}{4}{e^{4x}}} \right|_{\frac{1}{4}}^1 = \frac{1}{4}\left( {{e^4} – {e^1}} \right) = \frac{1}{4}\left( {{e^4} – e} \right)$.

Ví dụ 10. Biết tích phân $I = \int\limits_0^4 {\left( {3{e^x} + 4x} \right)dx} = a.{e^b} + c$ với $a$, $b$, $c$ là số nguyên. Tính giá trị $a + b + c$.

Lời giải

$I = \int\limits_0^4 {\left( {3{e^x} + 4x} \right)dx} = \left. {\left( {3{e^x} + 2{x^2}} \right)} \right|_0^4$

$ = \left( {3{e^4} + {{2.4}^2}} \right) – \left( {3{e^0} + {{2.0}^2}} \right) = 3{e^4} + 29$

Dạng 4. Tích phân sử dụng các tính chất

Chú ý:

• $\int\limits_a^b {kf\left( x \right)dx} = k\int\limits_a^b {f\left( x \right)dx} $, với $k$ là hằng số.

• $\int\limits_a^b {\left[ {f\left( x \right) + g\left( x \right)} \right]\operatorname{dx} } = \int\limits_a^b {f\left( x \right)\operatorname{dx} } + \int\limits_a^b {g\left( x \right)\operatorname{dx} } $

• $\int\limits_a^b {\left[ {f\left( x \right) – g\left( x \right)} \right]\operatorname{dx} } = \int\limits_a^b {f\left( x \right)\operatorname{dx} } – \int\limits_a^b {g\left( x \right)\operatorname{dx} } $

• $\int\limits_a^b {f\left( x \right)\operatorname{dx} } = \int\limits_a^c {f\left( x \right)\operatorname{dx} } + \int\limits_c^b {f\left( x \right)\operatorname{dx} } $ với $c \in \left( {a;b} \right)$

Ví dụ 11. Cho $\int\limits_1^3 {f(x)dx = 5} $. Tính các tích phân sau

a) $\int\limits_1^3 {7f(x)dx} $ b) $\int\limits_1^3 {\left[ {1 + f(x)} \right]dx} $ c) $\int\limits_1^3 {\left[ {2x – 5f(x)} \right]dx} $ d) $\int\limits_1^3 {\left[ {2f(x) – \frac{8}{x}} \right]dx} $

Lời giải

a) $\int\limits_1^3 {7f(x)dx = 7} \int\limits_1^3 {f(x)dx} = 7.5 = 35$

b) $\int\limits_1^3 {\left[ {1 + f(x)} \right]dx} = \int\limits_1^3 {1dx} + \int\limits_1^3 {f(x)dx} $$ = \left. x \right|_1^3 + 5 = 3 – 1 + 5 = 7$

c) $\int\limits_1^3 {\left[ {2x – 5f(x)} \right]dx} = \int\limits_1^3 {2xdx} + \int\limits_1^3 {5f(x)dx} $

$ = \left. {{x^2}} \right|_1^3 + 5\int\limits_1^3 {f(x)dx} = 8 + 5.5 = 33$

d) $\int\limits_1^3 {\left[ {2f(x) – \frac{8}{x}} \right]dx} = \int\limits_1^3 {2f(x)dx} – \int\limits_1^3 {\frac{8}{x}dx} $

$ = 2\int\limits_1^3 {f(x)dx} – 8\int\limits_1^3 {\frac{1}{x}dx} = 2.5 – 8\left. {\ln \left| x \right|} \right|_1^3 = 10 – 8\ln 3$

Ví dụ 12. Cho $\int\limits_1^2 {f(x)dx = 3} $ và $\int\limits_2^5 {f(x)dx = 11} $. Tính tích phân sau $\int\limits_1^5 {f(x)dx} $.

Lời giải

Ta có $\int\limits_1^5 {f(x)dx} = \int\limits_1^2 {f(x)dx + \int\limits_2^5 {f(x)dx} } = 3 + 11 = 14$

Ví dụ 13. Cho $\int\limits_0^1 {f(x)dx = 10} $ và $\int\limits_0^7 {f(x)dx} = 18$. Tính tích phân sau $\int\limits_1^7 {f(x)dx} $.

Lời giải

Ta có $\int\limits_0^7 {f(x)dx} = \int\limits_0^1 {f(x)dx + \int\limits_1^7 {f(x)dx} } $

$ \Rightarrow \int\limits_1^7 {f(x)dx} = \int\limits_0^7 {f(x)dx} – \int\limits_0^1 {f(x)dx} = 18 – 10 = 8$

Ví dụ 14. Cho $\int\limits_1^9 {f(x)dx = 4} $ và $\int\limits_7^9 {f(x)dx = } 1$. Tính tích phân sau $\int\limits_1^7 {6f(x)dx} $.

Lời giải

Ta có $\int\limits_1^7 {6f(x)dx} = 6\int\limits_1^7 {f(x)dx} = 6\left( {\int\limits_1^9 {f(x)dx – \int\limits_7^9 {f(x)dx} } } \right)$

$ = 6\left( {4 – 1} \right) = 18$

Dạng 5. Tích phân có chứa giá trị tuyệt đối

Ví dụ 15. Tính các tích phân sau

a) $\int\limits_0^3 {\left| {2x – 2} \right|dx} $ b) $\int_{ – 2}^3 | 2 – x|dx$ c) $\int\limits_0^2 {\left| {1 – {x^2}} \right|dx} $ d) $\int_0^{2\pi } | \sin x|dx$

Lời giải

a) $\int\limits_0^3 {\left| {2x – 2} \right|dx} $

Ta có: $\left| {2x – 2} \right| = \left\{ \begin{gathered}
2x – 2\,\,khi\,\,2x – 2 \geqslant 0\, \hfill \\
– 2x + 2\,\,khi\,\,2x – 2 < 0\,\,\, \hfill \\
\end{gathered} \right.$

$ = \left\{ \begin{gathered}
2x – 2\,\,khi\,\,x \geqslant 1\, \hfill \\
– 2x + 2\,\,khi\,\,x < 1\,\,\, \hfill \\
\end{gathered} \right.$

Khi đó $\int\limits_0^3 {\left| {2x – 2} \right|dx} = \int\limits_0^1 {\left| {2x – 2} \right|dx} + \int\limits_1^3 {\left| {2x – 2} \right|dx} $

$ = – \int\limits_0^1 {\left( {2x – 2} \right)dx} + \int\limits_1^3 {\left( {2x – 2} \right)dx} $$ = – \left. {\left( {{x^2} – 2x} \right)} \right|_0^1 + \left. {\left( {{x^2} – 2x} \right)} \right|_1^3$

$ = 1 + 4 = 5$

b) Ta có: $\left| {2 – x} \right| = \left\{ \begin{gathered}
2 – x\,\,khi\,\,2 – x \geqslant 0\, \hfill \\
– \left( {2 – x} \right)\,\,khi\,\,2 – x < 0\,\,\, \hfill \\
\end{gathered} \right.$$ = \left\{ \begin{gathered}
2 – x\,\,khi\,\,x \leqslant 2\, \hfill \\
– \left( {2 – x} \right)\,\,khi\,\,x > 2\,\,\, \hfill \\
\end{gathered} \right.$

Khi đó $\int_{ – 2}^3 | 2 – x|dx = \int_{ – 2}^2 | 2 – x|dx + \int_2^3 | 2 – x|dx$

$ = \int_{ – 2}^2 {(2 – x)} dx – \int_2^3 {(2 – x)} dx$

$ = \left. {\left( {2x – \frac{{{x^2}}}{2}} \right)} \right|_{ – 2}^2 – \left. {\left( {2x – \frac{{{x^2}}}{2}} \right)} \right|_2^3 = \frac{{17}}{2}$

c) $\int\limits_0^2 {\left| {1 – {x^2}} \right|dx} $

Ta có $1 – {x^2} = 0 \Leftrightarrow \left[ \begin{gathered}
x = 1 \hfill \\
x = – 1 \hfill \\
\end{gathered} \right.$

Bảng xét dấu

Khi đó $\int\limits_0^2 {\left| {1 – {x^2}} \right|dx} = \int\limits_0^1 {\left| {1 – {x^2}} \right|dx} + \int\limits_1^2 {\left| {1 – {x^2}} \right|dx} $

$ = \int\limits_0^1 {\left( {1 – {x^2}} \right)dx} – \int\limits_1^2 {\left( {1 – {x^2}} \right)dx} $

$ = \left. {\left( {x – \frac{{{x^2}}}{3}} \right)} \right|_0^1 – \left. {\left( {x – \frac{{{x^2}}}{3}} \right)} \right|_1^3 = \frac{2}{3} – \left( { – \frac{2}{3}} \right) = \frac{4}{3}$

d) $\int_0^{2\pi } | \sin x|dx = \int_0^\pi | \sin x|dx + \int_\pi ^{2\pi } | \sin x|dx$

$ = \int_0^\pi {\sin } x\;dx – \int_\pi ^{2\pi } {\sin } x\;dx = – \left. {\cos x} \right|_0^\pi + \left. {\cos x} \right|_\pi ^{2\pi } = 4$

Ví dụ 16. Cho $\int\limits_1^2 {h(x)dx = 9} $ và $\int\limits_2^{10} {h(x)dx = } – 3$. Biết $h(x) = \left\{ \begin{gathered}
h(x)\,\,khi\,\,1 \leqslant x \leqslant 2\, \hfill \\
– h(x)\,\,khi\,\,2 < x \leqslant 10 \hfill \\
\end{gathered} \right.$. Tính các tích phân sau:

a) $\int\limits_1^{10} {h(x)dx} $;    b) $\int\limits_1^{10} {\left| {h(x)} \right|dx} $

Lời giải

a) $\int\limits_1^{10} {h(x)dx} = \int\limits_1^2 {h(x)dx} + \int\limits_2^{10} {h(x)dx} = 9 – 3 = 6$.

b) Ta có $\int\limits_1^{10} {\left| {h(x)} \right|dx} = \int\limits_1^2 {\left| {h(x)} \right|dx} + \int\limits_2^{10} {\left| {h(x)} \right|dx} $

$ = \int\limits_1^2 {h(x)dx} – \int\limits_2^{10} {h(x)dx} = 9 + 3 = 12$

Dạng 6. Một số bài toán ứng dụng thực tiễn

Phương pháp:

– Quảng đường di chuyển của một vật trong khoảng thời gian từ $a$ đến $b$ là $s = \int\limits_a^b {v(t)dt} $

– Cho hàm số $f\left( x \right)$ liên tục trên đoạn $\left[ {a;b} \right]$. Khi đó $\frac{1}{{b – a}}\int\limits_a^b {f\left( x \right)dx} $ được gọi là giá trị trung bình của hàm số $f\left( x \right)$ trên đoạn $\left[ {a;b} \right]$.

Ví dụ 17. Một vật chuyển động với vận tốc $v(t) = 2 – \sin t(\;m/s)$. Tính quãng đường vật di chuyển trong khoảng thời gian từ thời điểm $t = 0$ (s) đến thời điểm $t = \frac{\pi }{2}(\;s)$.

Lời giải

Quãng đường vật di chuyển trong khoảng thời gian từ thời điểm $t = 0$ (s) đến thời điểm $t = \frac{\pi }{2}(\;s)$ là:

$s = \int\limits_a^b {v(t)dt} = \int\limits_0^{\frac{\pi }{2}} {\left( {2 – \sin t} \right)dt} = \left. {\left( {2t + cost} \right)} \right|_0^{\frac{\pi }{2}}$

$ = \left( {2.\frac{\pi }{2} + cos\frac{\pi }{2}} \right) – \left( {2.0 + cos0} \right) = \pi – 1\,(m)$

Ví dụ 18. Một ô tô đang di chuyển với tốc độ 20 m/s thì hãm phanh nên tốc độ ($m/s$) của xe thay đổi theo thời gian $t$ (giây) được tính theo công thức $v(t) = 20 – 5t$ $(0 \leqslant t \leqslant 4)$.

Kể từ khi hãm phanh đến khi dừng, ô tô đi được quãng đường bao nhiêu?

Lời giải

Xe dừng khi $v(t) = 0 \Leftrightarrow 20 – 5t = 0 \Leftrightarrow t = 4$

Khi đó, quãng đường xe di chuyển từ khi bắt đầu hãm phanh đến khi dừng là

$s = \int_0^4 v (t)dt = \int_0^4 {(20 – 5t)} dt = \left. {\left( {20t – \frac{{5{t^2}}}{2}} \right)} \right|_0^4 = 40(\;m).$

Ví dụ 19. Một chất điểm $A$ xuất phát từ $O$, chuyển động thẳng với vận tốc biến thiên theo thời gian bởi quy luật $v\left( t \right) = \frac{1}{{100}}{t^2} + \frac{{13}}{{30}}t \left( {m/s} \right)$, trong đó $t$ (giây) là khoảng thời gian tính từ lúc $A$ bắt đầu chuyển động. Từ trạng thái nghỉ, một chất điểm $B$ cũng xuất phát từ $O$, chuyển động thẳng cùng hướng với $A$ nhưng chậm hơn $10$ giây so với $A$ và có gia tốc bằng $a \left( {m/{s^2}} \right)$ ($a$ là hằng số). Sau khi $B$ xuất phát được $15$ giây thì đuổi kịp $A$. Vận tốc của $B$ tại thời điểm đuổi kịp $A$ bằng bao nhiêu?

Lời giải

Ta có ${v_B}\left( t \right) = \int {a.dt} = at + C$, ${v_B}\left( 0 \right) = 0 \Rightarrow C = 0$ $ \Rightarrow {v_B}\left( t \right) = at$.

Quãng đường chất điểm $A$ đi được trong $25$ giây là

${S_A} = \int\limits_0^{25} { \left( {\frac{1}{{100}}{t^2} + \frac{{13}}{{30}}t } \right)dt} $$\left. { = \left( {\frac{1}{{300}}{t^3} + \frac{{13}}{{60}}{t^2}} \right)} \right|_0^{25} = \frac{{375}}{2}$
Quãng đường chất điểm $B$ đi được trong $15$ giây là

${S_B} = \int\limits_0^{15} {at.dt} $$\left. { = \frac{{a{t^2}}}{2}} \right|_0^{15} = \frac{{225a}}{2}$.

Ta có $\frac{{375}}{2} = \frac{{225a}}{2} \Leftrightarrow a = \frac{5}{3}$.

Vận tốc của $B$ tại thời điểm đuổi kịp $A$ là ${v_B}\left( {15} \right) = \frac{5}{3}.15 = 25 \left( {m/s} \right)$.

Ví dụ 20. Một vật chuyển động với vận tốc được cho bởi đồ thị ở hình dưới.

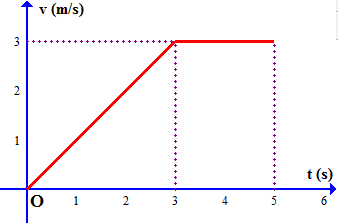
a) Tính quãng đường và vận tốc trung bình mà vật di chuyển được trong 3 giây đầu tiên.

b) Tính quãng đường mà vật di chuyển được trong 5 giây đầu tiên.

Lời giải

a) Trong 3 giây đầu tiên, đồ thị hàm vận tốc $v(t)$ là đường thẳng nên có dạng $v(t) = at + b$.

Do đồ thị đi qua hai điểm $(0;0)$ và $(3;3)$ nên ta có: $\left\{ \begin{gathered}
0 = a.0 + b \hfill \\
3 = a.3 + b \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
b = 0 \hfill \\
a = 1 \hfill \\
\end{gathered} \right.$

Suy ra, $v(t) = t$.

Vậy

– Quãng đường mà vật di chuyển được trong 3 giây đầu tiên là:

${s_1} = \int\limits_a^b {v(t)dt} = \int\limits_0^3 {tdt} = \left. {\frac{{{t^2}}}{2}} \right|_0^3 = \frac{9}{2}\,(m)$

– Vận tốc trung bình mà vật di chuyển được trong 3 giây đầu tiên là:

${v_1} = \frac{{{s_1}}}{{3 – 0}} = \frac{{\frac{9}{2}}}{3} = \frac{3}{2}\,(m/s)$

b) Tính quãng đường mà vật di chuyển được trong khoảng thời gian từ giây thứ 3 đến giây thứ 5.

Trong giây thứ 3 đến giây thứ 5, đồ thị hàm vận tốc $v(t)$ là đường thẳng đi qua điểm $(0;3)$ và song song với trục $Ot$ nên có phương trình $v(t) = 3$

Suy ra, quãng đường mà vật di chuyển được trong khoảng thời gian từ giây thứ 3 đến giây thứ 5 là:

${s_2} = \int\limits_3^5 {v(t)dt} = \int\limits_3^5 {3dt} = \left. {3t} \right|_3^5 = 6\,(m)$

Vậy quãng đường mà vật di chuyển được trong 5 giây đầu tiên là $s = {s_1} + {s_2} = \frac{9}{2} + 6 = 10,5\,m$.