Chuyên Đề Hình Học Không Gian Ôn Thi Tốt Nghiệp THPT 2025 Giải Chi Tiết

Chuyên đề hình học không gian ôn thi tốt nghiệp THPT 2025 giải chi tiết được soạn dưới dạng file word và PDF gồm 20 trang. Các bạn xem và tải về ở dưới.

CHUYÊN ĐỀ: HÌNH HỌC KHÔNG GIAN

A. KIẾN THỨC CẦN NHỚ

I. QUAN HỆ VUÔNG GÓC TRONG KHÔNG GIAN

1. Hai đường thẳng vuông góc

Hai đường thẳng $a$ và $b$ được gọi là vuông góc với nhau nếu góc giữa chúng bằng $90^\circ $, kí hiệu $a \bot b$.

2. Đường thẳng vuông góc với mặt phẳng

a) Định nghĩa

Đường thẳng $d$ được gọi là vuông góc với mặt phẳng $\left( P \right)$ nếu đường thẳng $d$ vuông góc với mọi đường thẳng trong mặt phẳng $\left( P \right)($Hình 1$)$, kí hiệu $d \bot \left( P \right)$ hoặc $\left( P \right) \bot d$.

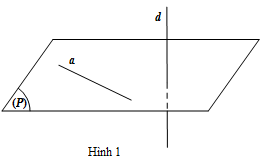
b) Dấu hiệu nhận biết

Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau cùng thuộc một mặt phẳng thì nó vuông góc với mặt phẳng ấy.

c) Tính chất

• Có duy nhất một mặt phẳng đi qua một điểm cho trước và vuông góc với một đường thẳng cho trước.

• Có duy nhất một đường thẳng đi qua một điểm cho trước và vuông góc với một mặt phẳng cho trước

• Cho hai đường thẳng song song. Một mặt phẳng vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.

• Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.

• Cho hai mặt phẳng song song. Một đường thẳng vuông góc với mặt phẳng này thì cũng vuông góc với mặt phẳng kia.

• Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì song song với nhau.

d) Định lí ba đường vuông góc

Cho đường thẳng $a$ không vuông góc với mặt phẳng $\left( P \right)$ và đường thẳng $d$ nằm trong mặt phẳng $\left( P \right)$. Khi đó, $d$ vuông góc với $a$ khi và chi khi $d$ vuông góc với hình chiếu vuông góc $a’$ của $a$ trên $\left( P \right)$ (Hình 2).

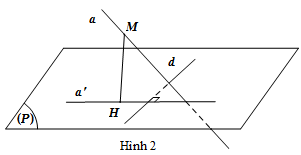
3. Hai mặt phẳng vuông góc

a) Định nghĩa

Hai mặt phẳng $\left( P \right),\left( Q \right)$ cắt nhau tạo nên bốn góc nhị diện. Nếu một trong các góc nhị diện đó là góc nhị diện vuông thì hai mặt phẳng $\left( P \right),\left( Q \right)$ gọi là vuông góc với nhau, kí hiệu $\left( P \right) \bot \left( Q \right)$.

b) Dấu hiệu nhận biết

Nếu mặt phẳng này chứa một đường thẳng mà đường thẳng đó vuông góc với mặt phẳng kia thì hai mặt phẳng đó vuông góc với nhau.

c) Tính chất

• Nếu hai mặt phẳng vuông góc với nhau thì bất cứ đường thẳng nào nằm trong mặt phẳng này và vuông góc với giao tuyến cũng vuông góc với mặt phẳng kia.

• Nếu hai mặt phẳng cắt nhau và cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba đó.

II. GÓC TRONG KHÔNG GIAN

1. Góc giữa hai đường thẳng trong không gian

Góc giữa hai đường thẳng $a$ và $b$ trong không gian là góc giữa hai đường thẳng $a’$ và $b’$ cùng đi qua một điểm $O$ và lần lượt song song (hoặc trùng) với $a$ và $b$ (Hình 3$)$, kí hiệu $\left( {a,b} \right)$ hoặc $(\widehat {a,b)}$.

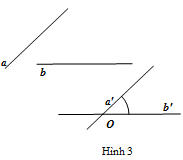
Nhận xét: Góc giữa hai đường thẳng trong không gian có số đo từ $0^\circ $ đến $90^\circ $.

2. Góc giữa đường thẳng và mặt phẳng

Cho đường thẳng $d$ và mặt phẳng $\left( P \right)$, ta có định nghĩa sau:

• Nếu đường thẳng $d$ vuông góc với mặt phẳng $\left( P \right)$ thì góc giữa $d$ và $\left( P \right)$ bằng $90^\circ $.

• Nếu đường thẳng $d$ không vuông góc với mặt phẳng $\left( P \right)$ thì góc giữa đường thẳng $d$ và mặt phẳng $\left( P \right)$ là góc giữa $d$ và hình chiếu $d’$của đường thẳng $d$ trên $\left( P \right)$ (Hình 4$)$, kí hiệu $\left( {d,\left( P \right)} \right)$.

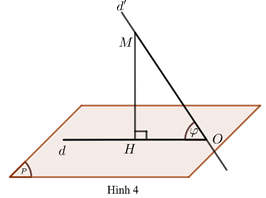Nhận xét: Góc giữa đường thẳng và mặt phẳng có số đo từ $0^\circ $ đến $90^\circ $.

3. Góc nhị diện

• Góc nhị diện là hình gồm hai nửa mặt phẳng có chung bờ; kí hiệu $\left[ {P,d,Q} \right]$ hoặc $\left[ {M,d,N} \right]$, trong đó $\left( P \right),\left( Q \right)$ là hai nửa mặt phẳng có chung bờ là đường thẳng $d$ và $M,N$ là các điểm lần lượt thuộc hai nửa mặt phẳng $\left( P \right),\left( Q \right)$. Đường thẳng $d$ gọi là cạnh của góc nhị diện, mỗi nửa mặt phẳng $\left( P \right),\left( Q \right)$ gọi là một mặt của góc nhị diện.

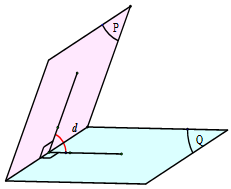
Cho góc nhị diện. Một góc có đỉnh thuộc cạnh của góc nhị diện, hai cạnh của góc đó lần lượt thuộc hai mặt nhị diện và cùng.vuông góc với cạnh của góc nhị diện, được gọi là góc phẳng nhị diện của góc nhị diện đã cho.

• Số đo của một góc phẳng nhị diện được gọi là số đo của góc nhị diện đó.

• Nếu số đo góc phẳng nhị diện bằng $90^\circ $ thì góc nhị diện đó gọi là góc nhị diện vuông.

Nhận xét: Góc nhị diện có số đo từ $0^\circ $ đến $180^\circ $.

III. KHOẢNG CÁCH TRONG KHÔNG GIAN

1. Khoảng cách từ một điểm đến một đường thẳng

Khoảng cách từ điểm $M$ đến đường thẳng $\Delta $ là khoảng cách từ điểm $M$ đến hình chiếu vuông góc $H$ của $M$ trên $\Delta $, kí hiệu $d\left( {M,\Delta } \right)$.

2. Khoảng cách từ một điểm đến một mặt phẳng

Khoảng cách từ điểm $M$ đến mặt phẳng $\left( P \right)$ là khoảng cách từ điểm $M$ đến hình chiếu vuông góc $H$ của $M$ trên $\left( P \right)$, kí hiệu $d\left( {M,\left( P \right)} \right)$.

3. Khoảng cách giữa hai đường thẳng song song

Khoảng cách giữa hai đường thẳng song song $\Delta $ và $\Delta ‘$ là khoảng cách từ một điểm bất kì thuộc đường thẳng này đến đường thẳng kia, kí hiệu $d\left( {\Delta ,\Delta ‘} \right)$.

4. Khoảng cách giữa đường thẳng và mặt phẳng song song

Cho đường thẳng $\Delta $ song song với mặt phẳng $\left( P \right)$. Khoảng cách giữa đường thẳng $\Delta $ và mặt phẳng $\left( P \right)$ là khoảng cách từ một điểm bất kì thuộc đương thẳng $\Delta $ đến mặt phẳng $\left( P \right)$, kí hiệu $d\left( {\Delta ,\left( P \right)} \right)$.

5. Khoảng cách giữa hai mặt phẳng song song

Khoảng cách giữa hai mặt phẳng song song $\left( P \right)$ và $\left( Q \right)$ là khoảng cách từ một điểm bất kì thuộc mặt phẳng này đến mặt phẳng kia, kí hiệu $d\left( {\left( P \right),\left( Q \right)} \right)$.

6. Khoảng cách giữa hai đường chéo nhau

Cho hai đường thẳng $a,b$ chéo nhau.

• Có và chỉ có một đường thẳng $c$ vừa vuông góc, vừa cắt cả hai đường thẳng $a,b$, gọi là đường vuông góc chung của hai đường thẳng đó.

• Đoạn thẳng có hai đầu mút là giao điểm của đường thẳng $c$ với hai đường thẳng $a,b$ gọi là đoạn vuông góc chung của hai đường thẳng đó.

• Độ dài đoạn vuông góc chung của hai đường thẳng $a,b$ gọi là khoảng cách giữa hai đường thẳng đó, kí hiệu $d\left( {a,b} \right)$.

Nhận xét

• Gọi $\left( P \right)$ là mặt phẳng chứa $b$ và song song với $a$, hình chiếu của $a$ trên $\left( P \right)$ là $a’$, giao điểm của $a’$ và $b$ là $K$, hình chiếu của $K$ trên $a$ là $H$ (Hình Ø). Khi đó $HK$ là đoạn vuông góc chung của $a$ và $b$. Ngoài ra, $d\left( {a,b} \right) = HK = d\left( {a,\left( P \right)} \right)$.

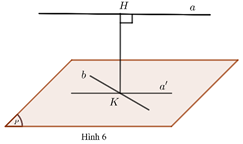
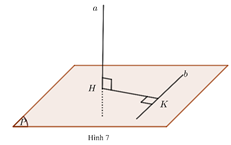
Trong trường hợp đặc biệt $ab$, ta có thể xác định như sau: Gọi $\left( P \right)$ là mặt phẳng chứa $b$ và vuông góc với $a$, giao điểm của $a$ và $\left( P \right)$ là $H$, hình chiếu của $H$ trên $b$ là $K$ (Hình 7 ). Khi đó, $HK$ là đoạn vuông góc chung của $a$ và $b$.

IV. THỂ TÍCH CỦA MỘT SỐ KHỐI ĐA DIỆN

• Công thức tính thể tích của khối lăng trụ: $V = Sh$.

Trong đó $V,S,h$ lần lượt là thể tích, diện tích đáy, chiều cao của khối lăng trụ.

• Công thức tính thể tích của khối chóp: $V = \frac{1}{3}Sh$.

Trong đó $V,S,h$ lần lượt là thể tích, diện tích đáy, chiều cao của khối chóp.

• Công thức tính thế tích của khối chóp cụt đều: $V = \frac{1}{3}h\left( {{S_1} + \sqrt {{S_1}{S_2}} + {S_2}} \right)$.

Trong đó $V,h,{S_1},{S_2}$ lần lượt là thể tích, chiều cao, diện tích hai đáy của khối chóp cut đều.

B. MỘT SỐ VÍ DỤ

Dạng 1. Câu trắc nghiệm nhiều phương án lựa chọn

Mỗi câu hỏi thí sinh chi chọn một phuơng án.

Ví du 1. Cho hai đường thẳng $a$ và $b$ chéo nhau. Có bao nhiêu đường thẳng vừa vuông góc vừa cắt cả hai đường thẳng $a$ và $b$ ?

A. 0. B. 1. C. 2. D. Vô số.

Lời giải

Có và chỉ có một đường thẳng $c$ vừa vuông góc, vừa cắt cả hai đường thẳng $a,b$. Chọn B.

Ví du 2. Cho hình chóp $S.ABC$ có $SA \bot \left( {ABC} \right)$, $SB \bot BC$. Trong tất cả các mặt của hình chóp $S.ABC$, có bao nhiêu mặt là tam giác vuông?

A. 1. B. 2. C. 3. D. 4.

Lời giải

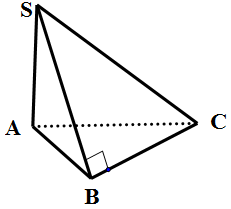
Vì $SA \bot \left( {ABC} \right)$ nên $SA \bot AB,SA \bot AC,SA \bot BC$.

Mà $BC \bot SB$ nên $BC \bot \left( {SAB} \right)$, suy ra $BC \bot BA$.

Vậy bốn tam giác $SAB,SAC,SBC,ABC$ đều là tam giác vuông. Chọn D.

Dạng 2. Câu trắc nghiệm đúng sai

Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoăc sai.

Ví du 3. Cho hình chóp $S.ABC$ có $SA \bot \left( {ABC} \right),AB \bot BC$, $SA = AB = a,AC = a\sqrt 3 $.

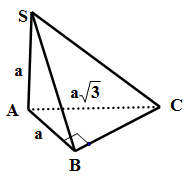
a) $BC \bot \left( {SAB} \right)$.

b) Góc giữa đường thẳng $SC$ và mặt phẳng $\left( {SAB} \right)$ bằng $\widehat {CSA}$.

c) $tan\widehat {CSB} = 1$.

d) Góc giữa đường thẳng $SC$ và mặt phẳng $\left( {SAB} \right)$ bằng ${60^0}$.

Lời giải

a) Vì $SA \bot \left( {ABC} \right)$ nên $SA \bot BC$. Mà $BC \bot AB$ nên $BC \bot \left( {SAB} \right)$. $ \Rightarrow $a) Đ

b) Vì $$$BC \bot (SAB)$ nên góc giữa đường thẳng $SC$ và mặt phẳng $\left( {SAB} \right)$ bằng $\widehat {CSB}$. $ \Rightarrow $b) S

c) Tam giác $ABC$ vuông tại $B$ có $BC = \sqrt {A{C^2} – A{B^2}} = a\sqrt 2 $, tam giác $SAB$ vuông tại $A$ có $SB = \sqrt {S{A^2} + A{B^2}} = a\sqrt 2 $.

Xét tam giác $SBC$ vuông tại $B$ có $tan\widehat {CSB} = \frac{{BC}}{{SB}} = \frac{{a\sqrt 2 }}{{a\sqrt 2 }} = 1$ $ \Rightarrow $c) Đ

d) Vì $tan\widehat {CSB} = 1$nên $\widehat {CSB} = {45^ \circ }$. Vậy góc giữa đường thẳng $SC$ và mặt phẳng $\left( {SAB} \right)$ bằng ${45^ \circ }$. $ \Rightarrow $d) S

Đáp án: a) Đ, b) S, c) Đ, d) S.

Ví du 4. Cho hình lăng trụ tam giác đều $ABC.A’B’C’$ có $AB = a,AA’ = 2a$.

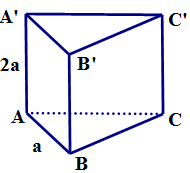
a) Khoảng cách giữa hai mặt phẳng $\left( {ABC} \right)$ và $\left( {A’B’C’} \right)$ bằng $2a$.

b) Khoảng cách giữa đường thẳng $B’C’$ và mặt phẳng $\left( {ABC} \right)$ bằng $a$.

c) Khoảng cách từ điểṃ $A$ đến mặt phẳng $\left( {BCC’B’} \right)$ bằng $a$.

d) Khoảng cách giữa hai đường thẳng $AA’$ và $BC$ bằng $a\sqrt 3 $.

Lời giải

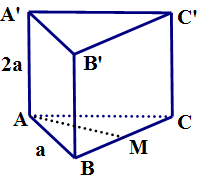
a) Vì $\left( {ABC} \right)//\left( {A’B’C’} \right),AA’ \bot \left( {ABC} \right),AA’ \bot \left( {A’B’C’} \right)$ nên$d\left( {\left( {ABC} \right),\left( {A’B’C’} \right)} \right) = d\left( {A,\left( {A’B’C’} \right)} \right) = AA’ = 2a$. $ \Rightarrow $a) Đúng

b) Vì $B’C’//\left( {ABC} \right),BB’ \bot \left( {ABC} \right)$ nên $d\left( {B’C’,\left( {ABC} \right)} \right) = d\left( {B’,\left( {ABC} \right)} \right) = BB’ = 2a.$$ \Rightarrow $b) Sai

c) Lấy $M$ là trung điểm của $BC$. Do tam giác $ABC$ đều nên $AM \bot BC$. Mà $\left( {ABC} \right) \bot \left( {BCC’B’} \right)$ nên $AM \bot \left( {BCC’B’} \right)$.

Do đó $d\left( {A,\left( {BC{C^\prime }{B^\prime }} \right)} \right) = AM = \frac{{a\sqrt 3 }}{2}$.

d) Vì $AM \bot A{A^\prime },AM \bot BC$ nên $AM$là đoạn vuông góc chung của $A{A^\prime }$ và $BC$. Do đó $d\left( {A{A^\prime },BC} \right) = AM = \frac{{a\sqrt 3 }}{2}$.

Dạng 3: Câu trắc nghiệm trả lời ngắn

Ví dụ 5: Để chuẩn bị cho hoạt động cắm trại, bạn An tìm hiểu các mẫu lều cắm trại có kích thước như trong Hình 11.

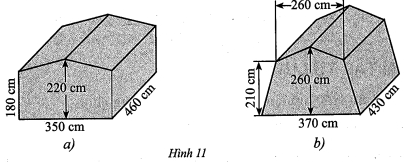
Bạn An muốn biết thể tích chênh lệch của hai lều nên thực hiện tính ${V_1} – {V_2}$, trong đó ${V_1},{V_2}$ lần lượt là thể tích của mẫu lều cắm trại ở Hình 11a, 11b. Giá trị của ${V_1} – {V_2}$ bằng bao nhiêu decimét khối (làm tròn kết quả đến hàng đơn vị)?

Lời giải

Cả hai lều đều có dạng khối lăng trụ đứng ngũ giác.

– Xét khối lăng trụ ở Hình 11a. Chia mặt đáy thành hai phần bao gồm: hình chữ nhật có chiều rộng $180\;cm$, chiều dài $350\;cm$; tam giác cân có cạnh đáy dài $350\;cm$, chiều cao $40\;cm$như Hình 12.

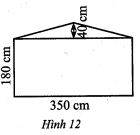
Diện tích mặt đáy của lăng trụ đó là:

${S_1} = 180 \cdot 350 + \frac{1}{2} \cdot 40 \cdot 350 = 70000\left( {\;c{m^2}} \right).$

Vậy thể tích của khối lăng trụ ngũ giác đó là:

${V_1} = {S_1} \cdot {h_1} = 70000 \cdot 460 = 32200000\left( {\;c{m^3}} \right)$

– Xét khối lăng trụ ở Hình 11b. Chia mặt đáy thành hai phần bao gồm: hình thang cân có đáy lớn dài $370\;cm$, đáy nhỏ dài $260\;cm$, chiều cao $210\;cm$; tam giác cân có cạnh đáy dài $260\;cm$, chiều cao $50\;cm$như Hình 13.

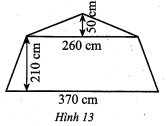
Diện tích mặt đáy của lăng trụ đó là:

${S_2} = \frac{1}{2}(370 + 260) \cdot 210 + \frac{1}{2} \cdot 260 \cdot 50 = 72650\left( {\;c{m^2}} \right).$

Vậy thể tích của khối lăng trụ ngũ giác đó là:

${V_2} = {S_2} \cdot {h_2} = 72650.430 = 31239500\left( {\;c{m^3}} \right).$

Do đó ${V_1} – {V_2} = 960500\left( {\;c{m^3}} \right) \approx 961\left( {d{m^3}} \right)$.

C. BÀI TẬP LUYỆN TẬP

Dạng 1: Câu hỏi trắc nghiệm nhiều phương án lựa chọn

Mỗi câu thí sinh chỉ chọn một phương án.

Câu 1. [MĐ1] Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông và $SD \bot (ABCD)$. Đường thẳng $AC$ vuông góc với mặt phẳng nào trong các mặt phẳng sau?

A. $(SAB)$. B. $(SAD)$. C. $(SCD)$. D. $(SBD)$.

Lời giải

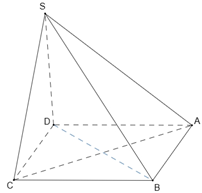
Chọn D

Do $\left\{ \begin{gathered}
SD \bot AC \hfill \\
BD \bot AC \hfill \\
\end{gathered} \right. \Rightarrow AC \bot \left( {SBD} \right)$

Câu 2. [MĐ2] Cho hình chóp tứ giác đều $S.ABCD$, $O$ là giao điểm của $AC$ và $BD$,$M$ là trung điểm $AD$. Góc nào sau đây là góc phẳng nhị diện của góc nhị diện$[B,AD,S]$?

A. $\widehat {SAB}$. B. $\widehat {SDB}$. C. $\widehat {SMO}$. D. $\widehat {SMB}$.

Lời giải

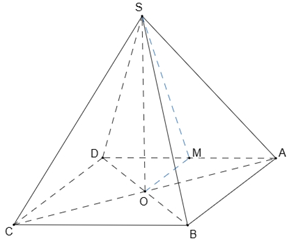
Chọn C

$O,M$lần lượt là trung điểm của$BD,AD$nên song song với $AB$mà $AB \bot AD \Rightarrow OM \bot AD$

$S.ABCD$đều $ \Rightarrow SAD$cân tại $S$$ \Rightarrow SM \bot AD$

Có: $\left\{ \begin{gathered}
OM \bot AD \hfill \\
SM \bot AD \hfill \\
\end{gathered} \right.$$ \Rightarrow \left[ {B,AD,S} \right] = \widehat {SMO}$

Câu 3. [MĐ1] Cho đường thẳng $a$ và hai mặt phẳng $(P),(Q)$ vuông góc với nhau. Phát biểu nào sau đây là đúng về đường thẳng $a$ ?

A. Đường thẳng $a$ nằm trong mặt phẳng $(P)$ thì vuông góc với mọi đường thẳng nằm trong $(Q)$.

B. Đường thẳng $a$ nằm trong mặt phẳng $(P)$ thì vuông góc với giao tuyến của $(P)$ và $(Q)$.

C. Đường thẳng $a$ vuông góc với mặt phẳng $(Q)$ thì $a$ nằm trong mặt phẳng $(P)$

D. Đường thẳng $a$ nằm trong mặt phẳng $(P)$ và vuông góc với giao tuyến của $(P),(Q)$ thì $a$ vuông góc với mặt phẳng $(Q)$.

Lời giải

Chọn D

A. Sai, vì chỉ khi $a$vuông góc với giao tuyến của $\left( P \right),\left( Q \right)$ thì $a$mới vuông góc với mọi đường thẳng nằm trong $\left( Q \right)$

B. Sai, vì $a$có thể song song với giao tuyến của $\left( P \right),\left( Q \right)$

C. Sai, vì $a$có thể song song với $\left( P \right)$

D. Đúng (theo SGK)

Câu 4. [MĐ2] Cho hình lập phương $ABCD.A’B’C’D’$. Góc giữa hai đường thẳng $AC$ và $A’B$ bằng:

A. $30^\circ $. B. $45^\circ $. C. $60^\circ $. D. $90^\circ $.

Lời giải

Chọn C

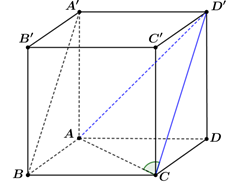
Do $A’B\,//\,D’C$ nên góc giữa hai đường thẳng $AC$ và $A’B$ bằng góc giữa hai đường thẳng $AC$ và $D’C$.

Xét tam giác $ACD’$, ta có $AC = AD’ = CD’$ (cùng là đường chéo của 3 hình vuông bằng nhau) nên tam giác $ACD’$ đều. Do đó $\widehat {ACD’} = 60^\circ $.

Vậy, $\left( {AC,A’B} \right) = \left( {AC,D’C} \right) = \widehat {ACD’} = 60^\circ .$

Câu 5. [MĐ3] Cho hình chóp tứ giác đều $S.ABCD$ có tất cả các cạnh đều bằng $a$. Góc giữa đường thẳng $SA$ với mặt phẳng $\left( {ABCD} \right)$ bằng:

A. $30^\circ $. B. $45^\circ $. C. $60^\circ $. D. $90^\circ $.

Lời giải

Chọn B

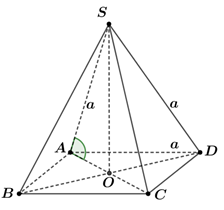
Gọi $O$ là giao điểm của hai đường chéo $AO$ và $BD$.

Do $S.ABCD$ là hình chóp đều nên $SO \bot \left( {ABCD} \right)$. Khi đó hình chiếu của $SA$ lên mặt phẳng $\left( {ABCD} \right)$ là $OA$.

Do đó, góc giữa đường thẳng $SA$ và $\left( {ABCD} \right)$ bằng góc giữa hai đường thẳng $SA$ và $OA$.

Xét tam giác $SAO$ vuông tại $O$, ta có $OA = \frac{{a\sqrt 2 }}{2}$, $SA = a$.

$\cos \widehat {SAO} = \frac{{OA}}{{SA}} = \frac{{\frac{{a\sqrt 2 }}{2}}}{a} = \frac{{\sqrt 2 }}{2}$.

Do đó $\widehat {SAO} = 45^\circ $.

Vậy, $\left( {SA,\left( {ABCD} \right)} \right) = \left( {SA,AO} \right) = \widehat {SAO} = 45^\circ .$

Câu 6. [MĐ2] Cho hình chóp tứ giác đều $S.ABCD$ có tất cả các cạnh đều bằng $a$. Khoảng cách từ đỉnh đến mặt đáy bằng:

A. $a$. B. $\frac{{a\sqrt 2 }}{2}$. C. $a\sqrt 2 $. D. $\frac{a}{2}$.

Lời giải

Chọn B

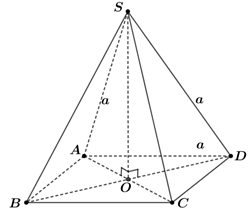
Gọi $O$ là giao điểm của hai đường chéo $AO$ và $BD$. Do $S.ABCD$ là hình chóp đều nên $SO \bot \left( {ABCD} \right)$. Khi đó khoảng cách từ đỉnh đến mặt đáy bằng độ dài đoạn $SO$.

Xét tam giác $SAO$ vuông tại $O$, ta có $OA = \frac{{a\sqrt 2 }}{2}$, $SA = a$.

Áp dụng định lí Pitago, ta được

$SO = \sqrt {S{A^2} – A{O^2}} = \sqrt {{a^2} – {{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}} = \frac{{a\sqrt 2 }}{2}$.

Vậy, $d\left( {S,\left( {ABCD} \right)} \right) = SA = \frac{{a\sqrt 2 }}{2}$.

Câu 7. [MĐ3] Cho hình hộp chữ nhật $ABCD.A’B’C’D’$ có $AA’ = 2a$, $A’B’ = 2a$, $A’D’ = a$. Khoảng cách từ đường thẳng $AA’$ đến mặt phẳng $\left( {BDD’B’} \right)$ bằng:

A. $\frac{{2a\sqrt 5 }}{5}$. B. $a\sqrt 2 $. C. $\frac{a}{2}$. D. $\frac{{a\sqrt 2 }}{2}$.

Lời giải

Chọn A

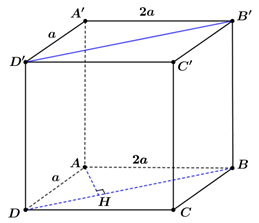
Gọi $H$ là hình chiếu của $A$ trên $BD$.

Do $AA’\,//\,\left( {BDD’B’} \right)$ nên khoảng cách từ đường thẳng $AA’$ đến mặt phẳng $\left( {BDD’B’} \right)$ bằng khoảng cách từ điểm $A$ đến mặt phẳng $\left( {BDD’B’} \right)$.

Ta có $\left\{ {\begin{array}{*{20}{c}}
{AH \bot BD} \\
{AH \bot BB’}
\end{array}} \right. \Rightarrow AH\, \bot \,\left( {BDD’B’} \right)$.

Do đó $d\left( {AA’,\left( {BDD’B’} \right)} \right) = d\left( {A,\left( {BDD’B’} \right)} \right) = AH$.

Xét tam giác $ABD$ vuông tại $A$, ta có $AH$ là đường cao.

$AH = \frac{1}{{\sqrt {\frac{1}{{A{B^2}}} + \frac{1}{{A{D^2}}}} }}$$ = \frac{1}{{\sqrt {\frac{1}{{{{\left( {2a} \right)}^2}}} + \frac{1}{{{a^2}}}} }} = \frac{{2a\sqrt 5 }}{5}$.

Vậy, $d\left( {AA’,\left( {BDD’B’} \right)} \right) = d\left( {A,\left( {BDD’B’} \right)} \right)$

$ = AH = \frac{{2a\sqrt 5 }}{5}$.

Câu 8. [MĐ2] Cho khối chóp có diện tích đáy là $3{a^2}$ và chiều cao là $a$. Thể tích của khối chóp đó bằng:

A. $3{a^3}$. B. ${a^3}$. C. $\frac{{{a^3}}}{3}$. D. $9{a^3}$.

Lời giải

Chọn B

Ta có thể tích khối chóp $V = \frac{1}{3}Bh = \frac{1}{3} \cdot 3{a^2} \cdot a = {a^3}$.

Câu 9. [MĐ1] Cho khối lăng trụ có diện tích đáy là $3{a^2}$ và chiều cao là $a$. Thể tích của khối lăng trụ đó bằng:

A. $3{a^3}$. B. ${a^3}$. C. $\frac{{{a^3}}}{3}$. D. $9{a^3}$.

Lời giải

Chọn A

Ta có thể tích của khối lăng trụ: $V = Bh = 3{a^2} \cdot a = 3{a^3}$.

Dạng 2: Trắc nghiệm đúng-sai

Trong mỗi ý a) b) c) d) ở mỗi câu thí sinh chọn đúng hoặc sai.

Câu 10. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, $SAB$ là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng $\left( {ABCD} \right)$. Gọi $H$ là trung điểm của $AB$.

a) $SH \bot \left( {ABCD} \right)$.

b) Góc giữa đường thẳng $SC$ và mặt phẳng $\left( {ABCD} \right)$ bằng $\widehat {SCA}$.

c) $CH = \frac{{a\sqrt 5 }}{2}$.

d) Gọi $\alpha $ là góc giữa đường thẳng $SC$ và mặt phẳng $\left( {ABCD} \right)$. Giá trị $cos\alpha $ bằng $\frac{3}{4}$.

Lời giải

Ý	a)	b)	c)	d)
Kết quả	Đ	S	Đ	S

a) Vì $\left( {SAB} \right) \bot \left( {ABCD} \right)$ và $SH \bot AB$ nên $SH \bot \left( {ABCD} \right)$. Suy ra câu a) Đúng.

b) Khi đó, $\left( {SC,\left( {ABCD} \right)} \right) = \left( {SC,HC} \right) = \widehat {SCH} = \alpha $. Suy ra câu b) Sai.

c) Xét tam giác vuông $CBH$ có $CH = \sqrt {{{\left( {\frac{a}{2}} \right)}^2} + {a^2}} = \frac{{a\sqrt 5 }}{2}.$ Suy ra câu c) Đúng.

d) Xét tam giác đều $SAB$ có $SH = \frac{{a\sqrt 3 }}{2}$. Tam giác vuông $SHC$ có

$SC = \sqrt {{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2} + {{\left( {\frac{{a\sqrt 5 }}{2}} \right)}^2}} = a\sqrt 2 $ và $cos\alpha = cos\widehat {SCH} = \frac{{CH}}{{SC}} = \frac{{\frac{{a\sqrt 5 }}{2}}}{{a\sqrt 2 }} = \frac{{\sqrt {10} }}{4}$.

Suy ra câu d) Sai.

Câu 11. Cho hình chóp $S.ABCD$ có $SA \bot \left( {ABCD} \right),ABCD$ là hình thoi cạnh $a,AC = a$, $SA = \frac{a}{2}$. Gọi $H$ là hình chiếu của $S$ trên cạnh $CD$.

a) $AH \bot CD$.

b) $AH = \frac{{a\sqrt 3 }}{2}$.

c) Góc $SDC$ là góc phẳng nhị diện của góc nhị diện $\left[ {S,CD,A} \right]$.

d) Số đo của góc nhị diện $\left[ {S,CD,A} \right]$ bằng ${30^ \circ }$.

Lời giải:

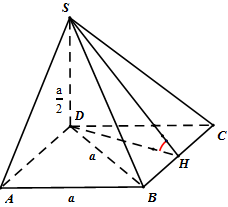
Vì $SA \bot \left( {ABCD} \right)$ nên $SA \bot CD$. Mà $SH \bot CD$ nên $CD \bot \left( {SHA} \right)$.

Do đó, $CD \bot AH$ và góc $\widehat {SHA}$ là góc phẳng nhị diện của góc nhị diện $\left[ {S,CD,A} \right]$.

Xét tam giác $ACD$ đều cạnh $a$ có $AH = \frac{{a\sqrt 3 }}{2}$. Tam giác $SAH$ vuông có

$tan\widehat {SHA} = \frac{{SA}}{{AH}} = \frac{{\frac{a}{2}}}{{\frac{{a\sqrt 3 }}{2}}} = \frac{{\sqrt 3 }}{3}.$

Suy ra $\widehat {SHA} = {30^ \circ }$. Vậy số đo của góc nhị diện $\left[ {S,CD,A} \right]$ bằng ${30^ \circ }$.

Đáp án: a) Đ, b) Đ, c) S, d) Đ.

Câu 12. Cho hình lâp phương $ABCD.A’B’C’D’$.

a) Góc giữa hai đường thẳng $AB$ và $A’C’$ bằng ${45^ \circ }$.

b) Gọi $\alpha $ là góc giữa đường thẳng $A’C$ và mặt phẳng $\left( {A’B’C’D} \right.$). Giá trị $tan\alpha $ bằng $\sqrt 2 $.

c) Gọi $\beta $ là số đo của góc nhị diện $\left[ {B,A’C’,B’} \right]$. Giá trị $tan\beta $ bằng $\frac{{\sqrt 2 }}{2}$.

d) Số đo của góc nhị diện $\left[ {B’,A’C,D’} \right]$ bằng ${120^ \circ }$.

Lời giải:

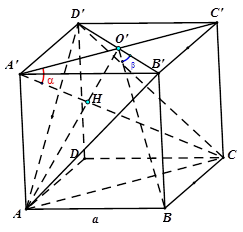
Vì $AB//A’B’$nên

$\left( {AB,A’C’} \right) = \left( {A’B’,A’C’} \right) = \widehat {B’A’C’} = {45^ \circ }$.

Vậy góc giữa hai đường thẳng $AB$ và $A’C’$ bằng ${45^ \circ }$. Vì $CC’ \bot \left( {A’B’C’D’} \right)$ nên $\left( {A’C,\left( {A’B’C’D’} \right)} \right) = \widehat {C’A’C} = \alpha $.

Xét tam giác vuông $A’C’C$ có $tan\widehat {C’A’C} = \frac{{C’C}}{{C’A’}} = \frac{a}{{a\sqrt 2 }} = \frac{{\sqrt 2 }}{2}.$

Suy ra $tan\alpha = tan\widehat {C’A’C} = \frac{{\sqrt 2 }}{2}$.

Gọi $O’$ ‘à giao điểm của $A’C’$ và $B’D’$.

Vì tam giác $A’BC’$ đều nên $BO’ \bot A’C’$.

Mà $B’O’ \bot A’C’$.

Suy ra số đo góc nhị diện $\left[ {B,A’C’,B’} \right]$ bằng $\widehat {B’O’B} = \beta $.

Xét tam giác vuông $B’O’B$ có $tan\widehat {B’O’B} = \frac{{B’B}}{{B’O’}} = \frac{a}{{\frac{{a\sqrt 2 }}{2}}} = \sqrt 2 $.

Vậy $tan\beta = \sqrt 2 $.

Vì $B’D’ \bot \left( {A’C’C} \right)$ nên $B’D’ \bot A’C$. Do $AD’ \bot \left( {A’DC} \right)$ nên $AD’ \bot A’C$.

Suy ra $A’C \bot \left( {AB’D’} \right)$. Gọi $H$ là giao điểm của $A’C$ và $\left( {AB’D’} \right)$.

Khi đó, số đo góc nhị diện $\left[ {B’,A’C,D’} \right]$ bằng $\widehat {B’HD’}$.

Vi tứ diện $A’D’B’A$ có $A’B’ = A’D’ = A’A$ mà $A’H \bot \left( {AB’D’} \right)$ nên $HA = HB’ = HD’$, suy ra $H$ là tâm đường tròn ngoại tiếp tam giác đều $AB’D’$.

Suy ra $\widehat {B’HD’} = {120^ \circ }$.

Vậy số đo góc nhị diện $\left[ {B’,A’C,D’} \right]$ bằng ${120^ \circ }$.

Đáp án: a) Đ, b) S, c) S, d) Đ.

Câu 13. Cho hình lăng trụ $ABC.A’B’C’$ có $\left( {A’ABB’} \right) \bot \left( {ABC} \right),AA’ = 2a,\widehat {A’AB} = {60^ \circ }$. Gọi $H$ là hình chiếu của $A’$ trên $AB$.

a) Khoảng cách giữa hai đường thẳng chéo nhau $A’C’$ và $AB$ bằng khoảng cách giữa hai mặt phẳng $\left( {A’B’C’} \right)$ và $\left( {ABC} \right)$.

b) $A’H$ không phải là đoạn vuông góc chung của hai đường thẳng chéo nhau $A’C’$ ‘và $AB$.

c) $A’H = a\sqrt 3 $.

d) Khoảng cách giữa hai đường thẳng chéo nhau $A’C’$ và $AB$ bằng $a$.

Lời giải:

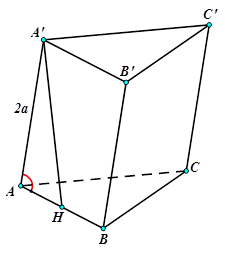
Xét tam giác $A’AH$ vuông có $A’H = A’Asin{60^ \circ } = a\sqrt 3 .$ Vậy $d\left( {A’C’,AB} \right) = a\sqrt 3 $.

Đáp án: a) Đ, b) S, c) Đ, d) ${\mathbf{S}}$.

Câu 14. Cho hình lập phương $ABCD.A’B’C’D’$ có cạnh bằng $a$.

a) Khoảng cách giữa hai đường thẳng $AB$ và $DD’$ bằng $a$.

b) Khoảng cách từ điểm $B$ đến mặt phẳng $\left( {ACC’A’} \right)$ bằng $\frac{{a\sqrt 2 }}{2}$.

c) Khoảng cách từ điểm $B$ đến đường thằng $A’C’$ bằng $\frac{{a\sqrt 3 }}{2}$.

d) Khoảng cách giữa hai đường thẳng $BD$ và $A’C$ bằng $\frac{a}{2}$.

Lời giải:

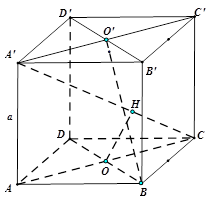
Gọi $O$ là giao điểm của $AC$ và $BD$, O’ là giao điểm của $A’C’$ và $B’D’$

Vì $AB \bot AD,$ $DD’ \bot AD$nên $d\left( {AB,DD’} \right) = AD = a.$

Vi $\left. {BO \bot {{\left( {ACC’A} \right)}’}} \right)$ nên $d\left( {B,\left( {ACC’A’} \right)} \right) = BO = \frac{{a\sqrt 2 }}{2}.$

Vi $A’C’ \bot B’O’,$ $A’C’ \bot BB’$ nên $A’C’ \bot BO’$.

Suy ra $d\left( {B,A’C’} \right) = BO’$.

Xét tam giác vuông $BB’O’$ có $BO’ = \sqrt {{{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2} + {a^2}} = \frac{{a\sqrt 6 }}{2}$.

Vậy $d\left( {B,A’C’} \right) = \frac{{a\sqrt 6 }}{2}$.

Gọi $H$ là hình chiếu của $O$ trên $A’C$. Vì $BD \bot \left( {ACA’} \right)$ nên $BD \bot OH$. Do đó, $OH$ là đoạn vuông góc chung của $BD$ và $A’C$.

Vì hai tam giác $CA’A$ và $COH$ đồng dạng với nhau nên $\frac{{OH}}{{A’A}} = \frac{{CO}}{{CA’}}$.

Suy ra $OH = \frac{{A’A \cdot CO}}{{CA’}} = \frac{{a \cdot \frac{{a\sqrt 2 }}{2}}}{{a\sqrt 3 }} = \frac{{a\sqrt 6 }}{6}$.

Vậy $d\left( {BD,A’C} \right) = \frac{{a\sqrt 6 }}{6}$.

Đáp án: a) Đ, b) Đ  c) S, d) S.

Câu 15. Cho hình lăng trụ $ABCD.A’B’C’D’$ có đáy là hình thoi cạnh $3a,\widehat {ABC} = {60^ \circ }$, $AA’ = 2a$. Đỉnh $A’$ cách đều ba đỉnh $A,B,C$. Gọi $G$ là trọng tâm của tam giác $ABC$.

a) $A’G$ là đường cao của hình lăng trư $ABCD.A’B’C’D’$.

b) Độ dài đường cao của hình lăng trụ $ABCD.A’B’C’D’$ bằng $a\sqrt 3 $.

c) Diện tích hình thoi $ABCD$ bằng $\frac{{9{a^2}\sqrt 3 }}{2}$.

d) Thể tích của khối lăng trụ $ABCD.A’B’C’D’$ bằng $\frac{{9{a^3}\sqrt 3 }}{2}$.

Lời giải:

a) Đúng.

Do $A’B = A’C = A’A$ nên hình chiếu của $A’$ lên mặt phẳng $\left( {ABC} \right)$ là tâm đường tròn ngoại tiếp tam giác $ABC$.

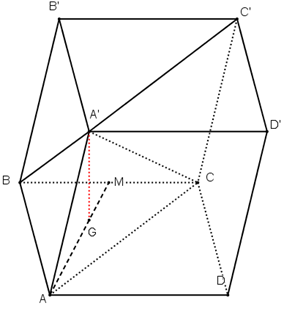
Do tam giác $ABC$ là tam giác đều nên trọng tâm $G$ cũng là tâm đường tròn ngoại tiếp.

Vậy $A’G \bot \left( {ABCD} \right)$.

Do đó $A’G$ là đường cao của hình hộp $ABCD.A’B’C’D’$.

b) Sai. Ta có tam giác $ABC$ có $AB = BC$ và $\widehat {ABC} = {60^ \circ }$ nên $ABC$ là tam giác đều cạnh $3a$, suy ra $AG = a\sqrt 3 $.

Tam giác $A’GA$ vuông tại $G$ và $AA’ = 2a$ nên $A’G = a$.

c) Đúng. Ta có ${S_{ABCD}} = 2{S_{ABC}} = 2.\frac{{{{\left( {3a} \right)}^2}\sqrt 3 }}{4} = \frac{{9{a^2}\sqrt 3 }}{2}$

d) Đúng. Thể tích khối lăng trụ là $V = A’G.{S_{ABCD}} = \frac{{9{a^3}\sqrt 3 }}{2}$

Dạng 3. Câu trắc nghiệm trả lời ngắn

Câu 16. Cho hình chóp tứ giác đều $S.ABCD$ có cạnh đáy bằng $a$, cạnh bên bằng $2a\sqrt 2 $. Gọi $M$ là trung điểm của $SA$. Góc giữa đường thẳng $BM$ với mặt phẳng $\left( {ABCD} \right)$ bằng bao nhiêu độ?

Lời giải:

Gọi $O$ là giao điểm $AC$ và $BD,I$ là trung điểm của $AO$.

Vì $S.ABCD$ là hình chóp tứ giác đều nên $SO \bot \left( {ABCD} \right)$.

Do $MI//SO$ nên $MI \bot \left( {ABCD} \right)$;

Suy ra $\left( {BM,\left( {ABCD} \right)} \right) = \widehat {MBI}$.

Xét tam giác $SAO$ vuông có $SO = \sqrt {S{A^2} – O{A^2}} = \frac{{a\sqrt {30} }}{2}.$

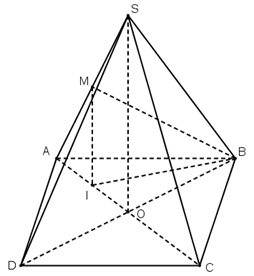
Suy ra $MI = \frac{1}{2}SO = \frac{{a\sqrt {30} }}{4}$.

Xét tam giác vuông $BIO$ có $BI = \sqrt {O{B^2} + O{I^2}} = \sqrt {O{B^2} + {{\frac{{OB}}{4}}^2}} = \frac{{a\sqrt {10} }}{4}$.

Khi đó, $tan\widehat {MBI} = \frac{{MI}}{{BI}} = \frac{{\frac{{a\sqrt {30} }}{4}}}{{\frac{{a\sqrt {10} }}{4}}} = \sqrt 3 $. Suy ra $\widehat {MBI} = {60^ \circ }$.

Vậy góc giữa đường thẳng $BM$ và mặt phẳng $\left( {ABCD} \right)$ là ${60^ \circ }$.

Câu 17. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi cạnh $a$, $\widehat {ABC} = {60^ \circ }$. Gọi $O$ là giao điểm của $AC$ và $BD$. Biết rằng $SO \bot \left( {ABCD} \right)$, $SO = \frac{{3a}}{4}$. Khoảng cách từ $O$ đến mặt phẳng $\left( {SCD} \right)$ bằng $\frac{{ma}}{n}$ với $\frac{m}{n}$ là phân số tối giản, $m > 0,n > 0$. Giá trị $m + n$ bằng bao nhiêu?

Lời giải:

Gọi $I$ là hình chiếu của $O$ trên $CD$. $H$ là hình chiếu của $O$ trên $SI$.

Thấy rằng $CD \bot \left( {SOI} \right)$ nên $CD \bot OH$.

Mà $OH \bot SI$ nên $OH \bot \left( {SCD} \right)$. Suy ra $d\left( {O,\left( {SCD} \right)} \right) = OH$.

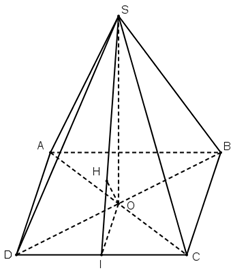
Vì $AB = BC$, $\widehat {ABC} = {60^ \circ }$ nên tam giác $ABC$ đều.

Suy ra $OB = OD = \frac{{a\sqrt 3 }}{2}$, $OA = OC = \frac{a}{2}$.

Xét tam giác vuông $DOC$ có $OI = \frac{{OC.OD}}{{CD}} = \frac{{a\sqrt 3 }}{4}.$

Xét tam giác vuông $SOI$ có $SI = \sqrt {{{\left( {\frac{{3a}}{4}} \right)}^2} + {{\left( {\frac{{a\sqrt 3 }}{4}} \right)}^2}} = \frac{{a\sqrt 3 }}{2}$.

Do đó $\;OH = \frac{{SO.OI}}{{SI}} = \frac{{3a}}{8}$.

Suy ra $\frac{m}{n} = \frac{3}{8}$. Vậy $m + n = 3 + 8 = 11$.

Câu 18. Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh $a$, $SA \bot \left( {ABCD} \right)$ và số đo của góc nhị diện $\left[ {S,BC,A} \right]$ bằng ${60^ \circ }$. Khoảng cách giữa hai đường thẳng $SC$ và $BD$ bằng $\frac{{a\sqrt {30} }}{n}$. Tìm giá trị của $n$.

Lời giải

Vì $BC \bot SA,BC \bot AB$ nên $BC \bot SB$.

Suy ra góc $SBA$ bằng số đo của góc nhị diện $\left[ {S,BC,A} \right]$, tức là $\widehat {SBA} = {60^ \circ }$.

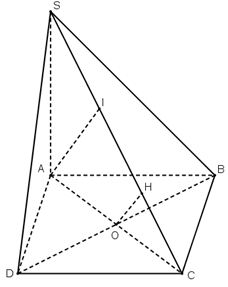
Xét tam giác vuông $SAB$ có $SA = a.tan{60^ \circ } = a\sqrt 3 .$

Gọi $H$ là hình chiếu của $O$ trên $SC$. Vì $BD \bot \left( {SAC} \right)$ nên $OH \bot BD$. Suy ra $OH$ là đoạn vuông góc chung của $BD$ và $SC$.

Gọi $I$ là hình chiếu của $A$ trên $SC$.

Xét tam giác vuông $SAC$ có $AI = \frac{{AC.AS}}{{SC}} = \frac{{a\sqrt {30} }}{5}$.

Ngoài ra, vì $OH//AI$ nên $\frac{{OH}}{{AI}} = \frac{{OC}}{{CA}} = \frac{1}{2}$, suy ra $OH = \frac{1}{2} \cdot \frac{{a\sqrt {30} }}{5} = \frac{{a\sqrt {30} }}{{10}}$. Vậy $n = 10$.

Câu 19. Người ta cần xây dựng công trình đê đề ngăn nước lũ của sông. Mặt cắt của đê được thiết kế với số đo như trong hình vẽ. Tồng thể tích vật liệu cần dùng để xây dựng đoạn đê đó bằng bao nhiêu mét khối (làm tròn kết quả đến hàng đơn vị)? Biết rằng đoạn đê thẳng và dài $100\;m$.

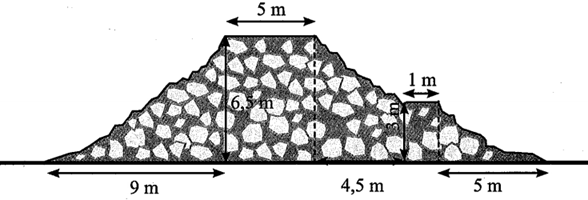
Lời giải

Chia mặt cắt đoạn đê thành các hình tam giác vuông, hình chữ nhật, hình thang như hình vẽ sau.

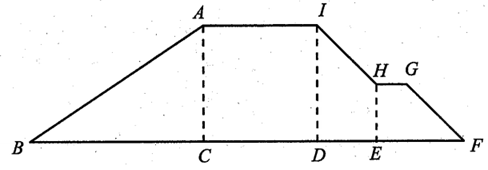
Đoạn đê được ghép bởi bốn khối lăng trụ đứng có cùng chiều cao $100\;m$ và có đáy lần lượt là tam giác vuông $ABC$, hình chữ nhật $ACDI$, các hình thang vuông $DEHI$ và $EFGH$.

Theo giả thiết, ta có:

• Tam giác vuông $ABC$ có kích thước hai cạnh góc vuông là $9$m và $6,5$ m

• Hình chữ nhật $ACDI$ có hai kích thước là $5$ m và $6,5$ m

• Hình thang vuông $DEHI$ có đáy lớn dài $6,5$ m đáy nhỏ dài $3$ m và chiều cao $4,5$ m.

• Hình thang vuông $EFGH$ có đáy lớn đài $6$ m, đáy nhỏ dài $1$ m và chiều cao $3$ m.

Thề tích của khối lăng trụ đứng có đáy là tam giác vuông $ABC$ bằng:

1. ${V_1} = \left( {\frac{1}{2} \cdot 9 \cdot 6,5} \right) \cdot 100 = 2925\left( {\;{m^3}} \right).$

Thề tích của khối lăng trụ đứng có đáy là hình chữ nhật $ACDI$ bằng:

2. ${V_2} = \left( {5 \cdot 6,5} \right) \cdot 100 = 3250\left( {\;{m^3}} \right).$

Thể tích của khối lăng trụ đứng có đáy là hình thang vuông $DEHI$ bằng:

3. ${V_3} = \frac{1}{2}\left( {6,5 + 3} \right) \cdot 4,5 \cdot 100 = 2137,5\left( {\;{m^3}} \right).$

Thể tích của khối lăng trụ đứng có đáy là hình thang vuông $DEHI$ bằng:

4. ${V_4} = \frac{1}{2}\left( {6 + 1} \right) \cdot 3 \cdot 100 = 1050\left( {\;{m^3}} \right).$

Vậy thể tích vật liệu cần dùng để xây dựng đoạn đê đó bằng:

5. $V = {V_1} + {V_2} + {V_3} + {V_4} = 2925 + 3250 + 2137,5 + 1050 = 9362,5 \approx 9363\left( {\;{m^3}} \right).$