Chuyên Đề Vectơ Và Phương Pháp Tọa Độ Trong Không Gian Ôn Thi Tốt Nghiệp THPT 2025 Giải Chi Tiết

Chuyên đề Vectơ và phương pháp tọa độ trong không gian ôn thi tốt nghiệp THPT 2025 giải chi tiết được soạn dưới dạng file word và PDF gồm 20 trang. Các bạn xem và tải về ở dưới.

CHUYÊN ĐỀ: VECTƠ VÀ PHƯƠNG PHÁP TỌA ĐỘ TRONG KHÔNG GIAN

A. KIẾN THỨC CẦN NHỚ

I. VECTƠ

1. Vectơ và các phép toán vectơ

a) Các khái niệm

• Vectơ là một đoạn thẳng có hướng.

• Giá của vectơ là đường thẳng đi qua hai đầu mút của vectơ; độ dài của vectơ là khoảng cách giữa hai đầu mút của vectơ; hai vectơ cùng phương nếu giá của chúng song song hoặc trùng nhau; hai vectơ bằng nhau nếu chúng cùng hướng và cùng độ dài; vectơ-không (kí hiệu $\vec 0$) là vectơ có điểm đầu và điểm cuối trùng nhau; hai vectơ đối nhau nếu chúng ngược hướng và cùng độ dài.

b) Các phép toán vectơ trong không gian

• Tổng và hiệu của hai vectơ:

Cho hai vectơ $\vec a,\vec b$.

– Lấy một điểm $A$ tuỳ ý, vẽ $\overrightarrow {AB} = \vec a,\overline {BC} = \vec b$. Vectơ $\overrightarrow {AC} $ được gọi là tổng của hai vectơ $\vec a,\,\vec b$ , kí hiệu là $\overrightarrow {AC} = \vec a + \vec b$ (Hình $1)$.

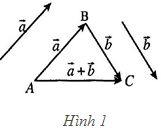
– Hiệu của vectơ $\vec a$ và vectơ $\vec b$ là tổng của vectơ $\vec a$ và vectơ đối của vectơ $\vec b$, kí hiệu là $\vec a – \vec b$.

Chú ý

– Nếu $ABCD$ là hình bình hành thì $\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} $ (Quy tắc hình bình hành).

– Nếu $ABCD.A’B’C’D’$ là hình hộp thì $\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA’} = \overrightarrow {AC’} $ (Quy tắc hình hộp).

– Với ba điểm $O,\,A,\,B$ trong không gian, ta có: $\overrightarrow {OA} – \overrightarrow {OB} = \overrightarrow {BA} $ (Quy tắc hiệu).

• Tích của một số với một vectơ:

Cho số thực $k \ne 0$ và vectơ $\vec a \ne \vec 0$. Tích của số $k$ với vectơ $\vec a$ là một vectơ, kí hiệu là $k\vec a$, được xác định như sau:

– Cùng hướng với vectơ $\vec a$ nếu $k > 0$, ngược hướng với vectơ $\vec a$ nếu $k < 0$;

– Có độ dài bằng $\left| k \right| \cdot \left| {\vec a} \right|$.

Chú ý:

– Ta có $k\vec a = 0$ khi và chỉ khi $k = 0$ hoặc $\vec a = \vec 0$.

– Với hai vectơ bất kì $\vec a,\,\vec b$ và hai số thực $h,\,k$, ta có:

$k\left( {\vec a + \vec b} \right) = k\vec a + k\vec b;\,k\left( {\vec a – \vec b} \right) = k\vec a – k\vec b$; $\left( {h + k} \right)\vec a = h\vec a + k\vec a;\,h\left( {k\vec a} \right) = \left( {hk} \right)\vec a;\,$

$1 \cdot \vec a = \vec a;\,\left( { – 1} \right) \cdot \vec a = – \vec a$.

– Hai vectơ $\vec a,\,\vec b$ khác $\vec 0$ là cùng phương khi và chỉ khi có một số thực $k \ne 0$ sao cho $\vec a = k\,\vec b$.

– Nếu $I$ là trung điểm của đoạn thẳng $AB$ thì $\overrightarrow {IA} + \overrightarrow {IB} = \overrightarrow 0 $.

– Nếu $G$ là trọng tâm của tam giác $ABC$ thì $\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 $.

– Điều kiện cần và đủ để ba điểm $A,B,C$ thẳng hàng là có số thực $k \ne 0$ sao cho $\overrightarrow {AB} = k\overrightarrow {AC} $.

• Tích vô hướng của hai vectơ:

Cho hai vectơ $\vec a,\,\vec b$ khác $\vec 0$. Tích vô hướng của hai vectơ $\vec a$ và $\vec b$, kí hiệu $\vec a \cdot \,\vec b$, là một số thực được xác định bởi công thức: $\vec a \cdot \vec b = \left| {\vec a} \right| \cdot \left| {\vec b} \right| \cdot \cos \left( {\vec a,\,\vec b} \right)$, ở đó $\left( {\vec a,\,\vec b} \right)$là góc giữa hai vectơ $\vec a,\,\vec b$.

Chú ý: Với các vectơ bất kì $\vec a,\,\vec b,\vec c$ và số thực $k$ tuỳ ý, ta có:

$\vec a \cdot \,\vec b = \,\vec b \cdot \vec a$

$\vec a \cdot \,\left( {\vec b + \vec c} \right) = \,\vec a \cdot \vec b + \vec a \cdot \vec c$

$\left( {k\vec a} \right) \cdot \,\vec b = k \cdot \left( {\vec a \cdot \,\vec b} \right) = \vec a \cdot \,\left( {k\vec b} \right)$

${\vec a^2} \geqslant 0$, trong đó ${\vec a^2} = \vec a \cdot \,\vec a$. Ngoài ra, ${\vec a^2} = 0 \Leftrightarrow \vec a = \vec 0$.

II. PHƯƠNG PHÁP TOẠ ĐỘ TRONG KHÔNG GIAN

Xét không gian với hệ trục tọa độ $Oxyz$.

1. Toạ độ của vectơ

• $\overrightarrow {OM} = \left( {a\,;\,b\,;\,c} \right) \Leftrightarrow M\left( {a\,;\,b\,;\,c} \right)$;

• Toạ độ của một vectơ $\vec u$ là toạ độ của điểm $A$, trong đó $A$ là điểm sao cho $\overrightarrow {OA} = \vec u$.

• Nếu $\vec u = \left( {a\,;\,b\,;\,c} \right)$ thì $\vec u = a\vec i + b\vec j + c\vec k$. Ngược lại, nếu $\vec u = a\vec i + b\vec j + c\vec k$ thì $\vec u = \left( {a\,;\,b\,;\,c} \right)$.

• Với $\vec a = \left( {{x_1}\,;\,{y_1}\,;\,{z_1}} \right)$ và $\vec b = \left( {{x_2}\,;\,{y_2}\,;\,{z_2}} \right)$, ta có: $\vec a = \vec b \Leftrightarrow \left\{ \begin{gathered}
{x_1} = {x_2} \hfill \\
{y_1} = {y_2} \hfill \\
{z_1} = {z_2} \hfill \\
\end{gathered} \right.$.

• Cho hai điểm $A\left( {{x_A}\,;\,{y_A}\,;\,{z_A}} \right)$ và $B\left( {{x_B}\,;\,{y_B}\,;\,{z_B}} \right)$. Khi đó, ta có:

$\overrightarrow {AB} = \left( {{x_B} – {x_A}\,;\,{y_B} – {y_A}\,;\,{z_B} – {z_A}} \right)$.

2. Biểu thức tọa độ của phép toán vec tơ.

• Cho hai vec tơ $\overrightarrow u = ({x_1};{y_1};{z_1})$ và $\overrightarrow v = \left( {{x_2};{y_2};{z_2}} \right)$. Khi đó:

$$ $\overrightarrow u \, + \,\overrightarrow v = ({x_1} + {x_2};{y_1} + {y_2};{z_1} + {z_2})$;

$\overrightarrow u \, – \,\overrightarrow v = ({x_1} – {x_2};{y_1} – {y_2};{z_1} – {z_2})$;

$m\overrightarrow u = (m{x_1};m{y_1};m{z_1})$ với $m \in \mathbb{R}$;

$\overrightarrow u .\overrightarrow v = {x_1}{x_2} + {y_1}{y_2} + {z_1}{z_2}$ ;

$$ $\,\left[ {\overrightarrow u ,\,\overrightarrow v } \right]\,\, = \,\,\left( {\left| {\begin{array}{*{20}{c}}
{{y_1}}&{{z_1}} \\
{{y_2}}&{{z_2}}
\end{array}} \right|\,\,;\,\,\left| {\begin{array}{*{20}{c}}
{{z_1}}&{{x_1}} \\
{{z_2}}&{{x_2}}
\end{array}} \right|\,\,;\,\,\left| {\begin{array}{*{20}{c}}
{{x_1}}&{{y_1}} \\
{{x_2}}&{{y_2}}
\end{array}} \right|} \right)$

$ = \left( {{y_1}{z_2} – {y_2}{z_1};{z_1}{x_2} – {x_1}{z_2};{x_1}{y_2} – {x_2}{y_1}} \right)$

Chú ý

– Hai vectơ $\overrightarrow u = ({x_1};{y_1};{z_1})$ và $\overrightarrow v = \left( {{x_2};{y_2};{z_2}} \right)$($\overrightarrow v \ne \overrightarrow 0 $) cùng phương khi và chỉ khi có một số thực $m$

sao cho $\left\{ \begin{gathered}
{x_1} = m{x_2} \hfill \\
{y_1} = m{y_2} \hfill \\
{z_1} = m{z_2} \hfill \\
\end{gathered} \right.$

– Nếu $\overrightarrow a = (x;y;z)$ thì $\left| {\overrightarrow a } \right| = \sqrt {\overrightarrow a \,.\,\overrightarrow a } = \sqrt {{x^2} + {y^2} + {z^2}} $

– Nếu $A({x_1};{y_1};{z_1})$ và $B({x_2};{y_2};{z_2})$ thì $AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{{({x_2} – {x_1})}^2} + {{({y_2} – {y_1})}^2} + {{\left( {{z_2} – {z_1}} \right)}^2}} $ .

– Với hai vectơ $\overrightarrow u = ({x_1};{y_1};{z_1})$ và $\overrightarrow v = \left( {{x_2};{y_2};{z_2}} \right)$khác vectơ $\overrightarrow 0 $ ta có

$cos\left( {\overrightarrow u \,,\,\overrightarrow v } \right) = \frac{{\overrightarrow u .\overrightarrow v }}{{\left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|}}$ $ = \frac{{{x_1}{x_2} + {y_1}{y_2} + {z_1}{z_2}}}{{\sqrt {x_1^2 + y_1^2 + z_1^2} \,.\,\sqrt {x_2^2 + y_2^2 + z_2^2} }}$

– Cho hai điểm $A({x_A};{y_A};{z_A})$ và $B({x_B};{y_B};{z_B})$. Nếu $M({x_M};{y_M};{z_M})$là trung điểm của đoạn thẳng AB thì ${x_M} = \frac{{{x_A} + {x_B}}}{2}$ ; ${y_M} = \frac{{{y_A} + {y_B}}}{2}$; ${z_M} = \frac{{{z_A} + {z_B}}}{2}$.

– Cho tam giác $ABC$ có $A({x_A};{y_A};{z_A})$, $B({x_B};{y_B};{z_B})$,$C({x_C};{y_C};{z_C})$. Nếu $G\left( {{x_G};{y_G};{z_G}} \right)$ là trọng tâm tam giác $ABC$thì: ${x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3}$; ${y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3}$; ${z_G} = \frac{{{z_A} + {z_B} + {z_C}}}{3}$.

3. Phương trình mặt phẳng

a) Vectơ pháp tuyến và cặp vectơ chỉ phương của mặt phẳng

• Nếu vectơ $\overrightarrow n $ khác $\overrightarrow 0 $ và có giá vuông góc với mặt phẳng $(P)$ thì $\overrightarrow n $ được gọi là vectơ pháp tuyến của mặt phẳng $(P)$.

• Hai vectơ không cùng phương có giá song song hoặc thuộc mặt phẳng $(P)$ được gọi là cặp vectơ chỉ phương của mặt phẳng $(P)$.

Chú ý: Nếu hai vectơ $\overrightarrow a = ({a_1};{a_2};{a_3})$ , $\overrightarrow b = \left( {{b_1};{b_2};{b_3}} \right)$ là cặp vectơ chỉ phương của mặt phẳng $(\alpha )$ thì $\overrightarrow n = \left[ {\overrightarrow a ,\overrightarrow b } \right]$ là một vectơ pháp tuyến của mặt phẳng $(\alpha )$.

b) Phương trình mặt phẳng

• Mặt phẳng $(P)$ đi qua điểm $I({x_0};{y_0};{z_0})$ và nhận $\overrightarrow n = (a;b;c)$làm vectơ pháp tuyến có phương trình tổng quát là: $ax + by + cz + d = 0$ với $d = – a{x_0} – b{y_0} – c{z_0}$.

• Mặt phẳng đi qua ba điểm $A(a\,;\,0\,;\,0),\,\,B(0\,;b\,;\,0),\,\,C(0\,;0\,;\,c)$ với $abc \ne 0$ có phương trình chính tắc là: $\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1$.

c) Điều kiện song song và vuông góc của hai mặt phẳng

Cho hai mặt phẳng $\left( {{P_1}} \right),\,\,\left( {{P_2}} \right)$ lần lượt có phương trình tổng quát là:

${A_1}x + {B_1}y + {C_1}z + {D_1} = 0$; ${A_2}x + {B_2}y + {C_2}z + {D_2} = 0$.

Gọi $\overrightarrow {{n_1}} = \left( {{A_1};{B_1};{C_1}} \right)$ , $\overrightarrow {{n_2}} = \left( {{A_2};{B_2};{C_2}} \right)$ lần lượt là vectơ pháp tuyến của hai mặt phẳng $\left( {{P_1}} \right),\,\,\left( {{P_2}} \right)$.

• $\left( {{P_1}} \right)\,//\,\left( {{P_2}} \right) \Leftrightarrow $ Tồn tại số thực $k \ne 0$sao cho $\left\{ {_{{D_1} \ne k{D_2}}^{\overrightarrow {{n_1}} = k\overrightarrow {{n_2}} }} \right.$.

• $({P_1}) \bot \,({P_2}) \Leftrightarrow {A_1}{A_2} + {B_1}{B_2} + {C_1}{C_2} = 0$.

d) Khoảng cách từ một điểm đến một mặt phẳng

Khoảng cách từ điểm ${M_0}({x_0};{y_0};{z_0})$ đến mặt phẳng$(P)$: $Ax + By + Cz + D = 0\,\,\,({A^2} + {B^2} + {C^2} > 0)$được tính theo công thức: $d\left( {{M_0},(P)} \right) = \frac{{\left| {A{x_0} + B{y_0} + C{z_0} + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}$.

4. Phương trình đường thẳng

a) Vectơ chỉ phương của đường thẳng

Nếu vectơ $\overrightarrow u $ khác $\overrightarrow 0 $ và có giá song song hoặc trùng với đường thẳng $\Delta $ thì $\overrightarrow u $ được gọi là vectơ chỉ phương của đường thẳng $\Delta $.

b) Phương trình đường thẳng

• Hệ phương trình $\left\{ \begin{gathered}
x = {x_0} + at \hfill \\
y = {y_0} + bt \hfill \\
z = {z_0} + ct \hfill \\
\end{gathered} \right.$, trong đó $a,\,b,\,c$ không đồng thời bằng 0, $t$ là tham số, được gọi là phương trình tham số của đường thẳng $\Delta $ đi qua ${M_0}\left( {{x_0}\,;\,{y_0}\,;\,{z_0}} \right)$ và có vectơ chỉ phương $\overrightarrow u = \left( {a\,;\,b\,;\,c} \right)$.

• Đường thẳng đi qua ${M_0}\left( {{x_0}\,;\,{y_0}\,;\,{z_0}} \right)$ và có vectơ chỉ phương $\overrightarrow u = \left( {a\,;\,b\,;\,c} \right)$( với $abc \ne 0$) thì có phương trình chính tắc là $\frac{{x – {x_0}}}{a} = \frac{{y – {y_0}}}{b} = \frac{{z – {z_0}}}{c}$.

c) Vị trí tương đối của hai đường thẳng

Cho hai đường thẳng phân biệt ${\Delta _1}\,,\,{\Delta _2}$ lần lượt đi qua các điểm ${M_1}\,,\,{M_2}$ và tương ứng có $\overrightarrow {{u_1}} \,,\,\overrightarrow {{u_2}} $ là hai vectơ chỉ phương. Khi đó, ta có:

• ${\Delta _1}\,//\,\,{\Delta _2} \Leftrightarrow \left\{ \begin{gathered}
\left[ {\overrightarrow {{u_1}} \,,\,\overrightarrow {{u_2}} } \right] = \overrightarrow 0 \hfill \\
\left[ {\overrightarrow {{u_1}} \,,\,\overrightarrow {{M_1}{M_2}} } \right] \ne \overrightarrow 0 \,\,; \hfill \\
\end{gathered} \right.\,\,$

• ${\Delta _1}$ cắt $\,{\Delta _2} \Leftrightarrow \left\{ \begin{gathered}
\left[ {\overrightarrow {{u_1}} \,,\,\overrightarrow {{u_2}} } \right] \ne \overrightarrow 0 \hfill \\
\left[ {\overrightarrow {{u_1}} \,,\,\overrightarrow {{u_2}} } \right]\,.\,\overrightarrow {{M_1}{M_2}} = 0\,; \hfill \\
\end{gathered} \right.\,\,$

• ${\Delta _1}$ và ${\Delta _2}$ chéo nhau $\,\left[ {\overrightarrow {{u_1}} \,,\,\overrightarrow {{u_2}} } \right]\,.\,\overrightarrow {{M_1}{M_2}} \ne 0.$

5. Phương trình mặt cầu

• Phương trình mặt cầu tâm $I\left( {a\,;\,b\,;\,c} \right)$ bán kính $R$ là: ${\left( {x – a} \right)^2} + {\left( {y – b} \right)^2} + {\left( {z – c} \right)^2} = {R^2}$

• Phương trình ${x^2} + {y^2} + {z^2} – 2ax – 2by – 2cz + d = 0$ xác định một mặt cầu khi và chỉ khi ${a^2} + {b^2} + {c^2} – d > 0$. Ngoài ra, nếu ${a^2} + {b^2} + {c^2} – d > 0$ thì phương trình đó xác định mặt cầu tâm $I\left( {a\,;\,b\,;\,c} \right)$ và bán kính $R = \sqrt {{a^2} + {b^2} + {c^2} – d} $.

6. Góc

a) Cosin của góc giữa hai đường thẳng

Cho hai đường thẳng ${\Delta _1}$ và ${\Delta _2}$ có vectơ chỉ phương lần lượt là $\overrightarrow {{u_1}} = \left( {{a_1}\,;\,\,{b_1};\,{c_1}} \right)\,,\,\overrightarrow {{u_2}} = \left( {{a_2}\,;\,\,{b_2};\,{c_2}} \right)\,$. Khi đó, ta có: $cos\,\left( {{\Delta _1}\,,\,\,{\Delta _2}} \right) = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2} + {c_1}{c_2}} \right|}}{{\sqrt {a_1^2 + b_1^2 + c_1^2} .\,\sqrt {a_2^2 + b_2^2 + c_2^2} }}$.

Nhận xét: ${\Delta _1}\, \bot \,{\Delta _2} \Leftrightarrow {a_1}{a_2} + {b_1}{b_2} + {c_1}{c_2} = 0$.

b) Sin của góc giữa đường thẳng và mặt phẳng

Cho đường thẳng $\Delta $ có vectơ chỉ phương $\overrightarrow u = \left( {{a_1}\,;\,\,{b_1};\,{c_1}} \right)\,$và mặt phẳng $\left( P \right)$ có vectơ pháp tuyến $\overrightarrow n = \left( {{a_2}\,;\,\,{b_2};\,{c_2}} \right)\,$. Khi đó, ta có:

$sin\,\left( {\Delta \,,\,\,\left( P \right)} \right) = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2} + {c_1}{c_2}} \right|}}{{\sqrt {a_1^2 + b_1^2 + c_1^2} .\,\sqrt {a_2^2 + b_2^2 + c_2^2} }}$.

c) Cosin của góc giữa hai mặt phẳng

Cho hai mặt phẳng $\left( {{P_1}} \right)$ và $\left( {{P_2}} \right)$ có vectơ pháp tuyến lần lượt là $\overrightarrow {{n_1}} = \left( {{A_1}\,;\,\,{B_1};\,{C_1}} \right)\,,\,$$\overrightarrow {{n_2}} = \left( {{A_2}\,;\,\,{B_2};\,{C_2}} \right)\,$. Khi đó, ta có:

$cos\,\left( {\left( {{P_1}} \right)\,,\,\,\left( {{P_2}} \right)} \right) = \frac{{\left| {{A_1}{A_2} + {B_1}{B_2} + {C_1}{C_2}} \right|}}{{\sqrt {A_1^2 + B_1^2 + C_1^2} .\,\sqrt {A_2^2 + B_2^2 + C_2^2} }}$.

B. MỘT SỐ VÍ DỤ

Dạng 1: Câu hỏi trắc nghiệm nhiều phương án lựa chọn

Mỗi câu thí sinh chỉ chọn một phương án.

Ví dụ 1. Cho hai vectơ $\overrightarrow u \,,\,\overrightarrow v $ có $\left| {\overrightarrow u } \right| = 2,\,\,\left| {\overrightarrow v } \right| = 3\,$và $\left( {\overrightarrow u ,\,\,\overrightarrow v } \right) = 60^\circ $ . Khi đó, $\overrightarrow u \,.\,\overrightarrow v $ bằng:

A. $3$. B. $6$. C. $3\sqrt 3 $. D. $12$.

Lời giải

Ta có: $\overrightarrow u \,.\,\overrightarrow v = \left| {\overrightarrow u } \right|\,.\,\left| {\overrightarrow v } \right|\,.\,\cos \left( {\overrightarrow u \,,\,\overrightarrow v } \right) = 2\,.\,3\,.\,\cos \,60^\circ = 3$.Chọn A.

Ví dụ 2. Trong không gian $Oxyz$, mặt cầu $\left( S \right):\,\,{\left( {x – 2} \right)^2} + {\left( {y – 3} \right)^2} + {\left( {z – 4} \right)^2} = 9$ có bán kính bằng:

A. $81$. B. $9$. C. $3$. D. $6$.

Lời giải

Bán kính mặt cầu $\left( S \right)$ bằng $R = \sqrt 9 = 3$.Chọn C.

Dạng 2: Câu trắc nghiệm đúng sai

Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Ví dụ 3. Một tháp trung tâm kiểm soát không lưu ở sân bay cao 80 m sử dụng ra đa có phạm vi theo dõi 500 km được đặt trên đỉnh tháp. Chọn hệ trục toạ độ $Oxyz$có gốc $O$ trùng với vị trí chân tháp, mặt phẳng $\left( {Oxy} \right)$ trùng với mặt đất sao cho trục $Ox$ hướng về phía tây, trục $Oy$ hướng về phía nam, trục $Oz$ hướng thẳng đứng lên phía trên (Hình 2) (đơn vị trên mỗi trục tính theo kilômét).

Một máy bay tại vị trí $A$ cách mặt đất 10 km, cách 300 km về phía đông và 200 km về phía bắc so với tháp trung tâm kiểm soát không lưu

a) Ra đa ở vị trí có toạ độ $\left( {0;\,0;\,0} \right)$

b) Vị trí $A$ có toạ độ $\left( {300;\,200;\,10} \right)$

c) Khoảng cách từ máy bay đến ra đa là khoảng 360,69 km (làm tròn kết quả đến hàng phần trăm).

d) Ra đa của trung tâm kiểm soát không lưu không phát hiện được máy bay tại vị trí $A$

Lời giải

Theo giả thiết, ra đa ở vị trí có toạ độ $\left( {0;\,0;\,0,08} \right)$; điểm $A\left( { – 300;\, – 200;\,10} \right)$

Vậy khoảng cách từ máy bay đến ra đa là:

$\sqrt {{{\left( { – 300 – 0} \right)}^2} + {{\left( { – 200 – 0} \right)}^2} + {{\left( {10 – 0,08} \right)}^2}} \approx 360,69$ (km).

Vì $360,69 < 500$ nên ra đa của trung tâm kiểm soát không lưu có phát hiện được máy bay tại vị trí $A$.

Đáp án: a) S, b) S, c) Đ, d) S

Ví dụ 4. Trong không gian $Oxyz$ (đơn vị trên mỗi trục tính theo kilômét), một trạm thu phát sóng điện thoại di động được đặt ở vị trí$A\left( {1;\,3;\,7} \right)$. Trạm thu phát sóng đó được thiết kế với bán kính phủ sóng là 3 km.

a) Phương trình mặt cầu $(S)$ để mô tả ranh giới bên ngoài của vùng phù sóng trong không gian là ${\left( {x + 1} \right)^2} + {\left( {y + 3} \right)^2} + {\left( {z + 7} \right)^2} = 9$.

b) Điểm $A\left( {2;\,2;\,7} \right)$ nằm ngoài mặt cầu $\left( S \right)$.

c) Nếu người dùng điện thoại ở vị trí có toạ độ $\left( {2;\,2;\,7} \right)$ thì có thể sử dụng dịch vụ của trạm thu phát sóng đó.

d) Nếu người dùng điện thoại ở vị trí có toạ độ $\left( {5;\,6;\,7} \right)$ thì không thể sử dụng dịch vụ của trạm thu phát sóng đó.

Lời giải

Phương trình mặt cầu $(S)$ tâm $I(1;\,3;\,7)$ bán kính 3 km mô tả ranh giới bên ngoài của vùng phủ sóng trong không gian là ${\left( {x – 1} \right)^2} + {\left( {y – 3} \right)^2} + {\left( {z – 7} \right)^2} = 9$.

Ta có: $IA = \sqrt {{{\left( {2 – 1} \right)}^2} + {{\left( {2 – 3} \right)}^2} + {{\left( {7 – 7} \right)}^2}} = \sqrt 2 < 3$ nên điểm $A$ nằm trong mặt cầu. Vì điểm $A$ nằm trong mặt cầu nên người dùng điện thoại ở vị trí có toạ độ $\left( {2;\,2;\,7} \right)$ có thể sử dụng dịch vụ của trạm thu phát sóng đó.

Ta có: $IB = \sqrt {{{\left( {5 – 1} \right)}^2} + {{\left( {6 – 3} \right)}^2} + {{\left( {7 – 7} \right)}^2}} = 5 > 3$ nên điểm $B$ nằm ngoài mặt cầu. Vậy người dùng điện thoại ở vị trí có toạ độ $\left( {5;\,6;\,7} \right)$ không thể sử dụng dịch vụ của trạm thu phát sóng đó.

Đáp án: $a)$S,$b)$S, $c)$Đ, $d)$Đ

Dạng 3: Câu trắc nghiệm trả lời ngắn

Ví dụ 5. Trong không gian $Oxyz$, cho tam giác $ABC$ có $A\left( {1;\, – 1;\,3} \right),\,B\left( { – 1;\, – 1;\,2} \right)$ và

$C\left( { – 3;\, – 2;\,2} \right)$. Tính $\cos \widehat {ABC}$.

Lời giải

Ta có: $\overrightarrow {BA} = \left( {2;\,0;\,1} \right),\,\,\overrightarrow {BC} = \left( { – 2;\, – 1;\,0} \right)$. Suy ra

$\cos \widehat {ABC} = \cos \left( {\overrightarrow {BA} ,\,\overrightarrow {BC} } \right)$

$ = \frac{{2.\left( { – 2} \right) + 0.\left( { – 1} \right) + 1.0}}{{\sqrt {{2^2} + {0^2} + {1^2}} .\sqrt {{{\left( { – 2} \right)}^2} + {{\left( { – 1} \right)}^2} + {0^2}} }} = – 0,8$

C. BÀI TẬP LUYỆN TẬP

Dạng 1: Câu hỏi trắc nghiệm nhiều phương án lựa chọn

Mỗi câu thí sinh chỉ chọn một phương án.

Câu 1. [MĐ2] Cho tứ diện$ABCD$. Lấy$G$ là trọng tâm của tam giác $ABC$. Phát biểu nào sau đây là sai?

A. $\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 $. B. $\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 $.

C. $\overrightarrow {GD} – \overrightarrow {GA} = \overrightarrow {AD} $. D. $\overrightarrow {DA} + \overrightarrow {DB} + \overrightarrow {DC} = 3\overrightarrow {DG} $.

Lời giải

Chọn B

Tính chất trọng tâm: $\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 $.

Câu B chỉ đúng khi $G$ là tâm tứ diện $ABCD$.

Câu 2. [MĐ2] Trong không gian $Oxyz$, cho điểm $M$ thỏa mãn $\overrightarrow {OM} = 2\overrightarrow i + 3\overrightarrow j – 4\overrightarrow k $.Tọa độ của điểm $M$ là

A. $( – 4 ;3 ;2)$. B. $(2 ;3 ; – 4)$. C. $(3 ; – 4 ;2)$. D. $( – 2 ; – 3 ;4)$

Lời giải

Chọn B

Với

$\left\{ \begin{gathered}
\vec i = \left( {1;0;0} \right) \hfill \\
\vec j = \left( {0;1;0} \right) \hfill \\
\vec k = \left( {0;0;1} \right) \hfill \\
\end{gathered} \right.$

Khi đó $\overrightarrow {OM} = 2\overrightarrow i + 3\overrightarrow j – 4\overrightarrow k = \left( {2;3; – 4} \right)$$$.

Câu 3. [MĐ2] Trong không gian $Oxyz$, cho hai vectơ $\overrightarrow u = \left( {3 ;2 ; – 1} \right), \overrightarrow v = \left( {5 ; – 4 ;2} \right)$. Tọa độ của vectơ $\overrightarrow u – \overrightarrow v $ là:

A. $\left( { – 2 ;6 ; – 3} \right)$. B. $\left( {2 ; – 6 ;3} \right)$. C. $\left( { – 2 ; – 2 ; – 3} \right)$. D. $\left( {2 ;2 ;1} \right)$

Lời giải

Chọn A

$\overrightarrow u – \overrightarrow v = \left( {3 – 5;2 – – 4; – 1 – 2} \right) = \left( { – 2;6; – 3} \right)$.

Câu 4. [MĐ2] Trong không gian $Oxyz$, cho vectơ $\overrightarrow u = \left( {1 ; – 2 ;3} \right)$. Tọa độ của vectơ $ – 3\overrightarrow u $ là:

A. $\left( {3 ; – 6 ;9} \right)$. B. $\left( { – 3 ; – 6 ; – 9} \right)$. C. $\left( {3 ;6 ;9} \right)$. D. $\left( { – 3 ;6 ; – 9} \right)$.

Lời giải

Chọn D

$ – 3\overrightarrow u = ( – 3.1 ; – 3. – 2 ; – 3.3) = \left( { – 3;6; – 9} \right)$.

Câu 5. [MĐ2] Trong không gian $Oxyz$, cho tam giác $MNP$ có $M\left( {2; – 3;4} \right),N\left( {1;2;3} \right)$ và $P\left( {3; – 2;2} \right)$. Trọng tâm của tam giác $MNP$ có tọa độ là:

A. $\left( {2; – 1;3} \right)$. B. $\left( {6; – 3;9} \right)$. C. $\left( { – 2;1; – 3} \right)$. D. $\left( { – 6;3; – 9} \right).$

Lời giải

Chọn A

Gọi $G$là trọng tâm tam giác$MNP$, khi đó:

$\left\{ \begin{gathered}
{x_G} = \frac{{{x_M} + {x_N} + {x_P}}}{3} = \frac{{2 + 1 + 3}}{3} = 2 \hfill \\
{y_G} = \frac{{{y_M} + {y_N} + {y_P}}}{3} = \frac{{ – 3 + 2 – 2}}{3} = – 1 \hfill \\
{z_G} = \frac{{{z_M} + {z_N} + {z_P}}}{3} = \frac{{4 + 3 + 2}}{3} = 3 \hfill \\
\end{gathered} \right.$.

Câu 6. [MĐ2] Trong không gian $Oxyz$, tích vô hướng của hai vectơ $\vec u = \left( {2;3; – 3} \right)$ và $\vec v = \left( { – 3; – 2;4} \right)$ bằng:

A. $\sqrt {22} .\sqrt {29} $. B. $ – \sqrt {22} .\sqrt {29} $. C. $24$. D. $ – 24$.

Lời giải

Chọn D

Ta có: $\vec u.\vec v = 2. – 3 + 3. – 2 + – 3.4 = – 24$.

Câu 7. [MĐ2] Trong không gian $Oxyz$, khoảng cách giữa hai điểm $I\left( {3;5; – 7} \right)$ và $K\left( { – 5;5; – 1} \right)$ bằng

A. $100$. B. $20$. C. $10$. D. $17$.

Lời giải

Chọn C

Khoảng cách giữa hai điểm $I$và $K$ là độ dài đoạn thẳng $IK$.

Ta có:

$IK = \sqrt {{{\left( { – 5 – 3} \right)}^2} + {{\left( {5 – 5} \right)}^2} + {{\left( { – 1 – – 7} \right)}^2}} = 10$.

Câu 8. [MĐ2] Trong không gian $Oxyz$, cho hai vectơ $\vec u = \left( {3;1; – 2} \right)$ và $\vec v = \left( { – 2;1;5} \right)$. Tọa độ của vectơ $\left[ {\vec u,\vec v} \right]$ là:

A. $\left( {5;7; – 11} \right).$ B. $\left( { – 7;11; – 5} \right).$ C. $\left( {7; – 11;5} \right).$ D. $\left( { – 5; – 7;11} \right).$

Lời giải

Chọn C

Ta có:

$\left[ {\vec u,\vec v} \right] = \left( {1.5 – \left( { – 2} \right).1; – \left( {3.5 – \left( { – 2} \right).\left( { – 2} \right)} \right);3.1 – 1.\left( { – 2} \right)} \right)$

$ = \left( {7; – 11;5} \right)$.

Câu 9. [MĐ1] Cho hình hộp chữ nhật $ABCD.A’B’C’D’$ Cặp vectơ nào sau đây là cặp vectơ chỉ phương của mặt phắng $\left( {ABB’A’} \right)$?

A. $\overrightarrow {AB} $ và $\overrightarrow {AD} $. B. $\overrightarrow {AB} $ và$\overrightarrow {AD’} $. C. $\overrightarrow {AB} $ và $\overrightarrow {A’B’} $ D. $\overrightarrow {AB} $ và $\overrightarrow {CC’} $

Lời giải

Chọn D

$\overrightarrow {AB} $có giá nắm trên $\left( {ABB’A’} \right)$ (1)

$\overrightarrow {CC’} $có giá song song với $\left( {ABB’A’} \right)$ (2)

Từ (1) và (2) suy ra $\overrightarrow {AB} $ và $\overrightarrow {CC’} $ là cặp vectơ chỉ phương của mặt phắng $\left( {ABB’A’} \right)$.

Câu 10. [MĐ1] Trong không gian $Oxyz$, vectơ nào sau đây là vectơ pháp tuyến của mặt phẳng $(P):x + 3y – 4z + 5 = 0$?

A. ${\vec n_1} = \left( {3;4;5} \right)$. B. ${\vec n_2} = \left( {1;3; – 4} \right)$. C. ${\vec n_3} = \left( {1;3;4} \right)$. D. ${\vec n_4} = \left( {3; – 4;5} \right)$.

Lời giải

Chọn B

Mặt phẳng $(P):x + 3y – 4z + 5 = 0$có 1 VTPT là ${\vec n_2} = \left( {1;3; – 4} \right)$.

Câu 11. [MĐ1] Trong không gian $Oxyz$, mặt phẳng đi qua điểm $K(1;1;1)$ nhận $\vec u = (1;0;1)$, $\vec v = (1;1;0)$ là cặp vectơ chỉ phương có phương trình tổng quát là:

A. $x + y + z – 3 = 0$. B. $x – y + z – 1 = 0$. C. $x + y – z – 1 = 0$. D. $ – x + y + z – 1 = 0$.

Lời giải

Chọn D

Ta có: $\left[ {\overrightarrow u ,\overrightarrow v } \right] = \left( { – 1\;;\;1\;;\;1} \right)$là 1 VTPT của mp cần tìm nên chỉ có phương án D thỏa mãn.

Câu 12. [MĐ2] Trong không gian $Oxyz$, mặt phẳng cắt ba trục toa độ tại ba điểm $D(3;0;0)$, $E(0; – 2;0),G(0;0; – 7)$ có phương trình chính tắc là:

A. $\frac{x}{3} – \frac{y}{2} – \frac{z}{7} + 1 = 0$. B. $\frac{x}{3} + \frac{y}{2} + \frac{z}{7} = 1$. C. $\frac{x}{3} – \frac{y}{2} – \frac{z}{7} = 1$. D. $\frac{x}{3} – \frac{y}{2} + \frac{z}{7} = 1$.

Lời giải

Chọn C

Phương trình mặt chắn là: $\frac{x}{3} – \frac{y}{2} – \frac{z}{7} = 1$.

Câu 13. [MĐ1] Trong không gian $Oxyz$, đường thẳng đi qua điểm $I(15; – 16;17)$ và nhận $\vec u = ( – 7;8; – 9)$ là vectơ chỉ phương có phương trình tham số là:

A. $\left\{ {\begin{array}{*{20}{l}}
{x = 15 – 7t} \\
{y = 16 + 8t} \\
{z = 17 – 9t}
\end{array}} \right.$. B. $\left\{ {\begin{array}{*{20}{l}}
{x = 15 – 7t} \\
{y = – 16 + 8t} \\
{z = 17 – 9{t^2}}
\end{array}} \right.$. C. $\left\{ {\begin{array}{*{20}{l}}
{x = 15 – 7{t^2}} \\
{y = – 16 + 8t} \\
{z = 17 – 9t}
\end{array}} \right.$. D. $\left\{ {\begin{array}{*{20}{l}}
{x = – 7 + 15t} \\
{y = 8 – 16t} \\
{z = – 9 + 17t}
\end{array}} \right.$.

Lời giải

Chọn A

Câu 14. [MĐ1] Trong không gian $Oxyz$, vectơ nào sau đây là vectơ chi phương cùa đường thằng $\Delta :\frac{{x – 5}}{8} = \frac{{y – 9}}{6} = \frac{{z – 12}}{3}$.

A. ${\bar u_1} = (8;6;3)$. B. ${\vec u_2} = (8;6; – 3)$. C. ${\vec u_3} = ( – 8;6; – 3)$. D. ${\vec u_4} = (5;9;12)$.

Lời giải

Chọn A

Đường thẳng $\Delta :\frac{{x – 5}}{8} = \frac{{y – 9}}{6} = \frac{{z – 12}}{3}$ có một VTCP là $\overrightarrow u = \left( {8;\;6\;;\;3} \right)$

Câu 15. [MĐ1] Trong không gian $Oxyz$, mặt cầu tâm $I\left( { – 6; – 9;15} \right)$ và đường kính bằng 10 có phương trình là:

A. ${\left( {x + 6} \right)^2} + {\left( {y + 9} \right)^2} + {\left( {z – 15} \right)^2} = 100$. B. ${\left( {x + 6} \right)^2} + {\left( {y + 9} \right)^2} + {\left( {z – 15} \right)^2} = 25$.

C. ${\left( {x – 6} \right)^2} + {\left( {y – 9} \right)^2} + {\left( {z + 15} \right)^2} = 100$. D. ${\left( {x – 6} \right)^2} + {\left( {y – 9} \right)^2} + {\left( {z + 15} \right)^2} = 25$.

Lời giải

Chọn B

Do mặt cầu có đường kính bằng 10 nên bán kính bằng 5.

Phương trình mặt cầu tâm $I\left( { – 6; – 9;15} \right)$ và đường kính bằng 10 có phương trình là:${\left( {x + 6} \right)^2} + {\left( {y + 9} \right)^2} + {\left( {z – 15} \right)^2} = 25$ .

Câu 16. [MĐ1] Trong không gian $Oxyz$, điểm nào sau đây thuộc mặt cầu $\left( S \right):{x^2} + {y^2} + {z^2} = 50$ ?

A. $M\left( {3;4;6} \right)$. B. $N\left( {4;4;5} \right)$. C. $P\left( {3;4; – 5} \right)$. D. $Q\left( { – 3;3; – 5} \right)$.

Lời giải

Chọn C

Thay tọa độ các điểm vào phương trình mặt cầu $\left( S \right):{x^2} + {y^2} + {z^2} = 50$ ta thấy tọa độ điểm $P\left( {3;4; – 5} \right)$ thỏa mãn.

Dạng 2: Trắc nghiệm đúng-sai

Trong mỗi ý a) b) c) d) ở mỗi câu thí sinh chọn đúng hoặc sai.

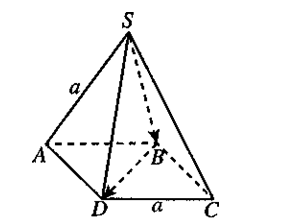
Câu 17. Cho hình chóp tứ giác đều $S.ABCD$ có độ dài tất cả các cạnh đều bằng $a$.

a) Tứ giác $ABCD$ là hình vuông.

b) Tam giác $SBD$ cân tại $S$.

c) $\left( {\overrightarrow {SB} ,\overrightarrow {BD} } \right) = {45^0}$.

d) $\overrightarrow {SB} \,.\,\overrightarrow {BD} = – {a^2}$.

Lời giải

Ý	a)	b)	c)	d)
Kết quả	Đ	Đ	S	Đ

a) Do $S.ABCD$ là hình chóp đều nên $ABCD$ là hình vuông. Suy ra a) đúng.

b) Do $S.ABCD$ là hình chóp đều tất cả các cạnh bằng $a$ $ \Rightarrow SB = SD = a$ . Suy ra b) đúng.

c) Do tứ giác $ABCD$ là hình vuông có độ dài cạnh bằng $a$ nên độ dài đường chéo $BD = a\sqrt 2 $.

Tam giác $SBD$ có $ \Rightarrow SB = SD = a$ và $BD = a\sqrt 2 $ nên tam giác $SBD$ vuông cân tại $S$, suy ra $\widehat {SBD} = {45^0}$.

Vậy $\left( {\overrightarrow {SB} ,\overrightarrow {BD} } \right) = {180^0} – \widehat {SBD} = {135^0}$. Suy ra c) sai.

d) Ta có$\overrightarrow {SB} \,.\,\overrightarrow {BD} = SB.BD.\cos \left( {\overrightarrow {SB} \,,\,\overrightarrow {BD} } \right) = a.a\sqrt 2 .\cos {135^0} = – {a^2}$ . Suy ra d) đúng.

Câu 18. Trong không gian $Oxyz$, cho các điểm $A\left( {1; – 2;3} \right),\,\,B\left( { – 2;1;2} \right),\,\,C\left( {3; – 1;2} \right)$.

a) $\overrightarrow {AB} = \left( { – 3;3 – 1} \right)$ .

b) $\overrightarrow {AC} = \left( { – 2; – 1;1} \right)$.

c) $\overrightarrow {AB} = 3\overrightarrow {AC} $.

d) Ba điểm $A,\,B,\,C$ không thẳng hàng.

Lời giải

Ý	a)	b)	c)	d)
Kết quả	Đ	S	S	Đ

a) Ta có $A\left( {1; – 2;3} \right),\,\,B\left( { – 2;1;2} \right)$$ \Rightarrow \overrightarrow {AB} = \left( { – 3;3; – 1} \right)$ . Suy ra a) đúng.

b) Ta có $A\left( {1; – 2;3} \right),\,\,C\left( {3; – 1;2} \right)$$ \Rightarrow \overrightarrow {AC} = \left( {2;1; – 1} \right)$. Suy ra b) sai.

c) Do $3\overrightarrow {AC} = \left( {6;3; – 3} \right);\,\overrightarrow {AB} = \left( { – 3;3; – 1} \right)$ . Suy ra c) sai..

d) Ta có$\overrightarrow {AB} = \left( { – 3;3; – 1} \right);\,\overrightarrow {AC} = \left( {2;1; – 1} \right)$$ \Rightarrow \frac{{ – 3}}{2} \ne \frac{3}{1}$$ \Rightarrow \overrightarrow {AB} $, $\overrightarrow {AC} $ không cùng phương. Suy ra ba điểm $A,\,B,\,C$ không thẳng hàng. Suy ra d) đúng.

Câu 19. Trong không gian $Oxyz$, cho hình bình hành $ABCD$ có $A\left( {2; – 1; – 2} \right),\,\,B\left( {3;1;2} \right),\,\,C\left( {1; – 1;1} \right)$ và $D\left( {{x_D};{y_D};{z_D}} \right)$.

a) $\overrightarrow {AB} = \left( {1;2;4} \right)$ .

b) $\overrightarrow {DC} = \left( {1 – {x_D}; – 1 – {y_D};1 – {z_D}} \right)$.

c) $\overrightarrow {DC} = \overrightarrow {AB} $.

d) Tọa độ điểm $D$ là $\left( {0;3;3} \right)$.

Lời giải

Ý	a)	b)	c)	d)
Kết quả	Đ	Đ	Đ	S

a) Ta có $A\left( {2; – 1; – 2} \right),\,\,B\left( {3;1;2} \right)$$ \Rightarrow \overrightarrow {AB} = \left( {1;2;4} \right)$ . Suy ra a) đúng.

b) Ta có $C\left( {1; – 1;1} \right);D\left( {{x_D};{y_D};{z_D}} \right)$$ \Rightarrow \overrightarrow {DC} = \left( {1 – {x_D}; – 1 – {y_D};1 – {z_D}} \right)$ . Suy ra b) đúng.

c) Do hình bình hành $ABCD$ có $\overrightarrow {AB} = \overrightarrow {DC} $ . Suy ra c) đúng.

d) Do hình bình hành $ABCD$ có $\overrightarrow {AB} = \overrightarrow {DC} $ .

Mà $\overrightarrow {AB} = \left( {1;2;4} \right)$ ; $\overrightarrow {DC} = \left( {1 – {x_D}; – 1 – {y_D};1 – {z_D}} \right)$

$ \Rightarrow \left\{ \begin{gathered}
1 = 1 – {x_D} \hfill \\
2 = – 1 – {y_D} \hfill \\
4 = 1 – {z_D} \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
{x_D} = 0 \hfill \\
{y_D} = – 3 \hfill \\
{z_D} = – 3 \hfill \\
\end{gathered} \right.$.

Vậy $D\left( {0; – 3; – 3} \right)$ . Suy ra d) sai.

Câu 20. Trong không gian $Oxyz$, cho hình lập phương $ABCD.A’B’C’D’$ có $A\left( {0;0;0} \right)$, $B\left( {2;0;0} \right)$, $D\left( {0;2;0} \right)$, $A’\left( {0;0;2} \right)$. Gọi $M,N$lần lượt là trung điểm của $AB$ và $AA’$ (Hình 3).

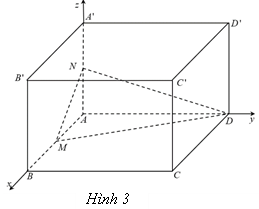
a) Toạ độ của điểm $M$ là $\left( {1;0;0} \right)$.

b) Toạ độ của điểm $N$ là $\left( {0;1;0} \right)$.

c) Phương trình mặt phẳng $\left( {DMN} \right)$ là $\frac{x}{1} + \frac{y}{2} + \frac{z}{1} = 1$.

d) Khoảng cách từ điểm $C’$ đến mặt phẳng $\left( {DMN} \right)$ bằng $\frac{8}{3}$.

Lời giải

Ý	a)	b)	c)	d)
Kết quả	Đ	S	Đ	Đ

a) Do $A\left( {0;0;0} \right)$,$B\left( {2;0;0} \right)$ và $M$ là trung điểm của $AB$ nên $M\left( {1;0;0} \right)$. Suy ra a) Đúng

b) Do $A\left( {0;0;0} \right)$,$A’\left( {0;0;2} \right)$ và $N$ là trung điểm của $AA’$ nên $N\left( {0;0;1} \right)$. Suy ra b) Sai.

c) Do $M\left( {1;0;0} \right)$,$N\left( {0;0;1} \right)$, $D\left( {0;2;0} \right)$. Phương trình mặt phẳng $\left( {DMN} \right)$ là

$\frac{x}{1} + \frac{y}{2} + \frac{z}{1} = 1$ ( phương trình đoạn chắn ). Suy ra c) Đúng

d) Ta có: Phương trình mặt phẳng $\left( {DMN} \right)$ là

$\frac{x}{1} + \frac{y}{2} + \frac{z}{1} = 1$$ \Leftrightarrow 2x + y + 2z – 2 = 0$. Mà điểm $C’\left( {2;2;2} \right)$ từ đó ta có:

$d\left( {C’;\left( {DMN} \right)} \right) = \frac{{\left| {2.2 + 2 + 2.2 – 2} \right|}}{{\sqrt {{2^2} + {1^2} + {2^2}} }} = \frac{8}{3}$. Suy ra d) Đúng

Câu 21. Trong không gian $Oxyz$, cho hai mặt phẳng $\left( P \right):y = 0,\left( Q \right):\sqrt 3 x – y – 2024 = 0$. Xét các véc tơ $\overrightarrow {{n_1}} = \left( {0;1;0} \right)$, $\overrightarrow {{n_2}} = \left( {\sqrt 3 ; – 1;0} \right)$.

a) $\overrightarrow {{n_1}} $ là một véctơ pháp tuyến của mặt phẳng $\left( P \right)$.

b) $\overrightarrow {{n_2}} $ không là một véctơ pháp tuyến của mặt phẳng $\left( Q \right)$.

c) $\overrightarrow {{n_1}} \,\,.\,\,\overrightarrow {{n_2}} = – 1$ .

d) Góc giữa hai mặt phẳng $\left( P \right),\left( Q \right)$ bằng $30^\circ $.

Lời giải

Ý	a)	b)	c)	d)
Kết quả	Đ	S	Đ	D

a) Do $\left( P \right):0.x + 1.y + 0.z = 0$ nên $\overrightarrow {{n_1}} = \left( {0;1;0} \right)$ là một véctơ pháp tuyến của mặt phẳng $\left( P \right)$. Suy ra a) Đúng.

b) Do $\left( Q \right):\sqrt 3 x – y + 0.z – 2024 = 0$ nên $\overrightarrow {{n_2}} = \left( {\sqrt 3 ; – 1;0} \right)$ là một véctơ pháp tuyến của mặt phẳng $\left( P \right)$. Suy ra b) Sai.

c) $\overrightarrow {{n_1}} \,\,.\,\,\overrightarrow {{n_2}} = 0.\sqrt 3 + 1\left( { – 1} \right) + 0.0 = – 1$. Suy ra c) Đúng.

d) $\cos \left( {\left( P \right),\left( Q \right)} \right) = \frac{{\left| {\overrightarrow {{n_1}} .\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}}$$ = \frac{{\left| { – 1} \right|}}{{\sqrt {{0^2} + {1^2} + {0^2}} \sqrt {{{\left( {\sqrt 3 } \right)}^2} + {{\left( { – 1} \right)}^2} + {0^2}} }}$

$ = \frac{1}{2}$$ \Rightarrow \left( {\left( P \right),\left( Q \right)} \right) = 60^\circ $

Suy ra d) Sai

Câu 22. Trong không gian $Oxyz$, cho đường thẳng $\Delta :\frac{{x – 2024}}{2} = \frac{y}{1} = \frac{{z + 2025}}{{ – 2}}$ và mặt phẳng $\left( P \right):2x + 2y – z + 1 = 0$. Xét các vectơ $\overrightarrow u = \left( {2;1; – 2} \right)$, $\overrightarrow n = \left( {2;2; – 1} \right)$.

a) $\overrightarrow u $ là một vectơ chỉ phương của đường thẳng $\Delta $.

b) $\overrightarrow n $ là một vectơ pháp tuyến của mặt phẳng $\left( P \right)$.

c) $\cos \left( {\Delta ,\left( P \right)} \right) = \frac{8}{9}$.

d) Góc giữa đường thẳng $\Delta $ và mặt phẳng $\left( P \right)$ bằng khoảng $63^\circ $ (làm tròn đến hàng đơn vị của độ).

Lời giải

Ý	a)	b)	c)	d)
Kết quả	Đ	Đ	S	Đ

a) Do $\Delta :\frac{{x – 2024}}{2} = \frac{y}{1} = \frac{{z + 2025}}{{ – 2}}$ nên $\overrightarrow u = \left( {2;1; – 2} \right)$ là một vectơ chỉ phương của đường thẳng $\Delta $. Suy ra a) Đúng.

b) Do $\left( P \right):2x + 2y – z + 1 = 0$ nên $\overrightarrow n = \left( {2;2; – 1} \right)$ là một vectơ pháp tuyến của đường thẳng $\left( P \right)$. Suy ra b) Đúng.

c) Ta có $\sin \left( {\Delta ,\left( P \right)} \right) = \frac{{\left| {\overrightarrow u .\overrightarrow n } \right|}}{{\left| {\overrightarrow u } \right|.\left| {\overrightarrow n } \right|}}$$ = \frac{{\left| {2.2 + 1.2 – 2\left( { – 1} \right)} \right|}}{{\sqrt {{2^2} + {1^2} + {{\left( { – 2} \right)}^2}} \sqrt {{2^2} + {2^2} + {{\left( { – 1} \right)}^2}} }}$$ = \frac{8}{9}$

${\cos ^2}\left( {\Delta ,\left( P \right)} \right) = 1 – {\sin ^2}\left( {\Delta ,\left( P \right)} \right) = 1 – \frac{{64}}{{81}} = \frac{{17}}{{81}} \Rightarrow \cos \left( {\Delta ,\left( P \right)} \right) = \frac{{\sqrt {17} }}{9}$. Suy ra c) Sai

d) Từ ý c) suy ra $\left( {\Delta ,\left( P \right)} \right) \approx {63^0}$. Suy ra d) Đúng.

Câu 23. Trong không gian $Oxyz$, cho hai đường thẳng

${\Delta _1}:\frac{x}{1} = \frac{{y – 3}}{{ – 1}} = \frac{{z + 3}}{2},\,\,{\Delta _2}:\frac{{x + 4}}{2} = \frac{{y + 2}}{1} = \frac{{z – 4}}{{ – 1}}$

Xét các vectơ $\overrightarrow {{u_1}} = \left( {1; – 1;2} \right)$ và $\overrightarrow {{u_2}} = \left( {2;1; – 1} \right)$.

a) Đường thẳng ${\Delta _1}$ đi qua điểm ${{\rm M}_1}\left( {0;3; – 3} \right)$ và có $\overrightarrow {{u_1}} = \left( {1; – 1;2} \right)$ là một vectơ chỉ phương.

b) Đường thẳng ${\Delta _2}$ đi qua điểm ${M_2}\left( { – 4; – 2;4} \right)$ và có $\overrightarrow {{u_2}} = \left( {2;1; – 1} \right)$ là một vectơ chỉ phương.

c) $\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] = \left( {1; – 5; – 3} \right)$.

d) hai đường thẳng ${\Delta _1}$ và ${\Delta _2}$ chéo nhau.

Lời giải

Ý	a)	b)	c)	d)
Kết quả	Đ	Đ	S	Đ

a) Do ${\Delta _1}:\frac{x}{1} = \frac{{y – 3}}{{ – 1}} = \frac{{z + 3}}{2}$ Nên ${\Delta _1}$ đi qua điểm ${M_1}\left( {0;3; – 3} \right)$ và có $\overrightarrow {{u_1}} = \left( {1; – 1;2} \right)$ là một vectơ chỉ phương. Suy ra a) Đúng.

b) Do ${\Delta _2}:\frac{{x + 4}}{2} = \frac{{y + 2}}{1} = \frac{{z – 4}}{{ – 1}}$ Nên ${\Delta _1}$ đi qua điểm ${M_2}\left( { – 4; – 2;4} \right)$ và có $\overrightarrow {{u_2}} = \left( {2;1; – 1} \right)$ là một vectơ chỉ phương. Suy ra b) Đúng.

c) Do $\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] = \left( {\left| {\begin{array}{*{20}{c}}
{ – 1}&2 \\
1&{ – 1}
\end{array}} \right|;\left| {\begin{array}{*{20}{c}}
2&1 \\
{ – 1}&2
\end{array}} \right|;\left| {\begin{array}{*{20}{c}}
1&{ – 1} \\
2&1
\end{array}} \right|} \right) = \left( { – 1;5;3} \right)$. Suy ra c) Sai.

d) $\overrightarrow {{M_1}{M_2}} = \left( { – 4; – 5;7} \right) \Rightarrow \left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right].\overrightarrow {{M_1}{M_2}} = 4 – 25 + 21 = 0$ suy ra hai đường thẳng ${\Delta _1}$ và ${\Delta _2}$ không chéo nhau. Suy ra d) Sai.

Câu 24. Trong không gian $Oxyz$ ( đơn vị trên mỗi trục tính theo mét ), một ngọn hải đăng được đặt ở vị trí $I\left( {17;20;45} \right)$. Biết rằng ngọn hải đăng đó được thiết kế với bán kính phủ sáng là $4\;km$.

a) Phương trình mặt cầu để mô tả ranh giới bên ngoài của vùng phủ sáng trên biển của hải đăng là:

${(x – 17)^2} + {(y – 20)^2} + {(z – 45)^2} = {4000^2}. $

b) Nếu người đi biển ở vị trí $M\left( {18;21;50} \right)$ thì không thể nhìn thấy được ánh sáng từ ngọn hải đăng.

c) Nếu người đi biển ở vị trí $N\left( {4019;21;44} \right)$ thì có thể nhìn thấy được ánh sáng từ ngọn hải đăng.

d Nếu hai người đi biển ở vị trí có thể nhìn thấy được ánh sáng từ ngọn hải đăng thì khoảng cách giữa hai người đó không quá $8 km$.

Lời giải

Ý	a)	b)	c)	d)
Kết quả	Đ	S	S	Đ

a) Do phương trình mặt cầu để mô tả ranh giới bên ngoài của vùng phủ sáng trên biển của hải đăng là: ${(x – 17)^2} + {(y – 20)^2} + {(z – 45)^2} = {4000^2}$ suy ra đúng.

b) Do ta có: $IM = \sqrt {{{(18 – 17)}^2} + {{(21 – 20)}^2} + {{(50 – 45)}^2}} = \sqrt {27} < 4000$ nên người đi biển ở vị trí $M(18;21;50)$ có thể nhìn thấy được ánh sáng từ ngọn hải đăng suy ra sai.

c) Do ta có: $IN = \sqrt {{{(4019 – 17)}^2} + {{(21 – 20)}^2} + {{(44 – 45)}^2}} \approx 4002 > 4000$ nên người đi biển ở vị trí $N(4019;21;44)$ không thể nhìn thấy được ánh sáng từ ngọn hải đăng suy ra sai.

d) Do đường kính của mặt cầu trên bằng $8000\;m$ hay $8\;km$ nên hai người đi biển ở vị trí có thể nhìn thấy được ánh sáng từ ngọn hải đăng thì khoảng cách giữa hai người đó không quá $8\;km$suy ra đúng.

Dạng 3: Câu trắc nghiệm trả lời ngắn

Câu 25. [MĐ3] Cho hình lập phương $ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }$. Gọi $M,N$ lần lượt là trung điểm của ${A^\prime }{D^\prime }$ và ${C^\prime }{D^\prime }$. Gọi $\varphi $ là góc giữa hai vectơ $\overrightarrow {MN} $ và $\overrightarrow {{A^\prime }B} $. Số đo của góc $\varphi $ bằng bao nhiêu độ?

Lời giải

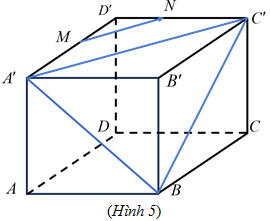
Trả lời: $60^\circ $

(Hinh 5). Vì $MN//{A^\prime }{C^\prime }$ nên $\left( {\overrightarrow {MN} ,\overrightarrow {{A^\prime }B} } \right) = \left( {\overrightarrow {{A^\prime }{C^\prime }} ,\overrightarrow {{A^\prime }B} } \right) = \widehat {{C^\prime }{A^\prime }B}$.

Tam giác ${C^\prime }{A^\prime }{B^\prime }$ là tam giác đều vì $ABCD.{A^\prime }{B^\prime }{C^\prime }{D^\prime }$ ‘ là hình lập phương.

Suy ra $\widehat {{C^\prime }{A^\prime }B} = 60^\circ $.

Vậy $\left( {\overrightarrow {MN} ,\overrightarrow {{A^\prime }B} } \right) = \overrightarrow {{C^\prime }{A^\prime }B} = 60^\circ $.

Câu 26. [MĐ3] Cho hình lâp phương $ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }$ có cạnh bằng $a$. Gọi $M,N$ lần lượt là trung điểm của ${A^\prime }{D^\prime }$ và ${C^\prime }{D^\prime }$. Tích vô hướng $\overrightarrow {MN} \cdot \overrightarrow {{C^\prime }B} = n{a^2}$ ( $n$ là số thập phân). Giá trị của $n$ bằng bao nhiêu?

Lời giải

Trả lời: $n = – 0,5$

(Hình 5). Vì $MN//{A^\prime }{C^\prime }$ nên $\left( {\overrightarrow {MN} ,\overrightarrow {{C^\prime }B} } \right) = \left( {\overrightarrow {{A^\prime }{C^\prime }} ,\overrightarrow {{C^\prime }B} } \right) = {180^\circ } – \widehat {{A^\prime }{C^\prime }B} = {120^\circ }$.

Ta có: $MN = \frac{{a\sqrt 2 }}{2},{C^\prime }B = a\sqrt 2 $. Suy ra

$\overrightarrow {MN} \cdot \overrightarrow {{C^\prime }B} = |\overrightarrow {MN} | \cdot \left| {\overrightarrow {{C^\prime }B} } \right| \cdot \cos \left( {\overrightarrow {MN} ,\overrightarrow {{C^\prime }B} } \right)$

$ = \frac{{a\sqrt 2 }}{2} \cdot a\sqrt 2 \cdot \cos {120^\circ } = – 0,5{a^2}$.

Vậy $n = – 0,5$.

Câu 27. [MĐ3] Trong không gian $Oxyz$ cho tam giác $ABC$ có $A(1;3;5),B(1;1;3),C(4; – 2;3)$. Số đo của góc $\widehat {ABC}$ bằng bao nhiêu độ?

Lời giải

Trả lời: $\widehat {ABC} = {120^\circ }$

Ta có: $\overrightarrow {BA} = (0;2;2),\overrightarrow {BC} = (3; – 3;0)$. Suy ra

$\cos \widehat {ABC} = \cos (\overrightarrow {BA} ,\overrightarrow {BC} ) = \frac{{\overrightarrow {BA} \cdot \overrightarrow {BC} }}{{|\overrightarrow {BA} | \cdot |\overrightarrow {BC} |}} $

$ = \frac{{0.3 + 2 \cdot ( – 3) + 2 \cdot 0}}{{\sqrt {{0^2} + {2^2} + {2^2}} \cdot \sqrt {{3^2} + {{( – 3)}^2} + {0^2}} }} = – \frac{1}{2}$

Suy ra góc $\widehat {ABC} = {120^\circ }$.

Câu 28. [MĐ3] Một người đứng ở mặt đất điều khiển hai flycam để phục vụ trong một chương trình của đài truyền hình. Flycam I ở vị trí $A$ cách vị trí điều khiển $150\;m$ về phía nam và $200\;m$ về phía đông, đồng thời cách mặt đất $50\;m$. Flycam II ở vị trí $B$ cách vị trí điều khiển $180\;m$ về phía bắc và $240\;m$ về phía tây, đồng thời cách mặt đất $60\;m$. Chọn hệ trục toạ độ $Oxyz$ với gốc $O$ là vị trí người điều khiển, mặt phẳng $\left( {Oxy} \right)$ trùng với mặt đất, trục $Ox$ có hướng trùng với hướng nam, trục $Oy$ trùng với hướng đông, trục $Oz$ vuông góc với mặt đất hướng lên bầu trời, đơn vị trên mỗi trục tính theo mét. Khoảng cách giữa hai flycam đó bằng bao nhiêu mét ( làm tròn đến hàng đơn vị )?

Lời giải

Trả lời: $550\left( { m } \right)$

Ta có: Vị trí $A,B$có tọa độ lần lượt là: $(150;200;50),( – 180; – 240;60)$. Suy ra khoảng cách giữa hai flycam đó bằng:

$AB = \sqrt {{{( – 180 – 150)}^2} + {{( – 240 – 200)}^2} + {{(60 – 50)}^2}} \approx 550(\;m)$.

Câu 29: [MĐ2] Trong không gian $Oxyz$, cho hai mặt phẳng $\left( P \right):3x + y + 4z – 2024 = 0$ và $\left( Q \right):x + 3y – 4z – 2025 = 0$. Góc giữa hai mặt phẳng $\left( P \right),\left( Q \right)$ bằng bao nhiêu độ (làm tròn kết quả đến hàng đơn vị)?

Lời giải

Trả lời: 67

Hai mặt phẳng $\left( P \right)$và $\left( Q \right)$ lần lượt có vectơ pháp tuyến là $\overrightarrow {{n_1}} = \left( {3;\,1;\,4} \right)$ và $\overrightarrow {{n_2}} = \left( {1;\,3;\, – 4} \right)$

Ta có:$\cos \left( {(P),(Q)} \right) = \frac{{\left| {3 \cdot 1 + 1 \cdot 3 + 4 \cdot ( – 4)} \right|}}{{\sqrt {{3^2} + {1^2} + {4^2}} \cdot \sqrt {{1^2} + {3^2} + {{( – 4)}^2}} }} = \frac{5}{{13}}$.

Suy ra $\left( {(P),(Q)} \right) \approx 67^\circ $.

Câu 30: [MĐ2] Trong không gian $Oxyz$, cho hai đường thẳng ${\Delta _1}:\frac{{x + 24}}{3} = \frac{{y – 25}}{4} = \frac{z}{{ – 5}}$ và ${\Delta _2}:\frac{{x – 26}}{5} = \frac{y}{3} = \frac{z}{4}$. Góc giữa hai đường thẳng ${\Delta _1},\,{\Delta _2}$ bằng bao nhiêu độ (làm tròn kết quả đến hàng đơn vị)?

Lời giải

Trả lời: 82

Hai đường thẳng ${\Delta _1}$ và ${\Delta _2}$ lần lượt có vectơ chỉ phương là ${\vec u_1} = (3;\,4;\, – 5)$ và${\vec u_2} = (5;\,3;\,4)$.

Тa có:$\cos \left( {{\Delta _1},{\Delta _2}} \right) = \frac{{\left| {3 \cdot 5 + 4 \cdot 3 + ( – 5) \cdot 4} \right|}}{{\sqrt {{3^2} + {4^2} + {{( – 5)}^2}} \cdot \sqrt {{5^2} + {3^2} + {4^2}} }} = \frac{7}{{50}}$.

Suy ra$\left( {{\Delta _1},{\Delta _2}} \right) \approx {82^\circ }$.

Câu 31: [MĐ2] Trong không gian $Oxyz$, cho đường thẳng $\Delta :\frac{{x + 2}}{1} = \frac{{y – 5}}{2} = \frac{z}{{ – 2}}$ và mặt phẳng $\left( P \right):12y + 5z + 1 = 0$. Góc giữa đường thẳng $\Delta $ và mặt phẳng $\left( P \right)$ bằng bao nhiêu độ (làm tròn kết quả đến hàng đơn vị)?

Lời giải

Trả lời: 21

Đường thẳng $\Delta $ có một vectơ chỉ phương là $\vec u = (1;\,2;\, – 2)$ và mặt phẳng $(P)$ có một vectơ pháp tuyến là $\vec n = (0;\,12;\,5)$.

Ta có:$\sin \left( {\Delta ,(P)} \right) = \frac{{\left| {1 \cdot 0 + 2 \cdot 12 + ( – 2) \cdot 5} \right|}}{{\sqrt {{1^2} + {2^2} + {{( – 2)}^2}} \cdot \sqrt {{0^2} + {{12}^2} + {5^2}} }} = \frac{{14}}{{39}}$.

Suy ra $\left( {\Delta ,(P)} \right) \approx 21^\circ $.

Câu 32: [MĐ2] Trong không gian $Oxyz$, cho tứ diện $ABCD$ có $A\left( {5;\,3;\,6} \right)$, $B\left( {1;\,1;\,4} \right)$, $C\left( {2;\,1;\,2} \right)$ và $D\left( {0;\,0;\,4} \right)$. Khoảng cách từ điểm $A$ đến mặt phẳng $\left( {BCD} \right)$ bằng bao nhiêu?

Lời giải

Trả lời: 2

Ta có: $\overrightarrow {BC} = (1;0; – 2),\overrightarrow {BD} = ( – 1; – 1;0)$ nên $\left[ {\overrightarrow {BC} ,\overrightarrow {BD} } \right] = \left( { – 2;2; – 1} \right)$ là một vectơ pháp tuyến của mặt phẳng$\left( {BCD} \right)$.

Vậy phương trình mặt phẳng $\left( {BCD} \right)$ là:$ – 2x + 2y – z + 4 = 0$.

Khi đó, khoảng cách từ điểm $A(5;\,3;\,6)$ đến mặt phẳng $(BCD)$ bằng: $\frac{{\left| { – 2 \cdot 5 + 2 \cdot 3 – 6 + 4} \right|}}{{\sqrt {{{( – 2)}^2} + {2^2} + {{( – 1)}^2}} }} = 2$.

Câu 33: [MĐ3] Khi gắn hệ tọa độ $Oxyz$ (đơn vị trên mỗi trục tính theo mét) vào một căn nhà sao cho nên nhà thuộc mặt phẳng $\left( {Oxy} \right)$, ngươi ta coi mỗi mái nhà là một phần của mặt phẳng và thấy ba vị trí $A,B,C$ ở mái nhà bên phải lần lượt có tọa độ $\left( {2;\,0;\,4} \right)$, $\left( {4;\,0;\,3} \right)$ và $\left( {4;\,9;\,3} \right)$. Góc giữa mái nhà bên phải và nên nhà bằng bao nhiêu độ (làm tròn kết quả đến hàng đơn vị)?

Lời giải

Trả lời: 27

Mặt phẳng $(ABC)$ và $(Oxy)$ có vectơ pháp tuyến lần lượt là:${\vec n_1} = (1;0;2)$,${\vec n_2} = (0;0;1)$.

Từ đó, góc có $\alpha $ giữa mái nhà bên phải và nền nhà có$\cos \alpha = \frac{2}{{\sqrt 5 }}$.

Suy ra $\alpha \approx 27^\circ $.

Câu 34: [MĐ3] Khi gắn hệ tọa độ $Oxyz$ (đơn vị trên mỗi trục tính theo kilômét) vào một sân bay, mặt phẳng $\left( {Oxy} \right)$ trùng với mặt sân bay. Một máy bay bay theo đường thẳng từ vị trí $A\left( {3;\, – 2;\,3} \right)$ đến vị trí $B\left( {8;\,8;\,0} \right)$. Góc giữa đường bay (một phần của đường thẳng $AB$ và sân bay (một phần của mặt phẳng $\left( {Oxy} \right)$) bằng bao nhiêu độ (làm tròn kết quả đến hàng đơn vị)?

Lời giải

Trả lời: 15

Đường thẳng $AB$ có vectơ chỉ phương là $\vec u = (5;\,10;\, – 3)$, mặt phẳng $\left( {Oxy} \right)$ có vectơ pháp tuyến là $\vec n = (0\,;0\,;1)$.

Từ đó, góc $\alpha $ giữa đường bay (một phần của đường thẳng $AB$) và sân bay (một phần của mặt phẳng$(Oxy))$ có $\sin \alpha = \frac{3}{{\sqrt {134} }}$.

Suy ra $\alpha \approx 15^\circ $.

Câu 35: [MĐ3] Khi gắn hệ tọa độ $Oxyz$ (đơn vị trên mỗi trục tính theo kilômét) vào một sân bay, mặt phẳng $\left( {Oxy} \right)$ trùng với mặt sân bay. Một máy bay bay theo đường thẳng từ vị trí $A\left( {5;\,0;\,5} \right)$ đến vị trí $B\left( {10;\,10;\,3} \right)$ và hạ cánh tại vị trí $M\left( {a;\,b;\,0} \right)$. Giá trị của $a + b$ bằng bao nhiêu (viết kết quả dưới dạng số thập phân)?

Lời giải

Trả lời: 42,5

Phương trình đường thẳng $AB$ là:$\frac{{x – 5}}{5} = \frac{y}{{10}} = \frac{{z – 5}}{{ – 2}}$.

Vì $M$thuộc $AB$ nên tồn tại số thực $t$ sao cho$M(5t + 5;\,10t;\, – 2t + 5)$.

Ngoài ra, $M$ thuộc mặt phẳng $\left( {Oxy} \right)$ nên $ – 2t + 5 = 0 \Leftrightarrow t = \frac{5}{2}$. Suy ra $M(17,5;\,25;\,0)$.

Vậy $a + b = 17,5 + 25 = 42,5$.