Cách Xét Tính Đơn Điệu Của Hàm Số y=f(u) Dựa Vào Bảng Biến Thiên

Cách xét tính đơn điệu của hàm số y=f(u) dựa vào bảng biến thiên được soạn dưới dạng file word và PDF gồm 7 trang. Các bạn xem và tải về ở dưới.

I. Phương pháp

+ Từ bảng biến thiên của hàm số $y = f(x)$, suy ra dấu của $f'(x)$.

+ Tính $g'(x)$ và lập bảng biến thiên của hàm số $y = g(x)$, suy ra dấu của $g'(x)$.

+ Kết luận về tính đơn điệu của hàm số $y = g(x)$.

Chú ý:

– Đối với các hàm số thường gặp thì trong mỗi khoảng $\left( {{x_i};{x_{i + 1}}} \right)$ đạo hàm giữ nguyên một dấu. Trong đó ${x_i}$ là các giá trị để đạo hàm bằng $0$ hoặc không xác định.

– Khi $x$ đi qua nghiệm đơn (hoặc bội lẻ) thì đạo hàm đổi dấu và khi đi qua nghiệm kép (hoặc bội chẵn) thì đạo hàm không đổi dấu.

II. Các ví dụ

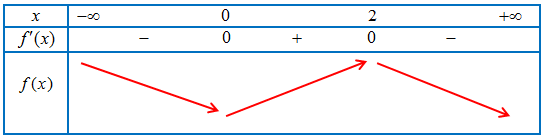
Ví dụ 1. Cho hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$ và có bảng biến thiên như sau:

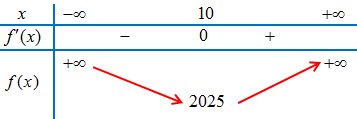
Tìm các khoảng đồng biến, nghịch biến của hàm số $y = g(x) = f\left( {4 – 3x} \right)$.

Lời giải

$y = g(x) = f\left( {4 – 3x} \right)$

Chú ý: $y = f(u) \Rightarrow y’ = {\left[ {f(u)} \right]^\prime } = u’f'(u)$

Ta có:

$g'(x) = {\left[ {f\left( {4 – 3x} \right)} \right]^\prime }$$ = {\left( {4 – 3x} \right)^\prime }f’\left( {4 – 3x} \right) = – 3f’\left( {4 – 3x} \right)$

$g'(x) = – 3f’\left( {4 – 3x} \right) = 0$$ \Leftrightarrow f’\left( {4 – 3x} \right) = 0 \Leftrightarrow 4 – 3x = 10 \Leftrightarrow x = – 2$.

Bảng biến thiên của hàm số $y = g(x)$

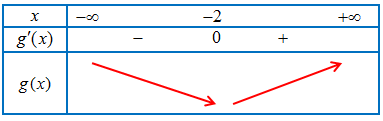
Vậy hàm số $y = g(x)$ đồng biến trên khoảng $\left( { – 2; + \infty } \right)$, nghịch biến trên khoảng $\left( { – \infty ; – 2} \right)$.

Lưu ý: Để xét dấu $g'(x)$ trong bảng biến thiên ví dụ 1 ở trên ta có thể xét dấu như sau:

– Chọn một giá trị ${x_0} \in \left( { – 2; + \infty } \right)$, chẳng hạn như ${x_0} = 0 \in \left( { – 2; + \infty } \right)$ .

Ta tính $g'(0)$ để kiểm tra dấu dương hay âm.

$g'(0) = – 3f’\left( {4 – 3.0} \right) = – 3f’\left( 4 \right)$.

Dựa vào bảng biến thiên của hàm số $y = f\left( x \right)$ ta thấy $f’\left( 4 \right) < 0$ nên $ – 3f’\left( 4 \right) > 0$.

Do đó, $g'(0) > 0$. Suy ra, $g'(x) > 0,\,\forall x \in \left( { – 2; + \infty } \right)$.

– Tiếp tục ta thấy $x = – 2$ là nghiệm đơn nên khi đi qua $x = – 2$ đạo hàm đổi dấu nên

$g'(x) < 0,\,\forall x \in \left( { – \infty ;2} \right)$.

Khi đó, ta lập được bảng biến thiên như trên.

Ta có thể làm tương tự như các ví dụ còn lại.

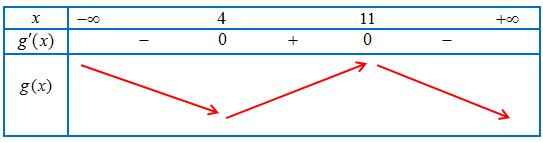
Ví dụ 2. Cho hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$ và có bảng biến thiên như sau:

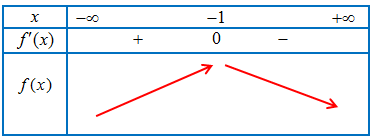
Tìm các khoảng đồng biến, nghịch biến của hàm số $y = g(x) = f\left( {x – 3} \right)$.

Lời giải

$y = g(x) = f\left( {x – 3} \right)$

Ta có:

$g'(x) = {\left[ {f\left( {x – 3} \right)} \right]^\prime }$$ = {\left( {x – 3} \right)^\prime }f’\left( {x – 3} \right) = f’\left( {x – 3} \right)$

$g'(x) = 0 \Leftrightarrow f’\left( {x – 3} \right) = 0$$ \Leftrightarrow x – 3 = – 1 \Leftrightarrow x = 2$.

Bảng biến thiên của hàm số $y = g(x)$

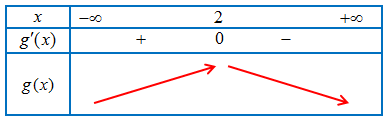
Vậy hàm số $y = g(x)$đồng biến trên khoảng $\left( { – \infty ;2} \right)$, nghịch biến trên khoảng $\left( {2; + \infty } \right)$.

Ví dụ 3. Cho hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$ và có bảng biến thiên như sau:

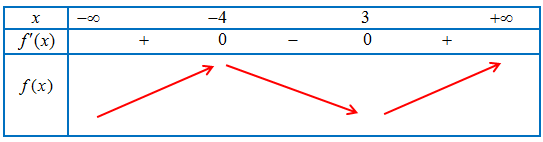
Tìm các khoảng đồng biến, nghịch biến của hàm số $y = g(x) = f\left( {7 – x} \right)$.

Lời giải

$y = g(x) = f\left( {7 – x} \right)$

Ta có:

$g'(x) = {\left[ {f\left( {7 – x} \right)} \right]^\prime }$$ = {\left( {7 – x} \right)^\prime }f’\left( {7 – x} \right) = – f’\left( {7 – x} \right)$

$g'(x) = 0 \Leftrightarrow – f’\left( {7 – x} \right) = 0 \Leftrightarrow f’\left( {7 – x} \right) = 0$$ \Leftrightarrow \left[ \begin{gathered}
7 – x = – 4 \hfill \\
7 – x = 3 \hfill \\
\end{gathered} \right. \Leftrightarrow \left[ \begin{gathered}
x = 11 \hfill \\
x = 4 \hfill \\
\end{gathered} \right.$.

Bảng biến thiên của hàm số $y = g(x)$

Vậy hàm số $y = g(x)$

– Đồng biến trên khoảng $\left( {4;11} \right)$.

– Nghịch biến trên các khoảng $\left( { – \infty ;4} \right)$ và $\left( {11; + \infty } \right)$.

Ví dụ 4. Cho hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$ và có bảng biến thiên như sau:

Tìm các khoảng đồng biến, nghịch biến của hàm số $y = g(x) = f\left( {{x^2} – 4x – 5} \right)$.

Lời giải

$y = g(x) = f\left( {{x^2} – 4x – 5} \right)$

Ta có:

$g'(x) = {\left[ {f\left( {{x^2} – 4x – 5} \right)} \right]^\prime }$$ = {\left( {{x^2} – 4x – 5} \right)^\prime }f’\left( {{x^2} – 4x – 5} \right)$

$ = \left( {2x – 4} \right)f’\left( {{x^2} – 4x – 5} \right)$

$g'(x) = 0 \Leftrightarrow \left( {2x – 4} \right)f’\left( {{x^2} – 4x – 5} \right) = 0$

$ \Leftrightarrow \left[ \begin{gathered}
2x – 4 = 0 \hfill \\
f’\left( {{x^2} – 4x – 5} \right) = 0 \hfill \\
\end{gathered} \right. \Leftrightarrow \left[ \begin{gathered}
2x = 4 \hfill \\
{x^2} – 4x – 5 = – 8 \hfill \\
\end{gathered} \right.$$ \Leftrightarrow \left[ \begin{gathered}
x = 2 \hfill \\
{x^2} – 4x + 3 = 0 \hfill \\
\end{gathered} \right. \Leftrightarrow \left[ \begin{gathered}
x = 2 \hfill \\
x = 3 \hfill \\
x = 1 \hfill \\
\end{gathered} \right.$.

Bảng biến thiên của hàm số $y = g(x)$

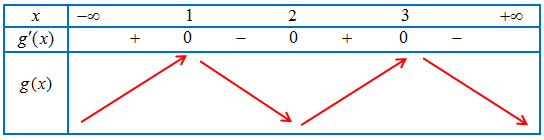
Vậy hàm số $y = g(x)$

– Đồng biến trên các khoảng $\left( { – \infty ;1} \right)$ và $\left( {2;3} \right)$.

– Nghịch biến trên các khoảng $\left( {1;2} \right)$ và $\left( {3; + \infty } \right)$.

Ví dụ 5. Cho hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$ và có bảng biến thiên như sau:

Tìm các khoảng đồng biến, nghịch biến của hàm số $y = g(x) = f\left( { – {x^3} + 3x} \right)$.

Lời giải

$y = g(x) = f\left( { – {x^3} + 3x} \right)$

Ta có:

$g'(x) = {\left[ {f\left( { – {x^3} + 3x} \right)} \right]^\prime }$$ = {\left( { – {x^3} + 3x} \right)^\prime }f’\left( { – {x^3} + 3x} \right)$

$ = \left( { – 3{x^2} + 3} \right)f’\left( { – {x^3} + 3x} \right)$

$g'(x) = 0 \Leftrightarrow \left( { – 3{x^2} + 3} \right)f’\left( { – {x^3} + 3x} \right) = 0$

$ \Leftrightarrow \left[ \begin{gathered}
– 3{x^2} + 3 = 0 \hfill \\
f’\left( { – {x^3} + 3x} \right) = 0 \hfill \\
\end{gathered} \right. \Leftrightarrow \left[ \begin{gathered}
\left[ \begin{gathered}
x = 1 \hfill \\
x = – 1 \hfill \\
\end{gathered} \right. \hfill \\
\left[ \begin{gathered}
– {x^3} + 3x = 0 \hfill \\
– {x^3} + 3x = 2 \hfill \\
\end{gathered} \right. \hfill \\
\end{gathered} \right.$$ \Leftrightarrow \left[ \begin{gathered}
\left[ \begin{gathered}
x = 1 \hfill \\
x = – 1 \hfill \\
\end{gathered} \right. \hfill \\
\left[ \begin{gathered}
x = 0 \hfill \\
x = \pm \sqrt 3 \hfill \\
x = – 2 \hfill \\
x = 1 \hfill \\
\end{gathered} \right. \hfill \\
\end{gathered} \right.$.

Bảng biến thiên của hàm số $y = g(x)$

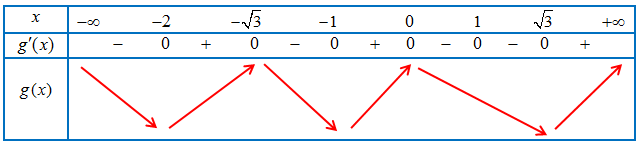
Vậy hàm số $y = g(x)$

– Đồng biến trên các khoảng $\left( { – 2; – \sqrt 3 } \right)$, $\left( { – 1;0} \right)$ và $\left( {\sqrt 3 ; + \infty } \right)$.

– Nghịch biến trên các khoảng $\left( { – \infty ; – 2} \right)$, $\left( { – \sqrt 3 ; – 1} \right)$ và $\left( {0;\sqrt 3 } \right)$.