Phương Pháp Tìm Cực Trị Của Hàm Số Cho Bởi Công Thức

Phương pháp tìm cực trị của hàm số cho bởi công thức: Hàm bậc hai, bậc ba, trùng phương; Hàm phân thức hữu tỉ.

I. Phương pháp

Bước 1. Tìm tập xác định của hàm số.

Bước 2. Tính $f’\left( x \right)$. Tìm các điểm tại đó $f’\left( x \right)$ bằng 0 hoặc $f’\left( x \right)$ không xác định.

Bước 3. Lập bảng biến thiên.

Bước 4. Từ bảng biến thiên suy ra các điểm cực trị.

II. Các ví dụ minh họa

Ví dụ 1. Tìm cực trị của hàm số $y = {x^2} – 4x – 9$.

Lời giải

Tập xác định: $D = \mathbb{R}$.

Ta có: $y’ = 2x – 4$.

$y’ = 0 \Leftrightarrow 2x – 4 = 0 \Leftrightarrow x = 2$

Bảng biến thiên

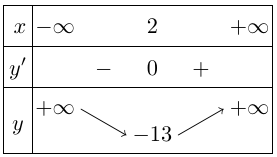
Vậy hàm số đạt cực tiểu tại $x = 2,{y_{CT}} = – 13$.

Ví dụ 2. Tìm cực trị của hàm số $y = – {x^3} + 3{x^2} + 5$.

Lời giải

Tập xác định: $D = \mathbb{R}$.

Ta có: $y’ = – 3{x^2} + 6x$.

$y’ = 0 \Leftrightarrow – 3{x^2} + 6x = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{x = 2} \\
{x = 0}
\end{array}} \right.$

Bảng biến thiên

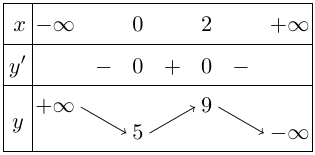
Vậy hàm số đạt cực đại tại $x = 2,{y_{CĐ}} = 9$ và đạt cực tiểu tại $x = 0,{y_{CT}} = 5$.

Ví dụ 3. Tìm cực trị của hàm số $y = {x^3} – 3{x^2} – 9x + 1$.

Lời giải

Tập xác định: $D = \mathbb{R}$.

Ta có: $y’ = 3{x^2} – 6x – 9$.

$y’ = 0 \Leftrightarrow 3{x^2} – 6x – 9 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{x = 3} \\
{x = – 1}
\end{array}} \right.$

Bảng biến thiên

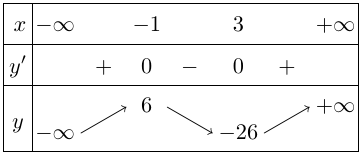
Vậy hàm số đạt cực đại tại $x = – 1,{y_{CĐ}} = 6$ và đạt cực tiểu tại $x = 3,{y_{CT}} = – 26$.

Ví dụ 4. Tìm cực trị của hàm số $y = – 2{x^3} – 3{x^2} – 6x + 1$.

Lời giải

Tập xác định $D = \mathbb{R}$.

Ta có: $y’ = – 6{x^2} – 6x – 6$.

$y’ = 0 \Leftrightarrow – 6{x^2} – 6x – 6 = 0$ (Phương trình vô nghiệm)

Bảng biến thiên

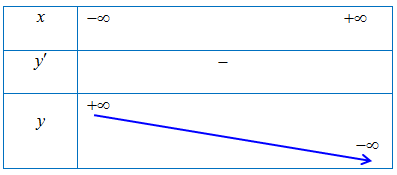
Vậy hàm số đã cho không có cực trị.

Ví dụ 5. Tìm cực trị của hàm số $y = {x^4} + 4{x^2} + 1$.

Lời giải

Tập xác định: $D = \mathbb{R}$.

Ta có: $y’ = 4{x^3} + 8x$.

$y’ = 0 \Leftrightarrow 4{x^3} + 8x = 0 \Leftrightarrow x = 0$.

Bảng biến thiên

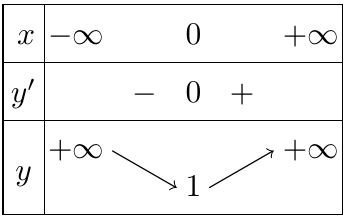
Vậy hàm số đạt cực tiểu tại $x = 0,{y_{CT}} = 1$.

Ví dụ 6. Tìm cực trị của hàm số $y = – {x^4} + 4{x^2} – 2$.

Lời giải

Tập xác định: $D = \mathbb{R}$.

Ta có: $y’ = – 4{x^3} + 8x$.

$y’ = 0 \Leftrightarrow – 4{x^3} + 8x = 0 \Leftrightarrow \left[ \begin{gathered}
x = \sqrt 2 \hfill \\
x = 0 \hfill \\
x = – \sqrt 2 \hfill \\
\end{gathered} \right.$.

Bảng biến thiên

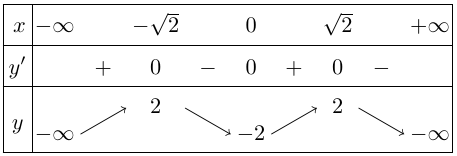
Vậy hàm số đạt cực đại tại $x = \pm \sqrt 2 ,{y_{CĐ}} = 2$ và đạt cực tiểu tại $x = 0,{y_{CT}} = – 2$.

Ví dụ 7. Tìm cực trị của hàm số $y = \frac{{5x – 3}}{{x + 4}}$.

Lời giải

Tập xác định .

$y’ = \frac{{23}}{{{{\left( {x + 4} \right)}^2}}} > 0,\,\forall x \in D$.

Vậy hàm số đã cho không có cực trị.

Chú ý: Hàm số $y = \frac{{ax + b}}{{cx + d}}$ không có cực trị.

Ví dụ 8. Tìm cực trị của hàm số $y = \frac{{{x^2} – 2x + 9}}{{x – 2}}$.

Lời giải

Tập xác định: $D = \mathbb{R}\backslash \left\{ 2 \right\}$.

Ta có: $y’ = \frac{{{{\left( {{x^2} – 2x + 9} \right)}^\prime }\left( {x – 2} \right) – \left( {{x^2} – 2x + 9} \right){{\left( {x – 2} \right)}^\prime }}}{{{{\left( {x – 2} \right)}^2}}}$

$ = \frac{{\left( {2x – 2} \right)\left( {x – 2} \right) – \left( {{x^2} – 2x + 9} \right).1}}{{{{\left( {x – 2} \right)}^2}}}$

$ = \frac{{2{x^2} – 4x – 2x + 4 – {x^2} + 2x – 9}}{{{{\left( {x – 2} \right)}^2}}}$$ = \frac{{{x^2} – 4x – 5}}{{{{\left( {x – 2} \right)}^2}}}$.

$y’ = 0 \Leftrightarrow {x^2} – 4x – 5 = 0 \Leftrightarrow \left[ \begin{gathered}
x = 5 \hfill \\
x = – 1 \hfill \\
\end{gathered} \right.$.

Bảng biến thiên

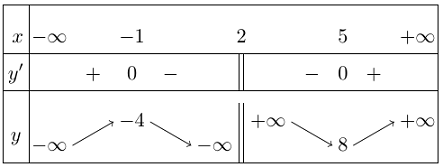
Vậy hàm số đạt cực đại tại $x = – 1,{y_{CĐ}} = – 4$ và đạt cực tiểu tại $x = 5,{y_{CT}} = 8$.

Ví dụ 9. Tìm cực trị của hàm số $y = \frac{{ – 4{x^2} + 12x – 1}}{{x – 3}}$.

Lời giải

Tập xác định: $D = \mathbb{R}\backslash \left\{ 2 \right\}$.

Ta có: $y’ = \frac{{{{\left( { – 4{x^2} + 12x – 1} \right)}^\prime }\left( {x – 3} \right) – \left( { – 4{x^2} + 12x – 1} \right){{\left( {x – 3} \right)}^\prime }}}{{{{\left( {x – 3} \right)}^2}}}$

$ = \frac{{{{\left( { – 4{x^2} + 12x – 1} \right)}^\prime }\left( {x – 3} \right) – \left( { – 4{x^2} + 12x – 1} \right){{\left( {x – 3} \right)}^\prime }}}{{{{\left( {x – 3} \right)}^2}}}$

$ = \frac{{\left( { – 8x + 12} \right)\left( {x – 3} \right) – \left( { – 4{x^2} + 12x – 1} \right).1}}{{{{\left( {x – 3} \right)}^2}}}$

$ = \frac{{ – 8{x^2} + 24x + 12x – 36 + 4{x^2} – 12x + 1}}{{{{\left( {x – 3} \right)}^2}}}$.

$ = \frac{{ – 4{x^2} + 24x – 35}}{{{{\left( {x – 3} \right)}^2}}}$

$y’ = 0 \Leftrightarrow – 4{x^2} + 24x – 35 = 0$$ \Leftrightarrow \left[ \begin{gathered}
x = \frac{7}{2} \hfill \\
x = \frac{5}{2} \hfill \\
\end{gathered} \right.$.

Bảng biến thiên

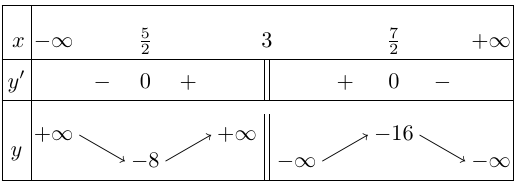
Vậy hàm số đạt cực đại tại $x = \frac{7}{2},{y_{CĐ}} = – 16$ và đạt cực tiểu tại $x = \frac{5}{2},{y_{CT}} = – 8$.

Ví dụ 10. Tìm cực trị của hàm số $y = \sqrt {{x^2} – 6x} $.

Lời giải

Tập xác định: $D = \left( { – \infty ;0} \right] \cup \left[ {6; + \infty } \right)$.

Ta có: $y’ = \frac{{{{\left( {{x^2} – 6x} \right)}^\prime }}}{{2\sqrt {{x^2} – 6x} }} = \frac{{2x – 6}}{{2\sqrt {{x^2} – 6x} }} = \frac{{x – 3}}{{\sqrt {{x^2} – 6x} }}$.

$y’ = 0 \Leftrightarrow x = 3$ (loại)

Bảng biến thiên

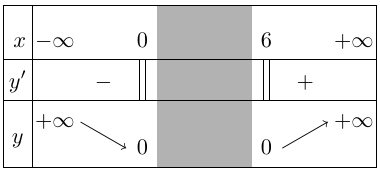
Vậy hàm số không có cực trị.

Ví dụ 11. Tìm cực trị của hàm số $y = \sqrt {8x – 2{x^2}} $.

Lời giải

Tập xác định: $D = \left[ {0;4} \right]$.

Ta có: $y’ = \frac{{{{\left( {8x – 2{x^2}} \right)}^\prime }}}{{2\sqrt {8x – 2{x^2}} }} = \frac{{8 – 4x}}{{2\sqrt {8x – 2{x^2}} }} = \frac{{4 – 2x}}{{\sqrt {8x – 2{x^2}} }}$.

$y’ = 0 \Leftrightarrow x = 2$ (nhận)

Bảng biến thiên

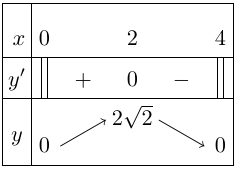
Vậy hàm số đạt cực đại tại $x = 2$, ${y_{CĐ}} = 2\sqrt 2 $.

Ví dụ 12. Tìm cực trị của hàm số $y = {(1 – x)^3}{(3x – 8)^2}$.

Lời giải

Tập xác định: $D = \mathbb{R}$.

Ta có: $y’ = 15{(1 – x)^2}\left( {3x – 8} \right)\left( {2 – x} \right)$.

$y’ = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = \frac{8}{3}} \\
{x = 1} \\
{x = 2}
\end{array}} \right.$

Ta có bảng biến thiên

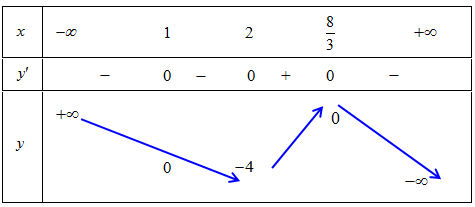
Suy ra hàm số đạt cực đại tại $x = \frac{8}{3},{y_{CĐ}} = 0$ và hàm số đạt cực tiểu tại $x = 2,{y_{CT}} = – 4$.