Phương Pháp Tìm GTLN Và GTNN Của Hàm Số Chứa Giá Trị Tuyệt Đối Lớp 12

Phương pháp tìm GTLN và GTNN của hàm số chứa giá trị tuyệt đối lớp 12 được soạn dưới dạng file word và PDF gồm 2 trang. Các bạn xem và tải về ở dưới.

I. Phương pháp: Để tìm Giá trị lớn nhất và nhỏ nhất của hàm số $y = | f(x)|$ ta làm như sau:

Bước 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = f(x)$.

Giả sử $\mathop {\min }\limits_D f(x) = m$; $\mathop {\max }\limits_D f(x) = M$.

Bước 2: Khi đó,

$\mathop {max}\limits_D |f(x)| = \frac{{|M + m| + |M – m|}}{2}$;

$\mathop {\min }\limits_D |f(x)| = \left\{ {\begin{array}{*{20}{l}}
{\frac{{|M + m| – |M – m|}}{2}}&{ khi\,\,m.M > 0} \\
0&{ khi\,\,m.M \leqslant 0}
\end{array}} \right.$.

II. Các ví dụ

Mức thông hiểu

Ví dụ 1: Gọi $M$ và $m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = \left| {{x^2} – 2x + 2} \right|$ trên đoạn $\left[ {0;2} \right]$. Tính $m + M$.

Lời giải

* Tìm GTLN và GTNN của hàm số $f(x) = {x^2} – 2x + 2$ trên đoạn $\left[ {0;2} \right]$.

Ta có:

$f'(x) = 2x – 2$; $f'(x) = 0 \Leftrightarrow x = 1$.

$f(0) = 2$; $f(1) = 1$; $f(2) = 2$.

Suy ra, $\mathop {\min }\limits_{\left[ {0;2} \right]} f(x) = 1$; $\mathop {max}\limits_{\left[ {0;2} \right]} f(x) = 2$

* Do đó, $m = \mathop {\min }\limits_{\left[ {0;2} \right]} \left| {{x^2} – 2x + 2} \right| = \frac{{\left| {2 + 1} \right| – \left| {2 – 1} \right|}}{2} = 1$; $M = \mathop {max}\limits_{\left[ {0;2} \right]} \left| {{x^2} – 2x + 2} \right| = \frac{{\left| {2 + 1} \right| + \left| {2 – 1} \right|}}{2} = 2$.

Vậy, $m + M = 1 + 2 = 3$.

Ví dụ 2: Gọi $M$ và $m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = \left| {\frac{{2x – 5}}{{4x – 5}}} \right|$ trên đoạn $\left[ { – 4; – 1} \right]$. Tính $m + M$.

Lời giải

* Tìm GTLN và GTNN của hàm số $f(x) = \frac{{2x – 5}}{{4x – 5}}$ trên đoạn $\left[ { – 4; – 1} \right]$.

Ta có:

$f'(x) = \frac{{10}}{{{{\left( {4x – 5} \right)}^2}}} > 0,\,\forall x \in \left[ { – 4; – 1} \right]$;

Suy ra, $\mathop {\min }\limits_{\left[ { – 4; – 1} \right]} f(x) = f( – 4) = \frac{{13}}{{21}}$; $\mathop {max}\limits_{\left[ { – 4; – 1} \right]} f(x) = f( – 1) = \frac{7}{9}$

* Do đó, $m = \mathop {\min }\limits_{\left[ { – 4; – 1} \right]} \left| {f(x)} \right| = \frac{{\left| {\frac{7}{9} + \frac{{13}}{{21}}} \right| – \left| {\frac{7}{9} – \frac{{13}}{{21}}} \right|}}{2} = \frac{{13}}{{21}}$; $\mathop {max}\limits_{\left[ { – 4; – 1} \right]} \left| {f(x)} \right| = \frac{{\left| {\frac{7}{9} + \frac{{13}}{{21}}} \right| + \left| {\frac{7}{9} – \frac{{13}}{{21}}} \right|}}{2} = \frac{7}{9}$.

Vậy, $m + M = \frac{{13}}{{21}} + \frac{7}{9} = \frac{{88}}{{63}}$.

Ví dụ 3: Gọi $M$ và $m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = \left| {{x^3} – 3x} \right|$ trên đoạn $\left[ { – 2;2} \right]$. Tính $m + M$.

Lời giải

* Tìm GTLN và GTNN của hàm số $f(x) = {x^3} – 3x$ trên đoạn $\left[ { – 2;2} \right]$.

Ta có:

$f'(x) = 3{x^2} – 3$; $f'(x) = 0 \Leftrightarrow \left[ \begin{gathered}
x = 1 \hfill \\
x = – 1 \hfill \\
\end{gathered} \right.$.

Khi đó, $f( – 2) = – 2$; $f(2) = 2$; $f(1) = – 2$; $f( – 1) = 2$.

Suy ra, $\mathop {\min }\limits_{\left[ { – 2;2} \right]} f(x) = – 2$; $\mathop {max}\limits_{\left[ { – 2;2} \right]} f(x) = 2$

* Do đó,

$m = \mathop {\min }\limits_{\left[ { – 2;2} \right]} \left| {{x^3} – 3x} \right| = 0$ (Do $\mathop {\min }\limits_{\left[ { – 2;2} \right]} f(x).\mathop {max}\limits_{\left[ { – 2;2} \right]} f(x) = – 2.2 = – 4 < 0$);

$M = \mathop {max}\limits_{\left[ { – 2;2} \right]} \left| {{x^3} – 3x} \right| = \frac{{\left| {2 + ( – 2)} \right| + \left| {2 – ( – 2)} \right|}}{2} = 2$.

Vậy, $m + M = 0 + 2 = 2$.

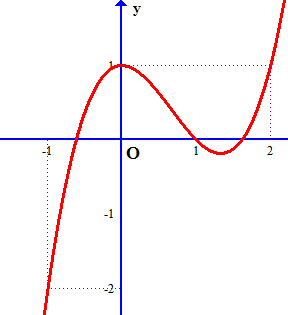
Ví dụ 4: Cho hàm số $y = f(x)$ có đồ thị như hình vẽ dưới. Gọi $M$ và $m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = \left| {f(x)} \right|$ trên đoạn $\left[ { – 1;2} \right]$. Tính $m + M$.

Lời giải

* Dựa vào đồ thị hàm số $y = f(x)$ ta thấy $\mathop {\min }\limits_{\left[ { – 2;2} \right]} f(x) = – 2$; $\mathop {max}\limits_{\left[ { – 2;2} \right]} f(x) = 1$

* Do đó,

$m = \mathop {\min }\limits_{\left[ { – 1;2} \right]} \left| {f(x)} \right| = 0$ (Do $\mathop {\min }\limits_{\left[ { – 1;2} \right]} f(x).\mathop {max}\limits_{\left[ { – 1;2} \right]} f(x) = – 2.1 = – 2 < 0$);

$M = \mathop {max}\limits_{\left[ { – 1;2} \right]} \left| {f(x)} \right| = \frac{{\left| {1 + ( – 2)} \right| + \left| {1 – ( – 2)} \right|}}{2} = 2$.

Vậy, $m + M = 0 + 2 = 2$.

Mức vận dụng

Ví dụ 5. Tính tổng các giá trị của tham số $m$ để giá trị lớn nhất của hàm số $y = \left| { – {x^4} + 8{x^2} + m} \right|$ trên đoạn $\left[ { – 1;3} \right]$ bằng $2025$.

A. $6$. B. $ – 6$. C. $ – 7$. D. $4$.

Lời giải

Ta có $f\left( x \right) = – {x^4} + 8{x^2} + m$ nên $f’\left( x \right) = – 4{x^3} + 16x$.

$f’\left( x \right) = 0 \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
x = \pm 2. \hfill \\
\end{gathered} \right.$

Khi đó, $f\left( { – 1} \right) = m + 7$; $f\left( 0 \right) = m$; $f\left( 2 \right) = m + 16$; $f\left( 3 \right) = m – 9$.

Suy ra, $\mathop {\max }\limits_{\left[ { – 1;3} \right]} f(x) = m + 16$ và $\mathop {\min }\limits_{\left[ { – 1;3} \right]} f(x) = m – 9$.

Do đó, $\mathop {\max }\limits_{\left[ { – 1;3} \right]} y = \frac{{\left| {(m + 16) + (m – 9)} \right| + \left| {(m + 16) – (m – 9)} \right|}}{2}$

$ = \frac{{\left| {2m + 7} \right| + 25}}{2} = 2025 \Leftrightarrow \left| {2m + 7} \right| = 4025$

$ \Leftrightarrow \left[ \begin{gathered}
2m + 7 = 4025 \hfill \\
2m + 7 = – 4025 \hfill \\
\end{gathered} \right. \Leftrightarrow \left[ \begin{gathered}
m = 2009 \hfill \\
m = – 2016 \hfill \\
\end{gathered} \right.$

Vậy tổng các giá trị của tham số $m$ là $2009 + ( – 2016) = – 7$.

Ví dụ 6. Gọi S là tập tất cả các giá trị nguyên của tham số thực m sao cho giá trị lớn nhất của hàm số $y = \left| {\frac{1}{4}{x^4} – 14{x^2} + 48x + {m^2} – 30} \right|$ trên đoạn $\left[ {0;2} \right]$ không vượt quá 30. Tìm số phần tử của S.

Lời giải

Xét hàm số $y = f\left( x \right) = \frac{1}{4}{x^4} – 14{x^2} + 48x + {m^2} – 30$ liên tục trên đoạn $\left[ {0;2} \right]$

$f’\left( x \right) = {x^3} – 28x + 48$; $f’\left( x \right) = 0 \Leftrightarrow \left[ \begin{gathered}
x = – 6 \notin \left[ {0;2} \right] \hfill \\
x = 4 \notin \left[ {0;2} \right] \hfill \\
x = 2 \in \left[ {0;2} \right] \hfill \\
\end{gathered} \right.$; $f\left( 0 \right) = {m^2} – 30,f\left( 2 \right) = 14 + {m^2}$

Do đó, $\mathop {\max }\limits_{\left[ {0;2} \right]} y = \frac{{\left| {(14 + {m^2}) + ({m^2} – 30)} \right| + \left| {(14 + {m^2}) – ({m^2} – 30)} \right|}}{2}$

$ = \frac{{\left| {2{m^2} – 16} \right| + 44}}{2} = \left| {{m^2} – 8} \right| + 22 \leqslant 30$

$ \Leftrightarrow 0 \leqslant {m^2} \leqslant 16 \Leftrightarrow – 4 \leqslant m \leqslant 4$$\mathop \Rightarrow \limits^{m \in \mathbb{Z}} m \in \left\{ { – 4; – 3; \cdots ;4} \right\}$

Vậy, có 9 phần tử $m$ nguyên thỏa yêu cầu bài toán.

Ví dụ 7. Có bao nhiêu số thực $m$ để hàm số $y = \left| {3{x^4} – 4{x^3} – 12{x^2} + m} \right|$ có giá trị lớn nhất trên đoạn $\left[ { – 3;2} \right]$ bằng $150$?

Lời giải

Đặt $f\left( x \right) = 3{x^4} – 4{x^3} – 12{x^2} + m$. Ta có $f’\left( x \right) = 12{x^3} – 12{x^2} – 24x = 0 \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
x = – 1 \hfill \\
x = 2 \hfill \\
\end{gathered} \right.$.

$f\left( { – 3} \right) = 243 + m$, $f\left( { – 1} \right) = – 5 + m$, $f\left( 0 \right) = m$, $f\left( 2 \right) = – 32 + m$.

Khi đó $\left\{ \begin{gathered}
A = \mathop {\max }\limits_{\left[ { – 3;2} \right]} f\left( x \right) = \max \left\{ {f\left( { – 3} \right);f\left( { – 1} \right);f\left( 0 \right);f\left( 2 \right)} \right\} \hfill \\
a = \mathop {\min }\limits_{\left[ { – 3;2} \right]} f\left( x \right) = \min \left\{ {f\left( { – 3} \right);f\left( { – 1} \right);f\left( 0 \right);f\left( 2 \right)} \right\} \hfill \\
\end{gathered} \right.$$ \Rightarrow \left\{ \begin{gathered}
A = f\left( { – 3} \right) = 243 + m \hfill \\
a = f\left( 2 \right) = – 32 + m \hfill \\
\end{gathered} \right.$

Vậy $\mathop {\max }\limits_{\left[ { – 3;2} \right]} y = \frac{{\left| {A + a} \right| + \left| {A – a} \right|}}{2} = \frac{{\left| {211 + 2m} \right| + 275}}{2} = 150 \Leftrightarrow \left| {211 + 2m} \right| = 25$

$ \Leftrightarrow \left[ \begin{gathered}
211 + 2m = 25 \hfill \\
211 + 2m = – 25 \hfill \\
\end{gathered} \right. \Leftrightarrow \left[ \begin{gathered}
m = – 93 \hfill \\
m = – 118 \hfill \\
\end{gathered} \right.$

Do đó có hai giá trị của $m$ thỏa mãn yêu cầu bài toán.

Ví dụ 8. Tìm $m$ để giá trị lớn nhất của hàm số $y = \left| {{x^3} – 3x + 2m – 1} \right|$ trên đoạn $\left[ {0\,;\,2} \right]$ là nhỏ nhất.

Lời giải

Đặt $f\left( x \right) = {x^3} – 3x + 2m – 1 \Rightarrow f’\left( x \right) = 3{x^2} – 3$.

Xét $f’\left( x \right) = 0 \Leftrightarrow 3{x^2} – 3 = 0 \Leftrightarrow \left[ \begin{gathered}
x = – 1 \notin \left[ {0\,;\,2} \right] \hfill \\
x = 1 \in \left[ {0\,;\,2} \right] \hfill \\
\end{gathered} \right.$.

Ta có : $\left\{ \begin{gathered}
f\left( 0 \right) = 2m – 1 \hfill \\
f\left( 1 \right) = 2m – 3 \hfill \\
f\left( 2 \right) = 2m + 1 \hfill \\
\end{gathered} \right.\,\,\,\,\, \Rightarrow \left\{ \begin{gathered}
\mathop {\max }\limits_{\left[ {0\,;\,2} \right]} f\left( x \right) = 2m + 1, \hfill \\
\mathop {\min }\limits_{\left[ {0\,;\,2} \right]} f\left( x \right) = 2m – 3. \hfill \\
\end{gathered} \right.$

Suy ra, $M = \mathop {\max }\limits_{\left[ {0\,;\,2} \right]} \left| {{x^3} – 3x + 2m – 1} \right| = \left| {2m – 1} \right| + 2 \geqslant 2$.

Do đó, $\min M = 2$.

Dấu “$ = $” xảy ra $ \Leftrightarrow \left| {2m – 1} \right| \Leftrightarrow m = \frac{1}{2}$.

Mức vận dụng cao

Ví dụ 9. Gọi $S$ là tập hợp tất cả các giá trị nguyên của tham số thực $m$ sao cho giá trị lớn nhất của hàm số $y = \left| {\frac{1}{4}{x^4} – 14{x^2} + 48x + m – 30} \right|$ trên đoạn $\left[ {0;2} \right]$ không vượt quá $30$. Tính tổng giá trị các phần tử của tập hợp $S$.

Lời giải

Đặt $g\left( x \right) = \frac{1}{4}{x^4} – 14{x^2} + 48x + m – 30$$ \Rightarrow g’\left( x \right) = {x^3} – 28x + 48$

$ \Rightarrow g’\left( x \right) = 0 \Leftrightarrow \left[ \begin{gathered}
x = – 6 \hfill \\
x = 2 \hfill \\
x = 4 \hfill \\
\end{gathered} \right.$

Suy ra, $\mathop {\min }\limits_{\left[ {0;2} \right]} g(x) = m – 30$; $\mathop {max}\limits_{\left[ {0;2} \right]} g(x) = m + 14$.

Do đó, $\mathop {max}\limits_{\left[ {0;2} \right]} y = \mathop {max}\limits_{\left[ {0;2} \right]} \left| {g(x)} \right| = \left| {m – 8} \right| + 22$

Theo đề, ta có $\mathop {max}\limits_{\left[ {0;2} \right]} y \leqslant 30 \Leftrightarrow \left| {m – 8} \right| + 22 \leqslant 30 \Leftrightarrow \left| {m – 8} \right| \leqslant 8 \Leftrightarrow 0 \leqslant m \leqslant 16$

Vậy $S = \left\{ {0;1;2;3;…;16} \right\}$.

Suy ra tổng giá trị các phần tử của tập hợp $S$ bằng $136$.

Ví dụ 10. Cho hàm số $f\left( x \right) = {x^2} – 2x + 1$. Gọi $S$ là tập hợp tất cả các giá trị thực của tham số $m$ để giá trị lớn nhất của hàm số $g\left( x \right) = \left| {{f^2}\left( x \right) – 2f\left( x \right) + m} \right|$ trên đoạn $\left[ { – 1;3} \right]$ bằng $8$. Tính tổng các phẩn tử của $S$.

Lời giải

Đặt $t = {x^2} – 2x + 1 \Rightarrow t’ = 2x – 2 \Rightarrow t = 0 \Leftrightarrow x = 1 \in \left[ { – 1;3} \right]$.

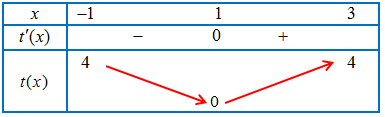
Dựa vào bảng biến thiên ta có: $t \in \left[ {0;4} \right]$.

Bài toán đưa về: Gọi $S$ là tập hợp tất cả các giá trị thực của tham số $m$ để giá trị lớn nhất của hàm số $g\left( t \right) = \left| {{t^2} – 2t + m} \right|$ trên đoạn $\left[ {0;4} \right]$ bằng $8$. Tính tổng các phẩn tử của $S$.

Đặt $h\left( t \right) = {t^2} – 2t + m \Rightarrow t’ = 2t – 2 \Rightarrow h’\left( t \right) = 0 \Leftrightarrow t = 1 \in \left[ {0;4} \right]$.

Ta có $h\left( 1 \right) = m – 1,h\left( 0 \right) = m – 1,h\left( 4 \right) = m + 8$

Do đó, $\mathop {max}\limits_{\left[ { – 1;3} \right]} g(x) = \frac{{\left| {\left( {m + 8} \right) + (m – 1)} \right| + \left( {m + 8} \right) + (m – 1)}}{2}$

$ = \frac{{\left| {2m + 7} \right| + 9}}{2} = 8$$ \Leftrightarrow \left[ \begin{gathered}
m = 0 \hfill \\
m = – 7 \hfill \\
\end{gathered} \right.$$ \Rightarrow S = \left\{ { – 7;0} \right\}$

Vậy, tổng các phần tử của $S$ bằng $ – 7 + 0 = – 7.$