Ứng Dụng Hệ Tọa Độ Không Gian Oxyz Để Giải Các Bài Toán Hình Học

Ứng dụng hệ tọa độ không gian oxyz để giải các bài toán hình học giải chi tiết được soạn dưới dạng file word và PDF gồm 8 trang. Các bạn xem và tải về ở dưới.

A. PHƯƠNG PHÁP

I. Gắn tọa độ đối với hình chóp

1. Hình chóp có cạnh bên (SA) vuông góc với mặt đáy:

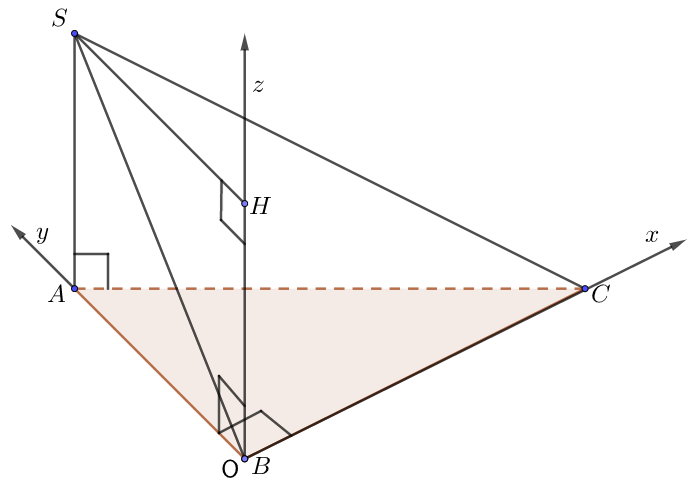
a) Đáy là tam giác đều

• Gọi O là trung điểm BC. Chọn hệ trục như hình vẽ, $AB = a = 1$.

• Tọa độ các điểm là: $O(0;0;0),\,\,A\left( {0;\frac{{\sqrt 3 }}{2};0} \right)$, $B\left( { – \frac{1}{2};0;0} \right)$, $C\left( {\frac{1}{2};0;0} \right)$, $S\left( {0;\frac{{\sqrt 3 }}{2};\underbrace {OH}_{ = SA}} \right)$

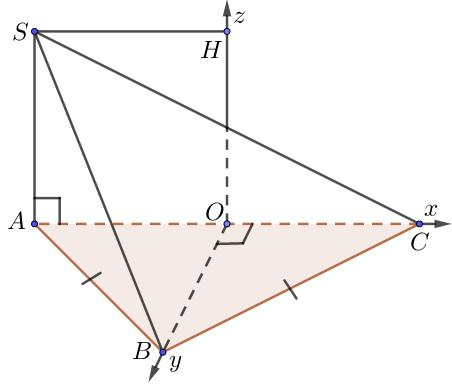
b) Đáy là tam giác cân tại A

• Gọi O là trung điểm BC. Chọn hệ trục như hình vẽ, $a = 1$.

• Tọa độ các điểm là: $O(0;0;0)$, $A\left( {0;OA;0} \right)$, $B\left( { – OB;0;0} \right)$, $C\left( {OC;0;0} \right)$, $S\left( {0;OA;\underbrace {OH}_{ = SA}} \right)$

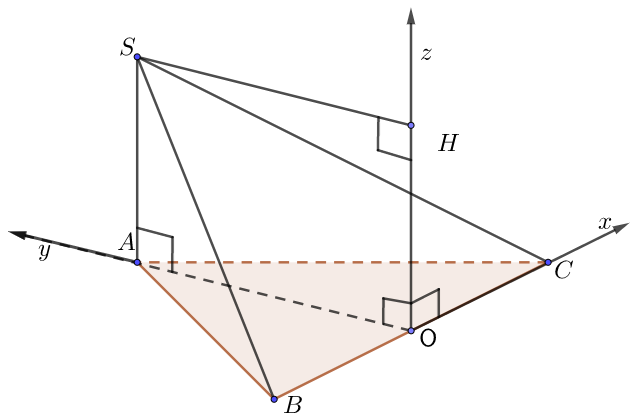
c) Đáy là tam giác cân tại B

• Gọi O là trung điểm AC. Chọn hệ trục như hình vẽ, $a = 1$.

• Tọa độ các điểm: $O\left( {0;0;0} \right)$, $A\left( { – OA;0;0} \right)$, $B\left( {0,OB;0} \right)$$C\left( {OC;0;0} \right)$, $S\left( { – OA;0;\underbrace {OH}_{ = SA}} \right)$.

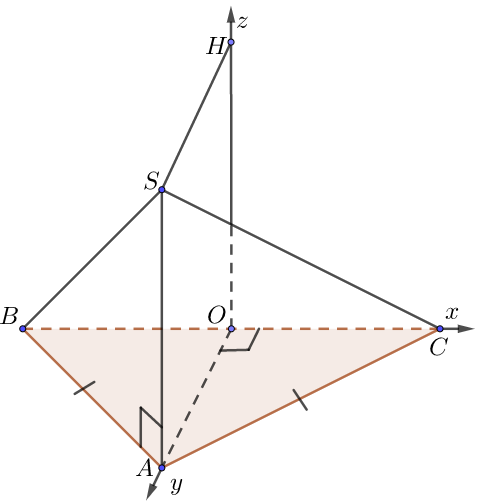
d) Đáy là tam giác vuông tại B

• Chọn hệ trục như hình vẽ, $a = 1$.

• Tọa độ các điểm: $B \equiv O\left( {0;0;0} \right)$, $C\left( {BC,0;0} \right)$, $A\left( {0;AB;0} \right)$, $S\left( {0;AB;\underbrace {BH}_{ = SA}} \right)$.

e) Đáy là tam giác vuông tại A

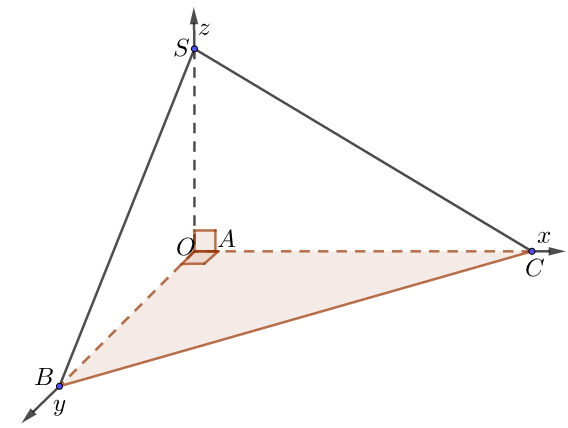
• Chọn hệ trục như hình vẽ, $a = 1$.

• Tọa độ các điểm: $A \equiv O\left( {0;0;0} \right)$, $B\left( {0;OB;0} \right),\,\,C\left( {AC;0;0} \right),$$S\left( {0;0;SA} \right)$.

e) Đáy là tam giác thường

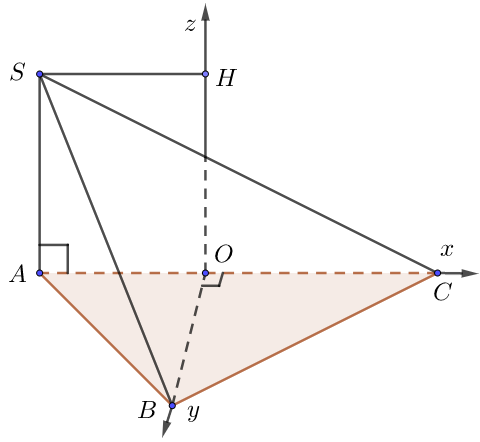
• Dựng đường cao BO của $\Delta ABC.$Chọn hệ trục như hình vẽ, $a = 1$.

• Tọa độ các điểm: $O\left( {0;0;0} \right)$,

$A\left( { – OA;0;0} \right)$, $B\left( {0,OB;0} \right)$, $C\left( {OC;0;0} \right)$, $S\left( { – OA;0;\underbrace {OH}_{ = SA}} \right)$

f) Đáy hình vuông, hình chữ nhật

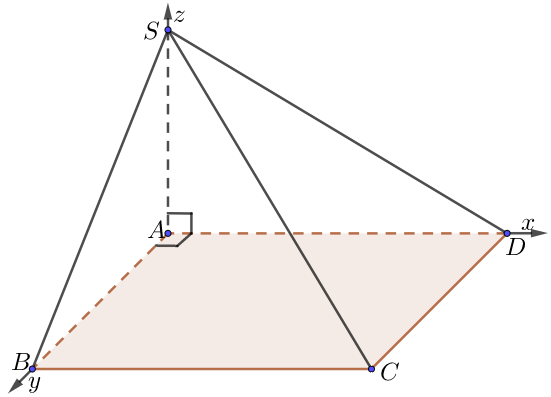
• Chọn hệ trục như hình vẽ, $a = 1.$

• Tọa độ $A \equiv O\left( {0;0;0} \right)$,$B\left( {0;AB;0} \right),$ $C\left( {AD;AB;0} \right)$, $\,D\left( {AD;0;0} \right)$, $S\left( {0;0;SA} \right)$

g) Đáy là hình thoi

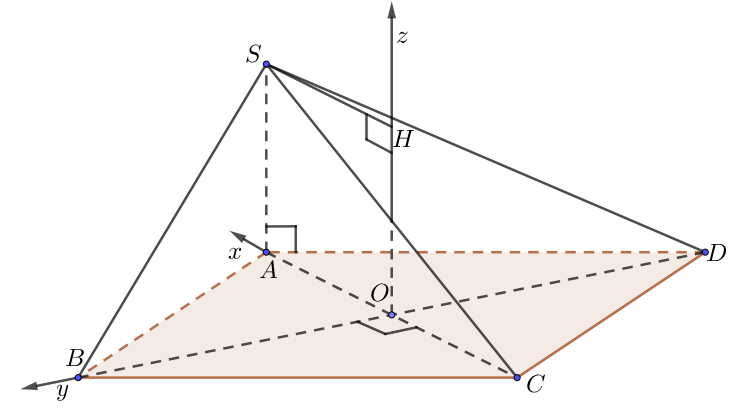
• Chọn hệ trục như hình vẽ, $a = 1.$

• Tọa độ $O\left( {0;0;0} \right)$, $A\left( {OA;0;0} \right),$ $B\left( {0;OB;0} \right)$,$C\left( { – OC;0;0} \right)$, $D\left( {0; – OD;0} \right)$, $S\left( {OA;0;\underbrace {OH}_{ = SA}} \right)$

h) Đáy là hình thang vuông

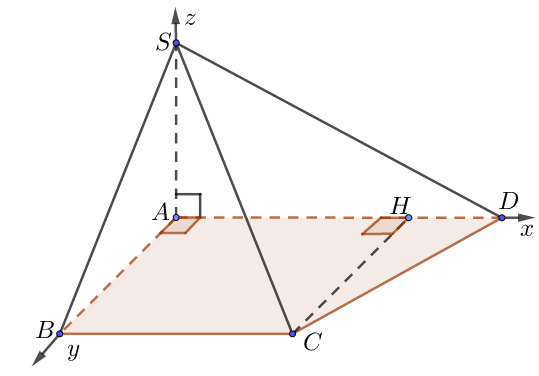
• Chọn hệ trục như hình vẽ, $a = 1.$

• Tọa độ $A \equiv O\left( {0;0;0} \right)$,$B\left( {0;AB;0} \right),\,\,C\left( {AH;AB;0} \right),$$D\left( {AD;0;0} \right),\,\,S\left( {0;0;SA} \right).$

2. Hình chóp có mặt bên (SAB) vuông góc với mặt đáy

a) Đáy là tam giác, mặt bên là tam giác thường

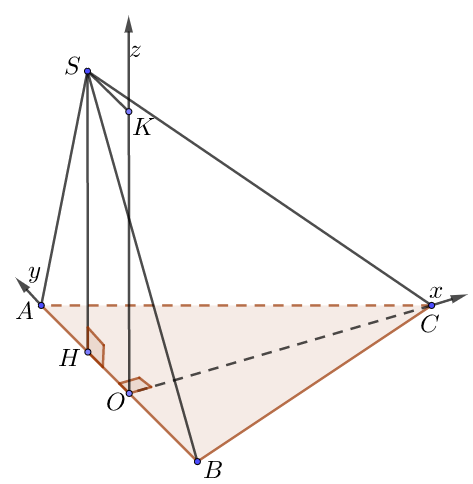
• Vẽ đường cao CO trong $\Delta ABC$. Chọn hệ trục như hình, a = 1.

• Ta có: $O\left( {0;0;0} \right),\,\,A\left( {0;OA;0} \right),$ $B\left( {0; – OB;0} \right)$, $C\left( {OC;0;0} \right)$,$S\left( {0;OH;\underbrace {OK}_{ = SH}} \right)$

b) Đáy là tam giác cân tại C (hoặc đều), mặt bên là tam giác cân tại S (hoặc đều)

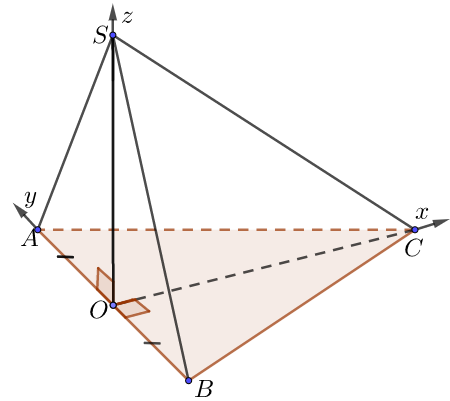
• Gọi O là trung điểm BC, chọn hệ trục như hình, a = 1.

• Ta có: $O\left( {0;0;0} \right),\,\,A\left( {0;OA;0} \right),$

$B\left( {0; – OB;0} \right),\,\,C\left( {OC;0;0} \right),\,\,S\left( {0;0;SO} \right)$

c) Đáy là hình vuông-hình chữ nhật

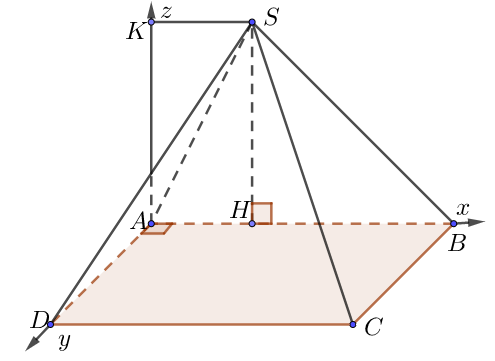
• Dựng hệ trục như hình, chọn a = 1.

• Ta có:

$A \equiv O\left( {0;0;0} \right),\,B\left( {AB;0;0} \right),C\left( {AB;AD;0} \right),\,$ $D\left( {0;AD;0} \right),\,$$S\left( {AH;0;\underbrace {AK}_{ = SH}} \right)$

3. Hình chóp đều

a) Hình chóp tam giác đều

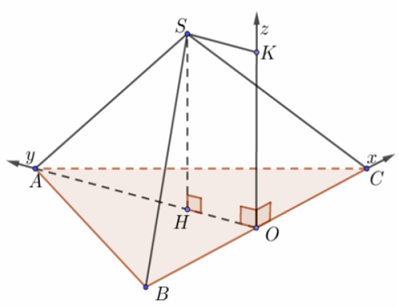
Gọi O là trung điểm một cạnh đáy. Dựng hệ trục như hình vẽ và a = 1.

Tọa độ điểm:

$O\left( {0;0;0} \right),$$A\left( {0;\frac{{AB\sqrt 3 }}{2};0} \right)$,$B\left( { – \frac{{BC}}{2};0;0} \right)$, $C\left( {\frac{{BC}}{2};0;0} \right)$, $S\left( {0;\underbrace {\frac{{AB\sqrt 3 }}{6}}_{ = OH};\underbrace {OK}_{ = SH}} \right)$.

b) Hình chóp tứ giác đều

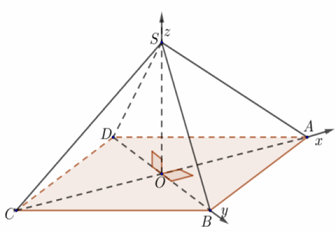
Chọn hệ trục như hình với a = 1.

Tọa độ điểm:

$O\left( {0;0;0} \right),$$A\left( {\underbrace {\frac{{AB\sqrt 2 }}{2}}_{ = OA};0;0} \right),$$B\left( {0;\underbrace {\frac{{AB\sqrt 2 }}{2}}_{ = OB};0} \right)$,$C\left( {\underbrace { – \frac{{AB\sqrt 2 }}{2}}_{ = – OA};0;0} \right),$ $D\left( {0; – \underbrace {\frac{{AB\sqrt 2 }}{2}}_{ = OB};0} \right);$$S\left( {0;0;SO} \right)$.

II. Gắn tọa độ đối với hình lăng trụ

1. Lăng trụ đứng

a) Hình lập phương, hình hộp chữ nhật

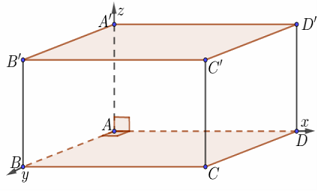
Dựng hệ trục như hình vẽ với a = 1. Tọa độ điểm:

$A \equiv O\left( {0;0;0} \right),$

$B\left( {0;AB;0} \right),$$C\left( {AD;AB;0} \right)$,

$D\left( {AD;0;0} \right)$,

$A’\left( {0;0;AA’} \right),$

$B’\left( {0;AB;AA’} \right),$$C’\left( {AD;AB;AA’} \right)$, $D’\left( {AD;0;AA’} \right).$

b) Lăng trụ đứng đáy là hình thoi

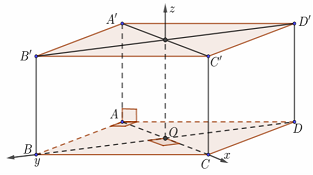
Gọi O là tâm hình thoi đáy, ta dựng hệ trục như hình với

$O\left( {0;0;0} \right),$$A\left( { – OA;0;0} \right),$$\,B\left( {0;OB;0} \right),$$\,C\left( {OC;0;0} \right),$$\,D\left( {0; – OD;0} \right),$$\,A’\left( { – OA;0;AA’} \right),$$\,B’\left( {0;OB;AA’} \right),$$\,C’\left( {OC;0;CC’} \right),$$\,D’\left( {0; – OD;DD’} \right)$

c) Lăng trụ tam giác đều

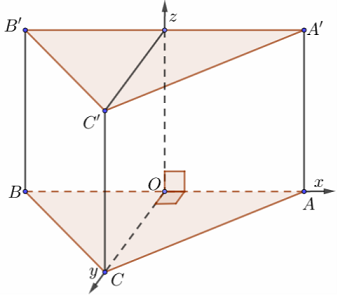
Gọi O là trung điểm một cạnh đáy, chọn hệ trục như hình vẽ với a = 1. Ta có:

$O\left( {0;0;0} \right),$$A\left( {\frac{{AB}}{2};0;0} \right),$$B\left( { – \frac{{AB}}{2};0;0} \right),$$C\left( {0;OC;0} \right),$$A’\left( {OA;0;AA’} \right),$$B’\left( { – \frac{{AB}}{2};0;BB’} \right),$$C’\left( {0;OC;CC’} \right).$

d) Lăng trụ đứng có đáy tam giác thường

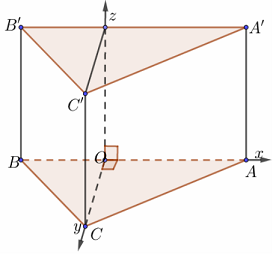
Vẽ đường cao CO trong tam giác ABC và chọn hệ trục như hình vẽ với a = 1.

Tọa độ điểm là:

$O\left( {0;0;0} \right),$$A\left( {OA;0;0} \right),$$B\left( { – OB;0;0} \right),$$C\left( {0;OC;0} \right),$$A’\left( {OA;0;AA’} \right),$$B’\left( { – OB;0;BB’} \right),$$C’\left( {0;OC;CC’} \right).$

2. Lăng trụ xiên:

a) Lăng trụ xiên có đáy là tam giác đều, hình chiếu của đỉnh trên mặt phẳng đối diện là trung điểm một cạnh tam giác đáy

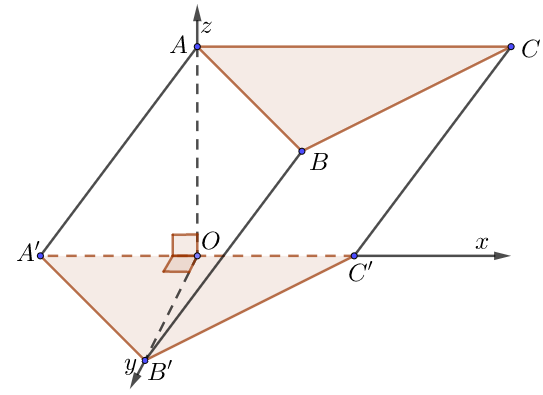
• Dựng hệ trục như hình vẽ, ta dễ dàng xác định được các điểm $O,\,\,A’,\,\,B’,\,\,C’,\,\,A$.

• Tìm tọa độ các điểm còn lại thông qua hệ thức vectơ bằng nhau: $\overrightarrow {AA’} = \overrightarrow {BB’} = \overrightarrow {CC’} $.

b) Lăng trụ xiên có đáy là hình vuông hoặc hình chữ nhật, hình chiếu của một đỉnh là một điểm thuộc cạnh đáy không chứa đỉnh đó

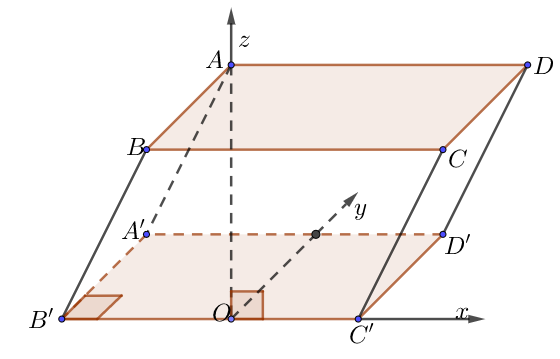
• Dựng hệ trục như hình vẽ, ta dễ dàng xác định được các điểm $O,\,\,A’,\,\,B’,\,\,C’,\,\,D’,\,\,A$.

• Tìm tọa độ các điểm còn lại thông qua hệ thức vectơ bằng nhau: $\overrightarrow {AA’} = \overrightarrow {BB’} = \overrightarrow {CC’} = \overrightarrow {DD’} $.

B. CÁC VÍ DỤ MINH HỌA

Ví dụ 1. Cho hình lập phương $ABCD.A’B’C’D’$ có độ dài cạnh bằng $1$. Gọi $M,N,P,Q$ lần lượt là trung điểm của $AB,BC,C’D’,DD’$. Chọn hệ tọa độ $Oxyz$ như hình vẽ, xác định tọa độ các điểm $M,N,P,Q$.

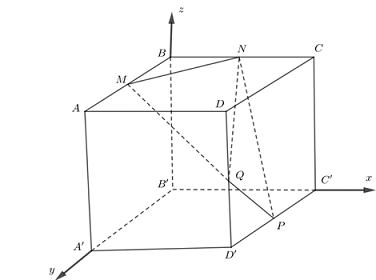
Lời giải

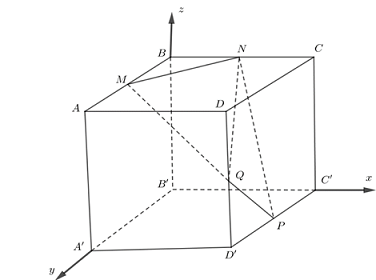
Thiết lập hệ tọa độ $Oxyz$ như hình vẽ, gốc $O \equiv B’$.

Khi đó:$M\left( {0\,;\,\frac{1}{2}\,;\,1} \right)$, $N\left( {\frac{1}{2}\,;\,0\,;\,1} \right)$, $P\left( {1\,;\,\frac{1}{2}\,;\,0} \right)$, $Q\left( {1\,;\,1\,;\,\frac{1}{2}} \right)$.

Ví dụ 2. Cho tứ diện đều $ABCD$ cạnh $a$. Gọi $K$ là trung điểm $AB$, gọi $M\,,\,N$ lần lượt là hình chiếu vuông góc của $K$ lên $AD\,,\,AC$. Chọn hệ tọa độ $Oxyz$ như hình vẽ, xác định tọa độ các điểm $K,M,N$ theo $a$.

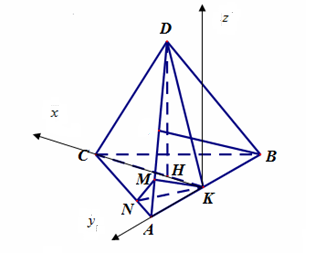
Lời giải

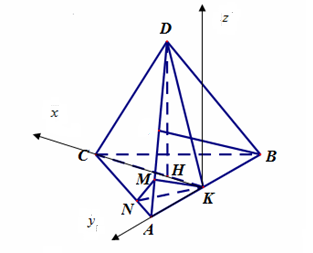
ta có: $KC = \frac{{\sqrt 3 }}{2}a\,;DH = \frac{{\sqrt 6 }}{3}a\,;\,HK = \frac{{\sqrt 3 }}{6}a$.

$AN = \frac{1}{4}AC\,;\,AM = \frac{1}{4}AD$

Chọn hệ trục $Oxyz$ sao cho $K \equiv O\left( {0\,;\,0\,;\,0} \right)$. $A\left( {0\,;\,\frac{a}{2}\,;\,0} \right)$, $\,C\left( {\frac{{a\sqrt 3 }}{2}\,;\,0\,;\,0} \right)$, $D\left( {\frac{{a\sqrt 3 }}{6}\,;\,0\,;\,\frac{{a\sqrt 6 }}{3}} \right)$

Ta có: $\overrightarrow {AN} = \frac{1}{4}\overrightarrow {AC} \Rightarrow N\left( {\frac{{a\sqrt 3 }}{{8\,}};\,\frac{{3a}}{8}\,;\,0} \right)$.

$\overrightarrow {AM} = \frac{1}{4}\overrightarrow {AD} \Rightarrow M\left( {\frac{{a\sqrt 3 }}{{24\,}};\,0\,;\,\frac{{a\sqrt 6 }}{{12\,}}} \right)$

Vậy$K\left( {0\,;\,0\,;\,0} \right),\,M\left( {\frac{{a\sqrt 3 }}{{24\,}};\,0\,;\,\frac{{a\sqrt 6 }}{{12\,}}} \right)$, $N\left( {\frac{{a\sqrt 3 }}{{8\,}};\,\frac{{3a}}{8}\,;\,0} \right)$.

Ví dụ 3. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, $SAD$ là tam giác đều và nằm trong mặt phẳng với đáy. Gọi $M$ và $N$ lần lượt là trung điểm của $BC$ và $CD$. Chọn hệ tọa độ $Oxyz$ như hình vẽ dưới.

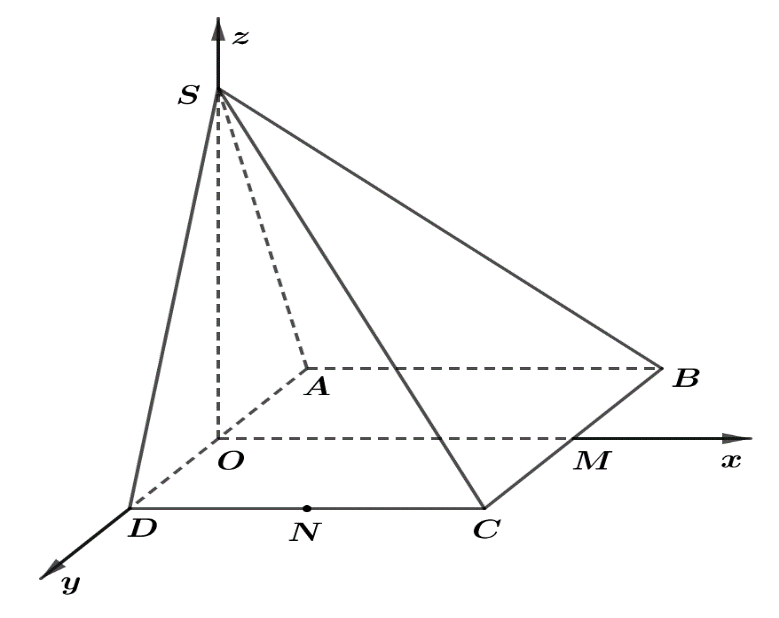
Xác định tọa độ các điểm $S,M,N$ theo $a$.

Lời giải

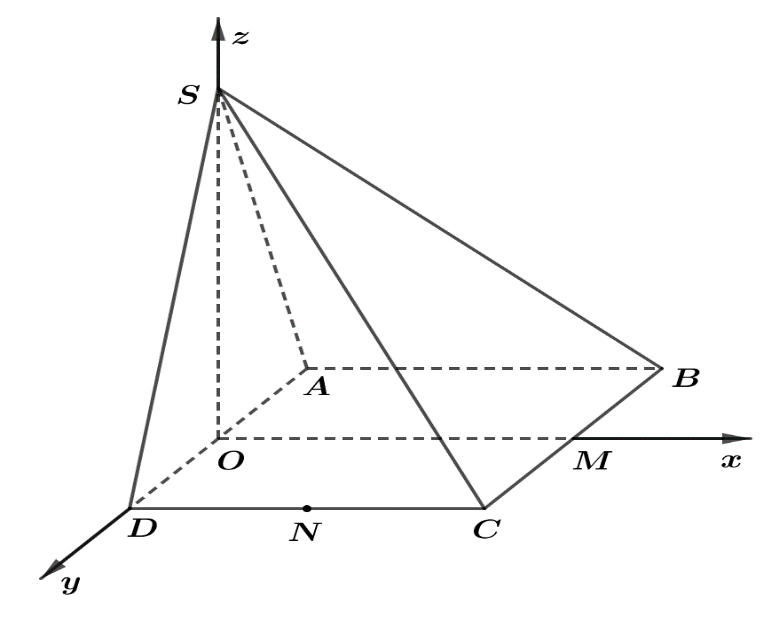
Chọn hệ tọa độ $Oxyz$ như hình vẽ.

$S\left( {0\,;\,0\,;\,\frac{{a\sqrt 3 }}{2}} \right);M\left( {a\,;\,0\,;\,0} \right);\,N\left( {\frac{a}{2}\,;\,\frac{a}{2}\,;\,0} \right).$.

Ví dụ 4. Cho tứ diện $OABC$, có $OA,OB,OC$đôi một vuông góc và $OA = 5,OB = 2,OC = 4$. Gọi $M,N$ lần lượt là trung điểm của $OB$và $OC$. Gọi $G,K$ lần lượt là trọng tâm của tam giác $ABC$ và $AMN$. Tính khoảng cách từ $G$ đến $K$.

Lời giải

Chọn hệ trục tọa độ $Oxyz$ như hình vẽ.

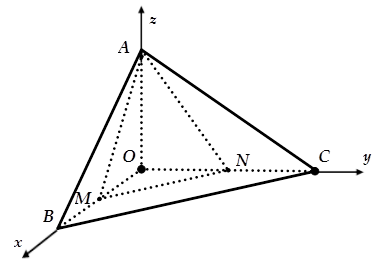
Ta có $O\left( {0;0;0} \right)$, $A \in {\text{Oz}},\;B \in Ox,\;C \in Oy$ sao cho $AO = 5,\;OB = 2,\;OC = 4$

$ \Rightarrow A\left( {0;0;5} \right),\;B\left( {2;0;0} \right),\;C\left( {0;4;0} \right)$.

Khi đó: $G$ là trọng tâm tam giác$ABC$ nên $G\left( {\frac{2}{3};\frac{4}{3};\frac{5}{3}} \right)$

$M$là trung điểm $OB$nên $M\left( {1;0;0} \right)$

$N$là trung điểm $OC$nên $N\left( {0;2;0} \right)$.

$K$ là trọng tâm tam giác$AMN$ nên $K\left( {\frac{1}{3};\frac{2}{3};\frac{5}{3}} \right)$

Khoảng cách từ $G$ đến $K$ là: $GK = \sqrt {{{\left( {\frac{1}{3} – \frac{2}{3}} \right)}^2} + {{\left( {\frac{2}{3} – \frac{4}{3}} \right)}^2} + {{\left( {\frac{5}{3} – \frac{5}{3}} \right)}^2}} = \frac{{\sqrt 5 }}{3}$

Ví dụ 5. Cho hình chóp $S.ABCD$ đáy là hình thang vuông tại $A$ và $D$, $SA \bot \left( {ABCD} \right)$. Góc giữa $SB$ và mặt phẳng đáy bằng ${45^{\text{o}}}$, $E$ là trung điểm của $SD$, $AB = 2a$, $AD = DC = a$. Gọi $G$ là trọng tâm của tam giác $ACE$. Tính độ dài đoạn $BG$.

Lời giải

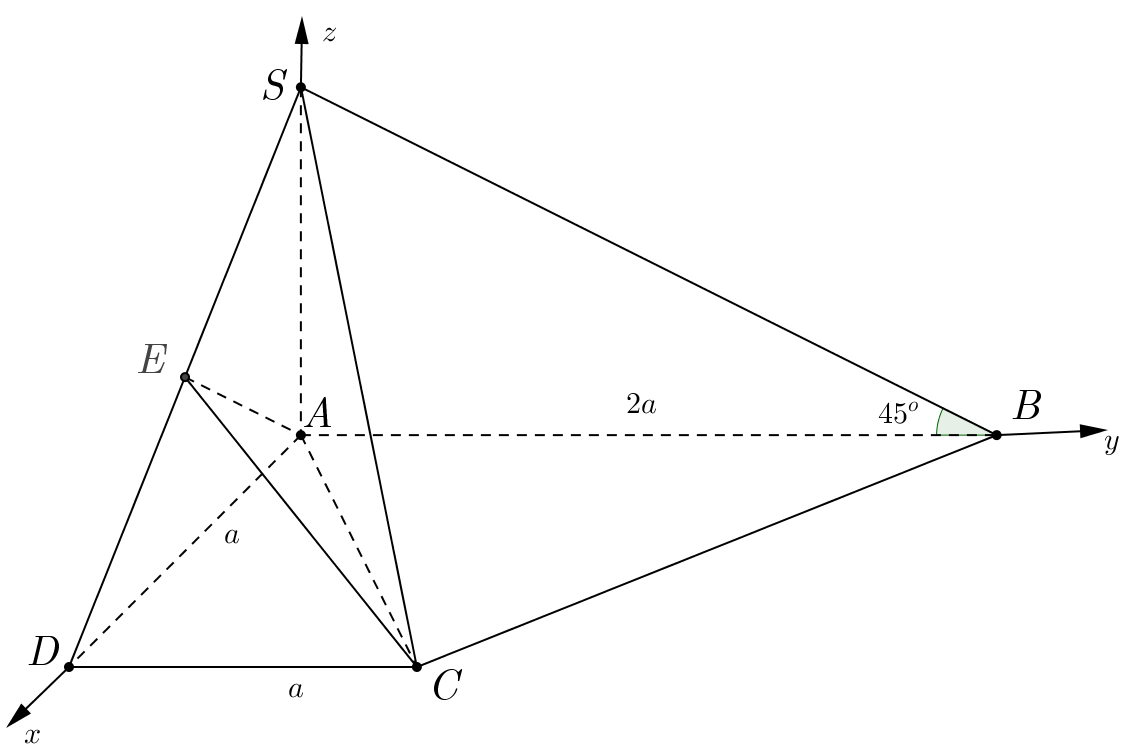
Hình chiếu của $SB$ trên mặt phẳng $\left( {ABCD} \right)$ là $AB$ $ \Rightarrow $ Góc giữa $SB$ và mặt đáy là góc giữa $SB$ và $AB$ và bằng góc $\widehat {SBA} = {45^o}$.

Tam giác $SAB$ vuông cân tại $A$ $ \Rightarrow SA = 2a$.

Chọn hệ trục tọa độ như hình vẽ ta có: $A\left( {0;0;0} \right)$, $B\left( {0;2a;0} \right)$, $C\left( {a;a;0} \right)$, $D\left( {a;0;0} \right)$, $S\left( {0;0;2a} \right)$, $E\left( {\frac{a}{2};0;a} \right)$.

Gọi $G$ là trọng tâm của tam giác $ACE \Rightarrow G\left( {\frac{a}{2};\frac{a}{3};\frac{a}{3}} \right)$

Độ dài $BG$ là: $BG = \sqrt {{{\left( {\frac{a}{2} – 0} \right)}^2} + {{\left( {\frac{a}{3} – 2a} \right)}^2} + {{\left( {\frac{a}{3} – 0} \right)}^2}} = \frac{{a\sqrt {113} }}{6}$

Ví dụ 6. Trong không gian với hệ tọa độ $Oxyz$, cho hình chóp $S.ABCD$, đáy $ABCD$ là hình chữ nhật. Biết $A\left( {0;0;0} \right)$,$D\left( {2;0;0} \right)$,$B\left( {0;4;0} \right)$,$S\left( {0;0;4} \right)$. Gọi $M$ là trung điểm của $SB$ và $G$ là trọng tâm của tam giác $SCD$. Tính độ dài đoạn $MG$.

Lời giải

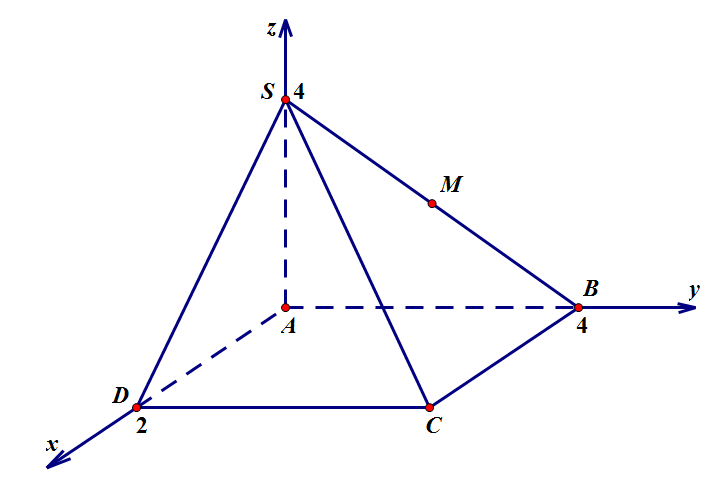
Chọn hệ trục tọa độ như hình vẽ : $A\left( {0;0;0} \right)$,$D\left( {2;0;0} \right)$,$B\left( {0;4;0} \right)$,$S\left( {0;0;4} \right)$.

$M$ là trung điểm của $SB$ $ \Rightarrow M\left( {0;2;2} \right)$.

Tứ giác $ABCD$ là hình chữ nhật nên $\left\{ \begin{gathered}
{x_A} + {x_C} = {x_B} + {x_D} \hfill \\
{y_A} + {y_C} = {y_B} + {y_D} \hfill \\
{z_A} + {z_C} = {z_B} + {z_D} \hfill \\
\end{gathered} \right.$$ \Rightarrow \left\{ \begin{gathered}
{x_C} = 2 \hfill \\
{y_C} = 4 \hfill \\
{z_C} = 0 \hfill \\
\end{gathered} \right.$$ \Rightarrow C\left( {2;4;0} \right)$.

$G$ là trọng tâm của tam giác $SCD$ $ \Rightarrow G\left( {\frac{4}{3};\frac{4}{3};\frac{4}{3}} \right)$

Độ dài $MG$ là: $MG = \sqrt {{{\left( {\frac{4}{3} – 0} \right)}^2} + {{\left( {\frac{4}{3} – 2} \right)}^2} + {{\left( {\frac{4}{3} – 2} \right)}^2}} = \frac{{2\sqrt 6 }}{3}$

Ví dụ 7. Cho hình hộp chữ nhật $ABCD.A’B’C’D’$ có các kích thước $AB = 4,\,AD = 3,AA’ = 5$. Gọi $G$ là trọng tâm của tam giác $ACB’$. Tính độ dài đoạn $BG$ là:

Lời giải

Chọn hệ trục tọa độ như hình vẽ.

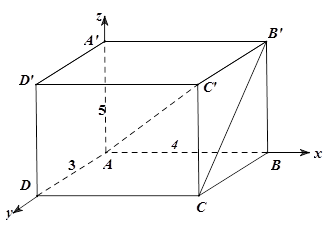
Có $A\left( {0\,0;\,0} \right),C\left( {4;3;0} \right),B’\left( {4;0;5} \right),B\left( {4;0;0} \right)$,

$G$ là trọng tâm của tam giác $ACB’$$ \Rightarrow G\left( {\frac{8}{3};1;\frac{5}{3}} \right)$

Độ dài $BG$ là: $BG = \sqrt {{{\left( {\frac{8}{3} – 4} \right)}^2} + {{\left( {1 – 0} \right)}^2} + {{\left( {\frac{5}{3} – 0} \right)}^2}} = \frac{{5\sqrt 2 }}{3}$

Ví dụ 8. Cho tứ diện $ABCD$ có $AB\,,AC\,,AD$ đôi một vuông góc với nhau và $AD = 2\,,AB = AC = 1$. Gọi $I$ là trung điểm của đoạn thẳng $BC$ và $G$ là trọng tâm của tam giác $ABD$. Tính độ dài $BI$.

Lời giải

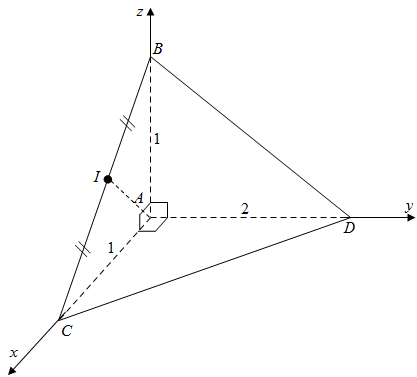
Vì tứ diện $ABCD$ có $AB\,,AC\,,AD$ đôi một vuông góc với nhau, nên ta chọn hệ trục tọa độ $Axyz$ như hình vẽ (với $A$ là gốc tọa độ, đường thằng $AC$ nằm trên trục $Ax$, $AD$ nằm trên trục $Ay$ và $AB$ nằm trên trục $Az$).

Từ đó suy ra: $A\left( {0\,;0\,;0} \right)$, $B\left( {0\,;0\,;1} \right)$ vì $B \in Az$, $C\left( {1\,;0\,;0} \right)$ vì $C \in Ax$, $D\left( {0\,;\,2\,;0} \right)$ vì $D \in Ay$.

Vì $I$ là trung điểm của $BC$ nên $I\left( {\frac{1}{2}\,;0\,;\frac{1}{2}} \right)$.

$G$ là trọng tâm của tam giác $ABD \Rightarrow G\left( {\frac{1}{6}\,;0\,;\frac{1}{2}} \right)$

Độ dài $BI$ là: $BI = \sqrt {{{\left( {\frac{1}{2} – \frac{1}{6}} \right)}^2} + {{\left( {0 – 0} \right)}^2} + {{\left( {\frac{1}{2} – \frac{1}{2}} \right)}^2}} = \frac{1}{3}$

Ví dụ 9. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, cạnh bên $SA = a$ và vuông góc với mặt phẳng đáy. Gọi $M,N$ lần lượt là trung điểm của $SB$ và $SD$ và $G$ là trọng tâm của tam giác $AMN$ . Tính tọa độ điểm $G$.

Lời giải

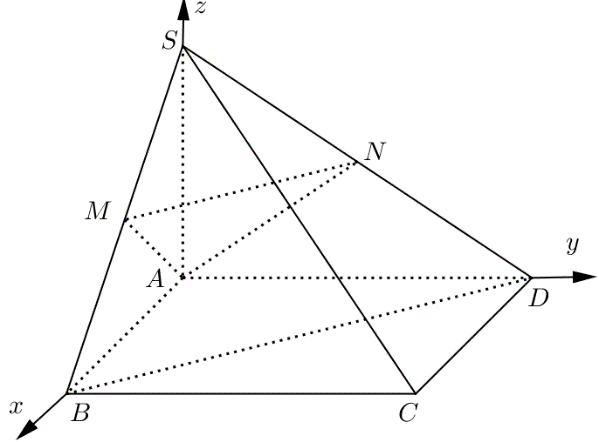
Chọn hệ trục tọa độ $Oxyz$ thỏa mãn: $A \equiv O,\,B\left( {a;0;0} \right),D\left( {0;a;0} \right),S\left( {0;0;a} \right)$(như minh họa hình vẽ),

suy ra $M\left( {\frac{a}{2};0;\frac{a}{2}} \right)$ và$N\left( {0;\frac{a}{2};\frac{a}{2}} \right)$.

$G$ là trọng tâm của tam giác $AMN$$ \Rightarrow G\left( {\frac{a}{6};\frac{a}{6};\frac{a}{3}} \right)$

Ví dụ 10. Cho hình lập phương $ABCD.A’B’C’D’$ có cạnh bằng $a$. Gọi $G$ là trọng tâm của tam giác $A’BD$. Tính độ dài $C’G$.

Lời giải

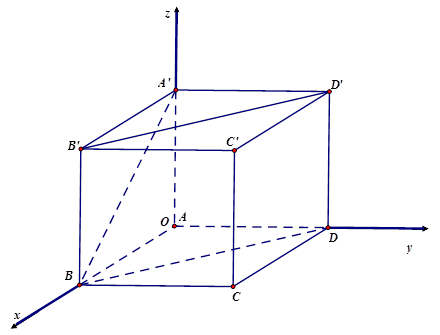
Chọn hệ trục tọa độ $Oxyz$ với $A \equiv O\left( {0;0;0} \right)$, $B\left( {a;0;0} \right)\,$, $C\left( {a;a;0} \right)\,$, $D\left( {0;a;0} \right)$, $A’\left( {0;0;a} \right)\,,\,$

$B’\left( {a;0;a} \right)\,,\,$$C’\left( {a;a;a} \right)$, $D’\left( {0;a;a} \right)$

$G$ là trọng tâm của tam giác $A’BD$$ \Rightarrow G\left( {\frac{a}{3};\frac{a}{3};\frac{a}{3}} \right)$

Độ dài $C’G$ là: $C’G = \sqrt {{{\left( {\frac{a}{3} – a} \right)}^2} + {{\left( {\frac{a}{3} – a} \right)}^2} + {{\left( {\frac{a}{3} – a} \right)}^2}} = \frac{{2a\sqrt 3 }}{3}$

Ví dụ 11. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, $AB = a$, $BC = a\sqrt 3 $, $SA = a$ và $SA$ vuông góc với đáy $ABCD$. Gọi $G$ là trọng tâm của tam giác $SBD$. Tính độ dài $CG$.

Lời giải

Đặt hệ trục tọa độ $Oxyz$ như hình vẽ.

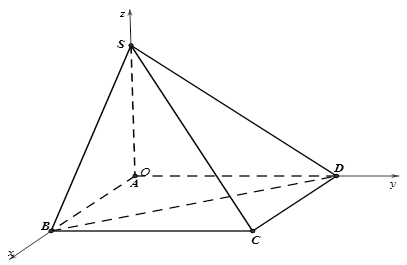
Khi đó, ta có:

$A\left( {0;0;0} \right)$, $B\left( {a;0;0} \right)$, $C\left( {a;a\sqrt 3 ;0} \right)$, $D\left( {0;a\sqrt 3 ;0} \right)$, $S\left( {0;0;a} \right)$.

$G$ là trọng tâm của tam giác $SBD$$ \Rightarrow G\left( {\frac{a}{3};\frac{{a\sqrt 3 }}{3};\frac{a}{3}} \right)$

Độ dài $CG$ là: $CG = \sqrt {{{\left( {\frac{a}{3} – a} \right)}^2} + {{\left( {\frac{{a\sqrt 3 }}{3} – a\sqrt 3 } \right)}^2} + {{\left( {\frac{a}{3} – 0} \right)}^2}} = \frac{{a\sqrt {17} }}{3}$

Ví dụ 12. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông có độ dài đường chéo bằng $a\sqrt 2 $ và $SA$ vuông góc với mặt phẳng $\left( {ABCD} \right)$. Gọi $\alpha $ là góc giữa hai mặt phẳng $\left( {SBD} \right)$ và $\left( {ABCD} \right)$. Nếu $\tan \alpha = \sqrt 2 $ thì tọa độ điểm $I$ là bao nhiêu? Biết $I = AC \cap BD$ và chọn hệ trục tọa độ $Oxyz$ như hình vẽ dưới.

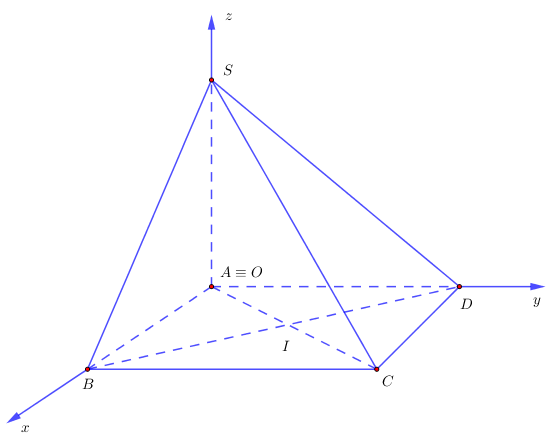
Lời giải

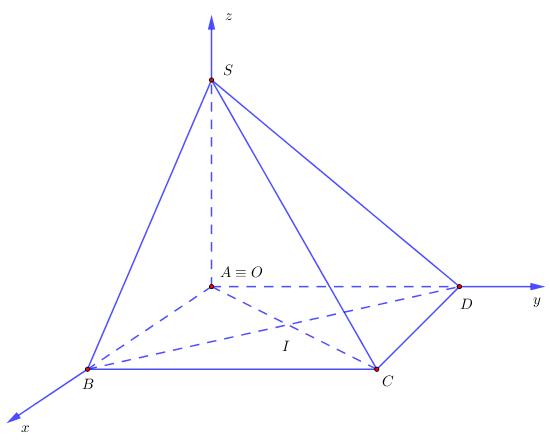
Gọi $I = AC \cap BD$.

Hình vuông $ABCD$ có độ dài đường chéo bằng $a\sqrt 2 $ suy ra hình vuông đó có cạnh bằng $a$.

Ta có $\left\{ \begin{gathered}
\left( {SBD} \right) \cap \left( {ABCD} \right) = BD \hfill \\
SI \bot BD \hfill \\
AI \bot BD \hfill \\
\end{gathered} \right.$$ \Rightarrow \widehat {\left( {\left( {SBD} \right);\,\left( {ABCD} \right)} \right)} = \widehat {\left( {SI;\,AI} \right)} = \widehat {SIA}$.

Ta có $\tan \alpha = \tan \widehat {SIA} = \frac{{SA}}{{AI}} \Leftrightarrow SA = a$.

Chọn hệ trục tọa độ $Oxyz$ như hình vẽ. Ta có $A\left( {0;\,0;\,0} \right)$, $B\left( {a;\,0;\,0} \right)$, $C\left( {a;\,a;\,0} \right)$, $S\left( {0;\,0;\,a} \right)$.

$ \Rightarrow I\left( {\frac{a}{2};0;\frac{a}{2}} \right)$

Ví dụ 13. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, mặt bên $SAB$ là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng $\left( {ABCD} \right)$. Gọi $G$ là trọng tâm của tam giác $SAB$ và $M,\,N$ lần lượt là trung điểm của $SC,\,SD$. Chọn hệ trục tọa độ $Oxyz$ như hình vẽ dưới, Tính tọa độ các điểm $G,M,\,N$theo $a$.

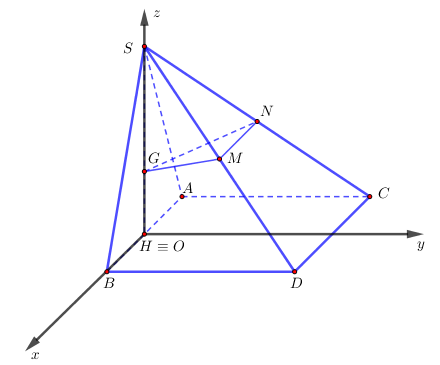
Lời giải

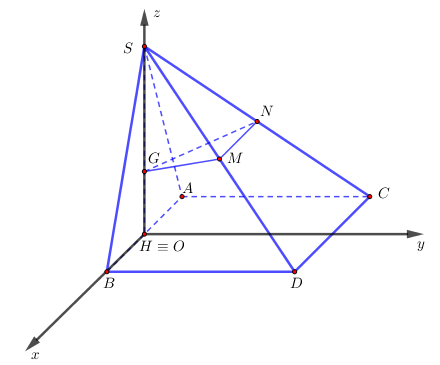
Chọn hệ trục tọa độ $Oxyz$ như hình vẽ. Khi đó

$S\left( {0;\,0;\,\frac{{\sqrt 3 }}{2}} \right)$; $A\left( {\frac{{ – a}}{2};0;\,0} \right)$; $B\left( {\frac{a}{2};0;\,0} \right)$;$C\left( {\frac{a}{2};a;\,0} \right)$; $D\left( {\frac{{ – a}}{2};a;\,0} \right)$

suy ra $G\left( {0;\,0;\,\frac{{a\sqrt 3 }}{6}} \right)$; $M\left( {\frac{a}{4};\frac{a}{2};\,\frac{{a\sqrt 3 }}{4}} \right)$; $N\left( { – \frac{a}{4};\frac{a}{2};\,\frac{{a\sqrt 3 }}{4}} \right)$

Ví dụ 14. Cho hình chóp $O.ABC$ có ba cạnh $OA$, $OB$, $OC$ đôi một vuông góc và $OA = OB = OC = a$. Gọi $M$ là trung điểm cạnh $AB$. Tính góc tạo bởi hai vectơ $\overrightarrow {BC} $ và $\overrightarrow {OM} $.

Lời giải

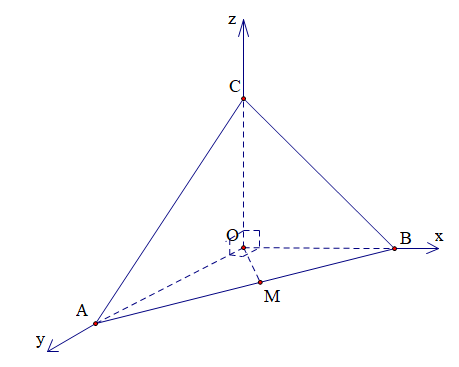
Chọn hệ trục tọa độ $Oxyz$ như hình vẽ.

Ta có: $O\left( {0\,;\,0\,;\,0} \right)$, $A\left( {0\,;\,a\,;\,0} \right)$, $B\left( {a\,;\,0\,;\,0} \right)$, $C\left( {0\,;\,0\,;\,a} \right)$, $M\left( {\frac{a}{2}\,;\,\frac{a}{2}\,;\,0} \right)$.

Khi đó ta có: $\overrightarrow {BC} = \left( { – a\,;\,0\,;\,a} \right)$,$\overrightarrow {OM} = \left( {\frac{a}{2}\,;\,\frac{a}{2}\,;\,0} \right)$

$ \Rightarrow $ $\cos \left( {\overrightarrow {BC} \,;\,\overrightarrow {OM} } \right)$ $ = \frac{{\overrightarrow {BC} .\overrightarrow {OM} }}{{BC.OM}}$$ = \frac{{ – \frac{{{a^2}}}{2}}}{{a.\sqrt 2 .\frac{{a\sqrt 2 }}{2}}}$$ = – \frac{1}{2}$$ \Rightarrow $$\left( {\overrightarrow {BC} \,;\,\overrightarrow {OM} } \right) = 120^\circ $.

Ví dụ 15. Cho hình chóp tứ giác đều $S.ABCD$ có $AB = a$, $SA = a\sqrt 2 $. Gọi $G$ là trọng tâm tam giác $SCD$. Tính $cosin$ góc giữa đường thẳng $BG$ với đường thẳng $SA$.

Lời giải

Gọi $O = AC \cap BD$.

Tam giác $SAO$ vuông : $SO = \sqrt {S{A^2} – A{O^2}} = \frac{{a\sqrt 6 }}{2}$

Gắn tọa độ như hình vẽ

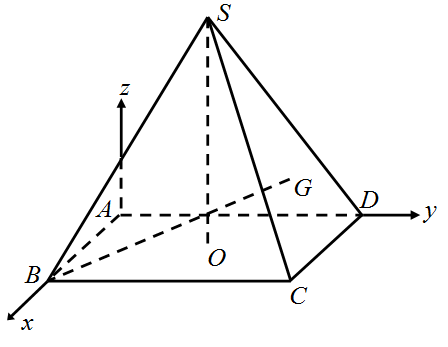
$A\left( {0;0;0} \right)$, $B\left( {a;0;0} \right)$, $C\left( {a;a;0} \right)$, $D\left( {0;a;0} \right)$, $O\left( {\frac{a}{2};\frac{a}{2};0} \right)$, $S\left( {\frac{a}{2};\frac{a}{2};\frac{{a\sqrt 6 }}{2}} \right)$.

Vì $G$ là trọng tâm tam giác $SCD$ nên $G\left( {\frac{a}{2};\frac{{5a}}{6};\frac{{a\sqrt 6 }}{6}} \right)$.

Ta có : $\overrightarrow {AS} = \left( {\frac{a}{2};\frac{a}{2};\frac{{a\sqrt 6 }}{2}} \right)$ $ = \frac{a}{2}\left( {1;1;\sqrt 6 } \right)$, $\overrightarrow {BG} = \left( {\frac{{ – a}}{2};\frac{{5a}}{6};\frac{{a\sqrt 6 }}{6}} \right) = \frac{a}{6}\left( { – 3;5;\sqrt 6 } \right)$.

Góc giữa đường thẳng $BG$ với đường thẳng $SA$ bằng:

$\cos \left( {BG;SA} \right) = \frac{{\left| {\overrightarrow {BG} .\overrightarrow {AS} } \right|}}{{BG.AS}} = \frac{{\left| { – 3 + 5 + 6} \right|}}{{\sqrt {40} .\sqrt 8 }} = \frac{{\sqrt 5 }}{5}$.

Ví dụ 16. Cho hình chóp $S.ABCD$ có đáy hình vuông. Cho tam giác $SAB$ vuông tại $S$ và góc $SBA$ bằng ${30^0}$. Mặt phẳng $\left( {SAB} \right)$ vuông góc mặt phẳng đáy. Gọi $M,N$ là trung điểm $AB,BC$. Tìm cosin góc tạo bởi hai đường thẳng $\left( {SM,DN} \right)$.

Lời giải

Trong $\left( {SAB} \right)$, kẻ $SH \bot AB$ tại $H$.

Ta có: $\left\{ \begin{gathered}
\left( {SAB} \right) \bot \left( {ABCD} \right) \hfill \\
\left( {SAB} \right) \cap \left( {ABCD} \right) = AB \hfill \\
SH \subset \left( {SAB} \right),SH \bot AB \hfill \\
\end{gathered} \right. \Rightarrow SH \bot \left( {ABCD} \right)$.

Kẻ tia $Az$//$SH$ và chọn hệ trục tọa độ $Axyz$ như hình vẽ sau đây.

Trong tam giác $SAB$ vuông tại $S$, $SB = AB.\cos \widehat {SBA} = a.\cos {30^0} = \frac{{a\sqrt 3 }}{2}$.

Trong tam giác $SBH$ vuông tại $H$, $BH = SB.\cos \widehat {SBH} = \frac{{3a}}{4}$ và $SH = BH.\sin \widehat {SBA} = \frac{{a\sqrt 3 }}{4}$.

$AH = AB – BH = a – \frac{{3a}}{4} = \frac{a}{4}$ $ \Rightarrow H\left( {0;\frac{a}{4};0} \right) \Rightarrow S\left( {0;\frac{a}{4};\frac{{a\sqrt 3 }}{4}} \right)$.

$M\left( {0;\frac{a}{2};0} \right)$, $D\left( {a;0;0} \right)$, $N\left( {\frac{a}{2};a;0} \right)$.

Ta có: $\overrightarrow {SM} = \left( {0;\frac{a}{4}; – \frac{{a\sqrt 3 }}{4}} \right)$, $\overrightarrow {DN} = \left( { – \frac{a}{2};a;0} \right)$

$ \Rightarrow $$\cos \left( {SM,DN} \right) = \frac{{\left| {\overrightarrow {SM} .\overrightarrow {DN} } \right|}}{{SN.DN}} = \frac{{\frac{{{a^2}}}{4}}}{{\frac{a}{2}.\frac{{a\sqrt 5 }}{2}}} = \frac{1}{{\sqrt 5 }}$.