20 Câu Trắc Nghiệm GTLN Và GTNN Lớp 12 Dạng Đúng Sai Giải Chi Tiết

20 câu trắc nghiệm GTLN và GTNN lớp 12 dạng đúng sai giải chi tiết được soạn dưới dạng file word và PDF gồm 6 trang. Các bạn xem và tải về ở dưới.

Câu 1. Cho hàm số $y = f\left( x \right)$ xác định, liên tục trên $\mathbb{R}$ và có bảng biến thiên:

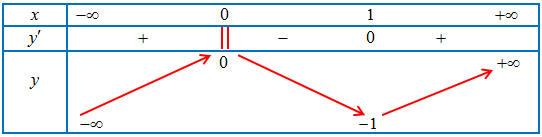
Khi đó:

a) Hàm số có giá trị cực tiểu bằng 1 .

b) Hàm số có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng -1 .

c) Hàm số đạt cực đại tại $x = 0$ và đạt cực tiểu tại $x = 1$.

d) Hàm số có đúng một cực trị.

Lời giải

a) Sai

b) Sai

c) Đúng

d) Sai

Đáp án a sai vì hàm số có giá trị cực tiểu $y = – 1$ khi $x = 0$.

Đáp án b sai vì hàm số không có GTLN và GTNN trên $\mathbb{R}$.

Đáp án c đúng vì hàm số đạt cực đại tại $x = 0$ và đạt cực tiểu tại $x = 1$.

Đáp án d sai vì hàm số có 2 điểm cực trị.

Câu 2. Xét hàm số $y = f\left( x \right)$ với $x \in \left[ { – 1;5} \right]$ có bảng biến thiên như sau:

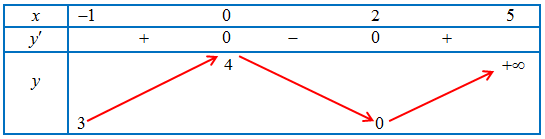
Khi đó:

a. Hàm số đã cho không tồn taị GTLN trên đoạn $\left[ { – 1;5} \right]$

b) Hàm số đã cho đạt GTNN tại $x = – 1$ và $x = 2$ trên đoạn $\left[ { – 1;5} \right]$

c) Hàm số đã cho đồng biến trên khoảng $\left( {2;5} \right)$

d) Hàm số đã cho đạt GTNN tại $x = 0$ trên đoạn $\left[ { – 1;5} \right]$

Lời giải

a) Đúng

b) Sai

c) Đúng

d) Sai

a) Đúng. Vì $\mathop {\lim }\limits_{x \to {5^ – }} y = + \infty $ nên hàm số không có GTLN trên đoạn $\left[ { – 1;5} \right]$.

b) Sai. Hàm số đã cho chỉ đạt GTNN tại $x = 2$ trên đoạn $\left[ { – 1;5} \right]$.

c) Đúng

d) Sai. Hàm số đã cho chỉ đạt GTNN tại $x = 2$ trên đoạn $\left[ { – 1;5} \right]$.

Câu 3. Cho hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$, có bảng biến thiên như hình sau:

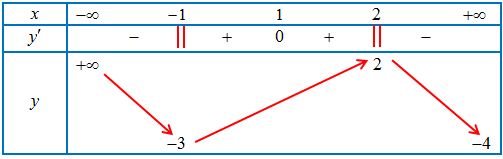
Khi đó:

a) Hàm số có hai điểm cực trị.

b) Hàm số có giá trị lớn nhất bằng 2 và giá trị nhỏ nhất bằng -3 .

c) Hàm số đạt cực đại tại $x = 2$

d) Hàm số nghịch biến trên mỗi khoảng $\left( { – \infty ; – 1} \right),\left( {2; + \infty } \right)$.

Lời giải

a) Đúng

b) Sai

c) Đúng

d) Đúng

Dựa vào BBT ta thấy hàm số không có GTLN, GTNN.

Câu 4. Cho hàm số $f\left( x \right) = – {x^4} + 12{x^2} + 1$, khi đó:

a) Hàm số đồng biến trên khoảng $\left( {1;37} \right)$.

b) Hàm số có 3 điểm cực trị.

c) Giá trị nhỏ nhất của hàm số $f\left( x \right) = – {x^4} + 12{x^2} + 1$ trên đoạn $\left[ { – 1;2} \right]$ bằng 12.

d) Giá trị lớn nhất của hàm số $f\left( x \right) = – {x^4} + 12{x^2} + 1$ trên đoạn $\left[ { – 1;2} \right]$ bằng 33.

Lời giải

a) Sai

b) Đúng

c) Sai

d) Đúng

Bảng biến thiên của hàm số

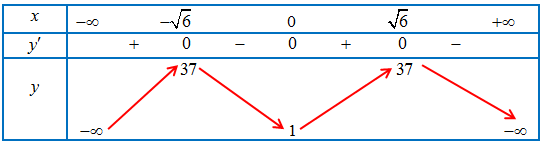
$f(x) = – {x^4} + 12{x^2} + 1$ liên tục trên $[ – 1;2]$.

$f'(x) = – 4{x^3} + 24{x^2} = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 0} \\
{x = \sqrt 6 \,\,(loại)} \\
{x = – \sqrt 6 \,\,(loại)}
\end{array}} \right.$

Ta có:

$f\left( { – 1} \right) = 12;f\left( 2 \right) = 33;f\left( 0 \right) = 1$

Giá trị lớn nhất của hàm số $f\left( x \right) = – {x^4} + 12{x^2} + 1$ trên đoạn $\left[ { – 1;2} \right]$ bằng 33 tại $x = 2$

Giá trị nhỏ nhất của hàm số $f\left( x \right) = – {x^4} + 12{x^2} + 1$ trên đoạn $\left[ { – 1;2} \right]$ bằng 1 tại $x = 0$

Câu 5. Cho hàm số $f\left( x \right) = {x^3} – 24x$, khi đó:

a) Hàm số nghịch biến trên khoảng $\left( { – \infty ;0} \right)$

b) Đồ thị hàm số có điểm cực tiểu là $A\left( {16; – 2048} \right)$

c) Giá trị lớn nhất của hàm số $f\left( x \right) = {x^3} – 24x$ trên đoạn $\left[ {2;19} \right]$ bằng 6403 .

d) Giá trị nhỏ nhất của hàm số $f\left( x \right) = {x^3} – 24x$ trên đoạn $\left[ {2;19} \right]$ bằng -40 .

Lời giải

a) Sai

b) Đúng

c) Đúng

d) Sai

Bảng biến thiên của hàm số

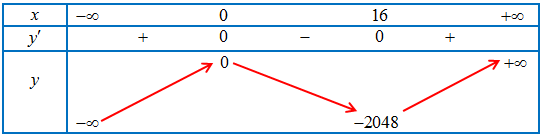
Ta có $f’\left( x \right) = 3{x^2} – 24 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 2\sqrt 2 \in \left[ {2;19} \right]} \\
{x = – 2\sqrt 2 \notin \left[ {2;19} \right]}
\end{array}} \right.$.

$f\left( 2 \right) = {2^3} – 24.2 = – 40$; $f\left( {2\sqrt 2 } \right) = {(2\sqrt 2 )^3} – 24.2\sqrt 2 = – 32\sqrt 2 $; $f\left( {19} \right) = {19^3} – 24.19 = 6403$.

Vậy giá trị nhỏ nhất của hàm số $f\left( x \right) = {x^3} – 24x$ trên đoạn $\left[ {2;19} \right]$ bằng $ – 32\sqrt 2 $.

Câu 6. Cho hàm số $f\left( x \right) = {x^4} – 10{x^2} – 4$. Khi đó

a) Hàm số nghịch biến trên khoảng $\left( {0;6} \right)$

b) Hàm số có 3 điểm cực trị
c) Giá trị lớn nhất của hàm số $f\left( x \right) = {x^4} – 10{x^2} – 4$ trên $\left[ {0;9} \right]$ bằng-4.

d) Giá trị nhỏ nhất của hàm số $f\left( x \right) = {x^4} – 10{x^2} – 4$ trên $\left[ {0;9} \right]$ bằng -29 .

Lời giải

a) Sai

b) Đúng

c) Sai

d) Đúng

Bảng biến thiên của hàm số

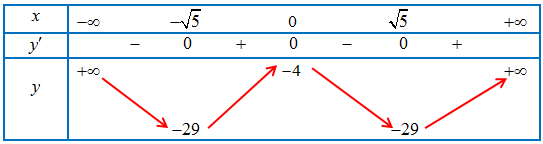Hàm số $y = f\left( x \right)$ liên tục trên $\left[ {0;9} \right]$.

Có $f’\left( x \right) = 4{x^3} – 20x$,

$f’\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 0} \\
{x = \sqrt 5 } \\
{x = – \sqrt 5 \notin \left[ {0;9} \right]}
\end{array}} \right.$

Ta có $f\left( 0 \right) = – 4$, $f\left( {\sqrt 5 } \right) = – 29$, $f\left( 9 \right) = 5747$

Câu 7. Cho hàm số $y = x + \frac{4}{x}$ trên khoảng $\left( {0; + \infty } \right)$. Khi đó:

a) Hàm số nghịch biến trên khoảng $\left( {0;2} \right)$

b) Hàm số có 1 điểm cực trị.

c) Hàm số đạt giá trị lớn nhất tại $x = 3$

d) Giá trị nhỏ nhất của hàm số bằng 4

Lời giải

a) Đúng

b) Đúng

c) Sai

d) Đúng

Hàm số $y = x + \frac{4}{x}$ liên tục và xác định trên $\left( {0; + \infty } \right)$.

Ta có $y’ = 1 – \frac{4}{{{x^2}}} = \frac{{{x^2} – 4}}{{{x^2}}} \Rightarrow $$y’ = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 2 \in \left( {0; + \infty } \right)} \\
{x = – 2 \notin \left( {0; + \infty } \right)}
\end{array}} \right.$.

Bảng biến thiên

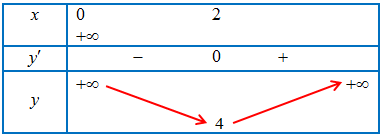
Vậy giá trị nhỏ nhất là $m = 4$ khi $x = 2$.

Hàm số không có giá trị lớn nhất.

Câu 8. Cho hàm số $y = f\left( x \right)$ xác định và liên tục trên $\mathbb{R}$, đồ thị của hàm số $y = f’\left( x \right)$ như hình vẽ.

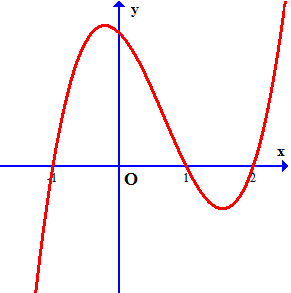
Khi đó:

a) Hàm số $y = f\left( x \right)$ có 2 điểm cực trị

b) Hàm số $y = f\left( x \right)$ nghịch biến trên khoảng $\left( {1;2} \right)$

c) Hàm số $y = f\left( x \right)$ đồng biến trên khoảng $\left( {2; + \infty } \right)$

d) Giá trị lớn nhất của hàm số $y = f\left( x \right)$ trên đoạn $\left[ { – 1;2} \right]$ là $f\left( 2 \right)$

Lời giải

a) Sai

b) Đúng

c) Đúng

d) Sai

$f’\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{x = – 1} \\
{x = 1} \\
{x = 2}
\end{array}} \right.$

Từ đồ thị hàm $y = f’\left( x \right)$ ta có bảng biến thiên

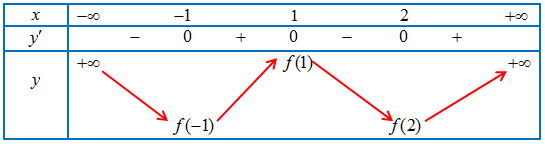
Từ đó suy ra giá trị lớn nhất của hàm số trên $\left[ { – 1;2} \right]$ là $f\left( 1 \right)$.

Câu 9. Cho hàm số $y = f\left( x \right)$ có đạo hàm liên tục trên $R$. Hàm số $y = f’\left( x \right)$ có đồ thị như hình sau:

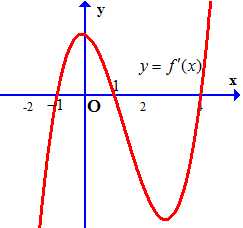
Khi đó:

a) Hàm số $y = f\left( x \right)$ có hai cực trị

b) Hàm số $y = f\left( x \right)$ đồng biến trên khoảng $\left( {1; + \infty } \right)$
c) $f\left( 1 \right) > f\left( 2 \right) > f\left( 4 \right)$.

d) Trên đoạn $\left[ { – 1;4} \right]$, giá trị lớn nhất của hàm số $y = f\left( x \right)$ là $f\left( 1 \right)$.

Lời giải

a) Sai

b) Sai

c) Đúng

d) Đúng

Dựa vào đồ thị của hàm số $y = f’\left( x \right)$ ta thấy:

$f’\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = – 1} \\
{x = 1} \\
{x = 4}
\end{array}} \right.$
$f’\left( x \right) < 0 \Leftrightarrow x \in \left( { – \infty ; – 1} \right) \cup \left( {1;4} \right)$

$f’\left( x \right) > 0 \Leftrightarrow x \in \left( { – 1;1} \right) \cup \left( {4; + \infty } \right)$

Ta có bảng biến thiên của hàm số $y = f\left( x \right)$

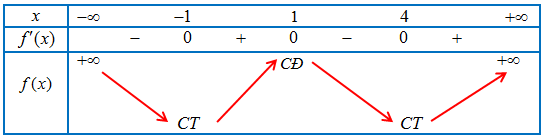
Dựa vào bảng biến thiên đáp án đúng là mệnh đề c và d

Câu 10. Cho hàm số $y = f\left( x \right)$ liên tục trên đoạn $\left[ {0;\frac{7}{2}} \right]$ có đồ thị hàm số $y = f’\left( x \right)$ như hình vẽ.

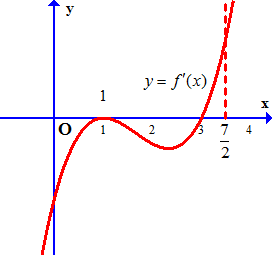
a) Hàm số $y = f\left( x \right)$ đồng biến trên khoảng $\left( {3;\frac{7}{2}} \right)$
b) $f\left( 0 \right) > f\left( 3 \right)$
c) $f\left( 3 \right) > f\left( {\frac{7}{2}} \right)$

d) Hàm số $y = f\left( x \right)$ đạt giá trị nhỏ nhất trên đoạn $\left[ {0;\frac{7}{2}} \right]$ tại điểm ${x_0} = \frac{7}{2}$

Lời giải

a) Đúng

b) Đúng

c) Sai

d) Sai

Dựa vào đồ thị hàm số $y = f’\left( x \right)$ ta có bảng biến thiên trên đoạn $\left[ {0;\frac{7}{2}} \right]$ như sau:

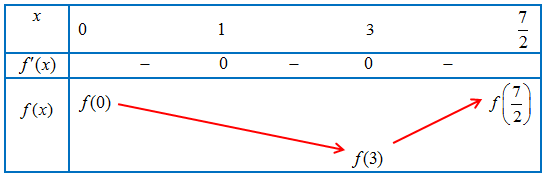
Do đó hàm số đạt giá trị nhỏ nhất tại ${x_0} = 3$.

Câu 11. Cho hàm số $y = \frac{{x – {m^2} – 2}}{{x – m}}$, (tham số $m$ ). Khi đó:

a) Tập xác định: $D = \mathbb{R}$.
b) Khi $m = 1$ hàm số đồng biến trên mỗi khoảng $\left( { – \infty ;1} \right)$ và $\left( {1; + \infty } \right)$.

c) Khi $m = 1$ thì trên đoạn $\left[ {1;4} \right]$ hàm số đạt giá trị lớn nhất bằng $\frac{1}{2}$

d) Có 1 giá trị của tham số $m$ để giá trị lớn nhất của hàm số $y = \frac{{x – {m^2} – 2}}{{x – m}}$ trên đoạn $\left[ {0;4} \right]$ bằng -1 .

Lời giải

a) Sai

b) Đúng

c) Sai

d) Đúng

Tập xác định: $D = \mathbb{R} \setminus \left\{ m \right\}$.

$y’ = \frac{{{m^2} – m + 2}}{{{{(x – m)}^2}}} > 0,\forall x \ne m$. Do đó hàm số đồng biến trên mỗi khoảng $\left( { – \infty ;m} \right)$ và $\left( {m; + \infty } \right)$.

Bảng biến thiên của hàm số:

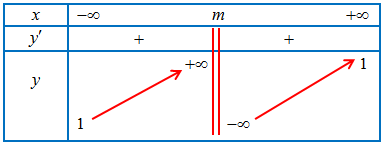
Từ bảng biến thiên suy ra, hàm số đạt giá trị lớn nhất trên đoạn $\left[ {0;4} \right]$ bằng -1 khi $\left\{ \begin{gathered}
\left[ {0;4} \right] \subset D \hfill \\
\mathop {\max y}\limits_{\left[ {0;4} \right]} = f(4) = – 1 \hfill \\
\end{gathered} \right.$ $ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{m < 0} \\
{\frac{{2 – {m^2}}}{{4 – m}} = – 1}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{m < 0} \\
{{m^2} + m – 6 = 0}
\end{array}} \right.} \right.$

$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{m < 0} \\
{m = 2,m = – 3}
\end{array} \Leftrightarrow m = – 3} \right.$.

Câu 12. Cho hàm số $y = \frac{{{x^2} + mx + 1}}{{x + m}}$ (tham số $m$ ). Khi đó:

a) Khi $m = 1$ hàm số có 2 điểm cực trị

b) Khi $m = 1$ hàm số đồng biến trên khoảng $\left( {0; + \infty } \right)$

c) Để hàm số liên tục trên $\left[ {0;2} \right]$ thì $\left[ {\begin{array}{*{20}{l}}
{m > 0} \\
{m < – 2}
\end{array}} \right.$

d) Để hàm số $y = \frac{{{x^2} + mx + 1}}{{x + m}}$ liên tục và đạt giá trị nhỏ nhất trên đoạn $\left[ {0;2} \right]$ tại một điểm ${x_0} \in \left( {0;2} \right)$ thì $m > 1$

Lời giải

a) Đúng

b) Đúng

c) Đúng

d) Sai

Tập xác định: $D = \mathbb{R} \setminus \left\{ { – m} \right\}$. Hàm số liên tục trên $\left[ {0;2} \right] \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{ – m < 0} \\
{ – m > 2}
\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{m > 0} \\
{m < – 2}
\end{array}} \right.} \right.$

Ta có $y’ = \frac{{{x^2} + 2mx + {m^2} – 1}}{{{{(x + m)}^2}}} = \frac{{{{(x + m)}^2} – 1}}{{{{(x + m)}^2}}}$.

Cho $y’ = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{{x_1} = – m – 1} \\
{{x_2} = – m + 1}
\end{array}} \right.$.

Ta có bảng biến thiên

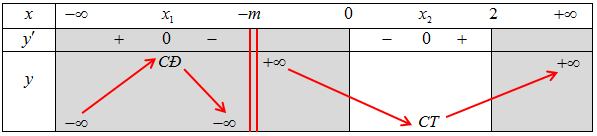
Hàm số đạt giá trị nhỏ nhất tại ${x_0} \in \left( {0;2} \right)$ nên $0 < – m + 1 < 2 \Leftrightarrow – 1 < m < 1$

So với điều kiện hàm số liên tục trên đoạn $\left[ {0;2} \right]$.

Ta có $0 < m < 1$.

Câu 13. Cho hàm số $y = {x^3} – 3m{x^2} + 3\left( {{m^2} – 1} \right)x + 2025$, (tham số $m$ ). Khi đó:

a) Khi $m = 1$ thì hàm số đạt cực tiểu tại $x = 2$

b) Khi $m = 1$ thì hàm số đồng biến trên khoảng $\left( {0;2} \right)$

c) Khi $m = 1$ thì hàm số có giá trị nhỏ nhất trên khoảng $\left( {0; + \infty } \right)$ bằng -4

d) Có tất cả 1 giá trị nguyên của $m$ để hàm số có giá trị nhỏ nhất trên khoảng $\left( {0; + \infty } \right)$

Lời giải

a) Đúng

b) Sai

c) Đúng

d) Sai

Ta có: $y’ = 3{x^2} – 6mx + 3\left( {{m^2} – 1} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{{x_1} = m – 1} \\
{{x_2} = m + 1}
\end{array}} \right.$.

Để hàm số có giá trị nhỏ nhất trên khoảng $\left( {0; + \infty } \right)$ thì ${x_1} \leqslant 0 < {x_2}$ hoặc $0 < {x_1} < {x_2}$.

TH1: ${x_1} \leqslant 0 < {x_2} \Leftrightarrow m – 1 \leqslant 0 < m + 1 \Leftrightarrow – 1 < m \leqslant 1$. Do $m \in \mathbb{Z} \Rightarrow m \in \left\{ {0;1} \right\}$.

BBT của hàm số:

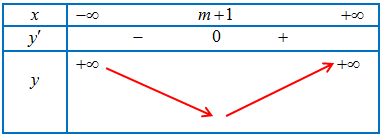
TH2: $0 < {x_1} < {x_2}$.

BBT của hàm số

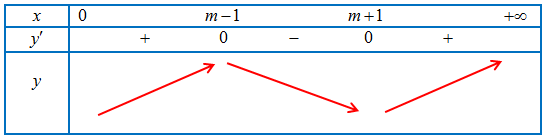
Hàm số có giá trị nhỏ nhất trên khoảng $\left( {0; + \infty } \right)$ khi và chỉ khi $\left\{ {\begin{array}{*{20}{l}}
{m – 1 > 0} \\
{y\left( {m + 1} \right) \leqslant y\left( 0 \right)}
\end{array}} \right.$.

$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{m > 1} \\
{{{(m + 1)}^3} – 3m{{(m + 1)}^2} + 3\left( {{m^2} – 1} \right)\left( {m + 1} \right) + 2025 \leqslant 2025}
\end{array}} \right.$

$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{m > 1} \\
{{{(m + 1)}^2}\left( {m – 2} \right) \leqslant 0}
\end{array}} \right.$

$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{m > 1} \\
{\left[ \begin{gathered}
m \leqslant 2 \hfill \\
m = – 1 \hfill \\
\end{gathered} \right.}
\end{array}} \right.$$ \Leftrightarrow 1 < m \leqslant 2$.

Do $m \in \mathbb{Z} \Rightarrow m = 2$.

Vậy $m \in \left\{ {0;1;2} \right\}$.

Câu 14. Cho hàm số $y = f\left( x \right) = {x^3} – 3x + m + 1$, (tham số $m$ ). Khi đó:

a) Khi $m = 0$ thì hàm số $y = – f\left( x \right)$ có 2 điểm cực trị

b) Khi $m = 0$ thì hàm số $y = f\left( x \right)$ nghịch biến trên khoảng $\left( {1; + \infty } \right)$

c) Khi $m = 0$ thì hàm số $y = – f\left( x \right)$ đạt giá trị lớn nhất trên khoảng $\left( { – 1; + \infty } \right)$ tại $x = 1$

d) Tổng tất cả các giá trị của tham số $m$ sao cho giá trị nhỏ nhất của hàm số $y = {[f\left( x \right)]^2}$ trên đoạn $\left[ { – 1;1} \right]$ bằng 1 là -2

Lời giải

a) Đúng

b) Sai

c) Đúng

d) Sai

Bảng biến thiên của $g\left( x \right)$

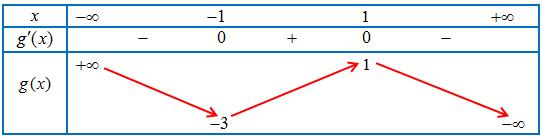
d) Đặt $y = f\left( x \right) = {\left( {{x^3} – 3x + m + 1} \right)^2}$ là hàm số xác định và liên tục trên đoạn $\left[ { – 1;1} \right]$.

Ta có $y’ = f’\left( x \right) = 2\left( {{x^3} – 3x + m + 1} \right)\left( {3{x^2} – 3} \right)$.

$f’\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = \pm 1} \\
{m = – {x^3} + 3x – 1 = g\left( x \right)}
\end{array}} \right.$.

Ta khảo sát hàm số $g\left( x \right)$ trên đoạn $\left[ { – 1;1} \right]$.

Bảng biến thiên của $g\left( x \right)$

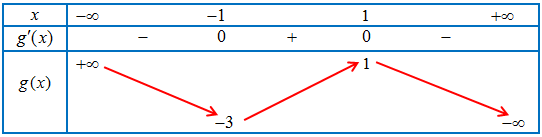
Nếu $m \in \left[ { – 3;1} \right]$ thì luôn tồn tại ${x_0} \in \left[ { – 1;1} \right]$ sao cho $m = g\left( {{x_0}} \right)$ hay $f\left( {{x_0}} \right) = 0$. Suy ra $\mathop {min}\limits_{\left[ { – 1;1} \right]} y = 0$, tức là không tồn tại $m$. thỏa mãn yêu cầu bài toán.

Nếu $m \notin \left[ { – 3;1} \right]$ thì $f’\left( x \right) = 0 \Leftrightarrow x = \pm 1 \in \left[ { – 1;1} \right]$.

Ta có: $\mathop {min}\limits_{\left[ { – 1;1} \right]} f\left( x \right) = min\left\{ {f\left( 1 \right);f\left( { – 1} \right)} \right\} = min\left\{ {{{(m – 1)}^2};{{(m + 3)}^2}} \right\}$

Trường hợp 1: $m > 1$ tức là $m + 3 > m – 1 > 0$ suy ra

$\mathop {min}\limits_{\left[ { – 1;1} \right]} f\left( x \right) = {\left( {m – 1} \right)^2} = 1$$ \Leftrightarrow \left[ \begin{gathered}
m = 2\,(TM) \hfill \\
m = 0\,(KTM) \hfill \\
\end{gathered} \right.$

Trường hợp 2: $m < – 3$ tức là $m – 1 < m + 3 < 0$ suy ra

$\mathop {min}\limits_{\left[ { – 1;1} \right]} f\left( x \right) = {(m + 3)^2} = 1 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{m = – 4\left( {TM} \right)} \\
{m = – 2\left( {KTM} \right)}
\end{array}} \right.$

Vậy có hai giá trị của $m$ thỏa mãn yêu cầu bài toán: $m = 2;m = – 4$, từ đó tổng tất cả các giá trị của $m$ là -2 .

Câu 15. Cho hàm số $f\left( x \right) = m{x^4} + 2\left( {m – 1} \right){x^2}$ với $m$ là tham số thực. Khi đó:

a) Khi $m = 1$ hàm số có 3 điểm cực trị

b) Khi $m = 0$ hàm số có 3 điểm cực trị

c) Khi $m = \frac{1}{2}$ thì giá trị nhỏ nhất của hàm số bằng $ – \frac{1}{2}$

d) Nếu thì bằng 3

Lời giải

a) Sai b) Đúng c) Đúng d) Sai

$f’\left( x \right) = 4m{x^3} + 4\left( {m – 1} \right)x$.

Do $f\left( x \right)$ là hàm đa thức và

$ \Leftrightarrow 4m + 4\left( {m – 1} \right) = 0 \Rightarrow m = \frac{1}{2}$.

Thay $m = \frac{1}{2}$ vào hàm số ban đầu ta được

$y = \frac{1}{2}{x^4} + 2\left( {\frac{1}{2} – 1} \right){x^2} = \frac{1}{2}{x^4} – {x^2}$

$ \Rightarrow y’ = 2{x^3} – 2x = 2x\left( {x – 1} \right)\left( {x + 1} \right)$

Ta có BBT:

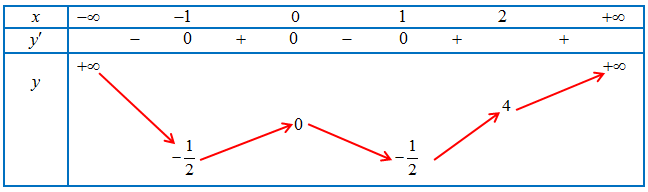
Vậy với $m = \frac{1}{2}$, thì $\mathop {min}\limits_{\left[ {0;2} \right]} f\left( x \right) = f\left( 1 \right)\left( {TM} \right)$.

Dựa vào BBT ta có .

Câu 16. Cho hàm số $f\left( x \right)$, đồ thị hàm số $y = f’\left( x \right)$ là đường cong trong hình bên.

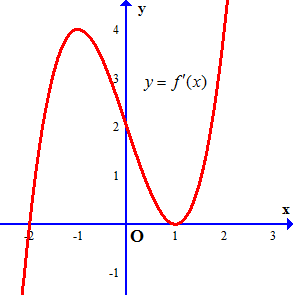
a) Hàm số $f\left( x \right)$ đồng biến trên khoảng $\left( {1; + \infty } \right)$ và $\left( { – \infty ; – 2} \right)$

b) Hàm số $f\left( x \right)$ có 2 điểm cực trị

c) Hàm số $g\left( x \right) = f\left( {\frac{x}{2}} \right)$ nghịch biến trên khoảng $\left( { – 5; – 4} \right)$

d) Giá trị nhỏ nhất của hàm số $g\left( x \right) = f\left( {\frac{x}{2}} \right)$ trên đoạn $\left[ { – 5;3} \right]$ bằng $f\left( { – 2} \right)$

Lời giải

a) Sai

b) Sai

c) Đúng

d) Đúng

${g^\prime }(x) = 0 \Leftrightarrow \frac{1}{2}{f^\prime }\left( {\frac{x}{2}} \right) = 0$

$ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{\frac{x}{2} = – 2} \\
{\frac{x}{2} = 1}
\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = – 4} \\
{x = 2}
\end{array} } \right.} \right.$.

${g^\prime }(x) < 0 \Leftrightarrow {f^\prime }\left( {\frac{x}{2}} \right) < 0 \Leftrightarrow \frac{x}{2} < – 2 \Leftrightarrow x < – 4$

Bảng biến thiên

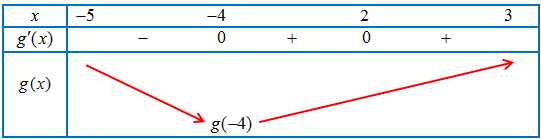
Giá trị nhỏ nhất của hàm số $g\left( x \right)$ trên $\left[ { – 5;3} \right]$ bằng $g\left( { – 4} \right) = f\left( { – 2} \right)$.

Câu 17. Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như hình dưới đây.

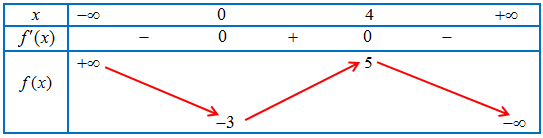
a) Hàm số $y = f\left( x \right)$ có 2 điểm cực trị

b) Hàm số $y = f\left( x \right)$ đồng biến trên khoảng $\left( { – 3;5} \right)$

c) Giá trị lớn nhất của hàm số $y = f\left( x \right)$ trên đoạn $\left[ {1;3} \right]$ bằng $f\left( 1 \right)$

d) Giá trị lớn nhất của hàm số $g\left( x \right) = f\left( {4x – {x^2}} \right) + \frac{1}{3}{x^3} – 3{x^2} + 8x + \frac{1}{3}$ trên đoạn $\left[ {1;3} \right]$ bằng 12
Lời giải

a) Đúng

b) Sai

c) Sai

d) Đúng

$g’\left( x \right) = \left( {4 – 2x} \right)f’\left( {4x – {x^2}} \right) + {x^2} – 6x + 8$

$ = \left( {2 – x} \right)\left[ {2f’\left( {4x – {x^2}} \right) + 4 – x} \right]$.

Với $x \in \left[ {1;3} \right]$ thì $4 – x > 0;3 \leqslant 4x – {x^2} \leqslant 4$ nên $f’\left( {4x – {x^2}} \right) > 0$.

Suy ra $2f’\left( {4x – {x^2}} \right) + 4 – x > 0,\forall x \in \left[ {1;3} \right]$.

Bảng biến thiên

Suy ra $\mathop {max}\limits_{\left[ {1;3} \right]} g\left( x \right) = g\left( 2 \right) = f\left( 4 \right) + 7 = 12$.

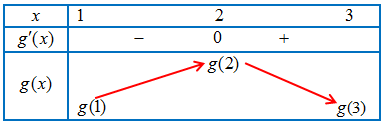
Câu 18. Cho hàm số $y = f\left( x \right)$ có đạo hàm liên tục trên $\mathbb{R}$ và $f\left( 0 \right) \geqslant – 1$. Đồ thị của hàm số $y = f’\left( x \right)$ như hình vẽ.

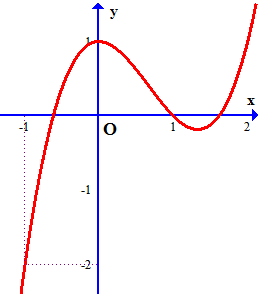
a) Hàm số $y = f\left( x \right)$ đồng biến trên khoảng $\left( {0;1} \right)$

b) Hàm số $y = f\left( x \right)$ có 2 điểm cực trị

c) Hàm số $y = f\left( x \right) – \frac{{{x^3}}}{3} + {x^2} – x + 2$ có 3 điểm cực trị

d) Hàm số $y = \left| {f\left( x \right) – \frac{{{x^3}}}{3} + {x^2} – x + 2} \right|$ có giá trị nhỏ nhất là $m \in \left( {0;1} \right)$ khi và chỉ khi $ – \frac{4}{3} < f\left( 2 \right) < \frac{1}{3}$

Lời giải

a) Đúng

b) Sai

c) Đúng

d) Đúng

Xét $g\left( x \right) = f\left( x \right) – \frac{{{x^3}}}{3} + {x^2} – x + 2$

$ \Rightarrow g’\left( x \right) = f’\left( x \right) – {x^2} + 2x – 1$;

$g’\left( x \right) = 0 \Leftrightarrow f’\left( x \right) = {x^2} – 2x + 1$.

Vẽ $\left( P \right):y = {x^2} – 2x + 1$ cắt $y = f’\left( x \right)$ tai ba điểm có hoành độ $x = 0;x = 1;x = 2$.

Ta có bảng biến thiên của $y = g\left( x \right)$ như sau

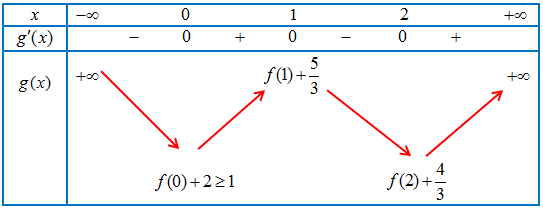
Từ bảng biến thiên ta thấy:

Nếu $f\left( 2 \right) + \frac{4}{3} < 0 \Rightarrow \left| {g\left( x \right)} \right| \geqslant 0 \Rightarrow Min\left| {g\left( x \right)} \right| = 0$.

Do đó để $min\left| {g\left( x \right)} \right| = m \in \left( {0;1} \right)$$ \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{f\left( 2 \right) + \frac{4}{3} > 0} \\
{f\left( 2 \right) + \frac{4}{3} < 1}
\end{array}} \right.$$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{f\left( 2 \right) > \frac{{ – 4}}{3}} \\
{f\left( 2 \right) < – \frac{1}{3}}
\end{array}} \right.$.

Vậy $ – \frac{4}{3} < f\left( 2 \right) < \frac{1}{3}$

Câu 19. Cho hàm số $y = f\left( x \right) = {x^3} – 3x + m$ (tham số thực $m$ ). Khi đó:

a) Khi $m = 0$ thì hàm số đồng biến trên khoảng $\left( { – 1;1} \right)$

b) Khi $m = 0$ thì hàm số có 2 điểm cực trị

c) Hàm số có giá trị nhỏ nhất trên đoạn $\left[ {0;2} \right]$ bằng $m – 2$
d) Gọi $S$ là tập hợp tất cả các giá trị của tham số thực $m$ sao cho giá trị lớn nhất của hàm số $y = \left| {f\left( x \right)} \right|$ trên đoạn $\left[ {0;2} \right]$ bằng 3 . Số phần tử của $S$ là 1

Lời giải

a) Sai

b) Đúng

c) Đúng

d) Sai

 

d) Xét hàm số $f\left( x \right) = {x^3} – 3x + m$, ta có $f’\left( x \right) = 3{x^2} – 3$. Ta có bảng biến thiên của $f\left( x \right)$ :

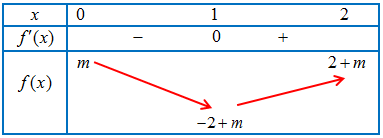
Cách 1. Dựa vào bảng biến thiên ta suy ra, $H = \mathop {max}\limits_{\left[ {0;2} \right]} f\left( x \right) = 2 + m$ và $K = \mathop {\min }\limits_{\left[ {0;2} \right]} f\left( x \right) =  – 2 + m$

Vậy, $\mathop {max}\limits_{\left[ {0;2} \right]} |f(x)| = \frac{{|H + K| + |H – K|}}{2}$

$ = \frac{{|(2 + m) + ( – 2 + m)| + |(2 + m) – ( – 2 + m)|}}{2} = \frac{{|2m| + 4}}{2}$

Theo đề cho $\mathop {max}\limits_{\left[ {0;2} \right]} |f(x)| = 3 \Leftrightarrow \frac{{|2m| + 4}}{2} = 3$

$ \Leftrightarrow |2m| = 2 \Leftrightarrow \left[ \begin{gathered}
2m = 2 \hfill \\
2m =  – 2 \hfill \\
\end{gathered}  \right. \Leftrightarrow \left[ \begin{gathered}
m = 1 \hfill \\
m =  – 1 \hfill \\
\end{gathered}  \right.$

Vậy, số phần tử của $S$ là $2$.

Chú ý: Để tìm Giá trị lớn nhất và nhỏ nhất của hàm số $y = \left| {f(x)} \right|$ ta làm như sau:

Bước 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = f(x)$.

Giả sử $\mathop {\min }\limits_D f(x) = m$; $\mathop {\max }\limits_D f(x) = M$.

Bước 2: $\mathop {max}\limits_D |f(x)| = \frac{{|M + m| + |M – m|}}{2}$;

$\mathop {\min }\limits_D |f(x)| = \left\{ {\begin{array}{*{20}{l}}
{\frac{{|M + m| – |M – m|}}{2}}&{ khi\,\, m.M \geqslant 0} \\
0&{ khi \,\,m.M < 0}
\end{array}} \right.$.

Cách 2. Dựa vào bảng biến thiên ta phân thành các trường hợp sau

TH 1 : $2 + m < 0 \Leftrightarrow m < – 2$. Khi đó $\mathop {max}\limits_{\left[ {0;2} \right]} \left| {f\left( x \right)} \right| = – \left( { – 2 + m} \right) = 2 – m$

$2 – m = 3 \Leftrightarrow m = – 1$ (loại).

TH 2: $\left\{ {\begin{array}{*{20}{l}}
{2 + m > 0} \\
{m < 0}
\end{array} \Leftrightarrow – 2 < m < 0} \right.$. Khi đó : $\;\left| {m – 2} \right| = 2 – m > 2 > 2 + m$

$2 – m = 3 \Leftrightarrow m = – 1$ (thỏa mãn).

TH 3: $\left\{ {\begin{array}{*{20}{l}}
{m > 0} \\
{ – 2 + m < 0}
\end{array} \Leftrightarrow 0 < m < 2} \right.$. Khi đó : $2 + m = 3 \Leftrightarrow m = 1$ (thỏa mãn).

TH 4: $ – 2 + m > 0 \Leftrightarrow m > 2$. Khi đó

$2 + m = 3 \Leftrightarrow m = 1$ (loại).

Vậy, số phần tử của $S$ là $2$.

Câu 20. Cho hàm số $y = {x^4} – 2{x^2} + 3m$ với $m$ là tham số. Khi đó :

a) Hàm số đồng biến trên khoảng $\left( {1; + \infty } \right)$

b) Hàm số có 3 điểm cực trị

c) Giá trị nhỏ nhất của hàm số trên đoạn $\left[ { – 1;2} \right]$ là $3m + 1$

d) Biết rằng có đúng hai giá trị ${m_1},{m_2}$ của $m$ để giá trị nhỏ nhất của hàm số $y = \left| {f\left( x \right)} \right|$ trên $\left[ { – 1;2} \right]$ bằng $2025$. Khi đó giá trị $\left| {{m_1} – {m_2}} \right|$ bằng $\frac{8}{3}$

Lời giải

a) Đúng

b) Đúng

c) Sai

d) Sai

d) Xét hàm số $f\left( x \right) = {x^4} – 2{x^2} + 3m$, ta có

$f’\left( x \right) = 4{x^3} – 4x = 4x\left( {{x^2} – 1} \right)f’\left( x \right) = 0$$ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 0} \\
{x = \pm 1}
\end{array}} \right.$

Bảng biến thiên của hàm số trên $\left[ { – 1;2} \right]$ :

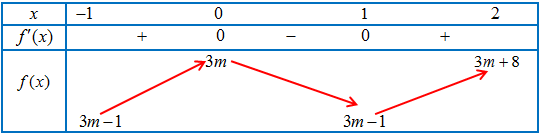
Suy ra, $H = \mathop {max}\limits_{\left[ { – 1;2} \right]} f(x) = 3m + 8$; $K = \mathop {\min }\limits_{\left[ { – 1;2} \right]} f(x) = 3m – 1$

TH1: $H.K \geqslant 0 \Leftrightarrow \left( {3m + 8} \right)\left( {3m – 1} \right) \geqslant 0 \Leftrightarrow \left[ \begin{gathered}
m \leqslant – \frac{8}{3} \hfill \\
m \geqslant \frac{1}{3} \hfill \\
\end{gathered} \right.$

Ta có: $\mathop {\min }\limits_{\left[ { – 1;2} \right]} \left| {f\left( x \right)} \right| = \frac{{\left| {(3m + 8) + (3m – 1)} \right| – \left| {(3m + 8) – (3m – 1)} \right|}}{2}$

$ = \frac{{\left| {6m + 7} \right| – 9}}{2} = 2025$

$\frac{{\left| {6m + 7} \right| – 9}}{2} = 2025$

$ \Leftrightarrow \left| {6m + 7} \right| = 4059 \Leftrightarrow \left[ \begin{gathered}
6m + 7 = 4059 \hfill \\
6m + 7 = – 4059 \hfill \\
\end{gathered} \right.$

$ \Leftrightarrow \left[ \begin{gathered}
m = \frac{{2026}}{3}\,(nhan) \hfill \\
m = – \frac{{2033}}{3}\,(nhan) \hfill \\
\end{gathered} \right.$

Khi đó giá trị $\left| {{m_1} – {m_2}} \right| = \left| {\frac{{2026}}{3} – \left( { – \frac{{2033}}{3}} \right)} \right| = 1353$

TH2: $H.K < 0 \Leftrightarrow \left( {3m + 8} \right)\left( {3m – 1} \right) < 0$ $ \Leftrightarrow – \frac{8}{3} < m < \frac{1}{3}$

$\mathop {\min }\limits_{\left[ { – 1;2} \right]} \left| {f\left( x \right)} \right| = 0$ (loại)

Vậy, $\left| {{m_1} – {m_2}} \right| = \left| {\frac{{2026}}{3} – \left( { – \frac{{2033}}{3}} \right)} \right| = 1353$. Do đó d) sai.