Trắc Nghiệm Bài Phép Chiếu Song Song Giải Chi Tiết

Trắc nghiệm bài phép chiếu song song giải chi tiết được soạn dưới dạng file word và PDF gồm 2 trang. Các bạn xem và tải về ở dưới.

Câu 1: Trong các mệnh đề sau, mệnh đề nào đúng?

A. Hình chiếu song song của hai đường thẳng cắt nhau là hai đường thẳng song song.

B. Hình chiếu song song của một hình bình hành là một hình bình hành.

C. Phép chiếu song song biến một tam giác thành một tam giác nếu mặt phẳng chứa tam giác không cùng phương với phương chiếu.

D. Phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng.

Câu 2: Trên hình A có $\left\{ \begin{gathered}
AH \bot BC \hfill \\
HB = HC \hfill \\
\end{gathered} \right.$ và hình B có $\left\{ \begin{gathered}
AB\parallel CD,AD\parallel BC \hfill \\
AC \bot BD \hfill \\
\end{gathered} \right.$

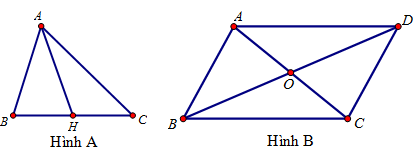
Hãy Chọn mệnh đề đúng trong các mệnh đề sau:

A. ABC là tam giác đều.

B. ABC là tam giác cân tại A

C. ABCD là hình thoi.

D. B và C đúng.

Câu 3: Trên hình $\mathcal{C}$, ta có phép chiếu song song theo phương d và mặt phẳng chiếu (P); $AB\parallel CG$ và $AB = DG$; A’, B’, C’, D’, E’, G’ lần lượt là hình chiếu của A, B, C, D, E, G qua phép chiếu nói trên.

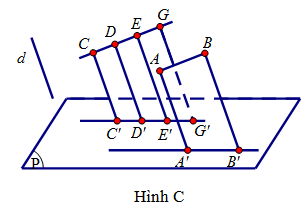Mệnh đề nào sau đây đúng?

A. $\frac{{DG}}{{AB}} = \frac{{D’G’}}{{A’B’}} = 1$. B. $\frac{{C’D’}}{{D’E’}} = \frac{{CD}}{{DE}}$.

C. $D’G’ = A’B’$. D. Tất cả A, B, C đều đúng.

Câu 4: Trong các mệnh đề sau, mệnh đề nào đúng?

A. Hình chiếu song song của hai đường thẳng chéo nhau có thể song song với nhau.

B. Hình chiếu song song của hai đường thẳng cắt nhau thì song song.

C. Hình chiếu song song của hai một hình vuông là một hình vuông.

D. Hình chiếu song song của một lục giác đều là một lục giác đều.

Câu 5: Qua phép chiếu song song lên mặt phẳng (P), hai đường thẳng chéo nhau a và b có hình chiếu là hai đường thẳng a’ và b’. Mệnh đề nào sau đây đúng?

A. a’ và b’ luôn luôn cắt nhau.

B. a’ và b’ có thể trùng nhau.

C. a và b không thể song song.

D. a’ và b’ có thể cắt nhau hoặc song song với nhau.

Câu 6: Qua phép chiếu song song lên mặt phẳng (P), hai đường thẳng a và b có hình chiếu là hai đường thẳng song song a’ và b’. Khi đó:

A. a và b phải song song với nhau.

B. a và b phải cắt nhau.

C. a và b có thể chéo nhau hoặc song song với nhau.

D. a và b không thể song song.

Câu 7: Cho bốn điểm không đồng phẳng A, B, C, D có hình chiếu song song trên mặt phẳng (P) lần lượt là bốn điểm A’, B’, C’, D’. Những trường hợp nào sau đây không thể xảy ra?

A. A’B’C’D’ là bốn đỉnh của một hình bình hành.

B. D’ là trọng tâm tam giác A’B’C’.

C. D’ là trung điểm cạnh A’B’.

D. Hai điểm B’, C’ nằm giữa hai điểm A’ và D’.

Câu 8: Hình chiếu song song của một hình thang ABCD không thể là hình nào dưới đây?

A. Hình bình hành. B. Hình tam giác cân.

C. Đoạn thẳng. D. Bốn điểm thẳng hàng.

ĐÁP ÁN

1	2	3	4
C	D	D	A
5	6	7	8
D	C	D	B

LỜI GIẢI CHI TIẾT

Câu 1: Trong các mệnh đề sau, mệnh đề nào đúng?

A. Hình chiếu song song của hai đường thẳng cắt nhau là hai đường thẳng song song.

B. Hình chiếu song song của một hình bình hành là một hình bình hành.

C. Phép chiếu song song biến một tam giác thành một tam giác nếu mặt phẳng chứa tam giác không cùng phương với phương chiếu.

D. Phép chiếu song song không làm thay đổi tỉ số độ dài của hai đoạn thẳng.

Lời giải

Chọn C

Câu 2: Trên hình A có $\left\{ \begin{gathered}
AH \bot BC \hfill \\
HB = HC \hfill \\
\end{gathered} \right.$ và hình B có $\left\{ \begin{gathered}
AB\parallel CD,AD\parallel BC \hfill \\
AC \bot BD \hfill \\
\end{gathered} \right.$

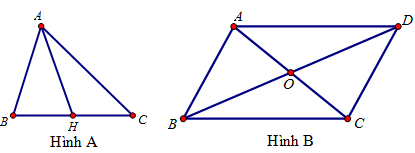
Hãy Chọn mệnh đề đúng trong các mệnh đề sau:

A. ABC là tam giác đều.

B. ABC là tam giác cân tại A

C. ABCD là hình thoi.

D. B và C đúng.

Lời giải

Chọn D

Nhìn hình vẽ, ta thấy:

– Tam giác ABC có AH vừa là đường cao vừa là trung tuyến nên cân tại A 🡪 B đúng.

– Tứ giác ABCD có $AB\parallel CD,\,\,AC\parallel BD$ nên là hình bình hành. Mặt khác hai đường chéo của nó vuông góc nên ABCD là hình thoi 🡪 C đúng.

Câu 3: Trên hình $\mathcal{C}$, ta có phép chiếu song song theo phương d và mặt phẳng chiếu (P); $AB\parallel CG$ và $AB = DG$; A’, B’, C’, D’, E’, G’ lần lượt là hình chiếu của A, B, C, D, E, G qua phép chiếu nói trên.

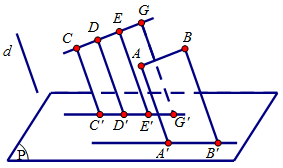
Hình $\mathcal{C}$

Mệnh đề nào sau đây đúng?

A. $\frac{{DG}}{{AB}} = \frac{{D’G’}}{{A’B’}} = 1$. B. $\frac{{C’D’}}{{D’E’}} = \frac{{CD}}{{DE}}$.

C. $D’G’ = A’B’$. D. Tất cả A, B, C đều đúng.

Lời giải

Chọn D

The định lí 2, ta thấy câu A và câu B đúng. Từ câu A đúng suy ra câu C đúng.

Câu 4: Trong các mệnh đề sau, mệnh đề nào đúng?

A. Hình chiếu song song của hai đường thẳng chéo nhau có thể song song với nhau.

B. Hình chiếu song song của hai đường thẳng cắt nhau thì song song.

C. Hình chiếu song song của hai một hình vuông là một hình vuông.

D. Hình chiếu song song của một lục giác đều là một lục giác đều.

Lời giải

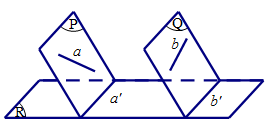
Chọn A

Dựng mặt phẳng (P) qua a và song song với b. Dựng mặt phẳng (Q) qua b và song song với a. Giả sử (P) song song với (Q). Ta Chọn phương chiếu d song song với (P) và mặt phẳng chiếu (R) sao cho (R) cắt (P) và (Q) lần lượt theo hai giao tuyến a’ và b’. Khi đó hình chiếu a’, b’ song song với nhau.

Câu 5: Qua phép chiếu song song lên mặt phẳng (P), hai đường thẳng chéo nhau a và b có hình chiếu là hai đường thẳng a’ và b’. Mệnh đề nào sau đây đúng?

A. a’ và b’ luôn luôn cắt nhau.

B. a’ và b’ có thể trùng nhau.

C. a và b không thể song song.

D. a’ và b’ có thể cắt nhau hoặc song song với nhau.

Lời giải

Chọn D

Gọi l là phương chiếu, $\left( \alpha \right)$ và $\left( \beta \right)$ là các mặt phẳng song song với l và lần lượt đi qua a và b. Khi đó nếu $\left( \alpha \right)$ và $\left( \beta \right)$ cắt nhau thì a’ và b’ cắt nhau, nếu $\left( \alpha \right)$ và $\left( \beta \right)$ song song thì a’ và b’ song song.

Câu 6: Qua phép chiếu song song lên mặt phẳng (P), hai đường thẳng a và b có hình chiếu là hai đường thẳng song song a’ và b’. Khi đó:

A. a và b phải song song với nhau.

B. a và b phải cắt nhau.

C. a và b có thể chéo nhau hoặc song song với nhau.

D. a và b không thể song song.

Lời giải

Chọn C

Nếu $a’\parallel b’$ thì $mp\left( {a,a’} \right)\parallel mp\left( {b,b’} \right)$. Bởi vậy a và b có thể song song hoặc chéo nhau.

Câu 7: Cho bốn điểm không đồng phẳng A, B, C, D có hình chiếu song song trên mặt phẳng (P) lần lượt là bốn điểm A’, B’, C’, D’. Những trường hợp nào sau đây không thể xảy ra?

A. A’B’C’D’ là bốn đỉnh của một hình bình hành.

B. D’ là trọng tâm tam giác A’B’C’.

C. D’ là trung điểm cạnh A’B’.

D. Hai điểm B’, C’ nằm giữa hai điểm A’ và D’.

Lời giải

Chọn D

Bốn điểm không đồng phẳng A’, B’, C’, D’ không thể thẳng hàng.

Câu 8: Hình chiếu song song của một hình thang ABCD không thể là hình nào dưới đây?

A. Hình bình hành. B. Hình tam giác cân.

C. Đoạn thẳng. D. Bốn điểm thẳng hàng.

Lời giải

Chọn B