Các Dạng Trắc Nghiệm Ứng Dụng Tích Phân Để Tính Diện Tích Hình Phẳng

Các dạng trắc nghiệm ứng dụng tích phân để tính diện tích hình phẳng có lời giải chi tiết được soạn dưới dạng file word và PDF gồm 6 trang. Các bạn xem và tải về ở dưới.

CÁC DẠNG TRẮC NGHIỆM ỨNG DỤNG HÌNH HỌC CỦA TÍCH PHÂN ĐỂ TÍNH DIỆN TÍCH HÌNH PHẲNG

Dạng 1: Tính diện tích giới hạn bởi các đường cong khi biết hàm số các đường cong

Chú ý: $\left\{ \begin{gathered}
y = f\left( x \right) \hfill \\
y = g\left( x \right) \hfill \\
x = a \hfill \\
x = b \hfill \\
\end{gathered} \right.$$ \Rightarrow S = \int\limits_a^b {\left| {f(x) – g\left( x \right)} \right|dx} $

Câu 1. Cho hàm số $y = f(x)$ liên tục trên $\left[ {a\,;\,b} \right]$. Diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = f(x)$, trục hoành và các đường thẳng $x = a$, $x = b$ bằng

A. $\left| {\int\limits_a^b {f(x)dx} } \right|$. B. $\int\limits_a^b {\left| {f(x)} \right|dx} $. C. $\int\limits_a^b {f(x)dx} $. D. $ – \int\limits_a^b {f(x)dx} $.

Lời giải

Chọn B.

Theo lý thuyết thì diện tích hình phẳng được giới hạn bởi đồ thị của các đường $y = f(x)$, trục hoành $y = 0$, $x = a$, $x = b$ được tính theo công thức $S = \int\limits_a^b {\left| {f\left( x \right) – 0} \right|dx} = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \,$.

Câu 2. Diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = {e^x}$, trục hoành và các đường thẳng $x = 0$, $x = \ln 5$ bằng

A. $\left| {\int\limits_a^b {f(x)dx} } \right|$. B. $\int\limits_a^b {\left| {f(x)} \right|dx} $. C. $\int\limits_a^b {f(x)dx} $. D. $ – \int\limits_a^b {f(x)dx} $.

Lời giải

$S = \int\limits_0^{\ln 5} {\left| {{e^x} – 0} \right|dx} = \int\limits_0^{\ln 5} {\left| {{e^x}} \right|dx} = \int\limits_0^{\ln 5} {\left| {{e^x}} \right|dx} $

$ = \int\limits_0^{\ln 5} {{e^x}dx} = \left. {{e^x}} \right|_0^{\ln 5} = {e^{\ln 5}} – {e^0} = 4$

Câu 3. Cho hai hàm số $f(x)$ và $g(x)$ liên tục trên $\left[ {a\,;\,b} \right]$. Diện tích hình phẳng giới hạn bởi đồ thị của các hàm số $y = f(x)$, $y = g(x)$ và các đường thẳng $x = a$, $x = b$ bằng

A. $\left| {\int\limits_a^b {\left[ {f(x) – g(x)} \right]dx} } \right|$. B. $\int\limits_a^b {\left| {f(x) + g(x)} \right|dx} $. C. $\int\limits_a^b {\left| {f(x) – g(x)} \right|dx} $. D. $\int\limits_a^b {\left[ {f(x) – g(x)} \right]dx} $.

Lời giải

Chọn C.

Theo lý thuyết thì diện tích hình phẳng được giới hạn bởi đồ thị của các đường $y = f(x)$, $y = g(x)$, $x = a$, $x = b$ được tính theo công thức $S = \int\limits_a^b {\left| {f\left( x \right) – g\left( x \right)} \right|dx} $.

Câu 4. Gọi $S$ là diện tích của hình phẳng giới hạn bởi các đường $y = {3^x}$, $y = 0$,$x = 0$,$x = 2$. Mệnh đề nào dưới đây đúng?

A. $S = \int\limits_0^2 {{3^x}} dx$. B. $S = \pi \int\limits_0^2 {{3^{2x}}} dx$. C. $S = \pi \int\limits_0^2 {{3^x}} dx$. D. $S = \int\limits_0^2 {{3^{2x}}} dx$.

Lời giải

Chọn A.

Diện tích hình phẳng đã cho được tính bởi công thức $S = \int\limits_0^2 {{3^x}} dx$

Câu 5. Diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = {\left( {x – 2} \right)^2} – 1$, trục hoành và hai đường thẳng $x = 1,\,x = 2$ bằng

A. $\frac{2}{3}$. B. $\frac{3}{2}$. C. $\frac{1}{3}$. D. $\frac{7}{3}$.

Lời giải

Chọn A.

Ta có:$S = \int\limits_1^2 {\left| {{{\left( {x – 2} \right)}^2} – 1} \right|dx} = \int\limits_1^2 {\left| {{x^2} – 4x + 3} \right|dx = } \left| {\int\limits_1^2 {\left( {{x^2} – 4x + 3} \right)dx} } \right| = \frac{2}{3}$.

Câu 6. Tính diện tích $S$ hình phẳng giới hạn bởi các đường $y = {x^2} + 1,\,x = – 1,\,x = 2$ và trục hoành.

A. $S = 6$. B. $S = 16$. C. $S = \frac{{13}}{6}$. D. $S = 13$.

Lời giải

Chọn A.

Ta có: $S = \int\limits_{ – 1}^2 {\left| {{x^2} + 1} \right|} \,dx = \int\limits_{ – 1}^2 {\left( {{x^2} + 1} \right)} \,dx = 6$.

Câu 7. Gọi $S$ là diện tích hình phẳng giới hạn bởi các đường $y = {x^2} + 5$,$y = 6x$, $x = 0$,$x = 1$. Tính $S$.

A. $\frac{4}{3}$ B. $\frac{7}{3}$ C. $\frac{8}{3}$ D. $\frac{5}{3}$

Lời giải

Chọn B.

Phương trình hoành độ giao điểm: ${x^2} + 5 = 6x \Leftrightarrow x = 5;x = 1$.

Diện tích hình phẳng cần tìm: $S = \int\limits_0^1 {\left| {{x^2} – 6x + 5} \right|dx} = \frac{7}{3}$.

Câu 8. Diện tích hình phẳng giới hạn bởi đồ thị các hàm số $y = \ln x,$ $y = 1$ và hai đường thẳng $x = 1,x = e$ bằng

A. ${e^2}$. B. $e + 2$. C. $2e$. D. $e – 2$.

Lời giải

Chọn D.

$S = \int\limits_1^e {\left| {\ln x – 1} \right|} dx = \left| {\int\limits_1^e {\left( {\ln x – 1} \right)dx} } \right| = \left| {\left. {x\left( {\ln x – 1} \right)} \right|_{\left. 1 \right|}^e – \int\limits_1^e {dx} } \right| = \left| {1 – \left. x \right|_1^e} \right| = \left| {1 – \left( {e – 1} \right)} \right| = \left| {2 – e} \right| = e – 2$

Câu 9. Diện tích hình phẳng giới hạn bởi đồ thị của hàm số $y = 4x – {x^2}$, $y = 2x$ và hai đường thẳng $x = 1,x = e$ bằng

A. $4$. B. $\frac{{20}}{3}$. C. $\frac{4}{3}$. D. $\frac{{16}}{3}$

Lời giải

Chọn C.

diện tích hình phẳng cần tìm là $S = \int\limits_0^2 {\left| {{x^2} – 2x} \right|dx} = \int\limits_0^2 {\left( {2x – {x^2}} \right)dx} = \left. {\left( {{x^2} – \frac{{{x^3}}}{3}} \right)} \right|_0^2 = \frac{4}{3}$.

Câu 10. Tính diện tích $S$ của hình phẳng giới hạn bởi các đường $y = {x^2} – 2x$, $y = 0$, $x = – 10$, $x = 10$.

A. $S = \frac{{2000}}{3}$. B. $S = 2008$. C. $S = 2000$. D. $S = \frac{{2008}}{3}$.

Lời giải

Chọn D.

Phương trình hoành độ giao điểm của hai đường $\left( C \right):y = {x^2} – 2x$ và $\left( d \right):y = 0$ là: ${x^2} – 2x = 0 \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
x = 2 \hfill \\
\end{gathered} \right.$.

Bảng xét dấu:

Diện tích cần tìm: $S = \int\limits_{ – 10}^{10} {\left| {{x^2} – 2x} \right|dx} = \int\limits_{ – 10}^0 {\left( {{x^2} – 2x} \right)dx} – \int\limits_0^2 {\left( {{x^2} – 2x} \right)dx} + \int\limits_2^{10} {\left( {{x^2} – 2x} \right)dx} $$ = \left. {\left( {\frac{{{x^3}}}{3} – {x^2}} \right)} \right|_{ – 10}^0 – \left. {\left( {\frac{{{x^3}}}{3} – {x^2}} \right)} \right|_0^2 + \left. {\left( {\frac{{{x^3}}}{3} – {x^2}} \right)} \right|_2^{10}$$ = \frac{{1300}}{3} + \frac{4}{3} + \frac{{704}}{3} = \frac{{2008}}{3}$.

Dạng 2: Tính diện tích giới hạn bởi các đường cong khi biết đồ thị hàm số của các đường cong

Chú ý:

– Nếu trên $\left( {a;b} \right)$ đồ thị hàm số $y = f(x)$ nằm phía trên trục hành $Ox$ thì $\int\limits_a^b {\left| {f(x)} \right|dx} = \int\limits_a^b {f(x)dx} $

– Nếu trên $\left( {a;b} \right)$ đồ thị hàm số $y = f(x)$ nằm phía dưới trục hành $Ox$ thì $\int\limits_a^b {\left| {f(x)} \right|dx} =- \int\limits_a^b {f(x)dx} $

– Nếu trên $\left( {a;b} \right)$ đồ thị hàm số $y = f(x)$ nằm phía trên đồ thị hàm số $y = g(x)$ thì $\int\limits_a^b {\left| {f(x) – g(x)} \right|dx} = \int\limits_a^b {\left[ {f(x) – g(x)} \right]dx} $

– Nếu trên $\left( {a;b} \right)$ đồ thị hàm số $y = f(x)$ nằm phía dưới đồ thị hàm số $y = g(x)$ thì $\int\limits_a^b {\left| {f(x) – g(x)} \right|dx} = – \int\limits_a^b {\left[ {f(x) – g(x)} \right]dx} $

Câu 11. Gọi $S$ là diện tích hình phẳng giới hạn bởi đồ thị hàm số $y = f\left( x \right)$, trục hoành, đường thẳng $x = a,x = b$ (như hình vẽ bên). Hỏi cách tính $S$ nào dưới đây đúng?

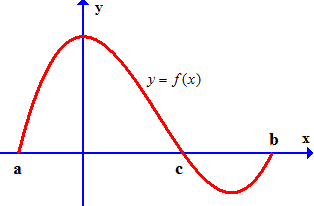
A. $S = \int\limits_a^b {f\left( x \right)dx} $. B. $S = \left| {\int\limits_a^c {f\left( x \right)dx} + \int\limits_c^b {f\left( x \right)dx} } \right|$.

C. $S = – \int\limits_a^c {f\left( x \right)dx} + \int\limits_c^b {f\left( x \right)dx} $. D. $S = \int\limits_a^c {f\left( x \right)dx} – \int\limits_c^b {f\left( x \right)dx} $.

Lời giải

Chọn D.

$S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} = \int\limits_a^c {\left| {f\left( x \right)} \right|dx} + \int\limits_c^b {\left| {f\left( x \right)} \right|dx} $

$ = \int\limits_a^c {f\left( x \right)dx} – \int\limits_c^b {f\left( x \right)dx} $

Câu 12. Cho hàm số $y = f\left( x \right)$ liên tục trên đoạn $\left[ {a;b} \right]$. Gọi $D$ là diện tích hình phẳng giới hạn bởi đồ thị $\left( C \right):y = f\left( x \right)$, trục hoành, hai đường thẳng $x = a$, $x = b$ (như hình vẽ dưới đây). Giả sử ${S_D}$ là diện tích hình phẳng $D$. đúng trong các phương án A, B, C, D cho dưới đây?

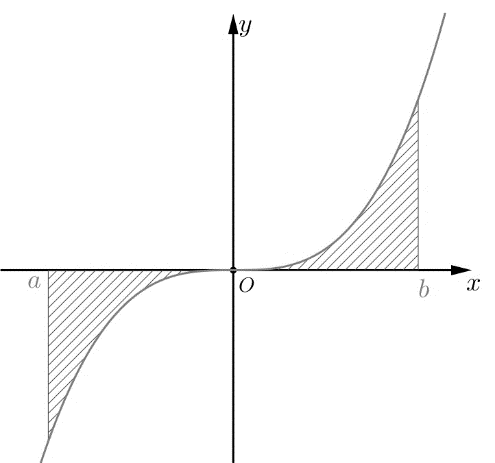
A. ${S_D} = \int\limits_a^0 {f\left( x \right)dx} + \int\limits_0^b {f\left( x \right)dx} $.

B. ${S_D} = – \int\limits_a^0 {f\left( x \right)dx} + \int\limits_0^b {f\left( x \right)dx} $.

C. ${S_D} = \int\limits_a^0 {f\left( x \right)dx} – \int\limits_0^b {f\left( x \right)dx} $.

D. ${S_D} = – \int\limits_a^0 {f\left( x \right)dx} – \int\limits_0^b {f\left( x \right)dx} $.

Lời giải

Chọn B.

Ta có ${S_D} = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} = \int\limits_a^0 {\left| {f\left( x \right)} \right|dx} + \int\limits_0^b {\left| {f\left( x \right)} \right|dx} $.

Vì $f\left( x \right) \leqslant 0,\,\forall x \in \left[ {a\,;\,0} \right]\,,\,f\left( x \right) \geqslant 0,\,\forall x \in \left[ {0\,;\,b} \right]$ nên:

${S_D} = \int\limits_a^0 {\left( { – f\left( x \right)} \right)dx} + \int\limits_0^b {f\left( x \right)dx} = – \int\limits_a^0 {f\left( x \right)dx} + \int\limits_0^b {f\left( x \right)dx} .$

Câu 13. Diện tích của hình phẳng được giới hạn bởi đồ thị hàm số $y = f\left( x \right)$, trục hoành và hai đường thẳng $x = a$, $x = b$$\left( {a < b} \right)$ (phần tô đậm trong hình vẽ) tính theo công thức nào dưới đây ?

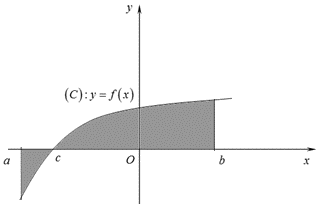
A. $S = \int\limits_a^c {f\left( x \right)dx + \int\limits_c^b {f\left( x \right)dx} } $. B. $S = \int\limits_a^b {f\left( x \right)dx} $.

C. $S = – \int\limits_a^c {f\left( x \right)dx + \int\limits_c^b {f\left( x \right)dx} } $. D. $S = \left| {\int\limits_a^b {f\left( x \right)dx} } \right|$.

Lời giải

Chọn C.

Diện tích của hình phẳng được giới hạn bởi đồ thị hàm số $y = f\left( x \right)$, trục hoành và hai đường thẳng $x = a$, $x = b$ là $S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} = $ $\int\limits_a^c {\left| {f\left( x \right)} \right|dx} + \int\limits_c^b {\left| {f\left( x \right)} \right|dx} $ $ = – \int\limits_a^c {f(x)dx} + \int\limits_c^b {f(x)dx} $.

Câu 14. Diện tích phần hình phẳng gạch chéo trong hình vẽ bên được tính theo công thức nào dưới đây?

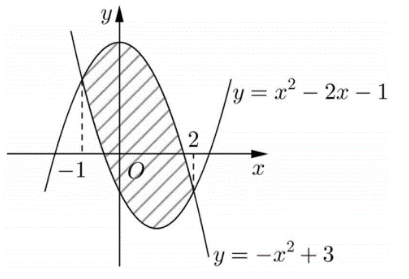
A. $\int\limits_{ – 1}^2 {\left( { – 2x + 2} \right)dx} $ B. $\int\limits_{ – 1}^2 {\left( {2x – 2} \right)dx} $ C. $\int\limits_{ – 1}^2 {\left( { – 2{x^2} + 2x + 4} \right)dx} $ D. $\int\limits_{ – 1}^2 {\left( {2{x^2} – 2x – 4} \right)dx} $

Lời giải

Chọn C.

Diện tích hình phẳng gạch chéo trong hình vẽ là:

$S = \int\limits_{ – 1}^2 {\left| {\left( { – {x^2} + 3} \right) – \left( {{x^2} – 2x – 1} \right)} \right|} dx = \int\limits_{ – 1}^2 {\left| { – 2{x^2} + 2x + 4} \right|} dx = \int\limits_{ – 1}^2 {\left( { – 2{x^2} + 2x + 4} \right)} dx$.

Câu 15. Cho hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}.$ Gọi $S$ là diện tích hình phẳng giới hạn bởi các đường $y = f\left( x \right),y = 0,x = – 1$ và $x = 5$ (như hình vẽ bên).

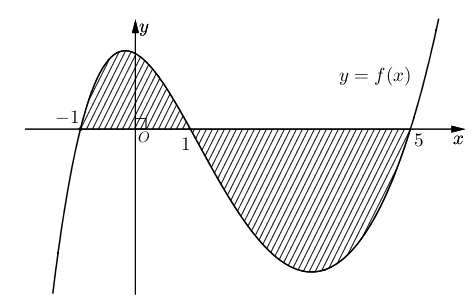
Mệnh đề nào sau đây đúng?

A. $S = – \int\limits_{ – 1}^1 {f(x)dx – } \int\limits_1^5 {f(x)dx} $. B. $S = \int\limits_{ – 1}^1 {f(x)dx + } \int\limits_1^5 {f(x)dx} $.

C. $S = \int\limits_{ – 1}^1 {f(x)dx – } \int\limits_1^5 {f(x)dx} $. D. $S = – \int\limits_{ – 1}^1 {f(x)dx + } \int\limits_1^5 {f(x)dx} $.

Lời giải

Chọn C.

Ta có: $S = \int\limits_{ – 1}^1 {\left| {f(x)} \right|dx} + \int\limits_1^5 {\left| {f\left( x \right)} \right|dx} = \int\limits_{ – 1}^1 {f\left( x \right)dx} – \int\limits_1^5 {f\left( x \right)dx} $.

Câu 16. Cho hàm số $f\left( x \right)$ liên tục trên $\mathbb{R}$. Gọi S là diện tích hình phẳng giới hạn bởi các đường $y = f\left( x \right),y = 0,x = – 1,x = 2$ (như hình vẽ bên). Mệnh đề nào dưới đây đúng?

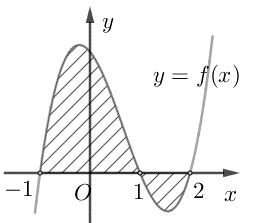
A. $S = \int\limits_{ – 1}^1 {f\left( x \right)} dx + \int\limits_1^2 {f\left( x \right)} dx$.

B. $S = – \int\limits_{ – 1}^1 {f\left( x \right)} dx – \int\limits_1^2 {f\left( x \right)} dx$.

C. $S = – \int\limits_{ – 1}^1 {f\left( x \right)} dx + \int\limits_1^2 {f\left( x \right)} dx$.

D. $S = \int\limits_{ – 1}^1 {f\left( x \right)} dx – \int\limits_1^2 {f\left( x \right)} dx$.

Lời giải

Chọn D.

$S = \int\limits_{ – 1}^2 {\left| {f\left( x \right)} \right|} dx = \int\limits_{ – 1}^1 {\left| {f\left( x \right)} \right|} dx + \int\limits_1^2 {\left| {f\left( x \right)} \right|} dx$

Nhìn hình ta thấy hàm số $f\left( x \right)$ liên tục và nhận giá trị không âm trên đoạn $\left[ { – 1;1} \right]$ nên $\int\limits_{ – 1}^1 {\left| {f\left( x \right)} \right|} dx = \int\limits_{ – 1}^1 {f\left( x \right)} dx$; hàm số $f\left( x \right)$ liên tục và nhận giá trị âm trên đoạn $\left[ {1;2} \right]$ nên $\int\limits_1^2 {\left| {f\left( x \right)} \right|} dx = – \int\limits_1^2 {f\left( x \right)} dx$

Vậy $S = \int\limits_{ – 1}^1 {f\left( x \right)} dx – \int\limits_1^2 {f\left( x \right)} dx$

Câu 17. Gọi$S$là diện tích hình phẳng $\left( H \right)$giới hạn bởi các đường $y = f\left( x \right)$, trục hoành và hai đường thẳng $x = – 1$, $x = 2$. Đặt $a = \int\limits_{ – 1}^0 {f\left( x \right)dx} $,$b = \int\limits_0^2 {f\left( x \right)dx} $, mệnh đề nào sau đây đúng?

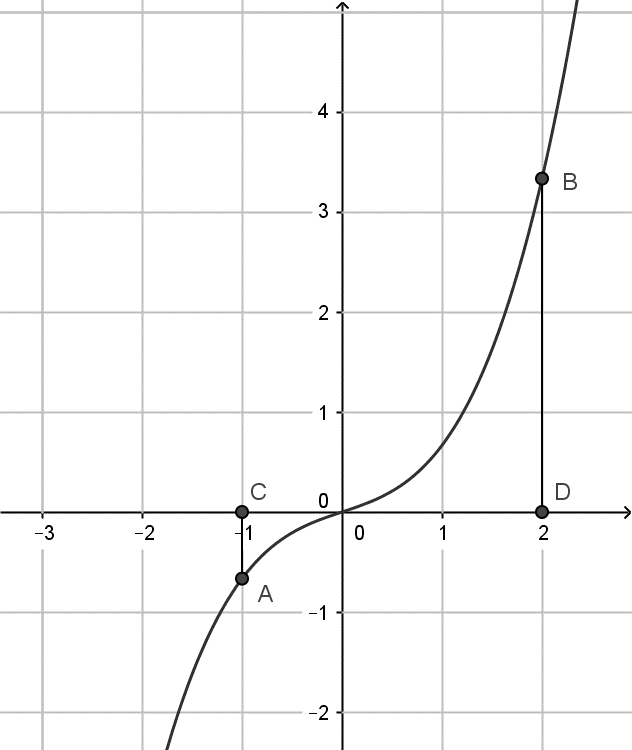
A. $S = b – a$ B. $S = b + a$ C. $S = – b + a$ D. $S = – b – a$

Lời giải

Chọn A.

Ta có:

$S = \int\limits_{ – 1}^2 {\left| {f\left( x \right)} \right|dx} = \int\limits_{ – 1}^0 {\left| {f\left( x \right)} \right|dx} + \int\limits_0^2 {\left| {f\left( x \right)} \right|dx} $$ = – \int\limits_{ – 1}^0 {f\left( x \right)dx} + \int\limits_0^2 {f\left( x \right)dx} = – a + b$.

Câu 18. Gọi $S$ là diện tích hình phẳng giới hạn bởi các đường $y = f\left( x \right)$, trục hoành và hai đường thẳng $x = – 3$, $x = 2$ (như hình vẽ bên). Đặt $a = \int\limits_{ – 3}^1 {f\left( x \right)\,dx} $, $b = \int\limits_1^2 {f\left( x \right)\,dx} $. Mệnh đề nào sau đây là đúng.

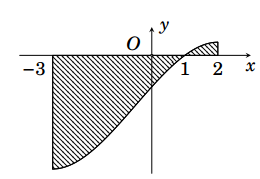
A. $S = a + b$. B. $S = a – b$. C. $S = – a – b$. D. $S = b – a$.

Lời giải

Chọn D.

Ta có $S = \int\limits_{ – 3}^2 {\left| {f\left( x \right)} \right|\,dx} $$ = \int\limits_{ – 3}^1 {\left| {f\left( x \right)} \right|\,dx} + \int\limits_1^2 {\left| {f\left( x \right)} \right|\,dx} $ $ = – \int\limits_{ – 3}^1 {\,f\left( x \right)dx} + \int\limits_1^2 {f\left( x \right)dx} $$ = – a + b$.

Câu 19. Cho các số $p,q$ thỏa mãn các điều kiện:$p > 1$, $q > 1$, $\frac{1}{p} + \frac{1}{q} = 1$ và các số dương $a,b$. Xét hàm số: $y = {x^{p – 1}}$$\left( {x > 0} \right)$có đồ thị là $\left( C \right)$. Gọi $\left( {{S_1}} \right)$ là diện tích hình phẳng giới hạn bởi $\left( C \right)$, trục hoành, đường thẳng $x = a$, Gọi $\left( {{S_2}} \right)$ là diện tích hình phẳng giới hạn bởi $\left( C \right)$, trục tung, đường thẳng $y = b$, Gọi $\left( S \right)$ là diện tích hình phẳng giới hạn bởi trục hoành, trục tung và hai đường thẳng $x = a$, $y = b$. Khi so sánh ${S_1} + {S_2}$ và $S$ ta nhận được bất đẳng thức nào trong các bất đẳng thức dưới đây?

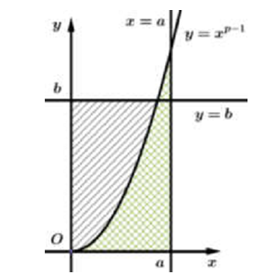
A. $\frac{{{a^p}}}{p} + \frac{{{b^q}}}{q} \leqslant ab$ B. $\frac{{{a^{p – 1}}}}{{p – 1}} + \frac{{{b^{q – 1}}}}{{q – 1}} \geqslant ab$. C. $\frac{{{a^{p + 1}}}}{{p + 1}} + \frac{{{b^{q + 1}}}}{{q + 1}} \leqslant ab$. D. $\frac{{{a^p}}}{p} + \frac{{{b^q}}}{q} \geqslant ab$.

Lời giải

Chọn D.

Ta có: $S \leqslant {S_1} + {S_2}$.

${S_1} = \int\limits_0^a {\left( {{x^{p – 1}}} \right)dx} = \left. {\left( {\frac{{{x^p}}}{p}} \right)\,} \right|_{\,0}^{\,a} = \frac{{{a^p}}}{p}$;

${S_2} = \int\limits_0^b {\left( {{y^{\frac{1}{{p – 1}}}}} \right)dy} = \left. {\left( {\frac{{{y^{\frac{1}{{p – 1}} + 1}}}}{{\frac{1}{{p – 1}} + 1}}} \right)\,} \right|_{\,0}^{\,b} = \left. {\left( {\frac{{{y^q}}}{q}} \right)\,} \right|_{\,0}^{\,b} = \frac{{{b^q}}}{q}$.

Vì: $\frac{1}{{p – 1}} + 1 = \frac{p}{{p – 1}} = \frac{1}{{1 – \frac{1}{p}}} = \frac{1}{{\frac{1}{q}}} = q$. Vậy $\frac{{{a^p}}}{p} + \frac{{{b^q}}}{q} \geqslant ab$.

Câu 20. Diện tích phần hình phẳng được tô đậm trong hình vẽ bên được tính theo công thức nào dưới đây?

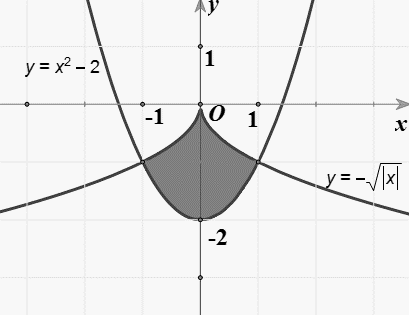
A. $\int\limits_{ – 1}^1 {\left( {{x^2} – 2 + \sqrt {\left| x \right|} } \right)dx} $.

B. $\int\limits_{ – 1}^1 {\left( {{x^2} – 2 – \sqrt {\left| x \right|} } \right)dx} $.

C. $\int\limits_{ – 1}^1 {\left( { – {x^2} + 2 + \sqrt {\left| x \right|} } \right)dx} $.

D. $\int\limits_{ – 1}^1 {\left( { – {x^2} + 2 – \sqrt {\left| x \right|} } \right)dx} $.

Lời giải

Chọn D.

Diện tích hình phẳng được tô đậm trong hình vẽ bên là:

$\int\limits_{ – 1}^1 {\left| {{x^2} – 2 – \left( { – \sqrt {\left| x \right|} } \right)} \right|dx} = \int\limits_{ – 1}^1 {\left( { – \sqrt {\left| x \right|} – {x^2} + 2} \right)dx} $ ( vì $x \in \left[ { – 1;1} \right] \Rightarrow – \sqrt {\left| x \right|} > {x^2} – 2$ ).