Cách Xét Tính Đơn Điệu Của Hàm Số y=f(u) Dựa Vào Hàm Số y=f'(x)

Cách xét tính đơn điệu của hàm số y=f(u) dựa vào hàm số y=f'(x) được soạn dưới dạng file word và PDF gồm 4 trang. Các bạn xem và tải về ở dưới.

I. Phương pháp

+ Lập bảng biến thiên của hàm số $y = f(x)$, suy ra dấu của $f'(x)$.

+ Tính $g'(x)$ và lập bảng biến thiên của hàm số $y = g(x)$, suy ra dấu của $g'(x)$.

+ Kết luận về tính đơn điệu của hàm số $y = g(x)$.

II. Các ví dụ:

Ví dụ 1. Cho hàm số $f\left( x \right)$ có đạo hàm là $f’\left( x \right) = \left( {x + 4} \right)\left( {x + 3} \right),\,\,\forall x \in \mathbb{R}$. Tìm các khoảng đồng biến, nghịch biến của hàm số $y = g(x) = f\left( {{x^2} + 4x} \right)$.

Lời giải

Ta có: $f’\left( x \right) = 0 \Leftrightarrow \left( {x + 4} \right)\left( {x + 3} \right) = 0$

$ \Leftrightarrow \left[ \begin{gathered}
x + 4 = 0 \hfill \\
x + 3 = 0 \hfill \\
\end{gathered} \right. \Leftrightarrow \left[ \begin{gathered}
x = – 4 \hfill \\
x = – 3 \hfill \\
\end{gathered} \right.$

Bảng xét dấu $f’\left( x \right)$

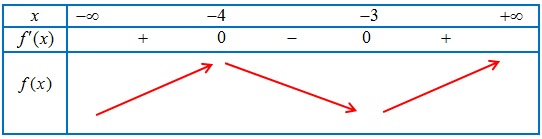
Ta có: $g'(x) = {\left( {{x^2} + 4x} \right)^\prime }f’\left( {{x^2} + 4x} \right)$ $ = (2x + 4)f’\left( {{x^2} + 4x} \right)$

$g'(x) = 0 \Leftrightarrow (2x + 4)f’\left( {{x^2} + 4x} \right) = 0$

$ \Leftrightarrow \left[ \begin{gathered}
2x + 4 = 0 \hfill \\
f’\left( {{x^2} + 4x} \right) = 0 \hfill \\
\end{gathered} \right. \Leftrightarrow \left[ \begin{gathered}
2x = – 4 \hfill \\
{x^2} + 4x = – 4 \hfill \\
{x^2} + 4x = – 3 \hfill \\
\end{gathered} \right.$

$ \Leftrightarrow \left[ \begin{gathered}
x = – 2 \hfill \\
{x^2} + 4x + 4 = 0 \hfill \\
{x^2} + 4x + 3 = 0 \hfill \\
\end{gathered} \right. \Leftrightarrow \left[ \begin{gathered}
x = – 2 \hfill \\
x = – 2 \hfill \\
x = – 1 \hfill \\
x = – 3 \hfill \\
\end{gathered} \right.$$ \Leftrightarrow \left[ \begin{gathered}
x = – 2 \hfill \\
x = – 1 \hfill \\
x = – 3 \hfill \\
\end{gathered} \right.$

Bảng xét dấu $g’\left( x \right)$

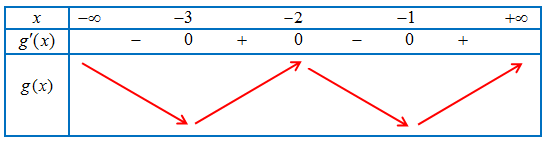
Vậy hàm số $y = g(x)$

– Đồng biến trên các khoảng $\left( { – 3; – 2} \right)$ và $\left( { – 1; + \infty } \right)$.

– Nghịch biến trên các khoảng $\left( { – \infty ; – 3} \right)$ và $\left( { – 2; – 1} \right)$.

Ví dụ 2. Cho hàm số $f\left( x \right)$ có đạo hàm là $f’\left( x \right) = – {x^2} + 3x – 2,\,\,\forall x \in \mathbb{R}$. Tìm các khoảng đồng biến, nghịch biến của hàm số $y = g(x) = f\left( {{x^3} + 2} \right)$.

Lời giải

Ta có: $f’\left( x \right) = 0 \Leftrightarrow – {x^2} + 3x – 2 = 0$$ \Leftrightarrow \left[ \begin{gathered}
x = 1 \hfill \\
x = 2 \hfill \\
\end{gathered} \right.$

Bảng xét dấu $f’\left( x \right)$

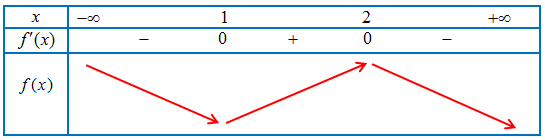
Ta có: $g'(x) = {\left( {{x^3} + 2} \right)^\prime }f’\left( {{x^3} + 2} \right)$ $ = 3{x^2}f’\left( {{x^3} + 2} \right)$

$g'(x) = 0 \Leftrightarrow 3{x^2}f’\left( {{x^3} + 2} \right) = 0$

$ \Leftrightarrow \left[ \begin{gathered}
3{x^2} = 0 \hfill \\
f’\left( {{x^3} + 2} \right) = 0 \hfill \\
\end{gathered} \right. \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
{x^3} + 2 = 1 \hfill \\
{x^3} + 2 = 2 \hfill \\
\end{gathered} \right.$ $ \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
x = – 1 \hfill \\
x = 0 \hfill \\
\end{gathered} \right. \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
x = – 1 \hfill \\
\end{gathered} \right.$

Bảng xét dấu $g’\left( x \right)$

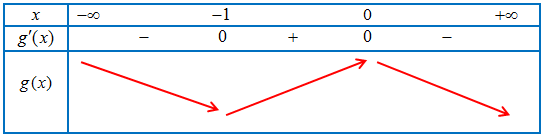
Vậy hàm số $y = g(x)$

– Đồng biến trên khoảng $\left( { – 1;0} \right)$.

– Nghịch biến trên các khoảng $\left( { – \infty ; – 1} \right)$ và $\left( {0; + \infty } \right)$.

Ví dụ 3. Cho hàm số $f\left( x \right)$ có đạo hàm trên $\mathbb{R}$ là $f’\left( x \right) = 25 – {x^2}.$ Tìm tất cả các giá trị của tham số $m$ để hàm số $y = g(x) = f\left( { – 2x + 7 – m} \right)$ đồng biến trên khoảng $\left( { – 3;6} \right)$.

Lời giải

Ta có: $f’\left( x \right) = 0 \Leftrightarrow 25 – {x^2} = 0$$ \Leftrightarrow \left[ \begin{gathered}
x = 5 \hfill \\
x = – 5 \hfill \\
\end{gathered} \right.$

Bảng xét dấu $f’\left( x \right)$

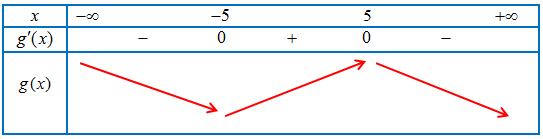
Ta có: $g’\left( x \right) = {\left( { – 2x + 7 – m} \right)^\prime }f’\left( { – 2x + 7 – m} \right)$

$ = – 2f’\left( { – 2x + 7 – m} \right)$

Hàm số đồng biến trên khoảng $\left( { – 3;6} \right)$ khi $g’\left( x \right) \geqslant 0$, $\forall x \in \left( { – 3;6} \right)$

$ \Leftrightarrow – 2f’\left( { – 2x + 7 – m} \right) \geqslant 0$, $\forall x \in \left( { – 3;6} \right)$

$ \Leftrightarrow f’\left( { – 2x + 7 – m} \right) \leqslant 0$, $\forall x \in \left( { – 3;6} \right)$

$ \Leftrightarrow \left[ \begin{gathered}
– 2x + 7 – m \leqslant – 5 \hfill \\
– 2x + 7 – m \geqslant 5 \hfill \\
\end{gathered} \right.$, $\forall x \in \left( { – 3;6} \right)$ ( Dựa vào bảng xét dấu $f’\left( x \right)$ )

$ \Leftrightarrow \left[ \begin{gathered}
m \geqslant – 2x + 12 \hfill \\
m \leqslant – 2x + 2 \hfill \\
\end{gathered} \right.$, $\forall x \in \left( { – 3;6} \right)$

$ \Leftrightarrow \left[ \begin{gathered}
m \geqslant \mathop {max}\limits_{\left[ { – 3;6} \right]} \left( { – 2x + 12} \right) \hfill \\
m \leqslant \mathop {\min }\limits_{\left[ { – 3;6} \right]} \left( { – 2x + 2} \right) \hfill \\
\end{gathered} \right. \Leftrightarrow \left[ \begin{gathered}
m \geqslant 18 \hfill \\
m \leqslant – 10 \hfill \\
\end{gathered} \right.$

Vậy $m \leqslant – 10$ hoặc $m \geqslant 18$ thỏa mãn yêu cầu bài toán.

Ví dụ 4. Cho hàm số $f\left( x \right)$ có đạo hàm trên $\mathbb{R}$ là $f’\left( x \right) = \left( {x – 1} \right)\left( {x + 3} \right).$ Có bao nhiêu giá trị nguyên của tham số $m$ thuộc đoạn $\left[ { – 10;20} \right]$ để hàm số $y = g(x) = f\left( {{x^2} + 3x – m} \right)$ đồng biến trên khoảng $\left( {0;2} \right)$.

Lời giải

Ta có: $f’\left( x \right) = 0 \Leftrightarrow \left( {x – 1} \right)\left( {x + 3} \right) = 0$$ \Leftrightarrow \left[ \begin{gathered}
x = 1 \hfill \\
x = – 3 \hfill \\
\end{gathered} \right.$

Bảng xét dấu $f’\left( x \right)$

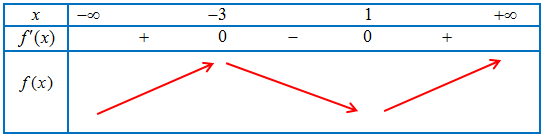
Ta có: $g’\left( x \right) = {\left( {{x^2} + 3x – m} \right)^\prime }f’\left( {{x^2} + 3x – m} \right)$

$ = \left( {2x + 3} \right)f’\left( {{x^2} + 3x – m} \right)$

Hàm số đồng biến trên khoảng $\left( {0;2} \right)$ khi $y’ \geqslant 0$, $\forall x \in \left( {0;2} \right)$

$ \Leftrightarrow \left( {2x + 3} \right)f’\left( {{x^2} + 3x – m} \right) \geqslant 0$, $\forall x \in \left( {0;2} \right)$

$ \Leftrightarrow f’\left( {{x^2} + 3x – m} \right) \geqslant 0$, $\forall x \in \left( {0;2} \right)$ (Do $x \in \left( {0;2} \right)$ suy ra, $2x + 3 > 0$)

$ \Leftrightarrow \left[ \begin{gathered}
{x^2} + 3x – m \leqslant – 3 \hfill \\
{x^2} + 3x – m \geqslant 1 \hfill \\
\end{gathered} \right.$, $\forall x \in \left( {0;2} \right)$ ( Dựa vào bảng xét dấu $f’\left( x \right)$ )

$ \Leftrightarrow \left[ \begin{gathered}
m \geqslant {x^2} + 3x + 3 \hfill \\
m \leqslant {x^2} + 3x – 1 \hfill \\
\end{gathered} \right.$, $\forall x \in \left( {0;2} \right)$

$ \Leftrightarrow \left[ \begin{gathered}
m \geqslant \mathop {\max }\limits_{\left[ {0;2} \right]} \left( {{x^2} + 3x + 3} \right) \hfill \\
m \leqslant \mathop {\min }\limits_{\left[ {0;2} \right]} \left( {{x^2} + 3x – 1} \right) \hfill \\
\end{gathered} \right.$$ \Leftrightarrow \left[ \begin{gathered}
m \geqslant 13 \hfill \\
m \leqslant – 1 \hfill \\
\end{gathered} \right.$

Mà $m \in \mathbb{Z},m \in \left[ { – 10;20} \right]$ nên $m \in \left\{ { – 10; – 9;…; – 1;13;14;…;19;20} \right\}$.

Vậy có $18$ giá trị của tham số $m$ thỏa mãn yêu cầu bài toán.