Ứng dụng tích phân phát triển câu 41 đề minh họa toán 2024 giải chi tiết được soạn dưới dạng file word và PDF gồm 5 trang. Các bạn xem và tải về ở dưới.
Câu 1: Xét $f\left( x \right) = a{x^4} + b{x^2} + c(a,b,c \in \mathbb{R},a > 0)$ sao cho đồ thị hàm số $y = f\left( x \right)$ có ba điểm cực trị là $A,B$ và $C\left( {2; – 1} \right)$. Gọi $y = g\left( x \right)$ là hàm số bậc hai có đồ thị đi qua ba điểm $A,B$ và $C$. Khi hình phẳng giới hạn bởi đồ thị của hai hàm số $y = f\left( x \right),y = g\left( x \right)$ và hai đường thẳng $x = 0,x = 2$ có diện tích bằng $\frac{{64}}{{15}}$, tích phân bằng
A. $\frac{{226}}{{15}}$. B. $\frac{{25}}{{13}}$. C. $ – \frac{{17}}{{15}}$. D. $ – \frac{{226}}{{15}}$.
Lời giải
Dễ thấy $f’\left( x \right)$ có ba nghiệm $x = 0,x = 2,x = – 2$ suy ra $f’\left( x \right) = 4ax\left( {{x^2} – 4} \right)$.
Từ đó ta có $f\left( x \right) = a{x^4} – 8a{x^2} + c$.
Đồ thị hàm số $y = f\left( x \right)$ đi qua điểm $C\left( {2; – 1} \right)$ nên ta có: $ – 1 = 16a – 32a + c \Leftrightarrow c = 16a – 1$.
Mặt khác, từ giả thiết đồ thị hàm số $y = f\left( x \right)$ và $y = g\left( x \right)$ cắt nhau tại hai điểm có hoành độ $x = \pm 2$ và tiếp xúc tại điểm có hoành độ $x = 0$ nên $f\left( x \right) – g\left( x \right) = a{x^2}\left( {{x^2} – 4} \right)$.
Từ hình phẳng giới hạn bởi đồ thị của hai hàm số $y = f\left( x \right),y = g\left( x \right)$ và hai đường thẳng $x = 0,x = 2$ có diện tích bằng $\frac{{64}}{{15}}$ ta có phường trình .
$ \Rightarrow c = 15 \Rightarrow f\left( x \right) = {x^4} – 8{x^2} + 15$.
Ta có: $\int\limits_0^2 {f(x)dx = } \int\limits_0^2 {({x^4} – 8{x^2} + 15)dx = \frac{{226}}{{15}}} $.
Câu 2: Có bao nhiêu số thực $c$ để hình phẳng giới hạn bởi đồ thị hàm số $y = {x^2} – 4x + c,$trục hoành và các đường thẳng $x = 2;\,\,\,x = 4$ có diện tích bằng 3?
A. $3$. B. 0. C. 1. D. 2.
Lời giải
Chọn D
Diện tích hình phẳng: $S = \int\limits_2^4 {\left| {{x^2} – 4x + c} \right|} \,dx$. Hàm số $y = f\left( x \right) = {x^2} – 4x + c$ trên đoạn $\left[ {2;4} \right]$có bảng biến thiên như sau:
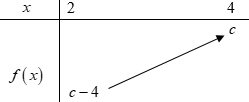
TH1: Nếu $c \geqslant 4$ $ \Rightarrow f\left( x \right) \geqslant {x^2} – 4x + 4 \geqslant 0\,\,\forall x \in \mathbb{R}$ nên $f\left( x \right) = {x^2} – 4x + 4 \geqslant 0\,\,\forall x \in [2;4]$.
Do đó $S = \int\limits_2^4 {\left| {{x^2} – 4x + c} \right|} \,dx = \left. {\left( {\frac{{{x^3}}}{3} – 2{x^2} + cx} \right)} \right|_2^4 = 2c – \frac{{16}}{3}$; $S = 3 \Leftrightarrow c = \frac{{25}}{6}$.
TH2: Nếu $c \leqslant 0$ $ \Rightarrow f\left( x \right) \leqslant {x^2} – 4x \leqslant 0\,\,\forall x \in [2;4].$
Do đó $S = \int\limits_2^4 {\left| {{x^2} – 4x + c} \right|} \,dx = \int\limits_2^4 {\left( { – {x^2} + 4x – c} \right)} \,dx = \left. {\left( { – \frac{{{x^3}}}{3} + 2{x^2} – cx} \right)} \right|_2^4 = \frac{{16}}{3} – 2c$; $S = 3 \Leftrightarrow c = \frac{7}{6}$.
TH3: Nếu $0 < c < 4$, $f\left( x \right) = {x^2} – 4x + c$ có 2 nghiệm, trong đó 1 nghiệm ${x_2} = 2 + \sqrt {4 – c} \in [2;4]$
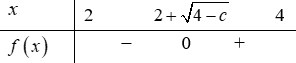
Đặt $F\left( x \right) = \int {\left( {{x^2} – 4x + c} \right)dx = } \int\limits_{}^{} {\left[ {{{\left( {x – 2} \right)}^2} + c – 4} \right]} dx = \frac{{{{\left( {x – 2} \right)}^3}}}{3} + \left( {c – 4} \right)x + C$
Do đó $S = – \int\limits_2^{{x_2}} {\left( {{x^2} – 4x + c} \right)} \,dx + \int\limits_{{x_2}}^4 {\left( {{x^2} – 4x + c} \right)} \,dx$ $ = F\left( 4 \right) + F\left( 2 \right) – 2F\left( {{x_2}} \right)$
$ = 6c – 24 + \frac{8}{3} – 2\left[ {\frac{{{{\left( {{x_2} – 2} \right)}^3}}}{3} + \left( {c – 4} \right){x_2}} \right]$.
Vì $S = 3$ và ${x_2} = 2 + \sqrt {4 – c} $ nên ta có phương trình: $4.{\sqrt {4 – c} ^3} = 25 – 6c\,\,\,\left( * \right)$.
Đặt $t = \sqrt {4 – c} ,\,\,t \in \left[ {0;2} \right]$, trở thành: $4{t^3} – 6t – 1 = 0$, tính được $t \approx 1.5979$ nên $c \approx 1.4467$.
Vậy có hai giá trị của $c$ thỏa mãn bài toán.
Câu 3: Xét $f\left( x \right) = a{x^4} + b{x^2} + c(a,b,c \in \mathbb{R},a < 0)$ sao cho đồ thị hàm số $y = f\left( x \right)$ có ba điểm cực trị là $A,B$ và $C\left( {2;1} \right)$. Gọi $y = g\left( x \right)$ là hàm số bậc hai có đồ thị đi qua ba điểm $A,B$ và $C$. Khi hình phẳng giới hạn bởi đồ thị của hai hàm số $y = f\left( x \right),y = g\left( x \right)$ và hai đường thẳng $x = 0,x = 2$ có diện tích bằng $\frac{{64}}{{15}}$, tích phân bằng
A. $\frac{{226}}{{15}}$.
B. $\frac{{25}}{{13}}$.
C. $ – \frac{{17}}{{15}}$.
D. $ – \frac{{226}}{{15}}$.
Lời giải
Dễ thấy $f’\left( x \right)$ có ba nghiệm $x = 0,x = 2,x = – 2$ suy ra $f’\left( x \right) = 4ax\left( {{x^2} – 4} \right)$.
Từ đó ta có $f\left( x \right) = a{x^4} – 8a{x^2} + c$.
Đồ thị hàm số $y = f\left( x \right)$ đi qua điểm $C\left( {2;1} \right)$ nên ta có: $1 = 16a – 32a + c \Leftrightarrow c = 16a + 1$.
Mặt khác, từ giả thiết đồ thị hàm số $y = f\left( x \right)$ và $y = g\left( x \right)$ cắt nhau tại hai điểm có hoành độ $x = \pm 2$ và tiếp xúc tại điểm có hoành độ $x = 0$ nên $f\left( x \right) – g\left( x \right) = a{x^2}\left( {{x^2} – 4} \right)$.
Từ hình phẳng giới hạn bởi đồ thị của hai hàm số $y = f\left( x \right),y = g\left( x \right)$ và hai đường thẳng $x = 0,x = 2$ có diện tích bằng $\frac{{64}}{{15}}$ ta có phương trình .
$ \Rightarrow c = – 15 \Rightarrow f\left( x \right) = – {x^4} + 8{x^2} – 15$
Ta có: $\int\limits_0^2 {f(x)dx = } \int\limits_0^2 {( – {x^4} + 8{x^2} – 15)dx = – \frac{{226}}{{15}}} $ .
Câu 4: Cho hàm số bậc bốn $y = f\left( x \right)$ có đồ thị $\left( C \right)$ như hình vẽ.
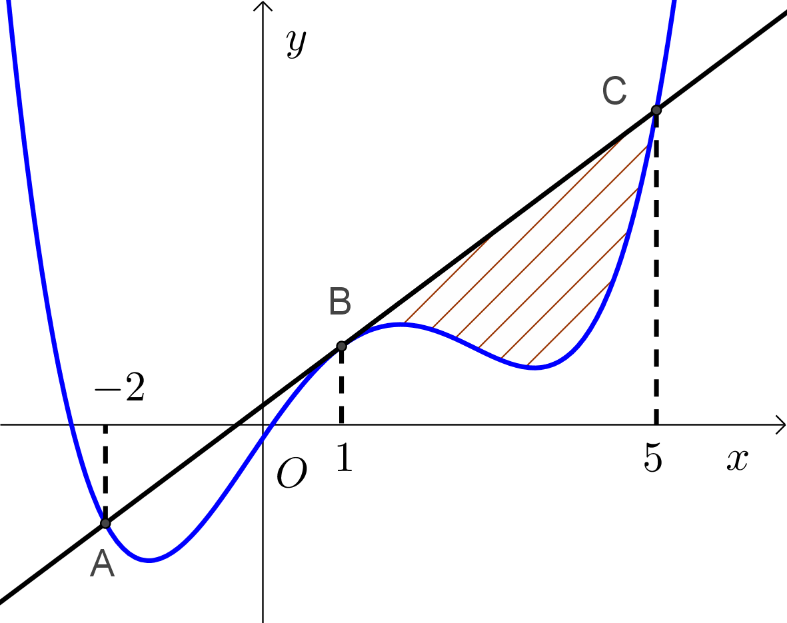
Đường thẳng $d:y = kx + \frac{1}{4}$ có đúng ba điểm chung với $\left( C \right)$ là $A,B,C$ và $BC – AB = \frac{5}{4}.$Biết diện tích hình phẳng $S$ là $\frac{{24}}{5}.$ Giá trị của $\int_{ – 2}^1 {f\left( x \right)dx} $ bằng
A. $ – 2$. B. $ – \frac{{321}}{{160}}$. C. $ – \frac{{161}}{{80}}$. D. $ – \frac{{159}}{{160}}$.
Lời giải
Chọn C
Phương trình giao điểm của $\left( C \right)$ và $d$ là:
$f\left( x \right) – g\left( x \right) = a\left( {x + 2} \right){\left( {x – 1} \right)^2}\left( {x – 5} \right)$
Theo giả thiết, ta có: $S = \frac{{24}}{5} \Leftrightarrow – a\int_1^5 {\left( {x + 2} \right){{\left( {x – 1} \right)}^2}\left( {x – 5} \right)dx} = \frac{{24}}{5} \Leftrightarrow a = \frac{1}{{24}}$
$ \Rightarrow f\left( x \right) = g\left( x \right) + \frac{1}{{24}}\left( {x + 2} \right){\left( {x – 1} \right)^2}\left( {x – 5} \right) = kx + \frac{1}{4} + \frac{1}{{24}}\left( {x + 2} \right){\left( {x – 1} \right)^2}\left( {x – 5} \right)$
* Gọi $A\left( { – 2;\frac{1}{4} – 2k} \right),\,B\left( {1;\frac{1}{4} + k} \right),\,C\left( {5;\frac{1}{4} + 5k} \right)$
$BC – AB = \frac{5}{4} \Leftrightarrow \sqrt {{4^2} + {{\left( {4k} \right)}^2}} – \sqrt {{3^2} + {{\left( {3k} \right)}^2}} = \frac{5}{4} \Leftrightarrow \left[ \begin{gathered}
k = \frac{3}{4} \hfill \\
k = – \frac{3}{4} \hfill \\
\end{gathered} \right.$
Đường thẳng nằm ở góc phần tư thứ nhất và thứ ba nên hệ số góc là dương nên ta chọn $k = \frac{3}{4}$
Vậy $f\left( x \right) = \frac{3}{4}x + \frac{1}{4} + \frac{1}{{24}}\left( {x + 2} \right){\left( {x – 1} \right)^2}\left( {x – 5} \right)$
Và $\int_{ – 2}^1 {f\left( x \right)dx} = – \frac{{321}}{{160}}$.
Câu 5: Xét $f\left( x \right) = a{x^4} + b{x^2} + c(a,b,c \in \mathbb{R},a > 0)$ sao cho đồ thị hàm số $y = f\left( x \right)$ có ba điểm cực trị là $A,B$ và $C\left( {1; – \frac{3}{5}} \right)$. Gọi $y = g\left( x \right)$ là hàm số bậc hai có đồ thị đi qua ba điểm $A,B$ và $C$. Khi hình phẳng giới hạn bởi đồ thị của hai hàm số $y = f\left( x \right),y = g\left( x \right)$ và hai đường thẳng $x = 0,x = 1$ có diện tích bằng $\frac{2}{5}$, tích phân bằng
A. $\frac{{27}}{{20}}$.
B. $\frac{{44}}{{15}}$.
C. 1 .
D. $\frac{{94}}{{30}}$.
Lời giải
Phương trình hàm số bậc hai đi qua 3 điểm $A,B$ và $C$. là: $y = g\left( x \right) = m{x^2} + nx + p$.
Hàm số bậc hai đi qua điểm $A\left( {0:c} \right)$ suy ra $p = c$
Hàm số bậc hai có trục tung là trục đối xứng $n = 0$ và đi qua $C\left( {\sqrt {\frac{{ – b}}{{2a}}} ; – \frac{{{b^2}}}{{4a}} + c} \right)$ suy ra $m = \frac{1}{2}b$
Suy ra $y = g\left( x \right) = \frac{1}{2}b{x^2} + c$
Ta có: $\left\{ {\begin{array}{*{20}{l}}
{f\left( 1 \right) = – \frac{3}{5}} \\
{f’\left( 1 \right) = 0}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{a + b + c = – \frac{3}{5}} \\
{4a + 2b = 0}
\end{array}} \right.} \right.$
Theo đề ta có:
Từ (II) và (III) ta có: $a = 3:b = – 6:c = \frac{{12}}{5}$
Vậy $\int\limits_0^1 {f(x)dx = } 1$.
Câu 6: Cho hàm số bậc hai $y = f\left( x \right)$ có đồ thị $\left( P \right)$ và đường thẳng $d$ cắt tại hai điểm như trong hình bên. Biết rằng hình phẳng giới hạn bởi $\left( P \right)$ và $d$ có diện tích $S = \frac{{125}}{6}$. Tích phân $\int\limits_2^7 {\left( {2x – 3} \right)f’\left( x \right)} dx$ bằng
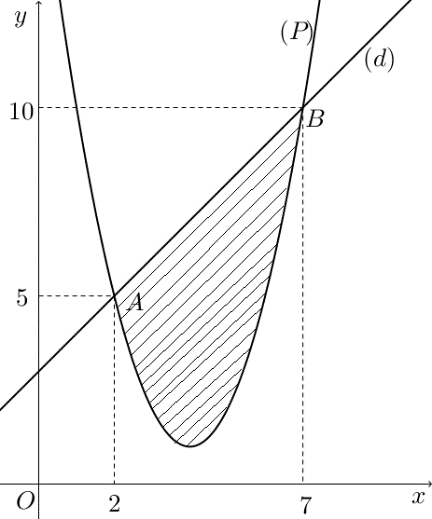
A. $\frac{{215}}{3}$. B. $\frac{{265}}{3}$. C. $\frac{{245}}{3}$. D. $\frac{{415}}{3}$.
Lời giải
Cách 1: Đặt $\left\{ \begin{gathered}
u = 2x – 3 \hfill \\
dv = f’\left( x \right)dx \hfill \\
\end{gathered} \right. \Rightarrow \left\{ \begin{gathered}
du = 2dx \hfill \\
v = f\left( x \right) \hfill \\
\end{gathered} \right.$.
Ta có: $\int\limits_2^7 {\left( {2x – 3} \right)f’\left( x \right)} {\kern 1pt} {\kern 1pt} dx = \left. {\left[ {\left( {2x – 3} \right)f\left( x \right)} \right]} \right|_2^7 – 2\int\limits_2^7 {f\left( x \right)} {\kern 1pt} {\kern 1pt} dx$
$ = 11f\left( 7 \right) – f\left( 2 \right) – 2\left[ {\frac{{\left( {5 + 10} \right).5}}{2} – \frac{{125}}{6}} \right] = \frac{{215}}{3}$.
Cách 2: Dựa vào đồ thị ta có điểm $A\left( {2;\,5} \right)$và $B\left( {7;\,10} \right)$ thuộc đường thẳng $d$ và Parabol $\left( P \right)$
Suy ra đường thẳng $d$ có vectơ chỉ phương $\overrightarrow {AB} = \left( {5;\,5} \right)$
Phương trình đường thẳng $d:y = x + 3$
Gọi $\left( P \right)$ có phương trình: $y = a{x^2} + bx + c,(a > 0)$
$A,B \in \left( P \right) \Rightarrow $ Hệ phương trình: $\left\{ \begin{gathered}
4a + 2b + c = 5 \hfill \\
49a + 7b + c = 10 \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
c = – 4a – 2b + 5 \hfill \\
49a + 7b + 5 – 4a – 2b = 10 \hfill \\
\end{gathered} \right.$
$ \Leftrightarrow \left\{ \begin{gathered}
c = – 4a – 2b + 5 \hfill \\
b = 1 – 9a \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
c = 3 + 14a \hfill \\
b = 1 – 9a \hfill \\
\end{gathered} \right.$
Hình phẳng giới hạn bởi $\left( P \right)$ và $d$ có diện tích $S = \frac{{125}}{6}$
$\begin{gathered}
\Rightarrow \int\limits_2^7 {\left| {x + 3 – \left( {a{x^2} + bx + c} \right)} \right|dx} = \frac{{125}}{6} \hfill \\
\Rightarrow \int\limits_2^7 {\left| {x + 3 – \left[ {a{x^2} + \left( {1 – 9a} \right)x + \left( {3 + 14a} \right)} \right]} \right|dx} = \frac{{125}}{6} \hfill \\
\Leftrightarrow \int\limits_2^7 {\left[ { – a{x^2} + 9ax – 14a} \right]dx} = \frac{{125}}{6} \Leftrightarrow \left. {\left( { – \frac{{a{x^3}}}{3} + \frac{{9a{x^2}}}{2} – 14ax} \right)} \right|_2^7 = \frac{{125}}{6} \hfill \\
\Leftrightarrow \frac{{125}}{6}a = \frac{{125}}{6} \Leftrightarrow a = 1 = > b = – 8;c = 17 \hfill \\
\end{gathered} $
$\left( P \right)$ có phương trình: $y = f\left( x \right) = {x^2} – 8x + 17 \Rightarrow f’\left( x \right) = 2x – 8$
$ \Rightarrow \int\limits_2^7 {\left( {2x – 3} \right)f’\left( x \right)} dx = \frac{{215}}{3}$
Câu 7: Xét $f\left( x \right) = a{x^4} + b{x^2} + c(a,b,c \in \mathbb{R},a < 0)$ sao cho đồ thị hàm số $y = f\left( x \right)$ có ba điểm cực trị là $A,B$ và $C\left( { – 2;\frac{{27}}{7}} \right)$. Gọi $y = g\left( x \right)$ là hàm số bậc hai có đồ thị đi qua ba điểm $A,B$ và $C$. Khi
hình phẳng giới hạn bởi đồ thị của hai hàm số $y = f\left( x \right),y = g\left( x \right)$ và hai đường thẳng $x = – 2,x = 0$ có diện tích bằng $\frac{{16}}{{15}}$, tích phân bằng
A. $\frac{{27}}{{20}}$.
B. $\frac{{44}}{{15}}$.
C. $\frac{{362}}{{105}}$.
D. $\frac{{94}}{{30}}$.
Lời giải
Phương trình hàm số bậc hai đi qua 3 điểm $A,B$ và $C$. là: $y = g\left( x \right) = m{x^2} + nx + p$.
Hàm số bậc hai đi qua điểm $A\left( {0:c} \right)$ suy ra $p = c$
Hàm số bậc hai có trục tung là trục đối xứng $n = 0$ và đi qua $C\left( {\sqrt {\frac{{ – b}}{{2a}}} ; – \frac{{{b^2}}}{{4a}} + c} \right)$ suy ra $m = \frac{1}{2}b$
Suy ra $y = g\left( x \right) = \frac{1}{2}b{x^2} + c$
Ta có: $\left\{ {\begin{array}{*{20}{l}}
{f\left( 2 \right) = – \frac{3}{5}} \\
{f’\left( 2 \right) = 0}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{16a + 4b + c = \frac{{27}}{7}} \\
{8a + b = 0}
\end{array}} \right.} \right.$
Theo đề ta có:
Từ (II) và (III) ta có: $a = – \frac{1}{4}:b = 2:c = – \frac{1}{7}$
Vậy $\int\limits_0^2 {f(x)dx = \frac{{362}}{{105}}} $
Câu 8: Cho hàm số $f(x) = a{x^3} + bx + c$và $g(x) = b{x^3} + ax + d,(a > 0)$có đồ thị như hình vẽ.
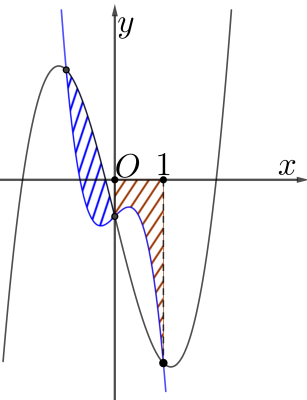
Biết rằng tổng diện tích miền kẻ sọc như hình vẽ bằng $\frac{7}{3}$. Giá trị của $\int\limits_1^e {\frac{{f(\ln x)}}{x}dx} $ bằng
A. $\frac{7}{6}$. B. $ – \frac{7}{3}$. C. $ – \frac{5}{3}$. D. $\frac{7}{3}$.
Lời giải
Xét $I = \int\limits_1^e {\frac{{f(\ln x)}}{x}dx} $Đặt $t = \ln x \Rightarrow dt = \frac{1}{x}dx$.
Đổi cận $x = 1 \Rightarrow t = 0$
$x = e \Rightarrow t = 1$
Vậy $I = \int\limits_0^1 {f\left( t \right)dt} $
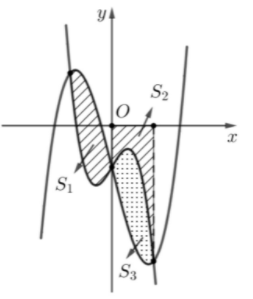
Dựa vào hình vẽ ta có ${S_1} = {S_3}$
Mà ${S_1} + {S_2} = \frac{7}{3} \Rightarrow {S_3} + {S_2} = \frac{7}{3} \Rightarrow \int\limits_0^1 {\left[ {g\left( x \right) – f\left( x \right)} \right]} + \int\limits_0^1 {\left[ { – g\left( x \right)} \right]} = \frac{7}{3}$
$ \Rightarrow \int\limits_0^1 {f\left( x \right)dx = – \frac{7}{3}} $.
Câu 9: Xét $f\left( x \right) = a{x^4} + b{x^2} + c(a,b,c \in \mathbb{R},a < 0)$ sao cho đồ thị hàm số $y = f\left( x \right)$ có ba điểm cực trị là $A,B$ và $C\left( {\frac{{\sqrt 2 }}{2};\frac{1}{{20}}} \right)$. Gọi $y = g\left( x \right)$ là hàm số bậc hai có đồ thị đi qua ba điểm $A,B$ và $C$. Khi hình phẳng giới hạn bởi đồ thị của hai hàm số $y = f\left( x \right),y = g\left( x \right)$ và hai đường thẳng $x = 0,x = \frac{{\sqrt 2 }}{2}$ có diện tích bằng $\frac{{\sqrt 2 }}{{60}}$, tích phân bằng
A. $\frac{{27}}{{20}}$.
B. $\frac{{44}}{{15}}$.
C. $ – \frac{{\sqrt 2 }}{{24}}$.
D. $\frac{{94}}{{30}}$.
Lời giải
Phương trình hàm số bậc hai đi qua 3 điểm $A,B$ và $C$. là: $y = g\left( x \right) = m{x^2} + nx + p$.
Hàm số bậc hai đi qua điểm $A\left( {0:c} \right)$ suy ra $p = c$
Hàm số bậc hai có trục tung là trục đối xứng $n = 0$ và đi qua $C\left( {\sqrt {\frac{{ – b}}{{2a}}} ; – \frac{{{b^2}}}{{4a}} + c} \right)$ suy ra $m = \frac{1}{2}b$
Suy ra $y = g\left( x \right) = \frac{1}{2}b{x^2} + c$
Ta có: $\left\{ {\begin{array}{*{20}{l}}
{f\left( {\frac{{\sqrt 2 }}{2}} \right) = \frac{1}{{20}}} \\
{f’\left( {\frac{{\sqrt 2 }}{2}} \right) = 0}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{\frac{1}{4}a + \frac{1}{2}b + c = \frac{1}{{20}}} \\
{a + b = 0}
\end{array}} \right.} \right.$
Theo đề ta có:
$\int_0^1 | g(x) – f(x)| \cdot dx = \frac{2}{5}$
$ \Leftrightarrow \int_0^{\frac{{\sqrt 2 }}{2}} {\left[ {a{x^4}\frac{1}{2}b{x^2}} \right]} \cdot dx = \frac{{\sqrt 2 }}{{60}} \Leftrightarrow \frac{a}{{40}} + \frac{b}{{24}} = \frac{1}{{60}}$
Từ (II) và (III) ta có: $a = – 1:b = 1:c = \frac{{ – 1}}{5}$
Vậy $\int\limits_0^{\frac{{\sqrt 2 }}{2}} {f(x)dx = } – \frac{{\sqrt 2 }}{{24}}$
Câu 10: Xét $f\left( x \right) = a{x^4} + b{x^2} + c(a,b,c \in \mathbb{R},a > 0)$ con cho đồ thị hàm số $y = f\left( x \right)$ có biểm cực trị là $A,B$ và $C\left( {\sqrt 2 ; – \frac{2}{3}} \right)$. Gọi $y = g\left( x \right)$ )lă hàm số bậc hai có đồ thị đi qua ba điểm $A,B$ và $C$. Khi hình phẳng giới hạn bởi đồ thị của hai hàm số $y = f\left( x \right),y = g\left( x \right)$ và hai đường thẳng $x = 0,x = \sqrt 2 $ có diện tích bằng $\frac{{2\sqrt 2 }}{{15}}$, tích phân bằng
A. $\frac{{27}}{{20}}$.
B. $\frac{{44}}{{15}}$.
C. $ – \frac{{2\sqrt 2 }}{{15}}$.
D. $\frac{{94}}{{30}}$.
Lời giải
Phương trình hàm số bậc hai đi qua 3 điểm $A,B$ và $C$. là: $y = g\left( x \right) = m{x^2} + nx + p$.
Hàm số bậc hai đi qua điểm $A\left( {0:c} \right)$ suy ra $p = c$
Hàm số bậc hai có trục tung là trục đối xứng $n = 0$ và đi qua $C\left( {\sqrt {\frac{{ – b}}{{2a}}} ; – \frac{{{b^2}}}{{4a}} + c} \right)$ suy ra $m = \frac{1}{2}b$
Suy ra $y = g\left( x \right) = \frac{1}{2}b{x^2} + c$
Ta có: $\left\{ {\begin{array}{*{20}{l}}
{f\left( {\sqrt 2 } \right) = – \frac{2}{3}} \\
{f’\left( {\sqrt 2 } \right) = 0}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{4a + 2b + c = – \frac{2}{3}} \\
{4a + b = 0}
\end{array}} \right.} \right.$
Theo đề ta có:
$\int_0^{\sqrt 2 } | g(x) – f(x)| \cdot dx = \frac{2}{5}{\text{ }}$
$ \Leftrightarrow \int_0^{\sqrt 2 } {\left[ { – a{x^4} – \frac{1}{2}b{x^2}} \right]} \cdot dx = \frac{{2\sqrt 2 }}{{15}} \Leftrightarrow – \frac{{4a}}{5} – \frac{b}{3} = \frac{2}{{15}}$
Từ (II) và (III) ta có: $a = \frac{1}{4}:b = – 1:c = \frac{1}{3}$
Vậy $\int\limits_0^{\sqrt 2 } {f(x)dx = } – \frac{{2\sqrt 2 }}{{15}}$
Câu 11: Xét $f\left( x \right) = a{x^4} + b{x^2} + c(a,b,c \in \mathbb{R},a > 0)$ sao cho đồ thị hàm số $y = f\left( x \right)$ có ba điểm cực trị là $A,B$ và $C\left( {1; – \frac{3}{5}} \right)$. Gọi $y = g\left( x \right)$ là hàm số bậc hai có đồ thị đi qua ba điểm $A,B$ và $C$. Khi hình phẳng giới hạn bởi đồ thị của hai hàm số $y = f\left( x \right),y = g\left( x \right)$ và hai đường thẳng $x = 0,x = 1$ có diện tích bằng $\frac{2}{5}$, tích phân bằng
A. 1.
B. -1 .
C. $ – \frac{{17}}{{15}}$.
D. $\frac{{17}}{{15}}$.
Lời giải
Dễ thấy $f’\left( x \right)$ có ba nghiệm $x = 0,x = 1,x = – 1$ suy ra $f’\left( x \right) = 4ax\left( {{x^2} – 1} \right)$.
Từ đó ta có $f\left( x \right) = a{x^4} – 2a{x^2} + c$.
Mặt khác, từ giả thiết đồ thị hàm số $x = \pm 1$ và tiếp xúc tại điểm có hoành độ $x = 0$ nên $f\left( x \right) – g\left( x \right) = a{x^2}\left( {{x^2} – 1} \right)$.
Từ hình phẳng giới hạn bởi đồ thị của hai hàm số $y = f\left( x \right),y = g\left( x \right)$ và hai đường thẳng $x = 0,x = 1$ có diện tích bằng $\frac{2}{5}$ ta có phương trình
$ \Rightarrow f\left( x \right) = 3{x^4} – 6{x^2} + \frac{{12}}{5}$
Câu 12: Cho hàm số bậc ba $y = f\left( x \right)$ và hàm số bậc nhất $y = g\left( x \right)$ có đồ thị như hình bên dưới.
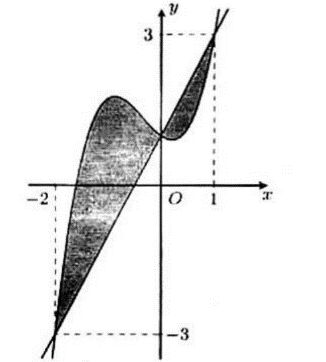
Biết diện tích phần tô đậm bằng $\frac{{37}}{{12}}$ và $\int_0^1 f \left( x \right)dx = \frac{{19}}{{12}}$. Giá trị $\int_{ – 1}^0 x .f’\left( {2x} \right)dx$ bằng
A. $ – \frac{5}{3}$. B. $ – \frac{{607}}{{348}}$. C. $ – \frac{5}{6}$. D. $ – \frac{{20}}{3}$.
Lời giải
$I = \int_{ – 1}^0 x .f’\left( {2x} \right)dx$
Đặt $t = 2x \Rightarrow dt = 2dx$ Suy ra $I = \int\limits_{ – 2}^0 {\frac{t}{2}f’\left( t \right)\frac{{dt}}{2}} = \frac{1}{4}\int\limits_{ – 2}^0 {xf’\left( x \right)dx} $.
Đặt $\left\{ \begin{gathered}
u = x \hfill \\
dx = f’\left( x \right)dx \hfill \\
\end{gathered} \right. \Rightarrow \left\{ \begin{gathered}
du = dx \hfill \\
v = f\left( x \right) \hfill \\
\end{gathered} \right.$.
Suy ra: $I = \frac{1}{4}\int\limits_{ – 2}^0 {xf’\left( x \right)dx} = \frac{1}{4}\left[ {\left. {xf\left( x \right)} \right|_{ – 2}^0 – \int\limits_{ – 2}^0 {f\left( x \right)dx} } \right] = \frac{1}{4}\left[ {2f\left( { – 2} \right) – \int\limits_{ – 2}^0 {f\left( x \right)dx} } \right]\left( {**} \right)$.
Quan sát đồ thị ta thấy:
$f\left( 1 \right) = 3;\,f\left( { – 2} \right) = – 3$.
Gọi $g\left( x \right) = ax + b \Rightarrow \left\{ \begin{gathered}
a + b = 3 \hfill \\
– 2a + b = – 3 \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
a = 2 \hfill \\
b = 1 \hfill \\
\end{gathered} \right. \Rightarrow g\left( x \right) = 2x + 1$.
$\int\limits_{ – 2}^1 {\left[ {f\left( x \right) – g\left( x \right)} \right]dx} = \int\limits_{ – 2}^0 {\left[ {f\left( x \right) – g\left( x \right)} \right]dx – } \int\limits_0^1 {\left[ {f\left( x \right) – g\left( x \right)} \right]dx} = \frac{{37}}{{12}}$
$ \Leftrightarrow \int\limits_{ – 2}^0 {\left[ {f\left( x \right) – 2x – 1} \right]dx – } \int\limits_0^1 {\left[ {f\left( x \right) – 2x – 1} \right]dx = } \frac{{37}}{{12}}$
$ \Leftrightarrow \int\limits_{ – 2}^0 {\left[ {f\left( x \right) – 2x – 1} \right]dx – } \int\limits_0^1 {\left[ {f\left( x \right) – 2x – 1} \right]dx = } \frac{{37}}{{12}}$
$\begin{gathered}
\Leftrightarrow \int\limits_{ – 2}^0 {f\left( x \right)dx – } \int\limits_0^1 {f\left( x \right)dx = } \frac{{37}}{{12}} – 4 \hfill \\
\Leftrightarrow \int\limits_{ – 2}^0 {f\left( x \right)dx – } \frac{{19}}{{12}} = \frac{{37}}{{12}} – 4 \Leftrightarrow \int\limits_{ – 2}^0 {f\left( x \right)dx} = \frac{2}{3} \hfill \\
\end{gathered} $.
$I = \frac{1}{4}\left[ {2f\left( { – 2} \right) – \int\limits_{ – 2}^0 {f\left( x \right)dx} } \right] = \frac{1}{4}\left[ {2\left( { – 3} \right) – \frac{2}{3}} \right] = – \frac{5}{3}$.
Câu 13: Xét $f\left( x \right) = a{x^4} + b{x^2} + c(a,b,c \in \mathbb{R},a > 0)$ sao cho đồ thị hàm số $y = f\left( x \right)$ có ba điểm cực trị là $A,B$ và $C\left( {1; – 1} \right)$. Gọi $y = g\left( x \right)$ là hàm số bậc hai có đồ thị đi qua ba điểm $A,B$ và $C$. Khi hình phẳng giới hạn bởi đồ thị của hai hàm số $y = f\left( x \right),y = g\left( x \right)$ và hai đường thẳng $x = 0,x = 1$ có diện tích bằng $\frac{4}{5}$, tích phân bằng
A. 1 .
B. 3 .
C. $ – \frac{8}{{15}}$.
D. $\frac{8}{{15}}$.
Lời giải
Dễ thấy $f’\left( x \right)$ có ba nghiệm $x = 0,x = 1,x = – 1$ suy ra $f’\left( x \right) = 4ax\left( {{x^2} – 1} \right)$.
Từ đó ta có $f\left( x \right) = a{x^4} – 2a{x^2} + c$.
Mặt khác, từ giả thiết đồ thị hàm số $y = f\left( x \right)$ và $y = g\left( x \right)$ cắt nhau tại hai điểm có hoành độ $x = \pm 1$ và tiếp xúc tại điểm có hoành độ $x = 0$ nên $f\left( x \right) – g\left( x \right) = a{x^2}\left( {{x^2} – 1} \right)$.
Từ hình phẳng giới hạn bởi đồ thị của hai hàm số $y = f\left( x \right),y = g\left( x \right)$ và hai đường thẳng $x = 0,x = 1$ có diện tích bằng $\frac{4}{5}$ ta có phương trình
$ \Rightarrow f\left( x \right) = 6{x^4} – 12{x^2} + 5$
Câu 14: Xét $f\left( x \right) = a{x^4} + b{x^2} + c(a,b,c \in \mathbb{R},a > 0)$ sao cho đồ thị hàm số $y = f\left( x \right)$ có ba điểm cực trị là $A,B$ và $C\left( {1;6} \right)$. Gọi $y = g\left( x \right)$ là hàm số bậc hai có đồ thị đi qua ba điểm $A,B$ và $C$. Khi hình phẳng giới hạn bởi đồ thị của hai hàm số $y = f\left( x \right),y = g\left( x \right)$ và hai đường thẳng $x = 0,x = 1$ có diện tích bằng $\frac{4}{{15}}$, tích phân bằng
A. 1.
B. 3 .
C. $ – \frac{{53}}{{15}}$.
D. $\frac{{53}}{{15}}$.
Lời giải
Dễ thấy $f’\left( x \right)$ có ba nghiệm $x = 0,x = 1,x = 1$ suy ra $\;’\left( x \right) = 4ax\left( {{x^2} – 1} \right)$.
Từ đó ta có $f\left( x \right) = a{x^4} – 2a{x^2} + c$.
Mặt khác, từ giả thiết đồ thị hàm số $x = \pm 1$ và tiếp xúc tại điểm có hoành độ $x = 0$ nên $f\left( x \right) – g\left( x \right) = a{x^2}\left( {{x^2} – 1} \right)$.
Từ hình phẳng giới hạn bởi đồ thị của hai hàm số $y = f\left( x \right),y = g\left( x \right)$ và hai đường thẳng $x = 0,x = 1$ có diện tích bằng $\frac{4}{{15}}$ ta có phương trình
$ \Rightarrow f\left( x \right) = 2{x^4} – 4{x^2} + 8$
Câu 15: Xét $f\left( x \right) = a{x^4} + b{x^2} + c(a,b,c \in \mathbb{R},a > 0)$ sao cho đồ thị hàm số $y = f\left( x \right)$ có ba điểm cực trị là $A,B$ và $C\left( {1; – 5} \right)$. Gọi $y = g\left( x \right)$ là hàm số bậc hai có đồ thị đi qua ba điểm $A,B$ và $C$. Khi hình phẳng giới hạn bởi đồ thị của hai hàm số $y = f\left( x \right),y = g\left( x \right)$ và hai đường thẳng $x = 0,x = 1$ có diện tích bằng $\frac{{14}}{{15}}$, tích phân bằng
A. 5 .
B. 3 .
C. $\frac{{23}}{{15}}$.
D. $\frac{{53}}{{15}}$.
Lời giải
Dễ thấy $f’\left( x \right)$ có ba nghiệm $x = 0,x = 1,x = – 1$ suy ra $f’\left( x \right) = 4ax\left( {{x^2} – 1} \right)$.
Từ đó ta có $f\left( x \right) = a{x^4} – 2a{x^2} + c$.
Mặt khác, từ giả thiết đồ thị hàm số $y = f\left( x \right)$ và $y = g\left( x \right)$ cắt nhau tại hai điểm có hoành độ $x = \pm 1$ và tiếp xúc tại điểm có hoành độ $x = 0$ nên $f\left( x \right) – g\left( x \right) = a{x^2}\left( {{x^2} – 1} \right)$.
Từ hình phẳng giới hạn bởi đồ thị của hai hàm số $y = f\left( x \right),y = g\left( x \right)$ và hai đường thẳng $x = 0,x = 1$ có diện tích bằng $\frac{{14}}{{15}}$ ta có phương trình
$ \Rightarrow f\left( x \right) = 7{x^4} – 14{x^2} + 2$
Câu 16: Xét $f\left( x \right) = a{x^4} + b{x^2} + c(a,b,c \in \mathbb{R},a > 0)$ sao cho đồ thị hàm số $y = f\left( x \right)$ có ba điểm cực trị là $A,B$ và $C\left( {2; – 12} \right)$. Gọi $y = g\left( x \right)$ là hàm số bậc hai có đồ thị đi qua ba điểm $A,B$ và $C$. Khi hình phẳng giới hạn bởi đồ thị của hai hàm số $y = f\left( x \right),y = g\left( x \right)$ và hai đường thẳng $x = 0,x = 2$ có diện tích bằng $\frac{{64}}{{15}}$,tích phân bằng
A. 5 .
B. 3 .
C. $\frac{{26}}{{15}}$.
D. $\frac{{23}}{{15}}$.
Lời giải
Dễ thấy $f’\left( x \right)$ có ba nghiệm $x = 0,x = 2,x = – 2$ suy ra $f’\left( x \right) = 4ax\left( {{x^2} – 4} \right)$.
Từ đó ta có $f\left( x \right) = a{x^4} – 8a{x^2} + c$.
Mặt khác, từ giả thiết đồ thị hàm số $y = f\left( x \right)$ và $y = g\left( x \right)$ cắt nhau tại hai điểm có hoành độ $x = \pm 2$ và tiếp xúc tại điểm có hoành độ $x = 0$ nên $f\left( x \right) – g\left( x \right) = a{x^2}\left( {{x^2} – 4} \right)$.
Từ hình phẳng giới hạn bởi đồ thị của hai hàm số $y = f\left( x \right),y = g\left( x \right)$ và hai đường thẳng $x = 0,x = 2$ có diện tích bằng $\frac{{64}}{{15}}$ ta có phương trình
$ \Rightarrow f\left( x \right) = {x^4} – 8{x^2} + 4$
Câu 17: Cho hàm số $y = f\left( x \right)$ có đạo hàm liên tục trên đoạn [1;3] thỏa mãn $f\left( 1 \right) = 4$ và $f\left( x \right) – \left( {x + 3} \right)f’\left( x \right) = 2x{f^2}\left( x \right),\forall x \in \left[ {1;3} \right]$. Giá trị của bằng
A. $1 + ln3$.
B. $2 – ln3$.
C. $2 + ln3$.
D. $1 – ln3$.
Xét $f\left( x \right) \ne 0$, theo giả thiết ta có
Lời giải
$f\left( x \right) – \left( {x + 3} \right)f’\left( x \right) = 2x{f^2}\left( x \right)$ $ \Leftrightarrow \frac{{f\left( x \right) – \left( {x + 3} \right)f’\left( x \right)}}{{{f^2}\left( x \right)}} = 2x \Leftrightarrow {\left[ {\frac{{x + 3}}{{f\left( x \right)}}} \right]’} = 2x$
$ \Rightarrow \frac{{x + 3}}{{f\left( x \right)}} = \smallint 2x\;dx \Leftrightarrow \frac{{x + 3}}{{f\left( x \right)}} = {x^2} + C\left( {{\;^*}} \right)$
Mà $f\left( 1 \right) = 4$, thay vào (8) ta được $\frac{{1 + 3}}{4} = {1^2} + C \Rightarrow C = 0 \Rightarrow \frac{{x + 3}}{{f\left( x \right)}} = {x^2} \Leftrightarrow f\left( x \right) = \frac{{x + 3}}{{{x^2}}}$.
Xét: $f\left( x \right) = 0 \Rightarrow x = – 3 \notin \left[ {0;2} \right] \Rightarrow f\left( x \right) \ne 0\forall x \in \left[ {1;3} \right]$.
Vậy $f\left( x \right) = \frac{{x + 3}}{{{x^2}}}\forall x \in \left[ {1;3} \right]$.
$ = \left. {\left( {lnx – \frac{3}{x}} \right)} \right|_1^3 = \left( {ln3 – 1} \right) – \left( {ln1 – 3} \right) = ln3 + 2$.
Câu 18: Cho hàm số $y = f\left( x \right)$ liên tục trên [-1;1] và thỏa mãn với $\forall x \in \left[ { – 1;1} \right]$. Khi đó bằng
A. $I = 3$.
B. $I = 4$.
C. $I = 2$.
D. $I = 1$.
Lời giải
Biến đổi
Do đó .
Thay ngược lại đẳng thức đã cho
$ = \frac{3}{2}x \times 2\left( {b – 1} \right) + \frac{3}{2} \times \frac{2}{3}a = 3\left( {b – 1} \right)x + a$
Từ đó ta có hệ phương trình $\left\{ {\begin{array}{*{20}{l}}
{a = 3\left( {b – 1} \right)} \\
{b = a}
\end{array} \Leftrightarrow a = b = \frac{3}{2}} \right.$ hay $f\left( x \right) = \frac{3}{2}x + \frac{1}{2}$ .
Câu 19: Cho hàm số bậc ba $y = f\left( x \right)$. Đường thẳng $y = ax + b$ tạo với đường cong $y = f\left( x \right)$ thành hai miền phẳng có diện tích lần lượt là ${S_1}$ và ${S_2}$ (hình vẽ bên). Biết rằng ${S_1} = \frac{5}{{12}}$ và $\int\limits_0^1 {\left( {1 – 2x} \right)f’\left( {3x} \right)dx} = – \frac{1}{2}$, khi đó giá trị của ${S_2}$ bằng
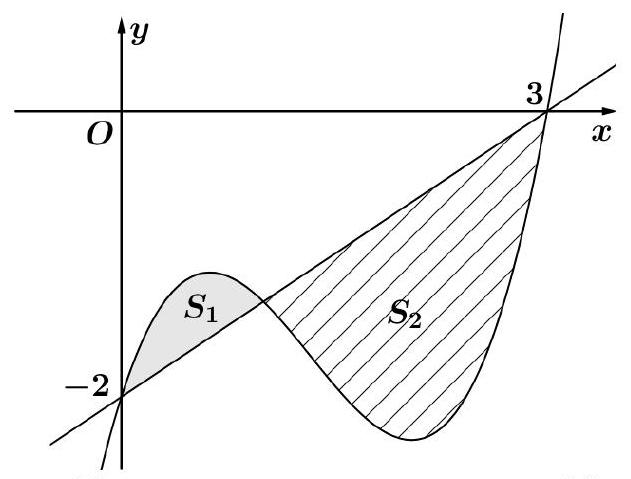
A. $\frac{8}{3}$ B. $\frac{{19}}{4}$. C. $\frac{{13}}{6}$. D. $\frac{{13}}{3}$.
Lời giải
Chọn A
Đầu tiên ta gọi phương trình đường thẳng cần tìm là: $\left( d \right):y = ax + b\left( {a \ne 0} \right)$
Dễ dàng giải ra được $\left( d \right):y = \frac{2}{3}x – 2$ với $\left( {a;b} \right) = \left( {\frac{2}{3}; – 2} \right)$ hoặc dùng tính chất đường đoạn chắn.
Tiếp đến ta có: $$
Suy ra: $\int\limits_0^3 {\left( {3 – 2x} \right)f’\left( x \right)dx} = – \frac{9}{2}$. Đặt $\left\{ {\begin{array}{*{20}{l}}
{u = 3 – 2x} \\
{dv = f’\left( x \right)dx}
\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{du = 2dx} \\
{v = f\left( x \right)}
\end{array}} \right.} \right.$ khi đó ta có được:
.
Ta có hình vẽ như sau:
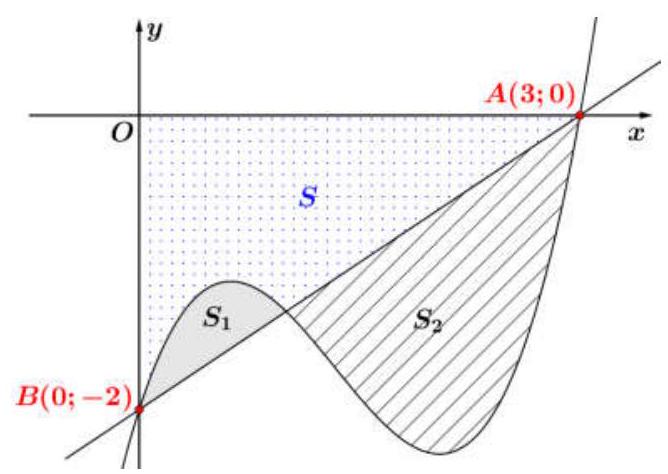
Gọi các điểm $A\left( { – 3;0} \right),B\left( {0; – 2} \right)$ và $S$ là phần diện tích giới hạn bởi đường cong $y = f\left( x \right)$ và $Ox$ với $x \in \left[ {0;3} \right]$
Khi đó ta có: và $S = {S_{\Delta OAB}} – {S_1} + {S_2} = \frac{1}{2}\left| {\overrightarrow {OA} \left| . \right|\overrightarrow {OB} } \right| – \frac{5}{{12}} + {S_2} = {S_2} + \frac{{31}}{{12}}$
Vậy ta suy ra: ${S_2} = S – \frac{{31}}{{12}} = \frac{{21}}{4} – \frac{{31}}{{12}} = \frac{8}{3}$.
Chọn đáp án A
Câu 20: Một biển quảng cáo có dạng hình vuông $ABCD$ cạnh $AB = 4m$. Trên tấm biển đó có các đường tròn tâm $A$ và đường tròn tâm $B$ cùng bán kính $R = 4m$, hai đường tròn cắt nhau như hình vẽ. Chi phí để sơn phần gạch chéo là $150 000$ đồng/m2, chi phí sơn phần màu đen là $100 000$ đồng/m2, chi phí để sơn phần còn lại là $250 000$ đồng/m2
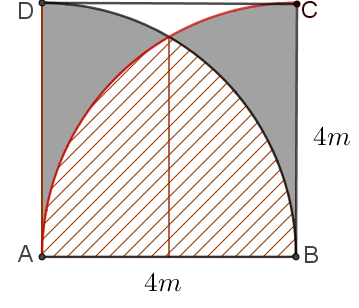
Hỏi số tiền để sơn biển quảng cáo theo cách trên gần nhất với số tiền nào dưới đây?
A. $3,017$triệu đồng. B. $1,213$triệu đồng. C. $2,06$triệu đồng. D. $2,195$triệu đồng.
Lời giải
Gọi $I$ là giao điểm của 2 cung tròn
Chọn gốc toạ độ $A\left( {0;0} \right)$$ \to B\left( {4,0} \right)$
– Xét cung tròn có phương trình $y = \sqrt {16 – {x^2}} $
– Phần diện tích gạch chéo $S = 2.\int\limits_2^4 {\sqrt {16 – {x^2}} } dx = 16\left. {\left( {x + \frac{1}{2}\sin 2x} \right)} \right|_{\frac{\pi }{6}}^{\frac{\pi }{2}} = \frac{{16\pi }}{3} – 4\sqrt 3 $
– Phần diện tích màu đen: $2.\left( {\frac{1}{4}\pi {{.4}^2} – \frac{{16\pi }}{3} + 4\sqrt 3 } \right) = \frac{{ – 8\pi }}{3} + 8\sqrt 3 $
– Phần diện tích còn lại: $16 – \left( {\frac{{16\pi }}{3} – 4\sqrt 3 + \frac{{ – 8\pi }}{3} + 8\sqrt 3 } \right) = 16 – \frac{{8\pi }}{3} – 4\sqrt 3 $
Số tiền để sơn biển quảng cáo:
$\left( {\frac{{16\pi }}{3} – 4\sqrt 3 } \right).150 000 + \left( {\frac{{ – 8\pi }}{3} + 8\sqrt 3 } \right).100 000 + \left( {16 – \frac{{8\pi }}{3} – 4\sqrt 3 } \right).250 000 = 2191480.378$triệu đồng.






