Chuyên Đề Phương Trình Và Bất Phương Trình Ôn Thi Tốt Nghiệp THPT 2025 Giải Chi Tiết

Chuyên đề phương trình và bất phương trình ôn thi tốt nghiệp THPT 2025 giải chi tiết được soạn dưới dạng file word và PDF gồm 18 trang. Các bạn xem và tải về ở dưới.

CHUYÊN ĐỀ PHƯƠNG TRÌNH VÀ BẤT PHƯƠNG TRÌNH

A. KIẾN THỨC CẦN NHỚ

I. PHƯƠNG TRÌNH LƯỢNG GIÁC

1. Phương trình lượng giác cơ bản

a) Phương trình $sinx = m\left( 1 \right)$

• Với $\left| m \right| > 1$, phương trình (1) vô nghiệm.

• Với $\left| m \right| \leqslant 1$, gọi $\alpha $ là số thực thuộc đoạn $\left[ { – \frac{\pi }{2};\frac{\pi }{2}} \right]$ sao cho $sinx = m$.

Khi đó, ta có: $sinx = m \Leftrightarrow sinx = sin\alpha $$ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = \alpha + k2\pi } \\
{x = \pi – \alpha + k2\pi }
\end{array}\left( {k \in \mathbb{Z}} \right)} \right.$.

Chú ý

• Ta có một số trường hợp đặc biệt sau của phương trình $sinx = m$ :

$sinx = 1 \Leftrightarrow x = \frac{\pi }{2} + k2\pi \left( {k \in \mathbb{Z}} \right)$

$sinx = – 1 \Leftrightarrow x = – \frac{\pi }{2} + k2\pi \left( {k \in \mathbb{Z}} \right)$

$\;sinx = 0 \Leftrightarrow x = k\pi \left( {k \in \mathbb{Z}} \right)$

• Nếu $x$ là góc lượng giác có đơn vị đo là độ thì ta có thể tìm góc lượng giác $x$ sao cho $sinx = sin{a^ \circ }$ nhu sau:

$sinx = sin{a^ \circ } \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = {a^ \circ } + k{{360}^ \circ }} \\
{x = {{180}^ \circ } – {a^ \circ } + k{{360}^ \circ }}
\end{array}\left( {k \in \mathbb{Z}} \right)} \right.$

b) Phương trình$cosx = m\left( 2 \right)$

• Với $\left| m \right| > 1$, phương trình (2) vô nghiệm.

• Với $\left| m \right| \leqslant 1$, gọi $\alpha $ là số thực thuộc đoạn $\left[ {0;\pi } \right]$ sao cho $cos\alpha = m$.

Khi đó, ta có: $cosx = m \Leftrightarrow cosx = cos\alpha \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = \alpha + k2\pi } \\
{x = – \alpha + k2\pi }
\end{array}\left( {k \in \mathbb{Z}} \right)} \right.$.

Chú ý

• Ta có một số trường hợp đặc biệt sau của phương trình $cosx = m$ :

$cosx = 1 \Leftrightarrow x = k2\pi \left( {k \in \mathbb{Z}} \right)$

$cosx = – 1 \Leftrightarrow x = \pi + k2\pi \left( {k \in \mathbb{Z}} \right)$

$cosx = 0 \Leftrightarrow x = \frac{\pi }{2} + k\pi \left( {k \in \mathbb{Z}} \right)$

• Nếu $x$ là góc lượng giác có đơn vị đo là độ thỉ ta có thể tìm góc lượng giác $x$ sao cho $cosx = cos{a^0}$ như sau:

$cosx = cos{a^ \circ } \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = {a^ \circ } + k{{360}^ \circ }} \\
{x = – {a^ \circ } + k{{360}^ \circ }}
\end{array}\left( {k \in \mathbb{Z}} \right)} \right.$

c) Phương trình $tanx = m$

Gọi $\alpha $ là số thực thuộc khoảng $\left( { – \frac{\pi }{2};\frac{\pi }{2}} \right)$ sao cho $tanx = m$. Khi đó, ta có:

$tanx = m \Leftrightarrow tanx = tan\alpha \Leftrightarrow x = \alpha + k\pi \left( {k \in \mathbb{Z}} \right)$

Chú ý: Nếu $x$ là góc lượng giác có đơn vị đo là độ thì ta có thể tìm góc lượng giác $x$ sao cho $tanx = tan{a^ \circ }$ nhu sau:

$tanx = tan{a^ \circ } \Leftrightarrow x = {a^ \circ } + k{180^ \circ }\left( {k \in \mathbb{Z}} \right)$

d) Phương trinh $cotx = m$

Gọi $\alpha $ là số thực thuộc đoạn $\left( {0;\pi } \right)$ sao cho $cotx = m$. Khi đó, ta có:

$cotx = m \Leftrightarrow cotx = cot\alpha \Leftrightarrow x = \alpha + k\pi \left( {k \in \mathbb{Z}} \right)$

Chú ý: Nếu $x$ là góc lượng giác có đơn vị đo là độ thì ta có thể tìm góc lượng giác $x$ sao cho $cotx = cot{a^0}$ như sau:

$cotx = cot{\alpha ^ \circ } \Leftrightarrow x = {\alpha ^ \circ } + k{180^ \circ }\left( {k \in Z} \right)$.

2. Phương trình lượng giác đưa về dạng cơ bản

$sinf\left( x \right) = sing\left( x \right) \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{f\left( x \right) = g\left( x \right) + k2\pi } \\
{f\left( x \right) = \pi – g\left( x \right) + k2\pi }
\end{array}\left( {k \in \mathbb{Z}} \right)} \right.$

$cosf\left( x \right) = cosg\left( x \right) \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{f\left( x \right) = g\left( x \right) + k2\pi } \\
{f\left( x \right) = – g\left( x \right) + k2\pi }
\end{array}\;\left( {k \in \mathbb{Z}} \right)} \right.$

với phương trình có dạng:

$si{n^2}u\left( x \right) = si{n^2}v\left( x \right),co{s^2}u\left( x \right) = co{s^2}v\left( x \right),si{n^2}u\left( x \right) = co{s^2}v\left( x \right)$

ta có thể dùng công thức hạ bậc để đưa về phương trình dạng $cosf\left( x \right) = cosg\left( x \right)$.

– Với một số phương trình lượng giác, ta có thể dùng các công thức lượng giác và các biến đổi để đưa về phương trình dạng tích $A\left( x \right) \cdot B\left( x \right) = 0$.

II. PHƯƠNG TRÌNH, BẤT PHƯƠNG TRÌNH MŨ VÀ LÔGARIT

1. Phương trình mũ

Với $a > 0,a \ne 1$ thì:

${a^{f\left( x \right)}} = b \Leftrightarrow f\left( x \right) = lo{g_a}b$ với $b > 0$;

${a^{f\left( x \right)}} = {a^{g\left( x \right)}} \Leftrightarrow f\left( x \right) = g\left( x \right)$.

2. Phương trình lôgarit

Với $a > 0,a \ne 1$ thì:

$lo{g_a}f\left( x \right) = b \Leftrightarrow f\left( x \right) = {a^b}$.

$lo{g_a}f\left( x \right) = lo{g_a}g\left( x \right) \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{f\left( x \right) = g\left( x \right)} \\
{f\left( x \right) > 0\;\;}
\end{array}} \right.$$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{f\left( x \right) = g\left( x \right)} \\
{g\left( x \right) > 0\;\;}
\end{array}} \right.$

3. Bất phương trình mũ

Với $a > 0,a \ne 1$ thì:

a) Xét bất phương trình: ${a^{f\left( x \right)}} > b$.

Nếu $b \leqslant 0$, tập nghiệm của bất phương trình là tập xác định của $f\left( x \right)$;

Nếu $b > 0,a > 1$ thì bất phương trình đưa về: $f\left( x \right) > lo{g_a}b$;

Nếu $b > 0,0 < a < 1$ thì bất phương trình đưa về: $f\left( x \right) < lo{g_a}b$.

b) Xét bất phương trình: ${a^{f\left( x \right)}} > {a^{g\left( x \right)}}$.

Nếu $a > 1$ thì bất phương trình đưa về: $f\left( x \right) > g\left( x \right)$;

Nếu $0 < a < 1$ thì bất phương trình đưa về: $f\left( x \right) < g\left( x \right)$.

Các bất phương trình mũ khác cùng loại được giải tương tự.

4. Bất phương trình lôgarit

Với $a > 0,a \ne 1$ thì:

a) Xét bất phương trình: $lo{g_a}f\left( x \right) > b$.

Nếu $a > 1$ thì bất phương trình đưa về: $f\left( x \right) > {a^b}$;

Nếu $0 < a < 1$ thì bất phương trình đưa về: $0 < f\left( x \right) < {a^b}$.

b) Xét bất phương trình: $lo{g_a}f\left( x \right) > lo{g_a}g\left( x \right)$.

Nếu $a > 1$ thì bất phương trình đưa về: $f\left( x \right) > g\left( x \right) > 0$;

Nếu $0 < a < 1$ thì bất phương trình đưa về: $0 < f\left( x \right) < g\left( x \right)$.

Các bất phương trình lôgarit khác cùng loại được giải tương tự.

B. MỘT SỐ VÍ DỤ

Dạng 1: Câu hỏi trắc nghiệm nhiều phương án lựa chọn

Mỗi câu thí sinh chỉ chọn một phương án.

Ví dụ 1: Nghiệm của phương trình $sin\left( {x + \frac{\pi }{3}} \right) = – \frac{{\sqrt 3 }}{2}$ là:

A. $x = – \frac{{2\pi }}{3} + k2\pi $ và $x = \pi + k2\pi \left( {k \in \mathbb{Z}} \right)$. B. $x = – \frac{\pi }{3} + k2\pi $ và $x = \frac{\pi }{3} + k2\pi \left( {k \in \mathbb{Z}} \right)$.

C. $x = k2\pi $ và $x = \pi + k2\pi \left( {k \in \mathbb{Z}} \right)$. D. $x = – \frac{\pi }{2} + k2\pi $ và $x = \frac{{5\pi }}{3} + k2\pi \left( {k \in \mathbb{Z}} \right)$.

Lời giải

Do $sin\left( { – \frac{\pi }{3}} \right) = – \frac{{\sqrt 3 }}{2}$ nên $sin\left( {x + \frac{\pi }{3}} \right) = – \frac{{\sqrt 3 }}{2} \Leftrightarrow sin\left( {x + \frac{\pi }{3}} \right) = sin\left( { – \frac{\pi }{3}} \right)$

$ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x + \frac{\pi }{3} = – \frac{\pi }{3} + k2\pi } \\
{x + \frac{\pi }{3} = \pi – \left( { – \frac{\pi }{3}} \right) + k2\pi }
\end{array}} \right.\;$$ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = – \frac{{2\pi }}{3} + k2\pi } \\
{x = \pi + k2\pi }
\end{array}\left( {k \in \mathbb{Z}} \right).\;} \right.$Chọn A

Ví dụ 2: Tổng các nghiệm của phương trình ${3^{{x^2} – 2x}} = 81$ là:

A. $4$. B. $ – 4$. C. $ – 2$. D. $2$.

Lời giải

${3^{{x^2} – 2x}} = 81 \Leftrightarrow {3^{{x^2} – 2x}} = {3^4} \Leftrightarrow {x^2} – 2x – 4 = 0.$

Phương trình ${x^2} – 2x – 4 = 0$ có hệ số $a,c$ trái dấu nên phương trình luôn có hai nghiệm phân biệt và tổng hai nghiệm bằng $2$. Chọn D

Ví dụ 3: Nghiệm của phương trình $lo{g_{16}}\left( {x + 5} \right) = \frac{1}{2}$ là:

A. $3$. B. $ – 1$. C. $ – 3$. D. $27$.

Lời giải

Ta có: $x + 5 = {16^{\frac{1}{2}}}$. Suy ra $x = – 1$. Chọn B

Ví dụ 4:  Số nghiệm của phương trình ${\log _2}\left( {x – 4} \right) = {\log _2}\left( {{x^2} – 5x + 4} \right)$là

A. $1$. B. $2$. C. $0$. D. $3$.

Lời giải

Chọn C

${\log _2}\left( {x – 4} \right) = {\log _2}\left( {{x^2} – 5x + 4} \right) \Leftrightarrow \left\{ \begin{gathered}
x – 4 = {x^2} – 5x + 4 \hfill \\
x – 4 > 0 \hfill \\
\end{gathered} \right.$ $ \Leftrightarrow \left\{ \begin{gathered}
{x^2} – 6x + 8 = 0 \hfill \\
x > 4 \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
\left[ \begin{gathered}
x = 2 \hfill \\
x = 4 \hfill \\
\end{gathered} \right. \hfill \\
x > 4 \hfill \\
\end{gathered} \right.$.

Vậy phương trình đã cho vô nghiệm.

Dạng 2: Trắc nghiệm đúng-sai

Trong mỗi ý a) b) c) d) ở mỗi câu thí sinh chọn đúng hoặc sai.

Ví dụ 5: Cho phương trình ${\sin ^2}\left( {2x + \frac{\pi }{4}} \right) = {\cos ^2}\left( {x + \frac{\pi }{2}} \right)$.

a) Hạ bậc hai vế, ta được phương trình : $\frac{{1 + \cos \left( {4x + \frac{\pi }{2}} \right)}}{2} = \frac{{1 – \cos \left( {2x + \pi } \right)}}{2}$.

b) Ta có : $\cos \left( {2x + \pi } \right) = – \cos 2x$.

c) Phương trình đã cho đưa về dạng : $\cos \left( {4x + \frac{\pi }{2}} \right) = \cos 2x$.

d) Nghiệm của phương trình đã cho là : $x = – \frac{\pi }{4} + k\pi $ và $x = \frac{\pi }{{12}} + k\frac{\pi }{3}\,(k \in \mathbb{Z})$

Lời giải

Ý	a)	b)	c)	d)
Kết quả	S	Đ	Đ	S

a) Hạ bậc hai vế, ta được phương trình: $\frac{{1 – \cos \left( {4x + \frac{\pi }{2}} \right)}}{2} = \frac{{1 + \cos \left( {2x + \pi } \right)}}{2}$. Suy ra sai

b) $\cos \left( {2x + \pi } \right) = – \cos 2x$ ( Áp dụng giá trị lượng giác của 2 cung hơn kém $\pi $). Suy ra đúng

c) $\frac{{1 – \cos \left( {4x + \frac{\pi }{2}} \right)}}{2} = \frac{{1 + \cos \left( {2x + \pi } \right)}}{2}$.

$ \Leftrightarrow – \cos \left( {4x + \frac{\pi }{2}} \right) = \cos \left( {2x + \pi } \right)$

$ \Leftrightarrow – \cos \left( {4x + \frac{\pi }{2}} \right) = – \cos \left( {2x} \right)$

Suy ra đúng

d) $\cos \left( {4x + \frac{\pi }{2}} \right) = \cos 2x \Leftrightarrow \left[ \begin{gathered}
4x + \frac{\pi }{2} = 2x + k2\pi \hfill \\
4x + \frac{\pi }{2} = – 2x + k2\pi \hfill \\
\end{gathered} \right. \Leftrightarrow \left[ \begin{gathered}
x = – \frac{\pi }{4} + k\pi \hfill \\
x = – \frac{\pi }{{12}} + k\frac{\pi }{3} \hfill \\
\end{gathered} \right.\left( {k \in Z} \right)$. Suy ra sai.

Ví dụ 6: Cho bất phương trình ${\left( {3 – 2\sqrt 2 } \right)^{{x^2} – 4x}} > {\left( {3 + 2\sqrt 2 } \right)^{5 – 2x}}$.

a) Ta có : $3 + 2\sqrt 2 = {\left( {3 – 2\sqrt 2 } \right)^{ – 1}}$.

b) Bất phương trình đã cho tương đương với bất phương trình : ${x^2} – 4x > 2x – 5$.

c) Số nghiệm nguyên của bất phương trình là 5.

d) Tổng các nghiệm nguyên của bất phương trình là 9.

Lời giải

Ý	a)	b)	c)	d)
Kết quả	Đ	S	S	Đ

a) $\left( {3 + 2\sqrt 2 } \right)\left( {3 – 2\sqrt 2 } \right) = 1$

$ \Rightarrow \left( {3 + 2\sqrt 2 } \right) = \frac{1}{{\left( {3 – 2\sqrt 2 } \right)}}$

$ \Rightarrow \left( {3 + 2\sqrt 2 } \right) = {\left( {3 – 2\sqrt 2 } \right)^{ – 1}}$ Suy ra đúng

b) ${\left( {3 – 2\sqrt 2 } \right)^{{x^2} – 4x}} > {\left( {3 + 2\sqrt 2 } \right)^{5 – 2x}}$

$ \Leftrightarrow {\left( {3 – 2\sqrt 2 } \right)^{{x^2} – 4x}} > {\left( {3 – 2\sqrt 2 } \right)^{2x – 5}}$

$ \Leftrightarrow {x^2} – 4x < 2x – 5$. Suy ra sai

c) ${x^2} – 4x < 2x – 5 \Leftrightarrow {x^2} – 6x + 5 < 0 \Leftrightarrow 1 < x < 5$

Vậy bất phương trình có 3 nghiệm nguyên là 2 ; 3 ; 4. Suy ra sai

d) Tổng các nghiệm nguyên là $2 + 3 + 4 = 9$. Suy ra đúng

Ví dụ 7: Cho bất phương trình ${\log _{\sqrt 2 – 1}}\left( {2{x^2} – 2} \right) \geqslant {\log _{\sqrt 2 – 1}}\left( {5x + 5} \right)$.

a) Ta có : $0 < \sqrt 2 – 1 < 1$.

b) Bất phương trình đã cho tương đương với: $\left\{ \begin{gathered}
2{x^2} – 2 \leqslant 5x + 5 \hfill \\
5x + 5 > 0 \hfill \\
\end{gathered} \right.$.

c) Số nghiệm nguyên của bất phương trình là 2.

d) Nghiệm nguyên nhỏ nhất của bất phương trình là 0.

Lời giải

Ý	a)	b)	c)	d)
Kết quả	Đ	S	Đ	S

a) Ta có : $0 < \sqrt 2 – 1 < 1$. Suy ra đúng

b) ${\log _{\sqrt 2 – 1}}\left( {2{x^2} – 2} \right) \geqslant {\log _{\sqrt 2 – 1}}\left( {5x + 5} \right)$$ \Leftrightarrow \left\{ \begin{gathered}
2{x^2} – 2 \leqslant 5x + 5 \hfill \\
2{x^2} – 2 > 0 \hfill \\
\end{gathered} \right.$. Suy ra sai

c) $\left\{ \begin{gathered}
2{x^2} – 2 \leqslant 5x + 5 \hfill \\
2{x^2} – 2 > 0 \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
2{x^2} – 5x – 7 \leqslant 0 \hfill \\
2{x^2} – 2 > 0 \hfill \\
\end{gathered} \right.$.$ \Leftrightarrow 1 < x \leqslant \frac{7}{2}$

Vậy bất phương trình có hai nghiệm nguyên là 2 và 3. Suy ra đúng.

d) Nghiệm nguyên nhỏ nhất là 2. Suy ra sai

Dạng 3: Câu trắc nghiệm trả lời ngắn

Ví dụ 8: Hàng ngày mực nước tại một cảng biển lên xuống theo thủy triều. Độ sâu $h\left( m \right)$ của mực nước theo thời gian $t$ (giờ) trong một ngày cho bởi công thức

$h = 16 + 7\sin \left( {\frac{\pi }{{12}}t} \right)$ với $0 \leqslant t \leqslant 24$

Tìm thời điểm mà mực nước tại cảng là cao nhất.

Lời giải

Do $ – 1 \leqslant \sin \left( {\frac{\pi }{{12}}t} \right) \leqslant 1$ nên $16 – 7 \leqslant 16 + 7\sin \left( {\frac{\pi }{{12}}t} \right) \leqslant 16 + 7$ hay $9 \leqslant h \leqslant 23$.

Vậy mực nước tại cảng cao nhất bằng 23m khi

$\sin \left( {\frac{\pi }{{12}}t} \right) = 1 \Leftrightarrow \frac{\pi }{{12}}t = \frac{\pi }{2} + k2\pi \Leftrightarrow t = 6 + 24k\,\,\,\left( {k \in \mathbb{Z}} \right)$.

Mà $0 \leqslant t \leqslant 24$ nên $t = 6$. Thời điểm mà mực nước tại cảng cao nhất là $t = 6$ (giờ).

Ví dụ 9: Công thức Định luật làm mát của Newton được cho như sau: $kt = \ln \frac{{T – S}}{{{T_0} – S}}$ trong đó $t$ là số giờ trôi qua, ${T_0}$ là nhiệt độ lúc đầu, $T$ là nhiệt độ sau $t$ giờ, $S$ là nhiệt độ môi trường (${T_0}\,,\,T\,,\,S$ theo cùng một đơn vị đo), $k$ là một hằng số. Một cốc trà có nhiệt độ $96^\circ C$, sau 2 phút nhiệt độ giảm còn $90^\circ C$. Biết nhiệt độ phòng là $24^\circ C$. Tính nhiệt độ của cốc trà sau 10 phút (làm tròn kết quả đến hàng phần mười).

Lời giải

Thay $t = 2$ phút $ = \frac{1}{{30}}$ giờ, ${T_0} = 96\,,\,T = 90\,,\,S = 24$ ta có $\frac{1}{{30}}k = \ln \frac{{90 – 24}}{{96 – 24}}$. Do đó $k = 30\ln \frac{{11}}{{12}}$.

Sau 10 phút $ = \frac{1}{6}$ giờ, ta có $\frac{1}{6}k = \ln \frac{{T – 24}}{{96 – 24}}$ hay $5\ln \frac{{11}}{{12}} = \ln \frac{{T – 24}}{{72}}$. Do đó $\frac{{T – 24}}{{72}} = {\left( {\frac{{11}}{{12}}} \right)^5}$.

Suy ra $T = 72.{\left( {\frac{{11}}{{12}}} \right)^5} + 24 \approx 70,6^\circ C$.

Vậy nhiệt độ của cốc trà sau 10 phút khoảng $70,6\,\left( {^\circ C} \right)$.

C. BÀI TẬP LUYỆN TẬP

Dạng 1: Câu hỏi trắc nghiệm nhiều phương án lựa chọn

Mỗi câu thí sinh chỉ chọn một phương án.

Câu 1. Các nghiệm của phương trình $\sin \left( {\frac{\pi }{5} – x} \right) = 0$ là:

A. $x = – \frac{\pi }{5} + k\pi \,\left( {k \in \mathbb{Z}} \right)$. B. $x = \frac{{2\pi }}{5} + k\pi \,\left( {k \in \mathbb{Z}} \right)$.

C. $x = – \frac{\pi }{5} + k2\pi \,\left( {k \in \mathbb{Z}} \right)$. D. $x = \frac{\pi }{5} + k\pi \,\left( {k \in \mathbb{Z}} \right)$.

Lời giải

Chọn D

Ta có $\sin \left( {\frac{\pi }{5} – x} \right) = 0 \Leftrightarrow \frac{\pi }{5} – x = k\pi \Leftrightarrow x = \frac{\pi }{5} – k\pi \,\,\left( {k \in \mathbb{Z}} \right)$, hay $x = \frac{\pi }{5} + k\pi \,\left( {k \in \mathbb{Z}} \right)$.

Câu 2.  Các nghiệm của phương trình $2\sin 3x + \sqrt 2 = 0$ là:

A. $x = \frac{\pi }{{12}} + k\frac{{2\pi }}{3}$ và $x = \frac{{3\pi }}{{12}} + k\frac{{2\pi }}{3}\,\,\left( {k \in \mathbb{Z}} \right)$. B. $x = – \frac{\pi }{{12}} + k\frac{{2\pi }}{3}$ và $x = \frac{{5\pi }}{{12}} + k\frac{{2\pi }}{3}\,\,\left( {k \in \mathbb{Z}} \right)$.

C. $x = \frac{\pi }{{12}} + k\frac{{2\pi }}{3}$ và $x = – \frac{\pi }{{12}} + k\frac{{2\pi }}{3}\,\,\left( {k \in \mathbb{Z}} \right)$. D. $x = – \frac{\pi }{{12}} + k\frac{{2\pi }}{3}$ và $x = \frac{{3\pi }}{{12}} + k\frac{{2\pi }}{3}\,\,\left( {k \in \mathbb{Z}} \right)$.

Lời giải

Chọn B

Ta có

$2\sin 3x + \sqrt 2 = 0 \Leftrightarrow \sin 3x = – \frac{{\sqrt 2 }}{2} \Leftrightarrow \sin 3x = \sin \left( { – \frac{\pi }{4}} \right)$

$ \Leftrightarrow \left[ \begin{gathered}
3x = – \frac{\pi }{4} + k2\pi \hfill \\
3x = \frac{{5\pi }}{4} + k2\pi \hfill \\
\end{gathered} \right.$$ \Leftrightarrow \left[ \begin{gathered}
x = – \frac{\pi }{{12}} + k\frac{{2\pi }}{3} \hfill \\
x = \frac{{5\pi }}{{12}} + k\frac{{2\pi }}{3} \hfill \\
\end{gathered} \right.\,\,\left( {k \in \mathbb{Z}} \right)$

Câu 3.  Các nghiệm của phương trình $\cos \left( {x + \frac{\pi }{6}} \right) = \frac{1}{2}$ là:

A. $x = \frac{\pi }{6} + k2\pi $ và $x = – \frac{\pi }{2} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)$. B. $x = – \frac{\pi }{6} + k2\pi $ và $x = \frac{\pi }{2} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)$.

C. $x = k2\pi $ và $x = – \frac{\pi }{3} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)$. D. $x = \frac{\pi }{6} + k\pi $ và $x = – \frac{\pi }{2} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)$.

Lời giải

Chọn A

Ta có

$\cos \left( {x + \frac{\pi }{6}} \right) = \frac{1}{2} \Leftrightarrow \cos \left( {x + \frac{\pi }{6}} \right) = \cos \frac{\pi }{3}$

$ \Leftrightarrow \left[ \begin{gathered}
x + \frac{\pi }{6} = \frac{\pi }{3} + k2\pi \hfill \\
x + \frac{\pi }{6} = – \frac{\pi }{3} + k2\pi \hfill \\
\end{gathered} \right.$$ \Leftrightarrow \left[ \begin{gathered}
x = \frac{\pi }{6} + k2\pi \hfill \\
x = – \frac{\pi }{2} + k2\pi \hfill \\
\end{gathered} \right.\,\,\left( {k \in \mathbb{Z}} \right)$

Câu 4. Các nghiệm của phương trình ${\sin ^2}2x = 1$ là:

A. $x = \frac{\pi }{4} + k\frac{\pi }{2} \left( {k \in \mathbb{Z}} \right)$. B. $x = k\frac{\pi }{2} \left( {k \in \mathbb{Z}} \right)$.

C. $x = \frac{\pi }{2} + k\pi \left( {k \in \mathbb{Z}} \right)$. D. $x = \frac{\pi }{8} + k\frac{\pi }{2} \left( {k \in \mathbb{Z}} \right)$.

Lời giải

$\begin{gathered}
{\sin ^2}2x = 1 \Leftrightarrow 1 – {\cos ^2}2x = 1 \Leftrightarrow {\cos ^2}2x = 0 \Leftrightarrow \cos 2x = 0 \hfill \\
\Leftrightarrow 2x = \frac{\pi }{2} + k\pi \Leftrightarrow x = \frac{\pi }{4} + k\frac{\pi }{2} \hfill \\
\end{gathered} $.

Câu 5.  Các nghiệm của phương trình $\tan \left( {x – \frac{\pi }{3}} \right) = \sqrt 3 $ là:

A. $x = \frac{{2\pi }}{3} + k2\pi \left( {k \in \mathbb{Z}} \right)$. B. $x = k\pi \left( {k \in \mathbb{Z}} \right)$.

C. $x = \frac{{2\pi }}{3} + k\pi \left( {k \in \mathbb{Z}} \right)$. D. $x = – \frac{{2\pi }}{3} + k\pi \left( {k \in \mathbb{Z}} \right)$.

Lời giải

$\tan \left( {x – \frac{\pi }{3}} \right) = \sqrt 3 \Leftrightarrow x – \frac{\pi }{3} = \frac{\pi }{3} + k\pi $$ \Leftrightarrow x = \frac{{2\pi }}{3} + k\pi $

Câu 6.  Các nghiệm của phương trình $\cot \left( {3x + \frac{\pi }{4}} \right) = – 1$ là:

A. $x = – \frac{\pi }{6} + k\pi \left( {k \in \mathbb{Z}} \right)$. B. $x = \frac{\pi }{6} + k\frac{\pi }{3} \left( {k \in \mathbb{Z}} \right)$.

C. $x = – \frac{\pi }{6} + k\frac{\pi }{6} \left( {k \in \mathbb{Z}} \right)$. D. $x = \frac{\pi }{6} + k\frac{\pi }{2} \left( {k \in \mathbb{Z}} \right)$.

Lời giải

Cách 1: $\cot \left( {3x + \frac{\pi }{4}} \right) = – 1 \Leftrightarrow 3x + \frac{\pi }{4} = \frac{{3\pi }}{4} + k\pi $

$ \Leftrightarrow 3x = \frac{\pi }{2} + k\pi \Leftrightarrow x = \frac{\pi }{6} + k\frac{\pi }{3}$

Cách 2: $\cot \left( {3x + \frac{\pi }{4}} \right) = – 1 \Leftrightarrow 3x + \frac{\pi }{4} = – \frac{\pi }{4} + l\pi $

$ \Leftrightarrow 3x = – \frac{\pi }{2} + l\pi $

$ \Leftrightarrow x = – \frac{\pi }{6} + l\frac{\pi }{3} = \frac{{ – \pi }}{6} + \frac{\pi }{3} + \left( {l – 1} \right)\frac{\pi }{3} = \frac{\pi }{6} + k\frac{\pi }{3}$

Câu 7. Các nghiệm của phương trình $\sin x + \sqrt 3 \cos x = 0$ là:

A. $x = – \frac{\pi }{6} + k\pi \left( {k \in \mathbb{Z}} \right)$. B. $x = \frac{\pi }{3} + k\pi \left( {k \in \mathbb{Z}} \right)$.

C. $x = \frac{\pi }{6} + k\pi \left( {k \in \mathbb{Z}} \right)$. D. $x = – \frac{\pi }{3} + k\pi \left( {k \in \mathbb{Z}} \right)$.

Lời giải

$\sin x + \sqrt 3 \cos x = 0 \Leftrightarrow \sin x = – \sqrt 3 \cos x \Leftrightarrow \tan x = – \sqrt 3 \Leftrightarrow x = \frac{{ – \pi }}{3} + k\pi $

Câu 8. Các góc lượng giác $x$ sao cho $\cos \left( {x – 15^\circ } \right) = – \frac{1}{2}$ là:

A. $x = 165^\circ + k360^\circ $ và $x = – 135^\circ + k360^\circ \left( {k \in \mathbb{Z}} \right)$.

B. $x = 165^\circ + k180^\circ $ và $x = – 135^\circ + k.180^\circ \left( {k \in \mathbb{Z}} \right)$.

C. $x = 135^\circ + k360^\circ $ và $x = – 105^\circ + k360^\circ \left( {k \in \mathbb{Z}} \right)$.

D. $x = 135^\circ + k180^\circ $ và $x = – 105^\circ + k180^\circ \left( {k \in \mathbb{Z}} \right)$.

Lời giải

$\cos \left( {x – 15^\circ } \right) = – \frac{1}{2}$$ \Leftrightarrow \left[ \begin{gathered}
x – 15^\circ = 120^\circ + k360^\circ \hfill \\
x – 15^\circ = – 120^\circ + k360^\circ \hfill \\
\end{gathered} \right.$

$ \Leftrightarrow \left[ \begin{gathered}
x = 135^\circ + k360^\circ \hfill \\
x = – 105^\circ + k360^\circ \hfill \\
\end{gathered} \right.$

Câu 9. Các góc lượng giác $x$ sao cho $\tan \left( {2x + 27^\circ } \right) = \tan 35^\circ $ là:

A. $x = 4^\circ + k180^\circ \left( {k \in \mathbb{Z}} \right)$ B. $x = – 4^\circ + k180^\circ \left( {k \in \mathbb{Z}} \right)$

C. $x = – 4^\circ + k90^\circ \left( {k \in \mathbb{Z}} \right)$ D. $x = 4^\circ + k90^\circ \left( {k \in \mathbb{Z}} \right)$.

Lời giải

$\tan \left( {2x + 27^\circ } \right) = \tan 35^\circ $

$ \Leftrightarrow 2x + 27^\circ = 35^\circ + k180^\circ \Leftrightarrow x = 4^\circ + k90^\circ $

Câu 10: Các góc lượng giác $x$ sao cho $\sin 2x = \sin \left( {{{36}^0} – x} \right)$ là:

A. $x = 12^\circ + k120^\circ $ và $x = 144^\circ + k360^\circ \left( {k \in \mathbb{Z}} \right)$.

B. $x = 12^\circ + k120^\circ $ và $x = 48^\circ + k120^\circ \left( {k \in \mathbb{Z}} \right)$.

C. $x = 12^\circ + k360^\circ $ và $x = 144^\circ + k120^\circ \left( {k \in \mathbb{Z}} \right)$.

D. $x = 35^\circ + k360^\circ $ và $x = 144^\circ + k360^\circ \left( {k \in \mathbb{Z}} \right)$.

Lời giải

$\sin 2x = \sin \left( {{{36}^0} – x} \right)$$ \Leftrightarrow \left[ \begin{gathered}
2x = {36^0} – x + k{360^0} \hfill \\
2x = {180^0} – \left( {{{36}^0} – x} \right) + k{360^0} \hfill \\
\end{gathered} \right.$

$ \Leftrightarrow \left[ \begin{gathered}
x = {12^0} + k{120^0} \hfill \\
x = {144^0} + k{360^0} \hfill \\
\end{gathered} \right.$

Câu 11: Số nghiệm của phương trình $\cos x = 1$ trên khoảng $\left( { – \frac{{3\pi }}{4};\frac{{9\pi }}{2}} \right)$ là:

A. $1.$ B. $2.$ C. $4.$ D. $3.$

Lời giải

$\cos x = 1 \Leftrightarrow x = k2\pi \,\,\left( {k \in \mathbb{Z}} \right)$

Giả thiết $x \in \left( { – \frac{{3\pi }}{4};\frac{{9\pi }}{2}} \right) \Rightarrow – \frac{{3\pi }}{4} < k2\pi < \frac{{9\pi }}{2} \Leftrightarrow – \frac{3}{8} < k < \frac{9}{4}$

Mà $k \in \mathbb{Z}$ nên chọn $k \in \left\{ {0;1;2} \right\}$. Vậy phương trình có 3 nghiệm thỏa bài toán.

Câu 12: Số nghiệm của phương trình $\sin x = \frac{1}{{\sqrt 3 }}$ trên khoảng $\left( { – \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right)$ là:

A. $2.$ B. $5.$ C. $4.$ D. $3.$

Lời giải

Cách 1: Tồn tại một giá trị $\alpha \in \left( {0;\frac{\pi }{2}} \right)$sao cho $\sin \alpha = \frac{1}{{\sqrt 3 }}$.

Phương trình $\sin x = \frac{1}{{\sqrt 3 }} \Leftrightarrow \sin x = \sin \alpha \Leftrightarrow \left[ \begin{gathered}
x = \alpha + k2\pi \hfill \\
x = \pi – \alpha + m2\pi \hfill \\
\end{gathered} \right.$ với $k,m \in \mathbb{Z}$

Vì $x \in \left( { – \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right)$ nên

$\left[ \begin{gathered}
– \frac{{5\pi }}{2} < \alpha + k2\pi < \frac{{5\pi }}{2} \hfill \\
\frac{{ – 5\pi }}{2} < \pi – \alpha + m2\pi < \frac{{5\pi }}{2} \hfill \\
\end{gathered} \right.$

$ \Leftrightarrow \left[ \begin{gathered}
– 3\pi < – \frac{{5\pi }}{2} – \alpha < k2\pi < \frac{{5\pi }}{2} – \alpha < \frac{{5\pi }}{2} \hfill \\
– \frac{{7\pi }}{2} < – \frac{{5\pi }}{2} – \pi + \alpha < m2\pi < \frac{{5\pi }}{2} – \pi + \alpha < 2\pi \hfill \\
\end{gathered} \right.$

$ \Leftrightarrow \left[ \begin{gathered}
– \frac{3}{2} < k < \frac{5}{4} \hfill \\
– \frac{7}{4} < k < 1 \hfill \\
\end{gathered} \right.$ với $k,m \in \mathbb{Z}$.

Suy ra: $k \in \left\{ { – 1;0;1} \right\}$; $m \in \left\{ { – 1;0} \right\}$. Vậy có 5 nghiệm thỏa bài toán.

Cách 2: Dùng đường tròn lượng giác:

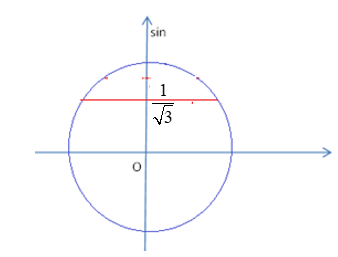
Trên hai vòng đường tròn $x \in \left[ { – 2\pi ;2\pi } \right]$ phương trình $\sin x = \frac{1}{{\sqrt 3 }}$ có 4 nghiệm.

Trên $\frac{1}{4}$ vòng đường tròn $x \in \left( {2\pi ;\frac{{5\pi }}{2}} \right)$ phương trình $\sin x = \frac{1}{{\sqrt 3 }}$ có 1 nghiệm

Trên $\frac{1}{4}$ vòng đường tròn $x \in \left( { – \frac{{5\pi }}{2}; – 2\pi } \right)$ phương trình $\sin x = \frac{1}{{\sqrt 3 }}$ vô nghiệm

Vậy phương trình $\sin x = \frac{1}{{\sqrt 3 }}$có 5 nghiệm trên $\left( { – \frac{{5\pi }}{2};\frac{{5\pi }}{2}} \right)$

Câu 13: Các nghiệm của phương trình ${\cos ^2}x – {\sin ^2}x = 0$ là:

A. $x = \frac{\pi }{4} + k\frac{\pi }{2} \left( {k \in \mathbb{Z}} \right)$. B. $x = \frac{\pi }{4} + k\pi \left( {k \in \mathbb{Z}} \right)$.

C. $x = \frac{\pi }{2} + k\pi \left( {k \in \mathbb{Z}} \right)$. D. $x = – \frac{\pi }{4} + k\pi \left( {k \in \mathbb{Z}} \right)$.

Lời giải

${\cos ^2}x – {\sin ^2}x = 0 \Leftrightarrow \cos 2x = 0 \Leftrightarrow 2x = \frac{\pi }{2} + k\pi \Leftrightarrow x = \frac{\pi }{4} + k\frac{\pi }{2}$.

Câu 14: Các nghiệm của phương trình $\cos \left( {2x – \frac{\pi }{2}} \right) = \cos 6x$ là:

A. $x = – \frac{{2\pi }}{3} + k2\pi $và $x = \pi + k2\pi \,\,\,\left( {k \in \mathbb{Z}} \right)$.

B. $x = – \frac{\pi }{3} + k2\pi $và $x = \frac{\pi }{3} + k2\pi \,\,\,\left( {k \in \mathbb{Z}} \right)$.

C. $x = k2\pi $và $x = \pi + k2\pi \,\,\,\left( {k \in \mathbb{Z}} \right)$.

D. $x = – \frac{\pi }{8} + k\frac{\pi }{2}$và $x = \frac{\pi }{{16}} + k\frac{\pi }{4}\,\,\,\left( {k \in \mathbb{Z}} \right)$.

Lời giải

$\cos \left( {2x – \frac{\pi }{2}} \right) = \cos 6x$$ \Leftrightarrow \left[ \begin{gathered}
2x – \frac{\pi }{2} = 6x + k2\pi \hfill \\
2x – \frac{\pi }{2} = – 6x + k2\pi \hfill \\
\end{gathered} \right.$

$ \Leftrightarrow \left[ \begin{gathered}
x = – \frac{\pi }{8} – k\frac{\pi }{2} \hfill \\
x = \frac{\pi }{{16}} + k\frac{\pi }{4} \hfill \\
\end{gathered} \right.$.

Câu 15: Nghiệm của phương trình ${\left( {\frac{3}{2}} \right)^x} = \frac{4}{9}$ là:

A. $x = – 2$. B. $x = – \sqrt 2 $. C. $x = \sqrt 2 $. D. $x = 2$.

Lời giải

${\left( {\frac{3}{2}} \right)^x} = \frac{4}{9} \Leftrightarrow {\left( {\frac{3}{2}} \right)^x} = {\left( {\frac{3}{2}} \right)^{ – 2}} \Leftrightarrow x = – 2$.

Câu 16: Nghiệm của phương trình ${2^{{x^2} – x}} = 4$ là:

A. $x = – 1$ và $x = 2$. B. $x = 0{\mkern 1mu} $ và $x = 1$.

C. $x = 1$và $x = – 2$. D. $x = 0$và $x = 2$

Lời giải

${2^{{x^2} – x}} = 4 \Leftrightarrow {2^{{x^2} – x}} = {2^2} \Leftrightarrow {x^2} – x = 2 \Leftrightarrow \left[ \begin{gathered}
x = – 1 \hfill \\
x = 2 \hfill \\
\end{gathered} \right.$.

Câu 17:  Tổng các nghiệm của phương trình ${5^{{x^2} – 3x}} = 10$ là :

A. $ – 3$. B. ${\log _5}10$. C. $3$. D. $ – {\log _5}10$.

Lời giải

${5^{{x^2} – 3x}} = 10 \Leftrightarrow {5^{{x^2} – 3x}} = {5^{{{\log }_5}10}} \Leftrightarrow {x^2} – 3x = {\log _5}10$

$ \Leftrightarrow {x^2} – 3x – {\log _5}10 = 0$ có $a = 1;c = – {\log _5}10 < 0 \Rightarrow $ phương trình có hai nghiệm trái dấu.

Vậy tổng các nghiệm của phương trình là $3$.

Câu 18: Nghiệm của phương trình ${\left( {\frac{1}{{25}}} \right)^{3 – 2x}} = {5^{x + 3}}$ là

A. $x = – 3$. B. $x = 5$. C. $x = – 5$. D. $x = 3$.

Lời giải

${\left( {\frac{1}{{25}}} \right)^{3 – 2x}} = {5^{x + 3}} \Leftrightarrow {5^{ – 2\left( {3 – 2x} \right)}} = {5^{x + 3}} \Leftrightarrow – 6 + 4x = x + 3 \Leftrightarrow x = 3$.

Câu 19: Nghiệm của phương trình ${\log _{27}}\left( {{x^2} – 1} \right) = \frac{1}{3}$ là

A. $x = \pm 2$. B. $x = \pm \sqrt {10} $. C. $x = 2$. D. $x = \sqrt {10} $.

Lời giải

Điều kiện: ${x^2} – 1 > 0 \Leftrightarrow \left[ \begin{gathered}
x < – 1 \hfill \\
x > 1 \hfill \\
\end{gathered} \right.$.

${\log _{27}}\left( {{x^2} – 1} \right) = \frac{1}{3} \Leftrightarrow {\log _{27}}\left( {{x^2} – 1} \right) = {\log _{27}}{27^{\frac{1}{3}}}$$ \Leftrightarrow {x^2} – 1 = 3 \Leftrightarrow x = \pm 2$.

Kết hợp điều kiện: nghiệm của phương trình là $x = \pm 2$.

Câu 20: Tích các nghiệm của phương trình ${\log _2}\left( {{x^2} – 2x} \right) = 3$ là :

A. $8$. B. $6$. C. $ – 8$. D. $ – 6$.

Lời giải

Điều kiện: ${x^2} – 2x > 0 \Leftrightarrow \left[ \begin{gathered}
x < 0 \hfill \\
x > 2 \hfill \\
\end{gathered} \right.$.

${\log _2}\left( {{x^2} – 2x} \right) = 3$$ \Leftrightarrow {\log _2}\left( {{x^2} – 2x} \right) = {\log _2}{2^3}$$ \Leftrightarrow {x^2} – 2x = 8$ (thỏa điều kiện)

$ \Leftrightarrow {x^2} – 2x – 8 = 0$ luôn có hai nghiệm trái dấu. Tích các nghiệm là $ – 8$.

Câu 21: Số nghiệm của phương trình ${\log _7}\left( {{x^2} – 2x} \right) = {\log _7}\left( {3x – 6} \right)$ là:

A. $2$. B. $0$. C. $3$. D. $1$.

Lời giải

Điều kiện $\left\{ \begin{gathered}
{x^2} – 2x > 0 \hfill \\
3x – 6 > 0 \hfill \\
\end{gathered} \right. \Leftrightarrow x > 2$.

${\log _7}\left( {{x^2} – 2x} \right) = {\log _7}\left( {3x – 6} \right)$$ \Leftrightarrow {x^2} – 2x = 3x – 6$$ \Leftrightarrow {x^2} – 5x + 6 = 0$$ \Leftrightarrow \left[ \begin{gathered}
x = 2 \hfill \\
x = 3 \hfill \\
\end{gathered} \right.$.

Kết hợp với điều kiện: $x = 3$ là nghiệm.

Câu 22: Nghiệm của bất phương trình ${\left( {0,5} \right)^x} > 3$ là:

A. $x > {\log _{0,5}}3$. B. $x < {\log _{0,5}}3$. C. $x < {\log _3}0,5$. D. $x > {\log _3}0,5$.

Lời giải

${\left( {0,5} \right)^x} > 3 \Leftrightarrow {\left( {0,5} \right)^x} > {\left( {0,5} \right)^{{{\log }_{0,5}}3}} \Leftrightarrow x < {\log _{0,5}}3$.

Câu 23: Tập nghiệm của bất phương trình ${\left( {0,2} \right)^{{x^2}}} > 1$ là:

A. $\emptyset $. B. $\mathbb{R}\backslash \left\{ 0 \right\}$. C. $\left( {0; + \infty } \right)$. D. $\mathbb{R}$.

Lời giải

${\left( {0,2} \right)^{{x^2}}} > 1 \Leftrightarrow {\left( {0,2} \right)^{{x^2}}} > {\left( {0,2} \right)^0} \Leftrightarrow {x^2} < 0$$ \Leftrightarrow x \in \emptyset $.

Câu 24: Tập nghiệm của bất phương trình ${\left( {2 – \sqrt 3 } \right)^{2x – 1}} > {\left( {2 + \sqrt 3 } \right)^{x – 5}}$ là:

A. $\left( {2; + \infty } \right)$. B. $\left( { – 4; + \infty } \right)$. C. $\left( { – \infty ;2} \right)$. D. $\left( { – \infty ; – 4} \right)$ .

Lời giải

${\left( {2 – \sqrt 3 } \right)^{2x – 1}} > {\left( {2 + \sqrt 3 } \right)^{x – 5}}$$ \Leftrightarrow {\left( {\frac{1}{{2 + \sqrt 3 }}} \right)^{2x – 1}} > {\left( {2 + \sqrt 3 } \right)^{x – 5}}$

$ \Leftrightarrow {\left( {2 + \sqrt 3 } \right)^{ – 2x + 1}} > {\left( {2 + \sqrt 3 } \right)^{x – 5}}$$ \Leftrightarrow – 2x + 1 > x – 5 \Leftrightarrow x < 2$.

Vậy tập nghiệm của bất phương trình là $\left( { – \infty ;2} \right)$.

Câu 25: Tập nghiệm của bất phương trình ${\log _{\frac{1}{2}}}\left( {2x – 6} \right) < – 2$ là

A. $\left( {3;5} \right)$. B. $\left( { – \infty ;5} \right)$. C. $\left( {3; + \infty } \right)$ D. $\left( {5; + \infty } \right)$.

Lời giải

Điều kiện: $2x – 6 > 0 \Leftrightarrow x > 3$.

${\log _{\frac{1}{2}}}\left( {2x – 6} \right) < – 2$$ \Leftrightarrow {\log _{\frac{1}{2}}}\left( {2x – 6} \right) < {\log _{\frac{1}{2}}}{\left( {\frac{1}{2}} \right)^{ – 2}}$.

$ \Leftrightarrow 2x – 6 > 4 \Leftrightarrow x > 5$

Kết hợp điều kiện: tập nghiệm của bất phương trình là $\left( {5; + \infty } \right)$.

Câu 26: Số nghiệm nguyên của bất phương trình ${\log _5}\left( {2x – 3} \right) < {\log _{25}}{x^2}$ là:

A. $1$. B. $2$. C. $0$. D. vô số.

Lời giải

Điều kiện: $\left\{ \begin{gathered}
2x – 3 > 0 \hfill \\
{x^2} > 0 \hfill \\
\end{gathered} \right. \Leftrightarrow x > \frac{3}{2}$.

${\log _5}\left( {2x – 3} \right) < {\log _{25}}{x^2}$$ \Leftrightarrow {\log _5}\left( {2x – 3} \right) < \frac{1}{2}.2.{\log _5}x$

$ \Leftrightarrow 2x – 3 < x \Leftrightarrow x < 3$.

Kết hợp điều kiện: tập nghiệm của bất phương trình là $\left( {\frac{3}{2};3} \right)$.

Số nghiệm nguyên của bất phương trình là $1$.

Dạng 2. Câu trắc nghiệm đúng sai

Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 27:  Cho phương trình ${\cos ^2}\left( {\frac{\pi }{2} – x} \right) = {\sin ^2}\left( {3x + \frac{\pi }{4}} \right)$.

a) Hạ bậc hai vế, ta được phương trình: $\frac{{1 + \cos \left( {\pi – 2x} \right)}}{2} = \frac{{1 – \cos \left( {6x + \frac{\pi }{2}} \right)}}{2}$.

b) Ta có: $\cos \left( {\pi – 2x} \right) = \cos 2x$.

c) Phương trình đã cho đưa về dạng: $\cos 2x = \cos 6x$.

d) Nghiệm của phương trình đã cho là: $x = k\frac{\pi }{4}(k \in \mathbb{Z})$.

Lời giải

Ta có: $\cos \left( {\pi – 2x} \right) = – \cos \left( {6x + \frac{\pi }{2}} \right) \Leftrightarrow \cos \left( {\pi – 2x} \right) = \cos \left( {\frac{\pi }{2} – 6x} \right)$

$ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{\pi – 2x = \frac{\pi }{2} – 6x + k2\pi } \\
{\pi – 2x = -\frac{\pi }{2} + 6x + k2\pi }
\end{array}} \right.$$ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = – \frac{\pi }{8} + k\frac{\pi }{2}} \\
{x = \frac{{3\pi }}{{16}} + k\frac{\pi }{4}}
\end{array}(k \in \mathbb{Z}).} \right.$

Đáp án: a) Đ, b) S, c) S, d) S

Câu 28:  Cho phương trình $\cos 2x = \sin \left( {\frac{\pi }{4} – x} \right)$ với $x \in \left[ {0;\pi } \right]$.

a) Ta có: $\cos 2x = \sin \left( {\frac{\pi }{2} – 2x} \right)$.

b) Phương trình $\sin \left( {\frac{\pi }{2} – 2x} \right) = \sin \left( {\frac{\pi }{4} – x} \right)$ có các nghiệm là: $x = \frac{\pi }{4} + k2\pi $ và

$x = \frac{{5\pi }}{4} + k2\pi (k \in \mathbb{Z})$.

c) Phương trình đã cho có hai nghiệm thuộc đoạn $\left[ {0;\pi } \right]$.

d) Tổng các nghiệm của phương trình đã cho trên đoạn $\left[ {0;\pi } \right]$ là $\frac{{5\pi }}{6}$.

Lời giải

Do $\cos 2x = \sin \left( {\frac{\pi }{2} – 2x} \right)$ nên phương trình đưa về dạng $\sin \left( {\frac{\pi }{2} – 2x} \right) = \sin \left( {\frac{\pi }{4} – x} \right)$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{\frac{\pi }{2} – 2x = \frac{\pi }{4} – x + k2\pi } \\
{\frac{\pi }{2} – 2x = \pi – \left( {\frac{\pi }{4} – x} \right) + k2\pi }
\end{array}} \right.$$ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = \frac{\pi }{4} + k2\pi } \\
{x = – \frac{\pi }{{12}} + k\frac{{2\pi }}{3}}
\end{array}(k \in \mathbb{Z})} \right.$.

Do $x \in \left[ {0;\pi } \right]$ nên $x = \frac{\pi }{4}$ và $x = \frac{{7\pi }}{{12}}$. Tổng các nghiệm của phương trình $\cos 2x = \sin \left( {\frac{\pi }{4} – x} \right)$ trên đoạn $\left[ {0;\pi } \right]$ là $\frac{\pi }{4} + \frac{{7\pi }}{{12}} = \frac{{5\pi }}{6}$.

Đáp án: a) Đ, b) S, c) Đ, d) Đ

Câu 29: Cho phương trình: $\sin 4x + \sin 2x = \cos 4x + \cos 2x$.

a) Dùng công thức biến đổi tổng thành tích, vế trái của phương trình đưa về dạng: $\sin 3x\cos x$.

b) Dùng công thức biến đổi tổng thành tích, vế phải của phương trình đưa về dạng: $\cos 3x\cos x$.

c) Nghiệm của phương trình đã cho là nghiệm của phương trình $\cos x = 0$ và phương trình $\sin 3x = \cos 3x$.

d) Nghiệm của phương trình đã cho là: $x = k2\pi $ và $x = \frac{\pi }{{12}} + k\frac{\pi }{3}(k \in \mathbb{Z})$.

Lời giải

Dùng công thức biến đổi tổng thành tích, phương trình đưa về dạng:

$2\sin 3x\cos x = 2\cos 3x\cos x \Leftrightarrow \cos x\left( {\sin 3x – \cos 3x} \right) = 0$

$ \Leftrightarrow \cos x = 0$ hoặc $\sin 3x – \cos 3x = 0$.

Với $\cos x = 0 \Leftrightarrow x = \frac{\pi }{2} + k\pi (k \in \mathbb{Z})$.

Với $\sin 3x – \cos 3x = 0 \Leftrightarrow \sin 3x = \cos 3x$.

+ Nếu $\cos 3x = 0$ thì phương trình đưa về dạng: $\sin 3x = 0$ (vô lí).

+ Với $\cos 3x \ne 0$, phương trình đưa về dạng:

$\tan 3x = 1 \Leftrightarrow 3x = \frac{\pi }{4} + k\pi \Leftrightarrow x = \frac{\pi }{{12}} + k\frac{\pi }{3}(k \in Z).$

Vậy nghiệm của phương trình đã cho là: $x = \frac{\pi }{2} + k\pi $ và $x = \frac{\pi }{{12}} + k\frac{\pi }{3}(k \in \mathbb{Z})$.

Đáp án: a) S, b) S, c) Đ, d) Đ

Câu 30: Hàng ngày mực nước tại một cảng biển lên xuống theo thủy chiều. Chiều cao $h\left( m \right)$ của mực nước theo thời gian $t$(giờ) trong một ngày được cho bởi công thức $h = 14 + 8\sin \left( {\frac{\pi }{{12}}t} \right)$ với $0 \leqslant t \leqslant 24.$

a) Lúc 6 giờ sáng thì chiều cao của mực nước biển là cao nhất

b) Chiều cao của mực nước biển thấp nhất vào lúc 12 giờ

c) Mực nước tại bến cảng cao 18 m vào lúc 2 giờ 10 phút

d) Biết tàu chỉ vào được cảng khi mực nước trong cảng không thấp hơn 18 m. Vậy thời gian tàu vào được cảng là từ 10 giờ sáng hôm trước đến 2 giờ sáng hôm sau.

Lời giải

Ý	a)	b)	c)	d)
Kết quả	Đ	S	Đ	S

+ Do $ – 1 \leqslant \sin \left( {\frac{\pi }{{12}}t} \right) \leqslant 1$ nên $14 – 8 \leqslant 14 + 8\sin \left( {\frac{\pi }{{12}}t} \right) \leqslant 14 + 8$

Hay $6 \leqslant h \leqslant 22.$ Vậy chiều cao của mực nước tại bến cảng cao nhất bằng $22m.$

Khi $\sin \left( {\frac{\pi }{{12}}t} \right) = 1 \Leftrightarrow \frac{\pi }{{12}}t = \frac{\pi }{2} + k2\pi \Leftrightarrow t = 6 + 24k\,\left( {k \in \mathbb{Z}} \right).$

Mà $0 \leqslant t \leqslant 24$ nên $t = 6$. Vậy lúc $6$ giờ sáng thì chiều cao của mực nước biển là cao nhất

+ Chiều cao của mực nước biển tại bến cảng thấp nhất bằng $6m$khi $\sin \left( {\frac{\pi }{{12}}t} \right) = – 1 \Leftrightarrow \frac{\pi }{{12}}t = – \frac{\pi }{2} + k2\pi \Leftrightarrow t = – 6 + 24k\,\left( {k \in \mathbb{Z}} \right).$

Mà $0 \leqslant t \leqslant 24$ nên $t = 18$. Vậy lúc $18$ giờ thì chiều cao của mực nước biển là thấp nhất.

Xét phương trình: $14 + 8\sin \left( {\frac{\pi }{{12}}t} \right) = 18 \Leftrightarrow \sin \left( {\frac{\pi }{{12}}t} \right) = \frac{1}{2}$

$ \Leftrightarrow \left[ \begin{gathered}
\frac{\pi }{{12}}t = \frac{\pi }{6} + k2\pi \hfill \\
\frac{\pi }{{12}}t = \frac{{5\pi }}{6} + k2\pi \hfill \\
\end{gathered} \right. \Leftrightarrow \left[ \begin{gathered}
t = 2 + 24k \hfill \\
t = 10 + 24k \hfill \\
\end{gathered} \right.\,\left( {k \in \mathbb{Z}} \right).$

Mà $0 \leqslant t \leqslant 24$ nên $t \in \left\{ {2;10} \right\}$.

+ Trong khoảng thời gian từ $2$ giờ đến $10$ giờ, mực nước tại bến cảng lớn hơn hoặc bằng $18m.$ Vậy thời gian tàu vào được cảng là từ $2$ giờ đến $10$ giờ.

Đáp án: a) Đ, b) S, c) Đ, d) S.

Câu 31: Cho bất phương trình ${4^{{x^2} + 5}} \geqslant {\left( {\frac{1}{8}} \right)^{x – {x^2}}}$

a) Ta có: $4 = {2^2};\,\frac{1}{8} = {2^{ – 3}}.$

b) Bất phương trình đã cho tương đương với bất phương trình

$2\left( {{x^2} + 50} \right) = – 3\left( {x – {x^2}} \right)$

c) Số nghiệm nguyên của bất phương trình là $6.$

d) Tích nghiệm nguyên lớn nhất và nghiệm nguyên nhỏ nhất của bất phương trình là $ – 4.$

Lời giải

Ý	a)	b)	c)	d)
Kết quả	Đ	Đ	S	S

Ta có:${4^{{x^2} + 5}} \geqslant {\left( {\frac{1}{8}} \right)^{x – {x^2}}} \Leftrightarrow {2^{2\left( {{x^2} + 5} \right)}} \geqslant {2^{ – 3\left( {x – {x^2}} \right)}}$

$ \Leftrightarrow 2\left( {{x^2} + 5} \right) \geqslant – 3\left( {x – {x^2}} \right)$

$ \Leftrightarrow {x^2} – 3x – 10 \leqslant 0 \Leftrightarrow – 2 \leqslant x \leqslant 5$

Vậy phương trình có $8$ nghiệm nguyên. Tích nghiệm lớn nhất và nghiệm nguyên nhỏ nhất của bất phương trình là $ – 10.$

Đáp án: a) Đ, b) Đ, c) S, d) S.

Câu 32: Cho bất phương trình ${\log _{\frac{1}{{3\sqrt 2 }}}}\left( { – {x^2} + 7x + 18} \right) \geqslant – 2.$

a) Ta có: $0 < \frac{1}{{3\sqrt 2 }} < 1.$

b) Bất phương trình đã cho là nghiệm của bất phương trình

$ – {x^2} + 7x + 18 \leqslant {\left( {\frac{1}{{3\sqrt 2 }}} \right)^{ – 2}}$

c) Số nghiệm nguyên của bất phương trình là $2.$

d) Tổng các nghiệm nguyên của bất phương trình là $14.$

Lời giải

Ý	a)	b)	c)	d)
Kết quả	Đ	Đ	S	Đ

Ta có: ${\log _{\frac{1}{{3\sqrt 2 }}}}\left( { – {x^2} + 7x + 18} \right) \geqslant – 2$

$ \Leftrightarrow \left\{ \begin{gathered}
– {x^2} + 7x + 18 \leqslant 18 \hfill \\
– {x^2} + 7x + 18 > 0 \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
\left[ \begin{gathered}
x \leqslant 0 \hfill \\
x \geqslant 7 \hfill \\
\end{gathered} \right. \hfill \\
– 2 < x < 9. \hfill \\
\end{gathered} \right.$

Vậy bất phương trình có nghiệm là: $ – 2 < x \leqslant 0$ hoặc $7 \leqslant x < 9.$

Bất phương trình có $4$ nghiệm nguyên là $ – 1;0;7;8$ và tổng các nghiệm nguyên của bất phương trình là $14.$

Đáp án: a) Đ, b) Đ, c) S, d) Đ.

Câu 33. Mức cường độ âm $L$( đơn vị dB) được tính bởi công thức $L = 10\log \frac{I}{{{{10}^{ – 12}}}}$, trong đó $I$( đơn vị: $W/{m^2}$) là cường độ của âm (Nguồn: R. Larson and B. Edwards, Calculus 10e Cengage). Một người đứng giữa hai loa A và B. Khi loa A bật thì người đó nghe được âm có mức cường độ 80 dB. Khi loa B bật thì nghe được âm có mức cường độ 90 dB. Nếu bật cả hai loa thì cường độ âm tác động vào tai người bằng tổng cường độ âm của hai loa đó.

a) Cường độ âm của loa A là ${10^{80}}{.10^{12}}(W/{m^2})$.

b) Cường độ âm của loa B là ${10^{90}}{.10^{ – 12}}(W/{m^2})$.

c) Cường độ âm tác động vào tai người khi bật cả hai loa là ${10^{170}}{.10^{ – 12}}(W/{m^2})$.

d) Nếu bật cả hai loa thì người đó nghe được âm có mức cường độ là 90,4 dB.

Lời giải

Ý	a)	b)	c)	d)
Kết quả	S	S	S	Đ

Đặt ${L_1} = 80(\;dB),{L_2} = 90(\;dB)$. ${I_1},{I_2}$lần lượt là cường

độ âm của loa $A$ và loa $B$. Ta có:

${L_1} = 10\log \frac{{{I_1}}}{{{{10}^{ – 12}}}}$$ \Rightarrow {I_1} = {10^{\frac{{{L_1}}}{{10}}}} \cdot {10^{ – 12}} = {10^8} \cdot {10^{ – 12}}$.

${L_2} = 10\log \frac{{{I_2}}}{{{{10}^{ – 12}}}}$$ \Rightarrow {I_2} = {10^{\frac{{{L_2}}}{{10}}}} \cdot {10^{ – 12}} = {10^9} \cdot {10^{ – 12}}$

Do đó, ${I_1} + {I_2} = \left( {{{10}^8} + {{10}^9}} \right) \cdot {10^{ – 12}}$.

Vậy:$L = 10\log \frac{{{I_1} + {I_2}}}{{{{10}^{ – 12}}}} = 10 \cdot \log \left( {{{10}^8} + {{10}^9}} \right) \approx 90,4(\;dB)$.

Dạng 3: Câu trắc nghiệm trả lời ngắn

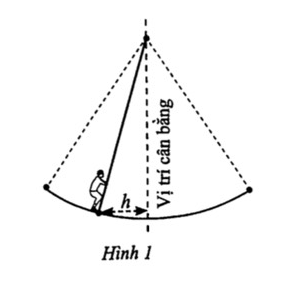
Câu 34. Mức cường Hội Lim ( tỉnh Bắc Ninh) vào mùa xuân thường có trò chơi đánh đu. Khi người chơi đu nhún đều, cây đu sẽ đưa người chơi đu dao động quanh vị trí cân bằng (Hình 1). Nghiên cứu trò chơi này, người ta thấy khoảng cách h (m) từ người chơi đu đến vị trí cân bằng được biểu diễn qua thời gian t (s) ( với $t \geqslant 0$) bởi hệ thức $h = \left| d \right|$ với $d = 3\cos \left[ {\frac{\pi }{3}\left( {2t – 1} \right)} \right]$, trong đó ta quy ước $d > 0$khi vị trí cân bằng ở phía sau lưng người chơi đu và $d < 0$trong trường hợp ngược lại (Nguồn: R. Larson and B. Edwards, Calculus 10e Cengage). Tìm thời điểm đầu tiên mà khoảng cách $h$ là lớn nhất. (Viết kết quả dưới dạng số thập phân).

Lời giải

Trả lời: $t = 0,5\;s$

Do $ – 1 \leqslant \cos \left[ {\frac{\pi }{3}(2t – 1)} \right] \leqslant 1$ nên $ – 3 \leqslant 3\cos \left[ {\frac{\pi }{3}(2t – 1)} \right] \leqslant 3$ hay $ – 3 \leqslant d \leqslant 3$.

Do đó, $0 \leqslant |d| \leqslant 3$. Vậy $h$ lớn nhất bằng 3 khi $|d| = 3$ hay

$\cos \left[ {\frac{\pi }{3}(2t – 1)} \right] = \pm 1 \Leftrightarrow \sin \left[ {\frac{\pi }{3}(2t – 1)} \right] = 0$

$ \Leftrightarrow \frac{\pi }{3}(2t – 1) = k\pi \Leftrightarrow t = \frac{{1 + 3k}}{2} $với $ k \in \mathbb{N}$

Thời điểm đầu tiên mà khoảng cách $h$ lớn nhất là $t = 0,5\;s$ (ứng với $k = 0$ ).

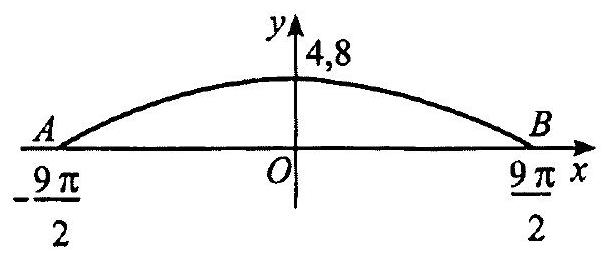
Câu 35. Một cây cầu có dạng cung $AB$của đồ thị hàm số $y = 4,8\cos \frac{x}{9}$ và được mô tả trong hệ trục toạ độ với đơn vị trục là mét như ở Hinh vẽ. Một sà lan chở khối hàng hoá được xếp thành hình hộp chữ nhật với độ cao $3,6m$ so với mực nước sông. Hỏi chiều rộng của khối hàng hoá đó lớn nhất là bao nhiêu mét đề sà lan có thể đi qua được gầm cầu (làm tròn kết quả đến hàng đơn vị)?

Lời giải

Trả lời: 13

Với mỗi điểm $M\left( {x;y} \right)$ nằm trên mặt cầu, khoảng cách từ điểm $M$ đến mặt nước tương ứng với giá trị tung độ $y$ của điểm $M$.

Xét phương trình:$4,8\cos \frac{x}{9} = 3,6 \Leftrightarrow \cos \frac{x}{9} = \frac{3}{4}$

Do $x \in \left[ { – \frac{{9\pi }}{2};\frac{{9\pi }}{2}} \right]$ nên $\frac{x}{9} \in \left[ { – \frac{\pi }{2};\frac{\pi }{2}} \right]$

Từ phương trình $4,8\cos \frac{x}{9} = 3,6 \Leftrightarrow \cos \frac{x}{9} = \frac{3}{4}$ với $\frac{x}{9} \in \left[ { – \frac{\pi }{2};\frac{\pi }{2}} \right]$

Ta có $\frac{x}{9} \approx \pm 0,7227$ Khi đó, $2\left| x \right| \approx 13,0086$

Vậy chiều rộng của khối hàng hoá đó lớn nhất là $13m$ để sà lan có thể đi qua được gầm cầu.

Câu 36. Trong một thí nghiệm, một quả cầu được gắn vào một đầu dây đàn hồi, đầu kia của sợi đây được gắn cố định vào một thanh treo nằm ngang. Sau khi quá cầu được kéo xuống và thả ra, nó bắt đầu di chuyển lên xuống. Khi đó, chiều cao $h\left( {cm} \right)$ của quả cầu so với mặt đất theo thời gian $t\left( s \right)$ được cho bởi công thức $h = 100 – 30\cos 20t$. Tính thời điểm đầu tiên mà quả cầu đạt chiều cao cao nhất kể từ khi quả cầu được thả ra (làm tròn kết quá đến hàng phần trăm).

Lời giải

Trả lời: 0,16

Do $ – 1 \leqslant \cos 20t \leqslant 1 \Rightarrow 70 \leqslant 100 – 30\cos 20t \leqslant 130$

Do đó quả cầu đạt chiều cao cao nhất khi $h = 130$

Khi $\cos 20t = – 1 \Leftrightarrow 20t = \pi + k2\pi \Leftrightarrow t = \frac{\pi }{{20}} + k\frac{\pi }{{10}};k \in \mathbb{N}$

Vậy thời điểm đầu tiên mà quả cầu đạt chiều cao cao nhất kể từ khi quả cầu được thả ra là $t = \frac{\pi }{{20}} \approx 0,16$

Câu 37. Trung bình sau mỗi năm sử dưng, giá trị còn lại của một chiếc ô tô giảm đi $6\% $so với năm trước đó. Giả sử một chiếc ô tô lúc mới mua là $800$ triệu đồng. Hỏi sau ít nhất bao nhiêu năm sử dụng thì giá trị còn lại của chiếc ô tô đó nhỏ hơn $600$triệu đồng (làm tròn kết quả đến hàng đơn vị)?

Lời giải

Trả lời: 5

Gọi $S$là giá trị còn lại của một chiếc ô tô sau $t$ năm sử dụng và

được tính bởi công thức:$S = {S_0}{\left( {0,94} \right)^t}$, trong đó ${S_0}$ là giá trị ban đầu của ô tô.

Xét phương trình: $800.{\left( {0,94} \right)^t} < 600 \Leftrightarrow {\left( {0,94} \right)^t} < 0,75$$ \Leftrightarrow t > {\log _{0,94}}\left( {0,75} \right) \approx 4,65$

Vậy sau khoảng $5$ năm sử dụng thì giá trị còn lại của một chiếc ô tô đó nhỏ hơn $600$ triệu đồng.

Câu 38. Các nhà khoa học xác định được chu kì bán rã của${}_6^{14}C$ là $5730$ năm, tức là sau $5730$ năm thì số nguyên tử ${}_6^{14}C$ giảm đi một nửa. Một cây còn sống có lượng ${}_6^{14}C$ trong cây được duy trì không đổi. Nhưng nếu cây chết thì lượng ${}_6^{14}C$ trong cây phân rã theo chu kì bán rã của nó. Các nhà khảo cổ đã tìm thấy một mẫu gỗ cổ và đo được tỉ lệ phần trăm lượng ${}_6^{14}C$ còn lại trong mẫu gỗ cổ đó so với lúc còn sinh trương là $75\% $. Hỏi mẫu gỗ cổ đó đã chết cách đây bao nhiêu năm (làm tròn kết quả đến hàng đơn vì)?

Lời giải

Trả lời: 2378

Gọi ${m_0}$ là khối lượng của ${}_6^{14}C$ trong cây tại thời điểm cây còn sống $\left( {t = 0} \right)$.

Khi đó, khối lượng $m\left( t \right)$ của ${}_6^{14}C$ trong cây sau khi chết $t$ (năm) được tính bởi công

thức:$m\left( t \right) = {m_o}{\left( {\frac{1}{2}} \right)^{\frac{t}{{5730}}}}$

Theo giả thiết, ta có: $\frac{{m\left( t \right)}}{{{m_o}}} = {m_o}{\left( {\frac{1}{2}} \right)^{\frac{t}{{5730}}}} = 0,75$

Do đó $\frac{t}{{5730}} = {\log _{0,5}}\left( {0,75} \right) \Leftrightarrow t \approx 2378$

Vậy mẫu gỗ cổ đó đã chết cách đây bao nhiêu $2378$ năm

Câu 39. Cô Liên gửi $100$triệu đồng vào ngân hàng theo hình thức lãi kép có kì hạn là $12$ tháng với lãi suất $6\% $ một năm. Giả sử qua các năm thì lãi suất không thay đổi và cô Liên không gửi thêm tiền vào mỗi năm. Hỏi sau ít nhất bao nhiêu năm thì số tiền cô Liên có được cả gốc và lãi nhiều hơn $150$ triệu đồng (làm tròn kết quả đến hàng đơn vị)?

Lời giải

Trả lời: 150

Số tiền sau $t$năm mà cô Liên có là: $S = 100.{\left( {1,06} \right)^t}$

Xét bất phương trình: $100.{\left( {1,06} \right)^t} > 150 \Leftrightarrow t > {\log _{1,06}}\left( {1,5} \right) \approx 6,96$

Vậy sau ít nhất $7$ năm thì số tiền cô Liên có được cả gốc và lãi nhiều hơn $150$ triệu đồng.