Đề Thi HK2 Toán 10 Kết Nối Tri Thức Theo Form Mới Giải Chi Tiết-Đề 6

Đề thi HK2 Toán 10 kết nối tri thức theo form mới giải chi tiết-Đề 6 được soạn dưới dạng file word và PDF gồm 4 trang. Các bạn xem và tải về ở dưới.
Phần 1. Câu trắc nghiệm nhiều phương án chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án đúng nhất.

Câu 1. Hàm số $y = 2{x^2} + 4x – 1$. Khi đó:

A. Hàm số đồng biến trên $\left( { – \infty ; – 2} \right)$ và nghịch biến trên $\left( { – 2; + \infty } \right)$.

B. Hàm số nghịch biến trên $\left( { – \infty ; – 2} \right)$ và đồng biến trên $\left( { – 2; + \infty } \right)$.

C. Hàm số đồng biến trên $\left( { – \infty ; – 1} \right)$ và nghịch biến trên $\left( { – 1; + \infty } \right)$.

D. Hàm số nghịch biến trên $\left( { – \infty ; – 1} \right)$ và đồng biến trên $\left( { – 1; + \infty } \right)$.

Câu 2. Phương trình $\left( {x + 5} \right)\left( {2 – x} \right) = 3\sqrt {{x^2} + 3x} $ có tổng bình phương các nghiệm bằng:

A. 26 . B. 17 . C. 10 . D. 25 .

Câu 3. Cho 2 điểm $A\left( {1; – 4} \right),B\left( {3;2} \right)$. Viết phương trình tổng quát đường trung trực của đoạn thẳng $AB$.

A. $3x + y + 1 = 0$. B. $x + 3y + 1 = 0$. C. $3x – y + 4 = 0$. D. $x + y – 1 = 0$.

Câu 4. Cho đường tròn $\left( C \right):{x^2} + {y^2} – 4x – 2y + 4 – {m^2} = 0$ và $\Delta : x + y – 1 = 0$.

A. Với $m < – 1 \vee m > 1$ thì $\Delta $ cắt $\left( C \right)$. B. $\Delta $ luôn tiếp xúc với $\left( C \right)\forall m$.

C. $\Delta $ đi qua tâm của $\left( C \right)\forall m$. D. Với $m > 3$ thì $\Delta $ không cắt $\left( C \right)$.

Câu 5. Phương trình chính tắc của parabol $\left( P \right)$ có đường chuẩn $x = – 2$ là:

A. ${y^2} = 8x$. B. ${y^2} = 6x$. C. ${y^2} = 4x$. D. ${y^2} = x$.

Câu 6. Có 10 cái bút khác nhau và 8 quyển sách giáo khoa khác nhau. Một bạn học sinh cần chọn 1 cái bút và 1 quyển sách. Hỏi bạn học sinh đó có bao nhiêu cách chọn?

A. 90 B. 70 C. 80 D. 60

Câu 7. Tập hợp tất cả giá trị của $n$ thoả mãn $C_{n + 2}^{n – 1} + C_{n + 2}^n > \frac{5}{2}A_n^2$ là:

A. $n \geqslant 5$. B. $n \geqslant 3$. C. $n \geqslant 2$. D. $n \geqslant 4$.

Câu 8. Số cách chọn ra 3 học sinh trong 10 học sinh bất kì là

A. 120 B. 6 C. 30 D. 720

Câu 9. Tính tổng các hệ số trong khai triển nhị thức Niu-tơn của ${(1 – 2x)^4}$.

A. 1 . B. -1 . C. 81 . D. -81 .

Câu 10. Với $n$ là số nguyên dương, gọi ${a_{3n – 3}}$ là hệ số của ${x^{3n – 3}}$ trong khai triển thành đa thức của $f\left( x \right) = {\left( {{x^2} + 1} \right)^n}{(x + 2)^n}$. Tìm $n$ để ${a_{3n – 3}} = 26n$.

A. $n = 11$. B. $n = 5$. C. $n = 12$. D. $n = 10$.

Câu 11. Gieo một đồng tiền 5 lần. Số phần tử của biến cố B: “Mặt sấp xuất hiện ít nhất một lần” bằng

A. $n\left( B \right) = 31$. B. $n\left( B \right) = 32$. C. $n\left( B \right) = 33$. D. $n\left( B \right) = 34$.

Câu 12. Gieo một con súc sắc. Xác suất để mặt chấm chẵn xuất hiện là:

A. 0,2 . B. 0,3 . C. 0,4 . D. 0,5 .

Phần 2. Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗ ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai

Câu 1. Xét tính đúng, sai của các khẳng định sau:

a) ${x^2} – 7x + 12 < 0$ có tập nghiệm là $S = \left( {3;4} \right)$

b) ${x^2} – 6x + 5 \geqslant 0$ có tập nghiệm là $S = \left( {1;5} \right)$

c) $ – 2{x^2} + 7x – 9 < 0$ có tập nghiệm là $\mathbb{R}$

d) ${x^2} – 6x + 9 \leqslant 0$ có tập nghiệm là $\left\{ 3 \right\}$

Câu 2. Cho ${\left( {1 – \frac{1}{2}x} \right)^5} = {a_0} + {a_1}x + {a_2}{x^2} + {a_3}{x^3} + {a_4}{x^4} + {a_5}{x^5}$.

a) ${a_3} = \frac{5}{2}$

b) ${a_5} = – \frac{1}{{32}}$

c) Hệ số lớn nhất trong tất cả hệ số là $\frac{5}{2}$

d) Tổng ${a_0} + {a_1} + {a_2} + {a_3} + {a_4} + {a_5} = \frac{1}{{16}}$

Câu 3. Cho elip $\left( E \right)$ có dạng $\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1$ $(a > b > 0)$, có một tiêu điểm là ${F_1}\left( { – 5;0} \right)$ và đi qua điểm $P\left( {6;0} \right)$. Khi đó:

a) ${a^2} = 36$

b) ${b^2} = 11$

c) Tiêu cự của elip bằng 5

d) Điểm $C\left( {1;1} \right)$ nằm bên trong elip $\left( E \right)$

Câu 4. Hộp thứ nhất đựng 1 thẻ xanh, 1 thẻ đỏ và 1 thẻ vàng. Hộp thứ hai đựng 1 thẻ xanh và 1 thẻ đỏ. Hộp thứ ba đựng 1 thẻ vàng và 1 thẻ đỏ. Các tấm thẻ có kích thước và khối lượng như nhau. Lần lượt lấy ra ngẫu nhiên từ mỗi hộp một tấm thẻ.

a) Số các kết quả có thể xảy ra của phép thử là $n\left( \Omega \right) = 12$

b) Xác suất của biến cố “Trong 3 thẻ lấy ra có ít nhất 1 thẻ màu đỏ” là: $\frac{5}{7}$

c) Xác suất của biến cố “Trong 3 thẻ lấy ra có nhiều nhất 1 thẻ màu xanh” là: $\frac{5}{7}$

d) Xác suất của biến cố “Trong 3 thẻ lấy ra tất cả đều là màu đỏ” là: $\frac{1}{{12}}$

Phần 3. Câu trả lời ngắn.
Thí sinh trả lời đáp án từ câu 1 đến câu 6.

Câu 1. Ông An muốn làm cái cửa bằng nhôm có dạng nửa hình tròn ở phía trên và phía dưới có dạng hình chữ nhật như hình vẽ. Biết rằng đường kính của nửa hình nửa hình tròn cũng là cạnh phía trên của hình chữ nhật và đường chéo của hình chữ nhật có độ dài 5,2 mét; diện tích của nửa hình tròn bằng $\frac{3}{{10}}$ diện tích của phần hình chữ nhật.

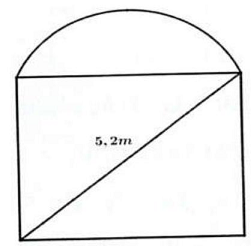
Tính số tiền ông An phải trả cho biết $1{m^2}$ cữa có giá 1300000 đồng (kết quả lấy gần đúng đến hàng phần mười).

Câu 2. Có hai con tàu $A,B$ xuất phát từ hai bến, chuyển động theo đường thẳng ngoài biển. Trên màn hình ra-đa của trạm điều khiển (xem như mặt phẳng tọa độ $Oxy$ với đơn vị trên các trục tính bằng ki-lômét), tại thời điểm $t$ (giờ), vị trí của tàu $A$ có tọa độ được xác định bởi công thức $\left\{ {\begin{array}{*{20}{l}}
{x = 3 – 33t} \\
{y = – 4 + 25t}
\end{array}} \right.$; vị trí tàu $B$ có tọa độ là $\left( {4 – 30t;3 – 40t} \right)$.

Nếu tàu $A$ đứng yên ở vị trí ban đầu, tàu $B$ chạy thì khoảng cách ngắn nhất giữa hai tàu bằng bao nhiêu?

Câu 3. Trong mặt phẳng tọa độ $Oxy$, cho hình thoi $ABCD$ có $AC = 2BD$ và đường tròn tiếp xúc với các cạnh của hình thoi có phương trình $\left( C \right):{x^2} + {y^2} = 4$. Viết phương trình chính tắc của elip $\left( E \right)$ đi qua các đỉnh $A,B,C,D$ của hình thoi với điểm $A$ nằm trên trục $Ox$.

Câu 4. Bạn Phú chọn mật khẩu cho tài khoản Microsoft Teams của mình gồm 8 kí tự đôi một khác nhau, trong đó 2 kí tự đầu tiên là hai chữ cái in thường, 2 kí tự tiếp theo là hai chữ cái in hoa (các chữ cái chọn từ bảng chữ cái Tiếng Anh gồm 26 chữ cái), 3 kí tự tiếp theo là các chữ số và kí tự cuối cùng là một trong các kí tự đặc biệt: @, #. Hỏi bạn Phú có bao nhiêu cách tạo ra một mật khẩu?

Câu 5. Một người có 500 triệu đồng gửi tiết kiệm ngân hàng với lãi suất $7,2\% /$năm. Với giả thiết sau mỗi tháng người đó không rút tiền thì số tiền lãi được nhập vào số tiền ban đầu. Đây được gọi là hình thức lãi kép. Biết số tiền cả vốn lẫn lãi $T$ sau $n$ tháng được tính bởi công thức $T = {T_0}{(1 + r)^n}$, trong đó ${T_0}$ là số tiênn gửi lúc đầu và $r$ là lãi suất của một tháng. Dùng hai số hạng đầu tiên trong khai triển của nhị thức Niu – tơn, tính gần đúng số tiên người đó nhận được (cả gốc lẫn lãi) sau 6 tháng.

Câu 6. Trong một chiếc hộp có 4 viên bi đỏ, 4 viên bi xanh và 2 viên bi vàng. Lấy ra ngẫu nhiên 2 viên bi từ trong hộp. Tính xác suất để lấy ra được 2 viên bi vàng.

ĐÁP ÁN VÀ LỜI GIẢI THAM KHẢO

Phần 1. Câu trắc nghiệm nhiều phương án chọn.

Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thi sinh chỉ chọn một phuơng án đúng nhất.

1D	2B	3B	4A	5A	6C
7C	8A	9A	10B	11A	12D

Câu 1. Hàm số $y = 2{x^2} + 4x – 1$. Khi đó:

A. Hàm số đồng biến trên $\left( { – \infty ; – 2} \right)$ và nghịch biến trên $\left( { – 2; + \infty } \right)$.

B. Hàm số nghịch biến trên $\left( { – \infty ; – 2} \right)$ và đồng biến trên $\left( { – 2; + \infty } \right)$.

C. Hàm số đồng biến trên $\left( { – \infty ; – 1} \right)$ và nghịch biến trên $\left( { – 1; + \infty } \right)$.

D. Hàm số nghịch biến trên $\left( { – \infty ; – 1} \right)$ và đồng biến trên $\left( { – 1; + \infty } \right)$.

Chọn D

Lời giải

Ta có $a = 2 > 0$ (bề lõm parabol hướng lên) và $ – \frac{b}{{2a}} = – 1$.

Hàm số nghịch biến trên khoảng $\left( { – \infty ; – 1} \right)$ và đồng biến trên khoảng $\left( { – 1; + \infty } \right)$.

Câu 2. Phương trình $\left( {x + 5} \right)\left( {2 – x} \right) = 3\sqrt {{x^2} + 3x} $ có tổng bình phương các nghiệm bằng:

A. 26 .

B. 17 .

C. 10 .

D. 25 .

Lời giải

Chọn B

Phương trình tương đương:

$ – {x^2} – 3x + 10 = 3\sqrt {{x^2} + 3x} $ $ \Leftrightarrow – \left( {{x^2} + 3x} \right) + 10 = 3\sqrt {{x^2} + 3x} $.

Đặt $t = \sqrt {{x^2} + 3x} \left( {t \geqslant 0} \right) \Rightarrow {t^2} = {x^2} + 3x$.

Phương trình trở thành: $ – {t^2} + 10 = 3t \Leftrightarrow {t^2} + 3t – 10 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{t = 2\;(n)\;} \\
{t = – 5\;(1)\;}
\end{array}} \right.$.

Với $t = 2$ thì $\sqrt {{x^2} + 3x} = 2 \Leftrightarrow {x^2} + 3x = 4 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 1} \\
{x = – 4}
\end{array}} \right.$.

Tổng bình phương các nghiệm là: ${1^2} + {( – 4)^2} = 17$.

Câu 3. Cho 2 điểm $A\left( {1; – 4} \right),B\left( {3;2} \right)$. Viết phương trình tổng quát đường trung trực của đoạn thẳng $AB$.

A. $3x + y + 1 = 0$.

B. $x + 3y + 1 = 0$.

C. $3x – y + 4 = 0$.

D. $x + y – 1 = 0$.

Chọn B

Lời giải

Gọi $I\left( {2; – 1} \right)$ là trung điểm $AB;\overrightarrow {AB} = \left( {2;6} \right) = 2\left( {1;3} \right)$.

Đường trung trực của đoạn $AB$ đi qua $I$ và nhận $\vec n = \left( {1;3} \right)$ làm vectơ pháp tuyến nên có phương trình tổng quát: $1\left( {x – 2} \right) + 3\left( {y + 1} \right) = 0 \Leftrightarrow x + 3y + 1 = 0$.

Câu 4. Cho đường tròn $\left( C \right):{x^2} + {y^2} – 4x – 2y + 4 – {m^2} = 0$ và $\Delta : x + y – 1 = 0$.

A. Với $m\left\langle { – 1 \vee m} \right\rangle 1$ thì $\Delta $ cắt $\left( C \right)$.

B. $\Delta $ luôn tiếp xúc với $\left( C \right)\forall m$.

C. $\Delta $ đi qua tâm của $\left( C \right)\forall m$.

D. Với $m > 3$ thì $\Delta $ không cắt $\left( C \right)$.

Khẳng định đúng là:

A. A.

B. B và C.

C. D.

D. A và C.

Lời giải

Chọn $A\left( C \right)$ : có tâm $I\left( {2;1} \right),R = \sqrt {{m^2} + 1} $ và $d\left[ {I,\Delta } \right] = \sqrt 2 $

Để $\Delta $ cắt $\left( C \right)$ thì $d\left[ {I,\Delta } \right] < R \Leftrightarrow \sqrt 2 < \sqrt {{m^2} + 1} \Leftrightarrow {m^2} > 1 \Leftrightarrow m < – 1 \vee m > 1$.

Câu 5. Phương trình chính tắc của parabol $\left( P \right)$ có đường chuẩn $x = – 2$ là:

A. ${y^2} = 8x$.

B. ${y^2} = 6x$.

C. ${y^2} = 4x$.

D. ${y^2} = x$.

Lời giải

Chọn A.

$P$ có đường chuẩn $x = – 2 \Rightarrow \frac{p}{2} = 2 \Rightarrow p = 4 \Rightarrow \left( P \right):{y^2} = 8x$.

Câu 6. Có 10 cái bút khác nhau và 8 quyển sách giáo khoa khác nhau. Một bạn học sinh cần chọn 1 cái bút và 1 quyển sách. Hỏi bạn học sinh đó có bao nhiêu cách chọn?

A. 90

B. 70

C. 80

D. 60

Chọn C

Lời giải

Số cách chọn 1 cái bút có 10 cách, số cách chọn 1 quyển sách có 8 cách. Vậy theo quy tắc nhân, số cách chọn 1 cái bút và 1 quyển sách là: $10.8 = 80$ cách.

Câu 7. Tập hợp tất cả giá trị của $n$ thoả mãn $C_{n + 2}^{n – 1} + C_{n + 2}^n > \frac{5}{2}A_n^2$ là:

A. $n \geqslant 5$.

B. $n \geqslant 3$.

C. $n \geqslant 2$.

D. $n \geqslant 4$.

Chọn C

Lời giải

Điều kiện: $n \geqslant 2,n \in \mathbb{N}$.

Ta có: $C_{n + 2}^{n – 1} + C_{n + 2}^n > \frac{5}{2}A_n^2$

$ \Leftrightarrow C_{n + 3}^n > \frac{5}{2}A_n^2 \Leftrightarrow \frac{{\left( {n + 3} \right)!}}{{n!3!}} > \frac{5}{2} \cdot \frac{{n!}}{{\left( {n – 2} \right)!}}$ $ \Leftrightarrow \frac{{\left( {n + 1} \right)\left( {n + 2} \right)\left( {n + 3} \right)}}{6} > \frac{5}{2} \cdot \left( {n – 1} \right)n$

$ \Leftrightarrow {n^3} + 6{n^2} + 11n + 6 > 15{n^2} – 15n$ $ \Leftrightarrow {n^3} – 9{n^2} + 26n + 6 > 0$

$ \Leftrightarrow n\left( {{n^2} – 9n + 26} \right) + 6 > 0$ $ \Leftrightarrow n\left[ {{{\left( {n – \frac{9}{2}} \right)}^2} + \frac{{23}}{4}} \right] + 6 > 0\left( {{\;^*}} \right)$.

Dễ thấy (*) luôn đúng với mọi $n \geqslant 2$.

Vậy nghiệm của bất phương trình là $n \geqslant 2$.

Câu 8. Số cách chọn ra 3 học sinh trong 10 học sinh bất kì là

A. 120

B. 6

C. 30

D. 720

Chọn A

Lời giải

Số cách chọn ra 3 học sinh trong 10 học sinh bất kì là $C_{10}^3 = 120$.

Câu 9. Tính tổng các hệ số trong khai triển nhị thức Niu-tơn của ${(1 – 2x)^4}$.

A. 1 .

B. -1 .

C. 81 .

D. -81 .

Lời giải

Chọn A

Tổng các hệ số trong khai triển nhị thức Niu-tơn của ${(2x – 3)^4}$ chính

là giá trị của biêu thức ${(2x – 3)^4}$ tại $x = 1$. Vậy $S = {(1 – 2 \cdot 1)^4} = 1$.

Câu 10. Với $n$ là số nguyên dương, gọi ${a_{3n – 3}}$ là hệ số của ${x^{3n – 3}}$ trong khai triển thành đa thức của $f\left( x \right) = {\left( {{x^2} + 1} \right)^n}{(x + 2)^n}$. Tìm $n$ để ${a_{3n – 3}} = 26n$.

A. $n = 11$.

B. $n = 5$.

C. $n = 12$.

D. $n = 10$

Chọn B

Lời giải

Yêu cầu $ \Leftrightarrow 3n – \left( {2k + i} \right) = 3n – 3$ $ \Leftrightarrow 2k + i = 3 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{k = i = 1} \\
{k = 0,i = 3}
\end{array}} \right.$.

$ \Rightarrow {a_{3n – 3}} = 2C_n^1C_n^1 + {2^3}C_n^0C_n^3 = 26n \Leftrightarrow n = 5.$

Câu 11. Gieo một đồng tiền 5 lần. Số phần tử của biến cố $B$ : “Mặt sấp xuất hiện ít nhất một lần”?

A. $n\left( B \right) = 31$.

B. $n\left( B \right) = 32$.

C. $n\left( B \right) = 33$.

D. $n\left( B \right) = 34$.

Chọn A

Lời giải

$n\left( \Omega \right) = 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 = 32$. Kết quả 5 lần gieo mà không có lần nào xuất hiện mặt sấp là 1 . Vậy $n\left( B \right) = 32 – 1 = 31$.

Câu 12. Gieo một con súc sắc. Xác suất để mặt chấm chẵn xuất hiện là:

A. 0,2 .

B. 0,3 .

C. 0,4 .

D. 0,5 .

Chon D

Lời giải

$\Omega = \left\{ {1;2;3;4;5;6} \right\}$.

Biến cố xuất hiện mặt chẵn: $A = \left\{ {2;4;6} \right\} \cdot P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{1}{2}$.

Phần 2. Câu trắc nghiệm đúng sai.

Thí sinh trả lời từ câu 1 đến câu 4. Trong mối ý a), b), c), d) ở mỗi câu, thi sinh chọn đúng hoặc sai

Câu 1. Xét tính đúng, sai của các khẳng định sau:

a) ${x^2} – 7x + 12 < 0$ có tập nghiệm là $S = \left( {3;4} \right)$

b) ${x^2} – 6x + 5 \geqslant 0$ có tập nghiệm là $S = \left( {1;5} \right)$

c) $ – 2{x^2} + 7x – 9 < 0$ có tập nghiệm là $\mathbb{R}$

d) ${x^2} – 6x + 9 \leqslant 0$ có tập nghiệm là $\left\{ 3 \right\}$

Lời giải

a) Đúng

b) Sai

c) Đúng

d) Đúng

a) Tam thức $f\left( x \right) = {x^2} – 7x + 12$ có 2 nghiệm là ${x_1} = 3;{x_2} = 4$ hệ số $a = 1 > 0$ nên ta có bảng xét dấu:

Từ bảng xét dấu ta thấy $f\left( x \right) < 0,\forall x \in \left( {3;4} \right)$.

Vậy tập nghiệm của bất phương trình đã cho là $S = \left( {3;4} \right)$.

b) Tam thức $f\left( x \right) = {x^2} – 6x + 5$ có 2 nghiệm là ${x_1} = 1;{x_2} = 5$, hệ số $a = 1 > 0$ nên ta có bảng xét dấu

Từ bảng xét dấu ta thấy $f\left( x \right) > 0,\forall x \in \left( { – \infty ;1} \right) \cup \left( {5; + \infty } \right)$.

Vậy tập nghiệm của bất phương trình đã cho là: $S = \left( { – \infty ;1\left] \cup \right[5; + \infty } \right)$.

c) Tam thức $f\left( x \right) = – 2{x^2} + 7x – 9$ có $\Delta = – 23 < 0$, hệ số $a = – 2 < 0$ nên ta có $f\left( x \right) < 0,\forall x \in \mathbb{R}$.

Vậy tập nghiệm của bất phương trình đã cho là $\mathbb{R}$.

d) Tam thức $f\left( x \right) = {x^2} – 6x + 9$ có $\Delta = 0$, hệ số $a = 1 > 0$ nên ta có bảng xét dấu:

Từ bảng xét dấu ta thấy $f\left( x \right) > 0,\forall x \in \mathbb{R} \setminus \left\{ 3 \right\}$ và $f\left( x \right) = 0 \Leftrightarrow x = 3$.

Vậy tập nghiệm của bất phương trình đã cho là $\left\{ 3 \right\}$.

Câu 2. Cho ${\left( {1 – \frac{1}{2}x} \right)^5} = {a_0} + {a_1}x + {a_2}{x^2} + {a_3}{x^3} + {a_4}{x^4} + {a_5}{x^5}$.

a) ${a_3} = \frac{5}{2}$

b) ${a_5} = – \frac{1}{{32}}$

c) Hệ số lớn nhất trong tất cả hệ số là $\frac{5}{2}$

d) Tổng ${a_0} + {a_1} + {a_2} + {a_3} + {a_4} + {a_5} = \frac{1}{{16}}$

Lời giải

a) Sai

b) Đúng

c) Đúng

d) Sai

${\left( {1 – \frac{1}{2}x} \right)^5} = C_5^0 + C_5^1\left( { – \frac{1}{2}x} \right) + C_5^2{\left( { – \frac{1}{2}x} \right)^2}$ $ + C_5^3{\left( { – \frac{1}{2}x} \right)^3} + C_5^4{\left( { – \frac{1}{2}x} \right)^4} + C_5^5{\left( { – \frac{1}{2}x} \right)^5}$

$ = 1 – \frac{5}{2}x + \frac{5}{2}{x^2} – \frac{5}{4}{x^3} + \frac{5}{{16}}{x^4} – \frac{1}{{32}}{x^5}$

$ = {a_0} + {a_1}x + {a_2}{x^2} + {a_3}{x^3} + {a_4}{x^4} + {a_5}{x^5}$

Suy ra: ${a_0} = 1,{a_1} = – \frac{5}{2},{a_2} = \frac{5}{2},{a_3} = – \frac{5}{4},{a_4} = \frac{5}{{16}},{a_5} = – \frac{1}{{32}}$.

Ta thấy hệ số lớn nhất tìm được là ${a_2} = \frac{5}{2}$.

Thay $x = 1$ vào $\left( * \right)$, ta được: ${\left( {1 – \frac{1}{2}} \right)^5} = {a_0} + {a_1} + {a_2} + {a_3} + {a_4} + {a_5}$.

Vậy ${a_0} + {a_1} + {a_2} + {a_3} + {a_4} + {a_5} = \frac{1}{{32}}$.

Câu 3. Cho elip $\left( E \right)$ có dạng $\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1(a > b > 0)$, có một tiêu điểm là ${F_1}\left( { – 5;0} \right)$ và đi qua điểm $P\left( {6;0} \right)$. Khi đó:

a) ${a^2} = 36$

b) ${b^2} = 11$

c) Tiêu cự của elip bằng 5

d) Điểm $C\left( {1;1} \right)$ nằm bên trong elip $\left( E \right)$

Lời giải

a) Đúng

b) Đúng

c) Sai

d) Đúng

Vì elip $\left( E \right)$ đi qua điểm $P\left( {6;0} \right)$ nên $\frac{{{6^2}}}{{{a^2}}} + \frac{{{0^2}}}{{{b^2}}} = 1 \Rightarrow {a^2} = 36$. Vì elip $\left( E \right)$ có một tiêu điểm là ${F_1}\left( { – 5;0} \right)$ nên $c = 5$ và ${b^2} = {a^2} – {c^2} = 36 – 25 = 11$. Vậy phương trình chính tắc của đường elip $\left( E \right)$ là: $\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{{11}} = 1$.

Câu 4. Hộp thứ nhất đựng 1 thẻ xanh, 1 thẻ đỏ và 1 thẻ vàng. Hộp thứ hai đựng 1 thẻ xanh và 1 thẻ đỏ. Hộp thứ ba đựng 1 thẻ vàng và 1 thẻ đỏ. Các tấm thẻ có kích thước và khối lượng như nhau. Lần lượt lấy ra ngẫu nhiên từ mỗi hộp một tấm thẻ.

a) Số các kết quả có thể xảy ra của phép thử là $n\left( \Omega \right) = 12$

b) Xác suất của biến cố “Trong 3 thẻ lấy ra có ít nhất 1 thẻ màu đỏ” là: $\frac{5}{7}$

c) Xác suất của biến cố “Trong 3 thẻ lấy ra có nhiều nhất 1 thẻ màu xanh” là: $\frac{5}{7}$

d) Xác suất của biến cố “Trong 3 thẻ lấy ra tất cả đều là màu đỏ” là: $\frac{1}{{12}}$

Lời giải

a) Đúng

b) Sai

c) Sai

d) Đúng

a)

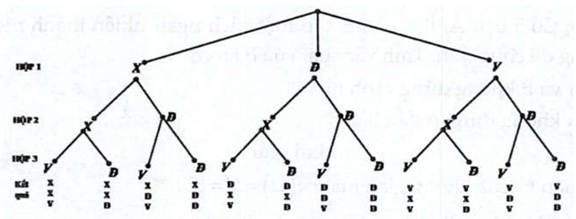
Kí hiệu $X$ là thẻ xanh, thẻ là đỏ và $V$ là thẻ vàng. Các kết quả có thể xảy ra trong 3 lần lấy thẻ từ hộp có thể được mô tả bởi sơ đồ hình cây ở trên.

b) Số các kết quả có thể xảy ra của phép thử là $n\left( \Omega \right) = 12$ Biến cố $A$ : “Trong 3 thẻ lây ra có ít nhất 1 thẻ màu đỏ”. $n\left( A \right) = 10$. Xác suất của biến cố $A:P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{5}{6}$.

c) Số các kết quả có thể xảy ra $n\left( \Omega \right) = 12$

Biến cố B: “Trong 3 thẻ lây ra có nhiêu nhất 1 thẻ màu xanh”. $n\left( B \right) = 10$. Xác suất của biến cố

$B:P\left( B \right) = \frac{{n\left( B \right)}}{{n\left( \Omega \right)}} = \frac{5}{6}$.

d) $P\left( D \right) = \frac{1}{{12}}$

Phần 3. Câu trả lời ngắn.
Thí sinh trả lời đáp án từ câu 1 đến câu 6.

Câu 1. Ông An muốn làm cái cửa bằng nhôm có dạng nửa hình tròn ở phía trên và phía dưới có dạng hình chữ nhật như hình vẽ. Biết rằng đường kính của nửa hình nửa hình tròn cũng là cạnh phía trên của hình chữ nhật và đường chéo của hình chữ nhật có độ dài 5,2 mét; diện tích của nửa hình tròn bằng $\frac{3}{{10}}$ diện tích của phần hình chữ nhật.

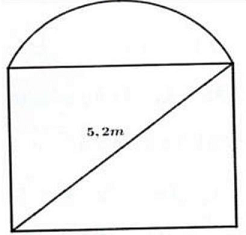
Tính số tiền ông An phải trả cho biết $1{m^2}$ cửa có giá 1300000 đồng (kết quả lấy gần đúng đến hàng phần mười).

Trả lời: 22230000 (đồng).

Lời giải

Gọi $x\left( m \right)(x > 0)$ là đường kính của nửa đường tròn.

Khi đó hình chữ nhật có hai kích thước là $x$ và $\sqrt {5,{2^2} – {x^2}} $.

Diện tích nửa hình tròn là $\frac{{\pi {x^2}}}{8}$ và diện tích hình chữ nhật là $x\sqrt {5,{2^2} – {x^2}} $.

Theo giả thiết ta có: $\frac{{\pi {x^2}}}{8} = \frac{3}{{10}}x\sqrt {5,{2^2} – {x^2}} \Leftrightarrow \frac{5}{{12}}\pi x = \sqrt {5,{2^2} – {x^2}} $

$ \Leftrightarrow \frac{{25}}{{144}}{\pi ^2}{x^2} = \frac{{676}}{{25}} – {x^2}$ $ \Leftrightarrow {x^2}\left( {\frac{{25}}{{144}}{\pi ^2} + 1} \right) = \frac{{676}}{{25}} \Leftrightarrow x \approx 3,2\left( m \right)$.

Diện tích cánh cửa là: $\frac{{\pi \cdot 3,{2^2}}}{8} + 3,2\sqrt {5,{2^2} – 3,{2^2}} \approx 17,1\left( {\;{m^2}} \right)$.

Do đó số tiên ông An phải trả là: $1300000 \cdot 17,1 = 22230000$ (đồng).

Câu 2. Có hai con tàu $A,B$ xuất phát từ hai bến, chuyển động theo đường thẳng ngoài biển. Trên màn hình ra-đa của trạm điều khiển (xem như mặt phẳng tọa độ $Oxy$ với đơn vị trên các trục tính bằng ki-lômét), tại thời điểm $t$ (giờ), vị trí của tàu $A$ có tọa độ được xác định bởi công thức $\left\{ {\begin{array}{*{20}{l}}
{x = 3 – 33t} \\
{y = – 4 + 25t}
\end{array}} \right.$; vị trí tàu $B$ có tọa độ là $\left( {4 – 30t;3 – 40t} \right)$.

Nếu tàu $A$ đứng yên ở vị trí ban đầu, tàu $B$ chạy thì khoảng cách ngắn nhất giữa hai tàu bằng bao nhiêu? Trả lời: $3,4\left( {\;km} \right)$

Lời giải

Khi tàu $A$ đứng yên, vị trí ban đầu của nó có tọa độ $P\left( {3; – 4} \right)$; vị trí tàu $B$ ứng với thời gian $t$ là $Q\left( {4 – 30t;3 – 40t} \right)$;

$PQ = \sqrt {{{(1 – 30t)}^2} + {{(7 – 40t)}^2}} = \sqrt {2500{t^2} – 620t + 50} $.

Đoạn $PQ$ ngắn nhất ứng với $t = – \frac{b}{{2a}} = \frac{{620}}{{2.2500}} = \frac{{31}}{{250}} = 0,124$ (giây).

Khi đó : $P{Q_{min}} = \sqrt {2500 \cdot {{(0,124)}^2} – 620 \cdot \left( {0,124} \right) + 50} $$ = \frac{{17}}{5} = 3,4\left( {\;km} \right)$.

Câu 3. Trong mặt phẳng tọa độ $Oxy$, cho hình thoi $ABCD$ có $AC = 2BD$ và đường tròn tiếp xúc với các cạnh của hình thoi có phương trình $\left( C \right):{x^2} + {y^2} = 4$. Viết phương trình chính tắc của elip $\left( E \right)$ đi qua các đỉnh $A,B,C,D$ của hình thoi với điểm $A$ nằm trên trục $Ox$.

Trả lời: $\frac{{{x^2}}}{{20}} + \frac{{{y^2}}}{5} = 1$

Lời giải

Giả sử phương trình elip $\left( E \right)$ là $\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1(a > b > 0)$.

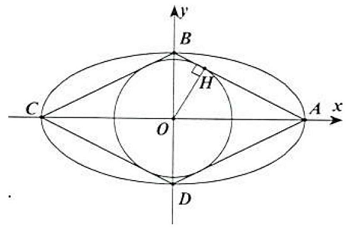
Đường tròn $\left( C \right):{x^2} + {y^2} = 4$ có tâm $O\left( {0;0} \right)$ và bán kính $R = 2$.

Vì $\left( C \right)$ tiếp xúc với các cạnh của hình thoi và $A \in Ox$ nên $C \in Ox$ và $B,D \in Oy$.

Các điểm $A,B,C,D \in \left( E \right)$ nên $A,B,C,D$ là các đỉnh của $\left( E \right)$.

$A,B \in \left( E \right) \Rightarrow A\left( {a;0} \right),B\left( {0;b} \right) \Rightarrow OA = a,OB = b$.

Vì $OA = 2OB$ nên $a = 2b$.

Kẻ $OH \bot AB\left( {H \in AB} \right)$.

Ta có $OH = R = 2$.

Tam giác $ABO$ vuông tại $O$ có $\frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} \Leftrightarrow \frac{1}{4} = \frac{1}{{{a^2}}} + \frac{4}{{{a^2}}}$$ \Leftrightarrow {a^2} = 20 \Rightarrow {b^2} = 5$.

Vậy phương trình $\left( E \right)$ là $\frac{{{x^2}}}{{20}} + \frac{{{y^2}}}{5} = 1$.

Câu 4. Bạn Phú chọn mật khẩu cho tài khoản Microsoft Teams của mình gồm 8 kí tự đôi một khác nhau, trong đó 2 kí tự đầu tiên là hai chữ cái in thường, 2 kí tự tiếp theo là hai chữ cái in hoa (các chữ cái chọn từ bảng chữ cái Tiếng Anh gồm 26 chữ cái), 3 kí tự tiếp theo là các chữ số và kí tự cuối cùng là một trong các kí tự đặc biệt:@,#,. Hỏi bạn Phú có bao nhiêu cách tạo ra một mật khẩu?

Trả lời: 912600000

Lời giải

Có 26 chữ cái và 10 chữ số. Chọn 2 kí tự đầu tiên là chữ cái in thường nên ta có $A_{26}^2$ cách chọn.

Chọn 2 kí tự tiếp theo là chữ cái in hoa nên ta có $A_{26}^2$ cách chọn.

Chọn 3 kí tự tiếp theo là chữ số trong 10 chữ số nên có $A_{10}^3$ cách chọn.

Chọn 1 kí tự cuối cùng có 3 cách.

Vậy ta có $3{\left( {A_{26}^2} \right)^2}A_{10}^3 = 912600000$ cách để bạn Phú tạo ra một mật khẩu.

Câu 5. Một người có 500 triệu đồng gửi tiết kiệm ngân hàng với lãi suất 7,2%/năm. Với giả thiết sau mỗi tháng người đó không rút tiền thì số tiền lãi được nhập vào số tiền ban đầu. Đây được gọi là hình thức lãi kép. Biết số tiền cả vốn lẫn lãi $T$ sau $n$ tháng được tính bởi công thức $T = {T_0}{(1 + r)^n}$, trong đó ${T_0}$ là số tiênn gửi lúc đầu và $r$ là lãi suất của một tháng. Dùng hai số hạng đầu tiên trong khai triển của nhị thức Niu – tơn, tính gần đúng số tiên người đó nhận được (cả gốc lẫn lãi) sau 6 tháng.

Trả Lời: 518000000 đồng.

Lời giải

Lãi suất của một tháng $r = \frac{{7,2}}{{12}}\% = 0,6\% $ / tháng.

Ta có: $T = {T_0}{(1 + r)^n}$.

Suy ra: $T = {500.10^6}{(1 + 0,006)^6} \approx {500.10^6}\left( {C_6^0 + C_6^1 \cdot 0,006} \right) \approx 518000000$ đồng.

Vậy: sau 6 tháng người đó nhận được hơn 518000000 đồng.

Câu 6. Trong một chiếc hộp có 4 viên bi đỏ, 4 viên bi xanh và 2 viên bi vàng. Lấy ra ngẫu nhiên 2 viên bi từ trong hộp. Tính xác suất để lấy ra được 2 viên bi vàng.

Trả Lời: $\frac{1}{{45}}$

Số viên bi có trong hộp là: $4 + 4 + 2 = 10$ (viên bi).

Lời giải

Lây ra ngẫu nhiên 2 viên bi từ hộp mà không quan trọng thứ tự nên số phần tử của không gian mẫu là: $n\left( \Omega \right) = C_{10}^2 = 45$.

Gọi $E$ là biến cố lấy được hai viên bi vàng. Vì chỉ có một cách lấy ra được hai viên bi vàng từ hộp nên ta có $n\left( E \right) = 1$. Vậy xác suất của biến cố $E$ là: $P\left( E \right) = \frac{{n\left( E \right)}}{{n\left( \Omega \right)}} = \frac{1}{{45}}$.