Giải Chi Tiết Đề Tham Khảo Môn Toán Tốt Nghiệp THPT 2024 Bộ GD&ĐT

Giải chi tiết đề tham khảo môn Toán tốt nghiệp THPT 2024 của Bộ GD&ĐT được soạn dưới dạng file word và PDF gồm 7 trang. Các bạn xem và tải về ở dưới.

BỘ GIÁO DỤC VÀ ĐÀO TẠO ĐỀ THI THAM KHẢO (Đề thi có 05 trang)

KÌ THI TỐT NGHIỆP THPT NĂM 2024 Bài thi: TOÁN Thời gian làm bài: 90 phút, không kể thời gian phát đề

Họ, tên thí sinh: ……………………………………………………………

Số báo danh: ……………………………………………………………….

Câu 1: Cho hàm số $f\left( x \right)$ có bảng biến thiên như sau:

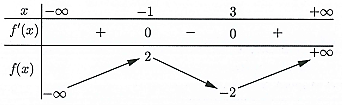
Giá trị cực tiểu của hàm số đã cho bằng

A. 3. B. -2 . C. 2 . D. -1 .

Lời giải

Chọn B

Câu 2: Cho hàm số $f\left( x \right) = 5 – 6{x^2}$. Khẳng định nào dưới đây đúng?

A. $\mathop \smallint \nolimits f\left( x \right)dx = 5 – 2{x^3} + C$. B. $\mathop \smallint \nolimits f\left( x \right)dx = 5x – 2{x^3} + C$.

C. $\mathop \smallint \nolimits f\left( x \right)dx = 5x – 6{x^3} + C$. D. $\mathop \smallint \nolimits f\left( x \right)dx = 5 – 3{x^3} + C$.

Lời giải

Chọn B

Câu 3: Tập nghiệm của phương trình $lo{g_3}\left( {{x^2} – 7} \right) = 2$ là

A. $\left\{ { – 4;4} \right\}$. B. $\left\{ 4 \right\}$. C. $\left\{ 2 \right\}$. D. $\left\{ {16} \right\}$.

Lời giải

$lo{g_3}\left( {{x^2} – 7} \right) = 2 \Leftrightarrow {x^2} – 7 = {3^2} \Leftrightarrow {x^2} = 16 \Leftrightarrow \left[ \begin{gathered}
x = 4 \hfill \\
x = – 4 \hfill \\
\end{gathered} \right.$

Chọn A

Câu 4: Trong không gian $Oxyz$, cho hai điểm $A\left( {1;1; – 2} \right)$ và $B\left( {3; – 1;2} \right)$. Tọa độ của vectơ $\overrightarrow {AB} $ là

A. $\left( {2; – 2;4} \right)$. B. $\left( {2;0;0} \right)$. C. $\left( {1; – 1;2} \right)$. D. $\left( { – 2;2; – 4} \right)$.

Lời giải

$\overrightarrow {AB} = \left( {{x_B} – {x_A};{y_B} – {y_A};{z_B} – {z_A}} \right) = \left( {2; – 2;4} \right)$

Chọn A

Câu 5: Cho hàm số $y = \frac{{ax + b}}{{cx + d}}\left( {a,b,c,d \in \mathbb{R}} \right)$ có đồ thị là đường cong trong hình bên. Tiệm cận ngang của đồ thị hàm số đã cho có phương trình là

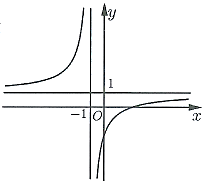
A. $y = 0$. B. $y = 2$.

C. $y = – 1$. D. $y = 1$.

Lời giải

Chọn D

Câu 6: Hàm số nào dưới đây có bảng biến thiên như sau?

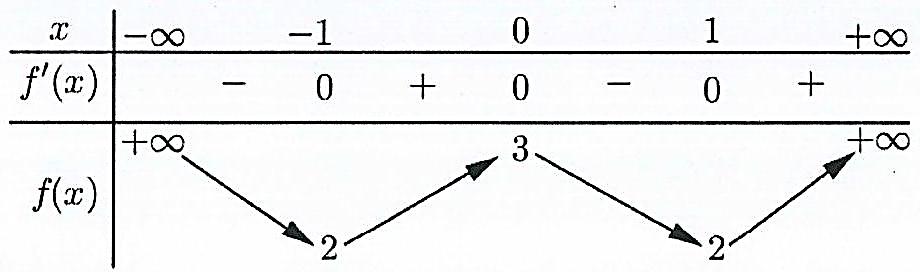
A. $y = – 2{x^4} + 4{x^2} + 1$. B. $y = {x^3} – 4{x^2} – 2$.

C. $y = {x^4} – 2{x^2} + 3$. D. $y = \frac{{2x – 1}}{{x – 1}}$.

Lời giải

+ Bảng biến thiên có dạng của đồ thị hàm số trùng phương.

+ Trên $\left( {1; + \infty } \right)$ hàm số đồng biến nên $a > 0$.

Chọn C

Câu 7: Tập xác định của hàm số $y = {(x + 1)^{\sqrt 2 }}$ là

A. $\mathbb{R}$. B. $\left( {0; + \infty } \right)$. C. $\left( { – 1; + \infty } \right)$. D. $\mathbb{R} \setminus \left\{ { – 1} \right\}$.

Lời giải

$\alpha = \sqrt 2 $ không nguyên nên hàm số xác định khi $x + 1 > 0 \Leftrightarrow x > – 1$

Chọn C

Câu 8: Trong không gian $Oxyz$, cho đường thẳng $d:\frac{{x – 1}}{2} = \frac{y}{1} = \frac{{z + 2}}{{ – 3}}$. Vectơ nào dưới đây là một vectơ chỉ phương của $d$ ?

A. $\overrightarrow {{u_2}} = \left( {1;0; – 2} \right)$. B. $\overrightarrow {{u_1}} = \left( {2;1; – 3} \right)$. C. $\overrightarrow {{u_3}} = \left( {2;1;3} \right)$. D. $\overrightarrow {{u_4}} = \left( {1;0;2} \right)$.

Lời giải

Chọn B

Câu 9: Điểm $M$ trong hình bên là điểm biểu diễn của số phức nào dưới đây?

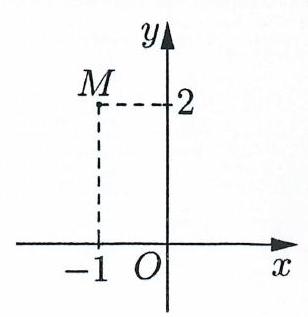
A. $2 + i$. B. $ – 1 + 2i$. C. $2 – i$. D. $ – 1 – 2i$.

Lời giải

Chọn B

Câu 10: Trong không gian $Oxyz$, cho mặt cầu $\left( S \right)$ có tâm $I\left( {1; – 2;1} \right)$ và bán kính $R = 5$. Phương trình của $\left( S \right)$ là

A. ${(x – 1)^2} + {(y + 2)^2} + {(z – 1)^2} = 25$. B. ${(x + 1)^2} + {(y – 2)^2} + {(z + 1)^2} = 25$.

C. ${(x – 1)^2} + {(y + 2)^2} + {(z – 1)^2} = 5$. D. ${(x + 1)^2} + {(y – 2)^2} + {(z + 1)^2} = 5$.

Lời giải

Chọn A

Câu 11: Với $a$ là số thực dương tùy ý, $lo{g_2}{a^{\frac{1}{3}}}$ bằng

A. $\frac{3}{2}lo{g_2}a$. B. $3lo{g_2}a$. C. $\frac{1}{3}lo{g_2}a$. D. $\frac{2}{3}lo{g_2}a$.

Lời giải

Chọn C

Câu 12: Cho hàm số bậc bốn $y = f\left( x \right)$ có đồ thị là đường cong trong hình bên. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

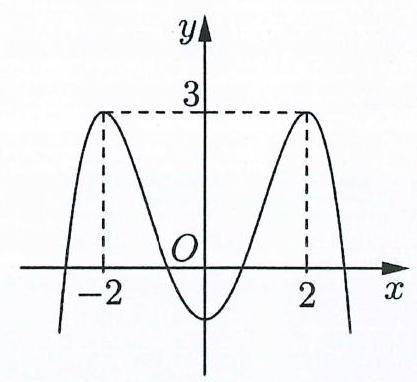
A. $\left( { – 2;2} \right)$. B. $\left( { – \infty ;2} \right)$.

C. $\left( { – 2;0} \right)$. D. $\left( {0;2} \right)$.

Lời giải

Chọn C

Câu 13: Cho khối lăng trụ có diện tích đáy bằng $5{a^2}$ và chiều cao bằng $6a$. Thể tích của khối lăng trụ đã cho bằng

A. $15{a^3}$. B. $5{a^3}$. C. $10{a^3}$. D. $30{a^3}$.

Lời giải

$v = \beta .h = 5{a^2}.6a = 30{a^3}$

Chọn D

Câu 14: Tập nghiệm của bất phương trình ${2^x} < 5$ là

A. $\left( { – \infty ;lo{g_2}5} \right]$. B. $\left( { – \infty ;lo{g_2}5} \right)$. C. $\left( { – \infty ;lo{g_5}2} \right]$. D. $\left( { – \infty ;lo{g_5}2} \right)$.

Lời giải

Chọn B

Câu 15: Hàm số nào dưới đây nghịch biến trên khoảng $\left( {0; + \infty } \right)$?

A. $y = lnx$. B. $y = lo{g_3}x$. C. $y = logx$. D. $y = lo{g_{\frac{1}{3}}}x$.

Lời giải

Do cơ số $a = \frac{1}{3} < 1$ nên hàm số $y = lo{g_{\frac{1}{3}}}x$ nghịch biến trên khoảng $\left( {0; + \infty } \right)$

Chọn D

Câu 16: Trong không gian $Oxyz$,vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng $\left( {Oxy} \right)$?

A. $\vec n = \left( {1;1;0} \right)$. B. $\overrightarrow j = \left( {0;1;0} \right)$. C. $\vec \imath = \left( {1;0;0} \right)$. D. $\vec k = \left( {0;0;1} \right)$.

Lời giải

Chọn D

Câu 17: Cho hàm số $y = f\left( x \right)$ có đạo hàm $f’\left( x \right) = \left( {x + 1} \right)\left( {x – 1} \right),\forall x \in \mathbb{R}$. Số điểm cực trị của hàm số đã cho là

A. 1 . B. 4 . C. 3. D. 2 .

Lời giải

Chọn D

Câu 18: Nếu $\int\limits_1^2 {f\left( x \right)dx = 3} $ và $\int\limits_1^2 {g\left( x \right)dx = 5} $ thì $\int\limits_1^2 {\left( {f\left( x \right) – g\left( x \right)} \right)dx} $ bằng

A. 2 . B. -2 . C. 8. D. $\frac{3}{5}$.

Lời giải

Chọn B

Câu 19: Nếu $\int\limits_{ – 1}^2 {f\left( x \right)dx = 3} $ thì $\int\limits_2^{ – 1} {f\left( x \right)dx} $ bằng

A. 3 . B. -3 . C. 1. D. -1 .

Lời giải

Chọn B

Câu 20: Cho khối chóp có diện tích đáy bằng $7{a^2}$ và chiều cao bằng $9a$. Thể tích của khối chóp đã cho bằng

A. $9{a^3}$. B. $21{a^3}$. C. $84{a^3}$. D. $63{a^3}$.

Lời giải

Chọn B

Câu 21: Cho hai số phức ${z_1} = 1 – 3i$ và ${z_2} = – 4 + i$. Số phức ${z_1} + {z_2}$ bằng

A. $ – 3 – 3i$. B. $3 – 4i$. C. $3 – 2i$. D. $ – 3 – 2i$.

Lời giải

Chọn D

Câu 22: Cho hình nón có bán kính đáy $r$, chiều cao $h$ và độ dài đường sinh $l$. Khẳng định nào dưới đây đúng?

A. $l = \sqrt {h + r} $. B. $l = \sqrt {{h^2} + {r^2}} $. C. $l = hr$. D. $l = {h^2} + {r^2}$.

Lời giải

Chọn B

Câu 23: Có bao nhiêu cách xếp 5 học sinh ngồi vào một dãy gồm 5 chiếc ghế sao cho mỗi chiếc ghế có đúng một học sinh ngồi?

A. 600 . B. 120. C. 3125 . D. 25 .

Lời giải

Số cách xếp là $5! = 120$

Chọn B

Câu 24: Hàm số $F\left( x \right) = {e^{2x}}$ là một nguyên hàm của hàm số nào dưới đây?

A. ${f_4}\left( x \right) = \frac{1}{2}{e^{2x}}$. B. ${f_1}\left( x \right) = {e^{2x}}$. C. ${f_2}\left( x \right) = {e^{{x^2}}}$. D. ${f_3}\left( x \right) = 2{e^{2x}}$.

Lời giải

Chọn D

Câu 25: Cho hàm số $y = \frac{{ax + b}}{{cx + d}}\left( {a,b,c,d \in \mathbb{R}} \right)$ có đồ thị là đường cong trong hình bên. Số giao điểm của đồ thị hàm số đã cho và trục tung là

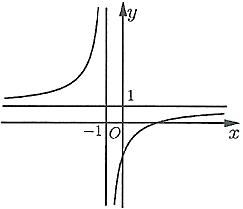
A. 2 . B. 0 . C. 1 . D. 3 .

Lời giải

Chọn C

Câu 26: Cho hình trụ có bán kính đáy bằng $r$ và diện tích xung quanh bằng $S$. Chiều cao của hình trụ đã cho bằng

A. $\frac{S}{{2\pi r}}$. B. $\frac{S}{{\pi r}}$. C. $\frac{{2S}}{{\pi r}}$. D. $\frac{S}{{2r}}$.

Lời giải

Chọn A

Câu 27: Cho cấp số cộng $\left( {{u_n}} \right)$ với ${u_1} = 3$ và ${u_2} = 7$. Công sai của cấp số cộng đã cho bằng

A. $\frac{7}{3}$. B. $\frac{3}{7}$. C. -4 . D. 4 .

Lời giải

Công sai $d = {u_2} – {u_1} = 7 – 3 = 4$

Chọn D

Câu 28: Số phức $z = 4 – 5i$ có phần ảo bằng

A. -5 . B. -4 . C. $ – 5i$. D. 4 .

Lời giải

Chọn A

Câu 29: Cho số phức $z = 3 – i$, phần thực của số phức $\left( {1 – i} \right)\bar z$ bằng

A. 4 . B. 2 . C. -4 . D. -2 .

Lời giải

$\left( {1 – i} \right)\bar z = \left( {1 – i} \right)\left( {3 + i} \right) = 3 + i – 3i – {i^2} = 4 – 2i$

Chọn A

Câu 30: Cho hình lập phương $ABCD.A’B’C’D’$ (tham khảo hình bên). Góc giữa hai đường thẳng $CD$ và $AB’$ bằng

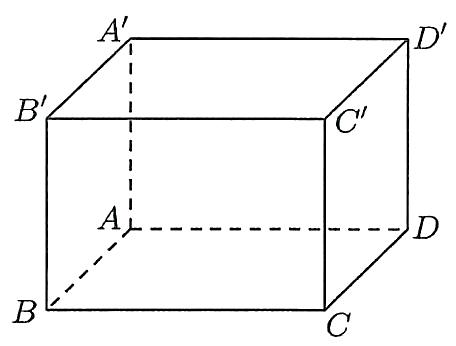
A. ${90^ \circ }$.

B. ${60^ \circ }$.

C. ${30^ \circ }$.

D. ${45^ \circ }$.

Lời giải

Ta có: $DC’//AB’$ nên $\left( {\widehat {CD;AB’}} \right) = \left( {\widehat {CD;DC’}} \right) = \widehat {CDC’} = {45^0}$

Chọn D

Câu 31: Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh bằng $a,SA$ vuông góc với mặt phẳng $\left( {ABCD} \right)$ và $SA = \frac{{\sqrt 3 a}}{3}$. Khoảng cách từ điểm $A$ đến mặt phẳng $\left( {SCD} \right)$ bằng

A. $\frac{a}{2}$. B. $a$. C. $\frac{{\sqrt 3 a}}{3}$. D. $\frac{{\sqrt {14} a}}{7}$.

Lời giải

Kẻ $AH \bot SD$ tại $H$

Ta có: $d(A;(SCD) = AH$

$\frac{1}{{A{H^2}}} = \frac{1}{{A{S^2}}} + \frac{1}{{A{D^2}}} = \frac{1}{{\frac{{{a^2}}}{3}}} + \frac{1}{{{a^2}}} = \frac{4}{{{a^2}}}$

$ \Rightarrow A{H^2} = \frac{{{a^2}}}{4} \Rightarrow AH = \frac{a}{2}$

Chọn A

Câu 32: Cho hàm số $y = f\left( x \right)$ có đạo hàm $f’\left( x \right) = \left( {x – 1} \right)\left( {x – 3} \right),\forall x \in \mathbb{R}$. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

A. $\left( {0;3} \right)$. B. $\left( {3; + \infty } \right)$. C. $\left( { – \infty ;2} \right)$. D. $\left( {1;3} \right)$.

Lời giải

Chọn D

Câu 33: Từ một hộp chứa 12 viên bi gồm 3 viên bi đỏ, 4 viên bi xanh và 5 viên bi vàng, lấy ngẫu nhiên đồng thời 4 viên bi. Xác suất để trong bốn viên bi được lấy có ít nhất một viên bi đỏ bằng

A. $\frac{{13}}{{55}}$. B. $\frac{{41}}{{55}}$. C. $\frac{{14}}{{55}}$. D. $\frac{{42}}{{55}}$.

Lời giải

Chọn B

$n(\Omega ) = C_{12}^4$

Gọi $A$ là biến cố “có ít nhất một viên bi đỏ”.

Suy ra $\overline A $ là biến cố “không có viên bi đỏ”.

$n\left( {\overline A } \right) = C_9^4 \Rightarrow P\left( {\overline A } \right) = \frac{{C_9^4}}{{C_{12}^4}} = \frac{{14}}{{55}}$

$ \Rightarrow P\left( A \right) = 1 – P\left( {\overline A } \right) = 1 – \frac{{14}}{{55}} = \frac{{41}}{{55}}$

Câu 34: Nếu $\int\limits_{ – 1}^2 {f\left( x \right)dx = 4} $ thì $\int\limits_{ – 1}^2 {\left( {3 – f\left( x \right)} \right)dx} $ bằng

A. 7 . B. 13. C. 5 . D. -1 .

Lời giải

Chọn C

Câu 35: Giá trị lớn nhất của hàm số $f\left( x \right) = – {x^4} + 6{x^2} – 4$ bằng

A. $ – \sqrt 3 $. B. -4 . C. 5 . D. $\sqrt 3 $.

Lời giải

Chọn C

Câu 36: Với $a$ là số thực dương tùy ý, $lo{g_2}\left( {32{a^4}} \right)$ bằng

A. $5 – 4lo{g_2}a$. B. $5 + 4a$. C. $5 – 4a$. D. $5 + 4lo{g_2}a$.

Lời giải

Chọn D

Câu 37: Trong không gian $Oxyz$, mặt cầu có tâm $I\left( {4;0;0} \right)$ và đi qua điểm $M\left( {0; – 3;0} \right)$ có phương trình là

A. ${(x – 4)^2} + {y^2} + {z^2} = 5$. B. ${(x + 4)^2} + {y^2} + {z^2} = 5$.

C. ${(x + 4)^2} + {y^2} + {z^2} = 25$. D. ${(x – 4)^2} + {y^2} + {z^2} = 25$.

Lời giải

Chọn D

Câu 38: Trong không gian $Oxyz$, cho ba điểm $A\left( { – 1;0;1} \right),B\left( {1;0;2} \right)$ và $C\left( {3;2;3} \right)$. Đường thẳng đi qua $A$ và song song với $BC$ có phương trình là

A. $\left\{ {\begin{array}{*{20}{l}}
{x = 2 – t} \\
{y = 2} \\
{z = 1 + t}
\end{array}} \right.$ B. $\left\{ {\begin{array}{*{20}{l}}
{x = – 1 + 4t} \\
{y = 2t} \\
{z = 1 + 5t}
\end{array}} \right.$. C. $\left\{ {\begin{array}{*{20}{l}}
{x = – 1 + 2t} \\
{y = 2t} \\
{z = 1 + t}
\end{array}} \right.$. D. $\left\{ {\begin{array}{*{20}{l}}
{x = 4 + 2t} \\
{y = 2 + 2t} \\
{z = 5 + t}
\end{array}} \right.$

Lời giải

Chọn C

Câu 39: Cho $a$ và $b$ là hai số thực dương phân biệt, khác 1 và thỏa mãn $log_a^2\left( {{a^2}b} \right).lo{g_a}\frac{b}{a} + 4 = 0$. Giá trị của $lo{g_b}a$ bằng

A. -3 . B. 3 . C. $\frac{1}{3}$. D. $ – \frac{1}{3}$.

Lời giải

$log_a^2\left( {{a^2}b} \right) \cdot lo{g_a}\frac{b}{a} + 4 = 0 $
$\Leftrightarrow {\left( {lo{g_a}\left( {{a^2}b} \right)} \right)^2} \cdot \left( {lo{g_a}b – 1} \right) + 4 = 0 $
$\Leftrightarrow {\left( {2 + lo{g_a}b} \right)^2}\left( {lo{g_a}b – 1} \right) + 4 = 0$
$ \Leftrightarrow \left( {4 + 4lo{g_a}b + log_a^2b} \right)\left( {lo{g_a}b – 1} \right) + 4 = 0$
$ \Leftrightarrow log_a^3b + 3log_a^2b = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{lo{g_a}b = 0} \\
{lo{g_a}b = – 3 \Leftrightarrow \frac{1}{{lo{g_b}a}} = – 3}
\end{array}} \right.$

$ \Leftrightarrow lo{g_b}a = – \frac{1}{3}$

Chọn D

Câu 40: Có bao nhiêu giá trị nguyên của tham số $m$ thuộc đoạn $\left[ {1;20} \right]$ sao cho ứng với mỗi $m$, hàm số $y = \frac{{ – {x^2} + 3x – m – 1}}{{3x – m}}$ đồng biến trên khoảng $\left( {2;3} \right)$ ?

A. 17. B. 14 . C. 15. D. 13.

Lời giải

Điều kiện: $x \ne \frac{m}{3}$.

Ta có $y’ = \frac{{ – 3{x^2} + 2mx + 3}}{{{{(3x – m)}^2}}}$.

Hàm số $y = \frac{{ – {x^2} + 3x – m – 1}}{{3x – m}}$ đồng biến trên khoảng $\left( {2;3} \right)$

$ \Leftrightarrow \frac{{ – 3{x^2} + 2mx + 3}}{{{{(3x – m)}^2}}} \geqslant 0;\forall x \in \left( {2;3} \right)$ $ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{ – 3{x^2} + 2mx + 3 \geqslant 0;\forall x \in \left( {2;3} \right)\,\,\,(1)} \\
{\frac{m}{3} \notin \left( {2;3} \right)\,\,\,(2)}
\end{array}} \right.$

Ta có:

$\left( 1 \right) \Leftrightarrow 2m \geqslant 3x – \frac{3}{x} = g\left( x \right),\forall x \in \left( {2;3} \right)$.

Mà $g’\left( x \right) = 3 + \frac{3}{{{x^2}}} > 0,\forall x \in \left( {2;3} \right) \Rightarrow g\left( x \right)$ luôn đồng biến frên $\left( {2;3} \right)$.

Do đó $2m \geqslant 3x – \frac{3}{x} = g\left( x \right),\forall x \in \left( {2;3} \right) \Leftrightarrow 2m \geqslant g\left( 3 \right) \Leftrightarrow 2m \geqslant 8 \Leftrightarrow m \geqslant 4$.

$\left( 2 \right)$$ \Leftrightarrow \left[ \begin{gathered}
\frac{m}{3} \geqslant 3 \hfill \\
\frac{m}{3} \leqslant 2 \hfill \\
\end{gathered} \right. \Leftrightarrow \left[ \begin{gathered}
m \geqslant 9 \hfill \\
m \leqslant 6 \hfill \\
\end{gathered} \right.$

Kết hợp hai điều kiện ta được $\left[ {\begin{array}{*{20}{l}}
{m \geqslant 9} \\
{4 \leqslant m \leqslant 6}
\end{array}} \right.$.

Vi $m \in \mathbb{Z}$ nên $m \in \left\{ {4;5;6;9;10; \ldots ;20} \right\}$.

Vậy có 15 số nguyên $m$ thỏa mãn.

Câu 41: Xét $f\left( x \right) = a{x^4} + b{x^2} + c(a,b,c \in \mathbb{R},a > 0)$ sao cho đồ thị hàm số $y = f\left( x \right)$ có ba điểm cực trị là $A,B$ và $C\left( {1; – \frac{3}{5}} \right)$. Gọi $y = g\left( x \right)$ là hàm số bậc hai có đồ thị đi qua ba điểm $A,B$ và $C$. Khi hình phẳng giới hạn bởi đồ thị của hai hàm số $y = f\left( x \right),y = g\left( x \right)$ và hai đường thẳng $x = 0,x = 1$ có diện tích bằng $\frac{2}{5}$, tích phân $\int\limits_0^1 {f\left( x \right)dx} $ bằng

A. 1 . B. -1 . C. $ – \frac{{17}}{{15}}$. D. $\frac{{17}}{{15}}$.

Lời giải

Phương trình đi qua 3 điểm $A,B,C$ là : $y = g(x) = \frac{1}{2}b{x^2} + c$.

Ta có: $\left\{ {\begin{array}{*{20}{l}}
{f(1) = \frac{{ – 3}}{5}} \\
{{f^\prime }(1) = 0}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{a + b + c = \frac{{ – 3}}{5}(1)} \\
{4a + 2b = 0}
\end{array}} \right.} \right.$

Theo đề ta có: $\int_0^1 {(g(} x) – f(x))dx = \frac{2}{5}$

$ \Leftrightarrow \int_0^1 {\left( { – a{x^4} – \frac{b}{2}{x^2}} \right)} dx = \frac{2}{5} \Leftrightarrow \frac{{ – a}}{5} – \frac{b}{6} = \frac{2}{5} \Leftrightarrow 6a + 5b = – 12(3)$

Từ (1) và (3) ta có: $a = 3,b = – 6,c = \frac{{12}}{5}$.

Vậy $\int_0^1 f (x)dx = 1$

Câu 42: Xét các số phức $z,w\left( {w \ne 2} \right)$ thỏa mãn $\left| z \right| = 1$ và $\frac{{w + 2}}{{w – 2}}$ là số thuần ảo. Khi $\left| {z – w} \right| = \sqrt 3 $, giá trị của $\left| {2z + w} \right|$ bằng

A. $\frac{{9\sqrt 7 }}{2}$. B. $\frac{{3\sqrt 7 }}{2}$. C. $\frac{{2\sqrt 3 }}{3}$. D. $2\sqrt 3 $.

Lời giải

Gọi $A$ là điểm biểu diễn của $z$. Theo đề ta có $\left| z \right| = 1$. Khi đó $A$ thuộc đường tròn tâm $O;R = 1$.

Gọi $B$ là điểm biểu diển của w. Theo đề ta có $\frac{{w + 2}}{{w – 2}}$ là số thuần ảo
$w = a + bi$. Khi đó $\frac{{w + 2}}{{w – 2}} = \frac{{a + 2 + bi}}{{{a^2} – 2 + bi}} = \frac{{\left( {a + 2 + bi} \right)\left( {a – 2 – bi} \right)}}{{{{(a – 2)}^2} + {b^2}}}$ là sổ thuẩn ảo nên

$\left( {x – 2} \right)\left( {x + 2} \right) + {y^2} = 0 \Leftrightarrow {x^2} + y = 4.0$
Khi đó $B$ thuộc đường tròn tàm $O;R = 2$.

Gọi $C$ là điểm biểu diễn của $2z$. Khi đó $C$ thuộc đường tròn tâm $O;R = 2$.

Theo đề ta có: $\left| {z – w} \right| = \sqrt 3 \Rightarrow BA = \sqrt 3 ,OB = 2;OC = 2OA = 2$

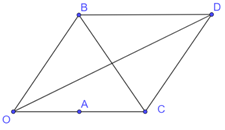
Trong tam giác OBA vuông tại A ta có: $cosO = \frac{{OA}}{{OB}} = \frac{1}{2}$

Khi đó $\left| {2z + w} \right| = OD = \sqrt {O{B^2} + O{C^2} + 2OB \cdot OC \cdot cosO} = 2\sqrt 3 $.

Câu 43: Cho khối lăng trụ $ABC.A’B’C’$ có đáy $ABC$ là tam giác vuông cân tại $A$, $A’A = A’B = A’C = a$. Biết góc giữa hai mặt phẳng $\left( {BCC’B’} \right)$ và $\left( {ABC} \right)$ bằng ${30^ \circ }$, thể tích của khối lăng trụ đã cho bằng

A. $\frac{{\sqrt 3 {a^3}}}{{24}}$. B. $\frac{{\sqrt 3 {a^3}}}{8}$. C. $\frac{{3{a^3}}}{8}$. D. $\frac{{{a^3}}}{8}$.

Lời giải

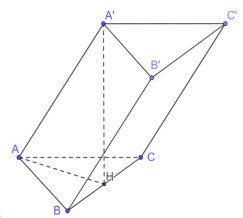
Đặt $AH = x \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{BC = 2x} \\
{A’H = \sqrt {{a^2} – {x^2}} }
\end{array}} \right.$.

Ta có $\left( {BCC’B’} \right)$ và $\left( {ABC} \right)$ bằng ${30^ \circ }$.

Suy ra $tan{30^ \circ } = \frac{{\sqrt {{a^2} – {x^2}} }}{x} \Leftrightarrow {x^2} = 3\left( {{a^2} – {x^2}} \right)$

$ \Leftrightarrow {x^2} = \frac{{3{a^2}}}{4}$. Suy ra $A’H = \frac{a}{2}$.

$V = A’H \cdot {S_{ABC}} = \frac{a}{2} \cdot \frac{{{a^2}}}{4} = \frac{{{a^3}}}{8}$

Câu 44: Trong không gian $Oxyz$, cho điểm $A\left( {1; – 2;2} \right)$ và mặt cầu $\left( S \right):{x^2} + {y^2} + {z^2} = 1$. Biết $B,C,D$ là ba điểm phân biệt trên $\left( S \right)$ sao cho các tiếp diện của $\left( S \right)$ tại mỗi điểm đó đều đi qua $A$. Hỏi mặt phẳng $\left( {BCD} \right)$ đi qua điểm nào dưới đây?

A. $M\left( {1;1;1} \right)$. B. $P\left( { – 3;1;1} \right)$. C. $N\left( { – 1;1;1} \right)$. D. $Q\left( {1;1; – 1} \right)$.

Lời giải

Biết $B,C,D$ là ba điểm phân biệt trên $\left( S \right)$ sao cho các tiếp diện của $\left( S \right)$ tại mỗi điểm đó đều đi qua $A$. Gọi $\left( {S’} \right)$ là mặt cầu đường kính $AO$.

$\left( {S’} \right):{\left( {x – \frac{1}{2}} \right)^2} + {(y + 2)^2} + {(z – 2)^2} = 9$

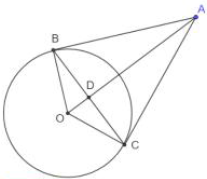
Khi đó 3 điểm $B,C,B$ đều nằm trên mặt cầu $\left( {S’} \right)$.

Vậy Mặt phẳng đi qua 3 điểm, $B,C,D$ thỏa mãn

$\left\{ {\begin{array}{*{20}{l}}
{{{\left( {x – \frac{1}{2}} \right)}^2} + {{(y + 2)}^2} + {{(z – 2)}^2} = 2} \\
{{x^2} + {y^2} + {z^2} = 1}
\end{array}} \right.$

$ \Rightarrow (BCD): – x + 2y – 2z + 1 = 0$ (*)

Thay tọa độ điểm $M\left( {1;1;1} \right)$ vào (*) ta thấy thỏa mãn.

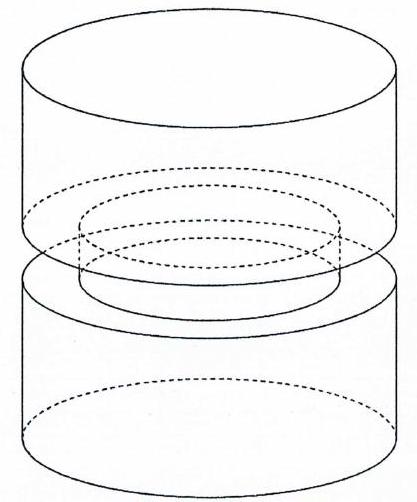
Câu 45: Để chế tạo một chi tiết máy, từ một khối thép hình trụ có bán kính $10\;cm$ và chiều cao $30\;cm$, người ta khoét bỏ một rãnh xung quanh rộng $1\;cm$ và sâu $1\;cm$ (tham khảo hình vẽ bên). Tính thể tích của chi tiết máy đó, làm tròn kết quả đến hàng phần nghìn.

A. $9110,619\;c{m^3}$. B. $9170,309\;c{m^3}$. C. $9365,088\;c{m^3}$. D. $8997,521\;c{m^3}$.

Lời giải

Thể tích của cái rãnh bỏ bị khoét bỏ đi là:

$\pi \cdot {10^2} \cdot 1 – \pi \cdot {9^2} \cdot 1 = 19\pi c{m^3}$.

Câu 46: Xét các số thực không âm $x$, $y$ thỏa mãn $ylo{g_3}\left( {3x + y + 9} \right) = \left( {{x^2} + 3x + y} \right)lo{g_3}\left( {x + 3} \right)$. Khi biểu thức $y – 5x$ đạt giá trị nhỏ nhất, giá trị của biểu thức $x – 2y$ bằng

A. -1 . B. 2 . C. -7 . D. -31 .

Lời giải

$ylo{g_3}\left( {3x + y + 9} \right) = \left( {{x^2} + 3x + y} \right)lo{g_3}\left( {x + 3} \right)$

$ \Leftrightarrow ylo{g_3}\left( {3x + y + 9} \right) – ylo{g_3}\left( {x + 3} \right) = \left( {{x^2} + 3x} \right)lo{g_9}\left( {x + 3} \right)$

$ \Leftrightarrow y\left( {lo{g_3}\left( {3x + y + 9} \right) – lo{g_3}\left( {x + 3} \right)} \right) = \left( {{x^2} + 3x} \right)log\left( {x + 3} \right)$

$ \Leftrightarrow y\left( {lo{g_3}\left( {\frac{{3x + y + 9}}{{x + 3}}} \right) = \left( {{x^2} + 3x} \right)lo{g_3}\left( {x + 3} \right)} \right.$

$ \Leftrightarrow y\left( {lo{g_3}\left( {\frac{{3\left( {x + 3} \right) + y}}{{x + 3}}} \right)} \right) = \left( {{x^2} + 3x} \right)lo{g_3}\left( {x + 3} \right)$

$y\left( {lo{g_3}\left( {3 + \frac{y}{{x + 3}}} \right)} \right) = x\left( {x + 3} \right)lo{g_3}\left( {x + 3} \right)$

$ \Leftrightarrow \frac{y}{{x + 3}}lo{g_3}\left( {1 + \frac{y}{{x + 3}}} \right) = xlog\left( {x + 3} \right)$

Suy ra: $\frac{y}{{x + 3}} = x \Leftrightarrow y = {x^2} + 3x$

Ta có $P = y – 5x = {x^2} – 2x$ đạt giá trị nhỏ nhất khi $x = 1$ Suy ra $y = 4$

Vậy $x – 2y = 1 – 2.4 = – 7$.

Chọn C

Câu 47: Xét các số phức $z,w$ thỏa mãn $\left| {z – w} \right| = 2\left| z \right| = 2$ và số phức $\bar z.w$ có phần thực bằng 1 . Giá trị lớn nhất của $P = \left| {z + w – 1 + 2i} \right|$ thuộc khoảng nào dưới đây?

A. $\left( {4;5} \right)$. B. $\left( {3;4} \right)$. C. $\left( {5;6} \right)$. D. $\left( {6;7} \right)$.

Lời giải

Đặt $\bar z \cdot w = 1 + bi$, suy ra $z \cdot \bar w = \overline {\bar z \cdot w} = \overline {1 + bi} = 1 – bi$ nên $\bar z \cdot w + z \cdot \bar w = 2$.

Ta có:

$|z – w| = 2$

$ \Rightarrow 4 = |z – w{|^2} = (z – w)(\overline {z – w} )$

$ = (z – w)(\bar z – \bar w) = z \cdot \bar z + w \cdot \bar w – (z \cdot \bar w + \bar z \cdot w)$

$ = |z{|^2} + |w{|^2} – (z \cdot \bar w + \bar z \cdot w)$

$ = 1 + |w{|^2} – 2 = |w{|^2} – 1 \Rightarrow |w| = \sqrt 5 $

$|z + w{|^2} = (z + w) \cdot (\overline {z + w} ) = (z + w) \cdot (\bar z + \bar w)$

$ = |z{|^2} + |w{|^2} + (z \cdot \bar w + \bar z \cdot w) = 1 + 5 + 2 = 8 \Rightarrow |z + w| = 2\sqrt 2 $

Khi đó: $P = \left| {z + w – 1 + 2i\left| = \right|\left( {z + w} \right) + \left( { – 1 + 2i} \right)\left| \leqslant \right|z + w\left| + \right| – 1 + 2i} \right| = 2\sqrt 2 + \sqrt 5 $.

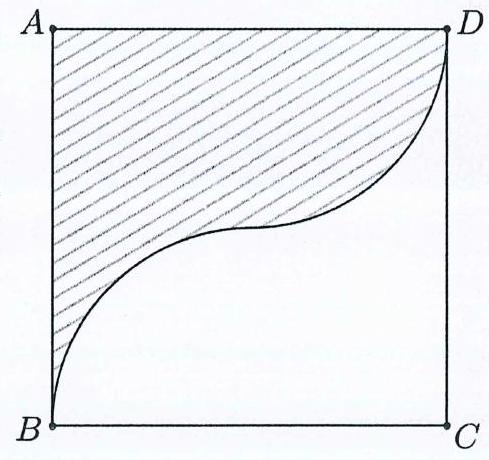
Câu 48: Một vật trang trí có dạng một khối tròn xoay được tạo thành khi quay miền $\left( R \right)$ (phần gạch chéo trong hình vẽ bên) quanh trục $AB$. Miền $\left( R \right)$ được giới hạn bởi các cạnh $AB,AD$ của hình vuông $ABCD$ và các cung phần tư của các đường tròn bán kính bằng $1\;cm$ với tâm lần lượt là trung điểm của các cạnh $BC,AD$. Tính thể tích của vật trang trí đó, làm tròn kết quả đến hàng phần mười.

A. $20,3\;c{m^3}$. B. $10,5\;c{m^3}$. C. $12,6\;c{m^3}$. D. $8,4\;c{m^3}$.

Lời giải

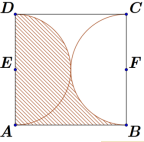
Chọn $AB$ chứa trong trục $Ox$ và $A \equiv O(0;0)$

Khi đó $E(0;1)$ và $F(2;1)$ với $E, F$ lần lượt là trung điểm của $AD, BC$.

Khi đó đường tròn tâm $E$ chứa cung tròn $AD$ là ${x^2} + {(y – 1)^2} = 1$ và đường tròn tâm $F$ chứa cung tròn $BC$ là $\left( {x – 2} \right)$

Suy ra phương trình cung trền của dương trôn fân $E$ là $y = \sqrt {1 – {x^2}} + 1$ và phương trình cung dưới của của đường tròn tâm $F$ là $y = – \sqrt {1 – {{(x – 2)}^2}} + 1$.

Khi đó, thể tích vật thể trang trí là

$V = \pi \int_0^1 {{{\left( {\sqrt {1 – {x^2}} + 1} \right)}^2}} \;dx + \pi \int_1^2 {{{\left( { – \sqrt {1 – {{(x – 2)}^2}} + 1} \right)}^2}} \;dx \approx 10,5\;c{m^3}$.

Câu 49: Cho hàm số $y = f\left( x \right)$ có đạo hàm $f’\left( x \right) = {x^2} – 3x – 4,\forall x \in \mathbb{R}$. Có bao nhiêu giá trị nguyên của tham số $m$ sao cho ứng với mỗi $m$, hàm số $g\left( x \right) = f\left( { – {x^3} + 3{x^2} + m} \right)$ có đúng hai điểm cực trị thuộc khoảng $\left( {1;4} \right)$ ?

A. 9 . B. 7. C. 8 . D. 10 .

Lời giải

Ta có $f’\left( x \right) = 0 \Leftrightarrow {x^2} – 3x – 4 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 4} \\
{x = – 1.}
\end{array}} \right.$

Mặt khác $g’\left( x \right) = \left( { – 3{x^2} + 6x} \right)f’\left( { – {x^3} + 3{x^2} + m} \right)$

suy ra $g’\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 0} \\
{x = 2 \in \left( {1;4} \right)} \\
{f’\left( { – {x^3} + 3{x^2} + m} \right) = 0}
\end{array}} \right.$.

Lại có $f’\left( { – {x^3} + 3{x^2} + m} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{ – {x^3} + 3{x^2} + m = 4} \\
{ – {x^3} + 3{x^2} + m = – 1}
\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{m = {x^3} – 3{x^2} + 4} \\
{m = {x^3} – 3{x^2} – 1}
\end{array}} \right.} \right.$

Vẽ đồ thị hai hàm số $y = {x^3} – 3{x^2} + 4$ và $y = {x^3} – 3{x^2} – 1$ lên cùng một mặt phẳng tọa độ.

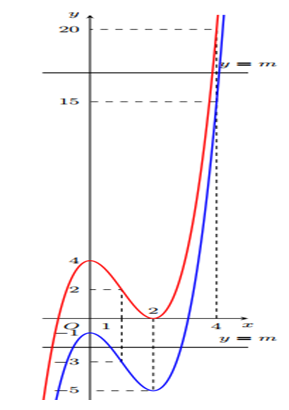
Yêu cầu bài toán tương đương $x’\left( { – {x^3} + 3{x^2} + m} \right) = 0$ có đúng một nghiệm đơn khác 2 trong khoảng $\left( {1;4} \right)$

suy ra $\left[ {\begin{array}{*{20}{l}}
{ – 3 \leqslant m \leqslant 0} \\
{15 \leqslant m < 20}
\end{array}} \right.$. Vậy có tất cà 9 giá tri

Câu 50: Trong không gian $Oxyz$, cho hình nón $\left( \mathcal{N} \right)$ có đỉnh $A\left( {2;3;0} \right)$, độ dài đường sinh bằng 5 và đường tròn đáy nằm trên mặt phẳng $\left( P \right):2x + y + 2z – 1 = 0$. Gọi $\left( C \right)$ là giao tuyến của mặt xung quanh của $\left( \mathcal{N} \right)$ với mặt phẳng $\left( Q \right):x – 4y + z + 4 = 0$ và $M$ là một điểm di động trên $\left( C \right)$. Hỏi giá trị nhỏ nhất của độ dài đoạn thẳng $AM$ thuộc khoảng nào dưới đây?

A. $\left( {\frac{3}{2};2} \right)$. B. $\left( {0;1} \right)$. C. $\left( {1;\frac{3}{2}} \right)$. D. $\left( {2;3} \right)$.

Lời giải

Gọi $l,h,r$ lần lượt là độ dài đường sinh, chiều cao và bán kính của hình nón.

Theo đề bài ta có $l = 5$ và $h = d\left( {A,\left( P \right)} \right) = 2$. Suy ra $r = \sqrt {{l^2} – {h^2}} = \sqrt {21} $.

Mặt khác $\left\{ {\begin{array}{*{20}{l}}
{\overline {{n_p}} = \left( {2;1;2} \right)} \\
{\overline {{n_Q}} = \left( {1; – 4;1} \right)}
\end{array} \Rightarrow \overline {{n_P}} ,\overline {{n_Q}} = 0 \Rightarrow \left( P \right) \bot \left( Q \right)} \right.$.

Khi đó giao tuyến $\left( C \right)$ là một parabol có đỉnh $H$ (như hình vẽ).

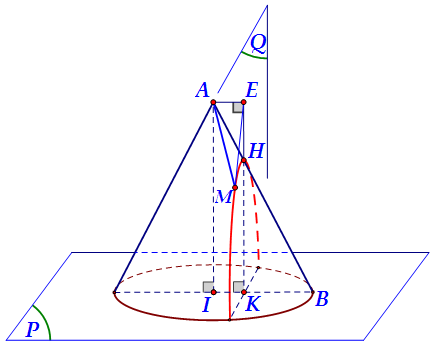
Gọi $E$ là hình chiếu vuông góc của $A$ lên $\left( Q \right)$.

Và $d\left( {A,\left( Q \right)} \right) = AE = \sqrt 2 \left( { = IK} \right)$ do $IA//\left( Q \right)$. Ta có: $AM = \sqrt {A{E^2} + E{M^2}} = \sqrt {2 + E{M^2}} $

Đồng thời $EM \geqslant EH$. Do đó $AM$ minin $ \Leftrightarrow AM = AH$ hay $M \equiv H$

Vì $IA//HK \Rightarrow \frac{{AH}}{{AB}} = \frac{{IK}}{{IB}}($ Thales $) \Rightarrow AH = \frac{{\sqrt 2 }}{{\sqrt {21} }} \cdot 5 = \frac{{5\sqrt {42} }}{{21}} \approx 1,54 \in \left( {\frac{3}{2};2} \right)$

Vậy giá trị nhỏ nhất độ dài đoạn thẳng $AM$ thuộc khoảng $\left( {\frac{3}{2};2} \right)$.
Cách khác

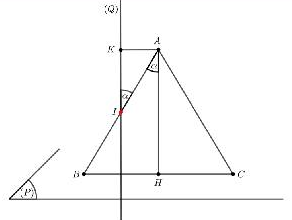
Ta có: $\left\{ {\begin{array}{*{20}{l}}
{AH = d(A;(P)) = 2} \\
{AK = d(A;(Q)) = \sqrt 2 }
\end{array}} \right.$.

Từ giả thiết, ta có $AB = AC = 5;BH = \sqrt {A{B^2} – A{H^2}} = \sqrt {21} $.

Mặt khác, ${\overrightarrow n _{_P}} = (21;2),{\overrightarrow n _{_Q}} = (1; – 4;1) \Rightarrow {\overrightarrow n _{_P}} \cdot {\overrightarrow n _{_Q}} = 0 \Rightarrow (P) \bot (Q)$ nên $AM$ đạt GTNN khi và chi khi $AM = AI \Leftrightarrow I \equiv M$.

Ta có: $\sin \alpha = \frac{{AK}}{{AI}} = \frac{{BH}}{{AB}} \Rightarrow AI = \frac{{AK \cdot AB}}{{BH}} = \frac{{\sqrt 2 \cdot 5}}{{\sqrt {21} }} \approx 1,54 \in \left( {\frac{3}{2};2} \right)$.