Giải Chi Tiết Đề Tham Khảo Vật Lí 2024 Tốt Nghiệp THPT Bộ GD&ĐT

Giải chi tiết đề tham khảo môn Vật lí tốt nghiệp THPT 2024 Bộ GD&ĐT được soạn dưới dạng file word và PDF gồm 9 trang. Các bạn xem và tải về ở dưới.

BỘ GIÁO DỤC VÀ ĐÀO TẠO ĐỀ THI THAM KHẢO (Đề thi có 04 trang)

KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG NĂM 2024 Bài thi: KHOA HỌC TỰ NHIÊN Môn thi thành phần: VẬT LÍ Thời gian làm bài: 50 phút, không kể thời gian phát đề

Họ, tên thí sinh:………………………………………

Số báo danh:…………………………………………

Câu 1: Đặt điện áp xoay chiều vào hai đầu đoạn mạch chỉ có cuộn cảm thuần. So với điện áp giữa hai đầu đoạn mạch, cường độ dòng điện trong đoạn mạch

A. trễ pha $\frac{\pi }{2}$. B. cùng pha. C. ngược pha. D. sớm pha $\frac{\pi }{2}$.

Lời giải

Chọn A

Câu 2: Một hạt nhân $\;_6^{13}C$ có số nuclôn bằng

A. 13 . B. 7 . C. 19 . D. 6 .

Lời giải

Chọn A

Câu 3: Đặt điện áp xoay chiều vào hai đầu đoạn mạch gồm điện trở $R$, cuộn cảm thuần và tụ điện mắc nối tiếp thì cảm kháng và dung kháng của đoạn mạch lần lượt là ${Z_L}$ và ${Z_C}$. Độ lệch pha $\varphi $ của điện áp giữa hai đầu đoạn mạch so với cường độ dòng điện trong đoạn mạch thỏa mãn công thức nào sau đây?

A. $tan\varphi = \frac{R}{{{Z_L} + {Z_C}}}$. B. $tan\varphi = \frac{{{Z_L} + {Z_C}}}{R}$. C. $tan\varphi = \frac{R}{{{Z_L} – {Z_C}}}$. D. $tan\varphi = \frac{{{Z_L} – {Z_C}}}{R}$.

Lời giải

Chọn D

Câu 4: Tốc độ truyền âm nhỏ nhất trong môi trường nào sau đây?

A. Sắt. B. Nước biển ở ${15^ \circ }C$. C. Nhôm. D. Không khí ở ${0^ \circ }C$.

Lời giải

Chọn D

Câu 5: Hệ vật cô lập về điện là hệ vật

A. có trao đổi điện tích dương với các vật khác ngoài hệ.

B. không có trao đổi điện tích giữa các vật trong hệ.

C. có trao đổi điện tích âm với các vật khác ngoài hệ.

D. không có trao đổi điện tích với các vật khác ngoài hệ.

Lời giải

Chọn D

Câu 6: Kim loại đồng là chất

A. dẫn điện tốt. B. không dẫn điện.

C. có điện trở suất không thay đổi theo nhiệt độ. D. có điện trở suất giảm khi nhiệt độ tăng.

Lời giải

Chọn A

Câu 7: Một vật dao động điều hòa với phương trình $x = Acos\left( {\omega t + \varphi } \right)$ ( $t$ tính bằng s). Tần số góc $\omega $ có đơn vị là

A. $rad/s$. B. $rad/{s^2}$. C. s/rad. D. ${s^2}/rad$.

Lời giải

Chọn A

Câu 8: Một con lắc lò xo gồm lò xo nhẹ có độ cứng $k$ và vật nhỏ có khối lượng $m$. Kích thích cho con lắc dao động điều hòa. Tần số $f$ của con lắc được tính bằng công thức nào sau đây?

A. $f = \frac{1}{{2\pi }}\sqrt {\frac{m}{k}} $. B. $f = \frac{1}{{2\pi }}\sqrt {\frac{k}{m}} $. C. $f = \sqrt {\frac{m}{k}} $. D. $f = \sqrt {\frac{k}{m}} $.

Lời giải

Chọn B

Câu 9: Hạt nhân nào sau đây bền vững nhất?

A. $\;_{92}^{235}U$. B. $\;_2^4He$. C. $\;_{28}^{56}Fe$. D. $\;_1^3H$.

Lời giải

Chọn C

Câu 10: Hiện tượng nhiễu xạ ánh sáng, giao thoa ánh sáng chứng tỏ ánh sáng

A. là sóng cơ. B. là chùm hạt êlectron.

C. có tính chất sóng. D. có tính chất hạt.

Lời giải

Chọn C

Câu 11: Theo thuyết lượng tử ánh sáng, phát biểu nào sau đây sai?

A. Trong chân không, phôtôn bay với tốc độ $3 \cdot {10^8}\;m/s$ dọc theo các tia sáng.

B. Năng lượng của các phôtôn ứng với các ánh sáng đơn sắc khác nhau luôn bằng nhau.

C. Ánh sáng được tạo thành bởi các hạt gọi là phôtôn.

D. Phôtôn chỉ tồn tại trong trạng thái chuyển động. Không có phôtôn đứng yên.

Lời giải

Chọn B

Câu 12: Trên một sợi dây đàn hồi đang có sóng dừng ổn định, nút sóng là các điểm trên dây mà phần tử ở đó

A. luôn luôn đứng yên. B. dao động với biên độ bằng một nửa bước sóng.

C. dao động với biên độ bằng một bước sóng. D. dao động với biên độ lớn nhất.

Lời giải

Chọn A

Câu 13: Hai dao động điều hòa cùng phương, có phương trình là ${x_1} = {A_1}cos\left( {\omega t + {\varphi _1}} \right)$ và ${x_2} = {A_2}cos\left( {\omega t + {\varphi _2}} \right)$ với ${A_1} > 0$ và ${A_2} > 0$. Khi ${\varphi _2} – {\varphi _1} = \left( {2n + 1} \right)\pi ,\left( {n = 0, \pm 1, \pm 2, \ldots } \right)$, thì hai dao động này

A. lệch pha nhau $\frac{\pi }{6}$. B. lệch pha nhau $\frac{\pi }{3}$. C. cùng pha nhau. D. ngược pha nhau.

Lời giải

Chọn D

Câu 14: Tại một nơi có gia tốc trọng trường $g$, một con lắc đơn có chiều dài $l$ đang dao động điều hòa với chu kì $T$. Công thức nào sau đây đúng?

A. $T = \sqrt {\frac{l}{g}} $. B. $T = 2\pi \sqrt {\frac{l}{g}} $. C. $T = 2\pi \sqrt {\frac{g}{l}} $. D. $T = \sqrt {\frac{g}{l}} $.

Lời giải

Chọn B

Câu 15: Công suất điện tiêu thụ của một đoạn mạch điện xoay chiều hình sin là $\mathcal{P}$. Điện năng tiêu thụ $W$ của đoạn mạch trong khoảng thời gian $t$ được tính bằng công thức nào sau đây?

A. $W = \mathcal{P}t$. B. $W = \mathcal{P}{t^2}$. C. $W = \frac{\mathcal{P}}{t}$. D. $W = \frac{\mathcal{P}}{{{t^2}}}$.

Lời giải

Chọn A

Câu 16: Một máy phát điện xoay chiều một pha có phần cảm là rôto và phần ứng là stato. Khi máy hoạt động ổn định, từ thông qua mỗi cuộn dây của stato biến thiên tuần hoàn với tần số $f$ thì trong các cuộn dây này xuất hiện suất điện động xoay chiều có tần số là

A. $1,5f$. B. $f$. C. $2f$. D. $2,5f$.

Lời giải

Chọn B

Câu 17: Bộ nguồn gồm hai nguồn điện một chiều giống nhau ghép nối tiếp, mỗi nguồn có suất điện động $\mathcal{E}$. Suất điện động của bộ nguồn là

A. ${\mathcal{E}_b} = 0,25\mathcal{E}$. B. ${\mathcal{E}_b} = 4\mathcal{E}$. C. ${\mathcal{E}_b} = 2\mathcal{E}$. D. ${\mathcal{E}_b} = 0,5\mathcal{E}$.

Lời giải

Chọn C

Câu 18: Trong sơ đồ khối của một máy phát thanh vô tuyến đơn giản không có bộ phận nào sau đây?

A. Micrô. B. Loa. C. Mạch biến điệu. D. Mạch khuếch đại.

Lời giải

Chọn B

Câu 19: Khi chiếu bức xạ có bước sóng $0,55\mu m$ vào một chất thì chất này phát quang. Bước sóng của ánh sáng phát quang có thể nhận giá trị nào sau đây?

A. $0,60\mu m$. B. $0,30\mu m$. C. $0,40\mu m$. D. $0,50\mu m$.

Lời giải

Chọn A

Câu 20: Khi nói về sóng cơ hình sin, phát biểu nào sau đây sai?

A. Bước sóng là quãng đường mà sóng truyền được trong một nửa chu kì.

B. Chu kì của sóng là chu kì dao động của một phần tử của môi trường có sóng truyền qua.

C. Biên độ của sóng là biên độ dao động của phần tử của môi trường có sóng truyền qua.

D. Năng lượng sóng là năng lượng dao động của các phần tử của môi trường có sóng truyền qua.

Lời giải

Chọn A

Câu 21: Tia hồng ngoại không có ứng dụng nào sau đây?

A. Chiếu điện, chụp điện. B. Chụp ảnh ban đêm.

C. Sấy khô, sưởi ấm. D. Dùng trong bộ điều khiển từ xa.

Lời giải

Chọn A

Câu 22: Quang phổ vạch phát xạ

A. do chất rắn hoặc chất lỏng phát ra khi bị kích thích bằng nhiệt hay bằng điện.

B. do chất khí ở áp suất lớn phát ra khi bị nung nóng.

C. là một hệ thống những vạch sáng riêng lẻ, ngăn cách nhau bởi những khoảng tối.

D. là một dải có màu từ đỏ đến tím nối liền nhau một cách liên tục.

Lời giải

Chọn C

Câu 23: Đặt điện áp xoay chiều vào hai đầu đoạn mạch gồm cuộn cảm thuần và tụ điện mắc nối tiếp. Biết cảm kháng của đoạn mạch lớn hơn dung kháng của đoạn mạch. So với cường độ dòng điện trong đoạn mạch thì điện áp giữa hai đầu đoạn mạch

A. sớm pha $\frac{\pi }{2}$. B. sớm pha $\frac{\pi }{4}$. C. trễ pha $\frac{\pi }{2}$. D. trê̂ pha $\frac{\pi }{4}$.

Lời giải

Chọn A

Câu 24: Một đoạn dây dẫn thẳng dài $0,4\;m$ được đặt trong một từ trường đều có cảm ứng từ $0,01\;T$. Biết đoạn dây vuông góc với hướng của từ trường. Cho dòng điện không đổi có cường độ $5\;A$ chạy trong đoạn dây. Lực từ tác dụng lên đoạn dây có độ lớn là

A. $0,02\;N$. B. $0,01\;N$. C. $0,03\;N$. D. $0,04\;N$.

Lời giải

Chọn A

Câu 25: Một mạch dao động lí tưởng gồm tụ điện có điện dung $0,300nF$ và cuộn cảm thuần có độ tự cảm $3,00mH$. Tần số dao động riêng của mạch là

A. $0,168kHz$. B. $0,168MHz$. C. $0,336MHz$. D. $0,336kHz$.

Lời giải

Chọn B

Câu 26: Trong thí nghiệm Y-âng về giao thoa với ánh sáng đơn sắc có bước sóng $0,50\mu m$, khoảng cách giữa hai khe hẹp là $1,0\;mm$, khoảng cách từ hai khe đến màn quan sát là $1,5\;m$. Trên màn, khoảng cách giữa hai vân sáng liên tiếp là

A. $3,0\;mm$. B. $0,75\;mm$. C. $2,0\;mm$. D. $0,33\;mm$.

Lời giải

Chọn B

Câu 27: Biết khối lượng của prôtôn; nơtron và hạt nhân $\;_{16}^{32}\;S$ lần lượt là $1,0073u;1,0087u$ và $31,9633u$. Độ hụt khối của hạt nhân $\;_{16}^{32}\;S$ là

A. $0,2207u$. B. $0,2351u$. C. $0,2927u$. D. $0,2783u$.

Lời giải

Chọn C

Câu 28: Một con lắc đơn dao động điều hòa tại nơi có $g = 9,87\;m/{s^2}$ với tần số $0,5\;Hz$. Chiều dài con lắc là

A. $0,5\;m$. B. $2,0\;m$. C. 1,0 m. D. 1,6 m.

Lời giải

Chọn C

Câu 29: Một sợi dây đàn hồi dài $l$, căng ngang có hai đầu cố định. Trên dây đang có sóng dừng với hai bụng sóng. Biết khoảng cách giữa hai nút sóng liên tiếp là $8,0\;cm$. Giá trị của $l$ là

A. $32\;cm$. B. $16\;cm$. C. $24\;cm$. D. $8,0\;cm$.

Lời giải

Chọn B

Câu 30: Xét nguyên tử hiđrô theo mẫu nguyên tủ Bo, quỹ đạo dừng $K$ có bán kính là ${r_0} = 5,3 \cdot {10^{ – 11}}\;m$. Quỹ đạo dừng có bán kính 132,5.10 ${\;^{ – 11}}\;m$ là quỹ đạo dừng

A. $N$. B. $P$. C. $O$. D. $M$.

Lời giải

$r = {k^2}{r_0} \Rightarrow k = 5$ (Quỹ đạo dừng 0 )

Chọn C

Câu 31: Trong thí nghiệm giao thoa sóng ở mặt chất lỏng, hai nguồn kết hợp đặt tại hai điểm $A$ và $B$, dao động cùng pha theo phương thẳng đứng với tần số $20\;Hz$. Sóng truyền trên mặt chất lỏng có bước sóng $\lambda $. Ở mặt chất lỏng, điểm $M$ là cực đại giao thoa cách $A$ và $B$ những khoảng $5,0\;cm$ và $14\;cm$. Biết tốc độ truyền sóng trên mặt chất lỏng có giá trị trong khoảng từ $55\;cm/s$ đến $81\;cm/s$. Giá trị của $\lambda $ là

A. $6,0\;cm$. B. $3,0\;cm$. C. $4,5\;cm$. D. $1,5\;cm$.

Lời giải

Điểm $M$ là cực đại giao thoa nên: $k = \frac{{{d_2} – {d_1}}}{\lambda } \in \mathbb{Z} \Rightarrow k = \frac{9}{\lambda } \in \mathbb{Z} \Rightarrow k = \frac{{9f}}{v} \Rightarrow v = \frac{{180}}{k}$

Mà: $55 < v < 81 \Rightarrow 55 < \frac{{180}}{k} < 81 \Rightarrow 2,2 < k < 3,2$

$ \Rightarrow k = 3 \Rightarrow v = \frac{{180}}{3} = 60\;cm/s \Rightarrow \lambda = \frac{v}{f} = 3\;cm$

Chọn B

Câu 32: Đặt điện áp $u = 120\sqrt 2 cos\left( {2\pi ft – \frac{\pi }{3}} \right)\left( V \right)(f$ thay đổi được) vào hai đầu đoạn mạch $AB$ gồm điện trở $R$, cuộn cảm thuần có $L = \frac{{0,6}}{\pi }H$và tụ điện $C$ như hình bên. Khi $f = {f_1} = 40,0\;Hz$ hoặc $f = {f_2} = 62,5\;Hz$ thì điện áp hiệu dụng giữa hai đầu đoạn mạch $AM$ có cùng giá trị. Khi $f = {f_0}$ thì công suất điện tiêu thụ của đoạn mạch $AB$ đạt cực đại và bằng $288\;W$. Trong trường hợp $f = {f_0}$ thì điện áp hiệu dụng giữa hai đầu đoạn mạch $AN$ là bao nhiêu?

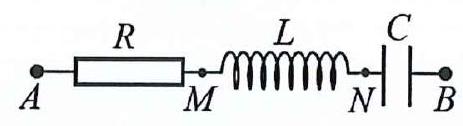
A. $144\;V$. B. $221\;V$. C. $187\;V$. D. $198\;V$.

Lời giải

Điện áp hiệu dụng hai đầu đoạn mạch $AM:{U_{AM}} = IR$

Công suất tiêu thụ đoạn mạch $AB:P = {I^2}R$

Khi $f = {f_1}$ hoặc $f = {f_2}$ thì ${U_{AM}}$ như nhau nên $I$ cùng giá trị.

Khi $f = {f_0}$ thì công suất đoạn mạch $AB$ cực đại nên ${I_{max}}$ nên mạch cộng hưởng

Từ đó ta có: $f_0^2 = {f_1}.{f_2} \Rightarrow {f_0} = 50\;Hz$

Khi xảy ra cộng hưởng:

$\left\{ {\begin{array}{*{20}{c}}
{{P_{max\;}} = \frac{{{U^2}}}{R} \Rightarrow R = \frac{{{U^2}}}{{{P_{max}}}} = 50\Omega } \\
{{Z_L} = 2\pi {f_0} \cdot L = 60\Omega } \\
{{I_{max}} = \frac{U}{R} = 2,4\;A}
\end{array}} \right.$

Điện áp hiệu dụng hai đầu đoạn mạch AN là: ${U_{AN}} = I\sqrt {{R^2} + Z_L^2} = 187\;V$

Chọn C

Câu 33: Một mạch dao động lí tưởng gồm cuộn cảm có độ tự cảm $8,00mH$ và tụ điện có điện dung $2,00nF$. Trong mạch đang có dao động điện từ tự do. Tại thời điểm $t$, hiệu điện thế giữa hai bản tụ điện là $0,640\;V$. Lấy $\pi \approx 3,14$. Tại thời điểm $t + 6,28\left( {\mu s} \right)$, cường độ dòng điện trong mạch có độ lớn là

A. $1,28\;mA$. B. $0,32\;mA$. C. 1,28 A. D. $0,32\;A$.

Lời giải

Ta có $T = 2\pi \sqrt {LC} = 8\pi \mu s$

Vì $\Delta t = 6,28\mu s = \frac{T}{4}$ nên $\frac{{{u_1}}}{{{U_0}}} = \frac{{{i_2}}}{{{I_0}}} \to {i_2} = \frac{{{u_1}}}{{{U_0}}}{I_0} = {u_1}\sqrt {\frac{C}{L}} = 0,32mA$.

Chọn B

Câu 34: Đặt điện áp $u = 200\sqrt 2 cos\left( {100\pi t + \frac{\pi }{4}} \right)\left( V \right)(t$ tính bằng $s)$ vào hai đầu đoạn mạch gồm điện trở, cuộn cảm thuần có độ tự cảm $L$ và tụ điện có điện dung $\frac{{100}}{\pi }\mu F$ mắc nối tiếp. Biết cường độ dòng điện trong đoạn mạch có biểu thức $i = \sqrt 2 cos\left( {100\pi t + \frac{\pi }{{12}}} \right)$ (A). Giá trị của $L$ là

A. $\frac{{1,78}}{\pi }H$. B. $\frac{4}{\pi }H$. C. $\frac{2}{\pi }H$. D. $\frac{{3,56}}{\pi }H$.

Lời giải

$tan\varphi = \frac{{{Z_L} – {Z_C}}}{R} \Rightarrow tan\left( {\frac{\pi }{4} – \frac{\pi }{{12}}} \right) = \frac{{{Z_L} – 100}}{R} \Rightarrow R = \left( {{Z_L} – 100} \right)\sqrt 3 $

$Z = \frac{U}{I} = 200 \Rightarrow {200^2} = {R^2} + {\left( {{Z_L} – 100} \right)^2} = 4.{\left( {{Z_L} – 100} \right)^2}$

$ \Rightarrow {Z_L} = 200 \Rightarrow L = \frac{{200}}{{100\pi }} = \frac{2}{\pi }H$

Chọn C

Câu 35: Một con lắc lò xo gồm lò xo nhẹ và vật nhỏ có khối lượng $400\;g$ đang dao động điều hòa. Lực kéo về tác dụng lên vật phụ thuộc vào thời gian $t$ theo biểu thức: $F = – 2cos\left( {10t + \frac{{2\pi }}{3}} \right)\left( N \right)(t$ tính bằng $s$ ). Quãng đường vật đi được tính từ thời điểm $t = 0$ đến thời điểm vật đi qua vị trí cân bằng lần thứ hai là

A. $15,0\;cm$. B. $17,5\;cm$. C. $20,0\;cm$. D. $12,5\;cm$.

Lời giải

Lực kéo về: $F = – m{\omega ^2}x = – m{\omega ^2}Acos\left( {\omega t + \varphi } \right) = – 2cos\left( {10t + \frac{{2\pi }}{3}} \right)$ $ \Rightarrow \left\{ {\begin{array}{*{20}{c}}
{A = \frac{2}{{0,{{4.10}^2}}} = 0,05m = 5\;cm} \\
{\varphi = \frac{{2\pi }}{3}}
\end{array}} \right.$

$t = 0,x = – 2,5\;cm,v < 0 \Rightarrow $ Vật đi qua vị trí cân bằng lần thứ 2 vật đi quãng đường:

$s = 4.A – 2,5 = 17,5\;cm$

Chọn B

Câu 36: Theo một lí thuyết của các nhà thiên văn học thì các nguyên tố nặng có trên các hành tinh trong vũ trụ được tạo ra từ các vụ nổ siêu tân tinh (cái chết của một ngôi sao nặng). Cho rằng ${\;^{235}}U$ và ${\;^{238}}U$ ược tạo ra từ mỗi vụ nổ siêu tân tinh đều có cùng số nguyên tử. Hiện nay, tỉ số về số nguyên tử giữa ${\;^{235}}U$ với ${\;^{238}}U$ trên Trái Đất là 0,00725 . Biết ${\;^{235}}U$ và ${\;^{238}}U$ là các chất phóng xạ với chu kì bán rã lần lượt là 0,704 tỉ năm và 4,47 tỉ năm. Thời điểm mà vụ nổ siêu tân tinh xảy ra để sản phẩm của nó tạo thành Trái Đất đã cách đây

A. 5,94 tỉ năm. B. 5,00 tỉ năm. C. 3,61 tỉ năm. D. 4,12 tỉ năm.

Lời giải

Gọi ${N_{01}},{N_1}$ là số nguyên tử lúc đầu và lúc sau của ${\;^{235}}U$

Gọi ${N_{02}},{N_2}$ là số nguyên tử lúc đầu và lúc sau của ${\;^{238}}U$

$\frac{{{N_1}}}{{{N_2}}} = \frac{{{N_{01}}}}{{{N_{02}}}} \cdot \frac{{{e^{ – {\lambda _1}t}}}}{{{e^{ – {\lambda _2}t}}}} = {e^{\left( {{\lambda _2} – {\lambda _1}} \right)t}} \to t = \frac{{ln\left( {\frac{{{N_1}}}{{{N_2}}}} \right)}}{{ln2\left( {\frac{1}{{{T_2}}} – \frac{1}{{{T_1}}}} \right)}} \approx 5,94\;\;$tỉ năm

Chọn A

Câu 37: Ba nguồn sáng phát ra ba bức xạ đơn sắc có bước sóng là $400\;nm,{\lambda _1}$ và ${\lambda _2}$ với $390\;nm \leqslant {\lambda _1} < {\lambda _2} \leqslant 760\;nm$ được sử dụng trong thí nghiệm Y-âng về giao thoa ánh sáng. Chiếu sáng hai khe hẹp đồng thời bằng bất kì hai trong ba bức xạ trên thì trên màn quan sát đều thấy: điểm $O$ là vị trí vân sáng trung tâm, tại điểm $M$ luôn là vị trí trùng nhau gần $O$ nhất của hai vân sáng. Nếu chiếu sáng hai khe đồng thời bằng cả ba bức xạ trên thì trong khoảng $OM$ (không kể $O$ và $M$ ) có 26 vân sáng. Giá trị của ${\lambda _2}$ gần nhất với giá trị nào sau đây?

A. $560\;nm$. B. $740\;nm$. C. $690\;nm$. D. $630\;nm$.

Lời giải

Tại $M$ là vân trùng của cả 3 bức xạa. Ta có: ${x_M} = {k_0}{i_0} = {k_1}{i_1} = {k_2}{i_2}\left( {{k_1} > {k_2}} \right)$

Điều kiện để $M$ luôn là vị trí vân sáng trùng nhau gần $O$ nhất là:

$UPCLN\;\left( {{k_0};{k_1}} \right) = $ ƯCLN $\left( {{k_1};{k_2}} \right) = $ ƯCLN$\left( {{k_0};{k_2}} \right) = 1$

Trên $OM$ có 26 vân sáng (không kể $O,M$ ) nên ta có: ${k_0} + {k_1} + {k_2} = 26 + 3 = 29$

Từ (1)(2) suy ra ${k_0};{k_1};{k_2}$ phải là ba số lẻ (Vì nếu có hai số chẵn thì sẽ có ước chung bằng 2)

Vì $390\;nm \leqslant {\lambda _0};{\lambda _1};{\lambda _2} \leqslant 760\;nm \Rightarrow {k_0};{k_1};{k_2}$ không chênh lệch nhau quá 2 lần.

Vì ${\lambda _0} = 400\;nm$ gần $390\;nm \Rightarrow {k_0}$ là lớn nhất $ \Rightarrow {k_0} > \frac{{29}}{3} \Rightarrow {k_0} > 9$, kết hợp với (2)(3) ta có bảng giá trị:

K0	K1	K2 (K1 > K2 )
11	9	9	Vi phạm (1)
11	11	7	Vi phạm (1)
11	13	5	Vi phạm (4)
13	9	7	Thỏa mãn
13	11	5	Vi phạm (4)

Suy ra: $13{\lambda _0} = 9{\lambda _1} = 7{\lambda _2}$ với ${\lambda _0} = 400\;nm \Rightarrow {\lambda _2} = 742\;nm$

Chọn B

Câu 38: Một lò xo nhẹ được đặt thẳng đứng có đầu trên gắn với vật nhỏ $A$ khối lượng $m$, đầu dưới gắn với vật nhỏ $B$ khối lượng $2m$, vật $B$ được đặt trên mặt sàn nằm ngang như hình H.I. Kích thích cho $A$ dao động điều hòa theo phương thẳng đứng. Lấy $g = 9,8\;m/{s^2}$. Hình H.II là đồ thị biểu diễn sự phụ thuộc của áp lực $F$ của $B$ lên mặt sàn theo thời gian $t$. Tốc độ cực đại của $A$ có giá trị gần nhất với giá trị nào sau đây?

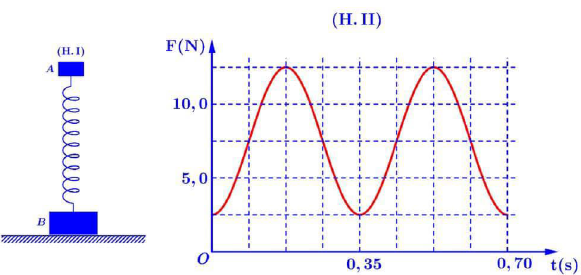
A. $1,4\;m/s$. B. $0,50\;m/s$. C. $1,1\;m/s$. D. $0,80\;m/s$.

Lời giải

Từ H.II suy ra khi $A$ dao động thì $B$ không bị nhấc lên khỏi sàn và

$T = 0,35\;s \Leftrightarrow \omega = \frac{{40\pi }}{7};{N_{max}} = 12,5\;N;{N_{min\;}} = 2,5\;N$

Các lực tác dụng lên $B$ : Trọng lực ${P_B}$, lực đàn hồi lò xo ${F_{dh}}$ và phản lực của sàn $N$

Ta có:

$N = {P_B} – {F_{dh}} = 2mg – \left( { – mg + m{\omega ^2}\;Acos\left( {\omega t + \varphi } \right)} \right)$

$ \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{{N_{max\;}} = 3mg + m{\omega ^2}\;A} \\
{\;{N_{min\;}} = 3mg – m{\omega ^2}\;A}
\end{array}} \right.$

$ \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{12,5 = 3mg + m{\omega ^2}\;A} \\
{2,5 = 3mg – m{\omega ^2}\;A}
\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{c}}
{mg = 2,5} \\
{\;m{\omega ^2}\;A = 5}
\end{array}} \right.} \right.$

$ \Rightarrow {\omega ^2}\;A = 2mg \Rightarrow {\omega ^2}\;A = 2\;g \Rightarrow {v_{max}} = \frac{{2\;g}}{\omega } = \frac{{2.9,8}}{{\frac{{2\pi }}{{0,35}}}} \simeq 1,09\;m/s$

Chọn C

Câu 39: Trong thí nghiệm giao thoa sóng ở mặt chất lỏng, hai nguồn kết hợp đặt tại hai điểm $A$ và $B$, dao động cùng pha theo phương thẳng đứng tạo ra hai sóng lan truyền trên mặt chất lỏng với bước sóng $\lambda $. Gọi $I$ là trung điểm của đoạn thẳng $AB$. Trên $AB$, điểm $P$ là cực đại giao thoa gần $I$ nhất. Trên đường trung trực của $AB$, điểm $Q$ là điểm gần $I$ nhất mà phần tử ở đó dao động ngược pha với dao động của phần tử ở $I$. Biết $QI = \sqrt {13} PI$. Mặt khác, trên nửa đường thẳng $Ax$ xuất phát từ $A$ và vuông góc với $AB$ có điểm $M$ và điểm $N$ là các cực tiểu giao thoa, giữa $M$ và $N$ có hai cực đại giao thoa, $MA = 17\;cm,NA = 5\;cm$. Giá trị của $\lambda $ gần nhất với giá trị nào sau đây?

A. $1,9\;cm$. B. $5,6\;cm$. C. $2,7\;cm$. D. $4,7\;cm$.

Lời giải

Ta có: $PI = \frac{\lambda }{2}$

Mà $Q$ là điểm gần $I$ nhất mà phần tử ở đó dao động ngược pha với dao động của phần tử ở $I$ :

$ \to \sqrt {{{\left( {\frac{{AB}}{2}} \right)}^2} + {{(QI)}^2}} – \frac{{AB}}{2} = \frac{\lambda }{2}$

$ \to \sqrt {{{\left( {\frac{{AB}}{2}} \right)}^2} + {{\left( {\sqrt {13} \frac{\lambda }{2}} \right)}^2}} – \frac{{AB}}{2} = \frac{\lambda }{2} \to AB = 6\lambda $

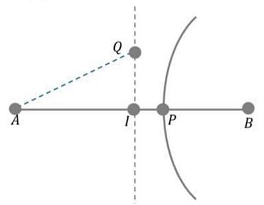
Giả sử $M$ là cực tiểu thứ $k$ ( $k$ bán nguyên), theo giả thiết giữa $M$ và $N$ có hai cực đại giao thoa suy ra $N$ nằm trên cực tiểu $\left( {k – 2} \right)$.

Tại $M:\sqrt {{{(6\lambda )}^2} + {{(17)}^2}} – 17 = \left( {k – 2} \right)\lambda $

Tại $N:\sqrt {{{(6\lambda )}^2} + {{(5)}^2}} – 5 = k\lambda $

Lấy (1) trừ (2) ta được:

$\sqrt {{{(6\lambda )}^2} + {{(17)}^2}} – \sqrt {{{(6\lambda )}^2} + {{(5)}^2}} = 12 – 2\lambda \Rightarrow \lambda = \frac{{20}}{7}\;cm$ thỏa mãn yêu cầu bài toán.

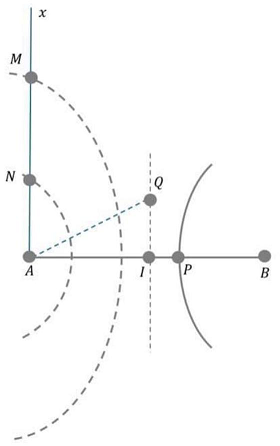
Chọn C

Câu 40: Đặt điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi vào hai đầu đoạn mạch $AB$ như hình H1, trong đó tụ điện có điện dung $C$ thay đổi được. Khi $C = {C_1}$ thì điện áp giữa hai đầu đoạn mạch $AB$ và đoạn mạch $AM$ phụ thuộc vào thời gian $t$ như đồ thị ở hình H2. Khi $C = {C_2}$ thì điện áp hiệu dụng giữa hai đầu đoạn mạch $AM$ là $25\;V$ và hệ số công suất của đoạn mạch $AB$ là $cos\varphi $. Giá trị của$cos\varphi $ là

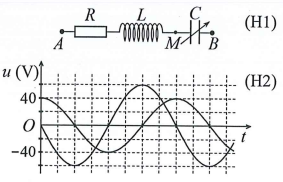
A. 0,87 . B. 0,55 . C. 0,49 . D. 0,83 .

Lời giải

Ta có: ${u_{AM}} = {u_{RL}}$ luôn sớm pha hơn ${u_{AB}} = $ ${u_{RLC}}$

– Khi $C = {C_1}$ thì ${U_{0AM}} = 60\left( {\;V} \right);{U_{0AB}} = 40\left( {\;V} \right)$ và từ đồ thị thấy ${u_{AM}}$ sớm pha $\frac{\pi }{2}$ hơn ${u_{AB}}$

Lúc này $\frac{{cos{\varphi _{AM}}}}{{cos{\varphi _{AB}}}} = \frac{{{U_{0AB}}}}{{{U_{0AM}}}} = \frac{2}{3}$ (do $\left. {cos{\varphi _{AM}} = \frac{{{U_{0R}}}}{{{U_{0AM}}}};cos{\varphi _{AB}} = \frac{{{U_{0R}}}}{{{U_{0AB}}}}} \right)$ và $cos\varphi _{AM}^2 + cos\varphi _{AB}^2 = 1$

$ \to $ giải được $cos{\varphi _{AM}} = \frac{{2\sqrt {13} }}{{13}}$ và $cos{\varphi _{AB}} = \frac{{3\sqrt {13} }}{{13}}$

– Khi C thay đổi thì $cos{\varphi _{AM}} = \frac{R}{{{Z_{AM}}}} = \frac{R}{{\sqrt {{R^2} + Z_L^2} }}$ không đồi $ \to $ khi $C = {C_2}$ thì $cos\varphi _{AM}’ = \frac{{2\sqrt {13} }}{{13}} = \frac{{U_R’}}{{U_{AM}’}}$

$ \to U_R’ = \frac{{2\sqrt {13} }}{{13}} \cdot U_{AM}’ = \frac{{2\sqrt {13} }}{{13}} \cdot 25 = \frac{{50\sqrt {13} }}{{13}}\left( {\;V} \right)$ và ${U_{AB}}$ luôn không đổi $ \to U_{AB}’ = {U_{AB}} = \frac{{40}}{{\sqrt 2 }} = 20\sqrt 2 \left( {\;V} \right)$

$ \to cos\varphi _{AB}’ = \frac{{U_R’}}{{U_{AB}’}} \approx 0,49$

Chọn C