Giải Chi Tiết Đề Thi Tốt Nghiệp THPT 2023 Môn Toán Mã Đề 202

BỘ GIÁO DỤC VÀ ĐÀO TẠO Đề chính thức

KỲ THI TỐT NGHIỆP TRUNG HOC PHỔ THÔNG NĂM 2023 Bài thi: TOÁN – Mã đề: 102 Thời gian làm bài: 90 phút (không kể thời gian phát đề)

HƯỚNG DẪN GIẢI CHI TIẾT THAM KHẢO

Câu 1: Trên mặt phẳng tọa độ, điểm $M\left( { – 2\,;\,2} \right)$ là điểm biểu diễn của số phức nào dưới đây?

A. $ – 2 + 2i$. B. $2 – 2i$. C. $2i$. D. $2 + 2i$.

Lời giải

Chọn A

Điểm $M\left( { – 2\,;\,2} \right)$ là điểm biễu diễn của số phức $ – 2 + 2i$ trên mặt phẳng tọa độ.

Câu 2: Khẳng định nào dưới đây đúng?

A. $\int {{x^5}{\text{d}}x} = 5{x^4} + C$. B. $\int {{x^5}{\text{d}}x} = {x^6} + C$. C. $\int {{x^5}{\text{d}}x} = \frac{1}{6}{x^6} + C$. D. $\int {{x^5}{\text{d}}x} = \frac{{{x^5}}}{{\ln 5}} + C$.

Lời giải

Chọn C

Ta có $\int {{x^5}{\text{d}}x} = \frac{1}{6}{x^6} + C$, với $C$ là hằng số.

Câu 3: Nếu $\int\limits_1^4 {f\left( x \right){\text{d}}x} = 6$ thì $\int\limits_1^4 {2f\left( x \right){\text{d}}x} $ bằng

A. $3$. B. $4$. C. $12$. D. $8$.

Lời giải

Chọn C

Ta có $\int\limits_1^4 {2f\left( x \right){\text{d}}x} = 2 \cdot \int\limits_1^4 {f\left( x \right){\text{d}}x} = 2 \cdot 6 = 12$.

Câu 4: Tập nghiệm của bất phương trình ${\log _2}\left( {3x} \right) > {\log _2}5$

A. $\left( {\frac{5}{3}; + \infty } \right)$. B. $\left( {0;\frac{5}{3}} \right)$. C. $\left( {\frac{3}{5}; + \infty } \right)$. D. $\left( {0;\frac{3}{5}} \right)$.

Lời giải

Chọn A

Ta có: ${\log _2}\left( {3x} \right) > {\log _2}5 \Leftrightarrow \left\{ \begin{gathered}
x > 0 \hfill \\
3x > 5 \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
x > 0 \hfill \\
x > \frac{5}{3} \hfill \\
\end{gathered} \right. \Leftrightarrow x > \frac{5}{3}$.

Câu 5: Với $a$ là số thực dương tùy ý, ${\log _7}\left( {7a} \right)$ là:

A. $1 – {\log _7}a$. B. $1 + {\log _7}a$. C. $1 + a$. D. $a$.

Lời giải

Chọn B

Ta có: ${\log _7}\left( {7a} \right) = 1 + {\log _7}a$

Câu 6: Cho khối chóp có diện tích đáy $B = 9{a^2}$ và chiều cao $h = 2a$. Thể tích của khối chóp đã cho bằng:

A. $3{a^3}$. B. $6{a^3}$. C. $18{a^3}$. D. $24{a^3}$.

Lời giải

Chọn B

Ta có: Thể tích khối chóp là: $V = \frac{1}{3}B.h = \frac{1}{3}.9{a^2}.2a = 6{a^3}$.

Câu 7: Cho hàm số $f\left( x \right)$ liên tục trên $\mathbb{R}$. Biết hàm số $F\left( x \right)$là một nguyên hàm của $f\left( x \right)$ trên $\mathbb{R}$ và $F\left( 1 \right) = 3,F\left( 3 \right) = 6$. Tích phân $\int\limits_1^3 {f\left( x \right)dx} $ bằng

A. $9$. B. $ – 3$. C. $3$. D. $2$.

Lời giải

Chọn C

$\int\limits_1^3 {f\left( x \right)dx} = F\left( 3 \right) – F\left( 1 \right) = 6 – 3 = 3$.

Câu 8: Diện tích đáy của khối lăng trụ có thể tích $V$ và chiều cao $h$ bằng.

A. $\frac{V}{h}$. B. $\frac{{3V}}{h}$. C. $\frac{V}{{3h}}$. D. $V.h$.

Lời giải

Chọn A

Thể tích của khối lăng trụ $V = B.h \Rightarrow B = \frac{V}{h}$ với $B$ là diện tích đáy.

Câu 9: Cho hàm số $y = f\left( x \right)$ có đạo hàm $f’\left( x \right) = {x^3},\,\forall x \in \mathbb{R}$. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

A. $\left( { – \infty ; + \infty } \right)$. B. $\left( { – \infty ;1} \right)$. C. $\left( {0; + \infty } \right)$. D. $\left( { – \infty ;0} \right)$.

Lời giải

Chọn D

Hàm số đã cho nghịch biến $ \Leftrightarrow {x^3} \leqslant 0 \Leftrightarrow x \leqslant 0$.

Câu 10: Đạo hàm của hàm số $y = {\log _3}\left( {x + 1} \right)$ là

A. $y’ = \frac{1}{{\ln 3}}$. B. $y’ = \frac{1}{{\left( {x + 1} \right)\ln 3}}$. C. $y’ = \frac{1}{{x + 1}}$. D. $y’ = \frac{{x = 1}}{{\ln 3}}$.

Lời giải

Chọn B

Áp dụng công thức ${\left( {{{\log }_a}u} \right)^\prime } = \frac{{u’}}{{u\ln a}}$. Ta có

$y’ = \frac{{{{\left( {x + 1} \right)}^\prime }}}{{\left( {x + 1} \right)\ln 3}} = \frac{1}{{\left( {x + 1} \right)\ln 3}}$.

Câu 11: Có bao nhiêu số tự nhiên gồm ba chữ số đôi một khác nhau mà các chữ số được lấy từ tập hợp $\left\{ {1,2,3,4,5,6} \right\}$?

A. $18$. B. $216$. C. $20$. D. $120$.

Lời giải

Chọn D

Số các chữ số thỏa mãn yêu cầu bài toán là một chỉnh hợp chập 3 của 6 phần tử.

Vậy có $A_6^3 = 120$ số.

Câu 12: Cho hàm số $y = a{x^3} + b{x^2} + cx + d$, $\left( {a,b,c,d \in \mathbb{R}} \right)$ có đồ thị là đường cong như hình bên.

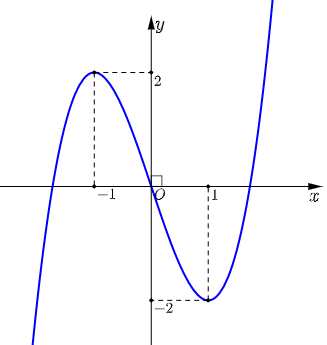
Điểm cực tiểu của hàm số đã cho là

A. $x = 1$. B. $x = – 2$. C. $x = – 1$. D. $x = 2$.

Lời giải

Chọn A

Từ đồ thị ta thấy điểm cực tiểu của hàm số đã cho là $x = 1$.

Câu 13: Tập nghiệm của bất phương trình ${2^x} \geqslant 8$ là

A. $\left[ { – 3; + \infty } \right)$. B. $\left[ {3; + \infty } \right)$. C. $\left( {3; + \infty } \right)$. D. $\left( { – 3; + \infty } \right)$.

Lời giải

Chọn B

Bất phương trình ${2^x} \geqslant 8 \Leftrightarrow {2^x} \geqslant {2^3} \Leftrightarrow x \geqslant 3$.

Vậy tập nghiệm của bất phương trình là $\left[ {3; + \infty } \right)$.

Câu 14: Hàm số nào dưới đây có đồ thị là đường cong trong hình bên?

A. $y = – {x^3} + 3{x^2} + 1$. B. $y = {x^4} – 2{x^2} + 1$. C. $y = {x^3} – 3{x^2}$. D. $y = – {x^4} + 2{x^2}$.

Lời giải

Chọn D

Quan sát đồ thị của hàm số thấy đồ thị trên là đồ thị của hàm số trùng phương và $\mathop {\lim }\limits_{x \to \pm \infty } f(x) = – \infty $ suy ra hệ số $a < 0$. Vậy nên chọn đáp án D.

Câu 15: Cho hàm số $y = f(x)$ có bảng biến thiên như sau

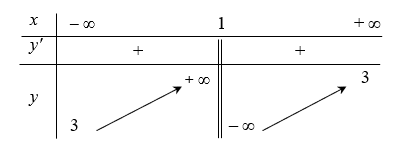
Tiệm cận đứng của đồ thị hàm số đã cho có phương trình là

A. $x = – 1$. B. $x = – 3$. C. $x = 3$. D. $x = 1$.

Lời giải

Chọn D

Quan sát bảng biến thiên ta thấy $\mathop {\lim }\limits_{x \to {1^ + }} f(x) = – \infty $; $\mathop {\lim }\limits_{x \to {1^ – }} f(x) = + \infty $.

Do đó đường thẳng $x = 1$ là tiệm cận đứng của đồ thị hàm số $y = f(x)$.

Câu 16: Với $a$ là số thực dương tùy ý, biểu thức ${a^{\frac{5}{3}}}.\,{a^{\frac{1}{3}}}$ bằng

A. ${a^5}$. B. ${a^{\frac{5}{9}}}$. C. ${a^{\frac{4}{3}}}$. D. ${a^2}$.

Lời giải

Chọn D

Ta có ${a^{\frac{5}{3}}}.\,{a^{\frac{1}{3}}} = {a^{\frac{5}{3} + \frac{1}{3}}} = {a^2}$.

Câu 17: Cho hình nón có bán kính đáy bằng $a$ và chiều cao bằng $\sqrt 3 a$. Độ dài đường sinh của hình nón đã cho bằng

A. $\sqrt 2 a$. B. $2a$. C. $\sqrt {10} a$. D. $4a$.

Lời giải

Chọn B

Độ dài đường sinh bằng $l = \sqrt {{r^2} + {h^2}} = \sqrt {{a^2} + {{\left( {\sqrt 3 a} \right)}^2}} = 2a$.

Câu 18: Cho hình trụ có bán kính đáy bằng $a$ và chiều cao $3a$. Diện tích xung quanh của hình trụ đã cho bằng

A. $8\pi {a^2}$. B. $7\pi {a^2}$. C. $6\pi {a^2}$. D. $14\pi {a^2}$.

Lời giải

Chọn C

Ta có diện tích xung quanh của hình trụ đã cho là $S = 2\pi rh = 2\pi a.3a = 6\pi {a^2}$.

Câu 19: Trong không gian $Oxyz$, hình chiếu vuông góc của điểm $M\left( { – 2;3;1} \right)$ trên trục $Ox$ có toạ độ là

A. $\left( {0;0;1} \right)$. B. $\left( { – 2;0;0} \right)$. C. $\left( {0;3;1} \right)$. D. $\left( {0;3;0} \right)$.

Lời giải

Chọn B

Hình chiếu vuông góc của điểm $M\left( { – 2;3;1} \right)$ trên trục $Ox$ có toạ độ là $\left( { – 2;0;0} \right)$.

Câu 20: Trong không gian $Oxyz$, mặt phẳng $\left( P \right):\frac{x}{3} + \frac{y}{5} + \frac{z}{2} = 1$ cắt trục $Oy$ tại điểm có tọa độ là

A. $\left( {0;5;0} \right)$. B. $\left( {0;3;0} \right)$. C. $\left( {0; – 1;0} \right)$. D. $\left( {0;2;0} \right)$.

Lời giải

Chọn A

Mặt phẳng $\left( P \right):\frac{x}{3} + \frac{y}{5} + \frac{z}{2} = 1$ cắt trục $Oy$, suy ra $\left\{ \begin{gathered}
x = 0 \hfill \\
y = 5 \hfill \\
z = 0 \hfill \\
\end{gathered} \right.$, nên giao điểm có tọa độ là $\left( {0;5;0} \right)$.

Câu 21: Số phức nào dưới đây là số thuần ảo?

A. $ – i$. B. $2$. C. $1 – i$. D. $1 + i$.

Lời giải

Chọn A

Số thuần ảo là $ – i$.

Câu 22: Số điểm giao điểm của đồ thị hàm số $y = {x^2} + 2x$ và trục hoành là

A. $3$. B. $2$. C. $1$. D. $0$.

Lời giải

Chọn B

Xét phương trình: ${x^2} + 2x = 0 \Leftrightarrow x\left( {x + 2} \right) = 0 \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
x = – 2 \hfill \\
\end{gathered} \right.$

Số điểm giao điểm của đồ thị hàm số và trục hoành là $2$.

Câu 23: Trong không gian $Oxyz$, mặt cầu $\left( S \right)$ có tâm $I\left( {1;0; – 1} \right)$ và có bán kính $R = \sqrt 2 $. Phương trình của $\left( S \right)$ là

A. ${\left( {x – 1} \right)^2} + {y^2} + {\left( {z + 1} \right)^2} = \sqrt 2 $. B. ${\left( {x + 1} \right)^2} + {y^2} + {\left( {z – 1} \right)^2} = 2$.

C. ${\left( {x – 1} \right)^2} + {y^2} + {\left( {z + 1} \right)^2} = 2$. D. ${\left( {x – 1} \right)^2} + {y^2} + {\left( {z – 1} \right)^2} = \sqrt 2 $.

Lời giải

Chọn C

Theo bài ra ta có: $\left\{ \begin{gathered}
I\left( {1;0; – 1} \right) \hfill \\
R = \sqrt 2 \hfill \\
\end{gathered} \right.$.

Do đó mặt cầu $\left( S \right)$có phương trình là: ${\left( {x – 1} \right)^2} + {y^2} + {\left( {z + 1} \right)^2} = 2$.

Câu 24: Cho hàm số $y = f(x)$ có đạo hàm $f'(x) = (x + 2)(x – 1)$, $\forall x \in \mathbb{R}$. Số điểm cực trị của hàm số đã cho là

A. $2$. B. $0$. C. $3$. D. $1$.

Lời giải

Chọn A

Xét phương trình $f'(x) = 0$

$ \Leftrightarrow f'(x) = (x + 2)(x – 1) = 0 \Leftrightarrow \left[ \begin{gathered}
x + 2 = 0 \hfill \\
x – 1 = 0 \hfill \\
\end{gathered} \right. \Leftrightarrow \left[ \begin{gathered}
x = – 2 \hfill \\
x = 1 \hfill \\
\end{gathered} \right.$

Ta có bảng xét dấu

Từ bảng xét dấu ta có số điểm cực trị của hàm số đã cho là $2$.

Câu 25: Cho số phức ${z_1} = 2 + 3i$ và ${z_2} = i$. Số phức ${z_1}{z_2}$ bằng

A. $ – 3 + 2i$. B. $2 + 4i$. C. $2 – 3i$. D. $3 – 2i$.

Lời giải

Chọn A

Ta có ${z_1}{z_2} = \left( {2 + 3i} \right)i = 2i + 3{i^2} = – 3 + 2i$

Câu 26: Cho hàm số $f\left( x \right) = 1 + 2\cos 2x$. Khẳng định nào dưới đây đúng?

A. $\int {f\left( x \right){\text{d}}x} = x + 2\sin 2x + C$. B. $\int {f\left( x \right){\text{d}}x} = x + \sin 2x + C$.

C. $\int {f\left( x \right){\text{d}}x} = x – \sin 2x + C$. D. $\int {f\left( x \right){\text{d}}x} = x – 2\sin 2x + C$.

Lời giải

Chọn B

Ta có $\int {f\left( x \right){\text{d}}x} = \int {\left( {1 + 2\cos 2x} \right){\text{d}}x} = \int {1{\text{d}}x{\text{ }}} {\text{ + 2}}\int {\cos 2x{\text{d}}x} = x + \sin 2x + C$

Câu 27: Trong không gian ${\text{Ox}}yz$, phương trình đường thẳng $d$ đi qua điểm $M\left( { – 3;\, – 1;\,2} \right)$ và có một vectơ chỉ phương $\overrightarrow u = \left( {4;3; – 2} \right)$ là

A. $\frac{{x – 4}}{{ – 3}} = \frac{{y – 3}}{{ – 1}} = \frac{{z + 2}}{2}$. B. $\frac{{x – 3}}{4} = \frac{{y – 1}}{3} = \frac{{z + 2}}{{ – 2}}$.

C. $\frac{{x + 3}}{4} = \frac{{y + 1}}{3} = \frac{{z – 2}}{{ – 2}}$. D. $\frac{{x + 4}}{{ – 3}} = \frac{{y + 3}}{{ – 1}} = \frac{{z – 2}}{2}$.

Lời giải

Chọn C

Đường thẳng $d$ đi qua điểm $M\left( { – 3;\, – 1;\,2} \right)$ và có một vectơ chỉ phương $\overrightarrow u = \left( {4;3; – 2} \right)$ có phương trình chính tắc là $\frac{{x + 3}}{4} = \frac{{y + 1}}{3} = \frac{{z – 2}}{{ – 2}}$.

Câu 28: Cho cấp số nhân $\left( {{u_n}} \right)$ với ${u_1} = 2$ và ${u_2} = 8$. Công bội của cấp số nhân bằng

A. $4$. B. $ – 6$. C. $\frac{1}{4}$. D. $6$.

Lời giải

Chọn A

Công bội của cấp số nhân là $q = \frac{{{u_2}}}{{{u_1}}} = \frac{8}{2} = 4$.

Câu 29: Đường gấp khúc $ABC$ trong hình bên dưới là đồ thị của hàm số $y = f\left( x \right)$ trên đoạn $\left[ { – 1;4} \right]$.

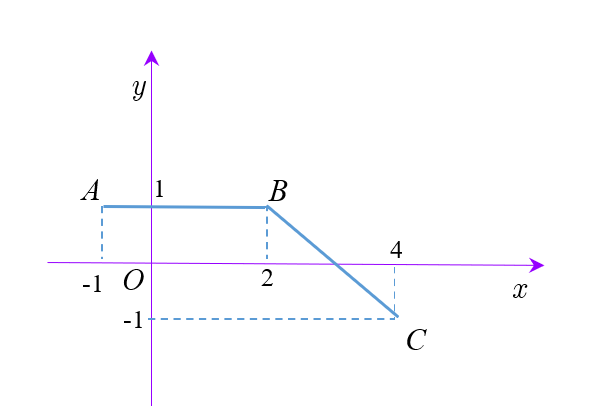
Tích phân $\int\limits_{ – 1}^4 {f\left( x \right)dx} $ bằng

A. $\frac{7}{2}$. B. $\frac{9}{2}$. C. $3$. D. $4$.

Lời giải

Chọn C

Đường thẳng đi qua $AB$ có phương trình $y = 1$.

Đường thẳng đi qua $BC$ có phương trình $y = – x + 3$.

Do đó $f\left( x \right) = \left\{ \begin{gathered}
1\,\,khi\,\,x \in \left[ { – 1;2} \right] \hfill \\
– x + 3\,\,khi\,\,x \in \left[ {2;4} \right] \hfill \\
\end{gathered} \right.$.

Vậy $\int\limits_{ – 1}^4 {f\left( x \right)dx} = \int\limits_{ – 1}^2 {f\left( x \right)dx} + \int\limits_2^4 {f\left( x \right)dx} = \int\limits_{ – 1}^2 {1dx} + \int\limits_2^4 {\left( { – x + 3} \right)dx} = 3$.

(*) Cách 2:

$\int\limits_{ – 1}^4 {f\left( x \right)dx} = {S_{ABED}} + {S_{BEI}} – {S_{ICJ}} = {S_{ABED}} = 3 \times 1 = 3$.

Câu 30: Hàm số $y = {x^4} – 2{x^2}$ nghịch biến trên khoảng nào dưới đây?

A. $\left( {1; + \infty } \right)$. B. $\left( { – \infty ; – 1} \right)$. C. $\left( { – 1;0} \right)$. D. $\left( { – \infty ;1} \right)$.

Lời giải

Chọn B

Ta có $y’ = 4{x^3} – 4x$, $y’ = 0 \Leftrightarrow 4{x^3} – 4x = 0 \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
x = – 1 \hfill \\
x = 1 \hfill \\
\end{gathered} \right.$

Bảng biến thiên

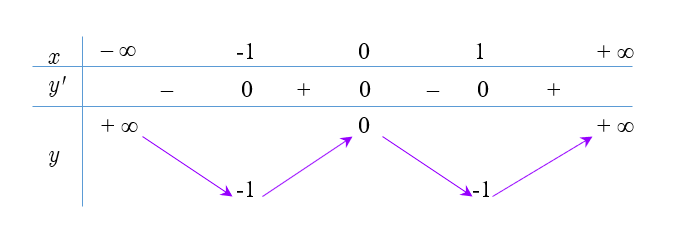
Hàm số $y = {x^4} – 2{x^2}$ nghịch biến trên khoảng $\left( { – \infty ; – 1} \right)$

Câu 31: Cho hình chóp đều $S.ABCD$ có độ dài tất cả các cạnh bằng $a$. Góc giữa hai đường thẳng $SB$ và $CD$ bằng

A. $30^\circ $. B. $45^\circ $. C. $60^\circ $. D. $90^\circ $.

Lời giải

Chọn C

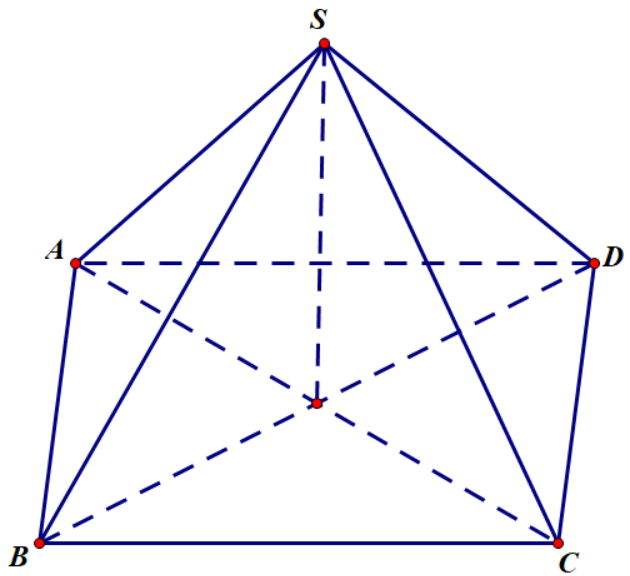
Ta có $CD{\text{ // }}AB$ nên $\left( {\widehat {SB,CD}} \right) = \left( {\widehat {SB,AB}} \right) = \widehat {SBA}$.

Vì tam giác $SAB$ là tam giác đều có tất cả cách cạnh đều bằng $a$ nên $\widehat {SBA} = 60^\circ $.

Vậy góc giữa hai đưởng thẳng $SB$ và $CD$ bằng $60^\circ $.

Câu 32: Trong không gian $Oxyz$, cho điển $A\left( {1; – 1;1} \right)$ và mặt phẳng $\left( P \right):2x + 3y + z – 5 = 0$. Đưởng thẳng đi qua $A$ và vuông góc với $\left( P \right)$ có phương trình là

A. $\left\{ \begin{gathered}
x = 2 + t \hfill \\
y = 3 – t \hfill \\
z = 1 + t \hfill \\
\end{gathered} \right.$. B. $\left\{ \begin{gathered}
x = 1 + 2t \hfill \\
y = – 1 + 3t \hfill \\
z = 1 + t \hfill \\
\end{gathered} \right.$. C. $\left\{ \begin{gathered}
x = 1 + 2t \hfill \\
y = – 1 + 3t \hfill \\
z = – 1 + t \hfill \\
\end{gathered} \right.$. D. $\left\{ \begin{gathered}
x = 1 + 2t \hfill \\
y = – 1 – 3t \hfill \\
z = 1 + t \hfill \\
\end{gathered} \right.$.

Lời giải

Chọn B

Đường thẳng đi qua $A\left( {1; – 1;1} \right)$ và vuông góc với $\left( P \right):2x + 3y + z – 5 = 0$ nhận vectơ pháp tuyến của $\left( P \right)$ là $\overrightarrow n = \left( {2;3;1} \right)$ làm vectơ chỉ phương nên có phương trình là $\left\{ \begin{gathered}
x = 1 + 2t \hfill \\
y = – 1 + 3t \hfill \\
z = 1 + t \hfill \\
\end{gathered} \right.$, $t \in \mathbb{R}$.

Câu 33: Cho hàm số bậc bốn $y = f\left( x \right)$ có đồ thị là đường cong trong hình bên dưới.

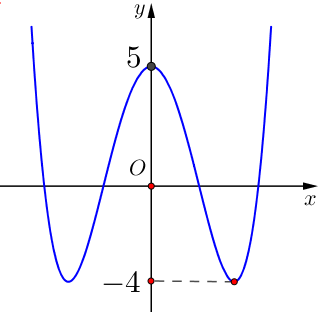
Có bao nhiêu giá trị nguyên của tham số $m$ sao cho ứng với mỗi $m$, phương trình $2f\left( x \right) = m$ có 4 nghiệm thực phân biệt?

A. $4$. B. $16$. C. $17$. D. $8$.

Lời giải

Chọn C

Ta có $2f\left( x \right) = m$$ \Leftrightarrow f\left( x \right) = \frac{m}{2}$.

Dựa vào đồ thị, phương trình trên có 4 nghiệm thực phân biệt khi và chỉ khi $ – 4 < \frac{m}{2} < 5 \Leftrightarrow – 8 < m < 10$.

Suy ra, các giá trị nguyên của tham số $m$ thỏa mãn yêu cầu bài toán là: $ – 7\,;\, – 6\,;\, \ldots \,;\, – 1\,;\,0\,;\,1\,;\, \ldots \,;\,9.$

Có tất cả $17$ số $m$ thỏa mãn.

Câu 34: Trong không gian $Oxyz$, cho hai điểm $A\left( {1;2;3} \right)$ và $B\left( { – 1;0;5} \right)$. Phương trình mặt cầu đường kính $AB$ là?

A. ${x^2} + {\left( {y – 1} \right)^2} + {\left( {z – 4} \right)^2} = 3$. B. ${x^2} + {\left( {y – 1} \right)^2} + {\left( {z – 4} \right)^2} = 12$.

C. ${x^2} + {\left( {y + 1} \right)^2} + {\left( {z + 4} \right)^2} = 3$. D. ${x^2} + {\left( {y + 1} \right)^2} + {\left( {z + 4} \right)^2} = 12$.

Lời giải

Chọn A

Mặt cầu đường kính $AB$ có tâm là trung điểm $I\left( {0;1;4} \right)$ của $AB$ và bán kính $R = \frac{{AB}}{2} = \frac{{\sqrt {{{\left( { – 1 – 1} \right)}^2} + {{\left( {0 – 2} \right)}^2} + {{\left( {5 – 3} \right)}^2}} }}{2} = \sqrt 3 $, có phương trình là ${x^2} + {\left( {y – 1} \right)^2} + {\left( {z – 4} \right)^2} = 3$.

Câu 35: Cho hình hộp chữ nhật $ABCD.A’B’C’D’$ có $AB = 1,BC = 2;AA’ = 3$ (tham khảo hình vẽ).

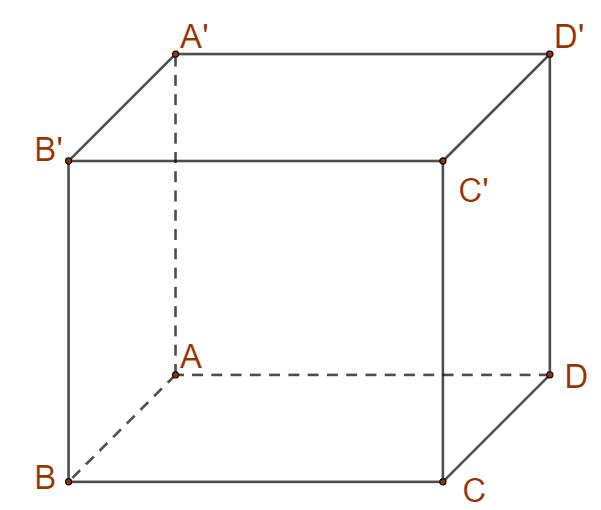
Khoảng cách giữa hai đường $AB’$ và $BC’$ bằng?

A. $\frac{6}{7}$. B. $\frac{{6\sqrt {13} }}{{13}}$. C. $\frac{7}{6}$. D. $\frac{{3\sqrt {10} }}{{10}}$.

Lời giải

Chọn A

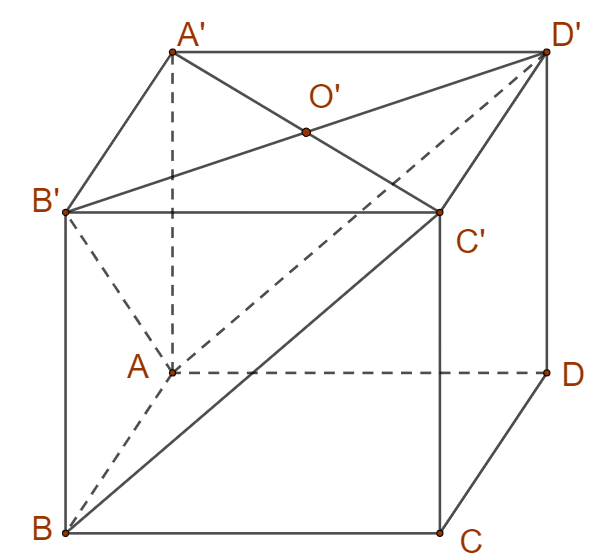
Ta có

$\begin{gathered}
BC’//AD’ \Rightarrow d\left( {AB’,BC’} \right) = d\left( {BC’,\left( {AB’D’} \right)} \right) = d\left( {C’;\left( {AB’D’} \right)} \right) \hfill \\
= \frac{{C’O’}}{{A’O’}}d\left( {A’,\left( {AB’D’} \right)} \right) = d\left( {A’,\left( {AB’D’} \right)} \right) \hfill \\
\end{gathered} $.

Lại có $A’B’,A’A,A’D$ đôi một vuông góc với nhau tại $A’,d\left( {A’,\left( {AB’D’} \right)} \right) = h$ thì $\frac{1}{{{h^2}}} = \frac{1}{{A’B{‘^2}}} + \frac{1}{{A’D{‘^2}}} + \frac{1}{{AA{‘^2}}} \Rightarrow h = \frac{6}{7}$.

Câu 36: Tập xác định của hàm số $f\left( x \right) = {\log _5}\left( {30 – {x^2}} \right)$ chứa bao nhiêu số nguyên?

A. $11$. B. $5$. C. $6$. D. $10$.

Lời giải

Chọn A

Điều kiện $30 – {x^2} > 0 \Leftrightarrow {x^2} < 30 \Leftrightarrow – \sqrt {30} < x < \sqrt {30} $.

Do $x \in \mathbb{Z} \Rightarrow x \in \left\{ { – 5; – 4; – 3; – 2; – 1;0;1;2;3;4;5} \right\}$. Vậy Chọn A

Câu 37: Cho số phức $z$ thỏa mãn $z – 2\overline z = 1 + 6i$. Môđun $z$ bằng

A. $5$. B. $\sqrt 3 $. C. $\sqrt 5 $. D. $3$.

Lời giải

Chọn C

Đặt $z = x + yi{\text{ }}\left( {x,y \in \mathbb{R}} \right)$.

Theo giả thiết ta có $x + yi – {\text{2}}\left( {x – yi} \right) = 1 + 6i \Leftrightarrow \left\{ \begin{gathered}
x = – 1 \hfill \\
y = 2 \hfill \\
\end{gathered} \right..$

Do đó $z = – 1 + 2i$.

Vậy $\left| z \right| = \sqrt 5 $.

Câu 38: Gọi $S$ là tập hợp tất cả các số tự nhiên có hai chữ số khác nhau. Chọn ngẫu nhiên một số từ $S$, xác suất để chọn được số có tổng hai chữ số bằng $8$ là

A. $\frac{4}{{81}}$. B. $\frac{1}{9}$. C. $\frac{7}{{81}}$. D. $\frac{8}{{81}}$.

Lời giải

Chọn C

Gọi $\overline {ab} $ là số tự nhiên có hai chữ số khác nhau.

Chọn $a$ có $9$cách.

Chọn $b$ có $9$ cách.

Do đó có $9.9 = 81$ số có hai chữ số khác nhau.

Gọi $A$ là biến cố: “Chọn được số có tổng hai chữ số bằng $8$”.

Khi đó $A = \left\{ {80,71,62,53,35,26,17} \right\}$

Vậy $P\left( A \right) = \frac{7}{{81}}$.

Câu 39: Cho hàm số bậc hai $y = f\left( x \right)$ có đồ thị $\left( P \right)$ và đường thẳng $d$ cắt $\left( P \right)$ tại hai điểm như trong hình bên dưới.

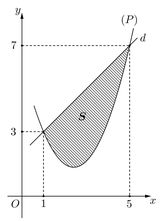
Biết rằng hình phẳng giới hạn bởi $\left( P \right)$ và $d$ có diện tích $S = \frac{{32}}{3}$. Tích phân $\int\limits_1^5 {\left( {2x – 5} \right)f’\left( x \right)} dx$ bằng:

A. $\frac{{104}}{3}$. B. $\frac{{76}}{3}$. C. $\frac{{22}}{3}$. D. $\frac{{188}}{3}$.

Lời giải

Chọn B

Đặt $\left\{ \begin{gathered}
u = 2x – 5 \hfill \\
{\text{d}}v = f’\left( x \right){\text{d}}x \hfill \\
\end{gathered} \right. \Rightarrow \left\{ \begin{gathered}
{\text{d}}u = 2{\text{d}}x \hfill \\
v = f\left( x \right) \hfill \\
\end{gathered} \right.$.

Ta có: $\int\limits_1^5 {\left( {2x – 5} \right)f’\left( x \right)} {\kern 1pt} {\kern 1pt} {\text{d}}x = \left. {\left[ {\left( {2x – 5} \right)f\left( x \right)} \right]} \right|_1^5 – 2\int\limits_1^5 {f\left( x \right)} {\kern 1pt} {\kern 1pt} {\text{d}}x$

$ = 5f\left( 5 \right) + 3f\left( 1 \right) – 2\left[ {\frac{{\left( {3 + 7} \right).4}}{2} – \frac{{32}}{3}} \right] = \frac{{76}}{3}$.

Câu 40: Có bao nhiêu giá trị nguyên của tham số $m$ sao cho ứng với mỗi $m$, hàm số $y = \frac{1}{3}{x^3} – {x^2} – mx + \frac{2}{3}$ có đúng một điểm cực trị thuộc khoảng $\left( {0;6} \right)$?

A. $24$. B. $25$. C. $26$. D. $23$.

Lời giải

Chọn A

Ta có: $y’ = {x^2} – 2x – m = 0 \Leftrightarrow f\left( x \right) = {x^2} – 2x = m\,\,\,\,\left( * \right)$.

BBT cho hàm số $f\left( x \right)$

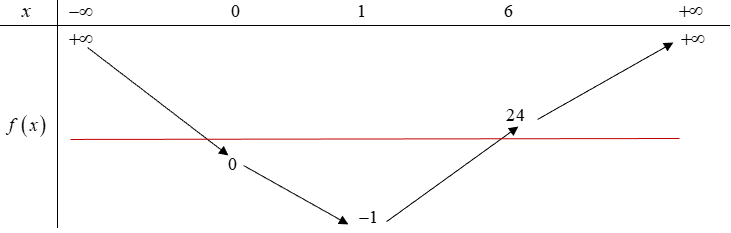
Hàm số có đúng một điểm cực trị thuộc khoảng $\left( {0;6} \right)$ khi $0 \leqslant m < 24$.

Vì $m \in \mathbb{Z}$ nên $m \in \left\{ {0;1;2;…;23} \right\}$. Vậy có tất cả 24 giá trị nguyên của $m$.

Câu 41: Có bao nhiêu giá trị số nguyên $x$ thỏa mãn $\left( {{3^x} – 27} \right)\left( {\log _3^2x – 7{{\log }_3}x + 10} \right) < 0$

A. $242$. B. $235$. C. $233$. D. $238$.

Lời giải

Chọn B

Đặt $f\left( x \right) = \left( {{3^x} – 27} \right)\left( {\log _3^2x – 7{{\log }_3}x + 10} \right)$. ĐK: $x > 0$.

$f\left( x \right) = 0 \Leftrightarrow \left[ \begin{gathered}
{3^x} = 27 \hfill \\
{\log _3}x = 2 \hfill \\
{\log _3}x = 5 \hfill \\
\end{gathered} \right. \Leftrightarrow \left[ \begin{gathered}
x = 3 \hfill \\
x = 9 \hfill \\
x = 243 \hfill \\
\end{gathered} \right.$.

Bảng xét dấu:

Dựa vào bảng xét dấu suy ra tập nghiệm của bất phương trình $S = \left( {0;3} \right) \cup \left( {9;243} \right)$.

Vậy $x \in \left\{ {1;2;10;11;…;242} \right\}$.

Câu 42: Trong không gian $Oxyz$, cho mặt cầu $\left( S \right):{\left( {x – 1} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z + 1} \right)^2} = 4$ và đường thẳng $d$ đi qua điểm $A\left( {1;0; – 2} \right)$ nhận $\overrightarrow u = \left( {1;a;4 – a} \right)$ (với $a \in \mathbb{R}$) làm vectơ chỉ phương. Biết rằng $d$ cắt $\left( S \right)$ tại hai điểm phân biệt mà các tiếp diện của $\left( S \right)$ tại hai điểm đó vuông góc với nhau. Hỏi ${a^2}$ thuộc khoảng nào dưới đây?

A. $\left( {8;\frac{{17}}{2}} \right)$. B. $\left( {25;\frac{{51}}{2}} \right)$. C. $\left( {\frac{{23}}{2};12} \right)$. D. $\left( {\frac{3}{2};2} \right)$.

Lời giải

Chọn C

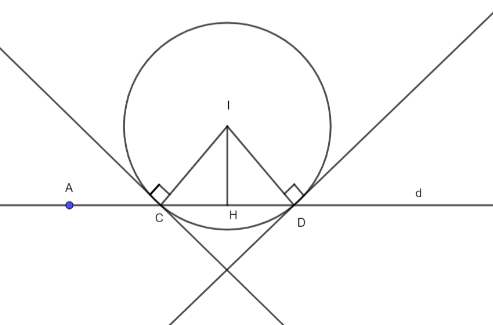
Mặt cầu $\left( S \right)$ có tâm $I\left( {1; – 2; – 1} \right)$ bán kính $R = 2$

Gọi $C,D$ là các giao điểm của $d$ với mặt cầu. Từ giả thiết bài ra suy ra $\Delta ICD$ vuông cân tại $I$, có $IC = ID = 2 \Rightarrow d\left( {I;d} \right) = IH = \frac{1}{2}CD = \frac{{2\sqrt 2 }}{2} = \sqrt 2 $.

Ta lại có $d\left( {I;d} \right) = \frac{{\left| {\left[ {\overrightarrow {IA} ,\overrightarrow u } \right]} \right|}}{{\left| {\overrightarrow u } \right|}} = \sqrt 2 \Leftrightarrow \frac{{\sqrt {{a^2} – 16a + 69} }}{{\sqrt {2{a^2} – 8a + 17} }} = \sqrt 2 $

$ \Leftrightarrow {a^2} – 16a + 69 = 4{a^2} – 16a + 34 \Leftrightarrow 3{a^2} = 35 \Leftrightarrow {a^2} = \frac{{35}}{3} \in \left( {\frac{{23}}{2};12} \right)$.

Câu 43: Cho hình lập phương $ABCD.A’B’C’D’$ có cạnh bằng $2$. Xét hình nón $\left( N \right)$ có đáy nằm trên mặt phẳng $\left( {ABCD} \right)$ và mặt xung quanh đi qua bốn điểm $A’;B’;C’;D’$. Khi bán kính đáy của $\left( N \right)$ bằng $2\sqrt 2 $, diện tích xung quanh của $\left( N \right)$ bằng

A. $8\sqrt 2 \pi $. B. $8\sqrt 3 \pi $. C. $8\sqrt 6 \pi $. D. $4\sqrt 2 \pi $.

Lời giải

Chọn B

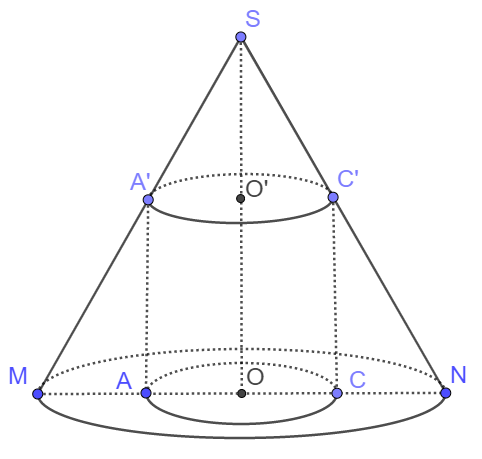
Theo đề ra, ta có: $MN = 4\sqrt 2 = 2R$$ \Rightarrow AC = 2\sqrt 2 $.

Mặt khắc: $\frac{{SO’}}{{SO}} = \frac{{O’A’}}{{OM}}$$ \Leftrightarrow \frac{{SO – 2}}{{SO}} = \frac{1}{2} \Leftrightarrow SO = 4 = h$.

Lại có: $l = \sqrt {{h^2} + {R^2}} = \sqrt {{4^2} + {{\left( {2\sqrt 2 } \right)}^2}} = 2\sqrt 6 $.

Vậy ${S_{xq}} = \pi Rl = 8\pi \sqrt 3 $.

Câu 44: Gọi $S$ là tập hợp các số phức $z = a + bi{\text{ }}\left( {a,b \in \mathbb{R}} \right)$ thỏa mãn $\left| {z + \overline z } \right| + \left| {z – \overline z } \right| = 4$ và $ab > 0.$ Xét ${z_1}$ và ${z_2}$ thuộc $S$ sao cho $\frac{{{z_1} – {z_2}}}{{1 + i}}$ là số thực dương. Giá trị nhỏ nhất của biểu thức $\left| {{z_1}} \right| + \left| {{z_2} – 2i} \right|$ bằng

A. $2\sqrt 2 $. B. $2$. C. $2\sqrt 5 $. D. $2 + 2\sqrt 2 $.

Lời giải

Chọn A

Đầu tiên ta có $z = a + bi{\text{ }}\left( {a,b \in \mathbb{R}} \right)$ thì khi đó$\left| {z + \overline z } \right| + \left| {z – \overline z } \right| = 4 \Leftrightarrow \left| a \right| + \left| b \right| = 2,{\text{ }}ab > 0.$

Do $\frac{{{z_1} – {z_2}}}{{1 + i}}$ là số thực dương nên khi $M\left( {{z_1}} \right),N\left( {{z_2}} \right)$ thì ta có:

$\overrightarrow {OM} – \overrightarrow {ON} = \overrightarrow {NM} = k\left( {1 + i} \right) = k\overrightarrow {OE} \left( {k \in {\mathbb{R}^ + }} \right)$ với $E\left( {1;1} \right).$

Do $ab > 0$ nên tập hợp các điểm $M,N$ thuộc $S$ biểu diễn như hình vẽ sau:

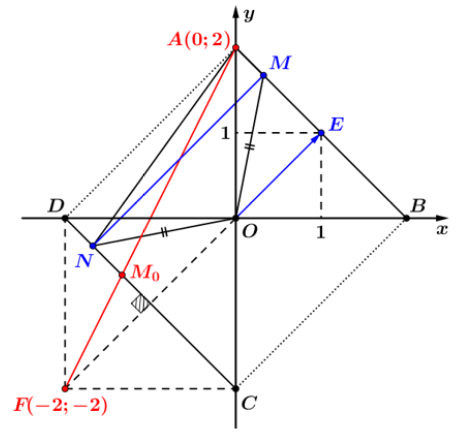
Gọi $F\left( { – 2; – 2} \right)$ là điểm đối xứng với $O$ qua đoạn thẳng $CD$

Suy ra $P = \left| {{z_1}} \right| + \left| {{z_2} – 2i} \right| = MO + NA = NO + NA = NF + NA \geqslant FA = 2\sqrt 5 $

Dấu bằng xảy ra khi và chỉ khi $M \equiv {M_0} = AF \cap CD.$ Chọn đáp án $C$.

Câu 45: Trên tập số phức, xét phương trình ${z^2} + az + b = 0$ $\left( {a,b \in \mathbb{R}} \right)$. Có bao nhiêu cặp số $\left( {a,b} \right)$ để phương trình đó có hai nghiệm phân biệt ${z_1},\,\,{z_2}$ thỏa mãn $\left| {{z_1} + 1} \right| = 2$ và $\left| {{z_2} – 3 + 2i} \right| = 4$?

A. $2$. B. $4$. C. $6$. D. $5$.

Lời giải

Chọn C

Ta có $\Delta = {a^2} – 4b$.

TH1: ${a^2} – 4b > 0$, phương trình có hai nghiệm thực ${z_1},\,\,{z_2}$. Khi đó

$\left\{ \begin{gathered}
\left| {{z_1} + 1} \right| = 2 \hfill \\
\left| {{z_2} – 3 + 2i} \right| = 4 \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
{z_1} + 1 = \pm 2 \hfill \\
\sqrt {{{\left( {{z_2} – 3} \right)}^2} + 4} = 4 \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
\left[ \begin{gathered}
{z_1} = 1 \hfill \\
{z_1} = – 3 \hfill \\
\end{gathered} \right. \hfill \\
{z_2} = 3 \pm 2\sqrt 3 \hfill \\
\end{gathered} \right.$, suy ra có 4 cặp $\left( {a,b} \right)$ thỏa mãn.

TH2: ${a^2} – 4b < 0$, phương trình có hai nghiệm phức liên hợp ${z_1} = x + yi$, ${z_2} = x – yi$. $x,\,\,y \in \mathbb{R}$; $y \ne 0$. Theo giả thiết, ta có: $\left\{ \begin{gathered}
\left| {{z_1} + 1} \right| = 2 \hfill \\
\left| {{z_2} – 3 + 2i} \right| = 4 \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
\sqrt {{{\left( {x + 1} \right)}^2} + {y^2}} = 2 \hfill \\
\sqrt {{{\left( {x – 3} \right)}^2} + {{\left( { – y + 2} \right)}^2}} = 4 \hfill \\
\end{gathered} \right.$

$ \Leftrightarrow \left\{ \begin{gathered}
{x^2} + {y^2} + 2x – 3 = 0 \hfill \\
{x^2} + {y^2} – 6x – 4y – 3 = 0 \hfill \\
\end{gathered} \right.$$ \Leftrightarrow \left\{ \begin{gathered}
2x + y = 0 \hfill \\
{x^2} + {y^2} + 2x – 3 = 0 \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
x = – 1 \hfill \\
y = 2 \hfill \\
\end{gathered} \right.$ hoặc $\left\{ \begin{gathered}
x = \frac{3}{5} \hfill \\
y = – \frac{6}{5} \hfill \\
\end{gathered} \right.$.

Suy ra ${z_1} = – 1 + 2i,\,\,{z_2} = – 1 – 2i$ hoặc ${z_1} = \frac{3}{5} – \frac{6}{5}i$, ${z_2} = \frac{3}{5} + \frac{6}{5}i$; do đó có 2 cặp $\left( {a,b} \right)$ thỏa mãn điều kiện ${a^2} – 4b < 0$ trong trường hợp này.

Vậy có tất cả có 6 cặp $\left( {a,b} \right)$ thỏa yêu cầu bài.

Câu 46: Cho khối lăng trụ $ABC.A’B’C’$ có $AC’ = 8$, diện tích của tam giác $A’BC$ bằng 9 và đường thẳng $AC’$ tạo với mặt phẳng $\left( {A’BC} \right)$ một góc $30^\circ $. Thể tích của khối lăng trụ đã cho bằng

A. $6$. B. $18$. C. $6\sqrt 3 $. D. $18\sqrt 3 $.

Lời giải

Chọn B

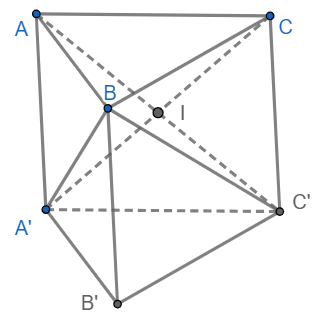
Gọi $I$ là giao điểm của $AC’$ và $A’C$ nên $I$ là trung điểm của $AC’$.

Dễ thấy ${V_{A.A’BC}} = {V_{C’.A’BC}} = {V_{B.A’B’C’}}$ ⇒ ${V_{ABC.A’B’C’}} = 3{V_{A.A’BC}}$.

Do đường thẳng $AC’$ tạo với mặt phẳng $\left( {A’BC} \right)$ một góc $30^\circ $

⇒$AI$ tạo với mặt phẳng $\left( {A’BC} \right)$ một góc $30^\circ $.

⇒ ${d_{\left( {A,\left( {A’BC} \right)} \right)}} = AI.\sin 30^\circ = \frac{{AC’}}{2}.\sin 30^\circ = 2$.

Vậy ${V_{ABC.A’B’C’}} = 3{V_{A.A’BC}} = 3.\frac{1}{3}.{S_{\Delta A’BC}}.{d_{\left( {A,\left( {A’BC} \right)} \right)}} = 9.2 = 18.$

Câu 47: Gọi $S$ là tập hợp các giá trị nguyên của $y$sao cho ứng với mỗi $y$, tồn tại duy nhất một giá trị $x \in \left[ {\frac{5}{2};\frac{{11}}{2}} \right]$thỏa mãn ${\log _2}\left( {{x^3} – 9{x^2} + 24x + y} \right) = {\log _3}\left( { – {x^2} + 8x – 7} \right)$. Số phần tử của $S$ bằng

A. $8$. B. $7$. C. $3$. D. $1$.

Lời giải

Chọn B

Ta có ${x^3} – 9{x^2} + 24x + y = {2^{{{\log }_3}\left( { – {x^2} + 8x – 7} \right)}}$$ \Leftrightarrow y = {2^{{{\log }_3}\left( { – {x^2} + 8x – 7} \right)}} – {x^3} + 9{x^2} – 24x$

Xét hàm số $f\left( x \right) = {2^{{{\log }_3}\left( { – {x^2} + 8x – 7} \right)}} – {x^3} + 9{x^2} – 24x,\forall x \in \left[ {\frac{5}{2};\frac{{11}}{2}} \right]$

$f’\left( x \right) = {2^{{{\log }_3}\left( { – {x^2} + 8x – 7} \right)}}.\ln 2.\frac{{ – 2x + 8}}{{\left( { – {x^2} + 8x – 7} \right)\ln 3}} – 3{x^2} + 18x – 24$

$ = – 3\left( {x – 2} \right)\left( {x – 4} \right) – \frac{{2\left( {x – 4} \right)}}{{\left( { – {x^2} + 8x – 7} \right)\ln 3}}{.2^{{{\log }_3}\left( { – {x^2} + 8x – 7} \right)}}.\ln 2$

$f’\left( x \right) = \Leftrightarrow \left[ \begin{gathered}
x = 4 \hfill \\
– 3\left( {x – 2} \right) – \frac{2}{{\left( { – {x^2} + 8x – 7} \right)\ln 3}}{.2^{{{\log }_3}\left( { – {x^2} + 8x – 7} \right)}}.\ln 2 = 0 \hfill \\
\end{gathered} \right.$.

Ta có:

$ – {x^2} + 8x – 7 > 0,\,\forall x \in \left[ {\frac{5}{2};\frac{{11}}{2}} \right] \Rightarrow – 3\left( {x – 2} \right) – \frac{2}{{\left( { – {x^2} + 8x – 7} \right)\ln 3}}{.2^{{{\log }_3}\left( { – {x^2} + 8x – 7} \right)}}.\ln 2 < 0,\,\,\forall x \in \left[ {\frac{5}{2};\frac{{11}}{2}} \right]$

Bảng biến thiên

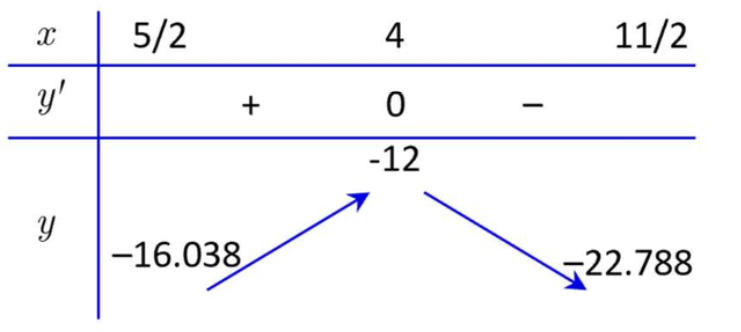
Yêu cầu bài toán suy ra $\left[ \begin{gathered}
y = – 12 \hfill \\
– 22.788 \leqslant y < 16.038 \hfill \\
\end{gathered} \right.$

Do $y \in \mathbb{Z}$nên ta được tập các giá trị của $y$là $\left\{ { – 22; – 21; – 20; – 19; – 18; – 17; – 12} \right\}.$

Vậy có 7 giá trị thỏa mãn.

Câu 48: Cho hàm số $f(x)$ nhận giá trị dương trên khoảng $(0; + \infty )$, có đạo hàm trên khoảng đó và thỏa mãn $f(x)\ln f(x) = x\left( {f(x) – f'(x)} \right),\forall x \in (0; + \infty )$. Biết $f(1) = f(4)$, giá trị $f(2)$ thuộc khoảng nào dưới đây?

A. $\left( {1;3} \right)$. B. $\left( {8;10} \right)$. C. $\left( {6;8} \right)$. D. $\left( {13;15} \right)$.

Lời giải

Chọn C

Ta có $f(x)\ln f(x) = x\left( {f(x) – f'(x)} \right) \Leftrightarrow \ln f(x) = x\left( {1 – \frac{{f'(x)}}{{f(x)}}} \right) \Leftrightarrow \ln f(x) = x\left( {1 – (\ln f(x))’} \right)$

$ \Leftrightarrow (x)’\ln f(x) + x{\left[ {\ln f(x)} \right]^\prime } = x \Leftrightarrow {\left[ {x\ln f(x)} \right]^\prime } = x$$ \Rightarrow $ $x\ln f(x) = \int x dx = \frac{1}{2}{x^2} + C$.

Cho $x = 1$ ta được $\ln f(1) = \frac{1}{2} + C$.

Cho $x = 4$ ta được $4\ln f(4) = 8 + C$.

Theo đề $f\left( 1 \right) = f\left( 4 \right)$ nên suy ra $2 + 4C = 8 + C \Rightarrow C = 2$ nên $f\left( x \right) = {e^{\frac{x}{2} + \frac{2}{x}}}$.

Vậy $f\left( 2 \right) = {e^2} \approx 7,39$.

Câu 49: Trong không gian $Oxyz$, xét mặt cầu $\left( S \right)$ có tâm $I\left( {3;7;12} \right)$ và bán kính $R$ thay đổi. Có bao nhiêu giá trị nguyên của $R$ sao cho ứng với mỗi giá trị đó, tồn tại hai tiếp tuyến của $\left( S \right)$ trong mặt phẳng $\left( {Oyz} \right)$ mà hai tiếp tuyến đó cùng đi qua $O$ và góc giữa chúng không nhỏ hơn $60^\circ $?

A. $11$. B. $7$. C. $5$. D. $3$.

Lời giải

Chọn C

Để tồn tại tiếp tuyến thì mặt cầu $\left( S \right)$ phải cắt hoặc tiếp xúc mặt phẳng $\left( {Oyz} \right)$ nên $R \geqslant 3$.

Gọi $J$ là hình chiếu của $I$ lên mặt phẳng $\left( {Oyz} \right)$ ta có $J\left( {0;7;12} \right)$ và $IJ = 3$ và $OJ = \sqrt {193} $.

Xét 2 tiếp tuyến đi qua $O$ và tiếp xúc với $\left( C \right)$ tại $K,H$ như hình vẽ.

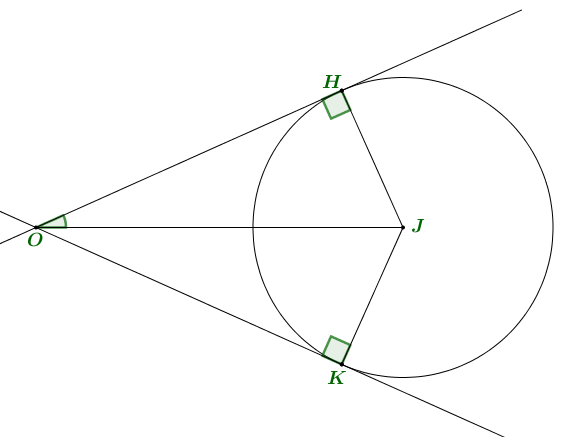
Từ đề bài ta có $OJ.\sin 60^\circ > r \geqslant OJ.\sin 30^\circ \Leftrightarrow \frac{{\sqrt {193} }}{2} \leqslant r < \sqrt {193} .\frac{{\sqrt 3 }}{2}$, với $r = JK = JH$.

Mà $d\left( {I\,,\,\left( {Oyz} \right)} \right) = IJ = 3$ nên:

$\frac{{193}}{4} + {d^2}\left( {I\,,\,\left( {Oyz} \right)} \right) \leqslant {r^2} + {d^2}\left( {I\,,\,\left( {Oyz} \right)} \right) < \frac{{579}}{4} + {d^2}\left( {I\,,\,\left( {Oyz} \right)} \right)$

$ \Leftrightarrow \frac{{193}}{4} + 9 \leqslant {R^2} < \frac{{579}}{4} + 9 \Leftrightarrow \frac{{229}}{4} \leqslant {R^2} < \frac{{615}}{4}$

$ \Leftrightarrow 7,6 \approx \sqrt {\frac{{229}}{4}} \leqslant R < \sqrt {\frac{{615}}{4}} \approx 12,4$, do $R \in \mathbb{Z} \Rightarrow R \in \left\{ {8;9;10;11;12} \right\}$.

Vậy, có 5 giá trị nguyên thỏa yêu cầu.

Câu 50: Cho hàm số $f\left( x \right) = {x^4} – 18{x^2} + 4$. Có bao nhiêu giá trị nguyên của tham số $m$ sao cho ứng với mỗi $m$, tổng giá trị các nghiệm phân biệt thuộc khoảng $\left( { – 4;\,1} \right)$ của phương trình $f\left( {{x^2} + 4x + 5} \right) = m$ bằng $ – 8$?

A. $63$. B. $65$. C. $62$. D. $64$.

Lời giải

Chọn A

Đặt $t = {x^2} + 4x + 5$, vì $x \in \left( { – 4;\,1} \right) \Rightarrow \,t \in \left( {1;\,10} \right)$.

Nhận xét: với $1 < t < 5$ ta suy ra có 2 giá trị $x$ có tổng bằng $ – 4$ ( vì ${x_1} + {x_2} = – 4$).

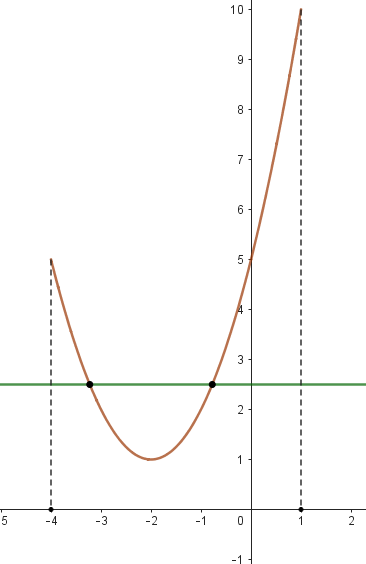
Yêu cầu bài toán tương đương $f\left( t \right) = m$ có 2 nghiệm phân biệt lớn hơn 1.

Bảng biến thiên của hàm số $f\left( x \right)$ trên khoảng $\left( {1;\,10} \right)$

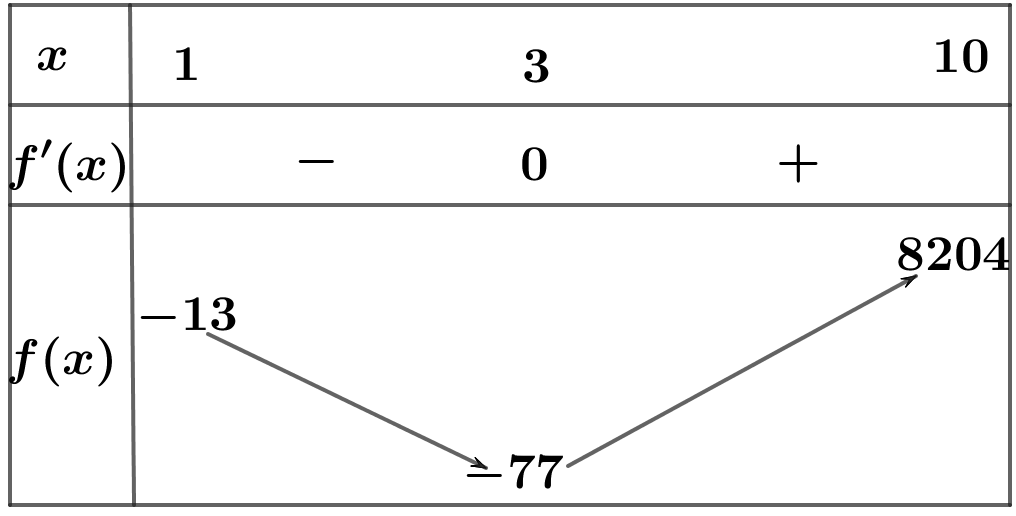
Nhận xét: $f\left( 1 \right) = f\left( {\sqrt {17} } \right)$ và phương trình $f\left( t \right) = m$ có tối đa 2 nghiệm $t \in \left( {1;\,10} \right)$.

TH1: Nếu $f\left( t \right) = m$ chỉ có 1 nghiệm $t \in \left( {1;\,10} \right)$ thì tổng các nghiệm của phương trình ${x^2} + 4x + 5 = {t_0}$ sẽ là $ – 4$.

TH2: Nếu $f\left( t \right) = m$ có 2 nghiệm phân biệt ${t_1};\,{t_2} \in \left( {1;\,10} \right) \Rightarrow \,{t_1};\,{t_2} \in \left( {1;\,\sqrt {17} } \right)$

Khi đó mỗi phương trình $\left\{ \begin{gathered}
{x^2} + 4x + 5 = {t_1} \hfill \\
{x^2} + 4x + 5 = {t_2} \hfill \\
\end{gathered} \right.$ có 2 nghiệm phân biệt thuộc khoảng $\left( { – 4;\,1} \right)$. Từ đó suy ra tổng các nghiệm là $ – 8$.

Vậy $m \in \left( { – 77;\, – 13} \right)$ và $m \in \mathbb{Z} \Rightarrow m \in \left\{ { – 76;…; – 14} \right\} \Rightarrow $ có 63 giá trị nguyên của tham số $m$ thỏa mãn.