Lời Giải Chi Tiết Đề Thi Tốt Nghiệp THPT Môn Toán Năm 2023

BỘ GIÁO DỤC VÀ ĐÀO TẠO ĐỀ CHÍNH THỨC

KỲ THI TỐT NGHIỆP TRUNG HOC PHỔ THÔNG NĂM 2023 Bài thi: TOÁN – Mã đề: 101 Thời gian làm bài: 90 phút (không kể thời gian phát đề)

HƯỚNG DẪN GIẢI CHI TIẾT

Câu 1: Tập nghiệm của bất phương trình ${2^{2x}} < 8$ là

A. $\left( { – \infty ;\frac{3}{2}} \right)$. B. $\left( {\frac{3}{2}; + \infty } \right)$. C. $( – \infty ;2)$. D. $\left( {0;\frac{3}{2}} \right)$.

Lời giải

Chọn A

Ta có ${2^{2x}} < 8 \Leftrightarrow {2^{2x}} < {2^3} \Leftrightarrow 2x < 3 \Leftrightarrow x < \frac{3}{2}$.

Câu 2: Khẳng định nào dưới đây đúng?

A. $\int {{x^{\frac{1}{3}}}} dx = {x^{\frac{4}{3}}} + C$. B. $\int {{x^{\frac{1}{3}}}\;{\text{d}}x} = \frac{3}{4}{x^{\frac{4}{3}}} + C$. C. $\int {{x^{\frac{1}{3}}}} \;{\text{d}}x = {x^{\frac{2}{3}}} + C$. D. $\int {{x^{\frac{1}{3}}}} dx = \frac{3}{2}{x^{\frac{2}{3}}} + C$.

Lời giải

Chọn B

Ta có $\int {{x^{\frac{1}{3}}}\;{\text{d}}x} = \frac{1}{{\frac{1}{3} + 1}}{x^{\frac{1}{3} + 1}} + C = \frac{3}{4}{x^{\frac{4}{3}}} + C$ với $C \in \mathbb{R}$.

Câu 3: Có bao nhiêu tam giác mà ba đỉnh của nó được lấy từ các đỉnh của một lục giác đều?

A. $729$. B. $20$. C. $120$. D. $216$.

Lời giải

Chọn B

Số tam giác là số cách chọn 3 đỉnh của tam giác. Số tam giác mà ba đỉnh của nó được lấy từ các đỉnh của một lục giác đều là $C_6^3 = 20$ tam giác.

Câu 4: Cho hàm số $f(x) = \cos x – x$. Khẳng định nào dưới đây đúng?

A. $\int f (x){\text{d}}x = – \sin x + {x^2} + C$. B. $\int f (x){\text{d}}x = – \sin x – \frac{{{x^2}}}{2} + C$.

C. $\int f (x){\text{d}}x = \sin x – {x^2} + C$. D. $\int {f(x){\text{d}}x} = \sin x – \frac{{{x^2}}}{2} + C$.

Lời giải

Chọn D

Ta có $\int {f(x)dx = \int {\left( {\cos x – x} \right)dx = \sin x – \frac{1}{2}{x^2} + C} } $ với $C \in \mathbb{R}$.

Câu 5: Đạo hàm của hàm số $y = {\log _2}(x – 1)$ là

A. $y’ = \frac{{x – 1}}{{\ln 2}}$. B. $y’ = \frac{1}{{\ln 2}}$. C. $y’ = \frac{1}{{(x – 1)\ln 2}}$. D. $y’ = \frac{1}{{x – 1}}$.

Lời giải

Chọn C

Ta có $y = {\log _2}(x – 1) \Rightarrow y’ = \frac{{{{\left( {x – 1} \right)}^\prime }}}{{\left( {x – 1} \right)\ln 2}} = \frac{1}{{\left( {x – 1} \right)\ln 2}}$.

Câu 6: Với $b,\,c$ là hai số thực dương tùy ý thỏa mãn ${\log _5}b \geqslant {\log _5}c$, khẳng định nào dưới đây là đúng?

A. $b \geqslant c$. B. $b \leqslant c$. C. $b > c$. D. $b < c$.

Lời giải

Chọn A

Ta có: ${\log _5}b \geqslant {\log _5}c \Leftrightarrow b \geqslant c$.

Câu 7: Cho hàm số bậc ba $y = f\left( x \right)$ có đồ thị là đường cong trong hình bên.

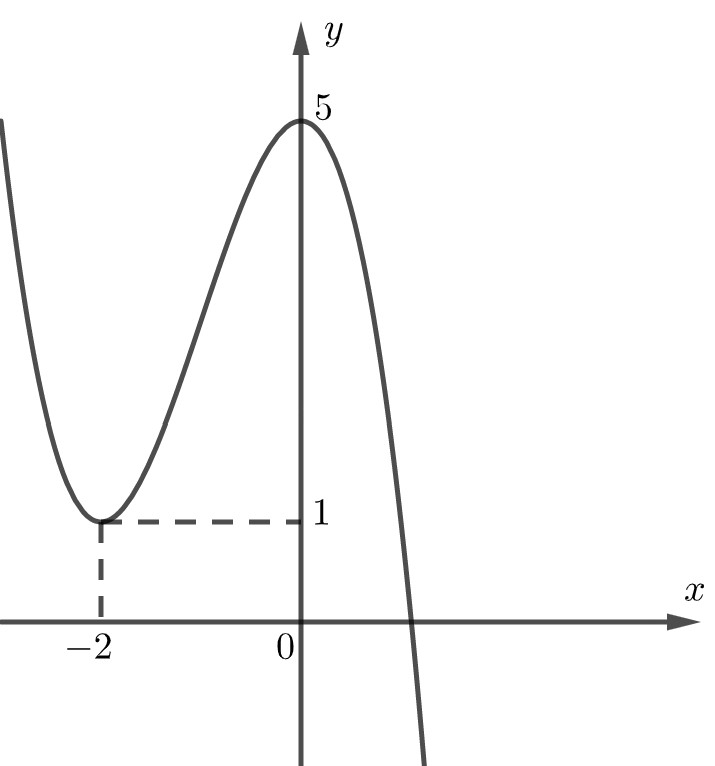
Số nghiệm thực của phương trình $f\left( x \right) = 2$ là

A. $1$. B. $0$. C. $2$. D. $3$.

Lời giải

Chọn D

Số nghiệm của phương trình bằng số giao điểm của hai đồ thị.

Do số giao điểm của đồ thị hàm số $y = f\left( x \right)$ và đường thẳng $y = 2$ là 3 nên số nghiệm thực của phương trình $f\left( x \right) = 2$ là 3.

Câu 8: Tiệm cận đứng của đồ thị hàm số $y = \frac{{3x – 1}}{{x – 2}}$ có phương trình là

A. $x = 2$. B. $x = – 2$. C. $x = 3$. D. $x = \frac{1}{2}$.

Lời giải

Chọn A

Ta có $\mathop {\lim }\limits_{x \to {2^ + }} \frac{{3x – 1}}{{x – 2}} = + \infty $ và $\mathop {\lim }\limits_{x \to {2^ – }} \frac{{3x – 1}}{{x – 2}} = – \infty $ nên tiệm cận đứng của đồ thị hàm số $y = \frac{{3x – 1}}{{x – 2}}$ có phương trình là $x = 2$.

Câu 9: Nếu khối lăng trụ $ABC.A’B’C’$ có thể tích $V$ thì khối chóp $A’.ABC$ có thể tích bằng

A. $\frac{V}{3}$. B. $V$. C. $\frac{{2V}}{3}$. D. $3V$.

Lời giải

Chọn A

Gọi $h$ là chiều cao của khối lăng trụ $ABC.A’B’C’$.

Khi đó $V = h.{S_{ABC}}$.

Ta có ${V_{A’.ABC}} = \frac{1}{3}h.{S_{ABC}} = \frac{1}{3}V$.

Câu 10: Cho hàm số $f\left( x \right)$ liên tục trên $\mathbb{R}$. Biết hàm số $F\left( x \right)$ là một nguyên hàm của $f\left( x \right)$ trên $\mathbb{R}$ và $F\left( 2 \right) = 6,F\left( 4 \right) = 12.$ Tích phân $\int\limits_2^4 {f\left( x \right)} \,dx$ bằng

A. $2$. B. $6$. C. $18$. D. $ – 6$.

Lời giải

Chọn B

$\int\limits_2^4 {f\left( x \right)} \,dx = F\left( 4 \right) – F\left( 2 \right) = 12 – 6 = 6$.

Câu 11: Điểm $M$ trong hình bên là điểm biểu diễn của số phức nào dưới đây?

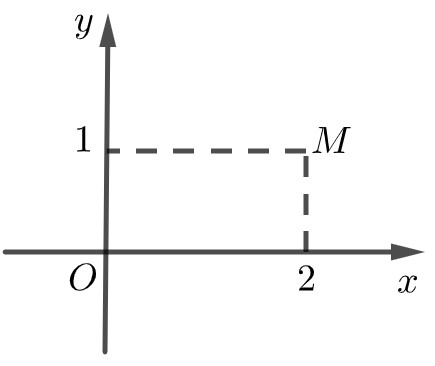
A. $2 – i$. B. $1 + 2i$. C. $1 – 2i$. D. $2 + i$.

Lời giải

Chọn D

Điểm $M\left( {2;1} \right)$ biểu diễn số $2 + i$.

Câu 12: Cho hàm số $y = f\left( x \right)$ có bảng xét dấu đạo hàm như sau:

Hàm số đã cho đồng biến trên khoảng nào dưới đây?

A. $\left( { – \infty ;0} \right)$. B. $\left( {2; + \infty } \right)$. C. $\left( {0; + \infty } \right)$. D. $\left( { – 1;2} \right)$.

Lời giải

Chọn B

Hàm số đã cho đồng biến trên khoảng $\left( {2; + \infty } \right)$.

Câu 13: Cho hình trụ có chiều cao $h = 3$ và bán kính đáy $r = 4$. Diện tích xung quanh của hình trụ đã cho bằng

A. $48\pi $. B. $16\pi $. C. $24\pi $. D. $56\pi $.

Lời giải

Chọn C

Diện tích xung quanh của hình trụ đã cho bằng $S = 2\pi hr = 2.\pi .3.4 = 24\pi $.

Câu 14: Cho khối nón có thể tích bằng $12$ và diện tích đáy bằng $9$. Chiều cao của khối nón đã cho bằng:

A. $\frac{{4\pi }}{3}$. B. $\frac{4}{3}$. C. $4\pi $. D. $4$.

Lời giải

Chọn D

Chiều cao của khối nón đã cho bằng: $h = \frac{{3V}}{S} = \frac{{3.12}}{9} = 4$.

Câu 15: Cho hai số phức ${z_1} = 2 – i$ và ${z_2} = 1 + 3i$. Phần thực của số phức ${z_1} – {z_2}$ bằng

A. $3$. B. $ – 4$. C. $1$. D. $ – 1$.

Lời giải

Chọn C

${z_1} – {z_2} = 2 – i – \left( {1 + 3i} \right) = 1 – 4i$.

Phần thực của số phức ${z_1} – {z_2}$ bằng $1$.

Câu 16: Cho khối chóp $S.ABCD$ có chiều cao bằng $4$ và đáy $ABCD$ có diện tích bằng $3$. Thể tích khối chóp đã cho bằng

A. $7$. B. $5$. C. $4$. D. $12$.

Lời giải

Chọn C

Ta có ${V_{S.ABCD}} = \frac{1}{3}.h.{S_{ABCD}} = \frac{1}{3}.4.3 = 4$.

Câu 17: Cho hàm số $y = {\left( {2{x^2} – 1} \right)^{\frac{1}{2}}}$. Giá trị của hàm số đã cho tại điểm $x = 2$ bằng

A. $3$. B. $\sqrt 7 $. C. $\sqrt 3 $. D. $7$.

Lời giải

Chọn B

Giá trị của hàm số $y = f\left( x \right) = {\left( {2{x^2} – 1} \right)^{\frac{1}{2}}}$ tại điểm $x = 2$ là:

$f\left( 2 \right) = {\left( {{{2.2}^2} – 1} \right)^{\frac{1}{2}}} = {7^{\frac{1}{2}}} = \sqrt 7 $.

Câu 18: Cho dãy số $\left( {{u_n}} \right)$ với ${u_n} = \frac{1}{{n + 1}}$, $\forall n \in {\mathbb{N}^*}$. Giá trị của ${u_3}$ bằng

A. $4$. B. $\frac{1}{4}$. C. $\frac{1}{3}$. D. $\frac{1}{2}$.

Lời giải

Chọn B

Ta có ${u_3} = \frac{1}{{3 + 1}} = \frac{1}{4}$.

Câu 19: Trong không gian $Oxyz$, cho mặt cầu $\left( S \right)$ có tâm $I\left( {1;2; – 1} \right)$ và bán kính $R = 2$. Phương trình của $\left( S \right)$ là

A. ${\left( {x – 1} \right)^2} + {\left( {y – 2} \right)^2} + {\left( {z + 1} \right)^2} = 4$. B. ${\left( {x – 1} \right)^2} + {\left( {y – 2} \right)^2} + {\left( {z + 1} \right)^2} = 2$.

C. ${\left( {x + 1} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z – 1} \right)^2} = 2$. D. ${\left( {x + 1} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z – 1} \right)^2} = 4$.

Lời giải

Chọn A

Phương trình mặt cầu $\left( S \right)$ có tâm $I\left( {1;2; – 1} \right)$ và bán kính $R = 2$ là${\left( {x – 1} \right)^2} + {\left( {y – 2} \right)^2} + {\left( {z + 1} \right)^2} = {2^2} \Leftrightarrow {\left( {x – 1} \right)^2} + {\left( {y – 2} \right)^2} + {\left( {z + 1} \right)^2} = 4$.

Câu 20: Trong không gian $Oxyz$, cho hai vecto $\overrightarrow u = \left( {1;2; – 2} \right)$ và $\overrightarrow v = \left( {2; – 2;3} \right)$. Tọa độ của vecto $\overrightarrow u + \overrightarrow v $ là

A. $\left( { – 1;4; – 5} \right)$. B. $\left( {1; – 4;5} \right)$. C. $\left( {3;0;1} \right)$. D. $\left( {3;0; – 1} \right)$.

Lời giải

Chọn C

Ta có $\overrightarrow u + \overrightarrow v = \left( {1 + 2;2 + \left( { – 2} \right); – 2 + 3} \right) = \left( {3;0;1} \right)$.

Câu 21: Cho số phức $z = 1 – 2i$. Phần ảo của số phức $\overline z $ bằng

A. $ – 1$. B. $2$. C. $1$. D. $ – 2$

Lời giải

Chọn B

Ta có $\overline z = 1 + 2i$ nên phần ảo của số phức $\overline z $ là $2$.

Câu 22: Nếu $\int\limits_0^1 {f\left( x \right)} {\text{d}}x = 2$ và $\int\limits_1^3 {f\left( x \right)} {\text{d}}x = 5$ thì $\int\limits_0^3 {f\left( x \right)} {\text{d}}x$ bằng

A. $10$. B. $3$. C. $7$. D. $ – 3$

Lời giải

Chọn C

Ta có:$\int\limits_0^3 {f\left( x \right)} {\text{d}}x = \int\limits_0^1 {f\left( x \right)} {\text{d}}x + \int\limits_1^3 {f\left( x \right)} {\text{d}}x = 2 + 5 = 7$.

Câu 23: Tập nghiệm của bất phương trình ${\log _3}\left( {2x} \right) \geqslant {\log _3}2$ là

A. $\left( {0\,;\, + \infty } \right)$. B. $\left[ {1\,;\, + \infty } \right)$. C. $\left( {1\,;\, + \infty } \right)$. D. $\left( {0\,;\,1} \right]$.

Lời giải

Chọn B

Điều kiện : $x > 0$.

Ta có: ${\log _3}\left( {2x} \right) \geqslant {\log _3}2$$ \Leftrightarrow 2x \geqslant 2$$ \Leftrightarrow x \geqslant 1$.

Câu 24: Hàm số nào dưới đây có bảng biến thiên như sau?

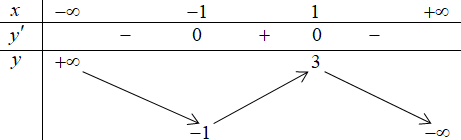
A. $y = \frac{{x + 2}}{x}$. B. $y = – {x^3} + 3x + 1$. C. $y = {x^4} – 3{x^2}$. D. $y = – 2{x^2} + 1$

Lời giải

Chọn B

Ta có : $y = – {x^3} + 3x + 1$ có $y’ = – 3{x^2} + 3 = 0$$ \Leftrightarrow x = \pm 1$. Vậy $x = \pm 1$là các điểm cực trị của hàm số.

Câu 25: Trong không gian $Oxyz$, mặt phẳng $\left( {Oxz} \right)$ có phương trình là.

A. $x = 0$. B. $z = 0$. C. $x + y + z = 0$. D. $y = 0$.

Lời giải

Chọn D

Mặt phẳng $\left( {Oxz} \right)$ có phương trình là: $y = 0$.

Câu 26: Cho hàm số $y = a{x^3} + b{x^2} + cx + d\left( {a,b,c,d \in \mathbb{R}} \right)$có đồ thị là đường cong trong hình bên. Giá trị cực đại của hàm số đã cho bằng:

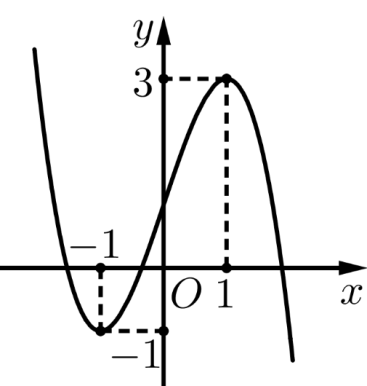
A. $0$. B. $1$. C. $3$. D. $ – 1$.

Lời giải

Chọn C

Giá trị cực đại của hàm số là $3$.

Câu 27: Trong không gia $Oxyz$ phương trình đường thẳng $d$ đi qua điểm $M(2;1; – 1)$ và có một véc tơ chỉ phương $\overrightarrow u = \left( {1; – 2;3} \right)$ là

A. $\frac{{x – 1}}{2} = \frac{{y + 2}}{1} = \frac{{z – 3}}{{ – 1}}$. B. $\frac{{x – 2}}{1} = \frac{{y – 1}}{{ – 2}} = \frac{{z + 1}}{3}$.

C. $\frac{{x + 1}}{2} = \frac{{y – 2}}{1} = \frac{{z + 3}}{{ – 1}}$. D. $\frac{{x + 2}}{1} = \frac{{y + 1}}{{ – 2}} = \frac{{z – 1}}{3}$.

Lời giải

Chọn B

Phương trình đường thẳng $d$ đi qua điểm $M(2;1; – 1)$ và có một véc tơ chỉ phương $\overrightarrow u = \left( {1; – 2;3} \right)$ là:
$\frac{{x – 2}}{1} = \frac{{y – 1}}{{ – 2}} = \frac{{z + 1}}{3}$.

Câu 28: Cho hàm số bậc bốn $y = f(x)$ có đồ thị là đường cong trong hình bên. Số điểm cực tiểu của hàm số đã cho là

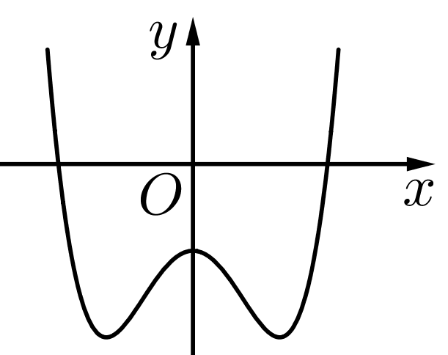
A. $1$. B. $3$. C. $0$. D. $2$.

Lời giải

Chọn D

Số điểm cực tiểu của hàm số đã cho là 2.

Câu 29: Với $a$, $b$ là các số thực dương tùy ý thỏa mãn $a \ne 1$ và ${\log _a}b = 2$, giá trị của ${\log _{{a^2}}}\left( {a{b^2}} \right)$ bằng

A. 2. B. $\frac{3}{2}$. C. $\frac{1}{2}$. D. $\frac{5}{2}$.

Lời giải

Chọn D

Ta có ${\log _{{a^2}}}\left( {a{b^2}} \right) = {\log _{{a^2}}}a + {\log _{{a^2}}}{b^2} = {\log _{{a^2}}}a + {\log _a}b = \frac{1}{2} + 2 = \frac{5}{2}$.

Câu 30: Trong không gian $Oxyz$, cho hai điểm $A(5;2;1)$ và $B(1;0;1)$. Phương trình của mặt cầu đường kính $AB$ là

A. ${\left( {x + 3} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z + 1} \right)^2} = 5$. B. ${\left( {x – 3} \right)^2} + {\left( {y – 1} \right)^2} + {\left( {z – 1} \right)^2} = 20$.

C. ${\left( {x – 3} \right)^2} + {\left( {y – 1} \right)^2} + {\left( {z – 1} \right)^2} = 5$. D. ${\left( {x + 3} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z + 1} \right)^2} = 20$.

Lời giải

Chọn C

Do $AB$ là đường kính của mặt cầu nên trung điểm $I\left( {3;1;1} \right)$ của $AB$ là tâm mặt cầu, bán kính của mặt cầu là: $R = \frac{{AB}}{2} = \frac{{\sqrt {{{\left( {5 – 1} \right)}^2} + {{\left( {2 – 0} \right)}^2} + {{\left( {1 – 1} \right)}^2}} }}{2} = \sqrt 5 $.

Ta có phương trình mặt cầu: $\left( C \right):{\left( {x – 3} \right)^2} + {\left( {y – 1} \right)^2} + {\left( {z – 1} \right)^2} = 5$. Chọn đáp án C.

Câu 31: Trong không gian $Oxyz$, cho điểm $A(1;2; – 1)$ và mặt phẳng $(P):x + 2y + z = 0$. Đường thẳng đi qua $A$ và vuông góc với $(P)$ có phương trình là

A. $\left\{ {\begin{array}{*{20}{l}}
{x = 1 + t} \\
{y = 2 – 2t} \\
{z = – 1 + t}
\end{array}} \right.$. B. $\left\{ {\begin{array}{*{20}{l}}
{x = 1 + t} \\
{y = 2 + 2t} \\
{z = 1 – t}
\end{array}} \right.$. C. $\left\{ {\begin{array}{*{20}{l}}
{x = 1 + t} \\
{y = 2 + 2t} \\
{z = 1 + t}
\end{array}} \right.$. D. $\left\{ {\begin{array}{*{20}{l}}
{x = 1 + t} \\
{y = 2 + 2t} \\
{z = – 1 + t}
\end{array}} \right.$.

Lời giải

Chọn D

Đường thẳng vuông góc với mặt phẳng $(P):x + 2y + z = 0$ nên nhận vector pháp tuyến $\overrightarrow n = \left( {1;2;1} \right)$ của $\left( P \right)$là vector chỉ phương.

Mặt khác đường thẳng đi qua $A\left( {1;2; – 1} \right)$ nên ta có phương trình $\left\{ \begin{gathered}
x = 1 + t \hfill \\
y = 2 + 2t \hfill \\
z = – 1 + t \hfill \\
\end{gathered} \right.\left( {t \in \mathbb{R}} \right)$.

Câu 32: Biết đường thẳng $y = x – 1$ cắt đồ thị hàm số $y = \frac{{ – x + 5}}{{x – 2}}$ tại hai điểm phân biệt có hoành độ là ${x_1},{x_2}$. Giá trị ${x_1} + {x_2}$ bằng

A. $ – 1$. B. 3. C. 2. D. 1.

Lời giải

Chọn C

Phương trình hoành độ giao điểm là:

$x – 1 = \frac{{ – x + 5}}{{x – 2}} \Leftrightarrow \left\{ \begin{gathered}
x \ne 2 \hfill \\
\left( {x – 1} \right)\left( {x – 2} \right) + x – 5 = 0 \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
x \ne 2 \hfill \\
{x^2} – 3x + 2 + x – 5 = 0 \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
x \ne 2 \hfill \\
{x^2} – 2x – 3 = 0 \hfill \\
\end{gathered} \right.$

$ \Leftrightarrow \left[ \begin{gathered}
x = 3 \hfill \\
x = – 1 \hfill \\
\end{gathered} \right.$.

Suy ra ${x_1} + {x_2} = – 1 + 3 = 2$.

Câu 33: Cho hàm số $y = f\left( x \right)$ có đạo hàm $f’\left( x \right) = x\left( {x – 4} \right),\forall x \in \mathbb{R}$. Khẳng định nào dưới đây đúng?

A. $f\left( 4 \right) > f\left( 0 \right)$. B. $f\left( 0 \right) > f\left( 2 \right)$. C. $f\left( 5 \right) > f\left( 6 \right)$. D. $f\left( 4 \right) > f\left( 2 \right)$.

Lời giải

Chọn B

$f’\left( x \right) = x\left( {x – 4} \right)$ nên $f’\left( x \right) = 0 \Leftrightarrow \left[ \begin{gathered}
x = 0 \hfill \\
x = 4 \hfill \\
\end{gathered} \right.$.

Bảng biến thiên

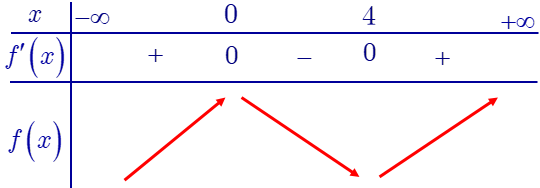
Dựa vào bảng biến thiên ta được $f\left( 0 \right) > f\left( 2 \right)$.

Câu 34: Cho hình hộp chữ nhật $ABCD.A’B’C’D’$ có $AB = 1$, $BC = 2$, $AA’ = 2$ (tham khảo hình bên).

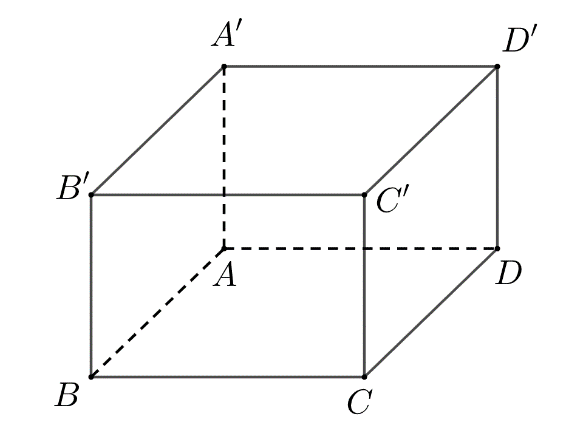
Khoảng cách giữa hai đường thẳng $AD’$ và $DC’$ bằng

A. $\sqrt 2 $. B. $\frac{{\sqrt 6 }}{2}$. C. $\frac{{2\sqrt 5 }}{5}$. D. $\frac{{\sqrt 6 }}{3}.$

Lời giải

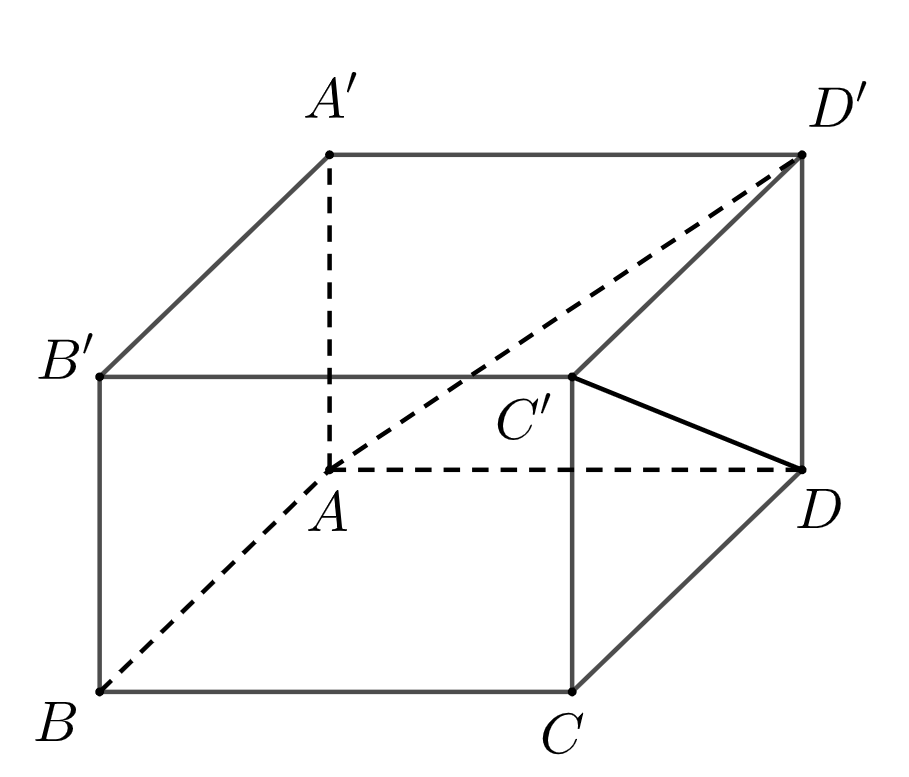
Chọn D

Ta có $AD’ \subset \left( {AD’B’} \right)$, $DC’ \subset \left( {DC’B} \right)$ và $\left( {AD’B’} \right){\text{ // }}\left( {DC’B} \right)$ nên khoảng cách giữa hai đường thẳng $AD’$ và $DC’$ bằng khoảng cách giữa $\left( {AD’B’} \right)$ và $\left( {DC’B} \right)$.

$d\left( {\left( {AD’B’} \right);\left( {DC’B} \right)} \right) = d\left( {A;\left( {DC’B} \right)} \right) = d\left( {C;\left( {DC’B} \right)} \right) = h$

Xét tứ diện $C.BC’D$ có các cạnh $CD,CB,CC’$ đôi một vuông góc nên ta có

$\frac{1}{{{h^2}}} = \frac{1}{{C{B^2}}} + \frac{1}{{C{D^2}}} + \frac{1}{{CC{‘^2}}} = \frac{1}{{{2^2}}} + \frac{1}{{{1^2}}} + \frac{1}{{{2^2}}} = \frac{3}{2}$ $ \Rightarrow h = \frac{{\sqrt 6 }}{3}$.

Câu 35: Từ một nhóm học sinh gồm 5 nam và 8 nữ, chọn ngẫu nhiên 4 học sinh. Xác suất để 4 học sinh được chọn có cả nam và nữ bằng

A. $\frac{{72}}{{143}}$. B. $\frac{{15}}{{143}}$. C. $\frac{{128}}{{143}}$. D. $\frac{{71}}{{143}}$.

Lời giải

Chọn C

Số cách để chọn ngẫu nhiên 4 học sinh từ $5 + 8 = 13$ học sinh là $C_{13}^4$.

Khi đó $n\left( \Omega \right) = C_{13}^4$.

Gọi $A$ là biến cố để 4 học sinh được chọn có cả nam và nữ.

Khi nó $n\left( A \right) = C_5^1C_8^3 + C_5^2C_8^2 + C_5^3C_8^1 = 640$

Nên $P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{C_5^1C_8^3 + C_5^2C_8^2 + C_5^3C_8^1}}{{C_{13}^4}} = \frac{{128}}{{143}}$.

Câu 36: Gọi ${z_1},{z_2}$là hai nghiệm phức của phương trình ${z^2} – 6z + 14 = 0$và $M,N$lần lượt là điểm biểu diễn của ${z_1},{z_2}$ trên mặt phẳng toạ độ.Trung điểm của đoạn $MN$có toạ độ là

A. $\left( {3;7} \right)$. B. $\left( { – 3;0} \right)$. C. $\left( {3;0} \right)$. D. $\left( { – 3;7} \right)$.

Lời giải

Chọn C

Phương trình ${z^2} – 6z + 14 = 0$

Có $\Delta ‘ = 9 – 14 = – 5 = 5{i^2}$

Suy ra $\sqrt {\Delta ‘} = \sqrt {5{i^2}} = i\sqrt 3 $

Phương trình có 2 nghiệm là ${z_1} = 3 + i\sqrt 3 ;\,{z_2} = 3 – i\sqrt 3 $

Tọa độ $M\left( {3;\sqrt 3 } \right);N\left( {3; – \sqrt 3 } \right)$

Trung điểm của đoạn thẳng $MN$ có tọa độ là$\left( {3;0} \right)$.

Câu 37: Đường gấp khúc $ABC$trong hình vẽ bên là đồ thị của hàm số $y = f\left( x \right)$trên đoạn $\left[ { – 2;3} \right]$.

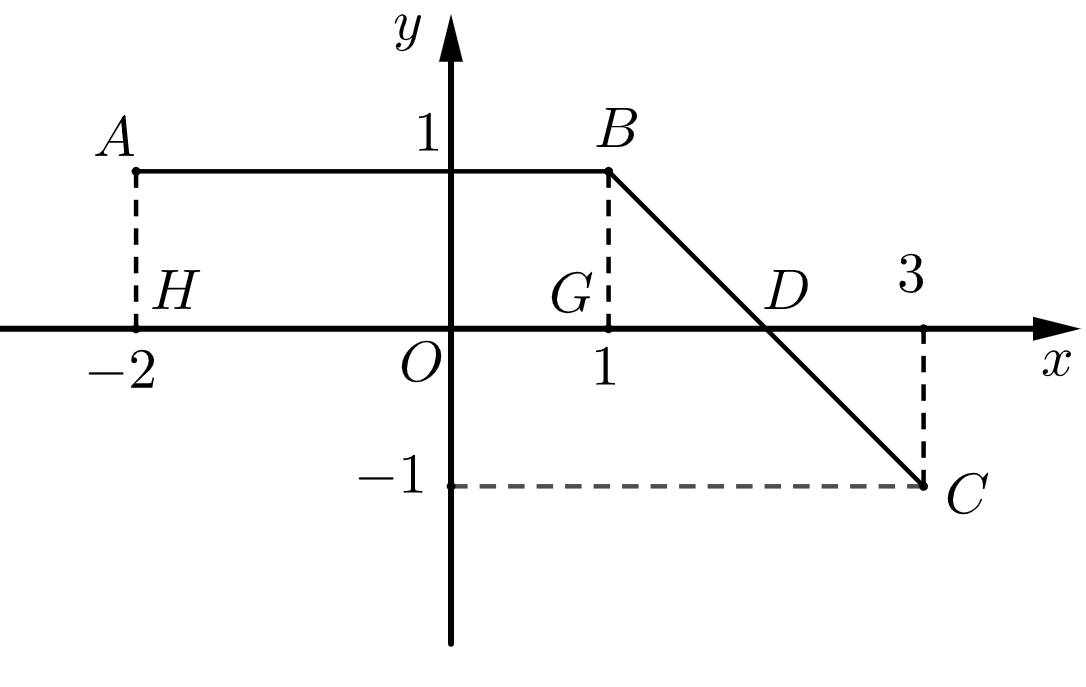
Tích phân $\int\limits_{ – 2}^3 {f\left( x \right)} dx$bằng

A. $4$. B. $\frac{9}{2}$. C. $\frac{7}{2}$. D. $3$.

Lời giải

Chọn D

Ta có

$\int\limits_{ – 2}^3 {f\left( x \right)} dx = {S_{ABGH}} + {S_{BGD}} – {S_{CDE}}$

$\int\limits_{ – 2}^3 {f\left( x \right)} dx = 3.1 + \frac{1}{2}.1.1 – \frac{1}{2}.1.1 = 3$.

Câu 38: Cho hình chóp đều$S.ABC{\text{D}}$có đáy bằng a chiều cao bằng $\frac{{\sqrt 3 a}}{6}$.Góc giữa mặt phẳng $\left( {SCD} \right)$và mặt phẳng đáy bằng

A. $45^\circ $. B. $90^\circ $. C. $60^\circ $. D. $30^\circ $.

Lời giải

Chọn D

Gọi $O$ là tâm mặt đáy, $H$ là trung điểm cạnh $CD$

Suy ra $\left( {SOH} \right) \bot CD \Rightarrow SHO = \left( {\left( {SCD} \right),\left( {ABCD} \right)} \right)$

$SO = \frac{{\sqrt 3 a}}{6};OH = \frac{a}{2} \Rightarrow \tan \left( {SHO} \right) = \frac{{SO}}{{OH}} = \frac{{\frac{{\sqrt 3 a}}{6}}}{{\frac{a}{2}}} = \frac{{\sqrt 3 }}{3}$ Suy ra $\widehat {SHO} = 30^\circ $

Vậy góc giữa mặt phẳng $\left( {SCD} \right)$ và $\left( {ABCD} \right)$là $30^\circ $.

Câu 39: Có bao nhiêu số nguyên $x$ thoả mãn điều kiện $\left( {{7^x} – 49} \right)\left( {\log _3^2x – 7{{\log }_3}x + 6} \right) < 0$?

A. $728$. B. $726$. C. $725$. D. $729$.

Lời giải

Chọn B

Điều kiện: $x > 0$

$\left( {{7^x} – 49} \right)\left( {\log _3^2x – 7{{\log }_3}x + 6} \right) < 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{\left\{ {\begin{array}{*{20}{c}}
{{7^x} – 49 > 0} \\
{\log _3^2x – 7{{\log }_3}x + 6 < 0}
\end{array}} \right.} \\
{\left\{ {\begin{array}{*{20}{c}}
{{7^x} – 49 < 0} \\
{\log _3^2x – 7{{\log }_3}x + 6 > 0}
\end{array}} \right.}
\end{array}} \right.$

$ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{\left\{ {\begin{array}{*{20}{c}}
{{7^x} > 49} \\
{1 < {{\log }_3}x < 6}
\end{array}} \right.} \\
{\left\{ {\begin{array}{*{20}{c}}
{{7^x} < 49} \\
{\left[ {\begin{array}{*{20}{c}}
{{{\log }_3}x < 1} \\
{{{\log }_3}x > 6}
\end{array}} \right.}
\end{array}} \right.}
\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{\left\{ {\begin{array}{*{20}{c}}
{x > 2} \\
{3 < x < {3^6}}
\end{array}} \right.} \\
{\left\{ {\begin{array}{*{20}{c}}
{x < 2} \\
{\left[ {\begin{array}{*{20}{c}}
{0 < x < 3} \\
{x > {3^6}}
\end{array}} \right.}
\end{array}} \right.}
\end{array}} \right.} \right.$

$ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{0 < x < 2} \\
{3 < x < {3^6}}
\end{array}} \right.$

Mà $x \in \mathbb{Z} \Rightarrow x \in \left\{ {1;4;5;…;728} \right\}$

Vậy có 726 số thỏa mãn.

Câu 40: Cho hàm số bậc hai $y = f\left( x \right)$ có đồ thị $\left( P \right)$ và đường thẳng $d$ cắt $\left( P \right)$ tại hai điểm như trong hình vẽ bên. Biết rằng hình phẳng giới hạn bởi $\left( P \right)$ và $d$ có diện tích $S = \frac{{125}}{9}$. Tích phân $\int\limits_1^6 {\left( {2x – 5} \right)f’\left( x \right)} {\text{d}}x$ bằng

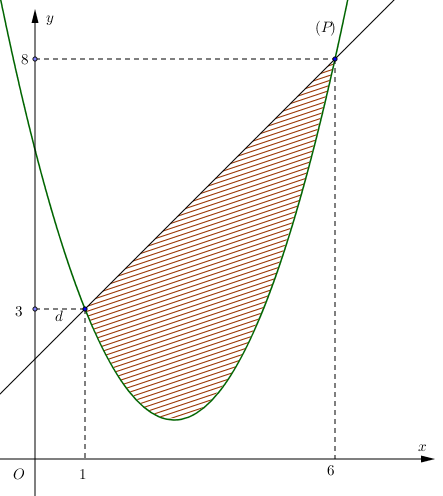
A. $\frac{{830}}{9}$. B. $\frac{{178}}{9}$. C. $\frac{{340}}{9}$. D. $\frac{{925}}{{18}}$.

Lời giải

Chọn C

Ta có $S_{_{hthang}}^{} = \frac{{\left( {8 + 3} \right).5}}{2} = \frac{{55}}{2} \Rightarrow \int\limits_1^6 {f\left( x \right)dx} = \frac{{55}}{2} – \frac{{125}}{9} = \frac{{245}}{{18}}$.

Đặt $\left\{ {\begin{array}{*{20}{c}}
{u = 2x – 5 \Rightarrow du = 2dx} \\
{dv = f’\left( x \right)dx \Rightarrow v = f\left( x \right)}
\end{array}} \right.$

$\int\limits_1^6 {\left( {2x – 5} \right)f’\left( x \right)} {\text{d}}x = \left. {\left( {2x – 5} \right)f\left( x \right)} \right|_1^6 – 2\int\limits_1^6 {f\left( x \right)} dx = 7.f\left( 6 \right) + 3.f\left( 1 \right) – 2.\frac{{245}}{{18}}$

$ = 7.8 + 3.3 – 2.\frac{{245}}{{18}} = \frac{{340}}{9}$.

Câu 41: Có bao nhiêu giá trị nguyên của tham số $m$ sao cho ứng với mỗi $m$, hàm số $y = – {x^3} + 3{x^2} – 3mx + \frac{5}{3}$ có đúng một cực trị thuộc khoảng $\left( { – 2;5} \right)$?

A. $16$. B. $6$. C. $17$. D. $7$.

Lời giải

Chọn D

$y’ = – 3{x^2} + 6x – 3m$

hàm số $y = – {x^3} + 3{x^2} – 3mx + \frac{5}{3}$ có đúng một cực trị thuộc khoảng $\left( { – 2;5} \right)$ khi và chỉ khi

$y’ = 0$ có một nghiệm thuộc khoảng $\left( { – 2;5} \right) \Leftrightarrow {x^2} – 2x + m = 0$ có một nghiệm thuộc khoảng $\left( { – 2;5} \right)$

$ \Leftrightarrow {x^2} – 2x = – m$

$g\left( x \right) = {x^2} – 2x \Rightarrow g’\left( x \right) = 2x – 2$

$g’\left( x \right) = 0 \Leftrightarrow 2x – 2 = 0 \Leftrightarrow x = 1$

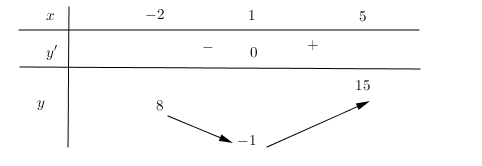
Để hàm số có 1 cực trị $ \Rightarrow 8 \leqslant – m < 15 \Leftrightarrow – 15 < m \leqslant – 8 \Rightarrow m \in \left\{ { – 14; – 13; – 12; – 11; – 10; – 9; – 8} \right\}$

Câu 42: Cho hàm số $f\left( x \right)$ nhận giá trị dương trên khoảng $\left( {0; + \infty } \right)$, có đạo hàm trên khoảng đó và thỏa mãn $f\left( x \right)\ln f\left( x \right) = x\left( {f\left( x \right) – f’\left( x \right)} \right),\,\,\forall x \in $$\left( {0; + \infty } \right)$. Biết $f\left( 1 \right) = f\left( 3 \right)$, giá trị $f\left( 2 \right)$ thuộc khoảng nào dưới đây?

A. $\left( {12;14} \right).$ B. $\left( {4;6} \right).$ C. $\left( {1;3} \right).$ D. $\left( {6;8} \right).$

Lời giải

Chọn B

Ta có

$f\left( x \right)\ln f\left( x \right) = x\left( {f\left( x \right) – f’\left( x \right)} \right) \Leftrightarrow \ln f\left( x \right) = x\left( {1 – \frac{{f’\left( x \right)}}{{f\left( x \right)}}} \right) \Leftrightarrow \ln f\left( x \right) = x\left( {1 – {{\left( {\ln f\left( x \right)} \right)}^\prime }} \right)$

$ \Leftrightarrow {\left( x \right)^\prime }\ln f\left( x \right) + x{\left( {\ln f\left( x \right)} \right)^\prime } = x \Leftrightarrow {\left( {x\ln f\left( x \right)} \right)^\prime } = x$.

Từ đó $x\ln f\left( x \right) = \int {xdx} = \frac{1}{2}{x^2} + C$.

Cho $x = 1$ ta được $\ln f\left( 1 \right) = \frac{1}{2} + C$

Cho $x = 3$ ta được $3\ln f\left( 3 \right) = \frac{9}{2} + C$

Theo bài ra thì $f\left( 1 \right) = f\left( 3 \right)$, từ đó suy ra $C = \frac{3}{2}$ nên $f\left( x \right) = {e^{\frac{1}{2}x + \frac{3}{{2x}}}}$.

Cho $x = 2$ ta được $f\left( 2 \right) = {e^{\frac{7}{4}}} \simeq 5,75$

Câu 43: Gọi $S$ là tập hợp các số phức $z = a + bi\,\,\left( {a,b \in \mathbb{R}} \right)$ thỏa mãn $\left| {z + \overline z } \right| + \left| {z – \overline z } \right| = 6$ và $ab \leqslant 0$. Xét ${z_1}$ và ${z_2}$ thuộc $S$ sao cho $\frac{{{z_1} – {z_2}}}{{ – 1 + i}}$ là số thực dương. Giá trị nhỏ nhất của biểu thức $\left| {{z_1} + 3i} \right| + \left| {{z_2}} \right|$ bằng

A. $3\sqrt 2 .$ B. $3.$ C. $3\sqrt 5 .$ D. $3 + 3\sqrt 2 .$

Lời giải

Chọn C

Cách 1

Từ giả thiết suy ra $\left| a \right| + \left| b \right| = 3 \Rightarrow a – b = \pm 3$ (do $ab \leqslant 0$)

Do $\frac{{{z_1} – {z_2}}}{{ – 1 + i}}$ là số thực dương nên ${a_1} – {a_2} = – \left( {{b_1} – {b_2}} \right) < 0$ suy ra ${a_1} < {a_2}$ và ${a_1} + {b_1} = {a_2} + {b_2}$ (1)

Nếu ${a_1} – {b_1} = {a_2} – {b_2}$ thì ${z_1} = {z_2}$ (loại);

Vậy ${a_1} – {b_1} = – \left( {{a_2} – {b_2}} \right)$ (2)

Từ (1) và (2) suy ra ${a_1} = {b_2}\,,\,\,{a_2} = {b_1} \Rightarrow {a_1} < {a_2} = {b_1}$

Do đó ${a_1} – {b_1} = – 3 \Rightarrow {b_1} = {a_1} + 3 = x + 3$

$ \Rightarrow {z_1} = x + \left( {x + 3} \right)i$, ${z_2} = x + 3 + xi$

Vậy $\left| {{z_1} + 3i} \right| + \left| {{z_2}} \right| = \sqrt {{x^2} + {{\left( {x + 6} \right)}^2}} + \sqrt {{{\left( {x + 3} \right)}^2} + {x^2}} \geqslant \sqrt {{3^2} + {6^2}} = 3\sqrt 5 $

Dấu “=” xảy ra khi $x = – 2$.

Cách 2

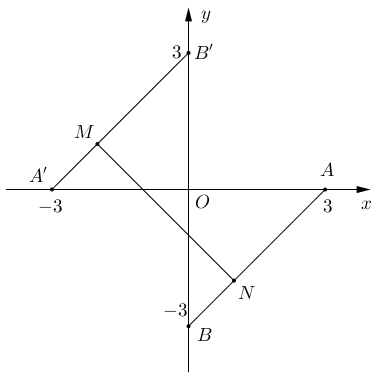
Từ giả thiết suy ra $\left| a \right| + \left| b \right| = 3 \Rightarrow a – b = \pm 3$ (do $ab \leqslant 0$)

Trên mặt phẳng Oab, vẽ 2 đoạn thẳng

[AB]: $a – b = 3\,\,\left( {0 \leqslant a \leqslant 3} \right)$ với $A\left( {3;0} \right),\,\,B\left( {0; – 3} \right)$

[A’B’]: $a – b = – 3\,\,\left( { – 3 \leqslant a \leqslant 0} \right)$ với $A’\left( { – 3;0} \right),\,\,B’\left( {0;3} \right)$

Gọi $M\left( {a;b} \right)$ biểu diễn cho số phức ${z_1}$, $N\left( {a’;b’} \right)$ biểu diễn cho số phức ${z_2}$. Thế thì $M,N$ chạy trên [AB] hoặc [A’B’].

Ta có $\frac{{{z_1} – {z_2}}}{{ – 1 + i}} = \frac{1}{2}\left[ {\left( {b – b’} \right) – \left( {a – a’} \right) – \left( {a – a’} \right)i – \left( {b – b’} \right)i} \right]$

Do $\frac{{{z_1} – {z_2}}}{{ – 1 + i}}$ là số thực dương nên
$\left\{ \begin{array}{l}
\left( {b – b’} \right) – \left( {a – a’} \right) > 0\\
\left( {b – b’} \right) + \left( {a – a’} \right) = 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
a < a’\\ b > b’\\
a + b = a’ + b’
\end{array} \right.$

Khi đó $M \in \left[ {A’B’} \right],\,\,N \in \left[ {AB} \right]$.

Vậy $M\left( {a;a + 3} \right)$, $N\left( {a’;a’ – 3} \right)$

Ta có $a + b = a’ + b’ \Leftrightarrow a + a – 3 = a’ + a’ + 3 \Leftrightarrow a’ = a + 3$ nên $N\left( {a + 3;a} \right)$

Do vậy

$\left| {{z_1} + 3i} \right| + \left| {{z_2}} \right| = \sqrt {{a^2} + {{\left( {a + 6} \right)}^2}} + \sqrt {{{\left( {a + 3} \right)}^2} + {a^2}} = \sqrt {{{\left( { – a} \right)}^2} + {{\left( {a + 6} \right)}^2}} + \sqrt {{{\left( {a + 3} \right)}^2} + {{\left( { – a} \right)}^2}} $

$ \geqslant \sqrt {{3^2} + {6^2}} = 3\sqrt 5 $

Dấu “=” xảy ra khi $\frac{{a + 6}}{{ – a}} = \frac{{ – a}}{{a + 3}} > 0 \Leftrightarrow a = – 2$.

Câu 44: Cho khối chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành, $SA = SB = SC = AC = a,$ $SB$ tạo với mặt phẳng $\left( {SAC} \right)$ một góc $30^\circ $. Thể tích khối chóp đã cho bằng

A. $\frac{{{a^3}}}{4}$. B. $\frac{{{a^3}}}{8}$. C. $\frac{{\sqrt 3 {a^3}}}{{12}}$. D. $\frac{{\sqrt 3 {a^3}}}{{24}}$.

Lời giải

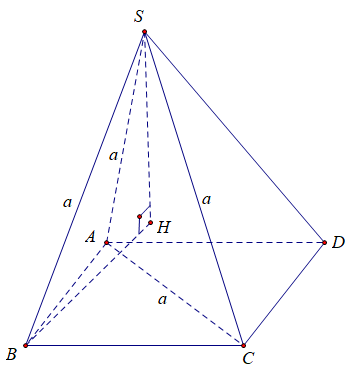
Chọn C

Vẽ $BH \bot \left( {SAC} \right)$ tại $H$ suy ra $\left( {SB;\left( {SAC} \right)} \right) = \left( {SB;BH} \right) = \widehat {BSH} = 30^\circ $

Từ đó ta có ${V_{S.ABCD}} = 2{V_{S.ABC}} = 2{V_{B.SAC}}$

Xét $\Delta SHB$ vuông tại $H$ ta có $\sin \widehat {BSH} = \frac{{BH}}{{SB}} \Rightarrow \sin 30^\circ = \frac{{BH}}{a} \Leftrightarrow BH = \frac{a}{2}$

Ta có ${V_{B.SAC}} = \frac{1}{3}BH.{S_{\Delta SAC}} = \frac{1}{3}.\frac{a}{2}.\frac{{{a^2}\sqrt 3 }}{4} = \frac{{{a^3}\sqrt 3 }}{{24}}$

Vậy ${V_{S.ABCD}} = 2{V_{B.SAC}} = 2.\frac{{{a^3}\sqrt 3 }}{{24}} = \frac{{{a^3}\sqrt 3 }}{{12}}$.

Câu 45: Trong không gian $Oxyz,$ cho mặt cầu $\left( S \right):{\left( {x – 1} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z + 1} \right)^2} = 4$ và đường thẳng $d$ đi qua điểm $A\left( {1;0; – 2} \right),$ nhận $\overrightarrow u = \left( {1;a;1 – a} \right)$ (với $a \in \mathbb{R}$) làm vectơ chỉ phương. Biết rằng $d$ cắt $\left( S \right)$ tại hai điểm phân biệt mà các tiếp diện của $\left( S \right)$ tại hai điểm đó vuông góc với nhau. Hỏi ${a^2}$ thuộc khoảng nào dưới đây?

A. $\left( {\frac{1}{2};\frac{3}{2}} \right)$. B. $\left( {\frac{3}{2};2} \right)$. C. $\left( {7;\frac{{15}}{2}} \right)$. D. $\left( {0;\frac{1}{4}} \right)$.

Lời giải

Chọn B

Mặt cầu $\left( S \right)$ có tâm $I\left( {1; – 2; – 1} \right)$, bán kính $R = 2$

Gọi $B,C$ là giao điểm giữa $d$ và $\left( S \right)$, và $O$ là hình chiếu vuông góc của I trên giao tuyến hai mặt tiếp diện.

Theo đề $d$ cắt $\left( S \right)$ tại hai điểm phân biệt mà các tiếp diện của $\left( S \right)$ tại hai điểm đó vuông góc với nhau, nghĩa là tứ giác $OBIC$ là hình vuông, từ đó suy ra $BC = 2\sqrt 2 $

Gọi $H$ là trung điểm $BC$ suy ra $BH = \frac{{BC}}{2} = \sqrt 2 $

Kẻ $IH \bot BC$, ta có $IH = \sqrt {I{B^2} – B{H^2}} = \sqrt 2 $

Từ đó ta có $d\left( {I;d} \right) = \sqrt 2 $

Ta có $\overrightarrow {AI} = \left( {0; – 2;1} \right)$, $\overrightarrow u = \left( {1;a;1 – a} \right)$ suy ra $\left[ {\overrightarrow {AI} ;\overrightarrow u } \right] = \left( {a – 2;1;2} \right)$

Từ đó ${\text{d}}\left( {I;d} \right) = \sqrt 2 \Leftrightarrow \frac{{\left| {\left[ {\overrightarrow {AI} ;\overrightarrow u } \right]} \right|}}{{\left| {\overrightarrow u } \right|}} = \sqrt 2 \Leftrightarrow \frac{{\sqrt {{{\left( {a – 2} \right)}^2} + {1^2} + {2^2}} }}{{\sqrt {1 + {a^2} + {{\left( {1 – a} \right)}^2}} }} = \sqrt 2 \Leftrightarrow {a^2} = \frac{5}{3} \in \left( {\frac{3}{2};2} \right)$.

Câu 46: Trên tập số phức, xét phưong trình ${z^2} + az + b = 0\,\,\left( {a,b \in \mathbb{R}} \right)$. Có bao nhiêu cặp số $\left( {a,b} \right)$ để phương trình đó có hai nghiệm phân biệt ${z_1},{z_2}$ thỏa mãn $\left| {{z_1} – 2} \right| = 2$và $\left| {{z_2} + 1 – 4i} \right| = 4$?

A. 2. B. 3. C. 6. D. 4.

Lời giải

Chọn D

Ta có $\Delta = {a^2} – 4b$

TH1. $\Delta > 0 \Rightarrow {z_1},{z_2} \in \mathbb{R}$
$\left| {{z_1} – 2} \right| = 2 \Leftrightarrow \left[ \begin{gathered}
{z_1} – 2 = 2 \hfill \\
{z_1} – 2 = – 2 \hfill \\
\end{gathered} \right. \Leftrightarrow \left[ \begin{gathered}
{z_1} = 4 \hfill \\
{z_1} = 0 \hfill \\
\end{gathered} \right.$

$\left| {{z_2} + 1 – 4i} \right| = 4 \Rightarrow {\left( {{z_2} + 1} \right)^2} + 16 = 16 \Leftrightarrow {z_2} + 1 = 0 \Leftrightarrow {z_2} = – 1.$

Với ${z_1} = 4,{z_2} = – 1$ có $\left\{ \begin{gathered}
{z_1} + {z_2} = – a \hfill \\
{z_1}{z_2} = b \hfill \\
\end{gathered} \right. \Rightarrow \left\{ \begin{gathered}
a = – 3\,\,\left( {{\text{tm}}} \right) \hfill \\
b = – 4\,\,\left( {{\text{tm}}} \right) \hfill \\
\end{gathered} \right.$

Với ${z_1} = 0,{z_2} = – 1$ có $\left\{ \begin{gathered}
{z_1} + {z_2} = – a \hfill \\
{z_1}{z_2} = b \hfill \\
\end{gathered} \right. \Rightarrow \left\{ \begin{gathered}
a = 1\,\,\left( {{\text{tm}}} \right) \hfill \\
b = 0\,\,\left( {{\text{tm}}} \right) \hfill \\
\end{gathered} \right.$

Vậy TH1 có 2 cặp số $\left( {a;b} \right)$ thỏa mãn.

TH2. $\Delta < 0 \Rightarrow \left\{ \begin{gathered}
{z_1} = x + yi \hfill \\
{z_2} = x – yi \hfill \\
\end{gathered} \right.$

Vì $\left\{ \begin{gathered}
\left| {{z_1} – 2} \right| = 2 \hfill \\
\left| {{z_2} + 1 – 4i} \right| = 4 \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
\left| {x + yi – 2} \right| = 2 \hfill \\
\left| {x – yi + 1 – 4i} \right| = 4 \hfill \\
\end{gathered} \right.$

$ \Leftrightarrow \left\{ \begin{gathered}
{\left( {x – 2} \right)^2} + {y^2} = 4 \hfill \\
{\left( {x + 1} \right)^2} + {\left( {y + 4} \right)^2} = 16 \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
{x^2} + {y^2} – 4x = 0{\text{ }}\left( 1 \right) \hfill \\
{x^2} + {y^2} + 2x + 8y + 1 = 0{\text{ }}\left( 2 \right) \hfill \\
\end{gathered} \right.$

Lấy (2) – (1) vế theo vế ta được: $6x + 8y + 1 = 0 \Rightarrow y = \frac{{ – 6x – 1}}{8}$

$ \Rightarrow {x^2} + {\left( {\frac{{6x + 1}}{8}} \right)^2} – 4x = 0$

$ \Leftrightarrow 100{x^2} – 244x + 1 = 0$

$ \Leftrightarrow \left\{ \begin{gathered}
{x_1} = \frac{{61 + 4\sqrt {231} }}{{50}} \hfill \\
{x_2} = \frac{{61 – 4\sqrt {231} }}{{50}} \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
{y_1} = \frac{{ – 416 – 24\sqrt {231} }}{{400}} \hfill \\
{y_2} = \frac{{ – 416 + 24\sqrt {231} }}{{400}} \hfill \\
\end{gathered} \right.$

Vậy TH2 có $2$ cặp số $\left( {a;b} \right)$ thỏa mãn.

Vậy có $4$ cặp số $\left( {a;b} \right)$ thỏa mãn.

Câu 47: Gọi $S$ là tập họp các giá trị nguyên của $y$ sao cho ứng với mỗi $y$, tồn tại duy nhất một giá trị $x \in \left[ {\frac{3}{2};\frac{9}{2}} \right]$ thỏa mãn ${\text{lo}}{{\text{g}}_3}\left( {{x^3} – 6{x^2} + 9x + y} \right) = {\text{lo}}{{\text{g}}_2}\left( { – {x^2} + 6x – 5} \right)$. Số phần tử của $S$ là

A. 7. B. 1. C. 8. D. 3.

Lời giải

Chọn C

Xét hàm số

$f\left( x \right) = {\log _3}\left( {{x^3} – 6{x^2} + 9x + y} \right) – {\log _2}\left( { – {x^2} + 6x – 5} \right)$

$ \Rightarrow f’\left( x \right) = \frac{{3{x^2} – 12x + 9}}{{\left( {{x^3} – 6{x^2} + 9x + y} \right)\ln 3}} + \frac{{2x – 6}}{{\left( { – {x^2} + 6x – 5} \right)\ln 2}}$

$ \Leftrightarrow f’\left( x \right) = \left( {x – 3} \right)\left[ {\frac{{3x – 3}}{{\left( {{x^3} – 6{x^2} + 9x + y} \right)\ln 3}} + \frac{2}{{\left( { – {x^2} + 6x – 5} \right)\ln 2}}} \right]$

Xét trên tập $x \in \left[ {\frac{3}{2};\frac{9}{2}} \right]$ thì ta dễ thấy

$f’\left( x \right) > 0$ với $x > 3$

$f’\left( x \right) < 0$ với $x < 3$

Nếu $x = 3$ thỏa mãn điều kiện.

Ta có $f\left( 3 \right) = {\log _3}y – 2;f\left( {\frac{3}{2}} \right) = {\log _3}\left( {\frac{{27}}{8} + y} \right) – {\log _2}\frac{7}{4}$;$f\left( {\frac{9}{2}} \right) = {\log _3}\left( {\frac{{81}}{8} + y} \right) – {\log _2}\frac{7}{4}$

TH1. $f\left( 3 \right) > 0 \Leftrightarrow y > 9 \Rightarrow $Phương trình $f\left( x \right) = 0$ vô nghiệm.

TH2. $f\left( 3 \right) = 0 \Leftrightarrow y = 9 \Rightarrow $Phương trình có nghiệm duy nhất $x = 3.$

TH3. $f\left( 3 \right) < 0$ hoặc $x = 3$ không thuộc tập xác định của phương trình, khi đó phương trình có nghiệm duy nhất $ \Leftrightarrow \left\{ \begin{gathered}
f\left( {\frac{3}{2}} \right) < 0 \hfill \\
f\left( {\frac{9}{2}} \right) \geqslant 0 \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
{\log _3}\left( {\frac{{27}}{8} + y} \right) < {\log _2}\frac{7}{4} \hfill \\
{\log _3}\left( {\frac{{81}}{8} + y} \right) \geqslant {\log _2}\frac{7}{4} \hfill \\
\end{gathered} \right. \Rightarrow – 7,7 < y < – 0,9$

Do $y$ nguyên $ \Rightarrow y \in \left\{ { – 7; – 6; – 5; – 4; – 3; – 2; – 1} \right\}.$

Vậy số phần tử của $S$ là $8.$

Câu 48: Xét khối nón $\left( \mathcal{N} \right)$ có đỉnh và đường tròn đáy cùng nằm trên một mặt cầu bán kính bằng 2. Khi $\left( \mathcal{N} \right)$ có độ dài đường sinh bằng $2\sqrt 3 $, thể tích của nó bằng

A. $2\sqrt 3 \pi $. B. $3\pi $. C. $6\sqrt 3 \pi $. D. $\pi $.

Lời giải

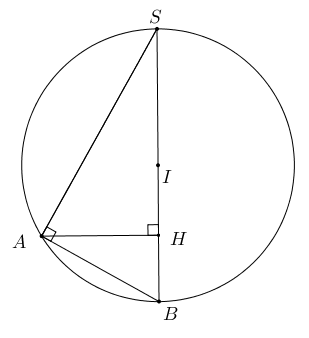
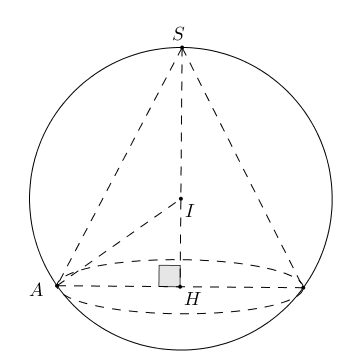Chọn B

Gọi $H$ là tâm đường tròn đáy của $\left( N \right)$, đỉnh $S$

TH1: $I$ thuộc đoạn $SH$. Đặt $IH = x,\,\,\left( {0 < x < 2} \right)$, suy ra $AH = \sqrt {I{A^2} – I{H^2}} = \sqrt {4 – {x^2}} $

Ta có $S{A^2} = S{H^2} + H{A^2}$

Suy ra $12 = {\left( {2 + x} \right)^2} + 4 – {x^2} \Leftrightarrow x = 1\,\left( {t.m} \right)$

Suy ra $SH = 3,AH = \sqrt 3 \Rightarrow V = \frac{1}{3}\pi {R^2}h = \frac{1}{3}\pi .3.3 = 3\pi $

TH2: $H$ thuộc đoạn $SI$. Đặt $IH = x,\,\,\left( {0 < x < 2} \right)$, suy ra $AH = \sqrt {I{A^2} – I{H^2}} = \sqrt {4 – {x^2}} $

Ta có $S{A^2} = S{H^2} + H{A^2}$

Suy ra ${\left( {2\sqrt 3 } \right)^2} = {\left( {2 – x} \right)^2} + 4 – {x^2} \Leftrightarrow x = – 1\,$(loại)

Câu 49: Trong không gian $Oxyz$, xét mặt cầu $\left( S \right)$ có tâm $I\left( {4;\,8;\,12} \right)$ và bán kính $R$ thay đổi. Có bao nhiêu giá trị nguyên của $R$ sao cho ứng với mỗi giá trị đó, tồn tại hai tiếp tuyến của $\left( S \right)$ trong mặt phẳng $\left( {Oyz} \right)$ mà hai tiếp tuyến đó cùng đi qua $O$ và góc giữa chúng không nhỏ hơn $60^\circ $?

A. $6$. B. $2$. C. $10$. D. $5$.

Lời giải

Chọn D

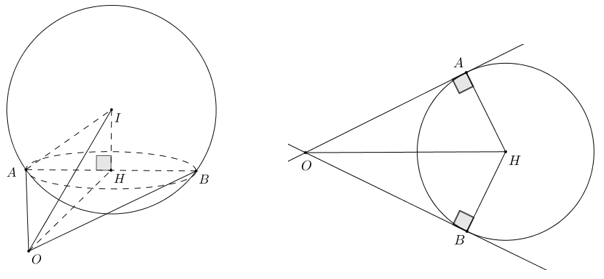
Giả sử 2 tiếp tuyến $OA,OB$, theo giả thiết suy ra $\left( {\overrightarrow {OA} ,\,\overrightarrow {OB} } \right) \geqslant 60^\circ $. Suy ra $30^\circ \leqslant \widehat {AOH} \leqslant 60^\circ $

Gọi $H$ là hình chiếu của $I$ trên $\left( {Oyz} \right)$, suy ra $H\left( {0;\,8;\,12} \right)$, suy ra $OH = 4\sqrt {13} $

Xét tam giác $OAH$ có: $HA = OH\sin \widehat {AOH} \geqslant 4\sqrt {13} \sin 30^\circ = 2\sqrt {13} $

Ta có $2\sqrt {13} \leqslant HA < 2\sqrt {39} $ $ \Rightarrow 52 \leqslant A{H^2} \leqslant 156$

$ \Rightarrow 52 + 16 \leqslant A{H^2} + I{H^2} \leqslant 156 + 16$

$ \Rightarrow 68 \leqslant I{A^2} \leqslant 172 \Rightarrow 68 \leqslant {R^2} \leqslant 172$ hay $8,24 \leqslant R \leqslant 13,11$.

Do $R$ là số nguyên $ \Rightarrow R \in \left\{ {9;\,10;\,…;\,13} \right\}$.

Vậy có tất cả 5 giá trị của $R$.

Câu 50: Cho hàm số $f\left( x \right) = {x^4} – 32{x^2} + 4$. Có bao nhiêu giá trị nguyên của tham số $m$ sao cho ứng với mỗi $m$, tổng giá trị các nghiệm phân biệt thuộc khoảng $\left( { – 3;2} \right)$ của phương trình $f\left( {{x^2} + 2x + 3} \right) = m$ bằng $ – 4$?

A. 145. B. 142. C. 144. D. 143.

Lời giải

Chọn D

Phương trình ${x^2} + 2x + 3 = a\,\,\left( {a \in \mathbb{R}} \right)$ có hai nghiệm ${x_1},{x_2}$ thì ta có: ${x_1} + {x_2} = – 2$

Phương trình $f\left( {{x^2} + 2{\text{x}} + 3} \right) = m\left( 1 \right)$ có tổng nghiệm bằng $ – 4$

$ \Leftrightarrow $phương trình $\left( 1 \right)$ có nghiệm xảy ra ở trường hợp: 4 nghiệm phân biệt ${x_1},{x_2},{x_3},{x_4}\,\,\left( 2 \right)$

( do khi đó: $\left( {{x_1} + {x_2}} \right) + \left( {{x_3} + {x_4}} \right) = – 2 + \left( { – 2} \right) = – 4\,\,$)

Đặt ${x^2} + 2x + 3 = t$

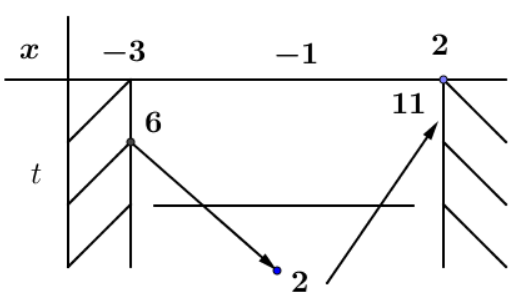
Điều kiện $\,\left( 2 \right)$$ \Leftrightarrow $Tìm $m$ để phương trình $f\left( t \right) = m$ có 2 nghiệm $2 < t < 6\,\,\,(2)$

Xét $f\left( t \right) = {t^4} – 32{t^2} + 4$
$ \Rightarrow f’\left( t \right) = 4{t^3} – 64t \Rightarrow f’\left( t \right) = 0 \Leftrightarrow \left[ \begin{gathered}
t = 0 \hfill \\
t = \pm 4 \hfill \\
\end{gathered} \right.$

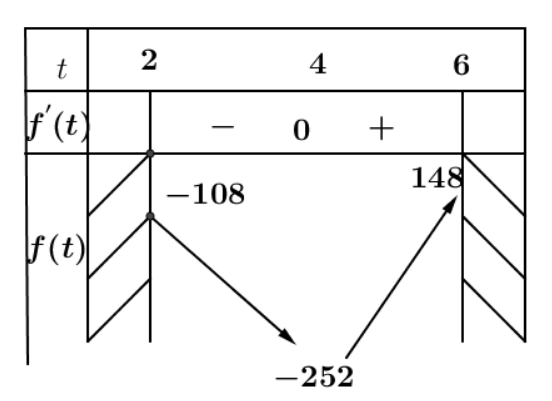
Yêu cầu bài toán $ \Leftrightarrow – 252 < m < – 108$$ \Rightarrow \,143$ số.