Phương Pháp Tìm m Để Hàm Số Đồng Biến Nghịch Biến Trên Một Khoảng

Phương pháp tìm m để hàm số đồng biến nghịch biến trên một khoảng gồm 3 dạng hàm số cơ bản: Hàm số bậc ba, hàm số bậc bốn, hàm số bậc nhất trên bậc nhất.

I. Phương pháp

1. Hàm số bậc ba $y = f\left( x \right) = a{x^3} + b{x^2} + cx + d$.

• Bước 1. Tập xác định: $D = \mathbb{R}$.

• Bước 2. Tính đạo hàm $y’ = f’\left( x \right) = 3a{x^2} + 2bx + c$.

• Để $f\left( x \right)$ đồng biến trên $\mathbb{R} \Leftrightarrow y’ = f’\left( x \right) \geqslant 0,\forall x \in \mathbb{R}$ $ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{{a_{f’\left( x \right)}} = 3a > 0} \\
{{\Delta _{f’\left( x \right)}} = 4{b^2} – 12ac \leqslant 0}
\end{array} \Rightarrow m} \right.$?

• Để $f\left( x \right)$ nghịch biến trên $\mathbb{R} \Leftrightarrow y’ = f’\left( x \right) \leqslant 0,\forall x \in \mathbb{R}$ $ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{{a_{f’\left( x \right)}} = 3a < 0} \\
{{\Delta _{f’\left( x \right)}} = 4{b^2} – 12ac \leqslant 0}
\end{array} \Rightarrow m} \right.$?

Lưu ý: Dấu của tam thức bậc hai $f\left( x \right) = a{x^2} + bx + c$.

• $f\left( x \right) \geqslant 0,\forall x \in \mathbb{R} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{a > 0} \\
{\Delta \leqslant 0}
\end{array}} \right.$.

• $f\left( x \right) \leqslant 0,\forall x \in \mathbb{R} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{a < 0} \\
{\Delta \leqslant 0}
\end{array}} \right.$.

2. Hàm số nhất biến $y = f\left( x \right) = \frac{{ax + b}}{{cx + d}}$.

• Bước 1. Tập xác định: $D = \mathbb{R} \setminus \left\{ { – \frac{d}{c}} \right\}$.

• Bước 2. Tính đạo hàm $y’ = f’\left( x \right) = \frac{{a.d – b.c}}{{{{(cx + d)}^2}}}$.

• Để $f\left( x \right)$ đồng biến trên $D \Leftrightarrow y’ = f’\left( x \right) > 0,\forall x \in D$ $ \Leftrightarrow a.d – b.c > 0 \Rightarrow m$?

• Để $f\left( x \right)$ nghịch biến trên $D \Leftrightarrow y’ = f’\left( x \right) < 0,\forall x \in D$$ \Leftrightarrow a.d – b.c < 0 \Rightarrow m$ ?

• Để $f\left( x \right)$ đồng biến trên $\left( {h;k} \right)$ $ \Leftrightarrow \left\{ \begin{gathered}
a.d – b.c > 0 \hfill \\
\left( {h;k} \right) \subset D \hfill \\
\end{gathered} \right. \Rightarrow m$?

• Để $f\left( x \right)$ nghịch biến trên $\left( {h;k} \right)$ $ \Leftrightarrow \left\{ \begin{gathered}
a.d – b.c < 0 \hfill \\
\left( {h;k} \right) \subset D \hfill \\
\end{gathered} \right. \Rightarrow m$?

3. Chú ý: Một số bài toán thì ta phải cô lập tham số $m$, tức là biến đổi $f’\left( {x,m} \right) \geqslant 0\left( { \leqslant 0} \right)$$ \Leftrightarrow g\left( x \right) \geqslant m\left( { \leqslant m} \right)$.

Bước 1. Xác định tham số để hàm số $f$ xác định trên khoảng đã cho.

Bước 2. Tính $f’\left( {x,m} \right)$.

Bước 3. Để giải bài toán dạng này, ta thường sử dụng các tính chất sau.

Nếu hàm số đồng biến trên $\left( {a;b} \right)$ thì

$f’\left( x \right) \geqslant 0,\forall x \in \left[ {a;b} \right]$$ \to g\left( x \right) \geqslant h\left( m \right),\forall x \in \left[ {a;b} \right]$$ \Leftrightarrow \mathop {\min }\limits_{\left[ {a;b} \right]} g(x) \geqslant h(m)$.

Nếu hàm số nghịch biến trên $\left( {a;b} \right)$ thì $f’\left( x \right) \leqslant 0,\forall x \in \left[ {a;b} \right]$$ \to g\left( x \right) \leqslant h\left( m \right),\forall x \in \left[ {a;b} \right]$$ \Leftrightarrow \mathop {max}\limits_{\left[ {a;b} \right]} g(x) \leqslant h(m)$.

II. Các ví dụ minh họa
1. Tìm $m$ để hàm số bậc ba đơn điệu trên một khoảng:

Ví dụ 1. Tìm $m$ để hàm số $y = {x^3} + \left( {m + 1} \right){x^2} + 3x + 2025$ đồng biến trên $\mathbb{R}$.

Lời giải

Tập xác định: $D = \mathbb{R}$.

Ta có: $y’ = 3{x^2} + 2\left( {m + 1} \right)x + 3$.

Hàm số $y = {x^3} + \left( {m + 1} \right){x^2} + 3x + 2$ đồng biến trên $\mathbb{R}$ khi và chỉ khi $y’ \geqslant 0,\forall x \in \mathbb{R}$.

$ \Leftrightarrow \Delta ‘ = {(m + 1)^2} – 9 \leqslant 0$$ \Leftrightarrow {m^2} + 2m – 8 \leqslant 0 \Leftrightarrow – 4 \leqslant m \leqslant 2$.

Vậy $m \in \left[ { – 4;2} \right]$.

Ví dụ 2. Tìm điều kiện của $m$ để hàm số $y = \left( {{m^2} – 1} \right){x^3} + \left( {m – 1} \right){x^2} – x – 10$ nghịch biến trên khoảng $\left( { – \infty ; + \infty } \right)$.

Lời giải

TH1: $m = 1$. Ta có: $y = – x + 4$ là phương trình của một đường thẳng có hệ số góc âm nên hàm số luôn nghịch biến trên $\mathbb{R}$. Do đó nhận $m = 1$.

TH2: $m = – 1$. Ta có: $y = – 2{x^2} – x + 4$ là phương trình của một đường Parabol nên hàm số không thể nghịch biến trên $\mathbb{R}$. Do đó loại $m = – 1$.

TH3: $m \ne \pm 1$. Khi đó hàm số nghịch biến trên khoảng $\left( { – \infty ; + \infty } \right) \Leftrightarrow y’ \leqslant 0\forall x \in \mathbb{R}$, dấu ” $ = $ ” chỉ xảy ra ở hữu hạn điểm trên $\mathbb{R}$.

$ \Leftrightarrow 3\left( {{m^2} – 1} \right){x^2} + 2\left( {m – 1} \right)x – 1 \leqslant 0,\forall x \in \mathbb{R}$

$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{a < 0} \\
{\Delta ‘ \leqslant 0}
\end{array}} \right.$$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{{m^2} – 1 < 0} \\
{{{(m – 1)}^2} + 3\left( {{m^2} – 1} \right) \leqslant 0}
\end{array}} \right.$$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{{m^2} – 1 < 0} \\
{\left( {m – 1} \right)\left( {4m + 2} \right) \leqslant 0}
\end{array}} \right.$$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{ – 1 < m < 1} \\
{ – \frac{1}{2} \leqslant m \leqslant 1}
\end{array} \Leftrightarrow – \frac{1}{2} \leqslant m < 1} \right.$
Vậy $m \in \left[ { – \frac{1}{2};1} \right]$

Ví dụ 3. Tìm $m$ để hàm số $y = {x^3} + 3{x^2} – mx + 2$ đồng biến trên $\left( { – \infty ;2} \right)$.

Lời giải

Tập xác định: $D = \mathbb{R}$.

$y’ = 3{x^2} + 6x – m$

Hàm số đồng biến trên $\left( { – \infty ;2} \right)$$ \Leftrightarrow y’ \geqslant 0,\,\forall x \in \left( { – \infty ;2} \right)$

$ \Leftrightarrow 3{x^2} + 6x – m \geqslant 0,\,\forall x \in \left( { – \infty ;2} \right)$

$ \Leftrightarrow 3{x^2} + 6x \geqslant m,\,\forall x \in \left( { – \infty ;2} \right)$

$ \Leftrightarrow m \leqslant \mathop {\min }\limits_{\left( { – \infty ;2} \right]} \left( {3{x^2} + 6x} \right)$

Ta tìm $\mathop {\min }\limits_{(  – \infty ;2]} \left( {3{x^2} + 6x} \right)$.

Xét hàm số $g(x) = 3{x^2} + 6x$

Ta có: $g'(x) = 6x + 6$; $g'(x) = 0 \Leftrightarrow 6x + 6 = 0 \Leftrightarrow x = – 1$.

Bảng biến thiên trên $(  – \infty ;2]$:

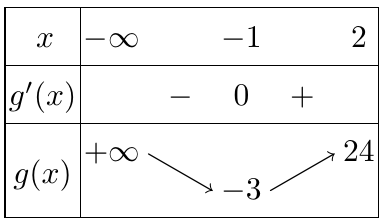
Dựa vào bảng biến thiên suy ra: $\mathop {\min }\limits_{(  – \infty ;2]} \left( {3{x^2} + 6x} \right) = – 3$.

Vậy, $m \leqslant – 3$ thỏa mãn yêu cầu bài toán.

Ví dụ 4. Tìm $m$ để hàm số $y = {x^3} – 3{x^2} + (2m – 3)x + 2025$ đồng biến trên $\left( { – 1; + \infty } \right)$.

Lời giải

Tập xác định: $D = \mathbb{R}$.

$y’ = 3{x^2} – 6x + 2m – 3$

Hàm số đồng biến trên $\left( { – 1; + \infty } \right)$$ \Leftrightarrow y’ \geqslant 0,\,\forall x \in \left( { – 1; + \infty } \right)$

$ \Leftrightarrow 3{x^2} – 6x + 2m – 3 \geqslant 0,\,\forall x \in \left( { – 1; + \infty } \right)$

$ \Leftrightarrow 2m \geqslant – 3{x^2} + 6x + 3,\,\forall x \in \left( { – 1; + \infty } \right)$

$ \Leftrightarrow 2m \geqslant \mathop {max}\limits_{[- 1; + \infty)} \left( { – 3{x^2} + 6x + 3} \right)$

Ta tìm $\mathop {max}\limits_{[- 1; + \infty)} \left( { – 3{x^2} + 6x + 2} \right)$.

Xét hàm số $g(x) = – 3{x^2} + 6x + 3$

Ta có: $g'(x) = – 6x + 6$; $g'(x) = 0 \Leftrightarrow – 6x + 6 = 0 \Leftrightarrow x = 1$.

Bảng biến thiên trên $[- 1; + \infty)$:

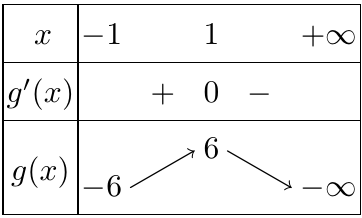
Dựa vào bảng biến thiên suy ra: $\mathop {max}\limits_{[- 1; + \infty)} \left( { – 3{x^2} + 6x + 2} \right) = 6$.

Vậy, $2m \leqslant 6 \Leftrightarrow m \geqslant 3$ thỏa mãn yêu cầu bài toán.

2. Tìm $m$ để hàm số bậc nhất trên bậc nhất đơn điệu trên một khoảng:

Ví dụ 5. Cho hàm số $y = \frac{{x – 3}}{{x – m}}$ với $m$ là tham số. Tìm $m$ để hàm số đồng biến trên mỗi khoảng xác định.

Lời giải

$D = \mathbb{R} \setminus \left\{ m \right\}$

$y’ = \frac{{ – m + 3}}{{{{(x – m)}^2}}}$

Hàm số đồng biến trên mỗi khoảng xác định$ \Leftrightarrow – m + 3 > 0 \Leftrightarrow m < 3$

Ví dụ 6. Cho hàm số $y = \frac{{mx + 4m}}{{x + m}}$ với $m$ là tham số. Tìm $m$ để hàm số nghịch biến trên các khoảng xác định.

Lời giải

$D = \mathbb{R} \setminus \left\{ { – m} \right\}$

$y’ = \frac{{{m^2} – 4m}}{{{{(x + m)}^2}}}$

Hàm số nghịch biến trên các khoảng xác định khi $y’ < 0,\forall x \in D \Leftrightarrow {m^2} – 4m < 0$$ \Leftrightarrow 0 < m < 4$.

Ví dụ 7. Tìm $m$ để hàm số $y = \frac{{x + 7}}{{2x + m}}$ nghịch biến trên $\left( { – 2; + \infty } \right)$.

Lời giải

Tập xác định: $D = \mathbb{R}\backslash \left\{ { – \frac{m}{2}} \right\}$

$y’ = \frac{{m – 14}}{{{{\left( {2x + m} \right)}^2}}}$

Hàm số nghịch biến trên $\left( { – 2; + \infty } \right) \Leftrightarrow \left\{ \begin{gathered}
m – 14 < 0 \hfill \\
\left( { – 2; + \infty } \right) \subset D \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
m – 14 < 0 \hfill \\
\frac{{ – m}}{2} \leqslant – 2 \hfill \\
\end{gathered} \right.$ $ \Leftrightarrow \left\{ \begin{gathered}
m < 14 \hfill \\
m \geqslant 4 \hfill \\
\end{gathered} \right. \Leftrightarrow 4 \leqslant m < 14$

Ví dụ 8. Tất cả giá trị của tham số $m$ để hàm số $y = \frac{{ – x + 1}}{{x – 2m}}$ đồng biến trên $\left( {2;10} \right)$.

Lời giải

Ta có: TXĐ: $D = \mathbb{R}\backslash \left\{ {2m} \right\}$.

$y’ = \frac{{2m – 1}}{{{{\left( {x – 2m} \right)}^2}}}$

Hàm số đồng biến trên $\left( {2;10} \right)$

$ \Leftrightarrow \left\{ \begin{gathered}
2m – 1 > 0 \hfill \\
\left( {2;10} \right) \subset D \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
2m > 1 \hfill \\
\left[ \begin{gathered}
2m \leqslant 2 \hfill \\
2m \geqslant 10 \hfill \\
\end{gathered} \right. \hfill \\
\end{gathered} \right.$

$ \Leftrightarrow \left\{ \begin{gathered}
m > \frac{1}{2} \hfill \\
\left[ \begin{gathered}
m \leqslant 1 \hfill \\
m \geqslant 5 \hfill \\
\end{gathered} \right. \hfill \\
\end{gathered} \right. \Leftrightarrow \left[ \begin{gathered}
\frac{1}{2} < m \leqslant 1 \hfill \\
m \geqslant 5 \hfill \\
\end{gathered} \right.$

Vậy, $\frac{1}{2} < m \leqslant 1$ hoặc $m \geqslant 5$.

Ví dụ 9. Tất cả giá trị của tham số $m$ để hàm số $y = \frac{{mx + 4}}{{x + m}}$ nghịch biến trong $\left( { – \infty ; – 1} \right)$.

Lời giải

Ta có: TXĐ: $D = \mathbb{R}\backslash \left\{ { – m} \right\}$.

$y’ = \frac{{{m^2} – 4}}{{{{\left( {x + m} \right)}^2}}}$

Hàm số $y = \frac{{mx + 4}}{{x + m}}$ nghịch biến trong $\left( { – \infty ; – 1} \right)$

$ \Leftrightarrow \left\{ \begin{gathered}
{m^2} – 4 < 0 \hfill \\
\left( { – \infty ; – 1} \right) \subset D \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
{m^2} – 4 < 0 \hfill \\
– m \geqslant – 1 \hfill \\
\end{gathered} \right.$

$ \Leftrightarrow \left\{ \begin{gathered}
– 2 < m < 2 \hfill \\
m \leqslant 1 \hfill \\
\end{gathered} \right.$$ \Leftrightarrow – 2 < m \leqslant 1$.

3. Tìm $m$ để hàm số bậc bốn đơn điệu trên một khoảng:

Ví dụ 10. Tìm tất cả các giá trị thực của tham số $m$ để hàm số $y = {x^4} – 6{x^2} + mx – 5$ nghịch biến trên khoảng $\left( {0;4} \right)$.

Lời giải

Tập xác định: $D = \mathbb{R}$.

$y’ = 4{x^3} – 12x + m$

Hàm số nghịch biến trên $\left( { – \infty ;2} \right)$$ \Leftrightarrow y’ \geqslant 0,\,\forall x \in \left( {0;4} \right)$

$ \Leftrightarrow 4{x^3} – 12x + m \geqslant 0,\,\forall x \in \left( {0;4} \right)$

$ \Leftrightarrow m \geqslant – 4{x^3} + 12x,\,\forall x \in \left( {0;4} \right)$

$ \Leftrightarrow m \geqslant \mathop {max}\limits_{[0;4]} \left( { – 4{x^3} + 12x} \right)$

Ta tìm $\mathop {max}\limits_{[0;4]} \left( { – 4{x^3} + 12x} \right)$.

Xét hàm số $g(x) = – 4{x^3} + 12x$

Ta có: $g'(x) = – 12{x^2} + 12$; $g'(x) = 0 \Leftrightarrow – 12{x^2} + 12 = 0 \Leftrightarrow \left[ \begin{gathered}
x = 1 \hfill \\
x = – 1 \hfill \\
\end{gathered} \right.$.

Bảng biến thiên trên $[0;4]$:

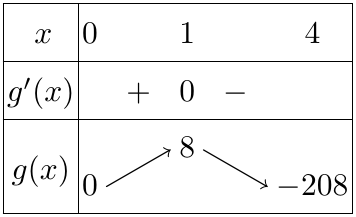
Vậy, $m \geqslant 8$.

Ví dụ 11. Tìm tất cả các giá trị thực của tham số $m$ để hàm số $y = {x^4} – 2\left( {m – 1} \right){x^2} + m – 2$ đồng biến trên khoảng $\left( {1;3} \right)$.

Lời giải

Hàm số đồng biến trên $\left( {1;3} \right)$

$ \Leftrightarrow \;y’ = 4{x^3} – 4\left( {m – 1} \right)x \geqslant 0,\forall x \in \left( {1;3} \right)$$ \Leftrightarrow \;y’ = 4x\left( {{x^2} – 4\left( {m – 1} \right)} \right) \geqslant 0,\forall x \in \left( {1;3} \right)$

$ \Leftrightarrow {x^2} – m + 1 \geqslant 0,\forall x \in \left( {1;3} \right)$ (vì trong khoảng $\left( {1;3} \right)$ ta có $x > 0$).

$ \Leftrightarrow {x^2} + 1 \geqslant m,\forall x \in \left( {1;3} \right)$$ \Leftrightarrow \mathop {\min }\limits_{[1;3]} \left( {{x^2} + 1} \right) \geqslant m$

Ta tìm $\mathop {\min }\limits_{[1;3]} \left( {{x^2} + 1} \right)$

Xét hàm số $g(x) = {x^2} + 1$

Ta có: $g'(x) = 2x$; $g'(x) = 0 \Leftrightarrow 2x = 0 \Leftrightarrow x = 0$.

Bảng biến thiên trên $[1;3]$:

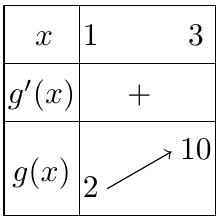
Vậy, $m \leqslant 2$