Các Dạng Trắc Nghiệm Biểu Thức Tọa Độ Của Các Phép Toán Vectơ Lớp 12

Các dạng trắc nghiệm biểu thức tọa độ của các phép toán vectơ lớp 12 giải chi tiết được soạn dưới dạng file word và PDF gồm 5 trang. Các bạn xem và tải về ở dưới.

DẠNG 1: CÁC PHÉP TOÁN VECTƠ

Câu 1. Trong không gian $Oxyz$, cho hai vectơ $\vec u = \left( {1; – 4;0} \right)$ và $\vec v = \left( { – 1; – 2;1} \right)$. Vectơ $\vec u + 3\vec v$ có tọa độ là

A. $\left( { – 2; – 10;3} \right)$. B. $\left( { – 2; – 6;3} \right)$. C. $\left( { – 4; – 8;4} \right)$. D. $\left( { – 2; – 10; – 3} \right)$.

Lời giải

Chọn A.

Ta có $3\vec v = \left( { – 3; – 6;3} \right)$.

Do đó $\vec u + 3\vec v = \left( { – 2; – 10;3} \right)$.

Câu 2. Trong không gian $Oxyz$, cho hai vectơ $\vec u = \left( {1;3; – 2} \right)$ và $\vec v = \left( {2;1; – 1} \right)$. Toạ độ vectơ $\vec u – \vec v$ là:

A. $\left( {3;4; – 3} \right)$. B. $\left( { – 1;2; – 3} \right)$. C. $\left( { – 1;2; – 1} \right)$. D. $\left( {1; – 2;1} \right)$.

Lời giải

Chọn C.

$\vec u – \vec v = \left( { – 1;2; – 1} \right)$

Câu 3. Trong không gian $Oxyz$ cho $\vec a = \left( {2;3;2} \right)$ và $\vec b = \left( {1;1; – 1} \right)$. Vectơ $\vec a – \vec b$ có tọa độ là

A. $\left( {3;4;1} \right)$. B. $\left( { – 1; – 2;3} \right)$. C. $\left( {3;5;1} \right)$. D. $\left( {1;2;3} \right)$.

Lời giải

Chọn D.

Ta có: $\vec a – \vec b = \left( {2 – 1;3 – 1;2 + 1} \right) = \left( {1;2;3} \right)$.

Câu 4. Trong không gian với hệ trục tọa độ $Oxyz$, cho ba vecto $\vec a\left( {1;2;3} \right);\vec b\left( {2;2; – 1} \right);\vec c\left( {4;0; – 4} \right)$. Tọa độ của vecto $\vec d = \vec a – \vec b + 2\vec c$ là

A. $\vec d\left( { – 7;0; – 4} \right)$ B. $\vec d\left( { – 7;0;4} \right)$ C. $\vec d\left( {7;0; – 4} \right)$ D. $\vec d\left( {7;0;4} \right)$

Lời giải

Chọn C.

Ta có: $\vec d = \vec a – \vec b + 2\vec c$

$ = \left( {1 – 2 + 2 \cdot 4;2 – 2 + 2 \cdot 0;3 + 1 + 2.\left( { – 4} \right)} \right) = \left( {7;0; – 4} \right)$.

Câu 5. Trong không gian với hệ trục tọa độ $Oxyz$, cho $\vec a = \left( {2; – 3;3} \right),\vec b = \left( {0;2; – 1} \right)$, $\vec c = \left( {3; – 1;5} \right)$. Tìm tọa độ của vectơ $\vec u = 2\vec a + 3\vec b – 2\vec c$.

A. $\left( {10; – 2;13} \right)$. B. $\left( { – 2;2; – 7} \right)$. C. $\left( { – 2; – 2;7} \right)$. D. $\left( { – 2;2;7} \right)$.

Lời giải

Chọn B.

Ta có: $2\vec a = \left( {4; – 6;6} \right),3\vec b = \left( {0;6; – 3} \right), – 2\vec c = \left( { – 6;2; – 10} \right)$

$ \Rightarrow \vec u = 2\vec a + 3\vec b – 2\vec c = \left( { – 2;2; – 7} \right)$.

Câu 6. Trong không gian với hệ tọa độ $Oxyz$, cho $\vec a = \left( {2; – 3;3} \right),\vec b = \left( {0;2; – 1} \right),\vec c = \left( {3; – 1;5} \right)$. Tìm tọa độ của vectơ $\vec u = 2\vec a + 3\vec b – 2\vec c$.

A. $\left( {10; – 2;13} \right)$. B. $\left( { – 2;2; – 7} \right)$. C. $\left( { – 2; – 2;7} \right)$. D. $\left( { – 2;2;7} \right)$.

Lời giải

Chọn B.

Có $2\vec a = \left( {4; – 6;6} \right);3\vec b = \left( {0;6; – 3} \right); – 2\vec c = \left( { – 6;2; – 10} \right)$.

Khi đó: $\vec u = 2\vec a + 3\vec b – 2\vec c = \left( { – 2;2; – 7} \right)$.

Câu 7. Trong không gian với hệ tọa độ $Oxyz$, cho hai vectơ $\vec x = \left( {2;1; – 3} \right)$ và $\vec y = \left( {1;0; – 1} \right)$. Tìm tọa độ của vectơ $\vec a = \vec x + 2\vec y$.

A. $\vec a = \left( {4;1; – 1} \right)$. B. $\vec a = \left( {3;1; – 4} \right)$. C. $\vec a = \left( {0;1; – 1} \right)$. D. $\vec a = \left( {4;1; – 5} \right)$.

Lời giải

Chọn D.

Ta có: $2\vec y = \left( {2;0; – 2} \right)$.

$\vec a = \vec x + 2\vec y = \left( {2 + 2;1 + 0; – 3 – 2} \right) = \left( {4;1; – 5} \right)$.

Câu 8. Trong không gian $Oxyz$ với $\vec i,\vec j,\vec k$ lần lượt là các vecto đơn vị trên các trục $Ox,Oy,Oz$. Tính tọa độ của vecto $\vec i + \vec j – \vec k$.

A. $\vec i + \vec j – \vec k = \left( { – 1; – 1;1} \right)$. B. $\vec i + \vec j – \vec k = \left( { – 1;1;1} \right)$. C. $\vec i + \vec j – \vec k = \left( {1;1; – 1} \right)$. D.

$\vec i + \vec j – \vec k = \left( {1; – 1;1} \right)$.

Lời giải

Chọn D.

Ta có $\vec i = \left( {1;0;0} \right),\vec j = \left( {0;1;0} \right),\vec k = \left( {0;0;1} \right)$.

Do đó, $\vec i + \vec j – \vec k = \left( {1;1; – 1} \right)$.

Câu 9. Trong không gian $Oxyz$, cho $\vec a = \left( {1;2;1} \right)$ và $\vec b = \left( { – 1;3;0} \right)$. Vectơ $\vec c = 2\vec a + \vec b$ có tọa độ là

A. $\left( {1;7;2} \right)$. B. $\left( {1;5;2} \right)$. C. $\left( {3;7;2} \right)$. D. $\left( {1;7;3} \right)$.

Lời giải

Chọn A.

Có $\vec c = 2\vec a + \vec b$, gọi $\vec c = \left( {{c_1};{c_2};{c_3}} \right)$

$ \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{{c_1} = 2.1 + \left( { – 1} \right) = 1} \\
{{c_2} = 2.2 + 3 = 7} \\
{{c_3} = 2.1 + 0 = 2}
\end{array}} \right.$

Vậy $\vec c = \left( {1;7;2} \right)$

Câu 10. Trong không gian Oxyz, cho $\vec a\left( { – 2;2;0} \right),\vec b\left( {2;2;0} \right),\vec c\left( {2;2;2} \right)$. Giá trị của $\left| {\vec a + \vec b + \vec c} \right|$ bằng

A. 6 . B. 11 . C. $2\sqrt {11} $. D. $2\sqrt 6 $.

Lời giải

Chọn C.

Ta có: $\vec a + \vec b + \vec c = \left( {2;6;2} \right)$.

Vậy $\left| {\vec a + \vec b + \vec c} \right| = 2\sqrt {11} $.

Câu 11. Trong không gian với hệ tọa độ $Oxyz$, cho các vectơ $\vec a = \left( {2;m – 1;3} \right),\vec b = \left( {1;3; – 2n} \right)$. Tìm $m,n$ để các vectơ $\vec a,\vec b$ cùng hướng.

A. $m = 7;n = – \frac{3}{4}$. B. $m = 4;n = – 3$. C. $m = 1;n = 0$. D. $m = 7;n = – \frac{4}{3}$

Lời giải

Chọn A.

$\vec a$ và $\vec b$ cùng hướng $ \Leftrightarrow \vec a = k\vec b(k > 0)$.

$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{2 = k} \\
{m – 1 = 3k} \\
{3 = k\left( { – 2n} \right)}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{k = 2} \\
{m = 7} \\
{n = – \frac{3}{4}}
\end{array}} \right.} \right.$

Vậy $m = 7;n = – \frac{3}{4}$

Câu 12. Trong không gian với hệ tọa độ $Oxyz$ cho các véc tơ $\vec u = 2\vec i – 2\vec j + \vec k,\vec v = \left( {m;2;m + 1} \right)$ với $m$ là tham số thực. Có bao nhiêu giá trị của $m$ để $\left| {\vec u\left| = \right|\vec v} \right|$.

A. 0 . B. 1. C. 2 . D. 3 .

Lời giải

Chọn C.

Ta có $\vec u = \left( {2; – 2;1} \right)$

Khi đó $\left| {\vec u} \right| = \sqrt {{2^2} + {{( – 2)}^2} + {1^2}} = 3$ và $\left| {\vec v} \right| = \sqrt {{m^2} + {2^2} + {{(m + 1)}^2}} = \sqrt {2{m^2} + 2m + 5} $

Do đó $\left| {\vec u\left| = \right|\vec v} \right| \Leftrightarrow 9 = 2{m^2} + 2m + 5 \Leftrightarrow {m^2} + m – 2 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{m = 1} \\
{m = – 2}
\end{array}} \right.$

Vậy có 2 giá trị của $m$ thỏa yêu cầu bài toán.

Câu 13. Trong không gian với hệ tọa độ $Oxyz$, cho các vectơ $\vec a = \left( {2;m – 1;3} \right),\vec b = \left( {1;3; – 2n} \right)$. Tìm $m,n$ để các vectơ $\vec a,\vec b$ cùng phương.

A. $m = 7;n = – \frac{3}{4}$. B. $m = 7;n = – \frac{4}{3}$. C. $m = 4;n = – 3$. D. $m = 1;n = 0$.

Lời giải

Chọn A.

Các vectơ $\vec a,\vec b$ cùng phương khi và chỉ khi tồn tại số thực dương $k$ sao cho $\vec a = k\vec b$

$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{2 = k} \\
{m – 1 = 3k} \\
{3 = k\left( { – 2n} \right)}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{2 = k} \\
{m – 1 = 6} \\
{3 = 2\left( { – 2n} \right)}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{2 = k} \\
{m = 7} \\
{n = \frac{{ – 3}}{4}}
\end{array}} \right.} \right.} \right.$

Câu 14. Trong không gian với hệ trục $Oxyz$ cho ba điểm $A\left( { – 1;2; – 3} \right),B\left( {1;0;2} \right),C\left( {x;y; – 2} \right)$ thẳng hàng. Khi đó $x + y$ bằng

A. $x + y = 1$. B. $x + y = 17$. C. $x + y = – \frac{{11}}{5}$. D. $x + y = \frac{{11}}{5}$.

Lời giải

Chọn A.

Có $\overrightarrow {AB} = \left( {2; – 2;5} \right),\overrightarrow {AC} = \left( {x + 1;y – 2;1} \right)$.

$A,B,C$ thẳng hàng $ \Leftrightarrow \overrightarrow {AB} ,\overrightarrow {AC} $ cùng phương $ \Leftrightarrow \frac{{x + 1}}{2} = \frac{{y – 2}}{{ – 2}} = \frac{1}{5}$

$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x = – \frac{3}{5}} \\
{y = \frac{8}{5}}
\end{array} \Rightarrow x + y = 1} \right.$.

Câu 15. Trong không gian với hệ tọa độ Oxyz , cho ba điểm $A\left( {2; – 1;5} \right),B\left( {5; – 5;7} \right),M\left( {x;y;1} \right)$ . Với giá trị nào của $x,y$ thì $A,B,M$ thẳng hàng.

A. $x = 4;y = 7$ B. $x = – 4;y = – 7$ C. $x = 4;y = – 7$ D. $x = – 4;y = 7$

Lời giải

Chọn A

Ta có $\overrightarrow {AB} = \left( {3; – 4;2} \right),\overrightarrow {AM} = \left( {x – 2;y + 1; – 4} \right)$

$A,B,M$ thẳng hàng $ \Leftrightarrow \overrightarrow {AB} ,\overrightarrow {AM} $ cùng phương $ \Leftrightarrow \frac{{x – 2}}{3} = \frac{{y + 1}}{{ – 4}} = \frac{{ – 4}}{2} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x = – 4} \\
{y = 7}
\end{array}} \right.$.

Câu 16. Trong không gian $Oxyz$, cho hai điểm $A\left( {2; – 2;1} \right),B\left( {0;1;2} \right)$. Tọa độ điểm $M$ thuộc mặt phẳng $\left( {Oxy} \right)$ sao cho ba điểm $A,B,M$ thẳng hàng là

A. $M\left( {4; – 5;0} \right)$. B. $M\left( {2; – 3;0} \right)$. C. $M\left( {0;0;1} \right)$. D. $M\left( {4;5;0} \right)$.

Lời giải

Chọn A

Ta có $M \in \left( {Oxy} \right) \Rightarrow M\left( {x;y;0} \right);\overrightarrow {AB} = \left( { – 2;3;1} \right);\overrightarrow {AM} = \left( {x – 2;y + 2; – 1} \right)$.

Để $A,B,M$ thẳng hàng thì $\overrightarrow {AB} $ và $\overrightarrow {AM} $ cùng phương, khi đó: $\frac{{x – 2}}{{ – 2}} = \frac{{y + 2}}{3} = \frac{{ – 1}}{1} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x = 4} \\
{y = – 5}
\end{array}} \right.$.

Vậy $M\left( {4; – 5;0} \right)$.

DẠNG 2: TÍCH VÔ HƯỚNG HAI VECTƠ

Câu 17. Trong không gian với hệ tọa độ Oxyz , cho vectơ $\vec u = \left( {3;0;1} \right)$ và $\vec v = \left( {2;1;0} \right)$. Tính tích vô hướng $\vec u \cdot \vec v$.

A. $\vec u \cdot \vec v = 8$. B. $\vec u \cdot \vec v = 6$. C. $\vec u \cdot \vec v = 0$. D. $\vec u \cdot \vec v = – 6$.

Lời giải

Chọn B.

Ta có $\vec u \cdot \vec v = 3.2 + 0.1 + 1.0 = 6$.

Câu 18. Trong hệ tọa độ $Oxy$, cho $\vec u = \vec i + 3\vec j$ và $\vec v = \left( {2; – 1} \right)$. Tính $\vec u \cdot \vec v$.

A. $\vec u \cdot \vec v = – 1$. B. $\vec u \cdot \vec v = 1$. C. $\vec u \cdot \vec v = \left( {2; – 3} \right)$. D. $\vec u \cdot \vec v = 5\sqrt 2 $.

Lời giải

Chọn A.

Từ $\vec u = \vec i + 3\vec j \Rightarrow \vec u = \left( {1;3} \right)$.

Do đó, $\vec u \cdot \vec v = 1 \cdot 2 + 3 \cdot \left( { – 1} \right) = – 1$.

Câu 19. Cho hai véc tơ $\vec a = \left( {1; – 2;3} \right),\vec b = \left( { – 2;1;2} \right)$. Khi đó, tích vô hướng $\left( {\vec a + \vec b} \right) \cdot \vec b$ bằng

A. 12. B. 2. C. 11. D. 10 .

Lời giải

Chọn C.

$\vec a + \vec b = \left( { – 1; – 1;5} \right) \Rightarrow \left( {\vec a + \vec b} \right) \cdot \vec b$

$ = – 1 \cdot \left( { – 2} \right) + \left( { – 1} \right) \cdot 1 + 5 \cdot 2 = 11$.

Câu 20. Trong không gian với hệ trục tọa độ $Oxyz$, cho $\vec u = \left( {2; – 1;1} \right)$ và $\vec v = \left( {0; – 3; – m} \right)$. Tìm số thực $m$ sao cho tích vô hướng $\vec u \cdot \vec v = 1$.

A. $m = 4$. B. $m = 2$. C. $m = 3$. D. $m = – 2$.

Lời giải

Chọn B.

Ta có: $\vec u \cdot \vec v = 1 \Leftrightarrow 3 – m = 1 \Leftrightarrow m = 2$.

Câu 21. Trong không gian $Oxyz$, cho hai vectơ $\vec u$ và $\vec v$ tạo với nhau một góc ${120^ \circ }$ và $\left| {\vec u} \right| = 2$ , $\left| {\vec v} \right| = 5$. Tính $\left| {\vec u + \vec v} \right|$

A. $\sqrt {19} $. B. -5 . C. 7 . D. $\sqrt {39} $.

Lời giải

Chọn A.

Ta có $:{(\left| {\vec u + \vec v} \right|)^2} = {(\vec u + \vec v)^2} = {\vec u^2} + 2\vec u\vec v + {\vec v^2}$

$ = \left| {{{\vec u}^2}} \right| + 2\left| {\vec u} \right|.\left| {\vec v} \right|cos\left( {\vec u;\vec v} \right) + {\left| {\vec v} \right|^2}$

$ = {2^2} + 2.2.5 \cdot \left( { – \frac{1}{2}} \right) + {5^2} = 19$.

Suy ra $\left| {\vec u + \vec v} \right| = \sqrt {19} $.

Câu 22. Trong không gian với hệ trục tọa độ $Oxyz$, cho hai vectơ $\vec a = \left( {2;1;0} \right)$ và $\vec b = \left( { – 1;0; – 2} \right)$. Tính $cos\left( {\vec a,\vec b} \right)$.

A. $cos\left( {\vec a,\vec b} \right) = – \frac{2}{{25}}$ B. $cos\left( {\vec a,\vec b} \right) = – \frac{2}{5}$ C. $cos\left( {\vec a,\vec b} \right) = \frac{2}{{25}}$ D. $cos\left( {\vec a,\vec b} \right) = \frac{2}{5}$

Lời giải

Chọn B.

Ta có: $cos\left( {\vec a,\vec b} \right) = \frac{{\vec a \cdot \vec b}}{{\left| {\vec a\left| \cdot \right|\vec b} \right|}} = \frac{{ – 2}}{{\sqrt 5 \cdot \sqrt 5 }} = – \frac{2}{5}$.

Câu 23. Trong không gian $Oxyz$, góc giữa hai vectơ $\vec i$ và $\vec u = \left( { – \sqrt 3 ;0;1} \right)$ là

A. ${120^ \circ }$. B. ${60^ \circ }$. C. ${150^ \circ }$. D. ${30^ \circ }$.

Lời giải

Chọn C.

Ta có $\vec i = \left( {1;0;0} \right)$.

Vậy: $cos\left( {\vec i,\vec u} \right) = \frac{{\vec i \cdot \vec u}}{{\left| {\vec i\left| \cdot \right|\vec u} \right|}} = \frac{{1 \cdot \left( { – \sqrt 3 } \right) + 0.0 + 0 \cdot 1}}{{1 \cdot \sqrt {{{( – \sqrt 3 )}^2} + {0^2} + {1^2}} }}$

$ = \frac{{ – \sqrt 3 }}{2} \Rightarrow \left( {\vec i,\vec u} \right) = {150^ \circ }$.

Câu 24. Trong không gian Oxyz , cho $\vec a = \left( { – 3;4;0} \right),\vec b = \left( {5;0;12} \right)$. Côsin của góc giữa $\vec a$ và $\vec b$ bằng

A. $\frac{3}{{13}}$. B. $\frac{5}{6}$. C. $ – \frac{5}{6}$. D. $ – \frac{3}{{13}}$.

Lời giải

Chọn D.

Ta có: $cos\left( {\vec a;\vec b} \right) = \frac{{\vec a \cdot \vec b}}{{\left| {\vec a\left| \cdot \right|\vec b} \right|}}$

$ = \frac{{ – 3.5 + 4.0 + 0.12}}{{\sqrt {{{( – 3)}^2} + {4^2} + {0^2}} \cdot \sqrt {{5^2} + {0^2} + {{12}^2}} }} = \frac{{ – 3}}{{13}}$.

Câu 25. Cho $\vec u = \left( { – 1;1;0} \right),\vec v = \left( {0; – 1;0} \right)$, góc giữa hai véctơ $\vec u$ và $\vec v$ là

A. ${120^ \circ }$. B. ${45^ \circ }$. C. ${135^ \circ }$. D. ${60^ \circ }$.

Lời giải

Chọn C.

Ta có $cos\left( {\vec u,\vec v} \right) = \frac{{\vec u \cdot \vec v}}{{\left| {\vec u\left| \cdot \right|\vec v} \right|}} = \frac{{ – 1}}{{\sqrt 2 }} \Rightarrow \left( {\vec u,\vec v} \right) = {135^ \circ }$.

Câu 26. Trong không gian $Oxyz$ cho 2 véc tơ $\vec a = \left( {2;1; – 1} \right);\vec b = \left( {1;3;m} \right)$. Tìm $m$ để $\left( {\vec a;\vec b} \right) = {90^ \circ }$.

A. $m = – 5$. B. $m = 5$. C. $m = 1$. D. $m = – 2$

Lời giải

Chọn B.

$\left( {\vec a;\vec b} \right) = {90^ \circ } \Leftrightarrow \vec a \cdot \vec b = 0 \Leftrightarrow 5 – m = 0 \Leftrightarrow m = 5$.

Câu 27. Trong không gian với hệ tọa độ $Oxyz$, cho véc tơ $\vec u = \left( {1;1; – 2} \right),\vec v = \left( {1;0;m} \right)$. Tìm tất cả giá trị của $m$ để góc giữa $\vec u,\vec v$ bằng ${45^ \circ }$.

A. $m = 2$. B. $m = 2 \pm \sqrt 6 $. C. $m = 2 – \sqrt 6 $. D. $m = 2 + \sqrt 6 $.

Lời giải

Chọn C.

$\; + \left( {\vec u,\vec v} \right) = {45^ \circ } \Leftrightarrow cos\left( {\vec u,\vec v} \right) = \frac{{\sqrt 2 }}{2} \Leftrightarrow \frac{{\vec u \cdot \vec v}}{{\left| {\vec u\left| \cdot \right|\vec v} \right|}} = \frac{{\sqrt 2 }}{2}$

$ \Leftrightarrow \frac{{1 – 2m}}{{\sqrt 6 \cdot \sqrt {1 + {m^2}} }} = \frac{1}{{\sqrt 2 }} \Leftrightarrow \sqrt {3\left( {{m^2} + 1} \right)} = 1 – 2m$

$ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}
{1 – 2m \geqslant 0} \\
{3{m^2} + 3 = 1 – 4m + 4{m^2}}
\end{array}} \right.$

$ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}
{m \leqslant \frac{1}{2}} \\
{{m^2} – 4m – 2 = 0}
\end{array} \Leftrightarrow m = 2 – \sqrt 6 .} \right.$

Câu 28. Trong không gian $Oxyz$, cho các vec tơ $\vec a = \left( {5;3; – 2} \right)$ và $\vec b = \left( {m; – 1;m + 3} \right)$. Có bao nhiêu giá trị nguyên dương của $m$ để góc giữa hai vec tơ $\vec a$ và $\vec b$ là góc tù?

A. 2. B. 3. C. 1. D. 5.

Lời giải

Chọn A.

Ta có $cos\left( {\vec a;\vec b} \right) = \frac{{\vec a \cdot \vec b}}{{\left| {\vec a\left| \cdot \right|\vec b} \right|}} = \frac{{3m – 9}}{{\sqrt {38} \cdot \sqrt {2{m^2} + 6m + 10} }}$.

Góc giữa hai vec tơ $\vec a$ và $\vec b$ là góc tù khi và chỉ khi $cos\left( {\vec a;\vec b} \right) < 0 \Leftrightarrow 3m – 9 < 0 \Leftrightarrow m < 3$.

Vì $m$ nguyên dương nên $m \in \left\{ {1;2} \right\}$.

Vậy có 2 giá trị $m$ thỏa mãn yêu cầu bài toán.

Câu 29. Trên mặt phẳng tọa độ $Oxy$, cho tam giác $ABC$ biết $A\left( {1;3} \right),B\left( { – 2; – 2} \right),C\left( {3;1} \right)$. Tính cosin góc $A$ của tam giác.

A. $cosA = \frac{2}{{\sqrt {17} }}$ B. $cosA = \frac{1}{{\sqrt {17} }}$ C. $cosA = – \frac{2}{{\sqrt {17} }}$ D. $cosA = – \frac{1}{{\sqrt {17} }}$

Lời giải

Chọn B

Ta có: $\overrightarrow {AB} = \left( { – 3; – 5} \right),\overrightarrow {AC} = \left( {2; – 2} \right)$.

Khi đó: $cosA = cos\left( {\overrightarrow {AB} ;\overrightarrow {AC} } \right)$

$ = \frac{{\overrightarrow {AB} \cdot \overrightarrow {AC} }}{{AB \cdot AC}} = \frac{{ – 3 \cdot 2 + 5 \cdot 2}}{{\sqrt {34} \cdot 2\sqrt 2 }} = \frac{1}{{\sqrt {17} }}$.

Câu 30. Trong không gian $Oxyz$, cho ba điểm $A\left( { – 1; – 2;3} \right)\;B\left( {0;3;1} \right),C\left( {4;2;2} \right)$. Cosin của góc $\widehat {BAC}$ là

A. $\frac{9}{{\sqrt {35} }}$. B. $ – \frac{9}{{\sqrt {35} }}$. C. $ – \frac{9}{{2\sqrt {35} }}$. D. $\frac{9}{{2\sqrt {35} }}$.

Lời giải

Chọn D

Ta có $\overrightarrow {AB} \left( {1;5; – 2} \right);\overrightarrow {AC} \left( {5;4; – 1} \right)$.

$cos\widehat {BAC} = \frac{{\overrightarrow {AB} \cdot \overrightarrow {AC} }}{{\left| {\overrightarrow {AB} \left| \cdot \right|\overrightarrow {AC} } \right|}} = \frac{{5 + 20 + 2}}{{\sqrt {30} \cdot \sqrt {42} }} = \frac{9}{{2\sqrt {35} }}$.

Câu 31. Trong không gian $Oxyz$ cho $A\left( {1;2;3} \right);B\left( { – 1;2;1} \right);C\left( {3; – 1; – 2} \right)$. Tính tích vô hướng $\overrightarrow {AB} \cdot \overrightarrow {AC} $.

A. -6. B. -14. C. 14. D. 6 .

Lời giải

Chọn D

Ta có: $\overrightarrow {AB} = \left( { – 2;0; – 2} \right);\overrightarrow {AC} = \left( {2; – 3; – 5} \right)$

$ \Rightarrow \overrightarrow {AB} \cdot \overrightarrow {AC} = 6$

Câu 32. Trong không gian với hệ tọa độ Oxyz cho ba điểm $M\left( {2;3; – 1} \right),N\left( { – 1;1;1} \right)$ và $P\left( {1;m – 1;2} \right)$. Tìm $m$ để tam giác $MNP$ vuông tại $N$.

A. $m = 2$ B. $m = – 6$ C. $m = 0$ D. $m = – 4$

Lời giải

Chọn C

$\overrightarrow {MN} \left( { – 3; – 2;2} \right);\overrightarrow {NP} \left( {2;m – 2;1} \right)$.

Tam giác $MNP$ vuông tại $N$

$ \Leftrightarrow \overrightarrow {MN} \cdot \overrightarrow {NP} = 0 \Leftrightarrow – 6 – 2\left( {m – 2} \right) + 2 = 0$

$ \Leftrightarrow m – 2 = – 2 \Leftrightarrow m = 0$.

Câu 33. Trong không gian tọa độ $Oxyz$, cho $A\left( {2;0;0} \right),B\left( {0;2;0} \right),C\left( {0;0;2} \right)$. Có tất cả bao nhiêu điểm $M$ trong không gian thỏa mãn $M$ không trùng với các điểm $A,B,C$ và $\widehat {AMB} = \widehat {BMC} = \widehat {CMA} = {90^ \circ }$

A. 0. B. 1. C. 2. D. 3.

Lời giải

Chọn C

Gọi $M\left( {x;y;z} \right)$.Ta có: $\widehat {AMB} = \widehat {BMC} = \widehat {CMA} = {90^ \circ }$

$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{\overrightarrow {AM} \cdot \overrightarrow {BM} = 0} \\
{\overrightarrow {BM} \cdot \overrightarrow {CM} = 0} \\
{\overrightarrow {CM} \cdot \overrightarrow {AM} = 0}
\end{array}} \right.$

$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x\left( {x – 2} \right) + y\left( {y – 2} \right) + {z^2} = 0} \\
{{x^2} + y\left( {y – 2} \right) + z\left( {z – 2} \right) = 0} \\
{x\left( {x – 2} \right) + {y^2} + z\left( {z – 2} \right) = 0}
\end{array}} \right.$

$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{{x^2} + {y^2} + {z^2} – 2x – 2y = 0} \\
{{x^2} + {y^2} + {z^2} – 2y – 2z = 0} \\
{{x^2} + {y^2} + {z^2} – 2x – 2z = 0}
\end{array}} \right.$

$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{{x^2} + {y^2} + {z^2} – 2x – 2y = 0} \\
{x = z} \\
{y = z}
\end{array}} \right.$

$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{3{x^2} – 4x = 0} \\
{x = y = z}
\end{array}} \right.$$ \Rightarrow \left[ {\begin{array}{*{20}{l}}
{M\left( {0;0;0} \right)} \\
{M\left( {\frac{4}{3};\frac{4}{3};\frac{4}{3}} \right)}
\end{array}} \right.$

Câu 34. Trong không gian với hệ tọa độ $Oxyz$, cho tam giác $ABC$, biết $A\left( {5;3; – 1} \right),B\left( {2;3; – 4} \right)$ , $C\left( {3;1; – 2} \right)$. Bán kính đường tròn nội tiếp tam giác $ABC$ bằng:

A. $9 – 2\sqrt 6 $. B. $9 – 3\sqrt 6 $. C. $9 + 3\sqrt 6 $. D. $9 + 2\sqrt 6 $.

Lời giải

Chọn B

Ta có $A{C^2} + B{C^2} = 9 + 9 = A{B^2} \Rightarrow $ tam giác $ABC$ vuông tại $C$.

Suy ra: $r = \frac{{{S_{ABC}}}}{p} = \frac{{\frac{1}{2}\;CA.CB\;}}{{\frac{1}{2}\left( {AB + BC + CA} \right)}}$

$ = \frac{{3.3\sqrt 2 }}{{3\sqrt 2 + \sqrt 3 + \sqrt 3 }} = 9 – 3\sqrt 6 $

DẠNG 3: ĐỘ DÀI ĐƯỜNG THẲNG-TÌM TỌA ĐỘ ĐIỂM

Câu 35. Trong không gian với hệ tọa độ $Oxyz$, cho điểm $A\left( {2;2;1} \right)$. Tính độ dài đoạn thẳng OA.

A. $OA = \sqrt 5 $ B. $OA = 5$ C. $OA = 3$ D. $OA = 9$

Lời giải

Chọn C

$OA = \sqrt {{2^2} + {2^2} + {1^2}} = 3$.

Câu 36. Trong không gian với hệ tọa độ $Oxyz$, cho hai điểm $A\left( {1; – 3;1} \right),B\left( {3;0; – 2} \right)$. Tính độ dài $AB$.

A. 26. B. 22. C. $\sqrt {26} $. D. $\sqrt {22} $.

Lời giải

Chọn D

$\overrightarrow {AB} = \left( {2;3; – 3} \right) \Rightarrow AB = \sqrt {{2^2} + {3^2} + {{( – 3)}^2}} = \sqrt {22} $

Câu 37. Trong không gian $Oxyz$, cho hai điểm $A\left( {1;1;2} \right)$ và $B\left( {3;1;0} \right)$. Trung điểm của đoạn thẳng $AB$ có tọa độ là

A. $\left( {4;2;2} \right)$. B. $\left( {2;1;1} \right)$. C. $\left( {2;0; – 2} \right)$. D. $\left( {1;0; – 1} \right)$.

Lời giải

Chọn B

Gọi $M$ là trung điểm của $AB$ ta có: $\left\{ {\begin{array}{*{20}{l}}
{{x_M} = \frac{{{x_A} + {x_B}}}{2} = \frac{{1 + 3}}{2} = 2} \\
{{y_M} = \frac{{{y_A} + {y_B}}}{2} = \frac{{1 + 1}}{2} = 1.\;} \\
{{z_M} = \frac{{{z_A} + {z_B}}}{2} = \frac{{2 + 0}}{2} = 1}
\end{array}} \right.$

Vậy $M\left( {2;1;1} \right)$.

Câu 38. Trong không gian với hệ tọa độ Oxyz cho hai điểm $A\left( { – 1;5;3} \right)$ và $M\left( {2;1; – 2} \right)$. Tọa độ điểm $B$ biết $M$ là trung điểm của $AB$ là

A. $B\left( {\frac{1}{2};3;\frac{1}{2}} \right)$. B. $B\left( { – 4;9;8} \right)$. C. $B\left( {5;3; – 7} \right)$. D. $B\left( {5; – 3; – 7} \right)$.

Lời giải

Chọn D

Giả sử $B\left( {{x_B};{y_B};{z_B}} \right)$.

Vì $M$ là trung điểm của $AB$ nên ta có: $\left\{ {\begin{array}{*{20}{l}}
{{x_M} = \frac{{{x_A} + {x_B}}}{2}} \\
{{y_M} = \frac{{{y_A} + {y_B}}}{2}} \\
{{z_M} = \frac{{{z_A} + {z_B}}}{2}}
\end{array}} \right.$

$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{2 = \frac{{ – 1 + {x_B}}}{2}} \\
{1 = \frac{{5 + {y_B}}}{2}} \\
{ – 2 = \frac{{3 + {z_M}}}{2}}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{{x_B} = 5} \\
{{y_B} = – 3} \\
{{z_B} = – 7}
\end{array}} \right.} \right.$

Vậy $B\left( {5; – 3; – 7} \right)$.

Câu 39. Trong không gian cho hệ trục toạ độ $Oxyz$, cho ba điểm $A\left( {1; – 2;3} \right),B\left( { – 1;2;5} \right),C\left( {0;0;1} \right)$. Tìm toạ độ trọng tâm $G$ của tam giác $ABC$.

A. $G\left( {0;0;3} \right)$. B. $G\left( {0;0;9} \right)$. C. $G\left( { – 1;0;3} \right)$. D. $G\left( {0;0;1} \right)$.

Lời giải

Chọn A

Toạ độ trong tâm $G$ của tam giác $ABC$ bằng: $\left\{ {\begin{array}{*{20}{l}}
{{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3} = \frac{{1 – 1 + 0}}{3} = 0} \\
{{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3} = \frac{{ – 2 + 2 + 0}}{3} = 0} \\
{{z_G} = \frac{{{z_A} + {z_B} + {z_C}}}{3} = \frac{{3 + 5 + 1}}{3} = 3}
\end{array}} \right.$

$ \Rightarrow G\left( {0;0;3} \right)$

Câu 40. Cho bốn điểm $S\left( {1,2,3} \right);A\left( {2,2,3} \right);B\left( {1,3,3} \right);C\left( {1,2,4} \right)$. Xác định tọa độ trọng tâm G của hình chóp $SABC$.

A. $\left( {5;9;13} \right)$. B. $\left( {\frac{5}{3};3;\frac{{13}}{3}} \right)$. C. $\left( {1;\frac{7}{4};\frac{9}{4}} \right)$ D. $\left( {\frac{5}{4};\frac{9}{4};\frac{{13}}{4}} \right)$

Lời giải

Chọn D

Gọi $G\left( {x,y,z} \right)$ là trọng tâm của hình chóp $SABC$ suy ra

Ta có: $\left\{ {\begin{array}{*{20}{l}}
{x = \frac{{{x_A} + {x_B} + {x_C} + {x_S}}}{4}} \\
{y = \frac{{{y_A} + {y_B} + {y_C} + {y_S}}}{4}} \\
{z = \frac{{{z_A} + {z_B} + {z_C} + {z_S}}}{4}}
\end{array}} \right.$

$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x = \frac{{2 + 1 + 1 + 1}}{4} = \frac{5}{4}} \\
{y = \frac{{2 + 3 + 2 + 2}}{4} = \frac{9}{4}} \\
{z = \frac{{3 + 3 + 4 + 3}}{4} = \frac{{13}}{4}}
\end{array}} \right.$

Câu 41. Trong không gian với hệ tọa độ Oxyz , cho 2 điểm $B\left( {1;2; – 3} \right),C\left( {7;4; – 2} \right)$ Nếu điểm $E$ thỏa mãn đẳng thức $\overrightarrow {CE} = 2\overrightarrow {EB} $ thì tọa độ điểm $E$ là:

A. $\left( {3;\frac{8}{3}; – \frac{8}{3}} \right)$ B. $\left( {\frac{8}{3};3; – \frac{8}{3}} \right)$. C. $\left( {3;3; – \frac{8}{3}} \right)$ D. $\left( {1;2;\frac{1}{3}} \right)$

Lời giải

Chọn A

Gọi $E\left( {x;y;z} \right)$

Ta có: $\overrightarrow {CE} = \left( {x – 7;y – 4;z + 2} \right)$; $2\overrightarrow {EB} = \left( {2 – 2x;4 – 2y; – 6 – 2z} \right)$

$\overrightarrow {CE} = 2\overrightarrow {EB} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x – 7 = 2 – 2x} \\
{y – 4 = 4 – 2y} \\
{z + 2 = – 6 – 2z}
\end{array}} \right.$

$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x = 3} \\
{y = \frac{8}{3}} \\
{z = – \frac{8}{3}}
\end{array}} \right.$

Câu 42. Trong không gian $Oxyz$, cho hai điểm $A\left( {3;1; – 2} \right),B\left( {2; – 3;5} \right)$. Điểm $M$ thuộc đoạn $AB$ sao cho $MA = 2MB$, tọa độ điểm $M$ là

A. $\left( {\frac{7}{3}; – \frac{5}{3};\frac{8}{3}} \right)$. B. $\left( {4;5; – 9} \right)$. C. $\left( {\frac{3}{2}; – 5;\frac{{17}}{2}} \right)$. D. $\left( {1; – 7;12} \right)$.

Lời giải

Chọn A

Gọi $M\left( {x;y;z} \right)$. Vì M thuộc đoạn AB nên:

$\overrightarrow {MA} = – 2\overrightarrow {MB} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{3 – x = – 2\left( {2 – x} \right)} \\
{1 – y = – 2\left( { – 3 – y} \right)} \\
{ – 2 – z = – 2\left( {5 – z} \right)}
\end{array}} \right.$

$ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}
{x = \frac{7}{3}} \\
{y = – \frac{5}{3}} \\
{z = \frac{8}{3}}
\end{array}} \right.$

Câu 43. Trong hệ trục tọa độ $Oxyz$, cho hai điểm là $A\left( {1;3; – 1} \right),B\left( {3; – 1;5} \right)$. Tìm tọa độ của điểm $M$ thỏa mãn hệ thức $\overrightarrow {MA} = 3\overrightarrow {MB} $.

A. $M\left( {\frac{5}{3};\frac{{13}}{3};1} \right)$. B. $M\left( {\frac{7}{3};\frac{1}{3};3} \right)$. C. $M\left( {\frac{7}{3};\frac{1}{3};3} \right)$. D. $M\left( {4; – 3;8} \right)$.

Lời giải

Chọn D

Ta có: $\overrightarrow {MA} = 3\overrightarrow {MB} \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{{x_M} = \frac{{{x_A} – 3{x_B}}}{{1 – 3}} = 4} \\
{{y_M} = \frac{{{y_A} – 3{y_B}}}{{1 – 3}} = – 3} \\
{{z_M} = \frac{{{z_A} – 3{z_B}}}{{1 – 3}} = 8}
\end{array}} \right.$$ \Rightarrow M(4; – 3;8)$

Câu 44. Trong không gian với hệ tọa độ $Oxyz$ cho hai điểm $A\left( {4;2;1} \right),B\left( { – 2; – 1;4} \right)$. Tìm tọa độ điểm $M$ thỏa mãn đẳng thức $\overrightarrow {AM} = 2\overrightarrow {MB} $.

A. $M\left( {0;0;3} \right)$. B. $M\left( {0;0; – 3} \right)$. C. $M\left( { – 8; – 4;7} \right)$. D. $M\left( {8;4; – 7} \right)$.

Lời giải

Chon A

Gọi điểm $M\left( {x;y;z} \right)$. Khi đó: $\overrightarrow {AM} = 2\overrightarrow {MB} $

$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x – 4 = 2\left( { – 2 – x} \right)} \\
{y – 2 = 2\left( { – 1 – y} \right)} \\
{z – 1 = 2\left( {4 – z} \right)}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x = 0} \\
{y = 0} \\
{z = 3}
\end{array}} \right.} \right.$

Vậy $M\left( {0;0;3} \right)$.

Câu 45. Trong không gian với hệ tọa độ $Oxyz$, cho các điểm $A\left( {3; – 4;0} \right),B\left( { – 1;1;3} \right),C\left( {3,1,0} \right)$ . Tìm tọa độ điểm $D$ trên trục hoành sao cho $AD = BC$.

A. $D\left( {6;0;0} \right),D\left( {12;0;0} \right)$ B. $D\left( {0;0;0} \right),D\left( {6;0;0} \right)$ C. $D\left( { – 2;1;0} \right),D\left( { – 4;0;0} \right)$ D. $D\left( {0;0;0} \right),D\left( { – 6;0;0} \right)$

Lời giải

Chọn B

Gọi $D\left( {x;0;0} \right) \in Ox$

$AD = BC \Leftrightarrow \sqrt {{{(x – 3)}^2} + 16} = 5 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 0} \\
{x = 6}
\end{array}} \right.$

Câu 46. Trong không gian với hệ tọa độ $Oxyz$, cho hai điểm $A\left( { – 2;3;1} \right)$ và $B\left( {5;6;2} \right)$. Đường thẳng $AB$ cắt mặt phẳng $\left( {Oxz} \right)$ tại điểm $M$. Tính tỉ số $\frac{{AM}}{{BM}}$.

A. $\frac{{AM}}{{BM}} = \frac{1}{2}$ B. $\frac{{AM}}{{BM}} = 2$ C. $\frac{{AM}}{{BM}} = \frac{1}{3}$ D. $\frac{{AM}}{{BM}} = 3$

Lời giải

Chọn A

$M \in \left( {Oxz} \right) \Rightarrow M\left( {x;0;z} \right);\overrightarrow {AB} = \left( {7;3;1} \right)$ $ \Rightarrow AB = \sqrt {59} ;\overrightarrow {AM} = \left( {x + 2; – 3;z – 1} \right)$và

$A,B,M$ thẳng hàng $ \Rightarrow \overrightarrow {AM} = k \cdot \overrightarrow {AB} \;\left( {k \in \mathbb{R}} \right)$

$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x + 2 = 7k} \\
{ – 3 = 3k} \\
{z – 1 = k}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x = – 9} \\
{ – 1 = k} \\
{z = 0}
\end{array} \Rightarrow M\left( { – 9;0;0} \right)} \right.} \right.$.

$\overrightarrow {BM} = \left( { – 14; – 6; – 2} \right);\overrightarrow {AM} = \left( { – 7; – 3; – 1} \right) \Rightarrow BM = 2AB$.

Câu 47. Trong không gian với hệ tọa độ $Oxyz$, cho hình hộp $ABCD.A’B’C’D’$ có $A\left( {0;0;0} \right)$, $B\left( {a;0;0} \right);D\left( {0;2a;0} \right),A’\left( {0;0;2a} \right)$ với $a \ne 0$. Độ dài đoạn thẳng $AC’$ là

A. $\left| a \right|$. B. $2\left| a \right|$. C. $3\left| a \right|$. D. $\frac{3}{2}\left| a \right|$.

Lời giải

Chọn C

Ta có $\overrightarrow {AB} = \left( {a;0;0} \right);\overrightarrow {AD} = \left( {0;2a;0} \right);\overrightarrow {AA’} = \left( {0;0;2a} \right)$.

Theo quy tắc hình hộp ta có $\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA’} = \overrightarrow {AC’} $

$ \Leftrightarrow \overrightarrow {AC’} = \left( {a;2a;2a} \right)$.

Suy ra $AC = \left| {\overrightarrow {AC} } \right| = \sqrt {{a^2} + {{(2a)}^2} + {{(2a)}^2}} = 3\left| a \right|$.

Vậy độ dài đoạn thẳng $AC’ = 3\left| a \right|$.

Câu 48. Trong không gian với hệ tọa độ $Oxyz$, cho hình vuông $ABCD,B\left( {3;0;8} \right),D\left( { – 5; – 4;0} \right)$. Biết đỉnh $A$ thuộc mặt phẳng $\left( {Oxy} \right)$ và có tọa độ là những số nguyên, khi đó $\left| {\overrightarrow {CA} + \overrightarrow {CB} } \right|$ bằng:

A. $10\sqrt 5 $. B. $6\sqrt {10} $. C. $10\sqrt 6 $. D. $5\sqrt {10} $.

Lời giải

Chọn B

$\overrightarrow {BD} = \left( { – 8; – 4; – 8} \right) \Rightarrow BD = 12 \Rightarrow AB = \frac{{12}}{{\sqrt 2 }} = 6\sqrt 2 $.

Gọi $M$ là trung điểm $AB \Rightarrow MC = 3\sqrt {10} $.

$\left| {\overrightarrow {CA} + \overrightarrow {CB} \left| = \right|2\overrightarrow {CM} } \right| = 2CM = 6\sqrt {10} $.

Câu 49. Trong không gian $Oxyz$ cho các điểm $A\left( {5;1;5} \right);B\left( {4;3;2} \right);C\left( { – 3; – 2;1} \right)$. Điểm $I\left( {a;b;c} \right)$ là tâm đường tròn ngoại tiếp tam giác $ABC$. Tính $a + 2b + c$ ?

A. 1. B. 3. C. 6. D. -9.

Lời giải

Chọn B

Ta có $\left\{ {\begin{array}{*{20}{l}}
{\overrightarrow {AB} = \left( { – 1;2; – 3} \right)} \\
{\overrightarrow {BC} = \left( { – 7; – 5; – 1} \right)}
\end{array} \Rightarrow \overrightarrow {AB} \cdot \overrightarrow {BC} = 0 \Rightarrow } \right.$ tam giác $ABC$ vuông tại $B$.

$ \Rightarrow $ tâm $I$ của đường tròn ngoại tiếp tam giác $ABC$ là trung điểm của cạnh huyền $AC$.

$ \Rightarrow I\left( {1; – \frac{1}{2};3} \right)$. Vậy $a + 2b + c = 3$.

Câu 50. Trong không gian với hệ trục tọa độ $Oxyz$, cho $\overrightarrow {OA} = 2\vec i + 2\vec j + 2\vec k,B\left( { – 2;2;0} \right)$ và $C\left( {4;1; – 1} \right)$. Trên mặt phẳng $\left( {Oxz} \right)$, điểm nào dưới đây cách đều ba điểm $A,B,C$.

A. $M\left( {\frac{3}{4};0;\frac{1}{2}} \right)$. B. $N\left( {\frac{{ – 3}}{4};0;\frac{{ – 1}}{2}} \right)$. C. $P\left( {\frac{3}{4};0;\frac{{ – 1}}{2}} \right)$. D. $Q\left( {\frac{{ – 3}}{4};0;\frac{1}{2}} \right)$.

Lời giải

Chọn C

Ta có: $A\left( {2;2;2} \right)$ và $PA = PB = PC = \frac{{3\sqrt {21} }}{4}$.

Câu 51. Trong không gian với hệ tọa độ $Oxyz$, cho tam giác $ABC$ có $A\left( {1;2; – 1} \right),B\left( {2; – 1;3} \right)$ , $C\left( { – 4;7;5} \right)$. Gọi $D\left( {a;b;c} \right)$ là chân đường phân giác trong góc $B$ của tam giác $ABC$. Giá trị của $a + b + 2c$ bằng

A. 5. B. 4 . C. 14 . D. 15 .

Lời giải

Chọn A

Ta có $AB = \sqrt {26} ,BC = \sqrt {104} = 2\sqrt {26} $.

Gọi $D\left( {x;y;z} \right)$, theo tính chất phân giác ta có $\frac{{DA}}{{DC}} = \frac{{BA}}{{BC}} = \frac{1}{2}$. Suy ra $\overrightarrow {DA} = – \frac{1}{2}\overrightarrow {DC} \left( * \right)$.

Ta có $\overrightarrow {DA} = \left( {1 – x;2 – y; – 1 – z} \right)$ và $\overrightarrow {DC} = \left( { – 4 – x;7 – y;5 – z} \right)$.

Do đó $\left( * \right) \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{1 – x = – \frac{1}{2}\left( { – 4 – x} \right)} \\
{2 – y = – \frac{1}{2}\left( {7 – y} \right)} \\
{ – 1 – z = – \frac{1}{2}\left( {5 – z} \right)}
\end{array}} \right.$

$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x = – \frac{2}{3}} \\
{y = \frac{{11}}{3}} \\
{z = 1}
\end{array} \Rightarrow D\left( { – \frac{2}{3};\frac{{11}}{3};1} \right)} \right.$$ \Rightarrow a + b + 2c = 5$.

Câu 52. Trong không gian với hệ tọa độ Oxyz, cho hai điểm $A\left( {1;2; – 2} \right)$ và $B\left( {\frac{8}{3};\frac{4}{3};\frac{8}{3}} \right)$. Biết $I\left( {a;b;c} \right)$ là tâm của đường tròn nội tiếp tam giác $OAB$. Giá trịi $a – b + c$ bằng

A. 1 B. 3 C. 2 D. 0

Lời giải

Chọn D

Ta có $\overrightarrow {OA} = \left( {1;2; – 2} \right),\overrightarrow {OB} = \left( {\frac{8}{3};\frac{4}{3};\frac{8}{3}} \right)$, do đó $OA = 3,OB = 4$.

Gọi $D$ là chân đường phân giác trong kẻ từ $O$, ta có $\overrightarrow {DA} = – \frac{{DA}}{{DB}} \cdot \overrightarrow {DB} = – \frac{{OA}}{{OB}} \cdot \overrightarrow {DB} $, suy ra

$\overrightarrow {DA} = – \frac{3}{4}\overrightarrow {DB} \Rightarrow \overrightarrow {OD} = \frac{{4 \cdot \overrightarrow {OA} + 3 \cdot \overrightarrow {OB} }}{7}$.

Do đó $D\left( {\frac{{12}}{7};\frac{{12}}{7};0} \right)$.

Ta có $\overrightarrow {AD} = \left( {\frac{5}{7}; – \frac{2}{7};2} \right) \Rightarrow AD = \frac{{15}}{7}$.

$\overrightarrow {ID} = – \frac{{AD}}{{AO}} \cdot \overrightarrow {IO} = – \frac{5}{7}\overrightarrow {IO} $

$ \Rightarrow \overrightarrow {OI} = \frac{7}{{12}}\overrightarrow {OD} $$ \Rightarrow D\left( {1;1;0} \right)$

Do đó $a – b + c = 0$.

Câu 53. Trong không gian $Oxyz$, cho hai điểm $M\left( {2;2;1} \right)$, $N\left( { – \frac{8}{3};\frac{4}{3};\frac{8}{3}} \right)$.Tìm tọa độ tâm đường tròn nội tiếp tam giác $OMN$.

A. $I\left( {1;1;1} \right)$. B. $I\left( {0;1;1} \right)$. C. $I\left( {0; – 1; – 1} \right)$. D. $I\left( {1;0;1} \right)$.

Lời giải

Chọn B

Ta có bài toán bài toán sau

Trong tam giác $ABC,I$ là tâm đường tròn nột tiếp $\vartriangle ABC$ ta có: a. $\overrightarrow {IA} + b \cdot \overrightarrow {IB} + c \cdot \overrightarrow {IC} = \vec 0$. với $BC = a;AC = b;AB = c$.

Thật vậy:

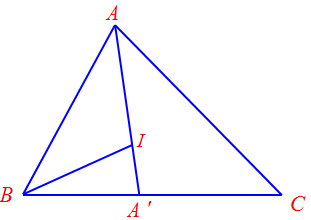
Gọi $A’$ là chân đường phân giác trong kẻ từ $A$.

$ \Rightarrow \overrightarrow {BA’} = \frac{c}{b}\overrightarrow {A’C} \Leftrightarrow b\overrightarrow {BA’} + c\overrightarrow {CA’} = \vec 0\left( 1 \right)$

$\overrightarrow {IA} = \frac{c}{{A’B}}\overrightarrow {A’I} = \frac{c}{{\frac{{ac}}{{b + c}}}}\overrightarrow {A’I} = \frac{{b + c}}{a}\overrightarrow {A’I} $

$ \Leftrightarrow a\overrightarrow {IA} + \left( {b + c} \right)\overrightarrow {IA’} = \vec 0$

$ \Leftrightarrow a\overrightarrow {IA} + b\overrightarrow {IB} + c\overrightarrow {IC} + b\overrightarrow {BA’} + c\overrightarrow {CA’} = \vec 0$

$ \Leftrightarrow a\overrightarrow {IA} + b\overrightarrow {IB} + c\overrightarrow {IC} = \vec 0\;\left( {do\left( 1 \right)} \right)$.

Áp dụng công thức trong tam giác $OMN$

ta được $OM \cdot \overrightarrow {IN} + ON \cdot \overrightarrow {IM} + MN \cdot \overrightarrow {IO} = \vec 0$

$ \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{{x_I} = \frac{{OM \cdot {x_N} + ON \cdot {x_M} + MN \cdot {x_O}}}{{OM + ON + MN}} = 0} \\
{{y_I} = \frac{{OM \cdot {y_N} + ON \cdot {y_M} + MN \cdot {y_O}}}{{OM + ON + MN}} = 1} \\
{{z_I} = \frac{{OM \cdot {z_N} + ON \cdot {z_M} + MN \cdot {z_O}}}{{OM + ON + MN}} = 1}
\end{array}} \right.$

Vậy điểm $I\left( {0;1;1} \right)$ là điểm cần tìm.

Câu 54. Trong không gian tọa độ $Oxyz$, cho $A\left( {2;0;0} \right),B\left( {0;2;0} \right),C\left( {0;0;2} \right)$. Có tất cả bao nhiêu điểm $M$ trong không gian thỏa mãn $M$ không trùng với các điểm $A,B,C$ và $\widehat {AMB} = \widehat {BMC} = \widehat {CMA} = {90^ \circ }$ ?

A. 0. B. 1. C. 2. D. 3 .

Lời giải

Chọn C

Gọi $I,J,K$ lần lượt là trung điểm của $AB,BC,CA$.

Do $\widehat {AMB} = \widehat {BMC} = \widehat {CMA} = {90^ \circ }$ nên các tam giác $\vartriangle AMB,\vartriangle BMC,\vartriangle CMA$ vuông tại $M$.

Khi đó $IM = \frac{{AB}}{2};JM = \frac{{BC}}{2};KM = \frac{{AC}}{2}$.

Mặt khác $AB = BC = AC = 2\sqrt 2 $.

Vậy $MI = MJ = MK = \sqrt 2 $. Khi đó $M$ thuộc trục của đường tròn ngoại tiếp đáy $IJK$ và cách $\left( {IJK} \right)$ một khoảng không đổi là $\sqrt 2 $. Khi đó có hai điểm $M$ thỏa mãn điều kiện trên.

Câu 55. Trong không gian với hệ toạ độ $Oxyz$, cho ba điểm $A\left( { – 2;3;1} \right),B\left( {2;1;0} \right)$, $C\left( { – 3; – 1;1} \right)$. Tìm tất cả các điểm $D$ sao cho $ABCD$ là hình thang có đáy $AD$ và diện tích tứ giác $ABCD$ bằng 3 lần diện tích tam giác $ABC$.

A. $D\left( { – 12; – 1;3} \right)$. B. $\left[ {\begin{array}{*{20}{l}}
{D\left( { – 8; – 7;1} \right)} \\
{D\left( {12;1; – 3} \right)}
\end{array}} \right.$. C. $D\left( {8;7; – 1} \right)$. D. $\left[ {\begin{array}{*{20}{l}}
{D\left( {8;7; – 1} \right)} \\
{D\left( { – 12; – 1;3} \right)}
\end{array}} \right.$

Lời giải

Chọn A

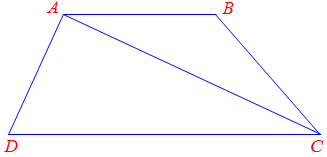
Ta có: ${S_{ABCD}} = \frac{1}{2}\left( {AD + BC} \right) \cdot d\left( {A,BC} \right)$

$ \Leftrightarrow {S_{ABCD}} = \frac{1}{2}\left( {AD + BC} \right) \cdot \frac{{2{S_{\vartriangle ABC}}}}{{BC}}$.

$ \Leftrightarrow 3{S_{\vartriangle ABC}} = \frac{{\left( {AD + BC} \right) \cdot {S_{\vartriangle ABC}}}}{{BC}}$

$ \Leftrightarrow 3BC = AD + BC \Leftrightarrow AD = 2BC$.

Mà $ABCD$ là hình thang có đáy $AD$ nên $\overrightarrow {AD} = 2\overrightarrow {BC} $ (1).

$\overrightarrow {BC} = \left( { – 5; – 2;1} \right),\overrightarrow {AD} = \left( {{x_D} + 2;{y_D} – 3;{z_D} – 1} \right)$.

(1) $ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{{x_D} + 2 = – 10} \\
{{y_D} – 3 = – 4} \\
{{z_D} – 1 = 2}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{{x_D} = – 12} \\
{{y_D} = – 1} \\
{{z_D} = 3}
\end{array}} \right.} \right.$.

Vậy $D\left( { – 12; – 1;3} \right)$.

Câu 56. Trong không gian với hệ trục tọa độ $Oxyz$ cho hình thang $ABCD$ vuông tại $A$ và $B$ . Ba đỉnh $A\left( {1;2;1} \right),B\left( {2;0; – 1} \right),C\left( {6;1;0} \right)$ Hình thang có diện tích bằng $6\sqrt 2 $. Giả sử đỉnh $D\left( {a;b;c} \right)$, tìm mệnh đề đúng?

A. $a + b + c = 6$. B. $a + b + c = 5$. C. $a + b + c = 8$. D. $a + b + c = 7$.

Lời giải

Chọn A

Ta có $\overrightarrow {AB} = \left( {1; – 2; – 2} \right) \Rightarrow \left| {\overrightarrow {AB} } \right| = 3$;

$\overrightarrow {BC} = \left( {4;1;1} \right) \Rightarrow \left| {\overrightarrow {BC} } \right| = 3\sqrt 2 $.

Theo giả thiết $ABCD$ là hình thang vuông tại $A$ và $B$ và có diện tích bằng $6\sqrt 2 $ nên $\frac{1}{2}AB\left( {AD + BC} \right) = 6\sqrt 2 $

$ \Leftrightarrow \frac{1}{2} \cdot 3 \cdot \left( {AD + 3\sqrt 2 } \right) = 6\sqrt 2 $

$ \Rightarrow AD = \sqrt 2 \Rightarrow AD = \frac{1}{3}BC$.

Do $ABCD$ là hình thang vuông tại $A$ và $B$ nên $\overrightarrow {AD} = \frac{1}{3}\overrightarrow {BC} $.

Giả sử $D\left( {a;b;c} \right)$ khi đó ta có $\left\{ {\begin{array}{*{20}{l}}
{a – 1 = \frac{4}{3}} \\
{b – 2 = \frac{1}{3}} \\
{c – 1 = \frac{1}{3}}
\end{array}} \right.$

$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{a = \frac{7}{3}} \\
{b = \frac{7}{3}} \\
{c = \frac{4}{3}}
\end{array} \Rightarrow a + b + c = 6} \right.$.