Chuyên Đề Cấp Số Cộng Cấp Số Nhân Ôn Thi Tốt Nghiệp THPT 2025 Giải Chi Tiết

Chuyên đề Cấp số cộng cấp số nhân ôn thi tốt nghiệp THPT 2025 giải chi tiết được soạn dưới dạng file word và PDF gồm 12 trang. Các bạn xem và tải về ở dưới.

CHUYÊN ĐỀ: CẤP SỐ CỘNG VÀ CẤP SỐ NHÂN

A. KIẾN THỨC CẦN NHỚ

I. CẤP SỐ CỘNG

1. Định nghĩa

Dãy số ( ${u_n}$ ) là cấp số công nếu ${u_n} = {u_{n – 1}} + d$ với $n \geqslant 2,$$d$là số không đổi.

Số $d$ gọi là công sai của cấp số công, $d = {u_n} – {u_{n – 1}}$ vơi $n \geqslant 2$.

Nếu $d = 0$ thì câp số cộng là một dãy số không đồi.

2. Số hạng tổng quát

Cho cấp số cộng $\left( {{u_n}} \right)$ có số hạng đầu ${u_1}$ và công sai $d$, ta có:

${u_n} = {u_1} + \left( {n – 1} \right)d\;$ với $\;n \geqslant 2.\;$

3. Tổng $n$ số hạng đầu

Cho cấp số cộng $\left( {{u_n}} \right)$ có số hạng đầu ${u_1}$ và công sai $d$. Đặt ${S_n} = {u_1} + {u_2} + \ldots + {u_n}$, ta có:

${S_n} = \frac{{\left( {{u_1} + {u_n}} \right)n}}{2}\;$ hoặc ${S_n} = \frac{{\left[ {2{u_1} + \left( {n – 1} \right)d} \right]n}}{2}.\;$

II. CẤP SỐ NHÂN

1. Định nghĩa

Dãy số $\left( {{u_n}} \right)$ là cấp số nhân nếu ${u_n} = {u_{n – 1}}.q$ với $n \geqslant 2,$$q$là số không đổi.

Số $q$ gọi là công bội của cấp số nhân. Nếu ${u_n} \ne 0$ với mọi $n \in {\mathbb{N}^*}$ thì

$q = \frac{{{u_n}}}{{{u_{n – 1}}}}$ với $n \geqslant 2.$

Nếu $q = 1$ thì cấp số nhân là một dãy số không đổi.

2. Số hạng tổng quát

Cho cấp số nhân $\left( {{u_n}} \right)$ có số hạng đầu ${u_1}$ và công bội $q$, ta có:

${u_n} = {u_1}.{q^{n – 1}}$ với $n \geqslant 2$.

3. Tổng $n$số hạng đầu

Cho cấp số nhân $\left( {{u_n}} \right)$ có số hạng đầu ${u_1}$ và công bội $q\left( {q \ne 1} \right)$.

Đặt ${S_n} = {u_1} + {u_2} + \ldots + {u_n}$, ta có:

${S_n} = \frac{{{u_1}\left( {1 – {q^n}} \right)}}{{1 – q}}$.

B. MỘT SỐ VÍ DỤ

Dạng 1. Câu trắc nghiệm nhiều phương án lựa chọn

Mỗi câu hỏi thi sinh chi chọn môt phương án.

Ví dụ 1. Trong các dãy số $\left( {{u_n}} \right)$ với số hạng tổng quát sau, dãy số nào là cấp số cộng?

A. ${u_n} = {5^n}$. B. ${u_n} = 2 – 5n$. C. ${u_n} = {5^n} – 2$. D. ${u_n} = 5 + {n^2}$.

Lời giải

Chọn B

Ở đáp án B, ta có: ${u_n} – {u_{n – 1}} = \left( {2 – 5n} \right) – \left[ {2 – 5\left( {n – 1} \right)} \right] = – 5$ với mọi $n \geqslant 2$. Vậy dãy số $\left( {{u_n}} \right)$ đã cho là một cấp số cộng có số hạng đầu ${u_1} = – 3$ và công sai $d = – 5$.

Ở đáp án $A$, ba số hạng đầu của dãy số là: $5;25;125$ nên dãy số cho ở đáp án $A$ không là cấp số cộng. Tương tự, dãy số cho ở đáp án $C,D$ cũng không là cấp số cộng.

Ví dụ 2. Cho cấp số công $\left( {{u_n}} \right)$ biết ${u_5} + {u_7} = 19$. Giá trị của ${u_2} + {u_{10}}$ là:

A. $38$. B. $29$. C. $12$. D. $19$.

Lời giải

Chọn D

Áp dụng công thức của số hạng tổng quát, ta có:

${u_5} + {u_7} = \left( {{u_1} + 4d} \right) + \left( {{u_1} + 6d} \right) = 2{u_1} + 10d = 19$.

Khi đó, ${u_2} + {u_{10}} = \left( {{u_1} + d} \right) + \left( {{u_1} + 9d} \right) = 2{u_1} + 10d = 19$.

Ví dụ 3. Cho cấp số nhân $\left( {{u_n}} \right)$ có công bội $q > 1$ với ${u_2} = – 3$ và ${u_1} + {u_2} + {u_3} = – 13$. Số hạng đầu ${u_1}$ và công bội $q$ của cấp số nhân đó là:

A. ${u_1} = 1,q = 3$. B. ${u_1} = – 1,q = – 3$.

C. ${u_1} = – 1,q = 3$. D. ${u_1} = 1,q = – 3$.

Lời giải

Chọn C

Từ giả thiết, ta có: $\left\{ {\begin{array}{*{20}{l}}
{{u_1}.q = – 3} \\
{{u_1}.\left( {1 + q + {q^2}} \right) = – 13\;.}
\end{array}} \right.$

Từ đó, suy ra: $\frac{{1 + q + {q^2}}}{q} = \frac{{13}}{3}$$ \Leftrightarrow 3{q^2} – 10q + 3 = 0$$ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{q = 3} \\
{q = \frac{1}{3}}
\end{array}} \right.$

Mà $q > 1$ nên $q = 3$. Thay $q = 3$ vào phương trình ${u_1} \cdot q = – 3$, ta được ${u_1} = – 1$.

Vậy cấp số nhân đó có số hạng đầu ${u_1} = – 1$ và công bội $q = 3$.

Dạng 2. Câu trắc nghiệm đúng sai

Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Ví dụ 4. Cho dãy số $\left( {{u_n}} \right)$ có tổng $n$ số hạng đầu được tính bởi công thức ${S_n} = 2{n^2} – 4n$.

a) Số hạng đầu ${u_1} = – 2$, số hạng thứ hai ${u_2} = 2$.

b) Với $n \geqslant 2$ thì ${S_n} – {S_{n – 1}} = 4n – 6$.

c) Dãy số $\left( {{u_n}} \right)$ là một cấp số cộng có công sai là $ – 6$.

d) Tổng ${u_2} + {u_4} + {u_6} + \ldots + {u_{100}}$ là 5000 .

Lời giải

+ Ta có: ${S_1} = {u_1} = – 2;{S_2} = {u_1} + {u_2} = 0$. Do đó, ${u_2} = {S_2} – {S_1} = 2$.

+ Với $n \geqslant 2$ thì ${S_n} – {S_{n – 1}}$$ = \left( {2{n^2} – 4n} \right) – \left[ {2{{(n – 1)}^2} – 4\left( {n – 1} \right)} \right]$$ = 4n – 6$.

${u_n} = {S_n} – {S_{n – 1}} = 4n – 6$. Do đó, ${u_n} – {u_{n – 1}}$ $ = 4n – 6 – \left[ {4\left( {n – 1} \right) – 6} \right] = 4$với $n \in {\mathbb{N}^*}$, $n \geqslant 2$.

Vậy $\left( {{u_n}} \right)$ là một cấp số cộng có công sai là 4 .

+ Các số ${u_2},{u_4},{u_6}, \ldots ,{u_{100}}$ lập thành cấp số cộng có số hạng đầu ${u_2} = 2$, công sai $d’ = 2d = 8,{u_{100}} = 4.100 – 6 = 394$.

Ta có, ${u_2} + {u_4} + {u_6} + \ldots + {u_{100}}$ là tổng của 50 số hạng.

Vậy ${u_2} + {u_4} + {u_6} + \ldots + {u_{100}}$$ = \frac{{\left( {{u_2} + {u_{100}}} \right).50}}{2} = 9900$.

Đáp án: a) Đ, b) Đ, c) S, d) ${\mathbf{S}}$.

Ví dụ 5. Cho dãy số $\left( {{u_n}} \right)$, biết ${u_1} = 8,{u_{n + 1}} = 4{u_n} – 9$ với $n \in {\mathbb{N}^*}$. Đặt ${v_n} = {u_n} – 3$ với $n \in {\mathbb{N}^*}$.

a) ${v_1} = 5$.

b) Dãy số $\left( {{v_n}} \right)$ là một cấp số nhân có công bội $q = – 3$.

c) Công thức của số hạng tổng quát ${v_n}$ là ${v_n} = 5.{( – 3)^{n – 1}}$.

d) Công thức của số hạng tổng quát ${u_n}$ là ${u_n} = 3 + 5 \cdot {( – 3)^{n – 1}}$.

Lời giải

+ Ta có: ${v_1} = {u_1} – 3 = 8 – 3 = 5$

+ ${v_{n + 1}} = {u_{n + 1}} – 3 = 4{u_n} – 9 – 3 = 4{u_n} – 12 = 4({u_n} – 3) = 4{v_n}$ với mọi $n \in {\mathbb{N}^*}$.

Vậy dãy số $\left( {{v_n}} \right)$là một cấp số nhân có số hạng đầu${v_1} = 5$, công bội ${q_1} = 4$.

+ ${v_n} = {5.4^{n – 1}};{u_n} = 3 + {v_n} = 3 + {5.4^{n – 1}}$

Đáp án: a) Đ, b) S, c) S, d) S.

Dạng 3. Câu trắc nghiệm trả lời ngắn

Vỉ dụ 6. Khi kí kết hợp đồng với người lao động, một doanh nghiệp đề xuất hai phương án trả lương như sau:

Phương án 1: Năm thứ nhất, tiền lương là $120$ triệu đồng. Kể từ năm thứ hai trở đi, mỗi năm tiền lương được tăng $18$ triệu đồng.

Phương án 2: Quý thứ nhất, tiền lương là $24$ triệu đồng. Kể từ quý thứ hai trở đi, mỗi quý tiền lương được tăng $1,8$ triệu đồng.

Tìm $n$ (với $n \in {\mathbb{N}^*}$) để từ năm thứ $n$ trở đi thì tổng số tiền lương nhận được trong $n$ năm đi làm ở phương án thứ hai sẽ nhiều hơn ở phương án thứ nhất?

Lời Giải

Ở phương án trả lương thứ nhất, số tiền lương mỗi năm người lao động nhận được lập thành cấp số cộng có số hạng đầu ${u_1} = 120$ triệu đồng, công sai $d = 18$ triệu đồng.

Ở phương án trả lương thứ hai, số tiền lương mỗi quý người lao động nhận được lập thành cấp số cộng có số hạng đầu ${v_1} = 24$ triệu đồng, công sai $d’ = 1,8$triệu đồng.

Tổng số tiền lương người lao động nhận được trong $n$ năm ở phương án thứ nhất là tổng $n$ số hạng đầu của cấp số cộng và bằng:

${S_n} = \frac{{\left[ {2.120 + (n – 1).18} \right].n}}{2} = 9{n^2} + 111n$ (triệu đồng).

Do $1$ năm có $4$ quý nên tổng số tiền lương người lao động nhận đựợc trong $n$ năm ở phương án thứ hai là tổng $4n$ số hạng đầu của cấp số cộng và bằng:

$S_{4n}’ = \frac{{\left[ {2.24 + (4n – 1).1,8} \right].4n}}{2}$ $ = 14,4{n^2} + 92,4n$ (triệu đồng).

Xét bất phương trình: $14,4{n^2} + 92,4n > 9{n^2} + 111n$$ \Leftrightarrow n > \frac{{31}}{9} \approx 3,44$

Vậy từ năm thứ $4$ trở đi thì tổng số tiền lương nhận được trong các năm đi làm ở phương án thứ hai sẽ nhiều hơn ở phương án thứ nhất.

Ví dụ 7. Cho hình vuông ${C_1}$ có cạnh bằng $1$. Gọi ${C_2}$ là hình vuông có các đỉnh là trung điểm các cạnh của hình vuông ${C_1}$; ${C_3}$ là hình vuông có các đỉnh là trung điểm các cạnh của hình vuông ${C_2}$ ;… Cứ tiếp tục quá trình như trên, ta được dãy các hình vuông ${C_1};{C_2};{C_3};…{C_n};…$. Diện tích của hình vuông ${C_{2025}}$ có dạng $\frac{1}{{{2^a}}}$. Tìm a.

Lời Giải

Gọi ${u_n}$ là cạnh của hình vuông ${C_n}$.

Ta có: ${u_1} = 1;{u_2} = \frac{1}{2}.{u_1}\sqrt 2 = {u_1}.\frac{{\sqrt 2 }}{2};$${u_3} = \frac{1}{2}.{u_2}\sqrt 2 = {u_2}.\frac{{\sqrt 2 }}{2}$; …

Cứ như vậy, dãy số $\left( {{u_n}} \right)$ lập thành cấp số nhân có số hạnh đầu ${u_1} = 1,$ công bội $q = \frac{{\sqrt 2 }}{2}$.

Do đó, ${u_{2025}} = {\left( {\frac{{\sqrt 2 }}{2}} \right)^{2024}}$ nên diện tích hình vuông ${C_{2025}}$ là:

$u_{2025}^2 = \frac{1}{{{2^{2024}}}}$. Vậy $a = 2024$.

C. BÀI TẬP TỰ LUYỆN

Dạng 1. Câu trắc nghiệm nhiều phương án lựa chọn

Mỗi câu hỏi thí sinh chỉ chọn một phương án.

Câu 1. (MĐ1)Trong các dãy số sau, dãy số nào không là cấp số cộng?

A. $2;0; – 2; – 4; – 5$. B. $\frac{1}{2}; – \frac{1}{2}; – \frac{3}{2}; – \frac{5}{2}; – \frac{7}{2}$.

C. $\sqrt 2 ;\sqrt 2 ;\sqrt 2 ;\sqrt 2 ;\sqrt 2 $. D. $ – 7; – 4; – 1;2;5$.

Lời giải

Chọn A

Xét $2;0; – 2; – 4; – 5$ ta có $0 – 2 = – 2 – 0 = – 4 + 2 \ne – 5 + 4$

Câu 2. (MĐ2) Trong các dãy số $\left( {{u_n}} \right)$ với số hạng tổng quát sau, dãy nào là cấp số cộng?

A. ${u_n} = {3.2^n}.$ B. ${u_n} = 3 – 2n.$ C. ${u_n} = {2^n} + 3.$ D. ${u_n} = 2 + {n^3}.$

Lời giải

Chọn B

Ta có ${u_n} = {3.2^n};{u_{n + 1}} = {3.2^{n + 1}}$$ \Rightarrow {u_{n + 1}} – {u_n} = {3.2^{n + 1}} – {3.2^n}$ không là cấp số cộng

Ta có ${u_n} = 3 – 2n$; ${u_{n + 1}} = 3 – 2(n + 1)$ $ \Rightarrow {u_{n + 1}} – {u_n} = 3 – 2(n + 1) – 3 – 2n = – 2$ là cấp số cộng

Câu 3. (MĐ2) Cho cấp số cộng $\left( {{u_n}} \right)$biết ${u_3} = – 2;{u_7} = 180$.  Số hạng ${u_{11}}$ bằng:

A.$38$. B. $20$. C. $43$. D. $33$.

Lời giải

Chọn A

Ta có: $\left\{ \begin{gathered}
{u_3} = – 2 \hfill \\
{u_7} = 18 \hfill \\
\end{gathered} \right.$$ \Leftrightarrow \left\{ \begin{gathered}
{u_1} + 2d = – 2 \hfill \\
{u_1} + 6d = 18 \hfill \\
\end{gathered} \right.$$ \Leftrightarrow \left\{ \begin{gathered}
{u_1} = – 12 \hfill \\
d = 5 \hfill \\
\end{gathered} \right.$.

Số hạng ${u_{11}} = {u_1} + 10d = – 12 + 10.5 = 38$.

Câu 4. (MĐ3) Cho $\left( {{u_n}} \right)$ là cấp số cộng có ${u_4} + {u_{16}} = 48$. Số hạng ${u_{10}}$ bằng:

A.$48$. B. $24$. C. $96$. D. $72$.

Lời giải

Chọn B

Ta có: ${u_4} + {u_{16}} = 48$$ \Leftrightarrow {u_1} + 3d + {u_1} + 15d = 48$

$ \Leftrightarrow 2{u_1} + 18d = 48$$ \Leftrightarrow {u_1} + 9d = 24 \Leftrightarrow {u_{10}} = 24$.

Câu 5. (MĐ3) Cho$\left( {{u_n}} \right)$ là cấp số cộng có ${u_9} = 5{u_2}$ và ${u_{13}} = 2{u_6} + 5$. Số hạng đầu ${u_1}$ và công sai $d$ của cấp số cộng đó là:

A. ${u_1} = – 3;d = 4.$ B. ${u_1} = 3;d = 4.$ C. ${u_1} = 4;d = 3.$ D. ${u_1} = – 4;d = 3.$

Lời giải

Chọn B

Ta có: $\left\{ \begin{gathered}
{u_9} = 5{u_2} \hfill \\
{u_{13}} = 2{u_6} + 5 \hfill \\
\end{gathered} \right.$$ \Leftrightarrow \left\{ \begin{gathered}
{u_1} + 8d = 5\left( {{u_1} + d} \right) \hfill \\
{u_1} + 12d = 2\left( {{u_1} + 5d} \right) + 5 \hfill \\
\end{gathered} \right.$

$ \Leftrightarrow \left\{ \begin{gathered}
4{u_1} – 3d = 0 \hfill \\
{u_1} – 2d = – 5 \hfill \\
\end{gathered} \right.$.$ \Leftrightarrow \left\{ \begin{gathered}
{u_1} = 3 \hfill \\
d = 4 \hfill \\
\end{gathered} \right.$

Câu 6. (MĐ3) Một cấp số cộng có số hạng đầu ${u_1} = \frac{1}{3}$, công sai $d = – 1$. Tổng $n$ số hạng đầu tiên của cấp số cộng đó bằng $ – 425$. Giá trị của $n$ bằng:

A. $30$. B. $60$. C. $45$. D. $15$.

Lời giải

Chọn A

Ta có: ${S_n} = \frac{{\left[ {2{u_1} + \left( {n – 1} \right)d} \right]n}}{2}$$ = \frac{{\left[ {2.\frac{1}{3} + \left( {n – 1} \right)\left( { – 1} \right)} \right]n}}{2} = – 425$

$ \Leftrightarrow \left( {\frac{5}{3} – n} \right)n = – 850$$ \Leftrightarrow {n^2} – \frac{5}{3}n – 850 = 0$

$ \Leftrightarrow \left[ \begin{gathered}
n = 30 \hfill \\
n = – \frac{{85}}{3}\,\,(loai) \hfill \\
\end{gathered} \right.$.

Câu 7. (MĐ3) Cho $({u_n})$ là cấp sổ cộng có ${u_2} + {u_9} = 15$. Tổng $10$ số hạng đầu tiên của cấp số cộng đó bằng:

A.$150$. B. $75$. C. $120$. D. $90$.

Lời giải

Chọn B

Ta có: ${u_2} + {u_9} = 15 \Leftrightarrow 2{u_1} + 9d = 15$.

Mà ${S_{10}} = \frac{{\left[ {2{u_1} + \left( {10 – 1} \right)d} \right]10}}{2}$$ = 5\left( {2{u_1} + 9d} \right) = 5.15 = 75$.

Câu 8. (MĐ3) Cho $({u_n})$ là cấp số cộng. Gọi ${S_n}$ là tổng $n$ số hạng đầu của cấp số đó. Biết ${S_{10}} = 365;{S_{15}} = 435$. Công thức của số hạng tổng quát ${u_n}$ là:

A.${u_n} = 50 – 3n.$ B. ${u_n} = 53 + 3n.$ C. ${u_n} = 50 + 3n.$ D. ${u_n} = 53 – 3n.$

Lời giải

Chọn D

Ta có: $\left\{ \begin{gathered}
{S_{10}} = \frac{{\left[ {2{u_1} + \left( {10 – 1} \right)d} \right]10}}{2} = 365 \hfill \\
{S_{15}} = \frac{{\left[ {2{u_1} + \left( {15 – 1} \right)d} \right]15}}{2} = 435 \hfill \\
\end{gathered} \right.$

$ \Leftrightarrow \left\{ \begin{gathered}
2{u_1} + 9d = 73 \hfill \\
2{u_1} + 14d = 58 \hfill \\
\end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered}
{u_1} = 50 \hfill \\
d = – 3 \hfill \\
\end{gathered} \right.$.

Vậy công thức của số hạng tổng quát là ${u_n} = {u_1} + \left( {n – 1} \right)d = 50 + \left( {n – 1} \right)\left( { – 3} \right) = 53 – 3n$.

Câu 9. (MĐ1)Cho dãy số $({u_n})$ với ${u_n} = 3{\left( {\frac{1}{2}} \right)^{n + 1}}$ là cấp số cộng. Khẳng định nào sau đây là đúng?

A. $\left( {{u_n}} \right)$ không phải là cấp số nhân.

B. $\left( {{u_n}} \right)$ là cấp số nhân có số hạng đầu ${u_1} = 3$ công bội $q = \frac{1}{2}$.

C. $\left( {{u_n}} \right)$ là cấp số nhân có số hạng đầu ${u_1} = \frac{3}{4}$ công bội $q = \frac{1}{2}$.

D. $\left( {{u_n}} \right)$ là cấp số nhân có số hạng đầu ${u_1} = \frac{3}{2}$ công bội $q = \frac{1}{2}$.

Lời giải

Chọn C

Ta có: ${u_n} = 3{\left( {\frac{1}{2}} \right)^{n + 1}}$$ \Rightarrow \left\{ \begin{gathered}
{u_1} = \frac{3}{4};{u_2} = \frac{3}{8} \hfill \\
d = \frac{{{u_2}}}{{{u_1}}} = \frac{1}{2} \hfill \\
\end{gathered} \right.$.

Câu 10. (MĐ3)Trong các dãy số $\left( {{u_n}} \right)$ với số hạng tổng quát sau, dãy số nào là cấp số nhân?

A.${u_n} = \frac{1}{{{5^n}}} – 1.$ B. ${u_n} = \frac{1}{5}n – 1.$ C. ${u_n} = \frac{1}{{{5^{n – 1}}}}.$ D. ${u_n} = \frac{1}{{5n – 1}}.$

Lời giải

Chọn C

Ta có: ${u_n} = \frac{1}{{{5^{n – 1}}}}$$ \Rightarrow {u_{n + 1}} = \frac{1}{{{5^{n + 1 – 1}}}} = \frac{1}{{{5^n}}}$

$ \Rightarrow \frac{{{u_{n + 1}}}}{{{u_n}}} = \frac{{\frac{1}{{{5^n}}}}}{{\frac{1}{{{5^{n – 1}}}}}} = \frac{1}{5}$.

Câu 11. (MĐ3) Cho cấp số nhân $\left( {{u_n}} \right)$ có ${u_1} = – 1$ và công bội $q = – \frac{1}{{10}}$. Số $ – \frac{1}{{{{10}^{2024}}}}$ là số hạng thứ mấy của cấp số nhân?

A. Số hạng thứ $2024$. B. Số hạng thứ $2025$. C. Số hạng thứ $2023$. D. Số hạng thứ $2026$.

Lời giải

Chọn B

Ta có: ${S_n} = \frac{{{u_1}\left( {1 – {q^n}} \right)}}{{1 – q}}$$ \Leftrightarrow – \frac{1}{{{{10}^{2024}}}} = \frac{{\left( { – 1} \right)\left( {1 – {{\left( { – \frac{1}{{10}}} \right)}^n}} \right)}}{{1 – \left( { – \frac{1}{{10}}} \right)}}$

$ \Leftrightarrow n = 2025$.

Câu 12. (MĐ3) Cho cấp số nhân $\left( {{u_n}} \right)$ có ${u_1} = \frac{1}{3};{u_4} = – 9$. Công bội $q$ của cấp số nhân là:

A.$\frac{1}{3}$. B. $ – \frac{1}{3}$. C. $ – 3$. D. $3$.

Lời giải

Chọn C

Ta có: ${u_4} = {u_1}.{q^{4 – 1}} = – 9 \Leftrightarrow \frac{1}{3}.{q^3} = – 9$

$ \Leftrightarrow {q^3} = – 27 = {\left( { – 3} \right)^3} \Leftrightarrow q = – 3$.

Câu 13. (MĐ3) Cho dãy số $\left( {{u_n}} \right)$ biết ${u_1} = 2$ và ${u_n} = \frac{1}{2} \cdot {u_{n – 1}}$ với $n \in {N^*}$. Số hạng tổng quát của dãy số là:

A. ${u_n} = \frac{1}{{{2^{n – 2}}}}$. B. ${u_n} = \frac{1}{{{2^{n – 1}}}}$. C. ${u_n} = \frac{1}{{{2^n}}}$. D. ${u_n} = \frac{1}{{{2^{n + 1}}}}$.

Lời giải

Chọn A

Ta có ${u_2} = \frac{1}{2} \cdot {u_1} = 1;{u_3} = \frac{1}{2} \cdot {u_2} = \frac{1}{2};{u_4} = \frac{1}{2} \cdot {u_3} = \frac{1}{4};…$

Vì $\frac{{{u_2}}}{{{u_1}}} = \frac{{{u_3}}}{{{u_2}}} = \frac{{{u_4}}}{{{u_3}}} = … = \frac{1}{2}.$ Nên $\left( {{u_n}} \right)$ là cấp số nhân có ${u_1} = 2$ và $q = \frac{1}{2}$. Số hạng tổng quát của dãy số $\left( {{u_n}} \right)$ là: ${u_n} = {u_1}.{q^{n – 1}} = 2.{\left( {\frac{1}{2}} \right)^{n – 1}}$

$ = {\left( {\frac{1}{2}} \right)^{ – 1}}.{\left( {\frac{1}{2}} \right)^{n – 1}} = \frac{1}{{{2^{n – 2}}}}$.

Câu 14. (MĐ3) Cho cấp số nhân $\left( {{u_n}} \right)$ biết ${u_2}.{u_5} = – 243$. Tích ${u_3}.{u_4}$ bằng:

A. $ – 81$. B. $ – 243$. C. $81$. D. $243$.

Lời giải

Chọn B

Ta có ${u_2}.{u_5} = – 243 \Leftrightarrow {u_1}q.{u_1}{q^4} = – 243$

$ \Leftrightarrow u_1^2.{q^5} = – 243$.

Mà ${u_3}.{u_4} = {u_1}{q^2}.{u_1}{q^3} = u_1^2.{q^3} = – 243$.

Câu 15. (MĐ2) Cho $\left( {{u_n}} \right)$ là cấp số nhân có số hạng đầu ${u_1} = – 3$, công bội $q = – 2$. Tổng 10 số hạng đầu của cấp số nhân đó là:

A. $1\,023$. B. $ – 1\,025$. C. $1\,025$. D. $ – 1\,023$.

Lời giải

Chọn A

Ta có ${S_n} = \frac{{{u_1}\left( {1 – {q^n}} \right)}}{{1 – q}}$$ \Leftrightarrow {S_{10}} = \frac{{{u_1}\left( {1 – {q^{10}}} \right)}}{{1 – q}}$$ = \frac{{ – 3.\left( {1 – {{\left( { – 2} \right)}^{10}}} \right)}}{{1 – \left( { – 2} \right)}} = 1023$.

Câu 16. (MĐ3) Bốn góc của một tứ giác tạo thành cấp số nhân và góc lớn nhất gấp $27$ lần góc nhỏ nhất. Tổng của góc lớn nhất và góc nhỏ nhất bằng:

A. ${243^\circ }$. B. ${252^\circ }$. C. ${102^\circ }$. D. ${168^\circ }$.

Lời giải

Chọn B

Gọi ${u_1};{u_2};{u_3};{u_4}\left( {{u_1} \ne 0} \right)$ lần lượt là số đo bốn góc của tứ giác tạo thành cấp số nhân và ${u_4}$ là góc có số đo lớn nhất. Theo đề bài, ta có: $\left\{ \begin{gathered}
{u_1} + {u_2} + {u_3} + {u_4} = 360 \hfill \\
{u_4} = 27{u_1} \hfill \\
\end{gathered} \right.$$ \Leftrightarrow \left\{ \begin{gathered}
{u_1} + {u_1}q + {u_1}{q^2} + {u_1}{q^3} = 360 \hfill \\
{u_1}{q^3} = 27{u_1} \hfill \\
\end{gathered} \right.$$ \Leftrightarrow \left\{ \begin{gathered}
q = 3 \hfill \\
{u_1} + 3{u_1} + 9{u_1} + 27{u_1} = 360 \hfill \\
\end{gathered} \right.$$ \Leftrightarrow \left\{ \begin{gathered}
q = 3 \hfill \\
{u_1} = 9 \hfill \\
\end{gathered} \right.$.

Vậy bốn góc của tứ giác là ${9^\circ };{27^\circ };{81^\circ };{243^\circ }.$

Tổng của góc lớn nhất và góc nhỏ nhất bằng ${252^\circ }$.

Dạng 2. Câu trắc nghiệm đúng sai

Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 17. Cho dãy số $\left( {{u_n}} \right)$ có tổng $n$ số hạng đầu được tính bởi công thức ${S_n} = {n^2} – \frac{3}{2}n$.

a) Ta có: ${S_1} = – \frac{1}{2};{S_2} = 1$.

b) Số hạng thứ hai của dãy số là ${u_2} = 1$.

c) Số hạng tổng quát của dãy số là ${u_n} = – \frac{5}{2} + 2n$.

d) Dãy số $\left( {{u_n}} \right)$ là một cấp số cộng có công sai là $2$.

Lời giải

+ Ta có: ${S_1} = {u_1} = – \frac{1}{2};{S_2} = {u_1} + {u_2} = 1$. Do đó, ${u_2} = {S_2} – {u_1} = \frac{3}{2}$.

+ Với $n \geqslant 2$ thì ${u_n} = {S_n} – {S_{n – 1}} = – \frac{5}{2} + 2n$. \

Mà ${u_1} = – \frac{1}{2} = – \frac{5}{2} + 2.1$ nên ${u_n} = – \frac{5}{2} + 2n$ với $n \in {\mathbb{N}^*}$.

+ Ta có: ${u_n} – {u_{n – 1}} = – \frac{5}{2} + 2n – \left( { – \frac{5}{2} + 2(n – 1)} \right) = 2$ với $n \in {N^*},n \geqslant 2$.

Vậy $\left( {{u_n}} \right)$ là một cấp số cộng có công sai là $2$.

Đáp án: a) Đ, b) S, c) Đ, d) Đ.

Câu 18. Cho dãy số $\left( {{u_n}} \right)$ biết ${u_1} = 1,{u_{n + 1}} = \frac{{{u_n}}}{{1 – 2{u_n}}}$ với $n \in {\mathbb{N}^*}$. Đặt ${v_n} = \frac{{{u_n} + 2}}{{{u_n}}}$ với $n \in {\mathbb{N}^*}$.

a) ${v_1} = 3$.

b) Dãy số $\left( {{v_n}} \right)$ là một cấp số cộng có công sai $d = 4$.

c) Công thức của số hạng tổng quát ${v_n}$ là ${v_n} = 7 – 4n$.

d) Công thức của số hạng tổng quát ${u_n}$ là ${u_n} = \frac{2}{{7 – 4n}}$.

Lời giải

+ Ta có: ${v_1} = \frac{{{u_1} + 2}}{{{u_1}}} = 3$.

+ Theo giả thiết, ta có ${v_n} = \frac{{{u_n} + 2}}{{{u_n}}} = 1 + \frac{2}{{{u_n}}}$ nên ${v_{n + 1}} = 1 + \frac{2}{{{u_{n + 1}}}}$.

Do ${u_{n + 1}} = \frac{{{u_n}}}{{1 – 2{u_n}}}$ nên $\frac{1}{{{u_{n + 1}}}} = \frac{{1 – 2{u_n}}}{{{u_n}}} = \frac{1}{{{u_n}}} – 2$. Suy ra ${v_{n + 1}} = 1 + 2\left( {\frac{1}{{{u_n}}} – 2} \right)$.

Khi đó, ${v_{n + 1}} – {v_n} = 1 + \frac{2}{{{u_n}}} – 4 – \left( {1 + \frac{2}{{{u_n}}}} \right) = – 4$ với mọi $n \in {\mathbb{N}^*}$.

Vậy dãy số $\left( {{v_n}} \right)$ là một cấp số cộng có số hạng đầu ${v_1} = 3$, công sai $d = – 4$.

+ Ta có: ${v_n} = {v_1} + (n – 1)d$$ = 3 + (n – 1)( – 4) = 7 – 4n$.

+ Từ ${v_n} = \frac{{{u_n} + 2}}{{{u_n}}}$ suy ra ${u_n} = \frac{2}{{{v_n} – 1}} = \frac{2}{{7 – 4n – 1}} = \frac{1}{{3 – 2n}}$.

Đáp án: a) Đ, b) S, c) Đ, d) S.

Câu 19. Cho dãy số $\left( {{u_n}} \right)$ có tổng $n$ số hạng đầu được tính bởi công thức: ${S_n} = \frac{{1 – {3^n}}}{{2 \cdot {3^{n – 2}}}}$ với $n \in {\mathbb{N}^*}$.

a) Số hạng thứ nhất của dãy số là ${u_1} = – 3$.

b) Số hạng thứ hai của dãy số là ${u_2} = – 4$.

c) Số hạng tổng quát của dãy số là ${u_n} = \frac{1}{{{3^{n – 2}}}}$.

d) Dãy số $\left( {{u_n}} \right)$ là một cấp số nhân có công bội là $ – \frac{1}{3}$.

Lời giải

+ ${S_1} = {u_1} = – 3$, ${S_2} = {u_1} + {u_2} = – 4$ nên ${u_2} = {S_2} – {S_1} = – 1$.

+ Ta có: ${u_n} = {S_n} – {S_{n – 1}} = – \frac{1}{{{3^{n – 2}}}}$ với mọi $n \geqslant 2$. Mà ${u_1} = – 3 = – \frac{1}{{{3^{1 – 2}}}}$ nên ${u_n} = – \frac{1}{{{3^{n – 2}}}}$ với $n \in {\mathbb{N}^ * }$. Lại có${u_n} = {u_{n – 1}}.\frac{1}{3}$ với mọi $n \geqslant 2$.

Vậy dãy số $\left( {{u_n}} \right)$ là một cấp số nhân có số hạng đầu ${u_1} = – 3$ và công bội $q = \frac{1}{3}$.

Đáp án: a) Đ, b) S, c) S, d) S.

Câu 20. Cho dãy số $\left( {{u_n}} \right)$, biết ${u_1} = – 17,\,\,{u_{n + 1}} = 5{u_n} – 12$ với $n \in {\mathbb{N}^*}$. Đặt ${v_n} = \frac{{3 – {u_n}}}{2}$ với $n \in {\mathbb{N}^*}$.

a) ${v_1} = 10$.

b) Dãy số ( ${v_n}$) là một cấp số nhân có công bội bằng $\frac{1}{5}$.

c) Công thức của số hạng tổng quát ${v_n}$ là ${v_n} = \frac{2}{{{5^n}}}$.

d) Công thức của số hạng tổng quát ${u_n}$ là ${u_n} = 3 – {4.5^n}$.

Lời giải

Ta có: ${v_1} = \frac{{3 – {u_1}}}{2} = 10$.

${v_{n + 1}} = \frac{{3 – {u_{n + 1}}}}{2} = \frac{{3 – \left( {5{u_n} – 12} \right)}}{2} = \frac{{5\left( {3 – {u_n}} \right)}}{2} = 5.{v_n}\;$với $n \in {\mathbb{N}^*}.$

Vậy dãy số $\left( {{v_n}} \right)$ là một cấp số nhân có số hạng đầu ${v_1} = 10$, công bội bằng $q = 5$.

Vậy ${v_n} = {2.5^n}$, ${u_n} = 3 – {4.5^n}$.

Đáp án: a) Đ, b) S, c) S, d) Đ.

Dạng 3. Câu trắc nghiệm trả lời ngắn

Câu 21. Một nhà thi đấu có $20$ hàng ghế dành cho khán giả. Hàng thứ nhất có $30$ ghế, hàng thứ hai có $31$ ghế, hàng thứ ba có $32$ ghế,… Cứ như thế, số ghế ở hàng sau nhiều hơn số ghế ở hàng ngay trước là $1$ ghế. Trong một giải thi đấu, ban tổ chức đã bán được hết số vé phát ra và số tiền thu được từ bán vé là $63\,200\,000$ đồng. Tính giá tiền của mỗi vé (đơn vị: nghìn đồng), biết số vé bán ra bằng số ghế dành cho khán giả của nhà thi đấu và các vé là đồng giá.

Lời giải

Trả lời: $80\,000$.

Số ghế ở mỗi hàng lập thành một cấp số cộng có số hạng đầu ${u_1} = 30$, công sai $d = 1$. Cấp số cộng này có 20 số hạng. Do đó, tổng số ghế trong nhà thi đấu là:

${S_{20}} = \frac{{\left[ {2.30 + \left( {20 – 1} \right).1} \right].20}}{2} = 790\;$(ghế).

Vì số vé bán ra bằng số ghế dành cho khán già của nhà thi đấu nên có 790 vé được bán ra. Vậy giá tiền của một vé là: $63\,200\,000:790 = 80\,000$ (đồng).

Câu 22. Cho tập hợp $A$ gồm $99$ số tự nhiên liên tiếp khác nhau $A = \left\{ {1;2;3; \ldots ;99} \right\}$. Tìm số cách chọn ba số khác nhau từ tập hợp $A$ để ba số đó lập thành cấp số cộng.

Lời giải

Trả lời: $2401.$

Gọi $a,b,c$ theo thứ tự lập thành cấp số cộng $\left( {a,b,c \in A} \right)$.

Khi đó, $b – a = c – b$ hay $2b = a + c$. Do đó, $a$ và $c$ phải cùng là số chã̃n hoặc cùng là số lẻ nên số cách chọn hai số $a,c$ cùng chẵn hoặc cùng lẻ là: $C_{49}^2 + C_{50}^2 = 1\,176 + 1\,225 = 2\,401$.

Với mỗi cách chọn hai số $a,c$ có duy nhất một cách chọn số $b$. Vậy số cách chọn ba số khác nhau từ tập hợp $A$ để ba số đó lập thành cấp số cộng là $2\,401$.

Câu 23. Anh Minh kí hợp đồng lao động có thời hạn ở một công ty với phương án trả lương như sau: Quý thứ nhất, tiền lương là $27$ triệu. Kể từ quý thứ hai trở đi, mỗi quý tiền lương được tăng $2,1$ triệu. Tổng số tiền lương anh nhận được trong các năm đã đi làm là $684$ triệu đồng. Hỏi anh Minh đã làm ở công ty đó bao nhiêu năm?

Lời giải

Trả lời: $4.$

Gọi số năm đã đi làm của anh Minh ở công ty đó là $n\left( {n \in {\mathbb{N}^*}} \right)$. Số quý làm việc là $4n$.

Khi đó, tổng số tiền thu được của anh Minh trong $n$ năm đi làm là:

$S = \frac{{\left[ {2.27 + \left( {4n – 1} \right).2,1} \right].4n}}{2} = 684$

$ \Leftrightarrow 84{n^2} + 519n – 3420 = 0$$ \Leftrightarrow n = 4$ hoặc $n = – \frac{{285}}{{28}}.$

Do $n$ nguyên dương nên $n = 4$ năm.

Câu 24. Một quả bóng được thả thẳng đứng từ độ cao $10\;m$ rơi xuống đất và nảy lên. Giả sử sau mỗi một lần rơi xuống, nó nảy lên được một độ cao bằng $75\% $ độ cao vừa rơi xuống. Tính tổng quãng đường quả bóng di chuyển được kể từ lúc thả xuống đến khi quả bóng chạm đất lần thứ $10\;$ (làm tròn kết quả đến hàng phần mười của mét).

Lời giải

Gọi ${u_n}$ (m) là độ cao mà quá bóng đạt được sau khi nảy lên ở lần thứ $n$. Ta có: ${u_1} = 10.0,75 = 7,5$. Ta có, dãy $\left( {{u_n}} \right)$ lập thành cấp số nhân có ${u_1} = 7,5$ và công bội $q = 0,75$. Kể từ lúc thả xuống đến khi quả bóng chạm đất lần thứ $10\;$, quả bóng đã được nảy lên $9$lần rồi lại rơi xuống. Do quãng đường quả bóng nảy lên và rơi xuống bằng nhau nên tổng quãng đường quả bóng di chuyển được kể từ lúc thả xuống đến khi quả bóng chạm đất lần thứ $10\;$là:

$S = 10 + 2\left( {{u_1} + {u_2} + \ldots + {u_9}} \right) = 10 + 2.7,5.\frac{{1 – {{(0,75)}^9}}}{{1 – 0,75}} \approx 65,5$ (m).

Câu 25. Một tam giác đều có cạnh bằng $4\;cm$. Chia tam giác đều đó thành $4\;$ tam giác đều bằng nhau và tô màu tam giác ở trung tâm. Với mỗi tam giác nhỏ chưa được tô màu, lại chia thành $4\;$ tam giác đều bằng nhau và tô màu tam giác ở trung tâm. Cứ như thế, quá trình trên được lặp lại. Tính tổng diện tích phần đã được tô màu ở hình tô thứ $5$ (đơn vị: $c{m^2}$, làm tròn kết quả đến hàng phần trăm).

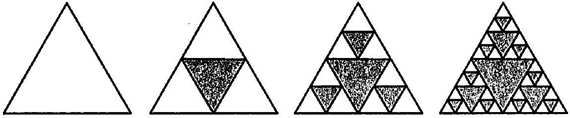
Lời giải

Gọi ${u_n}$ là diện tích phần không được tô màu ở hình tô thứ $n,$ ${S_0}$ là diện tích của tam giác ban đầu. Ta có: ${u_1} = \frac{3}{4} \cdot {S_0}$. Do ở hình tô thứ $n$, diện tích phần không được tô màu bằng $\frac{3}{4}$ diện tích phần không được tô màu ở hình tô trước đó nên dãy $\left( {{u_n}} \right)$ lập thành cấp số nhân có số hạng đầu ${u_1} = \frac{3}{4} \cdot {S_0}$, công bội $q = \frac{3}{4}$. Do đó,

${u_n} = \frac{3}{4} \cdot {S_0} \cdot {\left( {\frac{3}{4}} \right)^{n – 1}} = {S_0} \cdot {\left( {\frac{3}{4}} \right)^n}$

Vậy diện tích phần đã được tô màu ở hình tô thứ $n$ là: ${S_n} = {S_0}\left[ {1 – {{\left( {\frac{3}{4}} \right)}^n}} \right]$.

Thay $n = 5$, ta được ${S_5} = 4\sqrt 3 .\left( {1 – 0,{{75}^5}} \right) \approx 5,28$ (cm²).

Câu 26. Cho hình vuông ${C_1}$ có cạnh bằng $4\;cm$. Người ta chia mối cạnh hình vuông ${C_1}$ thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông ${C_2}$. Từ hình vuông ${C_2}$ lại làm tiếp tục như trên để có hình vuông ${C_3}$. Cứ tiếp tục quá trình như trên, ta nhận được dãy các hình vuông ${C_1},{C_2},{C_3}, \ldots ,{C_n}, \ldots $ như Hình dưới. Tính diện tích của hình vuông thứ $6\;$ (đơn vị: $c{m^2}$, làm tròn kết quả đến hàng phần trăm).

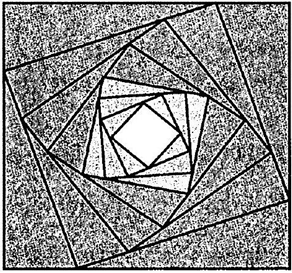
Lời giải

Gọi ${a_n}$(cm) là độ dài cạnh hình vuông thứ $n$.

Ta có: ${a_1} = 4,{a_2} = \sqrt {{{\left( {\frac{{{a_1}}}{4}} \right)}^2} + {{\left( {\frac{{3{a_1}}}{4}} \right)}^2}} = {a_1} \cdot \frac{{\sqrt {10} }}{4}$.

Cứ như thế, dãy $\left( {{a_n}} \right)$ lập thành cấp số nhân có công bội $q = \frac{{\sqrt {10} }}{4}$. Do đó, ${a_n} = 4 \cdot {\left( {\frac{{\sqrt {10} }}{4}} \right)^{n – 1}} \cdot $

Vậy diện tích hình vuông thứ 6 là $a_6^2 \approx 1,53$(cm²).