Các Dạng Toán Bài Công Thức Nhân Xác Suất Cho Hai Biến Cố Độc Lập Giải Chi Tiết

Các dạng toán bài công thức nhân xác suất cho hai biến cố độc lập giải chi tiết được soạn dưới dạng file word và PDF gồm 3 trang. Các bạn xem và tải về ở dưới.

Câu 1. Các học sinh lớp 11D làm thí nghiệm gieo hai loại hạt giống $A$ và $B$. Xác suất để hai loại hạt giống $A$ và $B$ nảy mầm tương ứng là 0,92 và 0,88 . Giả sử việc nảy mầm của hạt $A$ và hạt $B$ là độc lập với nhau. Dùng sơ đồ hình cây, tính xác suất để:

a) Hạt giống $A$ nảy mầm còn hạt giống $B$ không nảy mầm;

b) Hạt giống $A$ không nảy mầm còn hạt giống $B$ nảy mầm;

c) Ít nhất có một trong hai loại hạt giống nảy mầm.

Lời giải

Gọi $A$ là biến cố: “Hạt A nảy mầm”; $B$ là biến cố: “Hạt B nảy mầm”.

Suy ra,

+Biến cố:” “Hạt $A$ không nảy mầm, hạt $B$ nảy mầm” là biến cố $\overline A B$.

+Biến cố: “Có ít nhất một trong hai hạt nảy mầm” là biến cố $A \cup B$. Hai biến cố $A,B$ là độc lập.

$P\left( A \right) = 0,92;P\left( B \right) = 0,88$. Giải. Gọi $A$ là biến cố: “Hạt $A$ nảy mầm”; $B$ là biến cố: “Hạt $B$ nảy mầm”. Ta có sơ đồ hình cây như sau:

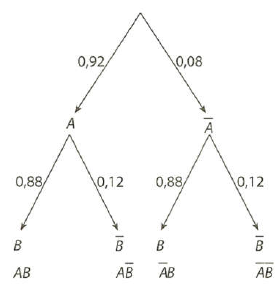
$P\left( A \right) = 0,92;P\left( B \right) = 0,88$. Ta có hai biến cố $A$ và $B$ độc lập.

a) Biến cố: “Hạt $A$ nảy mầm, hạt $B$ không nảy mầm” là biến cố $A\overline B $. Do đó:

$P\left( {A\overline B } \right) = 0,92 \cdot 0,12 = 0,1104$.

b) Biến cố: “Hạt $A$ không nảy mầm, hạt $B$ nảy mầm” là biến cố $\overline A B$.

Do đó:

$P\left( {\overline A B} \right) = 0,08 \cdot 0,88 = 0,0704$.

c) Biến cố: “Có ít nhất một trong hai hạt nảy mầm” là biến cố $A \cup B$.

$P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) – P\left( {AB} \right) = P\left( A \right) + P\left( B \right) – P\left( A \right)P\left( B \right)$

$ = 0,92 + 0,88 – 0,92 \cdot 0,88 = 0,9904$

Câu 2. Để nghiên cứu mối liên quan giữa thói quen hút thuốc lá với bệnh viêm phổi, nhà nghiên cứu chọn một nhóm 5000 người đàn ông. Với mỗi người trong nhóm, nhà nghiên cứu kiểm tra xem họ có nghiện thuốc lá và có bị viêm phổi hay không. Kết quả được thống kê trong bảng sau:

	Viêm phổi	Không viêm phổi
Nghiện thuốc lá	752 người	1236 người
Không nghiện thuốc lá	575 người	2437 người

Từ bảng thống kê trên, hãy chứng tỏ rằng việc nghiện thuốc lá và mắc bệnh viêm phổi có liên quan với nhau.

Lời giải

Chọn ngẫu nhiên một người trong nhóm 5000 người đang xét. Xét các biến cố sau:

$A$ : :Người đó nghiện thuốc lá”; $B$ : “Người đó mắc bệnh viêm phổi”.

Khi đó, $AB$ là biến cố: “Người đó nghiện thuốc lá và mắc bệnh viêm phổi”.

Số người nghiện thuốc là: $752 + 1236 = 1988$.

Số người mắc bệnh viêm phổi là: $752 + 575 = 1327$.

Số người nghiện thuốc lá và mắc bệnh viêm phổi là 752.

Ta có: $P\left( A \right) = \frac{{1988}}{{5000}};P\left( B \right) = \frac{{1327}}{{5000}};P\left( {AB} \right) = \frac{{752}}{{5000}}$.

$P\left( A \right)P\left( B \right) = \frac{{1988}}{{5000}} \cdot \frac{{1327}}{{5000}} \ne \frac{{752}}{{5000}} = P\left( {AB} \right)$. Vậy hai biến cố $A$ và $B$ không độc lập. Do đó, ta kết luận việc nghiện thuốc lá và mắc bệnh viêm phổi có liên quan với nhau.

Câu 3. Cho hai biến cố $A$ và $B$ là hai biến cố xung khắc với $P\left( A \right) > 0,P\left( B \right) > 0$. Chứng tỏ rằng hai biến cố $A$ và $B$ không độc lập.

Lời giải

Ta có $P\left( A \right)P\left( B \right) > 0;P\left( {AB} \right) = 0$. Do đó $P\left( {AB} \right) \ne P\left( A \right)P\left( B \right)$.

Vậy hai biến cố $A$ và $B$ không độc lập.

Câu 4. Một thùng đựng 60 tấm thẻ cùng loại được đánh số từ 1 đến 60 . Rút ngẫu nhiên một tấm thẻ trong thùng. Xét hai biến cố sau:

$A$ : “Số ghi trên tấm thẻ là ước của 60 ” và $B$ : “Số ghi trên tấm thẻ là ước của 48”.

Chứng tỏ rằng $A$ và $B$ là hai biến cố không độc lập.

Lời giải

a) Ta có: $A = \left\{ {1;2;3;4;5;6;10;12;15;20;30} \right\};B = \left\{ {1;2;3;4;6;8;12;16;24;48} \right\}$.

$AB = A \cap B = \left\{ {1;2;3;4;6;12} \right\}$.

Suy ra: $P\left( A \right) = \frac{{11}}{{60}};P\left( B \right) = \frac{{10}}{{60}} = \frac{1}{6};P\left( {AB} \right) = \frac{6}{{60}} = \frac{1}{{10}}$.

b) Ta có: $P\left( A \right)P\left( B \right) = \frac{{11}}{{60}} \cdot \frac{1}{6} = \frac{{11}}{{360}}$.

$P\left( {AB} \right) = \frac{1}{{10}} = \frac{{36}}{{360}} \ne \frac{{11}}{{360}} = P\left( A \right)P\left( B \right)$.

Do đó, hai biến cố $A$ và $B$ không độc lập.

Câu 5. Có hai túi đựng các viên bi có cùng kích thước và khối lượng. Túi $I$ có 3 viên bi màu xanh và 7 viên bi màu đỏ. Túi II có 10 viên bi màu xanh và 6 viên bi màu đỏ. Từ mỗi túi, lấy ngẫu nhiên ra một viên bi. Tính xác suất để:

a) Hai viên bi được lấy có cùng màu xanh;

b) Hai viên bi được lấy có cùng màu đỏ;

c) Hai viên bi được lấy có cùng màu;

d) Hai viên bi được lấy không cùng màu.

Lời giải

a) Gọi $A$ là biến cố: “Hai viên bi lấy ra cùng màu xanh”; ${A_1}$ là biến cố: “Viên bi lấy ra từ túi $I$ có màu xanh”; ${A_2}$ là biến cố: “Viên bi lấy ra từ túi II có màu xanh”.

Ta có: $A = {A_1}{A_2}$. Hai biến cố ${A_1}$ và ${A_2}$ độc lập nên $P\left( A \right) = P\left( {{A_1}} \right)P\left( {{A_2}} \right)$.

Dễ thấy $P\left( {{A_1}} \right) = \frac{3}{{10}};P\left( {{A_2}} \right) = \frac{{10}}{{16}}$. Suy ra $P\left( A \right) = P\left( {{A_1}} \right)P\left( {{A_2}} \right) = \frac{3}{{10}} \cdot \frac{{10}}{{16}} = \frac{{30}}{{160}}$.

b) Gọi $B$ là biến cố: “Hai viên bi lấy ra cùng màu đỏ”; ${B_1}$ là biến cố: “Viên bi lấy ra từ túi I có màu đỏ”; ${B_2}$ là biến cố: “Viên bi lấy ra từ túi II có màu đỏ”.

Ta có: $B = {B_1}{B_2}$. Hai biến cố ${B_1}$ và ${B_2}$ độc lập nên $P\left( B \right) = P\left( {{B_1}} \right)P\left( {{B_2}} \right) = \frac{7}{{10}} \cdot \frac{6}{{16}} = \frac{{42}}{{160}}$.

c) Gọi $E$ là biến cố: “Hai viên bi lấy ra cùng màu”. Ta có $E = A \cup B$. Hai biến cố $A$ và $B$ xung khắc nên $P\left( E \right) = P\left( A \right) + P\left( B \right)$.

Vậy $P\left( E \right) = P\left( A \right) + P\left( B \right) = \frac{{30}}{{160}} + \frac{{42}}{{160}} = \frac{{72}}{{160}} = \frac{9}{{20}}$.

d) Gọi $F$ là biến cố: “Hai viên bi lấy ra khác màu”. Ta có $F = \overline E $.

Vậy $P\left( F \right) = P\left( {\overline E } \right) = 1 – P\left( E \right) = 1 – \frac{9}{{20}} = \frac{{11}}{{20}}$.

Câu 6. Có hai túi mỗi túi đựng 10 quả cầu có cùng kích thước và khối lượng được đánh số từ 1 đến 10 . Từ mỗi túi, lấy ngẫu nhiên ra một quả cầu. Tính xác suất để trong hai quả cầu được lấy ra không có quả cầu nào ghi số 1 hoặc ghi số 5 .

Lời giải

Gọi $A$ là biến cố: “Hai quả cầu lấy ra không có quả cầu nào ghi số 1 “, ${A_1}$ là biến cố: “Quả cầu lấy ra từ túi $I$ không ghi số 1”; ${A_2}$ là biến cố: “Quả cầu lấy ra từ túi Il không ghi số 1”. Ta có: $A = {A_1}{A_2}$. Hai biến cố ${A_1}$ và ${A_2}$ độc lập nên $P\left( A \right) = P\left( {{A_1}} \right)P\left( {{A_2}} \right)$.

Dễ thấy $P\left( {{A_1}} \right) = P\left( {{A_2}} \right) = \frac{9}{{10}} = 0,9$. Vậy $P\left( A \right) = {(0,9)^2}$.

Gọi $B$ là biến cố: “Hai quả cầu lấy ra không có quả cầu nào ghi số 5 “.

Tương tự ta có $P\left( B \right) = {(0,9)^2}$.

Gọi $E$ là biến cố: “Trong hai quả cầu lấy ra không có quả cầu nào ghi số 1 hoặc số 5 “.

Ta có: $E = A \cup B$.

Theo công thức cộng xác suất: $P\left( E \right) = P\left( A \right) + P\left( B \right) – P\left( {AB} \right)$.

Gọi $AB$ là biến cố: “Hai quả cầu ra không có quả cầu nào ghi số 1 và ghi số 5 “;

${H_1}$ là biến cố: “Quả cầu lấy ra từ túi I không ghi số 1 và ghi số 5 “; ${H_2}$ là biến cố: “Quả cầu

Hai biến cố ${H_1}$ và ${H_2}$ độc lập nên $P\left( {AB} \right) = P\left( {{H_1}} \right)P\left( {{H_2}} \right)$.

Dễ thấy $P\left( {{H_1}} \right) = P\left( {{H_2}} \right) = \frac{8}{{10}} = 0,8$.

Từ đó $P\left( {AB} \right) = 0,{8^2} = 0,64$.

Vậy $P\left( E \right) = 0,81 + 0,81 – 0,64 = 0,98$.

Câu 7. Trong đợt kiểm tra cuối học kì Il lớp 11 của các trường trung học phổ thông, thống kê cho thấy có $93\% $ học sinh tỉnh $X$ đạt yêu cầu; $87\% $ học sinh tỉnh $Y$ đạt yêu cầu. Chọn ngẫu nhiên một học sinh của tỉnh $X$ và một học sinh của tỉnh $Y$. Giả thiết rằng chất lượng học tập của hai tỉnh là độc lập. Tính xác suất để:

a) Cả hai học sinh được chọn đều đạt yêu cầu;

b) Cả hai học sinh được chọn đều không đạt yêu cầu;

c) Chỉ có đúng một học sinh được chọn đạt yêu cầu;

d) Có ít nhất một trong hai học sinh được chọn đạt yêu cầu.

Lời giải

Gọi $A$ là biến cố: “Học sinh tỉnh $A$ đạt yêu cầu”; $B$ là biến cố: “Học sinh tỉnh $B$ đạt yêu cầu”.

a) $P\left( {AB} \right) = P\left( A \right)P\left( B \right) = 0,93 \cdot 0,87 = 0,8091$.

b) $P\left( {\overline {AB} } \right) = P\left( {\overline A } \right)P\left( {\overline B } \right) = 0,07 \cdot 0,13 = 0,0091$.

c) $P\left( {\overline A B} \right) + P\left( {A\overline B } \right) = 0,07 \cdot 0,87 + 0,93 \cdot 0,13 = 0,1818$.

d) $P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) – P\left( {AB} \right)$

$ = 0,93 + 0,87 – 0,8091 = 0,9909$.

Câu 8. Một vận động viên thi bắn súng. Biết rằng xác suất để vận động viên đó bắn trúng vòng 10 là 0,2 ; bắn trúng vòng 9 là 0,25 và bắn trúng vòng 8 là 0,3 . Nếu bắn trúng vòng $k$ thì được $k$ điểm. Vận động viên thực hiện bắn hai lần. Giả sử hai lần bắn của của vận động viên là độc lập. Vận động viên đạt huy chương vàng nếu được 20 điểm, đạt huy chương bạc nếu được 19 điểm và đạt huy chương đồng nếu được 18 điểm. Tính xác suất để vận động viên đạt được huy chương đồng.

Lời giải

Gọi $A,B,C$ tương ứng là các biến cố: “Vận động viên bắn trúng vòng 10 “, “Vận động viên bắn trúng vòng 9 “, “Vận động viên bắn trúng vòng 8 “.

Gọi $G$ là biến cố: “Vận động viên đạt được huy chương đồng”; $U$ là biến cố: “Vận động viên hai lần bắn trúng vòng 9 “, $V$ là biến cố: “Vận động viên một lần bắn trúng vòng 10 , một lần bắn trúng vòng 8 “.

Ta có: $G = U \cup V$.

$P\left( U \right) = P\left( B \right) \cdot P\left( B \right) = 0,25 \cdot 0,25 = 0,0625$.

$P\left( V \right) = P\left( {AC} \right) + P\left( {CA} \right) = 0,2 \cdot 0,3 + 0,3 \cdot 0,2 = 0,12$.

Do $U$ và $V$ xung khắc nên $P\left( G \right) = P\left( U \right) + P\left( V \right) = 0,0625 + 0,12 = 0,1825$.

Câu 9. Gieo ba xúc xắc cân đối và đồng chất. Xét các biến cố sau:

$A$ : “Số chấm xuất hiện trên mặt của ba xúc xắc khác nhau”.

$B$ : “Có ít nhất một xúc xắc xuất hiện mặt 6 chấm”.

Chứng minh rằng hai biến cố $A$ và $B$ không độc lập.

Lời giải

Ta cần chứng minh $P\left( {AB} \right) \ne P\left( A \right)P\left( B \right)$.

• Tính $P\left( A \right)$ : Ta có $\Omega = \left\{ {\left( {a,b,c} \right);1 \leqslant a,b,c \leqslant 6} \right\},n\left( \Omega \right) = 6 \cdot 6 \cdot 6 = 216$.

$A = \left\{ {\left( {a,b,c} \right);1 \leqslant a,b,c \leqslant 6} \right\}$ và $a,b,c$ là các số nguyên dương phân biệt.

Mỗi bộ $\left( {a,b,c} \right)$ là một chỉnh hợp chập 3 của 6 phần tử $\left\{ {1;2;3;4;5;6} \right\}$.

Ta có $n\left( A \right) = A_6^3 = 120$.

Vậy $P\left( A \right) = \frac{{120}}{{216}}$.

• Tính $P\left( B \right)$ :

Xét biến cố đối \[\overline B \] : “Số chấm xuất hiện trên mỗi xúc xắc đều khác 6 “. Mỗi kết quả thuận lợi cho \[\overline B \] là một bộ ba số $\left( {a,b,c} \right)$ trong đó $1 \leqslant a,b,c \leqslant 6$.

Do đó theo quy tắc nhân, số kết quả thuận lợi cho \[\overline B \] là $5 \cdot 5 \cdot 5 = 125$.

Vậy $P\left( {\overline B } \right) = \frac{{125}}{{216}}$. Suy ra $P\left( B \right) = 1 – P\left( {\overline B } \right) = \frac{{91}}{{216}}$.

• Tính $P\left( {AB} \right)$ :

Mỗi kết quả thuận lợi cho $AB$ là một bộ ba số $\left( {a,b,c} \right)$ trong đó $1 \leqslant a,b,c \leqslant 6$ và $a,b,c$ là các số nguyên dương khác nhau và có đúng một số bằng 6 . Có 3 cách chọn một số bằng 6 và $A_5^2 = 20$ cách chọn hai số còn lại trong 5 số $\left\{ {1;2;3;4;5} \right\}$. Theo quy tắc nhân, ta có $3 \cdot 20 = 60$ kết quả thuận lợi.

Do đó $P\left( {AB} \right) = \frac{{60}}{{216}} \ne P\left( A \right)P\left( B \right) = \frac{{120}}{{216}} \cdot \frac{{91}}{{216}}$.

Vậy $A,B$ không độc lập.

Câu 10. Cho $P\left( A \right) = 0,4;P\left( B \right) = 0,5;P\left( {A \cup B} \right) = 0,6$. Hỏi $A$ và $B$ có độc lập hay không?

Lời giải

$P\left( {AB} \right) = P\left( A \right) + P\left( B \right) – P\left( {A \cup B} \right) = 0,3 \ne P\left( A \right) \cdot P\left( B \right) = 0,2$.

Vậy $A$ và $B$ không độc lập.

Câu 11. Cho $P\left( A \right) = \frac{2}{5},P\left( B \right) = \frac{1}{3},P\left( {A \cup B} \right) = \frac{1}{2}$. Hỏi $A$ và $B$ có độc lập hay không?

Lời giải

$P\left( {AB} \right) = P\left( A \right) + P\left( B \right) – P\left( {A \cup B} \right) = \frac{7}{{30}} \ne P\left( A \right) \cdot P\left( B \right) = \frac{2}{{15}} = \frac{4}{{30}}$.

Vậy $A$ và $B$ không độc lập.

Câu 12. Gieo hai đồng xu cân đối. Xét các biến cố $A$ : “Cả hai đồng xu đều ra mặt sấp”, $B$ : “Có ít nhất một đồng xu ra mặt sấp”. Hỏi $A$ và $B$ có độc lập hay không?

Lời giải

Tính $P\left( A \right)$ : Ta có $\Omega = \left\{ {SS;SN;NS;NN} \right\},n\left( \Omega \right) = 4,A = \left\{ {SS} \right\},n\left( A \right) = 1$.

Vậy $P\left( A \right) = \frac{1}{4}$.

Tính $P\left( B \right)$ : Ta có $B = \left\{ {SS;SN;NS} \right\},n\left( B \right) = 3$. Vậy $P\left( B \right) = \frac{3}{4}$.

Tính $P\left( {AB} \right)$ : Ta có $AB = A \cap B = \left\{ {SS} \right\},n\left( {A \cap B} \right) = 1$.

Vậy $P\left( {AB} \right) = \frac{1}{4}$.

Ta có $P\left( {AB} \right) = \frac{1}{4} = \frac{4}{{16}} \ne P\left( A \right) \cdot P\left( B \right) = \frac{1}{4} \cdot \frac{3}{4} = \frac{3}{{16}}$.

Vậy $A$ và $B$ không độc lập.

Câu 13. Gieo hai con xúc xắc cân đối. Xét các biến cố $A$ : “Có ít nhất một con xúc xắc xuất hiện mặt 5 chấm”, $B$ : “Tổng số chấm xuất hiện trên hai con xúc xắc bằng 7 “. Chứng tỏ rằng $A$ và $B$ không độc lập.

Lời giải

Tính $P\left( A \right)$ : Xét biến cố đối \[\overline A \] : “Cả hai con xúc xắc không xuất hiện mặt 5 chấm”, $\overline A = \left\{ {\left( {a,b} \right):a,b \in \left\{ {1;2;3;4;6} \right\}} \right\}$. Ta có $n\left( {\overline A } \right) = 25;n\left( \Omega \right) = 36$.

Vậy $P\left( {\overline A } \right) = \frac{{25}}{{36}}$, do đó $P\left( A \right) = 1 – \frac{{25}}{{36}} = \frac{{11}}{{36}}$.

Tính $P\left( B \right)$ : Ta có $B = \left\{ {\left( {1,6} \right);\left( {2,5} \right);\left( {3,4} \right);\left( {4,3} \right);\left( {5,2} \right);\left( {6,1} \right)} \right\},n\left( B \right) = 6$.

Vậy $P\left( B \right) = \frac{6}{{36}}$.

Tính $P\left( {AB} \right)$ : Ta có $AB = A \cap B = \left\{ {\left( {2,5} \right);\left( {5,2} \right)} \right\},n\left( {A \cap B} \right) = 2$.

Vậy $P\left( {AB} \right) = \frac{2}{{36}}$.

Ta có: $P\left( {AB} \right) = \frac{2}{{36}} = \frac{{72}}{{{{36}^2}}};P\left( A \right) \cdot P\left( B \right) = \frac{{11}}{{36}} \cdot \frac{6}{{36}} = \frac{{66}}{{{{36}^2}}}$.

Suy ra $P\left( {AB} \right) \ne P\left( A \right) \cdot P\left( B \right)$.

Vậy $A$ và $B$ không độc lập.

Câu 14. Có 3 hộp I, II, III. Mỗi hộp chứa ba tấm thẻ đánh số 1,2,3. Từ mỗi hộp rút ngẫu nhiên một tấm thẻ. Xét các biến cố sau:

$A$ : “Tổng các số ghi trên ba tấm thẻ là 6 “; $B$ : “Ba tấm thẻ có ghi số bằng nhau”.

a) Tính $P\left( A \right),P\left( B \right)$.

b) Hỏi $A,B$ có độc lập không?

Lời giải

a) Ta có $\Omega = \left\{ {\left( {a,b,c} \right):1 \leqslant a,b,c \leqslant 3} \right\},n\left( \Omega \right) = 27$.

Tính $P\left( A \right):A = \left\{ {\left( {1,2,3} \right);\left( {2,1,3} \right);\left( {3,1,2} \right);\left( {1,3,2} \right);\left( {3,2,1} \right);\left( {2,3,1} \right);\left( {2,2,2} \right)} \right\},n\left( A \right) = 7$.

Suy ra $P\left( A \right) = \frac{7}{{27}}$.

Tính $P\left( B \right):B = \left\{ {\left( {1,1,1} \right);\left( {2,2,2} \right);\left( {3,3,3} \right)} \right\},n\left( B \right) = 3$.

Suy ra $P\left( B \right) = \frac{3}{{27}}$.

b) Tính $P\left( {AB} \right)$ : Ta có $A \cap B = \left\{ {\left( {2,2,2} \right)} \right\}$. Vậy $P\left( {AB} \right) = \frac{1}{{27}}$.

Vì $P\left( {AB} \right) = \frac{1}{{27}} = \frac{{27}}{{{{27}^2}}} \ne \frac{{21}}{{{{27}^2}}} = \frac{7}{{27}} \cdot \frac{3}{{27}} = P\left( A \right) \cdot P\left( B \right)$ nên $A$ và $B$ không độc lập.

Câu 15. Hai bạn An và Bình không quen biết nhau và đều học xa nhà. Xác suất để bạn An về thăm nhà vào ngày Chủ nhật là 0,2 và của bạn Bình là 0,25 . Dùng sơ đồ hình cây để tính xác suất vào ngày Chủ nhật:

a) Cả hai bạn đều về thăm nhà.

b) Có ít nhất một bạn về thăm nhà.

c) Cả hai bạn đều không về thăm nhà.

d) Chỉ có bạn An về thăm nhà.

e) Có đúng một bạn về thăm nhà.

Lời giải

Gọi $A,B$ tương ứng là các biến cố: “Bạn An về thăm nhà vào ngày Chủ nhật” và “Bạn Bình về thăm nhà vào ngày Chủ nhật”. $A$ và $B$ là hai biến cố độc lập. Ta có sơ đồ hình cây:

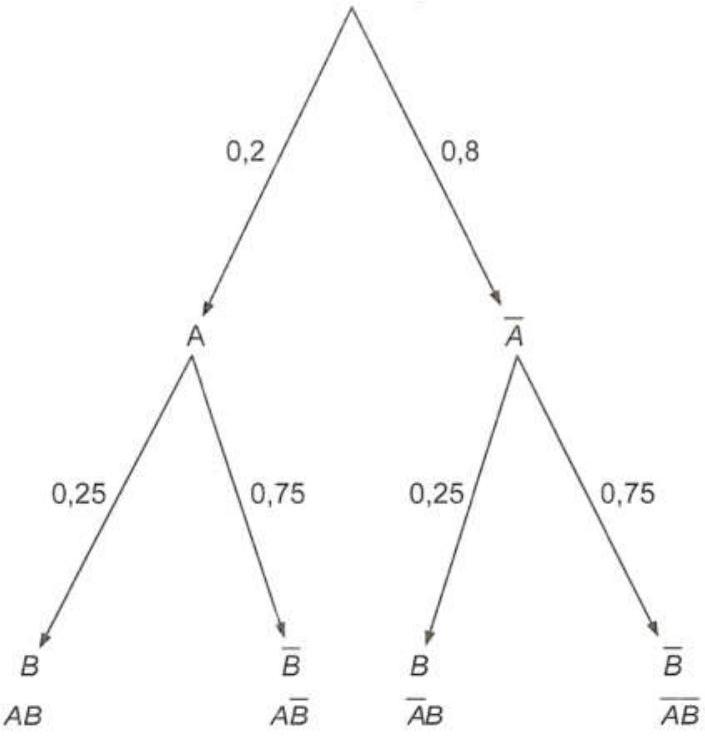
a) $P\left( {AB} \right) = 0,2 \cdot 0,25 = 0,05$.

b) $P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) – P\left( {AB} \right) = 0,2 + 0,25 – 0,05 = 0,4$.

c) $P\left( {\overline A \overline B } \right) = 0,8 \cdot 0,75 = 0,6$.

d) $P\left( {A\overline B } \right) = 0,2 \cdot 0,75 = 0,15$.

e) $P\left( {A\overline B \cup \overline A B} \right) = P\left( {A\overline B } \right) + P\left( {\overline A B} \right) = 0,2 \cdot 0,75 + 0,8 \cdot 0,25 = 0,35$.

Câu 16. Cho $A,B$ là hai biến cố độc lập và $P\left( {AB} \right) = 0,1;P\left( {A\overline B } \right) = 0,4$. Tìm $P\left( {A \cup \overline B } \right)$.

$P\left( {A \cup \overline B } \right) = P\left( A \right) + P\left( {\overline B } \right) – P\left( {A\overline B } \right)$.

Lời giải

$P\left( A \right) = P\left( {AB} \right) + P\left( {A\overline B } \right) = 0,1 + 0,4 = 0,5$.

$P\left( {AB} \right) = P\left( A \right) \cdot P\left( B \right) = 0,1$. Khi dó $0,1 = 0,5 \cdot P\left( B \right)$, suy ra $P\left( B \right) = 0,2$.

$P\left( {A \cup \overline B } \right) = P\left( A \right) + P\left( {\overline B } \right) – P\left( {A\overline B } \right) = 0,5 + 0,8 – 0,4 = 0,9$.

Câu 17. Hộp thứ nhất chứa 4 viên bi cùng loại được đánh số lần lượt từ 1 đến 4 . Hộp thứ hai chứa 6 viên bi cùng loại được đánh số lần lượt từ 1 đến 6 . Lấy ra ngẫu nhiên từ mỗi hộp 1 viên bi. Gọi $A$ là biến cố “Tổng các số ghi trên 2 viên bi bằng 8 “, $B$ là biến cố “Tích các số ghi trên 2 viên bi là số chẵn”.

a) Xác định không gian mẫu của phép thử.

b) Hãy tính xác suất của biến cố $AB$.

c) Tính xác suất của biến cố $A$ và biến cố $B$.

d) $A$ và $B$ có là hai biến cố độc lập không?

e) Hãy tìm một biến cố khác rỗng, xung khắc với biến cố $A$ nhưng không xung khắc với biến cố $B$.

Lời giải

a) Không gian mẫu của phép thử là $\Omega = \left\{ {\left( {i;j} \right)\;i \in \mathbb{N},j \in \mathbb{N},1 \leqslant i \leqslant 4,1 \leqslant j \leqslant 6} \right\}$, trong đó kí hiệu $\left( {i;j} \right)$ là kết quả viên bi lấy ra từ hộp thứ nhất được đánh số $i$, viên bi lấy ra từ hộp thứ hai được đánh số $j$.

b) Số phần tử của không gian mẫu là $n\left( \Omega \right) = 4 \cdot 6 = 24$.

Khi đó biến cố $AB = \left\{ {\left( {2;6} \right);\left( {4;4} \right)} \right\}$ nên số kết quả thuận lợi cho $AB$ là $n\left( {AB} \right) = 2$. Xác suất của biến cố $AB$ là: $P\left( {AB} \right) = \frac{{n\left( {AB} \right)}}{{n\left( \Omega \right)}} = \frac{2}{{24}} = \frac{1}{{12}}$.

c) Ta có $A = \left\{ {\left( {2;6} \right);\left( {3;5} \right);\left( {4;4} \right)} \right\}$ nên số kết quả thuận lợi cho $A$ là $n\left( A \right) = 3$.

Xác suất của biến cố $A$ là $P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{3}{{24}} = \frac{1}{8}$.

Biến cố đối của biến cố $B$ là \[\overline B \] : “Tích các số ghi trên hai viên bi là số lẻ”. Biến cố \[\overline B \] xảy ra khi cả hai viên bi lấy ra đều ghi số lẻ. Do đó, số kêt quả thuận lợi cho biến cố \[\overline B \] là $n\left( {\overline B } \right) = 2.3 = 6$.

Xác suất của biến cố \[\overline B \] là $P\left( {\overline B } \right) = \frac{{n\left( {\overline B } \right)}}{{n\left( \Omega \right)}} = \frac{6}{{24}} = \frac{1}{4}$.

Xác suất của biến cố $B$ là $P\left( B \right) = 1 – P\left( {\overline B } \right) = \frac{3}{4}$.

d) Ta có $P\left( A \right)P\left( B \right) = \frac{1}{8} \cdot \frac{3}{4} = \frac{3}{{32}}$.

Suy ra $P\left( {AB} \right) \ne P\left( A \right)P\left( B \right)$ nên $A$ và $B$ không là hai biến cố độc lập.

e) Gọi $C$ là biến cố “Cả 2 viên bi lấy ra đều ghi số 2 “. Biến cố $C$ xung khắc với $A$ nhưng không xung khắc với $B$.

Câu 18. Một hộp chứa 99 tấm thẻ cùng loại được đánh số từ 1 đến 99 . Chọn ra ngẫu nhiên 1 thẻ từ hộp. Gọi $A$ là biến cố “Số ghi trên thẻ được chọn chia hết cho 2 “, $B$ là biến cố “Số ghi trên thẻ được chọn chia hết cho 5.

a) Bình nói $AB$ là biến cố “Số ghi trên thẻ được chọn chia hết cho 10 “. Bình nói như vậy đúng hay sai? Tại sao?

b) Hai biến cố $A$ và $B$ có độc lập không? Tại sao?

Lời giải

a) Bình nói đúng. Vì nếu số ghi trên thẻ vừa chia hết cho 2 , vừa chia hết cho 5 khi và chỉ khi nó chia hết cho 10 .

b) Từ 1 đến 99 có 49 số chia hết cho 2 nên xác suất của biến cố $A$ là

$P\left( A \right) = \frac{{49}}{{99}}$.

Từ 1 đến 99 có 19 số chia hết cho 5 nên xác suất của biến cố $B$ là

$P\left( B \right) = \frac{{19}}{{99}}$.

Từ 1 đến 99 có 9 số chia hết cho 10 nên xác suất của biến cố $AB$ là

$P\left( {AB} \right) = \frac{9}{{99}} = \frac{1}{{11}}$.

Vậy $P\left( A \right)P\left( B \right) \ne P\left( {AB} \right)$. Do đó, hai biến cố $A$ và $B$ là không độc lập.

Câu 19. Cho $A$ và $B$ là hai biến cố độc lập.

a) Biết $P(A) = 0,3$ và $P(B) = 0,7$. Hãy tính xác suất của các biến cố $AB,\bar AB$ và $\bar A\bar B$.

b) Biết $P(A) = 0,8$ và $P(AB) = 0,4$. Hãy tính xác suất của các biến cố $B,\bar AB$ và $\bar A\bar B$.

Lời giải

a) Do $A$ và $B$ là hai biến cố độc lập nên xác suất của biến cố $A B$ là $P(AB) = P(A)P(B) = 0,3 \cdot 0,7 = 0,21$.

Vì $\bar A$ là biến cố đối của $A$ nên $P(\bar A) = 1 – P(A) = 0,7$.

Do $\bar A$ và $B$ là hai biến cố độc lập nên xác suất của biến cố $\bar AB$ là $P(\bar AB) = P(\bar A)P(B) = 0,7 \cdot 0,7 = 0,49$.

Vì $\bar B$ là biến cố đối của $B$ nên $P(\bar B) = 1 – P(B) = 0,3$.

Do $\bar A$ và $\bar B$ là hai biến cố độc lập nên xác suất của biến cố $\bar A\bar B$ là $P(\bar A\bar B) = P(\bar A)P(\bar B) = 0,7.0,3 = 0,21$.

b) Do $A$ và $B$ là hai biến cố độc lập nên $P(B) = \frac{{P(AB)}}{{P(A)}} = \frac{{0,4}}{{0,8}} = 0,5$.

Vì $\bar A$ là biến cố đối của $A$ nên $P(\bar A) = 1 – P(A) = 0,2$.

Do $\bar A$ và $B$ là hai biến cố độc lập nên xác suất của biến cố $\bar AB$ là $P(\bar AB) = P(\bar A)P(B) = 0,2 \cdot 0,5 = 0,1$

Vì $\bar B$ là biến cố đối của $B$ nên $P(\bar B) = 1 – P(B) = 0,5$.

Do $\bar A$ và $\bar B$ là hai biến cố độc lập nên xác suất của biến cố $\bar A\bar B$ là $P(\bar A\bar B) = P(\bar A)P(\bar B) = 0,2.0,5 = 0,1$.

Câu 20. Minh gieo 1 hạt đậu và 1 hạt ngô. Xác suất nảy mầm của hạt đậu và hạt ngô lần lượt là 0,7 và 0,6 . Biết rằng sự nảy mầm của hai hạt này là độc lập. Sử dụng sơ đồ hình cây, tính xác suất của các biến cố:

a) “Cả 2 hạt đều nảy mầm”;

b) “Cả 2 hạt đều không nảy mầm”;

c) “Hạt đậu nảy mầm, hạt ngô không nảy mầm”.

Lời giải

Ta có sơ đồ hình cây như sau:

a) Xác suất cả 2 hạt đều nảy mầm là 0,42 .

b) Xác suất cả 2 hạt đều không nảy mầm là 0,12 .

c) Xác suất hạt đậu nảy mầm, hạt ngô không nảy mầm là 0,28 .

Câu 21. Một hộp chứa 4 bút xanh, 1 bút đen và 1 bút đỏ. Các cây bút có cùng kích thước và khối lượng. Chọn ra ngẫu nhiên 3 cây bút từ hộp. Gọi $A$ là biến cố “Có 1 cây bút đỏ trong 3 cây bút được lấy ra”. Gọi $B$ là biến cố “Có 1 cây bút đen trong 3 cây bút được lấy ra”.

a) Hãy tìm một biến cố xung khắc với biến cố $A$ nhưng không xung khắc với biến cố $B$.

b) Tính xác suất của các biến cố $A,B$ và $AB$.

Lời giải

a) Biến cố “Lấy ra được 1 bút đen và 2 bút xanh” xung khắc với biến cố $A$ nhưng không xung khắc với biến cố $B$.

b) $P\left( A \right) = P\left( B \right) = \frac{{C_1^1C_5^2}}{{C_6^3}} = 0,5$.

$AB$ là biến cố “Lấy ra được 1 bút xanh, 1 bút đen và 1 bút đỏ.

Do đó $P\left( {AB} \right) = \frac{{C_4^1C_1^1C_1^1}}{{C_6^3}} = 0,2$.

Câu 22. Hộp thứ nhất chứa 4 viên bi xanh và 1 viên bi đỏ. Hộp thứ hai chứa 1 viên bi xanh và 3 viên bi đỏ. Các viên bi có cùng kích thước và khối lượng. Lấy ra ngẫu nhiên từ mỗi hộp 2 viên bi.

Gọi $A$ là biến cố “Cả 2 viên bi lấy ra từ hộp thứ nhất có cùng màu”; $B$ là biến cố “Cả 2 viên bi lấy ra từ hộp thứ hai có cùng màu”.

a) Minh nói $AB$ là biến cố “Trong 4 viên bi lấy ra có 2 viên bi xanh, 2 viên bi đỏ”. Minh nói đúng hay sai? Tại sao?

b) So sánh $P\left( {AB} \right)$ với $P\left( A \right)P\left( B \right)$.

c) Hãy tìm một biến cố khác rỗng, xung khắc với cả biến cố $A$ và biến cố $B$.

Lời giải

a) Minh nói sai vì nếu lấy ra từ hộp thứ nhất 1 viên bi xanh, 1 viên bi đỏ; lấy ra từ hộp thứ hai 1 viên bi xanh, 1 viên bi đỏ thì trong 4 viên bi lấy ra có 2 viên bi xanh, 2 viên bi đỏ nhưng cả hai biến cố $A$ và $B$ đều không xảy ra.

b) $P\left( A \right) = \frac{{C_4^2C_4^2}}{{C_5^2C_4^2}} = 0,6;P\left( B \right) = \frac{{C_5^2C_3^2}}{{C_5^2C_4^2}} = 0,5;$

$P\left( {AB} \right) = \frac{{C_4^2C_3^2}}{{C_5^2C_4^2}} = 0,3$.

Vậy $P\left( A \right)P\left( B \right) = P\left( {AB} \right)$.

c) Gọi $C$ là biến cố “Lấy ra từ mỗi hộp 1 viên bi xanh, 1 viên bi đỏ”. Biến cố $C$ xung khắc với cả hai biến cố $A$ và $B$.

Câu 23. Một hộp chứa 50 tấm thẻ cùng loại được đánh số từ 1 đến 50 . Chọn ra ngẫu nhiên 1 thẻ từ hộp. Gọi $A$ là biến cố “Số ghi trên thẻ được chọn chia hết cho 4”, $B$ là biến cố “Số ghi trên thẻ được chọn chia hết cho 6”.

a) Giang nói $AB$ là biến cố “Số ghi trên thẻ được chọn chia hết cho 24 “. Giang nói như vậy đúng hay sai? Tại sao?

b) Hai biến cố $A$ và $B$ có độc lập không? Tại sao?

Lời giải

a) Giang nói sai vì nếu lấy được thẻ ghi số 12 thì cả hai biến cố $A$ và $B$ xảy ra nhưng 12 không chia hết cho 24.

b) $P\left( A \right) = \frac{{12}}{{50}};P\left( B \right) = \frac{8}{{50}}$.

$AB$ là biến cố “Số ghi trên thẻ được chọn chia hết cho 12 ” nên $P\left( {AB} \right) = \frac{4}{{50}}$. Vì $P\left( A \right)P\left( B \right) \ne P\left( {AB} \right)$ nên $A$ và $B$ không là hai biến cố độc lập.

Câu 24. Cho $A$ và $B$ là hai biến cố độc lập.

a) Biết $P(\bar A) = 0,4$ và $P(B) = 0,1$. Hãy tính xác suất của các biến cố $AB,\bar AB$ và $\bar A\bar B$.

b) Biết $P(A) + P(B) = 0,8$ và $P(AB) = 0,16$. Hãy tính xác suất của các biến cố $B,\bar AB$ và $\bar A\bar B$.

Lời giải

a) $P(A) = 1 – P(\bar A) = 0,6;P(\bar B) = 1 – P(B) = 0,9$.

Do $A$ và $B$ là hai biến cố độc lập nên $P(AB) = P(A)P(B) = 0,06$.

Do $\bar A$ và $B$ là hai biến cố độc lập nên $P(\bar AB) = P(\bar A)P(B) = 0,04$.

Do $\bar A$ và $\bar B$ là hai biến cố độc lập nên $P(\bar A\bar B) = P(\bar A)P(\bar B) = 0,36$.

b) $P(A) + P(B) = 0,8$ và $P(AB) = P(A)P(B) = 0,16$. Suy ra $P(A) = P(B) = 0,4$.

$P(\bar A) = 1 – P(A) = 0,6;P(\bar B) = 1 – P(B) = 0,6$.

Do $\bar A$ và $B$ là hai biến cố độc lập nên $P(\bar AB) = P(\bar A)P(B) = 0,24$.

Do $\bar A$ và $\bar B$ là hai biến cố độc lập nên $P(\bar A\bar B) = P(\bar A)P(\bar B) = 0,36$.

Câu 25. Minh mua 2 bóng đèn. Theo một kết quả thống kê, tỉ lệ bị hỏng trong năm đầu sử dụng của loại bóng đèn Minh mua là $23\% $. Tính xác suất của các biến cố:

$A$ : “Cả hai bóng đèn đều bị hỏng trong năm đầu sử dụng”;

$B$ : “Cả hai bóng đèn đều không bị hỏng trong năm đầu sử dụng”.

Lời giải

Do tỉ lệ bóng bị hỏng trong năm đầu sử dụng là $23\% $ nên xác suất 1 bóng bị hỏng trong năm đầu sử dụng là 0,23 .

$P\left( A \right) = 0,23 \cdot 0,23 = 0,0529;P\left( B \right) = \left( {1 – 0,23} \right)\left( {1 – 0,23} \right) = 0,5929$.