40 Câu Trắc Nghiệm Cộng Xác Suất Theo Từng Dạng Giải Chi Tiết

40 câu trắc nghiệm cộng xác suất theo từng dạng giải chi tiết được soạn dưới dạng file word và PDF gồm 4 trang. Các bạn xem và tải về ở dưới.

I. PHƯƠNG PHÁP

1. Công thức cộng xác suất cho hai biến cố xung khắc

a. Biến cố xung khắc

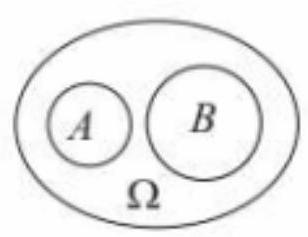
Biến cố $A$ và biến cố $B$ được gọi là xung khắc nếu $A$ và $B$ không đồng thời xảy ra.

Hai biến cố $A$ và $B$ là xung khắc khi và chỉ khi $A \cap B = \emptyset $

b. Công thức cộng xác suất cho hai biến cố xung khắc

Cho hai biến cố xung khắc $A$ và $B$. Khi đó: $P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right)$

Chú ý:

• Nếu các biến cố ${A_1},{A_2},{A_3}, \ldots ,{A_k}$ xung khắc nhau thì

$P\left( {{A_1} \cup {A_2} \cup \ldots \cup {A_k}} \right) = P\left( {{A_1}} \right) + P\left( {{A_2}} \right) + \ldots + P\left( {{A_k}} \right)$

• Xác suất của biến cố $\overline A $ của biến cố $A$ là : $P\left( {\overline A } \right) = 1 – P\left( A \right)$

2. Công thức cộng xác suất

Cho hai biến cố $A$ và $B$. Khi đó, ta có:

$P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) – P\left( {AB} \right)$

Công thức này được gọi là công thức cộng xác suất

II. TRẮC NGHIỆM

Câu 1. Cho $A,B$ là hai biến cố xung khắc. Đẳng thức nào sau đây đúng?
A. $P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right)$.
B. $P\left( {A \cup B} \right) = P\left( A \right) \cdot P\left( B \right)$.
C. $P\left( {A \cup B} \right) = P\left( A \right) – P\left( B \right)$.
D. $P\left( {A \cap B} \right) = P\left( A \right) + P\left( B \right)$.

Lời giải

Chọn A

Ta có $P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) – P\left( {A \cap B} \right)$.

Vì $A,B$ là hai biến cố xung khắc nên $A \cap B = \emptyset $. Từ đó suy ra $P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right)$.

Câu 2. Cho $A$ và $B$ là hai biến cố xung khắc. Mệnh đề nào dưới đây đúng?
A. $P\left( A \right) + P\left( B \right) = 1$.
B. Hai biến cố $A$ và $B$ không đồng thời xảy ra.
C. Hai biến cố $A$ và $B$ đồng thời xảy ra.
D. $P\left( A \right) + P\left( B \right) < 1$.

Lời giải

Chọn B

Vì $A$ và $B$ là hai biến cố xung khắc nên hai biến cố này không đồng thời xảy ra.

Câu 3. Cho $P\left( A \right) = \frac{1}{4},P\left( {A \cup B} \right) = \frac{1}{2}$. Biết $A,B$ là hai biến cố xung khắc, thì $P\left( B \right)$ bằng:
A. $\frac{1}{3}$.
B. $\frac{1}{8}$.
C. $\frac{1}{4}$.
D. $\frac{3}{4}$.

Lời giải

Chọn C.

$A,B$ là hai biến cố xung khắc: $P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) \Leftrightarrow P\left( B \right) = \frac{1}{4}$.
Câu 4. Cho $A,B$ là hai biến cố xung khắc. Biết $P\left( A \right) = \frac{1}{5},P\left( {A \cup B} \right) = \frac{1}{3}$. Tính $P\left( B \right)$
A. $\frac{3}{5}$.
B. $\frac{8}{{15}}$.
C. $\frac{2}{{15}}$.
D. $\frac{1}{{15}}$.
Lời giải
Chọn C.
$A,B$ là hai biến cố xung khắc
$P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) \Rightarrow P\left( B \right) = \frac{1}{3} – \frac{1}{5} = \frac{2}{{15}}$

Câu 5. Cho $A,B$ là hai biến cố xung khắc. Biết $P\left( A \right) = \frac{1}{3},P\left( B \right) = \frac{1}{4}$. Tính $P\left( {A \cup B} \right)$.
A. $\frac{7}{{12}}$.
B. $\frac{1}{{12}}$.
C. $\frac{1}{7}$.
D. $\frac{1}{2}$.

Lời giải

Chọn A

$P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) = \frac{7}{{12}}$.

Câu 6. Cho $P\left( A \right) = \frac{1}{4},P\left( {A \cup B} \right) = \frac{1}{2}$. Biết $A,B$ là hai biến cố độc lập, thì $P\left( B \right)$ bằng:
A. $\frac{1}{3}$.
B. $\frac{1}{8}$.
C. $\frac{1}{4}$.
D. $\frac{3}{4}$.

Lời giải

Chọn A.

Ta có $A,B$ là biến cố độc lập nên ta có

$P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) – P\left( {A \cap B} \right)$

$ \Leftrightarrow P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) – P\left( A \right) \cdot P\left( B \right)$

$ \Leftrightarrow \frac{1}{2} = \frac{1}{4} + P\left( B \right) – \frac{1}{4} \cdot P\left( B \right)$

$ \Leftrightarrow P\left( B \right) = \frac{1}{3}$

Vậy $P\left( B \right) = \frac{1}{3}$

Câu 7. $A,B$ là hai biến cố độc lập. $P\left( A \right) = 0,5.P\left( {A \cap B} \right) = 0,2$. Xác suất $P\left( {A \cup B} \right)$ bằng:
A. 0,3 .
B. 0,5
C. 0,6.
D. 0,7

Lời giải

Chọn D.

$A,B$ là hai biến cố độc lập nên: $P\left( {A \cap B} \right) = P\left( A \right) \cdot P\left( B \right) \Leftrightarrow P\left( B \right) = 0,4$

$P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) – P\left( {A \cap B} \right) = 0,7$.

Câu 8. Cho $A,B$ là hai biến cố. Biết $P\left( A \right) = \frac{1}{2},P\left( B \right) = \frac{3}{4} \cdot P\left( {A \cap B} \right) = \frac{1}{4}$. Biến cố $A \cup B$ là biến Cố
A. Sơ đẳng.
B. Chắc chắn.
C. Không xảy ra.
D. Có xác suất bằng $\frac{1}{8}$.

Lời giải

Chọn B.

$A,B$ là hai biến cố bất kỳ ta luôn có : $P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) – P\left( {A \cap B} \right) = \frac{1}{2} + \frac{3}{4} – \frac{1}{4} = 1$

Vậy $A \cup B$ là biến cố chắc chắn

Câu 9. Một xạ thủ bắn liên tục 4 phát đạn vào bia. Gọi ${A_k}$ là các biến cố “ xạ thủ bắn trúng lần thứ $k$ ” với $k = 1,2,3,4$. Gọi $B$ là các biến cố “Bắn trúng bia ít nhất một lần”. Hãy biểu diễn các biến cố $B$ sau qua các biến cố ${A_1},{A_2},{A_3},{A_4}$.
A. $B = {A_1} \cup {A_2} \cup {A_3} \cap {A_4}$
B. $B = {A_1} \cap {A_2} \cup {A_3} \cup {A_4}$
C. $B = {A_1} \cup {A_2} \cup {A_3} \cup {A_4}$
D. $B = {A_1} \cup {A_2} \cap {A_3} \cup {A_4}$

Lời giải

Chọn C.

Ta có: $\overline {{A_k}} $ là biến cố lần thứ $k\left( {k = 1,2,3,4} \right)$ bắn không trúng bia.

Do đó: $B = {A_1} \cup {A_2} \cup {A_3} \cup {A_4}$

Câu 10. Một xạ thủ bắn liên tục 4 phát đạn vào bia. Gọi ${A_k}$ là các biến cố “ xạ thủ bắn trúng lần thứ $k$ ” với $k = 1,2,3,4$. Gọi $C$ là các biến cố “ Chỉ bắn trúng bia hai lần”. Hãy biểu diễn các biến cố $C$ sau qua các biến cố ${A_1},{A_2},{A_3},{A_4}$.
A. $C = {A_i} \cup {A_j} \cap \overline {{A_k}} \cap \overline {{A_m}} ,i,j,k,m \in \left\{ {1,2,3,4} \right\}$ và đôi một khác nhau.
B. $C = {A_i} \cup {A_j} \cup \overline {{A_k}} \cup \overline {{A_m}} ,i,j,k,m \in \left\{ {1,2,3,4} \right\}$ và đôi một khác nhau.
C. $C = {A_i} \cap {A_j} \cup \overline {{A_k}} \cup \overline {{A_m}} ,i,j,k,m \in \left\{ {1,2,3,4} \right\}$ và đôi một khác nhau.

D. $C = {A_i} \cap {A_j} \cap \overline {{A_k}} \cap \overline {{A_m}} ,i,j,k,m \in \left\{ {1,2,3,4} \right\}$ và đôi một khác nhau.

Lời giải

Chọn D.

Ta có: $\overline {{A_k}} $ là biến cố lần thứ $k\left( {k = 1,2,3,4} \right)$ bắn không trúng bia.

Do đó:

$C = {A_i} \cap {A_j} \cap \overline {{A_k}} \cap \overline {{A_m}} $ với $i,j,k,m \in \left\{ {1,2,3,4} \right\}$ và đôi một khác nhau.

Câu 11. Hai cầu thủ sút phạt đền. Mỗi nười đá 1 lần với xác suất làm bàm tương ứng là 0,8 và 0,7 . Tính xác suất để có ít nhất 1 cầu thủ làm bàn
A. 0,42
B. 0,94
C. 0,234
D. 0,9

Lời giải

Chọn B.

Gọi $A$ là biến cố cầu thủ thứ nhất làm bàn

$B$ là biến cố cầu thủ thứ hai làm bàn

$X$ là biến cố ít nhất 1 trong hai cầu thủ làm bàn

Ta có: $X = \left( {A \cap \overline B } \right) \cup \left( {\overline A \cap B} \right) \cup \left( {A \cap B} \right)$

$ \Rightarrow P\left( X \right) = P\left( A \right) \cdot P\left( {\overline B } \right) + P\left( B \right) \cdot P\left( {\overline A } \right) + P\left( A \right) \cdot P\left( B \right) = 0,94$.

Câu 12. Một con súc sắc không đồng chất sao cho mặt bốn chấm xuất hiện nhiều gấp 3 lần mặt khác, các mặt còn lại đồng khả năng. Tìm xác suất để xuất hiện một mặt chẵn
A. $\frac{}5{8}$
B. $\frac{3}{8}$
C. $\frac{7}{8}$
D. $\frac{1}{8}$

Lời giải

Chọn A.

Gọi ${A_i}$ là biến cố xuất hiện mặt $i$ chấm $\left( {i = 1,2,3,4,5,6} \right)$

Ta có $P({A_1}) = P({A_2}) = P({A_3}) = P({A_5}) = P({A_6}) = \frac{1}{3}P({A_4}) = x$

Do $\sum\nolimits_{k = 1}^6 {P({A_k}} ) = 1 \Rightarrow 5x + 3x = 1 \Rightarrow x = \frac{1}{8}$

Gọi $A$ là biến cố xuất hiện mặt chẵn, suy ra $A = {A_2} \cup {A_4} \cup {A_6}$

Vì cá biến cố ${A_i}$ xung khắc nên:

$P\left( A \right) = P\left( {{A_2}} \right) + P\left( {{A_4}} \right) + P\left( {{A_6}} \right) = \frac{1}{8} + \frac{3}{8} + \frac{1}{8} = \frac{5}{8}$.

Câu 13. Gieo một con xúc sắc 4 lần. Tìm xác suất của biến cố $A$ : “ Mặt 3 chấm xuất hiện đúng một lần”.
A. $P\left( A \right) = \frac{5}{{24}}$
B. $P\left( A \right) = \frac{5}{{32}}$
C. $P\left( A \right) = \frac{5}{{324}}$
D. $P\left( A \right) = \frac{5}{{34}}$

Lời giải

Chọn C.

Gọi ${B_i}$ là biến cố “ mặt 3 chấm xuất hiện lần thứ $i$ ” với $i = 1,2,3,4$

Khi đó: $\overline {{B_i}} $ là biến cố “Mặt 3 chấm không xuất hiện lần thứ i”

Ta có: $A = \overline {{B_1}} \cdot {B_2} \cdot {B_3} \cdot {B_4} \cup {B_1} \cdot \overline {{B_2}} \cdot {B_3} \cdot {B_4} \cup {B_1} \cdot {B_2} \cdot \overline {{B_3}} \cdot {B_4} \cup {B_1} \cdot {B_2} \cdot {B_3} \cdot \overline {{B_4}} $

Suy ra $P\left( A \right) = P\left( {\overline {{B_1}} } \right)P\left( {{B_2}} \right)P\left( {{B_3}} \right)P\left( {{B_4}} \right) + P\left( {{B_1}} \right)P\left( {\overline {{B_2}} } \right)P\left( {{B_3}} \right)P\left( {{B_4}} \right)$

$ + P\left( {{B_1}} \right)P\left( {{B_2}} \right)P\left( {\overline {{B_3}} } \right)P\left( {{B_4}} \right) + P\left( {{B_1}} \right)P\left( {{B_2}} \right)P\left( {{B_3}} \right)P\left( {\overline {{B_4}} } \right)$

Mà $P\left( {{B_i}} \right) = \frac{1}{6},P\left( {\overline {{B_i}} } \right) = \frac{}5{6}$.

Do đó: $P\left( A \right) = 4 \cdot {\left( {\frac{1}{6}} \right)^3} \cdot \frac{}5{6} = \frac{}5{{324}}$.

Câu 14. Một hộp đựng 4 viên bi xanh, 3 viên bi đỏ và 2 viên bi vàng. Chọn ngẫu nhiên 2 viên bi, tính xác suất để chọn được 2 viên bi cùng màu.
A. $\frac{7}{{18}}$
B. $\frac{}5{8}$
C. $\frac{}5{{18}}$
D. $\frac{{11}}{{18}}$

Lời giải

Chọn C.

Gọi $A$ là biến cố “Chọn được 2 viên bi xanh”;

$B$ là biến cố “Chọn được 2 viên bi đỏ”,

$C$ là biến cố “Chọn được 2 viên bi vàng”

$X$ là biến cố “Chọn được 2 viên bi cùng màu”.

Ta có $X = A \cup B \cup C$ và các biến cố $A,B,C$ đôi một xung khắc.

Do đó, ta có: $P\left( X \right) = P\left( A \right) + P\left( B \right) + P\left( C \right)$.

Mà: $P\left( A \right) = \frac{{C_4^2}}{{C_9^2}} = \frac{1}{6};P\left( B \right) = \frac{{C_3^2}}{{C_9^2}} = \frac{1}{{12}};P\left( C \right) = \frac{{C_2^2}}{{C_9^2}} = \frac{1}{{36}}$

Vậy $P\left( X \right) = \frac{1}{6} + \frac{1}{{12}} + \frac{1}{{36}} = \frac{5}{{18}}$.

Câu 15. Một hộp đựng 40 viên bi trong đó có 20 viên bi đỏ, 10 viên bi xanh, 6 viên bi vàng, 4 viên bi trắng. Lấy ngẫu nhiên 2 bi, tính xác suất biến cố $A$ : “2 viên bi cùng màu”.
A. $P\left( A \right) = \frac{4}{{195}}$
B. $P\left( A \right) = \frac{6}{{195}}$
C. $P\left( A \right) = \frac{4}{{15}}$
D. $P\left( A \right) = \frac{{64}}{{195}}$

Lời giải

Ta có: $\left| \right| = C_{40}^2$

Gọi các biến cố: D: “lấy được 2 bi viên đỏ” ta có: $\left| {{_D}} \right| = C_{20}^2 = 190$;

X: “lấy được 2 bi viên xanh” ta có: $\left| {{_X}} \right| = C_{10}^2 = 45$;

V: “lấy được 2 bi viên vàng” ta có: $\left| {{_V}} \right| = C_6^2 = 15$;

T: “lấy được 2 bi màu trắng” ta có: $\left| {{_T}} \right| = C_4^2 = 6$.

Ta có $D, X, V, T$ là các biến cố đôi một xung khắc và $A = D \cup X \cup V \cup T$

$P\left( A \right) = P\left( \right) + P\left( X \right) + P\left( V \right) + P\left( T \right) = \frac{{256}}{{C_{40}^2}} = \frac{{64}}{{195}}$.

Câu 16. Một hộp đựng 10 viên bi trong đó có 4 viên bi đỏ, 3 viên bi xanh, 2 viên bi vàng, 1 viên bi trắng. Lấy ngẫu nhiên 2 bi tính xác suất biến cố C: “2 viên bi cùng màu”
A. $P\left( C \right) = \frac{1}{9}$
B. $P\left( C \right) = \frac{2}{9}$
C. $P\left( C \right) = \frac{4}{9}$
D. $P\left( C \right) = \frac{1}{3}$

Lời giải

Chọn B.

Ta có: $n\left( \right) = C_{10}^2$

Gọi các biến cố: D: “lấy được 2 viên đỏ”

X: “lấy được 2 viên xanh”

V: “lấy được 2 viên vàng”

Ta có $D, X, V$ là các biến cố đôi một xung khắc và $C = D \cup X \cup V$

$P\left( C \right) = P\left( \right) + P\left( X \right) + P\left( V \right) = \frac{2}{5 }+ \frac{{C_3^2}}{{45}} + \frac{1}{{15}} = \frac{{10}}{{45}} = \frac{2}{9}$.

Câu 17. Chọn ngẫu nhiên một vé xổ số có 5 chữ số được lập từ các chữ số từ 0 đến 9 . Tính xác suất của biến cố X: “lấy được vé không có chữ số 2 hoặc chữ số 7 ”
A. $P\left( X \right) = 0,8533$
B. $P\left( X \right) = 0,85314$
C. $P\left( X \right) = 0,8545$
D. $P\left( X \right) = 0,853124$

Lời giải

Chọn A.

Ta có $n(\Omega) = {10^5}$

Gọi A: “lấy được vé không có chữ số 2”

B: “lấy được vé số không có chữ số 7”

Suy ra $n\left( A \right) = n\left( B \right) = {9^5} \Rightarrow P\left( A \right) = P\left( B \right) = {(0,9)^5}$

Số vé số trên đó không có chữ số 2 và 7 là: ${8^5}$, suy ra $n\left( {A \cap B} \right) = {8^5}$

$ \Rightarrow P\left( {A \cap B} \right) = \frac{{n\left( {A \cap B} \right)}}{{n\left( {\text{\Omega }} \right)}} = {(0,8)^5}$

Do $X = A \cup B \Rightarrow P\left( X \right) = P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) – P\left( {A \cap B} \right) = 0,8533$.

Câu 18. Gieo ngẫu nhiên một con xúc xắc 6 lần. Tính xác suất để một số lớn hơn hay bằng 5 xuất hiện ít nhất 5 lần trong 6 lần gieo
A. $\frac{{23}}{{729}}$
B. $\frac{{13}}{{79}}$
C. $\frac{{13}}{{29}}$
D. $\frac{{13}}{{729}}$

Lời giải

Chọn D.

Gọi ${\text{A}}$ là biến cố một số lớn hơn hay bẳng 5 chấm trong mỗi lần gieo.A xảy ra,con xúc xắc xuất hiện mặt 5,chấm hoặc 6 chấm ta có $P\left( A \right) = \frac{2}{6} = \frac{1}{3}$.

Trong 6 lần gieo xác suất để biến cố ${\text{A}}$ xảy ra đúng 6 lần $P\left( {A \cdot A \cdot A \cdot A \cdot A \cdot A} \right) = {\left( {\frac{1}{3}} \right)^6}$

Xác suất để được đúng 5 lần xuất hiện ${\text{A}}$ và 1 lần không xuất hiện ${\text{A}}$ theo một thứ tự nào đó ${\left( {\frac{1}{3}} \right)^5} \cdot \frac{2}{3}$

Vì có 6 cách để biến cố này xuất hiện : $6 \cdot {\left( {\frac{1}{3}} \right)^5} \cdot \frac{2}{3} = \frac{{12}}{{729}}$

Vậy xác xuất để A xuất hiện ít nhất 5 lần là $\frac{{12}}{{729}} + {\left( {\frac{1}{3}} \right)^6} = \frac{{13}}{{729}}$.

Câu 19. Một bài trắc nghiệm có 10 câu hỏi, mỗi câu hỏi có 4 phương án lựa chọn trong đó có 1 đáp án đúng. Giả sử mỗi câu trả lời đúng được 5 điểm và mỗi câu trả lời sai bị trừ đi 2 điểm. Một học sinh không học bài nên đánh hú họa một câu trả lời. Tìm xác suất để học sinh này nhận điểm dưới 1.
A. $P\left( A \right) = 0,7124$
B. $P\left( A \right) = 0,7759$
C. $P\left( A \right) = 0,7336$
D. $P\left( A \right) = 0,783$

Lời giải

Chọn B.

Ta có xác suất để học sinh trả lời câu đúng là $\frac{1}{4}$ và xác suất trả lời câu sai là $\frac{3}{4}$.

Gọi $x$ là số câu trả lời đúng, khi đó số câu trả lời sai là $10 – x$

Số điểm học sinh này đạt được là : $4x – 2\left( {10 – x} \right) = 6x – 20$

Nên học sinh này nhận điểm dưới 1 khi $6x – 20 < 1 \Leftrightarrow x < \frac{{21}}{6}$

Mà $x$ nguyên nên $x$ nhận các giá trị: 0,1,2,3 .

Gọi ${A_i}\left( {i = 0,1,2,3} \right)$ là biến cố: “Học sinh trả lời đúng $i$ câu”

A là biến cố: “Học sinh nhận điểm dưới 1”

Suy ra: $A = {A_0} \cup {A_1} \cup {A_2} \cup {A_3}$ và $P\left( A \right) = P\left( {{A_0}} \right) + P\left( {{A_1}} \right) + P\left( {{A_2}} \right) + P\left( {{A_3}} \right)$

Mà: $P\left( {{A_i}} \right) = C_{10}^i \cdot {\left( {\frac{1}{4}} \right)^i}{\left( {\frac{3}{4}} \right)^{10 – i}}$ nên .

Câu 20. Một chiếc ôtô với hai động cơ độc lập đang gặp trục trặc kĩ thuật. Xác suất để động cơ 1 gặp trục trặc là 0,3. Xác suất để động cơ 2 gặp trục trặc là 0,4 . Biết rằng xe chỉ không thể chạy được khi cả hai động cơ bị hỏng. Tính xác suất để xe đi được.
A. 0,12
B. 0,7
C. 0,88
D.0,75

Lời giải

Chọn C

• Gọi A là biến cố “động cơ 1 bị hỏng” $ \Rightarrow {\text{P}}\left( {\text{A}} \right) = 0,3$
• Gọi $B$ là biến cố “động cơ 2 bị hỏng” $ \Rightarrow P\left( B \right) = 0,4$

Suy ra $AB$ là biến cố “cả hai động cơ bị hỏng” hay “ xe không chạy được nữa”.

• Do hai động cơ hoạt động độc lập nên ${\text{A}}$ và ${\text{B}}$ là hai biến cố độc lập.
• Áp dụng quy tắc nhân xác suất ta được xác suất để xe không đi được nữa là

${\text{P}}\left( {{\text{AB}}} \right) = {\text{P}}\left( {\text{A}} \right) \cdot {\text{P}}\left( {\text{B}} \right) = 0,3 \cdot 0,4 = 0,12$

Vậy xác suất để xe đi được là: $1 – 0,12 = 0,88$

Câu 21. Ba xạ thủ cùng bắn vào một tấm bia, xác suất trúng đích lần lượt là 0,$5;0,6$ và 0,7 . Xác suất để có đúng 2 người bắn trúng bia là:
A. 0,29 .
B. 0,44 .
C. 0,21 .
D. 0,79 .

Lời giải

Chọn B

Gọi $A$ là biến cố người thứ nhất bắn trúng.

$\overline A $ là biến cố người thứ nhất bắn trượt.

Vậy $P\left( A \right) = 0,5;P\left( {\overline A } \right) = 0,5$.

Gọi $B$ là biến cố người thứ hai bắn trúng.

Gọi $C$ là biến cố người thứ nhất bắn trúng.

Tương tự có $P\left( B \right) = 0,6;P\left( {\overline B } \right) = 0,4;P\left( C \right) = 0,7;P\left( {\overline C } \right) = 0,4$.

Để hai người bắn trúng bia có các khả năng sau xảy ra:

TH1. Người thứ nhất và thứ hai bắn trúng, người thứ ba bắn trượt.

$P\left( A \right) \cdot P\left( B \right) \cdot P\left( {\overline C } \right) = 0,5 \cdot 0,6 \cdot 0,3 = 0,09$.

TH2: Người thứ nhất và thứ ba bắn trúng, người thứ hai bắn trượt.

$P\left( A \right) \cdot P\left( {\overline B } \right) \cdot P\left( C \right) = 0,5 \cdot 0,4 \cdot 0,7 = 0,14$.

TH3: Người thứ hai và thứ ba bắn trúng, người thứ nhất bắn trượt.

$P\left( {\overline A } \right) \cdot P\left( B \right) \cdot P\left( C \right) = 0,5 \cdot 0,6 \cdot 0,7 = 0,21$.

Vậy xác suất để hai người bắn trúng bia là: 0,09+0,14+0, 21=0, 44 .

Lời giải

Câu 22. Trong phòng làm việc có hai máy tính hoạt động độc lập với nhau, khả năng hoạt động tốt trong ngày của hai máy này tương ứng là $75$ và $85$. Xác suất để có đúng một máy hoạt động không tốt trong ngày là
A. 0,425 .
B. 0,325 .
C. 0,625 .
D. 0,525 .

Lời giải

Chọn B

Gọi $A,B$ lần lượt là biến cố “khả năng hoạt động tốt trong ngày của hai máy đã cho”

Suy ra $H = A\overline B \cup \overline A B$ là biến cố “có đúng một máy hoạt động không tốt trong ngày”

Ta có $P\left( A \right) = 0,75,P\left( {\overline A } \right) = 0,25,P\left( B \right) = 0,85,P\left( {\overline B } \right) = 0,15$

Vậy $P\left( H \right) = P\left( A \right) \cdot P\left( {\overline B } \right) + P\left( {\overline A } \right) \cdot P\left( B \right) = \left( {0,7}5 \right) \cdot \left( {0,1}5 \right) + \left( {0,2}5 \right) \cdot \left( {0,8}5 \right) = 0,325$.

Câu 23. Một con súc sắc không cân đối, có đặc điểm mặt sáu chấm xuất hiện nhiều gấp hai lần các mặt còn lại. Gieo con súc sắc đó hai lần. Xác suất để tổng số chấm trên mặt xuất hiện trong hai lần gieo lớn hơn hoặc bằng 11 bằng:
A. $\frac{8}{{49}}$.
B. $\frac{4}{9}$.
C. $\frac{1}{{12}}$.
D. $\frac{3}{{49}}$.

Lời giải

Chọn A

Xác suất xuất hiện mặt 6 chấm là $\frac{2}{7}$, mỗi mặt còn lại là $\frac{1}{7}$.

Có các khả năng:

• Hai lần gieo được mặt 6 chấm.

• Lần thứ nhất được mặt 6 chấm, lần thứ hai được mặt 5 chấm.

• Lần thứ nhất được mặt 5 chấm, lần thứ hai được mặt 6 chấm.

Xác suất cần tính là $\frac{2}{7} \cdot \frac{2}{7} + \frac{2}{7} \cdot \frac{1}{7} + \frac{1}{7} \cdot \frac{2}{7} = \frac{8}{{49}}$.

Câu 24. Hai xạ thủ cùng bắn, mỗi người một viên đạn vào bia một cách độc lập với nhau. Xác suất bắn trúng bia của hai xạ thủ lần lượt là $\frac{1}{2}$ và $\frac{1}{3}$. Tính xác suất của biến cố có ít nhất một xạ thủ không bắn trúng bia.
A. $\frac{1}{2}$.
B. $\frac{1}{3}$.
C. $\frac{2}{3}$.
D. $\frac{5}{6}$.

Lời giải

Chọn D

Xác suất bắn trúng bia của xạ thủ ${\text{A}}$ và ${\text{B}}$ lần lượt là $P\left( A \right) = \frac{1}{2},P\left( B \right) = \frac{1}{3}$.

Suy ra xác suất bắn trượt bia của xạ thủ ${\text{A}}$ và ${\text{B}}$ lần lượt là $P\left( {\overline A } \right) = \frac{1}{2},P\left( {\overline B } \right) = \frac{2}{3}$. Gọi $H$ là biến cố “có ít nhất một xạ thủ không bắn trúng bia”.

Khi đó $P\left( H \right) = P\left( {\overline A B \cup A\overline B  \cup \overline A \overline B } \right) = P\left( {\overline A } \right) \cdot P\left( B \right) + P\left( A \right) \cdot P\left( {\overline B } \right) + P\left( {\overline A } \right) \cdot P\left( {\overline B } \right) = \frac{5}{6}$.

Câu 25. Một người gọi điện thoại nhưng quên mất chữ số cuối. Tính xác suất để người đó gọi đúng số điện thoại mà không phải thử quá hai lần.
A. $\frac{1}{}5$.
B. $\frac{1}{{10}}$.
C. $\frac{{19}}{{90}}$.
D. $\frac{2}{9}$.

Lời giải

Chọn A

Số phần tử của không gian mẫu là $n\left( \right) = 10 = 10$.

Để người đó gọi đúng số điện thoại mà không phải thử quá hai lần ta có 2 trường hợp:

TH1: Người đó gọi đúng ở lần thứ nhất.

TH2: Người đó gọi đúng ở lần thứ hai.

Gọi ${A_1}$ :” người đó gọi đúng ở lần thứ nhất” $ \Rightarrow $ xác suất người đó gọi đúng là $P\left( {{A_1}} \right) = \frac{1}{{10}}$ và xác suất người đó gọi không đúng là $P\left( {\overline {{A_1}} } \right) = \frac{9}{{10}}$.

Gọi ${A_2}$ :” người đó gọi đúng ở lần thứ hai” $ \Rightarrow $ xác suất người đó gọi đúng là $P\left( {{A_2}} \right) = \frac{1}{9}$.

Gọi $A$ :”người đó gọi đúng số điện thoại mà không phải thử quá hai lần” ta có $A = {A_1} \cup \overline {{A_1}} {A_2} \Rightarrow P\left( A \right) = P\left( {{A_1}} \right) + P\left( {\overline {{A_1}} } \right) \cdot P\left( {{A_2}} \right) = \frac{1}{{10}} + \frac{9}{{10}} \cdot \frac{1}{9} = \frac{1}{}5$.

Câu 26. Một người bắn súng, biết xác suất bắn trúng vào tâm của người đó là $\left( {\frac{3}{7}} \right)$. Hỏi cả thảy bắn ba lần, xác suất bắn trúng tâm đúng một lần là bao nhiêu?
A. $\frac{{48}}{{343}}$.
B. $\frac{{144}}{{343}}$.
C. $\frac{{199}}{{343}}$.
D. $\frac{{27}}{{343}}$.

Lời giải

Chọn B

Gọi ${A_i},i = \overline {1,3} $ lần lượt là biến cố bắn trúng vào tâm ở các lần thứ nhất, thứ hai và thứ ba.

Xác suất để người đó bắn ba lần và trúng mục tiêu một lần là

$P\left( {{A_1} \cdot \overline {{A_2}} \cdot \overline {{A_3}} \cup \overline {{A_1}} \cdot {A_2} \cdot \overline {{A_3}} \cup \overline {{A_1}} \cdot \overline {{A_2}} \cdot {A_3}} \right) = P\left( {{A_1} \cdot \overline {{A_2}} \cdot \overline {{A_3}} } \right) + P\left( {\overline {{A_1}} \cdot {A_2} \cdot \overline {{A_3}} } \right) + P\left( {\overline {{A_1}} \cdot \overline {{A_2}} \cdot {A_3}} \right)$

$\; = P\left( {{A_1}} \right) \cdot P\left( {\overline {{A_2}} } \right) \cdot P\left( {\overline {{A_3}} } \right) + P\left( {\overline {{A_1}} } \right) \cdot P\left( {{A_2}} \right) \cdot P\left( {\overline {{A_3}} } \right) + P\left( {\overline {{A_1}} } \right) \cdot P\left( {\overline {{A_2}} } \right) \cdot P\left( {{A_3}} \right)$

$\; = \frac{3}{7} \cdot \frac{4}{7} \cdot \frac{4}{7} + \frac{4}{7} \cdot \frac{3}{7} \cdot \frac{4}{7} + \frac{4}{7} \cdot \frac{4}{7} \cdot \frac{3}{7} = \frac{{144}}{{343}}.$

Câu 27. Một mạch điện gồm 4 linh kiện như hình vẽ, trong đó xác suất hỏng của từng linh kiện trong một khoảng thời gian $t$ nào đó tương ứng là 0,$2;0,1;0,05$ và 0,02 . Biết rằng các linh kiện làm việc độc lập với nhau và các dây luôn tốt. Tính xác suất để mạng điện hoạt động tốt trong khoảng thời gian $t$.

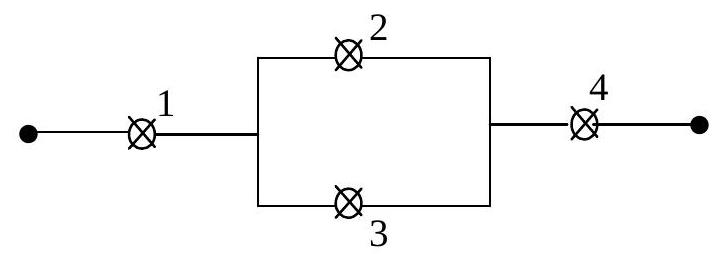
A. 0,37 .
B. 0,67032 .
C. 0,78008 .
D. 0,8 .

Lời giải

Chọn C:

Mạng điện hoạt động tốt khi xảy ra các trường hợp sau:

TH1: Mạng 1 , 2 , 4 tốt, 3 không tốt.

Xác suất là ${P_1} = \left( {1 – 0,2} \right) \cdot \left( {1 – 0,1} \right) \cdot 0,005 \cdot \left( {1 – 0,02} \right)$

TH2: Mạng 1, 3, 4 tốt, 2 không tốt.

Xác suất là ${P_2} = \left( {1 – 0,2} \right) \cdot 0,1 \cdot \left( {1 – 0,00}5 \right) \cdot \left( {1 – 0,02} \right)$

TH3: Mạng 1, 2, 3,4 tốt.

Xác suất là ${P_3} = \left( {1 – 0,2} \right) \cdot \left( {1 – 0,1} \right) \cdot \left( {1 – 0,00}5 \right) \cdot \left( {1 – 0,02} \right)$

Xác suất thỏa mãn ycbt là: $P = {P_1} + {P_2} + {P_3} = 0,78008$

Câu 28. Bạn Mạnh có 10 bông hoa hồng; 8 bông hoa lan và 9 bông hoa ly. Bạn Mạnh định chọn 7 bông hoa để đi tặng bạn. Tính xác suất để 7 bông hoa đó cùng loại.
A. $\frac{{186}}{{444015}}$.
B. $\frac{{254}}{{444015}}$.
C. $\frac{{82}}{{444015}}$.
D. $\frac{{143}}{{444015}}$.

Lời giải

Chọn C

• Gọi A là biến cố bạn Mạnh chọn 7 bông hoa hồng.
• Gọi B là biến cố bạn Mạnh chọn 7 bông hoa lan.
• Gọi C là biến cố bạn Mạnh chọn 7 bông hoa ly.

$ \Rightarrow A \cup B \cup C$ : bạn Mạnh chọn 7 bông hoa cùng loại.

Các biến cố ${\text{A}};{\text{B}}$; ${\text{C}}$ đôi một xung khắc.

• Số phần tử của không gian mẫu là: $n(\Omega) = C_{27}^7$

Ta có: $P\left( A \right) = \frac{{C_{10}^7}}{{C_{27}^7}};P\left( B \right) = \frac{{C_8^7}}{{C_{27}^7}};P\left( C \right) = \frac{{C_9^7}}{{C_{27}^7}}$

$ \Rightarrow P\left( {A \cup B \cup C} \right) = P\left( A \right) + P\left( B \right) + P\left( C \right) = \frac{{C_{10}^7}}{{C_{27}^7}} + \frac{{C_8^7}}{{C_{27}^7}} + \frac{{C_9^7}}{{C_{27}^7}} = \frac{{82}}{{444015}}$

Câu 29. Lớp 11A có 40 học sinh trong đó có 12 học sinh đạt điểm tổng kết môn Hóa học loại giỏi và 13 học sinh đạt điểm tổng kết môn Vật lí loại giỏi. Biết rằng khi chọn một học sinh của lớp đạt điểm tổng kết môn Hóa học hoặc Vật lí loại giỏi có xác suất là 0,5. Số học sinh đạt điểm tổng kết giỏi cả hai môn Hóa học và Vật lí là
A. 6 .
B. 5.
C. 4 .
D. 7 .

Lời giải

Chọn B

Gọi $A$ là biến cố “Học sinh được chọn đạt điểm tổng kết loại giỏi môn Hóa học”.

$B$ là biến cố “Học sinh được chọn đạt điểm tổng kết loại giỏi môn Vật lí”.

$A \cup B$ là biến cố “Học sinh được chọn đạt điểm tổng kết môn Hóa học hoặc Vật lí loại giỏi”.

$A \cap B$ là biến cố “Học sinh được chọn đạt điểm tổng kết loại giỏi cả hai môn Hóa học và Vật lí”.

Ta có: $n\left( {A \cup B} \right) = 0,5.40 = 20$.

Mặt khác: $n\left( {A \cup B} \right) = n\left( A \right) + n\left( B \right) – n\left( {A.B} \right)$

$ \Rightarrow n\left( {A.B} \right) = n\left( A \right) + n\left( B \right) – n\left( {A \cup B} \right) = 12 + 13 – 20 = 5$.

Câu 30. Trong kì thi thử THPT Quốc Gia, An làm để thi trắc nghiệm môn Toán. Đề thi gồm 50 câu hỏi, mỗi câu có 4 phương án trả lời, trong đó chỉ có một phương án đúng; trả lời đúng mỗi câu được 0,2 điểm. An trả lời hết các câu hỏi và chắc chắn đúng 45 câu, 5 câu còn lại An chọn ngẫu nhiên. Tính xác suất để điểm thi môn Toán của An không dưới 9, 5 điểm.
A. $\frac{9}{{22}}$.
B. $\frac{{13}}{{1024}}$.
C. $\frac{2}{{19}}$.
D. $\frac{{53}}{{512}}$.

Lời giải

Chọn B

Để An đúng được không dưới 9,5 điểm thì bạn ấy phải chọn đúng nhiều hơn 2 trong 5 câu còn lại.

Xác suất mỗi câu chọn đúng là $\frac{1}{4}$ và không chọn đúng là $\frac{3}{4}$.

Để An đúng được không dưới 9,5 điểm thì bạn ấy phải chọn đúng hoặc 3 hoặc 4 hoặc 5 trong 5 câu còn lại.

Do đó xác suất cần tìm là ${\left( {\frac{1}{4}} \right)^3}{\left( {\frac{3}{4}} \right)^2} + {\left( {\frac{1}{4}} \right)^4}\left( {\frac{3}{4}} \right) + {\left( {\frac{1}{4}} \right)^5} = \frac{{13}}{{1024}}$.

Câu 31. Có 3 chiếc hộp $A,B,C$. Hộp $A$ chứa 4 bi đỏ, 3 bi trắng. Hộp $B$ chứa 3 bi đỏ, 2 bi vàng. Hộp $C$ chứa 2 bi đỏ, 2 bi vàng. Lấy ngẫu nhiên một hộp từ 3 hộp này, rồi lấy ngẫu nhiên một bi từ hộp đó. Tính xác suất để lấy được một bi đỏ.
A. $\frac{1}{8}$.
B. $\frac{{13}}{{30}}$.
C. $\frac{1}{6}$.
D. $\frac{{39}}{{70}}$.

Lời giải

Xác suất để chọn hộp $A$ là $\frac{1}{3}$, xác suất để chọn được bi đỏ trong hộp $A$ là $\frac{4}{7}$

$ \Rightarrow $ Xác suất để chọn được bi đỏ trong hộp $A$ là $\frac{1}{3} \cdot \frac{4}{7}$.

Tương tự, xác suất để chọn được bi đỏ trong hộp $B$, hộp $C$ lần lượt là $\frac{1}{3} \cdot \frac{3}{}5,\frac{1}{3} \cdot \frac{2}{4}$.

Vậy xác suất để lấy được bi đỏ là $P = \frac{1}{3} \cdot \frac{4}{7} + \frac{1}{3} \cdot \frac{3}{}5 + \frac{1}{3} \cdot \frac{2}{4} = \frac{{39}}{{70}}$.

Câu 32. Hai người ngang tài ngang sức tranh chức vô địch của một cuộc thi cờ tướng. Người giành chiến thắng là người đầu tiên thắng được năm ván cờ. Tại thời điểm người chơi thứ nhất đã thắng 4 ván và người chơi thứ hai mới thắng 2 ván, tính xác suất để người chơi thứ nhất giành chiến thắng.
A. $\frac{3}{4}$.
B. $\frac{4}{5}$.
C. $\frac{7}{8}$.
D. $\frac{1}{2}$.

Lời giải

Chọn C

Theo giả thiết hai người ngang tài ngang sức nên xác suất thắng thua trong một ván đấu là 0,5;0,5.

Xét tại thời điểm người chơi thứ nhất đã thắng 4 ván và người chơi thứ hai thắng 2 ván.

Để người thứ nhất chiến thắng thì người thứ nhất cần thắng 1 ván và người thứ hai thắng không quá hai ván.

Có ba khả năng:

TH1: Đánh 1 ván. Người thứ nhất thắng xác suất là 0,5 .

TH2: Đánh 2 ván. Người thứ nhất thắng ở ván thứ hai xác suất là ${(0,5)^2}$.

TH3: Đánh 3 ván. Người thứ nhất thắng ở ván thứ ba xác suất là ${(0,5)^3}$.

Vậy $P = 0,5 + {(0,5)^2} + {(0,5)^3} = \frac{7}{8}.$.

Câu 33. Trong trận đấu bóng đá giữa 2 đội Real madrid và Barcelona, trọng tài cho đội Barcelona được hưởng một quả Penalty. Cầu thủ sút phạt ngẫu nhiên vào 1 trong bốn vị trí $1,2,3,4$ và thủ môn bay người cản phá ngẫu nhiên đến 1 trong 4 vị trí 1, 2, 3, 4 với xác suất như nhau (thủ môn và cầu thủ sút phạt đều không đoán được ý định của đối phương). Biết nếu cầu thủ sút và thủ môn bay cùng vào vị trí 1 (hoặc 2 ) thì thủ môn cản phá được cú sút đó, nếu cùng vào vị trí 3 (hoặc 4 ) thì xác suất cản phá thành công là 50%. Tính xác suất của biến cố “cú sút đó không vào lưới”?

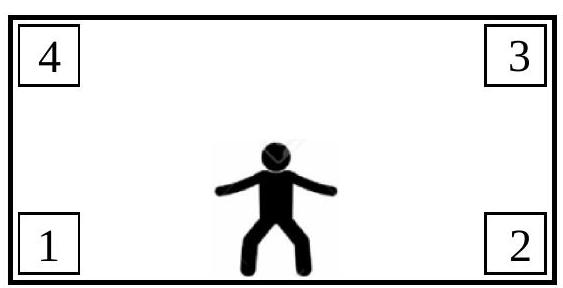
A. $\frac{5}{{16}}$.
B. $\frac{3}{{16}}$.
C. $\frac{1}{8}$.
D. $\frac{1}{4}$.

Lời giải

Chọn B

Cách 1:

• Số phần tử của không gian mẫu là $n\left( \right) = 4.4 = 16$

Gọi biến cố $A = $ “Cú sút đó không vào lưới”

Khi đó biến cố $\overline A = $ “Cú sút đó vào lưới”

Số phần tử của $n\left( {\overline A } \right)$ là

• Trường hợp 1: Cầu thủ sút vào vị trí 1 thủ môn bay vào 1 trong 3 vị trí còn lại

Cầu thủ có 1 cách sút

Thủ môn có 3 cách bay

Do đó, có 3 khả năng xảy ra

• Trường hợp 2: Cầu thủ sút vào vị trí 2 thủ môn bay vào 1 trong 3 vị trí còn lại

Cầu thủ có 1 cách sút

Thủ môn có 3 cách bay

Do đó, có 3 khả năng xảy ra

• Trường hợp 3: Cầu thủ sút vào vị trí 3 thủ môn bay vào 1 trong 3 vị trí còn lại

Cầu thủ có 1 cách sút

Thủ môn có 3 cách bay

Do đó, có 3 khả năng xảy ra

• Trường hợp 4: Cầu thủ sút vào vị trí 4 thủ môn bay vào 1 trong 3 vị trí còn lại

Cầu thủ có 1 cách sút

Thủ môn có 3 cách bay

Do đó, có 3 khả năng xảy ra

• Trường hợp 5: Cầu thủ sút vào vị trí 3 thủ môn bay vào vị trí 3

Cầu thủ có 1 cách sút

Thủ môn có 1 cách bay

Do đó, có 1 khả năng xảy ra

• Trường hợp 6: Cầu thủ sút vào vị trí 4 thủ môn bay vào vị trí 4

Cầu thủ có 1 cách sút

Thủ môn có 1 cách bay

Do đó, có 1 khả năng xảy ra

Khi đó $n\left( {\overline A } \right) = 4.3 + 2.1 = 14$.

Xác suất xảy ra biến cố $\overline A $ là $p\left( {\overline A } \right) = \frac{{4 \cdot 3}}{{16}} + \frac{{2 \cdot 1}}{{16}} \cdot \frac{1}{2} = \frac{{13}}{{16}}$ (Do 2 trường hợp 5,6 thì xác suất xảy ra chỉ là $50)$ Vậy $p\left( A \right) = 1 – p\left( {\overline A } \right) = 1 – \frac{{13}}{{16}} = \frac{3}{{16}}$.

Cách 2:

Gọi ${A_i}$ là biến cố “cầu thủ sút phạt vào vị trí $i$ ”

${B_i}$ là biến cố “thủ môn bay người cản phá vào vị trí thứ $i$ ”

Và $C$ là biến cố “Cú sút phạt không vào lưới””

Dễ thấy $P\left( {{A_i}} \right) = P\left( {{B_i}} \right) = \frac{1}{4}$.

Ta có $P\left( C \right) = P\left( {{A_1}} \right)P\left( {{B_1}} \right) + P\left( {{A_2}} \right)P\left( {{B_2}} \right) + \frac{1}{2}P\left( {{A_3}} \right)P\left( {{B_3}} \right) + \frac{1}{2}P\left( {{A_4}} \right)P\left( {{B_4}} \right)$

$ = {\left( {\frac{1}{4}} \right)^2} + {\left( {\frac{1}{4}} \right)^2} + \frac{1}{2}{\left( {\frac{1}{4}} \right)^2} + \frac{1}{2}{\left( {\frac{1}{4}} \right)^2} = \frac{3}{{16}}.$

Câu 34. Ba cầu thủ sút phạt đến $11$, mỗi người đá một lần với xác suất làm bàn tương ứng là $x,y$ và 0,6 (với $x > y$ ). Biết xác suất để ít nhất một trong ba cầu thủ ghi bàn là 0,976 và xác suất để cả ba cầu thủ đều ghi ban là 0,336 . Tính xác suất để có đúng hai cầu thủ ghi bàn.
A. 0,4525
B. 0,435
C. 0,452
D. 0,4245

Lời giải

Chọn C.

Gọi ${A_i}$ là biến cố “người thứ $i$ ghi bàn” với $i = 1,2,3$.

Ta có các ${A_i}$ độc lập với nhau và $P\left( {{A_1}} \right) = x,P\left( {{A_2}} \right) = y,P\left( {{A_3}} \right) = 0,6$.

Gọi A là biến cố: “ Có ít nhất một trong ba cầu thủ ghi bàn”

B: “Cả ba cầu thủ đều ghi bàn”

C: “Có đúng hai cầu thủ ghi bàn”

Ta có: $\overline A = \overline {{A_1}} \cdot \overline {{A_2}} \cdot \overline {{A_3}} \Rightarrow P\left( {\overline A } \right) = P\left( {\overline {{A_1}} } \right) \cdot P\left( {\overline {{A_2}} } \right) \cdot P\left( {\overline {{A_3}} } \right) = 0,4\left( {1 – x} \right)\left( {1 – y} \right)$

Nên $P\left( A \right) = 1 – P\left( {\overline A } \right) = 1 – 0,4\left( {1 – x} \right)\left( {1 – y} \right) = 0,976$

Suy ra $\left( {1 – x} \right)\left( {1 – y} \right) = \frac{3}{{50}} \Leftrightarrow xy – x – y = – \frac{{47}}{{50}}\left( 1 \right)$.

Tương tự: $B = {A_1} \cdot {A_2} \cdot {A_3}$, suy ra:

$P\left( B \right) = P\left( {{A_1}} \right) \cdot P\left( {{A_2}} \right) \cdot P\left( {{A_3}} \right) = 0,6xy = 0,336$ hay là $xy = \frac{{14}}{{2}}5$

Từ (1) và (2) ta có hệ: $\left\{ {\begin{array}{*{20}{l}}
{xy = \frac{{14}}{{2}}}5 \\
{x + y = \frac{3}{2}}
\end{array}} \right.$,
giải hệ này kết hợp với $x > y$ ta tìm được $x = 0,8$ và $y = 0,7$. Ta có: $C = \overline {{A_1}} {A_2}{A_3} + {A_1}\overline {{A_2}} {A_3} + {A_1}{A_2}\overline {{A_3}} $

Nên $P\left( C \right) = \left( {1 – x} \right)y \cdot 0,6 + x\left( {1 – y} \right) \cdot 0,6 + xy \cdot 0,4 = 0,452$.

Câu 35. Tung một đồng xu không đồng chất 2020 lần. Biết rằng xác suất xuất hiện mặt sấp là 0,6. Tính xác suất để mặt sấp xuất hiện đúng 1010 lần.
A. $\frac{1}{2}$.
B. ${(0,24)^{1010}}$.
C. $\frac{2}{3}$.
D. $C_{2020}^{1010} \cdot {(0,24)^{1010}}$.

Lời giải

Chọn D

Ta có $C_{2020}^{1010}$ cách chọn 1010 vị trí trong 2020 lần tung đồng xu để mặt xấp xuất hiện, các lần tung còn lại không xuất hiện mặt sấp. Ửng với mỗi cách chọn cố định 1010 vị trí xuất hiện mặt xấp ta có xác suất của trường hợp đó tính như sau:

+) Tại những lần mặt xấp xuất hiện thì xác suất xảy ra là 0,6 .

+) Tại những lần mặt ngửa xuất hiện thì xác suất xảy ra là 1-0,6.

Do có 1010 lần xuất hiện mặt sấp và 1010 xuất hiện mặt ngữa nên ứng với mỗi cách chọn cố định 1010 vị trí xuất hiện mặt xấp thì có xác xuất là $0,{6^{1010}}{(1 – 0,6)^{1010}} = {(0,24)^{1010}}$.

Vậy xác xuất cần tính là $C_{2020}^{1010} \cdot {(0,24)^{1010}}$.