- Giải Bài Tập Toán 12 Chân Trời Sáng Tạo Bài 1 Chương 1 Tính Đơn Điệu Và Cực Trị Của Hàm Số
- Giải Bài Tập Toán 12 Chân Trời Sáng Tạo Bài 2 Chương 1 Giá Trị Lớn Nhất Giá Trị Nhỏ Nhất Của Hàm Số
- Giải Bài Tập Toán 12 CTST Bài 3 Chương 1 Đường Tiệm Cận Của Đồ Thị Hàm Số
- Giải Toán 12 Chân Trời Sáng Tạo Bài 4 Chương 1 Bài Khảo Sát Và Vẽ Đồ Thị Một Số Hàm Số Cơ Bản
- Giải Toán 12 Chân Trời Sáng Tạo Bài Tập Cuối Chương 1
Câu 1. Tìm các khoảng đơn điệu và cực trị của các hàm số có đồ thị cho ở Hình 11.
a)
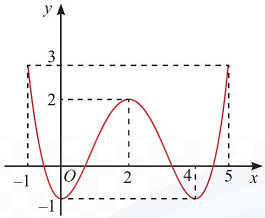
Hình 11a
b)
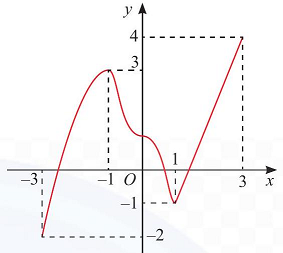
Hình 11b
Lời giải
Phương pháp:
+ Nếu đồ thị hàm số “đi lên” từ trái sang phải trên khoảng (a;b) thì hàm số đồng biến trên khoảng (a;b)
+ Nếu đồ thị hàm số “đi xuống” từ trái sang phải trên khoảng (a;b) thì hàm số nghịch biến trên khoảng (a;b)
a) + Hàm số đồng biến trên khoảng $\left( { 0;2} \right)$ và $\left( {4; + \infty } \right)$.
+ Hàm số nghịch biến trên khoảng $\left( { – \infty ; 0} \right)$ và $\left( {2;4} \right)$.
b) + Hàm số đồng biến trên khoảng $\left( { – \infty ;-1} \right)$ và $\left( {1; + \infty } \right)$.
+ Hàm số nghịch biến trên khoảng $\left( {-1;1} \right)$.
Câu 2. Xét tính đơn điệu và tìm điểm cực trị của các hàm số sau:
a) $y = 4{x^3} + 3{x^2} – 36x + 6$;
b) $y = \frac{{{x^2} – 2x – 7}}{{x – 4}}$.
Lời giải
a) $y = 4{x^3} + 3{x^2} – 36x + 6$;
Tập xác định: $D = \mathbb{R}$
$y’ = 12{x^2} + 6x – 36$
$y’ = 0 \Leftrightarrow 12{x^2} + 6x – 36 = 0 \Leftrightarrow \left[ \begin{gathered}
x = \frac{3}{2} \hfill \\
x = – 2 \hfill \\
\end{gathered} \right.$
Bảng biến thiên
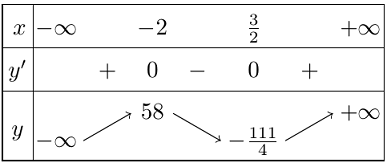
Vậy,
+ Hàm số đồng biến trên các khoảng $\left( { – \infty ; – 2} \right)$ và $\left( {\frac{3}{2}; + \infty } \right)$.
+ Hàm số nghịch biến trên khoảng $\left( { – 2;\frac{3}{2}} \right)$.
+ Hàm số đạt cực đại tại $x = – 2;\,{y_{CĐ}} = 58$.
+ Hàm số đạt cực tiểu tại $x = \frac{3}{2};\,{y_{CT}} = – \frac{{111}}{4}$.
b) $y = \frac{{{x^2} – 2x – 7}}{{x – 4}}$.
Tập xác định: $D = \mathbb{R}\backslash \left\{ 4 \right\}$
Lời giải
$y’ = \frac{{{{\left( {{x^2} – 2x – 7} \right)}^\prime }(x – 4) – \left( {{x^2} – 2x – 7} \right)(x – 4)’}}{{{{\left( {x – 4} \right)}^2}}}$
$ = \frac{{(2x – 2)(x – 4) – \left( {{x^2} – 2x – 7} \right).1}}{{{{\left( {x – 4} \right)}^2}}}$
$ = \frac{{2{x^2} – 8x – 2x + 8 – {x^2} + 2x + 7}}{{{{\left( {x – 4} \right)}^2}}} = \frac{{{x^2} – 8x + 15}}{{{{\left( {x – 4} \right)}^2}}}$
$y’ = 0 \Rightarrow \frac{{{x^2} – 8x + 15}}{{{{\left( {x – 4} \right)}^2}}} = 0 \Rightarrow {x^2} – 8x + 15 = 0 \Leftrightarrow \left[ \begin{gathered}
x = 5 \hfill \\
x = 3 \hfill \\
\end{gathered} \right.$
Bảng biến thiên
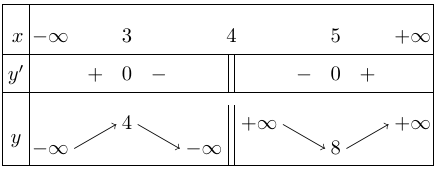
Vậy,
+ Hàm số đồng biến trên các khoảng $\left( { – \infty ;3} \right)$ và $\left( {5; + \infty } \right)$.
+ Hàm số nghịch biến trên các khoảng $\left( {3;4} \right)$ và $\left( {4;5} \right)$.
+ Hàm số đạt cực đại tại $x = 3;\,{y_{CĐ}} = 4$.
+ Hàm số đạt cực tiểu tại $x = 5;\,{y_{CT}} = 8$.
Câu 3. Tìm cực trị của các hàm số sau:
a) $y = 2{x^3} + 3{x^2} – 36x + 1$;
b) $y = \frac{{{x^2} – 8x + 10}}{{x – 2}}$
c) $y = \sqrt { – {x^2} + 4} $.
Lời giải
a) $y = 2{x^3} + 3{x^2} – 36x + 1$
Tập xác định: $D = \mathbb{R}$
$y’ = 6{x^2} + 6x – 36$
$y’ = 0 \Leftrightarrow 6{x^2} + 6x – 36 = 0 \Leftrightarrow \left[ \begin{gathered}
x = 2 \hfill \\
x = – 3 \hfill \\
\end{gathered} \right.$
Bảng biến thiên
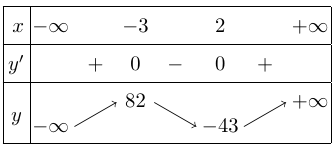
Vậy,
+ Hàm số đạt cực đại tại $x = – 3;\,{y_{CĐ}} = 82$.
+ Hàm số đạt cực tiểu tại $x = 2;\,{y_{CT}} = – 43$.
b) $y = \frac{{{x^2} – 8x + 10}}{{x – 2}}$
Tập xác định: $D = \mathbb{R}\backslash \left\{ 2 \right\}$
$y’ = \frac{{{{\left( {{x^2} – 8x + 10} \right)}^\prime }\left( {x – 2} \right) – \left( {{x^2} – 8x + 10} \right){{\left( {x – 2} \right)}^\prime }}}{{{{\left( {x – 2} \right)}^2}}}$
$ = \frac{{\left( {2x – 8} \right)\left( {x – 2} \right) – \left( {{x^2} – 8x + 10} \right).1}}{{{{\left( {x – 2} \right)}^2}}}$
$ = \frac{{2{x^2} – 4x – 8x + 16 – {x^2} + 8x – 10}}{{{{\left( {x – 2} \right)}^2}}}$
$ = \frac{{{x^2} – 4x + 6}}{{{{\left( {x – 2} \right)}^2}}}$
$y’ = 0 \Rightarrow \frac{{{x^2} – 4x + 6}}{{{{\left( {x – 2} \right)}^2}}} = 0$$ \Rightarrow {x^2} – 4x + 6 = 0$ (phương trình vô nghiệm)
Bảng biến thiên
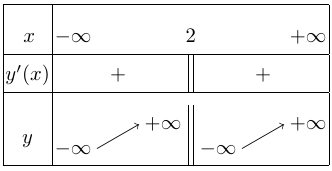
Vậy, hàm số không có cực trị.
c) $y = \sqrt { – {x^2} + 4} $.
Tập xác định: $D = \left[ { – 2;2} \right]$
$y’ = \frac{{ – x}}{{\sqrt { – {x^2} + 4} }}$
$y’ = 0 \Rightarrow x = 0\,(nhận)$
Bảng biến thiên
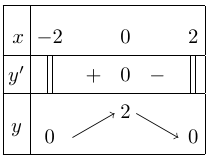
Vậy,
+ Hàm số đạt cực đại tại $x = 0;\,{y_{CĐ}} = 2$.
Câu 4. Chứng minh rằng hàm số $y = \frac{{2x + 1}}{{x – 3}}$ nghịch biến trên từng khoảng xác định của nó.
Lời giải
Tập xác định: $D = \mathbb{R}\backslash \left\{ 2 \right\}$
$y’ = \frac{{ – 7}}{{{{(x – 3)}^2}}} < 0,\,\forall x \ne 3$
Vậy, hàm số nghịch biến trên các khoảng $\left( { – \infty ;3} \right)$ và $\left( {3; + \infty } \right)$.
Câu 5. Kim ngạch xuất khẩu rau quả của Việt Nam trong các năm từ 2010 đến 2017 có thể được tính xấp xỉ bằng công thức $f\left( x \right) = 0,01{x^3} – 0,04{x^2} + 0,25x + 0,44$ (tỉ USD) với $x$ là số năm tính từ 2010 đến $2017\left( {0 \leqslant x \leqslant 7} \right)$.
(Theo: https://infographics.vn/interactive-xuat-khau-rau-quadu-bao-bung-no-dat-4-ty-usd-trong-nam-2023/116220.vna)
a) Tính đạo hàm của hàm số $y = f\left( x \right)$.
b) Chứng minh rằng kim ngạch xuất khẩu rau quả của Việt Nam tăng liên tục trong các năm từ 2010 đến 2017.
Lời giải
a) $f\left( x \right) = 0,01{x^3} – 0,04{x^2} + 0,25x + 0,44$
$f’\left( x \right) = 0,03{x^2} – 0,08x + 0,25$.
b) Ta có: $f’\left( x \right) = 0,03{x^2} – 0,08x + 0,25 > 0,\,\,\forall x \in \mathbb{R}$ (Do $\Delta = – \frac{{59}}{{2500}} < 0$ và $a = 0,03 > 0$)
$ \Rightarrow f'(x) > 0,\,\forall x \in \left[ {0;7} \right]$
$ \Rightarrow f(x)$ đồng biến trên $\left[ {0;7} \right]$
Do đó, kim ngạch xuất khẩu rau quả của Việt Nam tăng liên tục trong các năm từ 2010 đến 2017.
Câu 6. Xét một chất điểm chuyển động dọc theo trục $Ox$. Toạ độ của chất điểm tại thời điểm $t$ được xác định bởi hàm số $x\left( t \right) = {t^3} – 6{t^2} + 9t$ với $t \geqslant 0$. Khi đó $x’\left( t \right)$ là vận tốc của chất điểm tại thời điểm $t$, kí hiệu $v\left( t \right)$; $v’\left( t \right)$ là gia tốc chuyển động của chất điểm tại thời điểm $t$, kí hiệu $a\left( t \right)$.
a) Tìm các hàm $v\left( t \right)$ và $a\left( t \right)$.
b) Trong khoảng thời gian nào vận tốc của chất điểm tăng, trong khoảng thời gian nào vận tốc của chất điểm giảm?
a) Tìm các hàm $v\left( t \right)$ và $a\left( t \right)$.
$v\left( t \right) = x'(t) = 3{t^2} – 12t + 9$
$a\left( t \right) = v'(t) = 6t – 12$
b) Trong khoảng thời gian nào vận tốc của chất điểm tăng, trong khoảng thời gian nào vận tốc của chất điểm giảm?
$v\left( t \right) = 3{t^2} – 12t + 9$
$v'(t) = 6t – 12$
$v'(t) = 0 \Leftrightarrow 6t – 12 = 0 \Leftrightarrow t = 2$
Bảng biến thiên trên $ [0; + \infty )$
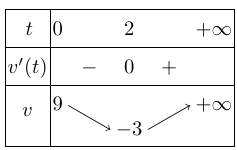
Vậy, trong khoảng thời gian$t > 2$ vận tốc của chất điểm tăng, trong khoảng thời gian $0 \leqslant t < 2$ vận tốc của chất điểm giảm.
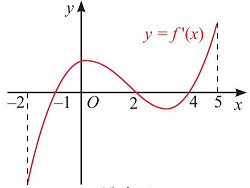
Câu 7. Đạo hàm $f’\left( x \right)$ của hàm số $y = f\left( x \right)$ có đồ thị như Hình 12. Xét tính đơn điệu và tìm điểm cực trị của hàm số $y = f\left( x \right)$.
Phương pháp
+ Nếu trên $(a;b)$ đồ thị hàm số $y = f'(x)$ nằm phía trên trục hoành thì $f'(x) > 0$ nên hàm số $y = f(x)$ đồng biến trên khoảng $(a;b)$.
+ Nếu trên $(a;b)$ đồ thị hàm số $y = f'(x)$ nằm phía dưới trục hoành thì $f'(x) < 0$ nên hàm số $y = f(x)$ nghịch biến trên khoảng $(a;b)$.
+ Nếu đồ thị hàm số $y = f'(x)$ cắt trục hoành tại điểm ${x_0}$ thì $f'({x_0}) = 0$.
Lời giải
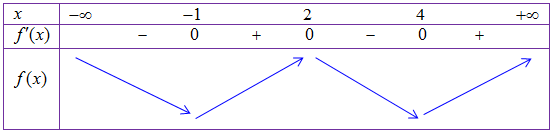
Dựa vào đồ thị hàm số $y = f’\left( x \right)$ ta có bảng xét dấu $f'(x)$ :
Vậy,
+ Hàm số đồng biến trên các khoảng $\left( { – 1;2} \right)$ và $\left( {4; + \infty } \right)$.
+ Hàm số nghịch biến trên các khoảng $\left( { – \infty ; – 1} \right)$ và $\left( {2;4} \right)$.
+ Hàm số đạt cực đại tại điểm $x = 2$.
+ Hàm số đạt cực tiểu tại các điểm $x = – 1;\,x = 4$.






