50 Câu Trắc Nghiệm Hệ Thức Lượng Trong Tam Giác Giải Chi Tiết

50 câu trắc nghiệm hệ thức lượng trong tam giác giải chi tiết được soạn dưới dạng file word và PDF gồm 4 trang. Các bạn xem và tải về ở dưới.

DẠNG 1: LÝ THUYẾT

Câu 1. Trong tam giác $ABC$ có:
A. $a = 2RcosA$.

B. $a = 2RsinA$.

C. $a = 2RtanA$.

D. $a = RsinA$.

Lời giải

Chọn B.

Định lý sin trong tam giác.

Câu 2. Cho tam giác $ABC$ bất kỳ có $BC = a,AC = b,AB = c$. Đẳng thức nào sai?
A. ${b^2} = {a^2} + {c^2} – 2accosB$.
B. ${a^2} = {b^2} + {c^2} – 2bccosA$.
C. ${c^2} = {b^2} + {a^2} + 2abcosC$.
D. ${c^2} = {b^2} + {a^2} – 2abcosC$.

Lời giải

Chọn C.

Theo định lí hàm số cosin, ${c^2} = {b^2} + {a^2} – 2abcosC$ nên $C$ sai.

Câu 3. Trong tam giác $ABC$ với $BC = a,AC = b,AB = c$. Mệnh đề nào dưới đây sai?
A. $a = \frac{{bsinA}}{{sinB}}$.
B. $sinC = \frac{{csinA}}{a}$.
C. $a = 2RsinA$.
D. $b = RtanB$.

Lời giải

Chọn D.

Theo định lý sin ta có $\frac{a}{{sinA}} = \frac{b}{{sinB}} = \frac{c}{{sinC}} = 2R$

$ \Rightarrow a = \frac{{bsinA}}{{sinB}},sinC = \frac{{csinC}}{a},a = 2RsinA$, nên các mệnh đề $A,B,C$ đúng.

Vậy mệnh đề $D$ là mệnh đề sai.

Câu 4. Cho tam giác $ABC$ có các cạnh $BC = a,AC = b,AB = c$. Diện tích của $\vartriangle ABC$ là
A. ${S_{\vartriangle ABC}} = \frac{1}{2}acsinC$.
B. ${S_{\vartriangle ABC}} = \frac{1}{2}bcsinB$.
C. ${S_{\vartriangle ABC}} = \frac{1}{2}acsinB$.
D. ${S_{\vartriangle ABC}} = \frac{1}{2}bcsinC$.

Lời giải

Chọn C.

Ta có: ${S_{\vartriangle ABC}} = \frac{1}{2}acsinB$.

Câu 5. Cho tam giác $ABC$, có độ dài ba cạnh là $BC = a,AC = b,AB = c$. Gọi ${m_a}$ là độ dài đường trung tuyến kẻ từ đỉnh $A,R$ là bán kính đường tròn ngoại tiếp tam giác và $S$ là diện tích tam giác đó. Mệnh đề nào sau đây sai?
A. $m_a^2 = \frac{{{b^2} + {c^2}}}{2} – \frac{{{a^2}}}{4}$.
B. ${a^2} = {b^2} + {c^2} + 2bccosA$.
C. $S = \frac{{abc}}{{4R}}$.
D. $\frac{a}{{sinA}} = \frac{b}{{sinB}} = \frac{c}{{sinC}} = 2R$.

Lời giải

Chọn B

Theo định lý hàm số cosin trong tam giác ta có ${a^2} = {b^2} + {c^2} – 2bccosA$

DẠNG 2: XÁC ĐỊNH CÁC YẾU TỐ TRONG TAM GIÁC

Câu 6. Cho tam giác $ABC$ có $a = 8,b = 10$, góc $C$ bằng ${60^ \circ }$. Độ dài cạnh $c$ là?
A. $c = 3\sqrt {21} $.
B. $c = 7\sqrt 2 $.
C. $c = 2\sqrt {11} $.
D. $c = 2\sqrt {21} $.

Lời giải

Chọn D

Ta có: ${c^2} = {a^2} + {b^2} – 2a \cdot b \cdot cosC = {8^2} + {10^2} – 2 \cdot 8 \cdot 10 \cdot cos{60^ \circ } = 84 \Rightarrow c = 2\sqrt {21} $.

Câu 7. Cho $\vartriangle ABC$ có $b = 6,c = 8,\hat A = {60^ \circ }$. Độ dài cạnh $a$ là:
A. $2\sqrt {13} $.
B. $3\sqrt {12} $.
C. $2\sqrt {37} $.
D. $\sqrt {20} $.

Lời giải

Chọn A

Ta có: ${a^2} = {b^2} + {c^2} – 2bccosA = 36 + 64 – 2 \cdot 6 \cdot 8 \cdot cos{60^ \circ } = 52 \Rightarrow a = 2\sqrt {13} $.

Câu 8. Cho $\vartriangle ABC$ có $B = {60^ \circ },a = 8,c = 5$. Độ dài cạnh $b$ bằng:
A. 7 .
B. 129 .
C. 49 .
D. $\sqrt {129} $.

Lời giải

Chọn A

Ta có: ${b^2} = {a^2} + {c^2} – 2accosB = {8^2} + {5^2} – 2 \cdot 8 \cdot 5 \cdot cos{60^ \circ } = 49 \Rightarrow b = 7$.

Câu 9. Cho $\vartriangle ABC$ có $AB = 9;BC = 8;\hat B = {60^ \circ }$. Tính độ dài $AC$.
A. $\sqrt {73} $.
B. $\sqrt {217} $.
C. 8 .
D. $\sqrt {113} $.

Lời giải

Chọn A

Theo định lý cosin có:

$A{C^2} = B{A^2} + B{C^2} – 2BA \cdot BC \cdot cos\widehat {ABC} = 73 \Rightarrow AC = \sqrt {73} $.

Vậy $AC = \sqrt {73} $.

Câu 10. Cho tam giác $ABC$ có $AB = 2,AC = 1$ và $A = {60^ \circ }$. Tính độ dài cạnh $BC$.
A. $BC = \sqrt 2 $.
B. $BC = 1$.
C. $BC = \sqrt 3 $.
D. $BC = 2$.

Lời giải

Chọn C

Theo định lý cosin ta có: $BC = \sqrt {A{B^2} + A{C^2} – 2AB \cdot AC \cdot cos{{60}^ \circ }} $

$ = \sqrt {{2^2} + {1^2} – 2 \cdot 2 \cdot 1 \cdot \frac{1}{2}} = \sqrt 3 $

Câu 11. Tam giác $ABC$ có $a = 8,c = 3,\hat B = {60^ \circ }$. Độ dài cạnh $b$ bằng bao nhiêu?
A. 49 .
B. $\sqrt {97} $
C. 7 .
D. $\sqrt {61} $.

Lời giải

Chọn C

Ta có: ${b^2} = {a^2} + {c^2} – 2accosB = {8^2} + {3^2} – 2 \cdot 8 \cdot 3 \cdot cos{60^0} = 49 \Rightarrow b = 7$.

Câu 12. Tam giác $ABC$ có $\hat C = {150^ \circ },BC = \sqrt 3 ,AC = 2$. Tính cạnh $AB$ ?
A. $\sqrt {13} $.
B. $\sqrt 3 $.
C. 10 .
D. 1 .

Lời giải

Chọn A

Theo định lí cosin trong $\vartriangle ABC$ ta có:

$A{B^2} = C{A^2} + C{B^2} – 2CA \cdot CB \cdot cos\hat C = 13 \Rightarrow AB = \sqrt {13} .$

Câu 13. Cho $a;b;c$ là độ dài 3 cạnh của tam giác $ABC$. Biết $b = 7;c = 5;cosA = \frac{4}{5}$. Tính độ dài của $a$.
A. $3\sqrt 2 $.
B. $\frac{{7\sqrt 2 }}{2}$.
C. $\frac{{23}}{8}$.
D. 6 .

Lời giải

Chọn A

Áp dụng định lí cosin cho tam giác $ABC$ ta có:

${a^2} = {b^2} + {c^2} – 2bc \cdot cosA = {7^2} + {5^2} – 2 \cdot 7 \cdot 5 \cdot \frac{4}{5} = 18$.

Suy ra: $a = \sqrt {18} = 3\sqrt 2 $.

Câu 14. Cho $\widehat {xOy} = {30^ \circ }$. Gọi $A,B$ là 2 điểm di động lần lượt trên $Ox,Oy$ sao cho $AB = 2$. Độ dài lớn nhất của $OB$ bằng bao nhiêu?
A. 4 .
B. 3 .
C. 6 .
D. 2 .

Lời giải

Chọn A

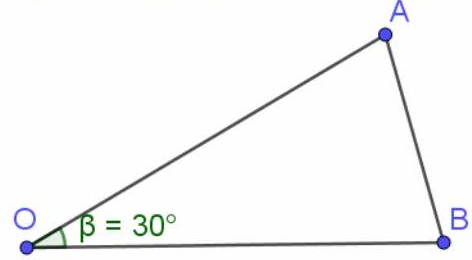
Áp dụng định lí cosin: $A{B^2} = O{A^2} + O{B^2} – 2OA \cdot OB \cdot cos{30^ \circ } \Leftrightarrow 4 = O{A^2} + O{B^2} – 2OA \cdot OB \cdot \frac{{\sqrt 3 }}{2}$

$ \Leftrightarrow O{A^2} – \sqrt 3 \cdot OB \cdot OA + O{B^2} – 4 = 0$.

Coi phương trình là một phương trình bậc hai ẩn $OA$. Để tồn tại giá trị lớn nhất của $OB$

thì ${\Delta _{\left( * \right)}} \geqslant 0 \Leftrightarrow {(\sqrt 3 OB)^2} – 4\left( {O{B^2} – 4} \right) \geqslant 0 \Leftrightarrow O{B^2} \leqslant 16 \Leftrightarrow OB \leqslant 4$.

Vậy $maxOB = 4$.

Câu 15. Tam giác $ABC$ có $AB = 9\;cm,BC = 15\;cm,AC = 12\;cm$. Khi đó đường trung tuyến $AM$ của tam giác có độ dài là
A. $10\;cm$.
B. $9\;cm$.
C. $7,5\;cm$.
D. $8\;cm$.

Lời giải

Chọn C

Ta có $A{M^2} = \frac{{A{B^2} + A{C^2}}}{2} – \frac{{B{C^2}}}{4} = \frac{{{9^2} + {{12}^2}}}{2} – \frac{{{{15}^2}}}{4} = \frac{{225}}{4} \Rightarrow AM = \frac{{15}}{2}$.

Câu 16. Cho tam giác $ABC$ có $AB = 3,BC = 5$ và độ dài đường trung tuyến $BM = \sqrt {13} $. Tính độ dài $AC$.
A. $\sqrt {11} $.
B. 4 .
C. $\frac{9}{2}$.
D. $\sqrt {10} $.

Lời giải

Chọn B

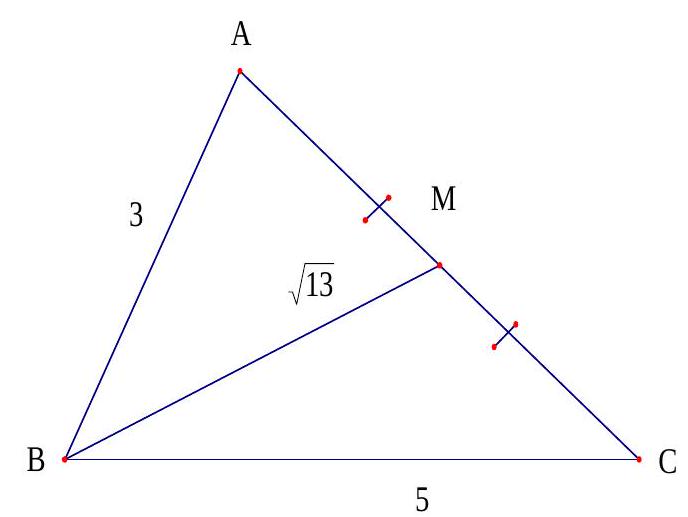
Theo công thức tính độ dài đường trung tuyến;ta có:

$B{M^2} = \frac{{B{A^2} + B{C^2}}}{2} – \frac{{A{C^2}}}{4} \Leftrightarrow {(\sqrt {13} )^2} = \frac{{{3^2} + {5^2}}}{2} – \frac{{A{C^2}}}{4} \Leftrightarrow AC = 4.$

Câu 17. Cho $\vartriangle ABC$ vuông ở $A$, biết $\hat C = {30^ \circ },AB = 3$. Tính độ dài trung tuyến $AM$ ?
A. 3 .
B. 4
C. $\frac{5}{2}$
D. $\frac{7}{2}$

Lời giải

Chọn A

$AM$ là trung tuyến ứng với cạnh huyền nên $AM = \frac{1}{2}BC = BM = MC$.

Xét $\vartriangle BAC$ có $\hat B = {90^ \circ } – {30^ \circ } = {60^ \circ }$.

Xét tam giác $ABM$ có $BM = AM$ và $\hat B = {60^ \circ }$ suy ra $\vartriangle ABM$ là tam giác đều.

$ \Rightarrow AM = AB = 3$.

Câu 18. Cho tam giác $ABC$ có $AB = 4\;cm,BC = 7\;cm,AC = 9\;cm$. Tính $cosA$.
A. $cosA = – \frac{2}{3}$.
B. $cosA = \frac{1}{2}$.
C. $cosA = \frac{1}{3}$.
D. $cosA = \frac{2}{3}$.

Lời giải

Chọn D

Ta có $cosA = \frac{{A{B^2} + A{C^2} – B{C^2}}}{{2 \cdot AB \cdot AC}} = \frac{{{4^2} + {9^2} – {7^2}}}{{2.4 \cdot 9}} = \frac{2}{3}$.

Câu 19. Cho tam giác $ABC$, biết $a = 24,b = 13,c = 15$. Tính góc $A$ ?
A. ${33^0}{34’}$.
B. ${117^0}{49’}$.
C. ${28^0}{37’}$.
D. ${58^0}24$.

Lời giải

Chọn B

Ta có: $cosA = \frac{{{b^2} + {c^2} – {a^2}}}{{2bc}} = \frac{{{{13}^2} + {{15}^2} – {{24}^2}}}{{2.13.15}} = – \frac{7}{{15}} \Rightarrow A \simeq {117^0}{49’}$.

Câu 20. Cho tam giác $ABC$, biết $a = 13,b = 14,c = 15$. Tính góc $B$ ?
A. ${59^0}{49’}$.
B. ${53^0}7’$.
C. ${59^0}{29’}$.
D. ${62^0}22$ ‘.

Lời giải

Chọn C

Ta có: $cosB = \frac{{{a^2} + {c^2} – {b^2}}}{{2ac}} = \frac{{{{13}^2} + {{15}^2} – {{14}^2}}}{{2.13.15}} = \frac{{33}}{{65}} \Rightarrow B \simeq {59^0}{29’}$.

Câu 21. Cho tam giác $ABC$ biết độ dài ba cạnh $BC,CA,AB$ lần lượt là $a,b,c$ và thỏa mãn hệ thức $b\left( {{b^2} – {a^2}} \right) = c\left( {{c^2} – {a^2}} \right)$ với $b \ne c$. Khi đó, góc $\widehat {BAC}$ bằng
A. ${45^ \circ }$.
B. ${60^ \circ }$.
C. ${90^ \circ }$.
D. ${120^ \circ }$.

Lời giải

Chọn D

Ta có $b\left( {{b^2} – {a^2}} \right) = c\left( {{c^2} – {a^2}} \right) \Leftrightarrow {b^3} – b{a^2} = {c^3} – c{a^2} \Leftrightarrow {b^3} – {c^3} – {a^2}\left( {b – c} \right) = 0$

$ \Leftrightarrow \left( {b – c} \right)\left( {{b^2} + bc + {c^2} – {a^2}} \right) = 0 \Leftrightarrow {b^2} + {c^2} – {a^2} = – bc$. Mặt khác $cos\widehat {BAC} = \frac{{{b^2} + {c^2} – {a^2}}}{{2bc}} = \frac{{ – bc}}{{2bc}} = – \frac{1}{2} \Rightarrow \widehat {BAC} = {120^ \circ }$.

Câu 22. Tam giác $ABC$ có $a = 6,b = 4\sqrt 2 ,c = 2$. $M$ là điểm trên cạnh $BC$ sao cho $BM = 3$. Độ dài đoạn $AM$ bằng bao nhiêu?
A. $\sqrt 9 $.
B. 9 .
C. 3 .
D. $\frac{1}{2}\sqrt {108} $.

Lời giải

Chọn C

Ta có: Trong tam giác $ABC$ có $a = 6 \Rightarrow BC = 6$ mà $BM = 3$ suy ra $M$ là trung điểm $BC$.

Suy ra: $A{M^2} = m_a^2 = \frac{{{b^2} + {c^2}}}{2} – \frac{{{a^2}}}{4} = 9 \Rightarrow AM = 3$.

Câu 23. Cho $\vartriangle ABC$ có $AB = 2;AC = 3;\hat A = {60^ \circ }$. Tính độ dài đường phân giác trong góc $A$ của tam giác $ABC$.
A. $\frac{{12}}{5}$.
B. $\frac{{6\sqrt 2 }}{5}$.
C. $\frac{{6\sqrt 3 }}{5}$.
D. $\frac{6}{5}$.

Lời giải

Chọn C

  A

Gọi $M$ là chân đường phân giác góc $A$.

Ta có $B{C^2} = A{B^2} + A{C^2} – 2AB \cdot AC \cdot cosA = 7 \Rightarrow BC = \sqrt 7 $.

Lại có $\frac{{BM}}{{CM}} = \frac{{AB}}{{AC}} = \frac{2}{3}$.

Suy ra $BM = \frac{{2\sqrt 7 }}{5}$.

Áp dụng định lý cosin trong tam giác $ABM$ ta được:

$A{M^2} = A{B^2} + B{M^2} – 2AB \cdot BM \cdot cos\widehat {ABC}$

$ = A{B^2} + B{M^2} – 2AB \cdot BM \cdot \frac{{A{B^2} + B{C^2} – A{C^2}}}{{2 \cdot AB \cdot BC}} = \frac{{108}}{{25}}$.

$ \Rightarrow AM = \frac{{6\sqrt 3 }}{5}$.

Cách khác

Gọi $M$ là chân đường phân giác trong của góc $A$. Vì đoạn thẳng $AM$ chia tam giác $ABC$ thành hai phần nên ta có:

${S_{ABC}} = {S_{ABM}} + {S_{ACM}}$

$ \Leftrightarrow \frac{1}{2}AB \cdot AC \cdot sin\widehat {BAC} = \frac{1}{2}AB \cdot AM \cdot sin\widehat {BAM} + \frac{1}{2}AC \cdot AM \cdot sin\widehat {MAC}$

$ \Leftrightarrow AM = \frac{{AB \cdot AC \cdot sin{{60}^ \circ }}}{{\left( {AB + AC} \right) \cdot sin{{30}^ \circ }}}$

$ \Leftrightarrow AM = \frac{{6\sqrt 3 }}{5}$.

Vậy $AM = \frac{{6\sqrt 3 }}{5}$.

Câu 24. Cho $\vartriangle ABC$ với các cạnh $AB = c,AC = b,BC = a$. Gọi $R,r,S$ lần lượt là bán kính đường tròn ngoại tiếp, nội tiếp và diện tích của tam giác $ABC$. Trong các phát biểu sau, phát biểu nào sai?
A. $S = \frac{{abc}}{{4R}}$.
B. $R = \frac{a}{{sinA}}$.
C. $S = \frac{1}{2}absinC$.
D. ${a^2} + {b^2} – {c^2} = 2abcosC$.

Lời giải

Chọn B

Theo định lí Sin trong tam giác, ta có $\frac{a}{{sinA}} = 2R$.

Câu 25. Cho tam giác $ABC$ có góc $\widehat {BAC} = {60^ \circ }$ và cạnh $BC = \sqrt 3 $. Tính bán kính của đường tròn ngoại tiếp tam giác $ABC$.
A. $R = 4$.
B. $R = 1$.
C. $R = 2$.
D. $R = 3$.

Lời giải

Chọn B

Ta có: $\frac{{BC}}{{sinA}} = 2R \Leftrightarrow R = \frac{{BC}}{{2sinA}} = \frac{{\sqrt 3 }}{{2 \cdot \frac{{\sqrt 3 }}{2}}} = 1$.

Câu 26. Trong mặt phẳng, cho tam giác $ABC$ có $AC = 4\;cm$, góc $\hat A = {60^ \circ },\hat B = {45^ \circ }$. Độ dài cạnh $BC$ là
A. $2\sqrt 6 $.
B. $2 + 2\sqrt 3 $.
C. $2\sqrt 3 – 2$.
D. $\sqrt 6 $.

Lời giải

Chọn A

Ta có $\frac{{BC}}{{sinA}} = \frac{{AC}}{{sinB}} \Leftrightarrow BC = \frac{{4 \cdot \frac{{\sqrt 3 }}{2}}}{{\frac{{\sqrt 2 }}{2}}} = 2\sqrt 6 $.

Câu 27. Tam giác $ABC$ có $\hat A = {68^0}{12’},\hat B = {34^0}{44’},AB = 117$. Tính $AC$ ?
A. 68 .
B. 168 .
C. 118 .
D. 200 .

Lời giải

Chọn A

Ta có: Trong tam giác $ABC:\hat A + \hat B + \hat C = {180^0} \Rightarrow \hat C = {180^0} – {68^0}{12’} – {34^0}{44’} = {77^0}4’$.

Mặt khác $\frac{a}{{sinA}} = \frac{b}{{sinB}} = \frac{c}{{sinC}} \Rightarrow \frac{{AC}}{{sinB}} = \frac{{AB}}{{sinC}} \Rightarrow AC = \frac{{AB \cdot sinB}}{{sinC}} = \frac{{117 \cdot sin{{34}^0}{{44}’}}}{{sin{{77}^0}4′}} \simeq 68$.

Câu 28. Cho hình thoi $ABCD$ có cạnh bằng $a$. Góc $\widehat {BAD} = {30^ \circ }$. Diện tích hình thoi $ABCD$ là
A. $\frac{{{a^2}}}{4}$.
B. $\frac{{{a^2}}}{2}$.
C. $\frac{{{a^2}\sqrt 3 }}{2}$.
D. ${a^2}$.

Lời giải

Chon B

Ta có ${S_{ABCD}} = AB \cdot AD \cdot sin\widehat {BAD} = a \cdot a \cdot sin{30^ \circ } = \frac{1}{2}{a^2}$.

Câu 29. Cho $\vartriangle ABC$ có $AB = 5;\hat A = {40^ \circ };\hat B = {60^ \circ }$. Độ dài $BC$ gần nhất với kết quả nào?
A. 3,7 .
B. 3,3 .
C. 3,5 .
D. 3,1 .

Lời giải

Chọn B

$\hat C = {180^ \circ } – \hat A – \hat B = {180^ \circ } – {40^ \circ } – {60^ \circ } = {80^ \circ }$

Áp dụng định lý sin: $\frac{{BC}}{{sinA}} = \frac{{AB}}{{sinC}} \Rightarrow BC = \frac{{AB}}{{sinC}} \cdot sinA = \frac{5}{{sin{{80}^ \circ }}}sin{40^ \circ } \approx 3,3$.

Câu 30. Tam giác $ABC$ có $a = 16,8;\hat B = {56^0}{13’};\hat C = {71^ \circ }$. Cạnh $c$ bằng bao nhiêu?
A. 29,9 .
B. 14,1 .
C. 17,5 .
D. 19,9.

Lời giải

Chọn D

Ta có: Trong tam giác $ABC:\hat A + \hat B + \hat C = {180^ \circ } \Rightarrow \hat A = {180^ \circ } – {71^0} – {56^0}{13’} = {52^0}{47’}$.

Mặt khác $\frac{a}{{sinA}} = \frac{b}{{sinB}} = \frac{c}{{sinC}} \Rightarrow \frac{a}{{sinA}} = \frac{c}{{sinC}} \Rightarrow c = \frac{{a \cdot sinC}}{{sinA}} = \frac{{16,8 \cdot sin{{71}^0}}}{{sin{{52}^0}{{47}’}}} \simeq 19,9$.

Câu 31. Tính diện tích tam giác $ABC$ biết $AB = 3,BC = 5,CA = 6$.
A. $\sqrt {56} $
B. $\sqrt {48} $.
C. 6 .
D. 8 .

Lời giải

Chọn A

Ta có: $p = \frac{{AB + AC + BC}}{2} = \frac{{3 + 5 + 6}}{2} = 7$.

Vậy diện tích tam giác $ABC$ là: $S = \sqrt {p\left( {p – AB} \right)\left( {p – AC} \right)\left( {p – BC} \right)} = \sqrt {7\left( {7 – 3} \right)\left( {7 – 6} \right)\left( {7 – 5} \right)} = \sqrt {56} $.

Câu 32. Cho $\vartriangle ABC$ có $a = 6,b = 8,c = 10$. Diện tích $S$ của tam giác trên là:
A. 48 .
B. 24 .
C. 12 .
D. 30 .

Lời giải

Chọn B

Ta có: Nửa chu vi $\vartriangle ABC:p = \frac{{a + b + c}}{2}$.

Áp dụng công thức Hê-rông: $S = \sqrt {p\left( {p – a} \right)\left( {p – b} \right)\left( {p – c} \right)} = \sqrt {12\left( {12 – 6} \right)\left( {12 – 8} \right)\left( {12 – 10} \right)} = 24$.

Câu 33. Cho $\vartriangle ABC$ có $a = 4,c = 5,B = {150^ \circ }$. Diện tích của tam giác là:
A. $5\sqrt 3 $.
B. 5. C. 10 .
D. $10\sqrt 3 $.

Lời giải

Chọn B

Ta có: ${S_{\vartriangle ABC}} = \frac{1}{2}$ a.c. $sinB = \frac{1}{2} \cdot 4 \cdot 5 \cdot sin{150^0} = 5$.

Câu 34. Cho tam giác $ABC$ có $a = 4,b = 6,c = 8$. Khi đó diện tích của tam giác là:
A. $9\sqrt {15} $.
B. $3\sqrt {15} $.
C. 105 .
D. $\frac{2}{3}\sqrt {15} $.

Lời giải

Chọn B

Ta có: $p = \frac{{a + b + c}}{2} = \frac{{4 + 6 + 8}}{2} = 9$.

Suy ra: $S = \sqrt {p\left( {p – a} \right)\left( {p – b} \right)\left( {p – c} \right)} = 3\sqrt {15} $.

Câu 35. Cho tam giác $ABC$. Biết $AB = 2;BC = 3$ và $\widehat {ABC} = {60^ \circ }$. Tính chu vi và diện tích tam giác $ABC$.
A. $5 + \sqrt 7 $ và $\frac{3}{2}$.
B. $5 + \sqrt 7 $ và $\frac{{3\sqrt 3 }}{2}$.
C. $5\sqrt 7 $ và $\frac{{3\sqrt 3 }}{2}$.
D. $5 + \sqrt {19} $ và $\frac{3}{2}$.

Lời giải

Chọn B

Ta có: $A{C^2} = A{B^2} + B{C^2} – 2 \cdot AB \cdot BC \cdot cos\widehat {ABC} = 4 + 9 – 2 \cdot 2 \cdot 3 \cdot cos{60^ \circ } = 13 – 6 = 7$.

Suy ra $AC = \sqrt 7 $.

Chu vi tam giác $ABC$ là $AB + AC + BC = 2 + 3 + \sqrt 7 $.

Diện tích tam giác $ABC$ là ${S_{\vartriangle ABC}} = \frac{1}{2}AB \cdot BC \cdot sin\widehat {ABC} = \frac{1}{2} \cdot 2 \cdot 3 \cdot sin{60^ \circ } = \frac{{3\sqrt 3 }}{2}$.

Câu 36. Cho tam giác $\vartriangle ABC$ có $b = 7;c = 5;cosA = \frac{3}{5}$. Độ dài đường cao ${h_a}$ của tam giác $\vartriangle ABC$ là.
A. $\frac{{7\sqrt 2 }}{2}$.
B. 8 .
C. $8\sqrt 3 $
D. $80\sqrt 3 $

Lời giải

Chọn A

$a = \sqrt {{b^2} + {c^2} – 2bccosA} = \sqrt {{7^2} + {5^2} – 2.7 \cdot 5 \cdot \frac{3}{5}} = \sqrt {32} = 4\sqrt 2 $

$si{n^2}A = 1 – co{s^2}A = 1 – {\left( {\frac{3}{5}} \right)^2} = \frac{{16}}{{25}}$. Suy ra $\left[ {\begin{array}{*{20}{l}}
{sinA = \frac{4}{5}} \\
{sinA = – \frac{4}{5}}
\end{array}} \right.$ vì nên $sinA = \frac{4}{5}$

$S = \frac{1}{2}bcsinA = \frac{1}{2} \cdot 7 \cdot 5 \cdot \frac{4}{5} = 14$ mà $S = \frac{1}{2}a \cdot {h_a} \Leftrightarrow 14 = \frac{1}{2} \cdot 4\sqrt 2 \cdot {h_a} \Leftrightarrow {h_a} = \frac{{7\sqrt 2 }}{2}$

Câu 37. Cho tam giác $ABC$ có $AB = 2a;AC = 4a$ và $\widehat {BAC} = {120^ \circ }$. Tính diện tích tam giác $ABC$ ?
A. $S = 8{a^2}$.
B. $S = 2{a^2}\sqrt 3 $.
C. $S = {a^2}\sqrt 3 $.
D. $S = 4{a^2}$.

Lời giải

Chọn B

Diện tích của tam giác $ABC$ là ${S_{ABC}} = \frac{1}{2}AB \cdot AC \cdot sin\widehat {BAC} = \frac{1}{2} \cdot 2a \cdot 4a \cdot sin{120^ \circ } = 2{a^2}\sqrt 3 $.

Câu 38. Cho tam giác $ABC$ đều cạnh $a$. Bán kính đường tròn ngoại tiếp tam giác $ABC$ bằng
A. $\frac{{a\sqrt 3 }}{2}$.
B. $\frac{{a\sqrt 3 }}{3}$.
C. $\frac{{a\sqrt 3 }}{4}$.
D. $\frac{{a\sqrt 2 }}{2}$.

Lời giải

Chọn B

Gọi $G$ là trọng tâm $ABC$. Bán kính đường tròn ngoại tiếp $R = AG = \frac{2}{3}\frac{{a\sqrt 3 }}{2} = \frac{{a\sqrt 3 }}{3}$.

Câu 39. Cho tam giác $ABC$ có chu vi bằng 12 và bán kính đường tròn nội tiếp bằng 1 . Diện tích của tam giác $ABC$ bằng
A. 12 .
B. 3 .
C. 6 .
D. 24 .

Lời giải

Chọn C

Theo đề bài tam giác $ABC$ có chu vi bằng 12 nên nửa chu vi là $p = \frac{{12}}{2}$; bán kính đường tròn nội tiếp bằng 1 , tức là ta có: $r = 1$.

Diện tích tam giác $ABC$ là: $S = p \cdot r = 6.1 = 6$.

Câu 40. Cho tam giác $ABC$ đều cạnh $2a$. Tính bán kính $R$ của đường tròn ngoại tiếp tam giác $ABC$.
A. $\frac{{2a}}{{\sqrt 3 }}$.
B. $\frac{{4a}}{{\sqrt 3 }}$.
C. $\frac{{8a}}{{\sqrt 3 }}$.
D. $\frac{{6a}}{{\sqrt 3 }}$.

Lời giải

Chọn A

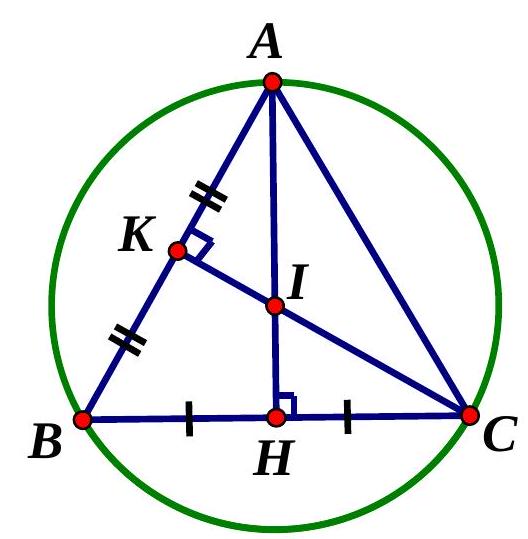
Gọi $H,K$ lần lượt là trung điểm cạnh $AB,BC$;

I là giao điểm của $AH$ và $CK$.

Lúc đó, I là tâm đường tròn ngoại tiếp tam giác $ABC$.

Ta có: $AH = \frac{{2a\sqrt 3 }}{2} = a\sqrt 3 $.

Do đó: $R = AI = \frac{2}{3}AH = \frac{2}{3}a\sqrt 3 = \frac{{2a}}{{\sqrt 3 }}$.

Câu 41. Cho tam giác $ABC$ có $BC = \sqrt 6 ,AC = 2$ và $AB = \sqrt 3 + 1$. Bán kính đường tròn ngoại tiếp tam giác $ABC$ bằng:
A. $\sqrt 5 $.
B. $\sqrt 3 $.
C. $\sqrt 2 $.
D. 2 .

Lời giải

Chọn C

Áp dụng định lý cosin ta có $cosA = \frac{{{b^2} + {c^2} – {a^2}}}{{2bc}} = \frac{1}{2}$ suy ra $A = {60^ \circ }$.

Áp dụng định lý sin ta có $R = \frac{a}{{2sinA}} = \sqrt 2 $.

Câu 42. Cho tam giác $ABC$ có $AB = 3,AC = 4,BC = 5$. Bán kính đường tròn nội tiếp tam giác bằng
A. 1 .
B. $\frac{8}{9}$.
C. $\frac{4}{5}$.
D. $\frac{5}{2}$.

Lời giải

Chọn A

Vì $A{B^2} + A{C^2} = B{C^2}$ nên tam giác $ABC$ vuông tại $A$.

Do đó bán kính đường tròn nội tiếp $r = \frac{S}{p} = \frac{{\frac{1}{2}AB \cdot AC}}{{\frac{1}{2}\left( {AB + AC + BC} \right)}} = \frac{{3.4}}{{3 + 4 + 5}} = 1$.

Câu 43. Cho $\vartriangle ABC$ có $S = 84,a = 13,b = 14,c = 15$. Độ dài bán kính đường tròn ngoại tiếp $R$ của tam giác trên là:
A. 8,125 .
B. 130 .
C. 8 .
D. 8,5 .

Lời giải

Chọn A

Ta có: ${S_{\vartriangle ABC}} = \frac{{a \cdot b \cdot c}}{{4R}} \Leftrightarrow R = \frac{{a \cdot b \cdot c}}{{4S}} = \frac{{13 \cdot 14 \cdot 15}}{{4.84}} = \frac{{65}}{8}$.

Câu 44. Tam giác với ba cạnh là 5;12;13 có bán kính đường tròn ngoại tiếp là?
A. 6 .
B. 8 .
C. $\frac{{13}}{2}$.
D. $\frac{{11}}{2}$.

Lời giải

Chọn C

Ta có: ${5^2} + {12^2} = {13^2} \Rightarrow R = \frac{{13}}{2}$.

Câu 45. Tam giác với ba cạnh là 5;12;13 có bán kính đường tròn nội tiếp tam giác đó bằng bao nhiêu?
A. 2 .
B. $2\sqrt 2 $.
C. $2\sqrt 3 $.
D. 3 .

Lời giải

Chọn A

Ta có: $p = \frac{{5 + 12 + 13}}{2} = 15$. Mà ${5^2} + {12^2} = {13^2} \Rightarrow S = \frac{1}{2} \cdot 5 \cdot 12 = 30$.

Mặt khác $S = p \cdot r \Rightarrow r = \frac{S}{p} = 2$.

Câu 46. Tam giác với ba cạnh là 6;8;10 có bán kính đường tròn ngoại tiếp bằng bao nhiêu?
A. 5 .
B. $4\sqrt 2 $.
C. $5\sqrt 2 $.
D. 6 .

Lời giải

Chọn A

Ta có: ${6^2} + {8^2} = {10^2} \Rightarrow R = \frac{{10}}{2} = 5$. .

Câu 47. Cho $\vartriangle ABC$ có $S = 10\sqrt 3 $, nửa chu vi $p = 10$. Độ dài bán kính đường tròn nội tiếp $r$ của tam giác trên là:
A. 3 .
B. 2 .
C. $\sqrt 2 $.
D. $\sqrt 3 $.

Lời giải

Chọn D

Ta có: $S = pr \Rightarrow r = \frac{S}{p} = \frac{{10\sqrt 3 }}{{10}} = \sqrt 3 $.

Câu 48. Cho hình chữ nhật $ABCD$ có cạnh $AB = 4,BC = 6,M$ là trung điểm của $BC,N$ là điểm trên cạnh $CD$ sao cho $ND = 3NC$. Khi đó bán kính của đường tròn ngoại tiếp tam giác $AMN$ bằng
A. $3\sqrt 5 $.
B. $\frac{{3\sqrt 5 }}{2}$.
C. $5\sqrt 2 $.
D. $\frac{{5\sqrt 2 }}{2}$.

Lời giải

Chọn D

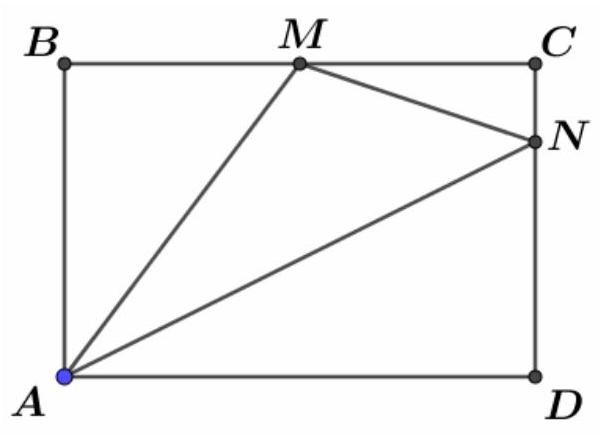
Ta có

$\begin{array}{*{20}{r}}
{}&{MC = 3,NC = 1 \Rightarrow MN = \sqrt {10} } \\
{}&{BM = 3,AB = 4 \Rightarrow AM = 5} \\
{}&{AD = 6,ND = 3 \Rightarrow AN = \sqrt {45} } \\
{}&{p = \frac{{AM + AN + MN}}{2} = \frac{{\sqrt {10} + 5 + \sqrt {45} }}{2}} \\
{}&{{S_{AMN}} = \sqrt {p\left( {p – AM} \right)\left( {p – AN} \right)\left( {p – MN} \right)} = \frac{{15}}{2}}
\end{array}$

Bán kính của đường tròn ngoại tiếp của tam giác $AMN$ là: $R = \frac{{AM \cdot AN \cdot MN}}{{4{S_{AMN}}}} = \frac{{5\sqrt 2 }}{2}$

Câu 49. Cho hình bình hành $ABCD$ có $AB = a,BC = a\sqrt 2 $ và $\widehat {BAD} = {135^ \circ }$. Diện tích của hình bình hành $ABCD$ bằng
A. ${a^2}$.
B. ${a^2}\sqrt 2 $.
C. ${a^2}\sqrt 3 $.
D. $2{a^2}$.

Lời giải

Chọn A.

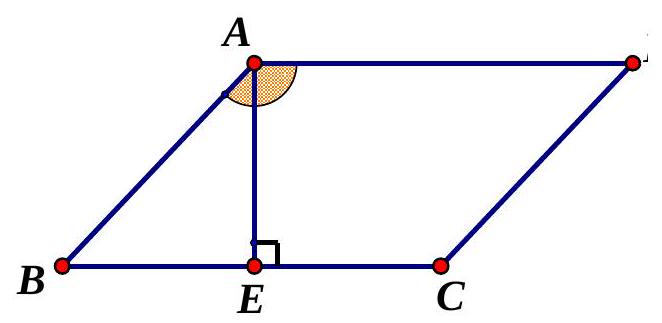
Ta có $\widehat {ABC} = {45^ \circ }$.

Gọi $AE$ kà đường cao của tam giác $ABC$, khi đó tam giác $AEB$ vuông cân tại $E$.

Suy ra $AE = \frac{1}{2}BC = \frac{{a\sqrt 2 }}{2}$.

Vậy diện tích hình bình hành $ABCD$ là $AE \cdot BC = \frac{{a\sqrt 2 }}{2} \cdot a\sqrt 2 = {a^2}$.

Câu 50. Cho tứ giác lồi $ABCD$ có $\widehat {ABC} = \widehat {ADC} = {90^ \circ },\widehat {BAD} = {120^ \circ }$ và $BD = a\sqrt 3 $. Tính $AC$.
A. $AC = 2a$.
B. $AC = a\sqrt 3 $.
C. $AC = a$.
D. $AC = a\sqrt 5 $.

Lời giải

Chọn A.

Cách 1:

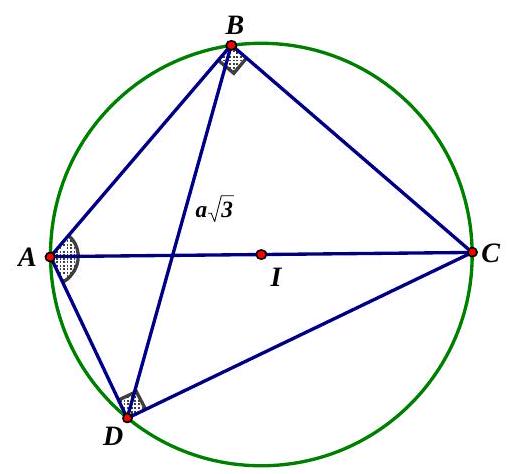
$\vartriangle ABD$ nội tiếp đường tròn đường kính $AC$

Áp dụng định sin trong $\vartriangle ABD$, ta có $AC = 2R = \frac{{BD}}{{sinBAD}} = \frac{{a\sqrt 3 }}{{sin{{120}^ \circ }}} = 2a$.

Cách 2:

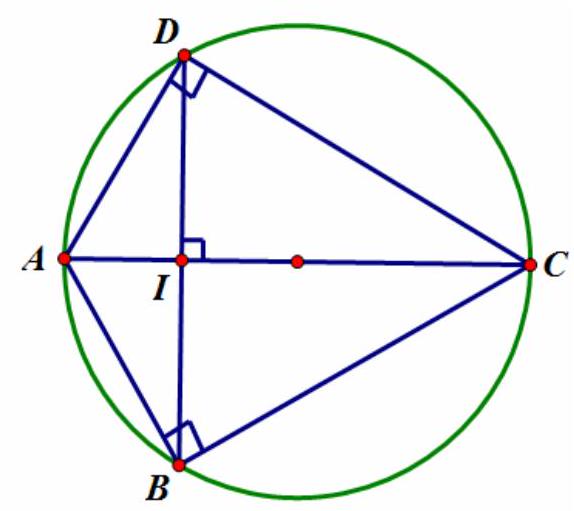
Đề không mất tính tổng quát ta có thể chọn $BD \bot AC$ tại $I$.

Ta có $\hat C = {360^ \circ } – \left( {\hat A + \hat B + \hat D} \right) = {360^ \circ } – \left( {{{120}^ \circ } + {{90}^ \circ } + {{90}^ \circ }} \right) = {60^ \circ }$.

Do $BD \bot AC \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{AB = AD} \\
{CB = CD}
\end{array}} \right.$.
Suy ra $\vartriangle BCD$ là tam giác đều cạnh bằng $a\sqrt 3 $.

Ta có $CI = \frac{{3a}}{2}$.

Xét $\vartriangle AID$ vuông tại $I,ID = \frac{1}{2}BD = \frac{{a\sqrt 3 }}{2}$.

Suy ra $AI = \frac{{ID}}{{tan\frac{A}{2}}} = \frac{{\frac{{a\sqrt 3 }}{2}}}{{tan{{60}^ \circ }}} = \frac{a}{2}$.

Ta có $AC = AI + CI = \frac{a}{2} + \frac{{3a}}{2} = 2a$.

Vậy $AC = 2a$.