Các Dạng Toán Bài Hệ Thức Lượng Trong Tam Giác Giải Chi Tiết

Các dạng toán bài hệ thức lượng trong tam giác giải chi tiết được soạn dưới dạng file word và PDF gồm 4 trang. Các bạn xem và tải về ở dưới.

DẠNG 1: XÁC ĐỊNH CÁC YẾU TỐ TRONG TAM GIÁC

Bài 1. Cho tam giác $ABC$ có $AB = 4,AC = 6,\hat A = {120^ \circ }$. Tính độ dài cạnh $BC$

Lời giải

$B{C^2} = A{B^2} + A{C^2} – 2AB \cdot AC \cdot cosA = {6^2} + {4^2} – 2 \cdot 6 \cdot 4 \cdot cos{120^0} = {6^2} + {4^2} – 2 \cdot 6 \cdot 4 \cdot \frac{{ – 1}}{2} = 76$

$ \Rightarrow BC = \sqrt {76} = 2\sqrt {19} $

Bài 2. Cho tam giác $ABC$ có $a = 10,\hat A = {45^ \circ },\hat B = {70^ \circ }$. Tính $R,b,c$.

Lời giải

Áp dụng định lý sin ta có $\frac{a}{{sinA}} = 2R \Rightarrow R = \frac{a}{{2sinA}} = \frac{{10}}{{2 \cdot sin{{45}^ \circ }}} = 5\sqrt 2 $.

Ta có $\frac{a}{{sinA}} = \frac{b}{{sinB}} \Rightarrow b = \frac{{asinB}}{{sinA}} = \frac{{10 \cdot sin{{70}^ \circ }}}{{sin{{45}^ \circ }}} \approx 13,289$

Vì $\hat A + \hat B + \hat C = {180^ \circ } \Rightarrow \hat C = {180^ \circ } – \hat A – \hat B = {65^ \circ } \Rightarrow c = \frac{{asinC}}{{sinA}} = \frac{{10 \cdot sin{{65}^ \circ }}}{{sin{{45}^ \circ }}} \approx 12,82$

Bài 3. Cho tam giác $ABC$ có $a = 7;b = 8;c = 5$. Tính $\hat A,S,{h_a},R$.

Lời giải

$ + S = \frac{1}{2}$ b.c. $sinA = \frac{1}{2} \cdot 8 \cdot 5 \cdot sin{60^ \circ } = 10\sqrt 3 $.

• Ta có: $S = \frac{1}{2}a \cdot {h_a} \Rightarrow {h_a} = \frac{{2S}}{a} = \frac{{2 \cdot 10\sqrt 3 }}{7} = \frac{{20\sqrt 3 }}{7}$.

• Ta có: $S = \frac{{a \cdot b \cdot c}}{{4R}} \Rightarrow R = \frac{{a \cdot b \cdot c}}{{4S}} = \frac{{7 \cdot 8 \cdot 5}}{{4 \cdot 10\sqrt 3 }} = \frac{{7\sqrt 3 }}{3}$.

Bài 4. Cho tam giác $ABC$ có $a = 6,b = 5,c = 8$. Tính $cosA,S,r$.

Lời giải

Ta có $cosA = \frac{{{b^2} + {c^2} – {a^2}}}{{2bc}} = \frac{{{5^2} + {8^2} – {6^2}}}{{2.5.8}} = \frac{{53}}{{80}}$

Nửa chu vi là $P = \frac{{a + b + c}}{2} = \frac{{6 + 5 + 8}}{2} = \frac{{19}}{2}$. Áp dụng công thức Heron ta có: $S = \sqrt {p\left( {p – a} \right)\left( {p – b} \right)\left( {p – c} \right)} = \sqrt {\frac{{19}}{2}\left( {\frac{{19}}{2} – 6} \right)\left( {\frac{{19}}{2} – 5} \right)\left( {\frac{{19}}{2} – 8} \right)} = \frac{{3\sqrt {399} }}{4}$

Do $S = p.r \Rightarrow r = \frac{S}{p} = \frac{{3\sqrt {399} }}{{38}}$.

Bài 5. Tam giác $ABC$ vuông tại $A$ có $AC = 6\;cm,BC = 10\;cm$. Tính bán kính đường tròn nội tiếp tam giác $ABC$.

Lời giải

Do tam giác $ABC$ vuông tại $A$ có $AC = 6\;cm,BC = 10\;cm$ nên

$AB = \sqrt {B{C^2} – A{C^2}} = \sqrt {{{10}^2} – {6^2}} = 8$.

Diện tích tam giác $ABC$ là ${S_{\vartriangle ABC}} = \frac{1}{2}AB \cdot AC = 24$.

Bán kính đường tròn nội tiếp tam giác $ABC$ là $r = \frac{{2{S_{\vartriangle ABC}}}}{{AB + BC + CA}} = \frac{{2.24}}{{6 + 8 + 10}} = 2$.

Bài 6. Cho tam giác $ABC$ có $b = 7,c = 5,cosA = \frac{3}{5}$. Tính độ dài đường cao ${h_a}$ của tam giác $ABC$.

Lời giải

Theo định lí hàm cos ta có ${a^2} = {b^2} + {c^2} – 2bccosA = 49 + 25 – 2.7 \cdot 5 \cdot \frac{3}{5} = 32 \Rightarrow a = 4\sqrt 2 $.

Ta lại có: $cosA = \frac{3}{5} \Rightarrow sinA = \frac{4}{5}$.

Diện tích tam giác $ABC$ là ${S_{\vartriangle ABC}} = \frac{1}{2}bcsinA = \frac{1}{2} \cdot 7 \cdot 5 \cdot \frac{4}{5} = 14$.

Vì ${S_{\vartriangle ABC}} = \frac{1}{2}a \cdot {h_a}$ nên ${h_a} = \frac{{2{S_{\vartriangle ABC}}}}{a} = \frac{{28}}{{4\sqrt 2 }} = \frac{{7\sqrt 2 }}{2}$

Vậy ${h_a} = \frac{{7\sqrt 2 }}{2}$.

Bài 7. Cho tam giác ABC có $a = 13,b = 8,c = 7$. Tính góc $A$, suy ra $S,{h_a},R,r$.

Lời giải

${a^2} = {b^2} + {c^2} – 2bccosA \Rightarrow cosA = \frac{{{b^2} + {c^2} – {a^2}}}{{2bc}} = – \frac{1}{2} \Rightarrow A = {120^ \circ }$

$S = \frac{1}{2}bcsinA = \frac{1}{2}56 \cdot \frac{{\sqrt 3 }}{2} = 14\sqrt 3 $

$S = \frac{1}{2}a \cdot {h_a} \Rightarrow {h_a} = \frac{{2S}}{a} = \frac{{28\sqrt 3 }}{{13}}$

$S = \frac{{abc}}{{4R}} \Rightarrow R = \frac{{abc}}{{4S}} = \frac{{7.8.13}}{{4.14\sqrt 3 }} = \frac{{13\sqrt 3 }}{3}$

$S = p.r \Rightarrow r = \frac{{2S}}{{a + b + c}} = \frac{{2.14\sqrt 3 }}{{7 + 8 + 13}} = \sqrt 3 $

Bài 8. Cho tam giác $ABC$ cân tại A biết $a = \sqrt 3 ;\hat B = \hat C = {30^0}$. Tính $R,r$, cạnh c, b, suy ra $S$

Lời giải

Áp dụng định lí sin:

$\frac{a}{{sinA}} = 2R \Rightarrow R = \frac{a}{{2sinA}} = \frac{{\sqrt 3 }}{{2\frac{{\sqrt 3 }}{2}}} = 1 \Rightarrow b = c = 2Rsin{30^ \circ } = 1$

$S = \frac{1}{2}b \cdot csinA = \frac{{\sqrt 3 }}{4}$

$r = \frac{S}{p} = \frac{{\sqrt 3 }}{2}\left( {2 – \sqrt 3 } \right)$.

DẠNG 2: GIẢI TAM GIÁC

Bài 1. Giải tam giác $ABC$ biết $\hat A = {60^ \circ },\hat B = {40^ \circ },c = 14$

Lời giải

Ta có $\hat C = {180^ \circ } – \hat A – \hat B = {180^ \circ } – {60^ \circ } – {40^ \circ } = {80^ \circ }$

Theo định lí sin ta có

$\begin{array}{*{20}{r}}
{}&{a = \frac{{csinA}}{{sinC}} = \frac{{14 \cdot sin{{60}^ \circ }}}{{sin{{80}^ \circ }}} \Rightarrow a \approx 12,3} \\
{}&{b = \frac{{csinB}}{{sinC}} = \frac{{14 \cdot sin{{40}^ \circ }}}{{sin{{80}^ \circ }}} \Rightarrow b \approx 9,1}
\end{array}$

Bài 2. Giải tam giác $ABC$, biết:

Lời giải

Ta có $\hat B = {180^ \circ } – \hat A – \hat C = {180^ \circ } – {30^ \circ } – {75^ \circ } = {75^ \circ } = \hat C$

suy ra tam giác $ABC$ cận tại $A \Rightarrow c = b = 4,5$.

Theo định lí sin ta có

$a = \frac{{bsinA}}{{sinB}} = \frac{{4,5 \cdot sin{{30}^ \circ }}}{{sin{{75}^ \circ }}} \Rightarrow a \approx 2,33.$

Bài 3. Giải tam giác $ABC$ và tính diện tích của tam giác đó, biết $\hat A = {15^ \circ },\hat B = {130^ \circ },c = 6$.

Lời giải

Ta có $\hat A + \hat B + \hat C = {180^ \circ } \Rightarrow \hat C = {180^ \circ } – \hat A – \hat B = {35^ \circ }$

Áp dụng định lý sin ta có: $\frac{a}{{sinA}} = \frac{b}{{sinB}} = \frac{c}{{sinC}} \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{a = \frac{{csinA}}{{sinC}} = \frac{{6sin{{15}^ \circ }}}{{sin{{35}^ \circ }}} \approx 2,71} \\
{b = \frac{{csinB}}{{sinC}} = \frac{{6sin{{130}^ \circ }}}{{sin{{35}^ \circ }}} \approx 8,01}
\end{array}} \right.$

Diện tích của tam giác là: $S = \frac{1}{2}$ a.c. $sinB = \frac{1}{2} \cdot 2,71 \cdot 6 \cdot sin{130^ \circ } \approx 6,228$

DẠNG 3: CHỨNG MINH HỆ THỨC-NHẬN DẠNG TAM GIÁC

Bài 1. Cho tam giác $ABC$ thỏa mãn $si{n^2}A = sinB \cdot sinC$.

a) Chứng minh ${a^2} = bc$

b) Chứng minh $cosA \geqslant \frac{1}{2}$

Lời giải

a) Áp dụng định lí $sin$ ta có $sinA = \frac{a}{{2R}},sinB = \frac{b}{{2R}},sinC = \frac{C}{{2R}}$

Suy ra $si{n^2}A = sinB \cdot sinC \Leftrightarrow {\left( {\frac{a}{{2R}}} \right)^2} = \frac{b}{{2R}} \cdot \frac{c}{{2R}} \Leftrightarrow {a^2} = bc$ đpcm

b) Áp dụng định lí côsin và câu a) ta có

$cosA = \frac{{{b^2} + {c^2} – {a^2}}}{{2bc}} = \frac{{{b^2} + {c^2} – bc}}{{2bc}} \geqslant \frac{{2bc – bc}}{{2bc}} = \frac{1}{2}Apcm$

Bài 2. Tam giác $ABC$ có $BC = a,CA = b,AB = c$. Chứng minh $si{n^2}A = 2\left( {si{n^2}B – si{n^2}C} \right)$

Lời giải

Theo định lí sin ta có

$\frac{a}{{sinA}} = \frac{b}{{sinB}} = \frac{c}{{sinC}} = 2R \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{{a^2} = 4{R^2}si{n^2}A} \\
{{b^2} = 4{R^2}si{n^2}B} \\
{{c^2} = 4{R^2}si{n^2}C}
\end{array}} \right.$

Thay vào (*) ta có đpcm

Bài 3. Chứng minh rằng trong mọi tam giác $ABC$ ta có;

a) $a = b \cdot cosC + c \cdot cosB$

b) $sinA = sinBcosC + sinCcosB$

Lời giải

a) Áp dụng định lí côsin ta có:

$\begin{array}{*{20}{r}}
{}&{VP = b \cdot \frac{{{a^2} + {b^2} – {c^2}}}{{2ab}} + c \cdot \frac{{{c^2} + {a^2} – {b^2}}}{{2ca}}} \\
{}&{\; = \frac{{{a^2} + {b^2} – {c^2} + {c^2} + {a^2} – {b^2}}}{{2a}} = a = VT}
\end{array}$

b) $sinA = sinBcosC + sinCcosB \Leftrightarrow \frac{a}{{2R}} = \frac{b}{{2R}} \cdot cosC + \frac{c}{{2R}} \cdot cosB$

$ \Leftrightarrow a = b \cdot cosC + c \cdot cosB$

Bài 4. Cho tam giác $ABC$. Chứng minh tam giác $ABC$ cân nếu ${h_a} = c$. sin $A$

Lời giải

Sử dụng công thức $S = \frac{1}{2}a{h_a} = \frac{1}{2}bcsinA\left( * \right)$ thay ${h_a} = c \cdot sinA$ vào $\left( * \right)$ được:

$b{h_a} = a{h_a} \Leftrightarrow a = $ b suy ra tam giác $ABC$ cân tại $C$

Bài 5. Chứng minh trong tam giác $ABC$ ta có: ${h_a} = 2R \cdot sinB \cdot sinC$

Lời giải

Áp dụng định lí sin trong tam giác ta có: $\frac{b}{{sinB}} = 2R \Rightarrow 2R \cdot sinB = b$

Do đó: ${h_a} = 2R \cdot sinB \cdot sinC \Leftrightarrow {h_a} = b \cdot sinC$ ( đúng)

Bài 6. Cho tam giác $ABC$ thỏa $\frac{{sinA}}{{sinB}} = 2cosC$. Tam giác $ABC$ là tam giác gì?

Lời giải

Ta có: $\frac{{sinA}}{{sinB}} = 2cosC$

$ \Leftrightarrow \frac{a}{b} = 2cosC$

$ \Leftrightarrow a = 2b \cdot cosC$

$ \Leftrightarrow a = 2b \cdot \frac{{{a^2} + {b^2} – {c^2}}}{{2ab}}$

$ \Leftrightarrow {a^2} = {a^2} + {b^2} – {c^2} \Leftrightarrow b = c$

Tam giác $ABC$ cân tại $A$.

Bài 7. Cho tam giác $ABC$. Chứng minh $S = $ R.r. $\left( {sinA + sinB + sinC} \right)$.

Lời giải

Ta có $:VP = R \cdot r \cdot \left( {\frac{a}{{2R}} + \frac{b}{{2R}} + \frac{c}{{2R}}} \right) = r \cdot \left( {\frac{{a + b + c}}{2}} \right) = r \cdot p = S($ đpcm $)$.

Bài 8. Cho tam giác $ABC$ thỏa $\left\{ {\begin{array}{*{20}{l}}
{\frac{{{b^3} + {c^3} – {a^3}}}{{b + c – a}} = {a^2}} \\
{a = 2b \cdot cosC}
\end{array}} \right.$. Chứng minh tam giác $ABC$ là tam giác đều.

Lời giải

Ta có:

$\left\{ {\begin{array}{*{20}{c}}
{\frac{{{b^3} + {c^3} – {a^3}}}{{b + c – a}} = {a^2}} \\
{a = 2b \cdot c\;o\;sC}
\end{array}} \right.$

$ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}
{{b^3} + {c^3} – {a^3} = {a^2}b + {a^2}c – {a^3}} \\
{a = 2b \cdot \frac{{{a^2} + {b^2} – {c^2}}}{{2ab}}}
\end{array}} \right.$

$ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}
{\left( {b + c} \right)\left( {{b^2} – bc + {c^2} – {a^2}} \right) = 0} \\
{a = \frac{{{a^2} + {b^2} – {c^2}}}{a}}
\end{array}} \right.$

$ \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}
{ – bc + 2bc \cdot c\;o\;sA = 0} \\
{{b^2} = {c^2}}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}
{c\;o\;sA = \frac{1}{2}} \\
{b = c}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}
{A = {{60}^ \circ }} \\
{b = c}
\end{array}} \right.} \right.} \right.$

Vì tam giác $ABC$ cân có 1 góc bằng ${60^ \circ }$ nên tam giác $ABC$ là tam giác đều.

Bài 9. Chứng minh trong tam giác $ABC$ ta có: $sinB \cdot cosC + sinC \cdot cosB = sinA$

Lời giải

$VT = \frac{b}{{2R}} \cdot \frac{{{a^2} + {b^2} – {c^2}}}{{2ab}} + \frac{c}{{2R}} \cdot \frac{{{a^2} + {c^2} – {b^2}}}{{2ac}} = \frac{{{a^2} + {b^2} – {c^2}}}{{4aR}} + \frac{{{a^2} + {c^2} – {b^2}}}{{4aR}} = \frac{{2{a^2}}}{{4aR}} = \frac{a}{{2R}} = sinA$

Bài 10. Tìm tính chất đặc biệt của tam giác $ABC$ biết: $2acosA = b \cdot cosC + c \cdot cosB$

Lời giải

Yêu cầu bài toán tương đương với:

$2\left( {2RsinA} \right)cosA = \left( {2RsinB} \right)cosC + 2RsinCcosB$

$ \Leftrightarrow 2sinA \cdot cosA = sin\left( {B + C} \right) = sinA$

$ \Leftrightarrow cosA = \frac{1}{2}\left( {do\;sinA \ne 0} \right) \Leftrightarrow \hat A = {60^ \circ }$

Bài 11. Nhận dạng tam giác $ABC$ biết: $\left\{ {\begin{array}{*{20}{l}}
{a = 2bcosC} \\
{{a^2} = \frac{{{a^3} – {b^3} – {c^3}}}{{a – b – c}}}
\end{array}} \right.$

Lời giải

$\left\{ {\begin{array}{*{20}{l}}
{a = 2bcosC} \\
{{a^2} = \frac{{{a^3} – {b^3} – {c^3}}}{{a – b – c}}}
\end{array}} \right.$

Áp dụng định lí cosin ở (1) và thế vào (2)

$\left( 1 \right) \Leftrightarrow a = \frac{{{a^2} + {b^2} – {c^2}}}{a} \Leftrightarrow b = c$

$\left( 2 \right) \Leftrightarrow {a^2} = {b^2} + {c^2} – bc$

$ \Leftrightarrow cosA = \frac{1}{2} \Leftrightarrow \hat A = {60^ \circ }$

Vây tam giác $ABC$ dều.

Bài 12. Nhận dạng tam giác $ABC$ biết: $a \cdot sinA + bsinB + csinC = {h_a} + {h_b} + {h_c}$

Lời giải

Áp dụng công thức diện tích ta có $S = \frac{1}{2}bcsinA = \frac{1}{2}a{h_a}$ suy ra

$a \cdot sinA + bsinB + csinC = {h_a} + {h_b} + {h_c} \Leftrightarrow a \cdot \frac{{2S}}{{bc}} + b \cdot \frac{{2S}}{{ca}} + c \cdot \frac{{2S}}{{ab}} = \frac{{2S}}{a} + \frac{{2S}}{b} + \frac{{2S}}{c}$

$ \Leftrightarrow {a^2} + {b^2} + {c^2} = ab + bc + ca$

$ \Leftrightarrow {(a – b)^2} + {(b – c)^2} + {(c – a)^2} = 0$

$ \Leftrightarrow a = b = c$

Vậy tam giác $ABC$ dều.

DẠNG 4: ỨNG DỤNG THỰC TẾ

Bài 1. Một tàu đánh cá xuất phát từ cảng $A$, đi theo hướng $S{70^ \circ }E$ với vận tốc $70\;km/h$. Đi được 90 phút thì động cơ của tàu bị hỏng nên tàu trôi tự do theo hướng nam với vận tốc $8\;km/h$. Sau 2 giờ kể từ khi động cơ bị hỏng, tàu neo đậu được vào một hòn đảo.

a) Tính khoảng cách từ cảng $A$ tới đảo nơi tàu neo đậu.

b) Xác định hướng từ cảng $A$ tới đảo nơi tàu neo đậu.

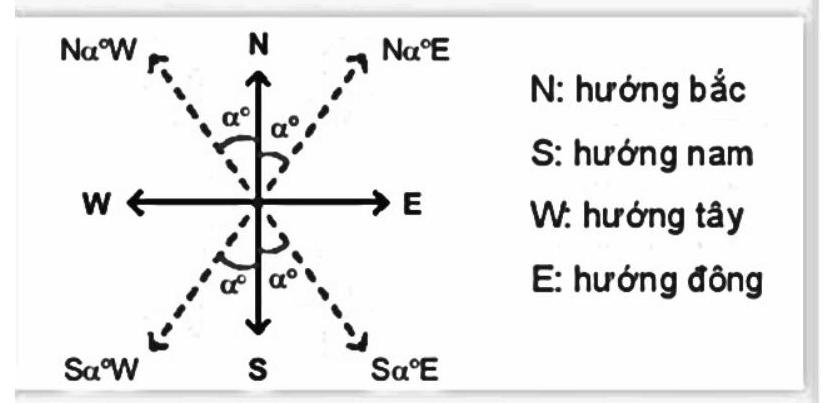
Hướng $S{\alpha ^ \circ }E$ là hướng tạo với hướng nam góc ${\alpha ^ \circ }$ và tạo với hướng đông góc ${90^ \circ } – {\alpha ^ \circ }$. Các hướng $S{\alpha ^ \circ }W,N{\alpha ^ \circ }E,N{\alpha ^ \circ }W$ cũng được định nghĩa một cách tương tự.

Lời giải

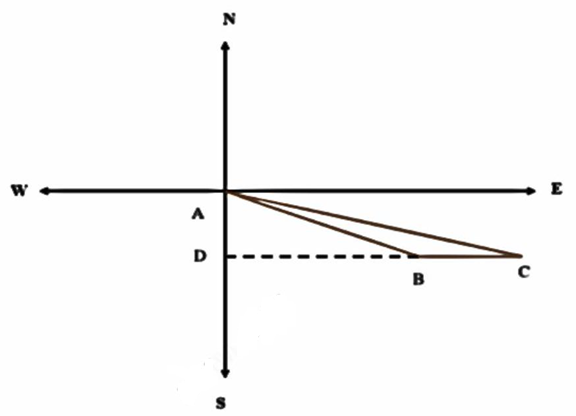
a) Theo giả thiết ta có: $AB = 105\;km,BC = 16\;km$,

Góc $\widehat {BAD} = {70^ \circ },\widehat {ABD} = {20^ \circ } \Rightarrow \widehat {ABC} = {160^ \circ }$

Khoảng cách từ $A$ tới đảo tàu neo đậu bằng đoạn $AC$.

Áp dụng định lý côsin ta có:

$AC = \sqrt {A{B^2} + B{C^2} – 2AB \cdot BC \cdot cosB} $

$ = \sqrt {{{105}^2} + {{16}^2} – 2 \cdot 105 \cdot 16 \cdot cos{{160}^ \circ }} = 120,16\;km$

b) Ta có $cosA = \frac{{A{B^2} + A{C^2} – B{C^2}}}{{2AB \cdot AC}} \approx 0,999 \Rightarrow \hat A \approx {2^ \circ }{37′} \Rightarrow \widehat {NAC} = {107^ \circ }{23′}$.

Vậy hướng từ cảng $A$ tới đảo nơi tàu neo đậu là hướng Đông.

Bài 2. Trên nóc một tòa nhà có một cột ăng-ten cao $5\;m$. Từ một vị trí quan sát $A$ cao $7\;m$ so với mặt đất có thể nhìn thấy đỉnh $B$ và chân $C$ của cột ăng-ten, với các góc tương ứng là ${50^ \circ }$ và ${40^ \circ }$ so với phương nằm ngang

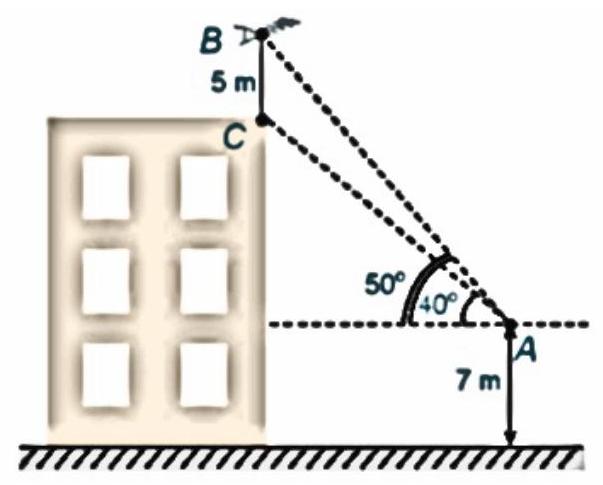
Hinh 3.18

a) Tính các góc của tam giác $ABC$.

b) Tính chiều cao của tòa nhà.

Lời giải

a) Ta có $\widehat {BAC} = {50^ \circ } – {40^ \circ } = {10^ \circ },\widehat {ABC} = {90^ \circ } – \widehat {BAD} = {40^ \circ } \Rightarrow \widehat {ACB} = {180^ \circ } – \widehat {ABC} – \widehat {BAC} = {130^ \circ }$

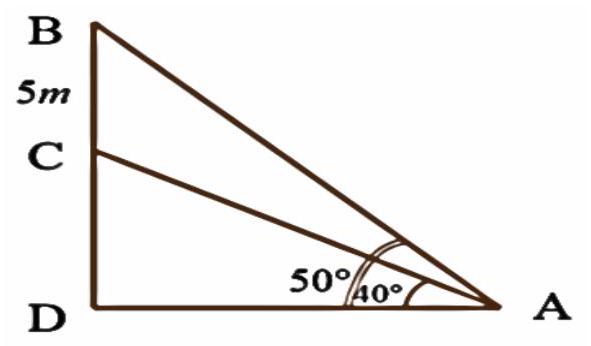
b) Áp dụng định lý sin trong tam giác $ABC$ ta có

$\frac{{BC}}{{sinA}} = \frac{{AC}}{{sinB}} \Rightarrow AC = \frac{{BC \cdot sinB}}{{sinA}} = \frac{{5 \cdot sin{{40}^ \circ }}}{{sin{{10}^ \circ }}} \approx 18,51$.

Xét tam giác $ACD$ vuông tại $D$ có $CD = AC \cdot sin{40^ \circ } \approx 11,9$

Vậy chiều cao của tòa nhà là: $11,9 + 7 = 18,9m$.

Bài 3. Từ bãi biển Vũng Chùa, Quảng Bình, ta có thể ngắm được Đảo Yến. Hãy đề xuất một cách xác định bề rộng của hòn đảo (theo chiều ta ngắm được). Đảo Yến nhìn tù bãi biển Vũng Chùa, Quảng Bình

Lời giải

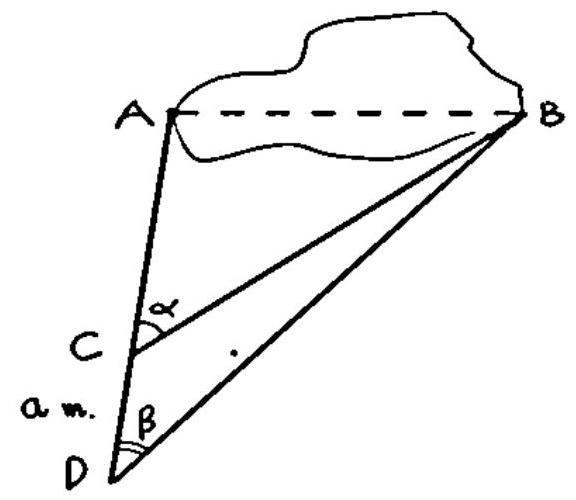
Gọi $A,B$ là hai vị trí ngoài cùng mà ta quan sát khi nhìn từ bãi biển

Từ một điểm $C$ trên bãi biển dùng giác kế ta xác định được góc $\widehat {ACB} = \alpha $.

Lấy điểm $D$ trên bãi biển sao cho $A,C,D$ thẳng hàng và có độ dài đoạn $CD = a$ mét. Ta xác định được $\widehat {ADB} = \beta $.

Từ đó áp dụng định lí sin cho hai tam giác $BCD$ và $ABC$ ta xác định được bề rộng $AB$ của hòn đảo.

Bài 4. Để tránh núi, đường giao thông hiện tại phải đi vòng như mô hình trong hình vẽ dưới. Để rút ngắn khoảng cách và tránh sạt lở núi, người ta dự định làm đường hầm xuyên núi, nối thẳng từ $A$ tới $D$. Hỏi độ dài đường mới sẽ giảm bao nhiêu kilômét so với đường cũ?

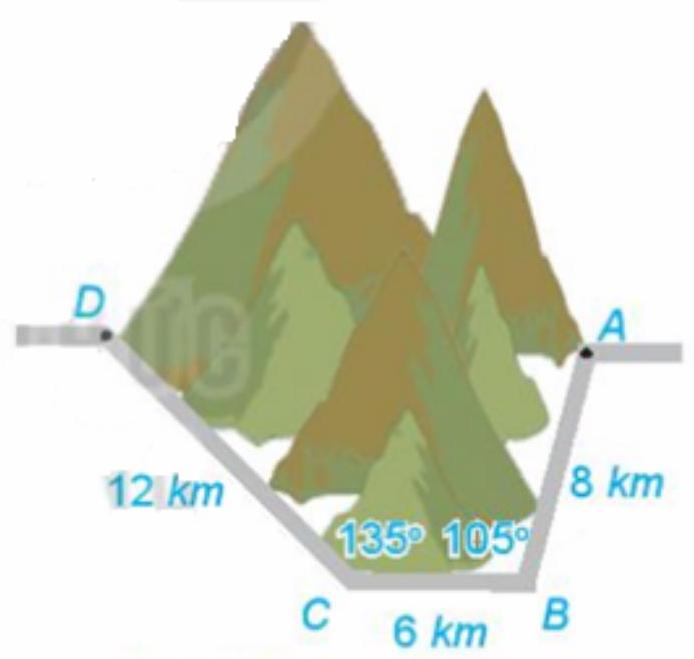
Lời giải

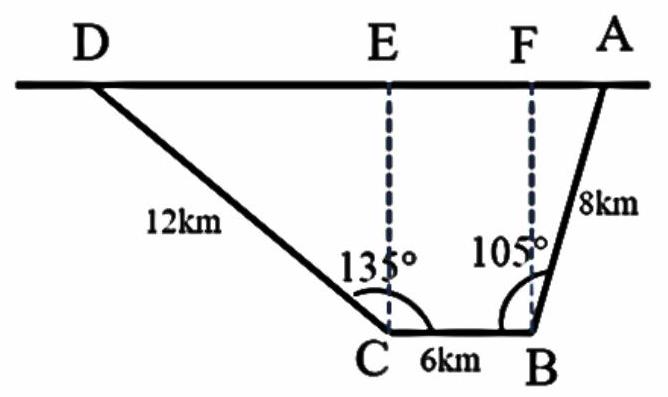
Dựng $CE,BF$ vuông góc với $AD$.

Xét tam giác $CDE$ vuông tại $E$ có $\hat D = \hat C = {45^ \circ }$

$ \Rightarrow DE = CD \cdot sin{45^ \circ } = 6\sqrt 2 \;km$. Xét tam giác $ABF$ vuông tại $F$ có $\hat B = {15^ \circ } \Rightarrow AF = AB \cdot sin{15^ \circ } = \left( {2\sqrt 6 – 2\sqrt 2 } \right)km$.

Mặt khác $EF = BC = 6\;km$

$ \Rightarrow AD = DE + EF + FA = 6 + 4\sqrt 2 + 2\sqrt 6 \approx 16,56\;km$.

Vậy độ dài đường mới sẽ giảm 9,44 km so với đường cũ.

Bài 5. Hai chiếc tàu thuỷ cùng xuất phát từ vị trí $A$, đi thẳng theo hai hướng tạo với nhau một góc ${60^ \circ }$. Tàu thứ nhất chạy với tốc độ $30\;km/h$, tàu thứ hai chạy với tốc độ $40\;km/h$. Hỏi sau 2 giờ hai tàu cách nhau bao nhiêu $km$ ?

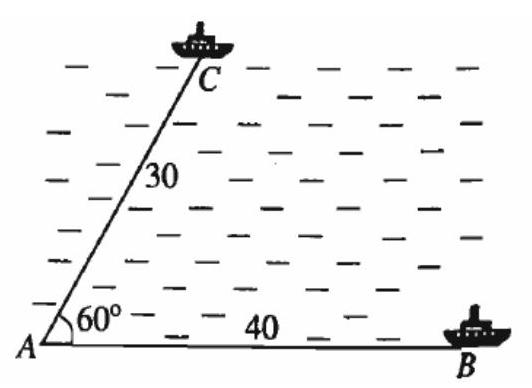
Lời giải

Ta có: Sau $2h$ quãng đường tàu thứ nhất chạy được là: ${S_1} = 30.2 = 60\;km$.

Sau $2h$ quãng đường tàu thứ hai chạy được là: ${S_2} = 40.2 = 80\;km$.

Vậy: sau $2h$ hai tàu cách nhau là: $S = \sqrt {S_1^2 + S_2^2 – 2{S_1} \cdot {S_2} \cdot cos{{60}^ \circ }} = 20\sqrt {13} $.

Bài 6. Từ một đỉnh tháp chiều cao $CD = 80\;m$, người ta nhìn hai điểm $A$ và $B$ trên mặt đất dưới các góc nhìn là ${72^0}{12′}$ và ${34^0}{26′}$ so với phương nằm ngang. Ba điểm $A,B,D$ thẳng hàng. Tính khoảng cách $AB$ (chính xác đến hàng đơn vị)?

Lời giải

Ta có: Trong tam giác vuông $CDA:tan{72^0}{12′} = \frac{{CD}}{{AD}} \Rightarrow AD = \frac{{CD}}{{tan{{72}^0}{{12}’}}} = \frac{{80}}{{tan{{72}^0}{{12}’}}} \simeq 25,7$.

Trong tam giác vuông $CDB:tan{34^ \circ }{26′} = \frac{{CD}}{{BD}} \Rightarrow BD = \frac{{CD}}{{tan{{34}^0}{{26}’}}} = \frac{{80}}{{tan{{34}^0}{{26}’}}} \simeq 116,7$.

Suy ra: khoảng cách $AB = 116,7 – 25,7 = 91m$.