20 Câu Trắc Nghiệm Nhận Dạng Tam Giác Lớp 10 Giải Chi Tiết

20 câu trắc nghiệm nhận dạng tam giác lớp 10 giải chi tiết được soạn dưới dạng file word và PDF gồm 2 trang. Các bạn xem và tải về ở dưới.

Câu 1: Cho $a;b;c$ là độ dài 3 cạnh của một tam giác. Mệnh đề nào sau đây không đúng?
A. ${a^2} < ab + ac$.
B. ${a^2} + {c^2} < {b^2} + 2ac$.
C. ${b^2} + {c^2} > {a^2} + 2bc$.
D. $ab + bc > {b^2}$.

Lời giải

Chọn C

Do nên mệnh đề $C$ sai.

Áp dụng bất đẳng thức tam giác ta có $a < b + c \Rightarrow {a^2} < ab + ac$;áp án A đúng.

Tương tự $a + c > b \Rightarrow ab + bc > {b^2}$;mệnh đề $D$ đúng.

Ta có: ${a^2} + {c^2} – {b^2} = 2ac \cdot cosB < 2ac \Rightarrow {a^2} + {c^2} < {b^2} + 2ac$;mệnh đề $B$ đúng.

Câu 2: Cho tam giác $ABC$ có ${a^2} + {b^2} – {c^2} > 0$. Khi đó:
A. Góc $C > {90^ \circ }$
B. Góc $C < {90^ \circ }$
C. Góc $C = {90^0}$
D. Không thể kết luận được gì về góc $C$.

Lời giải

Chọn B

Ta có: $cosC = \frac{{{a^2} + {b^2} – {c^2}}}{{2ab}}$.

Mà: ${a^2} + {b^2} – {c^2} > 0$ suy ra: $cosC > 0 \Rightarrow C < {90^ \circ }$.

Câu 3: Cho tam giác $ABC$ thoả mãn: ${b^2} + {c^2} – {a^2} = \sqrt 3 bc$. Khi đó:
A. $A = {30^ \circ }$.
B. $A = {45^0}$.
C. $A = {60^ \circ }$.
D. $A = {75^ \circ }$.

Lời giải

Chọn A

Ta có: $cosA = \frac{{{b^2} + {c^2} – {a^2}}}{{2bc}} = \frac{{\sqrt 3 bc}}{{2bc}} = \frac{{\sqrt 3 }}{2} \Rightarrow A = {30^0}$.

Câu 4: Tam giác $ABC$ có $AB = c,BC = a,CA = b$. Các cạnh $a,b,c$ liên hệ với nhau bởi đẳng thức $b\left( {{b^2} – {a^2}} \right) = c\left( {{a^2} – {c^2}} \right)$. Khi đó góc $\widehat {BAC}$ bằng bao nhiêu độ.
A. ${30^ \circ }$.
B. ${60^ \circ }$.
C. ${90^ \circ }$.
D. ${45^ \circ }$.

Lời giải

Chọn B

Theo bài ra, ta có: $b\left( {{b^2} – {a^2}} \right) = c\left( {{a^2} – {c^2}} \right) \Leftrightarrow {b^3} – {a^2}b = {a^2}c – {c^3} = 0$

$ \Leftrightarrow {b^3} + {c^3} – {a^2}b – {a^2}c = 0$

$ \Leftrightarrow \left( {b + c} \right)\left( {{b^2} – bc + {c^2}} \right) – {a^2}\left( {b + c} \right) = 0$

$ \Leftrightarrow \left( {b + c} \right)\left( {{b^2} – bc + {c^2} – {a^2}} \right) = 0 \Leftrightarrow {b^2} – bc + {c^2} – {a^2} = 0$$ \Leftrightarrow {b^2} + {c^2} – {a^2} = bc \Leftrightarrow \frac{{{b^2} + {c^2} – {a^2}}}{{2bc}} = \frac{1}{2} \Leftrightarrow cos\widehat {BAC} = \frac{1}{2} \Rightarrow \widehat {BAC} = {60^ \circ }$.

Câu 5: Cho tam giác $ABC$ vuông cân tại $A$ và $M$ là điểm nằm trong tam giác $ABC$ sao cho $MA:MB:MC = 1:2:3$ khi đó góc $AMB$ bằng bao nhiêu?
A. ${135^ \circ }$.
B. ${90^ \circ }$.
C. ${150^ \circ }$.
D. ${120^ \circ }$.

Lời giải

Chọn A

$MB = x \Leftrightarrow MA = 2x;MC = 3x$ với $0 < x < BC = \sqrt 2 $.

Ta có $cos\widehat {BAM} = \frac{{1 + 4{x^2} – {x^2}}}{{2.1.2x}} = \frac{{3{x^2} + 1}}{{4x}}$

$cos\widehat {MAC} = \frac{{1 + 4{x^2} – 9{x^2}}}{{4x}} = \frac{{1 – 5{x^2}}}{{4x}}$

$ \Rightarrow {\left( {\frac{{3{x^2} + 1}}{{4x}}} \right)^2} + {\left( {\frac{{1 – 5{x^2}}}{{4x}}} \right)^2} = 1 \Rightarrow 9{x^4} + 6{x^2} + 1 + 1 – 10{x^2} + 25{x^4} = 16$.

$ \Rightarrow 34{x^4} – 20{x^2} + 2 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{{x^2} = \frac{{5 + 2\sqrt 2 }}{{17}} > \frac{1}{5}\left( l \right)} \\
{{x^2} = \frac{{5 – 2\sqrt 2 }}{{17}}}
\end{array}} \right.$.

$ \Rightarrow cos\widehat {AMB} = \frac{{A{M^2} + B{M^2} – A{B^2}}}{{2AM \cdot BM}} = \frac{{4{x^2} + {x^2} – 1}}{{2.2x \cdot x}}$

$ = \frac{{5{x^2} – 1}}{{4{x^2}}} = \left( {\frac{{25 – 10\sqrt 2 }}{{17}} – 1} \right):\frac{{20 – 8\sqrt 2 }}{{17}} = \frac{{ – \sqrt 2 }}{2}$.

Vậy $\widehat {AMB} = {135^ \circ }$.

Câu 6: Cho tam giác $ABC$ thoả mãn hệ thức $b + c = 2a$. Trong các mệnh đề sau, mệnh đề nào đúng?
A. $cosB + cosC = 2cosA$.
B. $sinB + sinC = 2sinA$.
C. $sinB + sinC = \frac{1}{2}sinA$.
D. $sinB + cosC = 2sinA$.

Lời giải

Chọn B

Ta có:

$\frac{a}{{sinA}} = \frac{b}{{sinB}} = \frac{c}{{sinC}} = 2R$

$ \Rightarrow \frac{{\frac{{b + c}}{2}}}{{sinA}} = \frac{b}{{sinB}} = \frac{c}{{sinC}} $

$\Leftrightarrow \frac{{b + c}}{{2sinA}} = \frac{{b + c}}{{sinB + sinC}}$

$\Leftrightarrow sinB + sinC = 2sinA$.

Câu 7: Tam giác $ABC$ có các cạnh $a,b,c$ thỏa mãn điều kiện $\left( {a + b + c} \right)\left( {a + b – c} \right) = 3ab$. Tính số đo của góc $C$.
A. ${45^ \circ }$.
B. ${60^ \circ }$.
C. ${120^ \circ }$.
D. ${30^ \circ }$.

Lời giải

Chọn B.

Ta có: $\left( {a + b + c} \right)\left( {a + b – c} \right) = 3ab $

$\Leftrightarrow {(a + b)^2} – {c^2} = 3ab \Leftrightarrow {a^2} + {b^2} – {c^2} = ab$.

Mà $cosC = \frac{{{a^2} + {b^2} – {c^2}}}{{2ab}} = \frac{1}{2} \Rightarrow \hat C = {60^ \circ }$.

Câu 8: Cho tam giác $ABC$. Đẳng thức nào sai?
A. $sin\left( {A + B – 2C} \right) = sin3C$.
B. $cos\frac{{B + C}}{2} = sin\frac{A}{2}$.
C. $cos\frac{{A + B + 2C}}{2} = sin\frac{C}{2}$.
D. $sin\left( {A + B} \right) = sinC$.

Lời giải

Chọn C.

Do $cos\frac{{A + B + 2C}}{2} = cos\left( {\frac{{A + B}}{2} + C} \right) = cos\left( {\frac{\pi }{2} – \frac{C}{2} + C} \right) = cos\left( {\frac{\pi }{2} + \frac{C}{2}} \right) = – sin\frac{C}{2}$.

Câu 9: Cho tam giác $ABC$, các đường cao ${h_a},{h_b},{h_c}$ thỏa mãn hệ thức $3{h_a} = 2{h_b} + {h_c}$. Tìm hệ thức giữa $a,b,c$
A. $\frac{3}{a} = \frac{2}{b} – \frac{1}{c}$.
B. $3a = 2b + c$.
C. $3a = 2b – c$.
D. $\frac{3}{a} = \frac{2}{b} + \frac{1}{c}$.

Lời giải

Chọn D.

$3{h_a} = 2{h_b} + {h_c} \Leftrightarrow \frac{{6S}}{a} = \frac{{4S}}{b} + \frac{{2S}}{c} \Leftrightarrow \frac{3}{a} = \frac{2}{b} + \frac{1}{c}$.

Câu 10: Cho tam giác $ABC$, nếu $2{h_a} = {h_b} + {h_c}$ thì
A. $\frac{2}{{sinA}} = \frac{1}{{sinB}} + \frac{1}{{sinC}}$.
B. $2sinA = sinB + sinC$.
C. $sinA = 2sinB + 2sinC$.
D. $\frac{2}{{sinA}} = \frac{1}{{sinB}} – \frac{1}{{sinC}}$.

Lời giải

Chọn A.

$2{h_a} = {h_b} + {h_c} \Leftrightarrow \frac{{4S}}{a} = \frac{{2S}}{b} + \frac{{2S}}{c} \Leftrightarrow \frac{4}{{2RsinA}} = \frac{2}{{2RsinB}} + \frac{2}{{2RsinC}} \Leftrightarrow \frac{2}{{sinA}} = \frac{1}{{sinB}} + \frac{1}{{sinC}}.$

Câu 11: Diện tích $S$ của tam giác sẽ thỏa mãn hệ thức nào trong hai hệ thức sau đây?

I. ${S^2} = p\left( {p – a} \right)\left( {p – b} \right)\left( {p – c} \right)$

II. $16{S^2} = \left( {a + b + c} \right)\left( {a + b – c} \right)\left( {a – b + c} \right)\left( {b + c – a} \right)$
A. Chỉ I.
B. Chỉ II.
C. Cả I và II.
D. Không có.

Lời giải

Chọn A.

Áp dụng công thức Hê-rông $S = \sqrt {p\left( {p – a} \right)\left( {p – b} \right)\left( {p – c} \right)} \Leftrightarrow {S^2} = p\left( {p – a} \right)\left( {p – b} \right)\left( {p – c} \right)$

Nếu thay $p = \frac{{a + b + c}}{2}$ vào công thức Hê – rông thì ta có: $8{S^2} = \left( {a + b + c} \right)\left( {a + b – c} \right)\left( {a – b + c} \right)\left( {b + c – a} \right)$.

Câu 12: Cho tam giác $ABC$ không vuông ( đặt $BC = a,AB = c,AC = b$ ). Giá trị $\frac{{{a^2} + {c^2} – {b^2}}}{{{b^2} + {c^2} – {a^2}}}$ bằng
A. $\frac{{sinA}}{{cosB}}$.
B. $\frac{{tanA}}{{tanB}}$.
C. $\frac{{sinA}}{{sinB}}$.
D. $\frac{{cosA}}{{cosB}}$.

Lời giải

Chọn B.

$\frac{{{a^2} + {c^2} – {b^2}}}{{{b^2} + {c^2} – {a^2}}} = \frac{{2accosB}}{{2bccosA}}$ $ = \frac{{acosB}}{{bcosA}}$

$ = \frac{{2RsinAcosB}}{{2RsinBcosA}} = \frac{{tanA}}{{tanB}}$.

Câu 13: Cho tam giác $ABC$ có $\widehat {ABC} = {45^ \circ }$. Gọi $D$ là điểm trên đọ̣n $BC$ sao cho $CD = 2BD$ và $\widehat {DAB} = {15^0}$. Góc $\widehat {ACB}$ bằng
A. ${60^ \circ }$.
B. ${72^0}$.
C. ${75^0}$.
D. ${80^ \circ }$.

Lời giải

Chọn C.

Ta có: $\widehat {ADC} = {60^ \circ }$

Cách 1: Áp dụng định lý sin trong hai tam giác $ADC$ và $ABC$ ta có:

$\frac{{CD}}{{sin\widehat {CAD}}} = \frac{{CA}}{{sin{{60}^ \circ }}};\frac{{BC}}{{sin\left( {\widehat {CAD} + {{15}^ \circ }} \right)}} = \frac{{CA}}{{sin{{45}^ \circ }}}$

$ \Rightarrow \frac{{CDsin\left( {\widehat {CAD} + {{15}^ \circ }} \right)}}{{BCsin\widehat {CAD}}} = \frac{{sin{{45}^ \circ }}}{{sin{{60}^ \circ }}}$

$ \Rightarrow \frac{{sin\widehat {CAD}}}{{sin\left( {\widehat {CAD} + {{15}^ \circ }} \right)}} = \sqrt {\frac{2}{3}} = \frac{{sin{{45}^ \circ }}}{{sin{{60}^ \circ }}}$ Từ đây dễ dàng tìm được $\widehat {CAD} = {45^ \circ }$. Suy ra $\widehat {ACB} = {75^ \circ }$

Cách 2: Gọi $E$ trên đoạn $AD$ sao cho $CE \bot AD$. Xét tam giác $CDE$ ta có:

$\widehat {DCE} = {30^ \circ },DE = DC \cdot sin\widehat {DCE} \Rightarrow CD = 2DE$

Suy ra $BD = DE$, hay tam giác $BDE$ cân tại $D$. Suy ra $\widehat {DBE} = \widehat {DEB} = {30^ \circ }$

Khi đó:

$\widehat {CBE} = \widehat {DEB} = {30^ \circ }$

$\widehat {EBA} = \widehat {EAB} = {15^0}$

Suy ra hai tam giác BCE, BAE cân hay $EA = CE = BE$. Điều này suy ra tam giác $AEC$ vuông cân. Hay $\widehat {ACE} = {45^ \circ }$

Vậy $\widehat {ACB} = {75^ \circ }$

Câu 14: Đường tròn tâm $O$ nội tiếp xúc với cạnh $AB$ tại $D$. Biết $AC \cdot BC = 2AD \cdot BD$. Tam giác $ABC$ là:
A. Tam giác đều.
B. Tam giác vuông tại $A$.
C. Tam giác vuông tại $B$.
D. Tam giác vuông tại $C$.

Lời giải

Chọn D.

Ta có:

$AD = \frac{{b + c – a}}{2},BD = \frac{{a + c – b}}{2}$

Theo giả thiết:

$AC \cdot BC = 2AD \cdot BD$

$ \Rightarrow ab = 2 \cdot \frac{{b + c – a}}{2} \cdot \frac{{a + c – b}}{2} \Leftrightarrow 2ab = {c^2} – {(b – a)^2}$

$ \Leftrightarrow {c^2} = {a^2} + {b^2}$

Câu 15: Cho tam giác $ABC$ có tâm đường tròn nội tiếp là $I$. Gọi $R,{R_1},{R_2},{R_3}$ lần lượt là bán kính đường tròn ngoại tiếp tam giác $ABC,IBC,ICA,IAB$. Biết ${R_1} + {R_2} + {R_3} = 3R$. Khi đó tam giác $ABC$ là:
A. Tam giác đều.
B. Tam giác vuông.
C. Tam giác cân có $\widehat {BAC}$ tù.
D. Tam giác bất kỳ.

Lời giải

Chọn A.

Áp dụng định lý sin cho các tam giác IBC và $ABC$ ta có:

${R_1} = \frac{a}{{2sinBIC}} = \frac{{2RsinA}}{{2sin\frac{{B + 2}}{2}}} = 2Rsin\frac{A}{2}.$

Tương tự:

${R_2} = 2Rsin\frac{B}{2} = 2Rsin\frac{C}{2}$

Từ đó ta có: ${R_1} + {R_2} + {R_3}$

$ = 2R\left( {sin\frac{A}{2} + sin\frac{B}{2} + sin\frac{C}{2}} \right) \leqslant 3R$

Dấu bằng xảy ra khi và chỉ khi tam giác $ABC$ là tam giác đều.

Câu 16: Cho tam giác $ABC$. $AM,BN,CP$ là các đường phân giác trong $\left( {M \in BC,N \in CA,P \in AB} \right)$ của tam giác đó. Để PM vuông góc với $NM$ thì số đo của $\widehat {BAC}$ bằng
A. ${120^ \circ }$.
B. ${135^ \circ }$.
C. ${150^ \circ }$.
D. ${90^ \circ }$.

Lời giải

Theo định lý sin ta có: $\frac{{NA}}{{NM}} = sin\frac{{\widehat {AMN}}}{{sin\frac{A}{2}}}$

$\frac{{NM}}{{NC}} = \frac{{sinC}}{{sin\widehat {CMN}}};\frac{{BC}}{{BA}} = \frac{{sinA}}{{sinC}}$

Nhân ba đẳng thức trên theo vế với vế và để ý rằng $\frac{{NA}}{{NC}} = \frac{{BA}}{{BC}}$, suy ra:

$\frac{{sin\widehat {AMN}}}{{sin\frac{A}{2}}} = \frac{{sinA}}{{sin\frac{A}{2}}} = 1$

$ \Rightarrow \frac{{si{n^2}\widehat {AMN}}}{{si{n^2}\frac{A}{2}}} = \frac{{si{n^2}\widehat {CMN}}}{{si{n^2}A}}$

Tương tự:

$\frac{{si{n^2}\widehat {AMP}}}{{si{n^2}\frac{A}{2}}} = \frac{{si{n^2}\widehat {BMP}}}{{si{n^2}A}}\left( 2 \right)$

Mặt khác:

$\begin{array}{*{20}{r}}
{}&{si{n^2}\widehat {AMN} + si{n^2}\widehat {AMP} = 1} \\
{}&{si{n^2}\widehat {CMN} + si{n^2}\widehat {BMP} = 1}
\end{array}$

Cộng các đẳng thức (1), (2) theo vế đồng thời kết hợp với (3) ta suy ra:

$sin\frac{A}{2} = sinA \Rightarrow \widehat {BAC} = {120^ \circ }$

Câu 17: Tam giác $ABC$ có đặc điểm gì nếu $sinA = \frac{{sinB + 2sinC}}{{2cosB + cosC}}$.
A. Tam giác đều.
B. Tam giác có $\hat A = {120^ \circ }$.
C. Tam giác có $\hat A = {150^ \circ }$.
D. Tam giác có $\hat A = {90^ \circ }$.

Lời giải

Chọn D.

Ta có:

$sinA = \frac{{sinB + 2sinC}}{{2cosB + cosC}}$

$ \Leftrightarrow \frac{a}{{2R}} = \frac{{\frac{b}{{2R}} + \frac{{2c}}{{2R}}}}{{2 \cdot \frac{{{a^2} + {c^2} – {b^2}}}{{2ac}} + \frac{{{a^2} + {b^2} – {c^2}}}{{2ab}}}}$

$ \Leftrightarrow a\left( {\frac{{{a^2} + {c^2} – {b^2}}}{{2ac}} + \frac{{{a^2} + {b^2} – {c^2}}}{{2ab}}} \right) = b + 2c$

$ \Leftrightarrow \left( {\frac{{{a^2} + {c^2} – {b^2}}}{c} – 2c} \right) + \left( {\frac{{{a^2} + {b^2} – {c^2}}}{{2b}} – b} \right) = 0$

$ \Leftrightarrow \frac{{{a^2} + {c^2} – {b^2}}}{c} + \frac{{{a^2} + {b^2} – {c^2}}}{{2b}} = 0$

$ \Leftrightarrow \left( {\frac{{{a^2} + {c^2} – {b^2}}}{c} – 2c} \right) + \left( {\frac{{{a^2} + {b^2} – {c^2}}}{{2b}} – b} \right) = 0$

$ \Leftrightarrow \frac{{{a^2} + {c^2} – {b^2}}}{c} + \frac{{{a^2} + {b^2} – {c^2}}}{{2b}} = 0$

$ \Leftrightarrow \left( {{a^2} – {b^2} – {c^2}} \right)\left[ {\frac{1}{c} + \frac{1}{{2b}}} \right] = 0$

$ \Leftrightarrow {a^2} = {b^2} + {c^2}$.

Vậy tam giác ABC vuông tại A.

Câu 18: Cho $\vartriangle ABC$ thỏa mãn ${a^4} + {b^4} = {c^4}$ trong đó $a = BC,b = AC,c = AB$. ABC là tam giác
A. Vuông.
B. có góc $\widehat {ABC}$ tù.
C. có ba góc nhọn
D. có góc $\widehat {ACB}$ tù.

Lời giải

Chọn C.

Ta có:

${a^4} + {b^4} = {c^4} \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{c > a} \\
{c > b}
\end{array} \Rightarrow \widehat {ABC},\widehat {BAC}} \right.$ nhọn

Lại có: ${c^4} = {a^2}{a^2} + {b^2}{b^2} < {a^2}{c^2} + {b^2}{c^2}$

$ \Rightarrow {c^2}\left\langle {{a^2} + {b^2} = {c^2} + 2abcosC \Rightarrow cosC} \right\rangle 0 \Rightarrow \widehat {ACB}$ nhọn

Câu 19: *Xét $\vartriangle ABC$ nội tiếp đường tròn $\left( O \right)$ cho trước. Các trung tuyến xuất phát từ $A,B,C$ cắt đường tròn $\left( O \right)$ tương ứng tại $M,N,P$. Biểu thức $P = \frac{{A{M^2} + B{N^2} + C{P^2}}}{{A{B^2} + B{C^2} + C{A^2}}}$ đạt giá trị nhỏ nhất khi và chỉ khi tam giác ABC là
A. Tam giác đều.
B. Tam giác vuông.
C. Tam giác cân có $\widehat {BAC}$ tù.
D. Tam giác vuông cân.

Lời giải

Chọn A.

Gọi D,E,F lần lượt là trung điểm của $BC,CA,AB$.

Khi đó:

$AD \cdot DM = DB \cdot DC = \frac{{B{C^2}}}{4}$.

$ \Leftrightarrow AD\left( {AM – AD} \right) = \frac{{B{C^2}}}{4} \Leftrightarrow AD \cdot AM = A{D^2} + \frac{{B{C^2}}}{4}$

Theo công thức độ dài đường trung tuyến trong tam giác ta có: $A{B^2} + A{C^2} = 2A{D^2} + \frac{{B{C^2}}}{2} = 2AD \cdot AM$

Tương tự ta cũng ta:

$B{C^2} + B{A^2} = 2BE \cdot BN$,

$C{B^2} + A{C^2} = 2CF.CP$.

Từ đó, theo bất đẳng thức Cauchy – Schwars ta có:

$B{C^2} + B{A^2} + A{C^2} = CF \cdot CP + BE \cdot BN + AD \cdot AM \leqslant \sqrt {\left( {A{M^2} + B{N^2} + C{P^2}} \right)\left( {A{D^2} + B{E^2} + C{F^2}} \right)} $

$ \Rightarrow {\left( {B{A^2} + B{C^2} + A{C^2}} \right)^2} \leqslant \frac{3}{4}\left( {B{A^2} + B{C^2} + A{C^2}} \right)\left( {A{M^2} + B{N^2} + C{P^2}} \right) \Rightarrow P \geqslant \frac{4}{3}$

Đẳng thức xảy ra khi và chỉ khi tam giác $ABC$ đều.

Câu 20: Xét hình chữ nhật $ABCD$ và điểm $M$ di động trên $BC$. Phân giác góc $DAM$ cắt $BC$ tại $N$. $\frac{{AN}}{{MN}}$ đạt giá trị nhỏ nhất khi điểm $M$ :
A. Trùng điểm $B$.
B. Trùng điểm $C$.
C. Trùng với trung điểm của $BC$.
D. Trùng với giao điểm của phân giác trong góc $\widehat {BAC}$ với $BC$.

Lời giải

Chọn A.

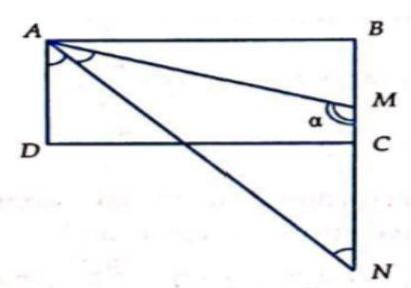
Đặt $AB = a,AD = b,AM = m > 0AN = n > m,\widehat {AMN} = \alpha $.

Theo giả thiết ta có: $AN$ là phân giác $\widehat {MAD} \Rightarrow \widehat {MAD} = \widehat {ANB}$ (cùng bằng $NAD$ )

Vậy $\vartriangle ANM$ cân tại $M \Rightarrow MN = AM = m$.

Theo định lý cosin cho $\vartriangle ANM$ có:

${n^2} = {m^2} + {m^2} – 2m \cdot m \cdot cos\alpha = 2{m^2}\left( {1 – cos\alpha } \right)$

$ \Leftrightarrow n = m\sqrt {2\left( {1 – cos\alpha } \right)} $

Theo bài ra ta có:

$\frac{{AN}}{{AM}} = \frac{n}{m} = \frac{{m\sqrt {2\left( {1 – cos\alpha } \right)} }}{m}$

$ = \sqrt {2\left( {1 – cos\alpha } \right)} $

Ta có: $\alpha > {90^ \circ }$ (vì $M$ di động trên đoạn $BC$ ) $ \Rightarrow cos\alpha \leqslant 0$

$ \Rightarrow \frac{{AN}}{{AM}} = \sqrt {2\left( {1 – cos\alpha } \right)} \geqslant \sqrt 2 $

$ \Rightarrow \frac{{AN}}{{MN}}$ đạt giá trị nhỏ nhất khi $\frac{{AN}}{{MN}} = \sqrt 2 $ xảy ra $ \Leftrightarrow cos\alpha = 0 \Leftrightarrow \alpha = {90^ \circ } \Leftrightarrow M \equiv B$.