Các Dạng Bài Toán Thực Tế Về Cấp Số Nhân Lớp 11 Có Lời Giải

Các dạng bài toán thực tế về cấp số nhân lớp 11 có lời giải được soạn dưới dạng file word và PDF gồm 6 trang. Các bạn xem và tải về ở dưới.

A. KIẾN THỨC CƠ BẢN

1. Cấp số nhân là một dãy số (hữu hạn hay vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều là tích của số hạng đứng ngay trước nó với một số không đổi $q$. Số $q$ được gọi là công bội của cấp số nhân.

2. Cấp số nhân $\left( {{u_n}} \right)$ với công bội $q$ được cho bởi hệ thức truy hồi: ${u_n} = {u_{n – 1}} \cdot q,\left( {n \geqslant 2} \right)$.

3. Nếu cấp số nhân $\left( {{u_n}} \right)$ có số hạng đầu ${u_1}$ và công bội $q$ thì số hạng tổng quát ${u_n}$ của nó được xác định bởi công thức: ${u_n} = {u_1} \cdot {q^{n – 1}},\left( {n \geqslant 2} \right)$.

4. Cho cấp số nhân $\left( {{u_n}} \right)$ với công bội $q \ne 1$. Đặt ${S_n} = {u_1} + {u_2} + \ldots + {u_n}$. Khi đó: ${S_n} = \frac{{{u_1}\left( {1 – {q^n}} \right)}}{{1 – q}}$.

B. BÀI TẬP VẬN DỤNG

Câu 1: Một tỉnh có 2 triệu dân vào năm 2020 với tỉ lệ tăng dân số là 1%/năm. Gọi ${u_n}$là số dân của tỉnh đó sau $n$ năm. Giả sử tỉ lệ tăng dân số là không đổi.

a) Viết công thức tính số dân của tỉnh đó sau $n$ năm kể từ năm 2020 .

b) Tính số dân của tỉnh đó sau 10 năm kể từ năm 2020.

Lời giải

a) Ta có dãy ${u_n}$ lập thành một cấp số nhân có số hạng đầu là ${u_o} = 2$ triệu dân và công sai $q = 1\% $.

Khi đó số hạng tổng quát của ${u_n} = 2 \cdot {(1 + 1\% )^{n – 1}}$ (triệu dân).

b) Số dân của tỉnh đó sau 10 năm kể từ năm 2020 là:

${u_{10}} = 2 \cdot {(1 + 1\% )^{10 – 1}} \approx 2,19$ (triệu dân).

Câu 2: Một gia đình mua một chiếc ô tô giá 800 triệu đồng. Trung bình sau mỗi năm sử dụng, giá trị còn lại của ô tô giảm đi $4\% $ (so với năm trước đó).

a) Viết công thức tính giá trị của ô tô sau 1 năm, 2 năm sử dụng.

b) Viết công thức tính giá trị của ô tô sau $n$ năm sử dụng.

c) Sau 10 năm, giá trị của ô tô ước tính còn bao nhiêu triệu đồng?

Lời giải

a) Sau 1 năm giá trị của ô tô còn lại là: ${u_1} = 800 – 800.4\% = 800.\left( {1 – 4\% } \right) = 768$ (triệu đồng).

Sau 2 năm giá trị của ô tô còn lại là: ${u_1} = 800.\left( {1 – 4\% } \right) – 800 \cdot \left( {1 – 4\% } \right) \cdot 4\% = 800 \cdot {(1 – 4\% )^2} = 737,28$ (triệu đồng).

b) Gọi $\;{u_n}$ là giá trị của ô tô sau n năm sử dụng.

Dãy số ${u_n}$ tạo thành một cấp số nhân với số hạng đầu là giá trị đầu của ô tô là ${u_0} = 800$ triệu đồng và công bội $q = 1 – 4\% $.

Khi đó công thức tổng quát để tính ${u_n} = 800.{(1 – 4\% )^n}$.

c) Sau 10 năm sử dụng giá trị của ô tô còn lại là: ${u_{10}} = 800 \cdot {(1 – 4\% )^{10}} \approx 531,87$ (triệu đồng).

Câu 3: Một người nhảy bungee (một trò chơi mạo hiểm mà người chơi nhảy từ một nơi có địa thế cao xuống với dây đai an toàn buộc xung quanh người) từ một cây cầu và căng một sợi dây dài $100m$. Sau mỗi lần rơi xuống, nhờ sự đàn hồi của dây, người nhảy được kéo lên một quãng đường có độ dài bằng $75\% $ so với lần rơi trước đó và lại bị rơi xuống đúng bằng quãng đường vừa được kéo lên (Hình 3). Tính tổng quãng đường người đó đi được sau 10 lần kéo lên và lại rơi xuống.

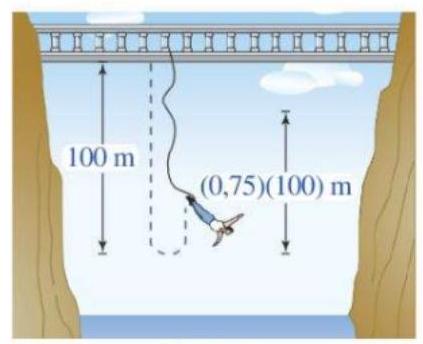
Hình 3

Lời giải

Gọi ${u_n}$ là độ dài dây kéo sau n lần rơi xuống $\left( {n \in N} \right)$

Ta có: ${u_0} = 100\left( {\;m} \right)$.

Sau lần rơi đầu tiên độ dài dây kéo còn lại là: ${u_1} = 100.75\% \left( m \right)$.

Sau cú nhảy tiếp theo độ dài dây kéo còn lại là: ${u_2} = 100.75\% .75\% = 100$. ${(75\% )^2}\left( {\;m} \right)$.

Dãy số này lập thành một cấp số nhân có số hạng đầu là 100 và công bội $q = 0,75\% $, có công thức tổng quát ${u_n} = 100 \cdot {(0,75\% )^{n – 1}}\left( {\;m} \right)$.

Tổng quãng đường người đó đi được sau 10 lần kéo lên và lại rơi xuống là:

${S_{10}} = \frac{{100\left( {1 – {{(75\% )}^{10}}} \right)}}{{1 – 75\% }} \approx 377,5\left( {\;m} \right)$.

Câu 4: Một loại vi khuẩn được nuôi cấy trong phòng thí nghiệm, cứ mỗi phút số lượng lại tăng lên gấp đôi số lượng đang có. Từ một vi khuẩn ban đầu, hãy tính tổng số vi khuẩn có trong ống nghiệm sau 20 phút.

Lời giải

Tổng số vi khuẩn có trong ống nghiệm sau 20 phút là:

${S_{20}} = \frac{{20 \cdot \left[ {1 – {2^{20}}} \right]}}{{1 – 2}} = 20971500$

Câu 5: Giả sử một thành phố có dân số năm 2022 là khoàng 2,1 triệu người và tốc độ gia tăng dân số trung bình mỗi năm là $0,75\% $.

a) Dự đoán dân số của thành phố đó vào năm 2032.

b) Nếu tốc độ gia tăng dân số vẫn giữ nguyên như trên thì ước tính vào năm nào dân số của thành phố đó sẽ tăng gấp đôi so với năm 2022?

Lời giải

Dân số của thành phố từ năm 2022 lần lượt tạo thành cấp số nhân có công bội là $1 + 0,0075 = 1,0075$

Dân số của thành phố vào năm $n$ là: ${u_n} = 2,1.1,{0075^{n – 2022}}$

a) ${u_{2032}} = 2,1.1,{0075^{2032 – 2022}} = 2,26$

b) Khi ${u_n} = 2 \cdot {u_{2022}} \Leftrightarrow 1,{0075^{n – 2022}} = 2 \Leftrightarrow n = 2115$

Vậy đến năm 2115 , dân số thành phố gấp đôi so với năm 2022.

Câu 6: Trong trò chơi mạo hiểm nhảy bungee, mỗi lần nhảy, người chơi sẽ được dây an toàn có tính đàn hồi kéo nảy ngược lên $60\% $ chiều sâu của cú nhảy. Một người chơi bungee thực hiện củ nhảy đầu tiên có độ cao nảy ngược lên là $9m$.

a) Tính độ cao nảy ngược lên của người đó ở lần nảy thứ ba.

b) Tính tổng các độ cao nảy ngược lên của người đó trong 5 lần nảy đầu.

Lời giải

Độ cao nảy ngược lên của người đó ở lần nảy thứ nhất là ${u_1} = 9$

Độ cao các lần nảy lần lượt tạo thành cấp số nhân có công bội là $q = 0,6{u_n} = 9.0,{6^{n – 1}}$

a) ${u_3} = 9.0,{6^{3 – 1}} = 3,24$

b) ${S_5} = \frac{{5 \cdot \left[ {1 – 0,{6^5}} \right]}}{{1 – 0,6}} = 11,528$

Câu 7: Một công ty xây dựng mua một chiếc máy ủi với giá 3 tỉ đồng. Cứ sau mỗi năm sử dụng, giá trị của chiếc máy ủi này lại giảm $20\% $ so với giá trị của nó trong năm liền trước đó. Tìm giá trị còn lại của chiếc máy ủi đó sau 5 năm sử dụng.

Lời giải

Giá trị của chiếc máy ủi mỗi năm lập thành một cấp số nhân với số hạng đầu bằng 3 và công bội $q = 0,8$

Giá trị của chiếc máy ủi sau 5 năm sử dụng là: ${u_5} = 3 \times 0,{8^{5 – 1}} = 0,1875$ (tỷ đồng)

Câu 8: Vào năm 2020, dân số của một quốc gia là khoảng 97 triệu người và tốc độ tăng trưởng dân số là $0,91\% $. Nếu tốc độ tăng trưởng dân số này được giữ nguyên hằng năm, hãy ước tính dân số của quốc gia đó vào năm 2030 .

Lời giải

Dân số hằng năm lập thành cấp số nhân với số hạng đầu là 97 và công bội $q = 1.0091$

Dân số của quốc gia đó năm 2030 (tức $n = 11$ ) là ${u_{11}} = 97 \times {1.0091^{11 – 1}} = 106.197$ (triệu người)

Câu 9: Một loại thuốc được dùng mỗi ngày một lần. Lúc đầu nồng độ thuốc trong máu của bệnh nhân tăng nhanh, nhưng mỗi liều kế tiếp có tác dụng ít hơn liều trước đó. Lượng thuốc trong máu ở ngày thứ nhất là $50mg$ , và mỗi ngày sau đó giảm chỉ còn một nửa so với ngày kề trước đó. Tính tổng lượng thuốc (tính bằng $mg$ ) trong máu của bệnh nhân sau khi dùng thuốc 10 ngày liên tiếp.

Lời giải

Lượng thuốc trong máu mỗi ngày cảu bệnh nhân lập thành cấp số nhân với số hạng đầu là 50 và công bội $q = 0.5$

Tổng lượng thuốc trong máu 10 ngày liên tiếp chính là tổng 10 số hạng đầu cảu cấp số nhân này và

bằng: ${S_n} = \frac{{50\left[ {1 – {{(0.5)}^{10}}} \right]}}{{1 – 0.5}} = 99.902\left( {mg} \right)$

Câu 10: Ban đầu, một quả lắc đồng hồ dao động theo một cung tròn dài$\;46cm$ (H. 2.1). Sau mỗi lần đu liên tiếp, độ dài của cung tròn bằng 0,98 độ dài cung tròn ở ngay lần trước đó.

a) Độ dài của cung tròn ở lần thứ 10 là bao nhiêu?

b) Sau 15 lần dao động, quả lắc sẽ đi được quãng đường tổng cộng là bao nhiêu?

(Kết quả tính theo centimét và làm tròn đến chữ số thập phân thứ hai).

Hình 2.1

Lời giải

Gọi ${u_n}$ là độ dài cung tròn ở lần thứ $n$ khi con lắc dao động. Do lần một, quả lắc đồng hồ dao động theo một cung tròn dài $46\;cm$, sau mỗi lần dao động liên tiếp, độ dài của cung tròn bằng 0,98 độ dài
cung tròn ở ngay lần trước đó nên dãy số $\left( {{u_n}} \right)$ lập thành cấp số nhân có ${u_1} = 46$ và công bội $q = 0,98$.

a) Độ dài của cung tròn ở lần thứ 10 là ${u_{10}} = {u_1}{q^9} = 46 \cdot 0,{98^9} \approx 38,35\left( {\;cm} \right)$.

b) Sau 15 lần dao động, quả lắc sẽ đi được quãng đường tổng cộng là

${S_{15}} = {u_1}\frac{{1 – {q^{15}}}}{{1 – q}} = 46 \cdot \frac{{1 – 0,{{98}^{15}}}}{{1 – 0,98}} \approx 601,29\left( {\;cm} \right)$.

Câu 11: Các bệnh truyền nhiễm có thể lây lan rất nhanh. Giả sử có năm người bị bệnh trong tuần đầu tiên của một đợt dịch, và mỗi người bị bệnh sễ lây bệnh cho bốn người vào cuối tuần tiếp theo. Tính đến hết tuần thứ 10 của đợt dịch, có bao nhiêu người đã bị lây bởi căn bệnh này?

Lời giải

Gọi ${u_n}$ là số người bị bệnh ở cuối tuần thứ $n$. Vì có năm người bị bệnh trong tuần đầu tiên của một đợt dịch, và mỗi người bị bệnh sẽ lây bệnh cho bốn người vào cuối tuần tiếp theo nên dãy số $\left( {{u_n}} \right)$ là một cấp số nhân có ${u_1} = 5$ và công bội $q = 4$.

Suy ra số người bị ảnh hướng bởi dịch bệnh ở cuối tuần 10 là ${u_{1n}} = {u_1}{q^9} = 5 \cdot {4^9} = 1310720$ (người).

Câu 12: Nếu một kĩ sư được một công ty thuê với mức lương hằng năm là 180 triệu đồng và nhận được mức tăng lương hằng năm là $5\% $, thì mức lương của người kĩ sư đó là bao nhiêu khi bắt đầu năm thứ sáu làm việc cho công ty?

Lời giải

Gọi ${u_n}$ là số triệu đồng mà người kĩ sư đó nhận được ở năm thứ $n$.

Vì người kĩ sư được công ty thuê với mức lương hằng năm là 180 triệu đồng và nhận được mức tăng lương hằng năm là 5% nên dãy số $\left( {{u_n}} \right)$ là một cấp số nhân có ${u_1} = 180$ và công bội $q = 1 + 5\% = 1,05$.

Khi bắt đầu năm thứ sáu làm việc cho công ty thì mức lương năm của người kĩ sư đó là ${u_6} = {u_1}{q^5} = 229,73$ (triệu đồng)

Câu 13: Để tích lũy tiền cho việc học đại học của con gái, cô Hoa quyết định hằng tháng bỏ ra 500 nghìn đồng vào tài khoản tiết kiệm, được trả lãi $0,5\% $cộng dồn hằng tháng. Có bắt đầu chương trình tích luỹ này khi con gái cô tròn 3 tuổi. Cô ấy sẽ tích luỹ được bao nhiêu tiền vào thời điểm gửi khoản tiên thứ 180 ? Lúc này con gái cô Hoa bao nhiêu tuổi?

Lời giải

Gọi ${u_n}$ là số triệu đồng mà cô Hoa có trong chương trình tích luỹ ở lần gửi thứ $n$ (vào đầu tháng thứ $n)$.

Kí hiệu $a = 0,5$ triệu đồng, $r = 0,5\% $.

Số tiền của cô Hoa trong chương trình ở đầu tháng 1 là ${u_1} = a$.

Số tiền của cô Hoa trong chương trình ở đầu tháng 2 là ${u_2} = {u_1}\left( {1 + r} \right) + a$.

Số tiền của cô Hoa trong chương trình ở đầu tháng 3 là
${u_3} = {u_2}\left( {1 + r} \right) + a = a{(1 + r)^2} + a\left( {1 + r} \right) + a$.

Tương tự cho các tháng tiếp theo, suy ra số tiền của cô Hoa trong chương trình ở đầu tháng $n$ là ${u_n} = a{(1 + r)^{n – 1}} + a{(1 + r)^{n – 2}} + \ldots + a\left( {1 + r} \right) + a$

$ = a\frac{{{{(1 + r)}^n} – 1}}{{\left( {1 + r} \right) – 1}} = a\frac{{{{(1 + r)}^n} – 1}}{r}$.

Vào thời điểm gửi khoản tiền thứ 180 , cô ấy sẽ tích luỹ được ${u_{180}} = a\frac{{{{(1 + r)}^{180}} – 1}}{r} = 145,41$ (triệu đồng).

Khi đó, tuổi của con gái cô Hoa là $3 + 180:12 = 18$ tuổi.

Câu 14: Các cạnh của hình vuông ban đầu có chiều dài $16\,cm$. Một hình vuông mợ được hình thành bằng cách nối các điểm giữa của các cạnh của hình vượng ban đầu và hai trong số các hình tam giác kết quả được tố mảu (hinh vẽ dưới). Nếu quá trinh này được lặp lại năm lần nữa, hãy xác định tổng diện tích của vùng được tô màu.

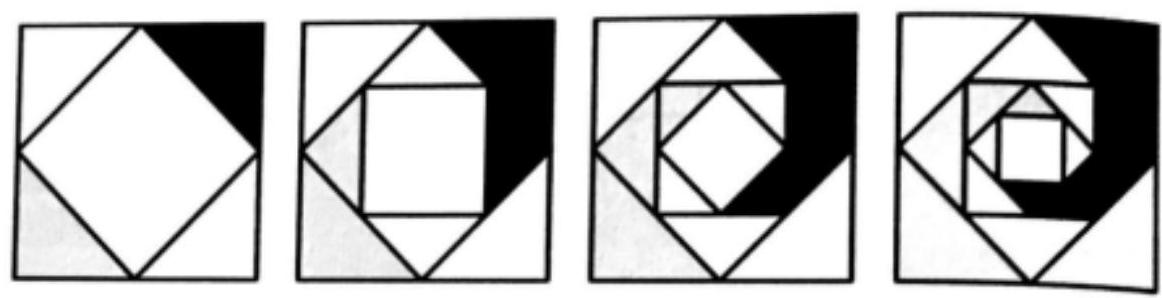
Lời giải

Gọi ${u_n}$ là diện tích hai tam giác được tô màu ở lần thực hiện thứ $n$. Gọi a là độ dài cạnh của hình vuông ban đầu.

Ở lần 1 thì độ dài cạnh tam giác vuông cân là $\frac{a}{2}$ nên ${u_1} = 2 \cdot \frac{1}{2}\frac{a}{2}\frac{a}{2} = \frac{{{a^2}}}{{{2^2}}}$

và độ dài cạnh hình vuông sau đó là $\frac{{a\sqrt 2 }}{2}$.

Ở lần 2 thì độ dài cạnh tam giác vuông cân là $\frac{a}{2} \cdot \frac{{\sqrt 2 }}{2}$ nên ${u_2} = \frac{{{a^2}}}{{{2^3}}}$.

Ở lần 3 thì độ dài cạnh tam giác vuông cân là $\frac{a}{2} \cdot \frac{{\sqrt 2 }}{2} \cdot \frac{{\sqrt 2 }}{2}$ nên ${u_3} = \frac{{{a^2}}}{{{2^4}}}$.

Như vậy, dãy số $\left( {{u_n}} \right)$ là cấp số nhân với ${u_1} = \frac{{{a^2}}}{4}$ và công bội $q = \frac{1}{2}$.

Vậy tổng diện tích sau năm lần thực hiện là ${S_5} = {u_1}\frac{{1 – {q^5}}}{{1 – q}} = 124\left( {\;c{m^2}} \right)$.

Chú ý. Diện tích cần tính bằng diện tích hình vuông ngoài cùng trừ đi diện tích hình vuông trong cùng rồi chia 2 .

Câu 15: Một loại vi khuẩn được nuôi cấy trong ống nghiệm, cứ 20 phút lại phân đôi một lần. Nếu ban đầu có 200 vi khuẩn, tính sô lượng vi khuẩn có trong ống nghiệm sau 2 giờ.

Lời giải

Ta có: 2 giờ $ = 120$ phút=6.20 phút. Do đó sau 2 giớ vi khuẩn phân đôi 6 lần.

Gọi ${u_n}$ là số lượng vi khuẩn có trong ống nghiệm sau lần phân đôi thứ $n – 1$.

Khi đó, dãy số $\left( {{u_n}} \right)$ là một cấp số nhân với ${u_1} = 200$ và $q = 2$.

Ta có ${u_7} = {u_1} \cdot {q^6} = 200 \cdot {2^6} = 12800$.

Vậy sau 2 giờ, trong ống nghiệm có 12800 vi khuẩn.

Câu 16: Bác Năm gửi tiết kiệm vào ngân hàng 100 triệu đồng với hình thức lãi kép, kì hạn một năm với lãi suất $8\% /$ năm. Tính số tiền cả gốc và lãi bác Năm nhận được sau 10 năm. (Giả sử lãi suất không thay đổi trong suốt thời gian gửi tiền.)

Lời giải

Khoảng 215892500 triệu đồng.

Câu 17: Một người chơi nhảy bungee trên một cây cầu với một sợi dây dài $100\;m$. Sau mỗi lần rơi xuống, người chơi được kéo lên một quãng đường có độ dài bằng $80\% $ so với lần rơi trước và lại rơi xuống đúng bằng quãng đường vừa được kéo lên. Tính tổng quãng đường đi lên của người đó sau 10 lần được kéo lên.

Lời giải

${S_{10}} = \frac{{80\left( {1 – 0,{8^{10}}} \right)}}{{1 – 0,8}} \approx 357,05\left( {\;m} \right)$

Câu 18: Một người nhảy bungee (một trò chơi mạo hiểm mà người chơi nhảy từ một nơi có địa thế cao xuống với dây đai an toàn buộc xung quanh người) từ một cây cầu và căng một sợi dây dài Giả sử sau mỗi lần rơi xuống, người nhảy được kéo lên một quãng đường có độ cao bằng so với lần rơi trước đó và lại bị rơi xuống đúng bằng quãng đường vừa được kéo lên (Hình 3 ). Tính tổng quãng đường người đó đi được sau 10 lần rơi xuống và lại được kéo lên, tính từ lúc bắt đầu nhảy (làm tròn kết quả đến hàng đơn vị).

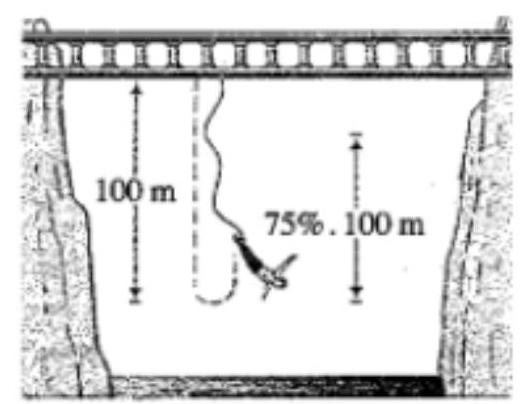
Hình 3

Lời giải

Gọi ${u_1}\left( {\;m} \right)$ là quãng đường người chơi rơi xuống ở lần thứ nhất, ta có: ${u_1} = 100$;

${v_1}\left( {\;m} \right)$ là quãng đường người chơi được kéo lên ở lần thứ nhất, ta có: ${v_1} = 100 \cdot 0,75 = 75$;

${u_2}\left( {\;m} \right)$ là quãng đường người chơi rơi xuống ở lần thứ hai, ta có: ${u_2} = {v_1} = 0,75{u_1}$;

${v_2}\left( {\;m} \right)$ là quãng đường người chơi được kéo lên ở lần thứ hai, ta có: ${v_2} = 0,75{u_2} = 0,75{v_1}$.

Như vậy, ta có hai cấp số nhân đều có công bội 0,75 là: ${u_1},{u_2}, \ldots ,{u_{10}}$ và ${v_1},{v_2}, \ldots ,{v_{10}}$ với ${u_1} = 100$ và ${v_1} = 75$

Ta có:

${u_1} + {u_2} + \ldots + {u_{10}} = 100 \cdot \left( {\frac{{1 – 0,{{75}^{10}}}}{{1 – 0,75}}} \right);$

${v_1} + {v_2} + \ldots + {v_{10}} = 75 \cdot \left( {\frac{{1 – 0,{{75}^{10}}}}{{1 – 0,75}}} \right)$.

Vậy quãng đường người đó đi được sau 10 lần rơi xuống và lại được kéo lên (tính từ lúc bắt đầu nhảy) là:

$\left( {{u_1} + {u_2} + \ldots + {u_{10}}} \right) + \left( {{v_1} + {v_2} + \ldots + {v_{10}}} \right)$$ = 175 \cdot \left( {\frac{{1 – 0,{{75}^{10}}}}{{1 – 0,75}}} \right) \approx 661\left( {\;m} \right)$

Câu 19: Anh Dũng kí hợp đồng lao động trong 10 năm với phương án trả lương như sau: Năm thứ nhất, tiền lương của anh Dũng là 120 triệu đồng. Kể từ năm thứ hai trở đi, mỗi năm tiền lương của anh Dũng được tăng lên . Tính tổng số tiền lương anh Dũng lĩnh được trong 10 năm đầu đi làm (làm tròn kết quả đến hàng đơn vị theo đơn vị triệu đồng).

Lời giải

Ta có tiền lương năm thứ nhất của anh Dũng là: 120 triệu đồng.

Tiền lương năm thứ hai của anh Dũng là:

$120 + 120 \cdot 10\% = 120\left( {1 + 0,1} \right) = 120 \cdot 1,1$ (triệu đồng).

Tiền lương năm thứ ba của anh Dũng là:

$120 \cdot 1,1 + 120 \cdot 1,1 \cdot 10\% = 120 \cdot 1,1\left( {1 + 0,1} \right) = 120 \cdot 1,{1^2}$ (triệu đồng).

Cứ tiếp tục như vậy, ta được tiền lương năm thứ 10 của anh Dũng là 120. 1,19 (triệu đồng).

Do vậy, tiền lương mỗi năm của anh Dũng nhận được trong 10 năm lập thành một cấp số nhân với số hạng đầu ${u_1} = 120$ và công bội $q = 1,1$.

Khi đó tổng số tiền lương anh Dũng lĩnh được trong 10 năm đầu đi làm là:

${S_{10}} = \frac{{{u_1}\left( {1 – {q^{10}}} \right)}}{{1 – q}} = \frac{{120 \cdot \left[ {1 – {{(1,1)}^{10}}} \right]}}{{1 – 1,1}} \approx 1912$ ( triệu đồng )

Vậy tổng số tiền lương anh Dũng lĩnh được trong 10 năm đầu đi làm là 1912 triệu đồng.

Câu 20: Một cái tháp có 11 tầng. Diện tích của mặt sàn tầng 2 bằng nửa diện tích của mặt đáy tháp và diện tích của mặt sàn mỗi tầng bằng nửa diện tích của mặt sàn mỗi tầng ngay bên dưới. Biêt mặt đáy tháp có
diện tích là . Tính diện tích của mặt sàn tầng trên cùng của tháp theo đơn vị mét vuông.

Lời giải

Diện tích mặt đáy tháp là ${u_1} = 12288\left( {\;{m^2}} \right)$.

Diện tích mặt sàn tầng 2 là: ${u_2} = 12$ 288. $\frac{1}{2} = 6144\left( {\;{m^2}} \right)$.

Gọi diện tích mặt sàn tầng $n$ là ${u_n}$ với $n \in {N^*}$.

Dãy ${u_n}$ lập thành một cấp số nhân là ${u_1} = 12288$ và công bội $q = \frac{1}{2}$, có số hạng tổng quát là: ${u_n} = 12288 \cdot {\left( {\frac{1}{2}} \right)^{n – 1}}$

Diện tích mặt tháp trên cùng chính là mặt tháp thứ 11 nên ta có:

${u_{11}} = 12288.{\left( {\frac{1}{2}} \right)^{11 – 1}} = 12\left( {\;{m^2}} \right)$.

Câu 21: Một khay nước có nhiệt độ ${23^0}C$ được đặt vào ngăn đá của tủ lạnh. Biết sau mỗi giờ, nhiệt độ của nước giảm 20%. Tính nhiệt độ của khay nước đó sau 6 giờ theo đơn vị độ $C$ .

Lời giải

Gọi ${u_n}$ là nhiệt độ của khay nước đó sau $n$ giờ (đơn vị độ $C$ ) với $n \in {N^*}$.

Ta có: ${u_1} = 23;$

${u_2} = 23 – 23.20\% = 23.\left( {1 – 20\% } \right) = 23.80\% ;$

${u_3} = 23.80\% .80\% = 23.{(80\% )^2}; \ldots $

Suy ra dãy ${u_n}$ lập thành một cấp số nhân với số hạng đầu ${u_1} = 23$ và công bội $q = 80\% $ có số hạng tổng quát ${u_n} = 23.{(80\% )^{n – 1}}$ độ C

Vậy sau 6 giờ thì nhiệt độ của khay là ${u_6} = 23 \cdot {(80\% )^5} \approx 7,{5^\;}C$.

Câu 22: Cho hình vuông ${C_1}$ có cạnh bằng 4. Người ta chia mỗi cạnh hình vuông thành bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông ${C_2}$ (Hình 4). Từ hình vuông ${C_2}$ lại làm tiếp tục như trên để có hình vuông ${C_3}$ . Cứ tiếp tục quá trình như trên, ta nhận được dãy các hình vuông ${C_1},\,{C_2},\,{C_3},\,…,{C_n}, \ldots \;$ Gọi ${a_n}$ là độ dài cạnh hình vuông ${C_n}$. Chứng minh rằng dãy số $({a_n})$ là cấp số nhân.

Lời giải

Độ dài cạnh của hình vuông đầu tiên là: ${a_1} = 4$.

Độ dài cạnh của hình vuông thứ hai là: $\;{a_2} = \sqrt {{{\left( {\frac{{{a_1}}}{4}} \right)}^2} + {{\left( {\frac{{3{a_1}}}{4}} \right)}^2}} = \frac{{{a_1}\sqrt {10} }}{4}$.

Độ dài cạnh của hình vuông thứ ba là: $\;{a_3} = \sqrt {{{\left( {\frac{{{a_2}}}{4}} \right)}^2} + {{\left( {\frac{{3{a_2}}}{4}} \right)}^2}} = \frac{{{a_2}\sqrt {10} }}{4}$.

……

Độ dài cạnh của hình vuông thứ $n$ là: $\;{a_n}$.

Độ dài cạnh của hình vuông thứ $n + 1$ là:

${a_{n + 1}} = \left( {\frac{{\sqrt {10} }}{4}} \right) \cdot {a_n}$

Suy ra: $\frac{{{a_{n + 1}}}}{{{a_n}}} = \frac{{\sqrt {10} }}{4}$

Vậy $\left( {{a_n}} \right)$ là một cấp số nhân với số hạng đầu ${a_1} = 4$ và công bội $q = \frac{{\sqrt {10} }}{4}$.

Câu 23: Ông An vay ngân hàng 1 tỉ đồng với lãi suất $12\% $/năm. Ông đã trả nợ theo cách: Bắt đầu từ tháng thứ nhất sau khi vay, cuối mỗi tháng ông trả ngân hàng cùng số tiền là $a$ (đồng) và đã trả hết nợ sau đúng 2 năm kể từ ngày vay. Hỏi số tiền mô̂i tháng mà ông An phải trả là bao nhiêu đồng (làm tròn kết quả đến hàng nghìn)?

Lời giải

Gọi ${u_n}$ là số tiền sau mỗi tháng ông An còn nợ ngân hàng.

Lãi suất mỗi tháng là $1\% $.

Ta có:

${u_1} = 1000000000$ đồng.

${u_2} = {u_1} + {u_1} \cdot 1\% – a = {u_1}\left( {1 + 1\% } \right) – a$ (đồng)

${u_3} = {u_1}\left( {1 + 1\% } \right) – a + \left[ {{u_1}\left( {1 + 1\% } \right) – a} \right].1\% – a$

$ = {u_1}{(1 + 1\% )^2} – a\left( {1 + 1\% } \right) – a$

$ \cdots $

${u_n} = {u_1}{(1 + 1\% )^{n – 1}} – a{(1 + 1\% )^{n – 2}} – a{(1 + 1\% )^{n – 3}} – a{(1 + 1\% )^{n – 4}} – \ldots – a$.

Ta thấy dãy $a{(1 + 1\% )^{n – 2}};a{(1 + 1\% )^{n – 3}};a{(1 + 1\% )^{n – 4}}; \ldots $; a lập thành một cấp số nhân với số hạng đầu ${a_1} = a$ và công bội $q = 1 + 1\% = 99\% $ có tổng $n – 2$ số hạng đầu là:

${S_{n – 2}} = \frac{{a\left( {1 – {{(\% )}^{n – 2}}} \right)}}{{1 – 99\% }} = 100a\left[ {1 – {{(99\% )}^{n – 2}}} \right]$.

Suy ra ${u_n} = {u_1}{(1 + 1\% )^{n – 1}} – 100a\left[ {1 – {{(99\% )}^{n – 2}}} \right]$

Vì sau 2 năm $ = 24$ tháng thì ông An trả xong số tiền nên $n = 24$ và ${u_{24}} = 0$.

Do đó ta có:

${u_{24}} = {u_1}{(1 + 1\% )^{23}} – 100a\left[ {1 – {{(99\% )}^{22}}} \right] = 0$

$ \Leftrightarrow 1000000000.{(99\% )^{23}} – 100a\left[ {1 – {{(99\% )}^{22}}} \right] = 0$

$ \Leftrightarrow a = 40006888,25$

Vậy mỗi tháng ông An phải trả 40006888,25 đồng.

Câu 24: Một cây đàn organ có tần số âm thanh các phim liên tiếp tạo thành một cấp số nhân. Cho biết tần số phim La Trung là $400Hz$ và tần số của phím LaCao cao hơn 12 phím là $800Hz$ (nguổn: https:// vi.wikipedia.org/wiki/Organ). Tìm công bội của cẩp số nhân nói trên (làm tròn kết quả đến hàng phần nghìn).

Lời giải

Ta có: ${q^{12}} = \frac{{800}}{{400}} = 2$. Suy ra: $q = 1,06$.

Câu 25: Dân số Việt Nam năm 2020 là khoảng 97,6 triệu người (theo Niên giảm thống kê năm 2020). Nếu trung bình mỗi năm tăng $1,14\% $ thì ước tính dân số Việt Nam năm 2040 là khoảng bao nhiêu người (làm tròn kết quả đến hàng trăm nghìn)?

Lời giải

Ước tính dân số Việt Nam năm 2040 là: $\;97,6.{(1 + 0,0114)^{20}} = 122,4$ (triệu người).

Câu 26: Tế bào E.Coli trong điều kiện nuôi cấy thích hợp cứ 20 phút lại phân đôi một lần. Hỏi sau 24 giờ, tế bào ban đầu sẽ phân chia thành bao nhiêu tế bào?

Lời giải

Số tế bào phân chia sau mỗi 20 phút tạo thành cấp số nhân với số hạng đầu là 2 , công bội là 2 .

Sau 24 giờ ( tức $n = \left( {24.60} \right):20 = 72$ ) tế bào ban đầu phân chia thành số tế bào là:

${u_{72}} = {2.2^{71}} = {4.722.10^{21}}$

${u_{72}} = {2.2^{71}} = {4.722.10^{21}}$

Câu 27: Mặt sàn tầng một (tầng trệt) của một ngôi nhà cao hơn mặt sân $0,5\,m$. Cầu thang đi từ tầng một lên tầng hai gồm 25 bậc, mổi bậc cao $16\,cm$

a) Viết công thức để tìm độ cao của bậc cầu thang thứ $n$ so với mặt sân.

b) Tính độ cao của sàn tầng hai so với mặt sân.

Lời giải

a. Mỗi bậc thang cao $16\;cm = 0,16\;m$.

$ \Rightarrow n$ bậc thang cao $0,16n\left( m \right)$

Vì mặt bằng sàn cao hơn mặt sân $0,5\;m$ nên công thức tính độ cao của bậc $n$ so với mặt sân sẽ là: ${h_n} = \left( {0,5 + 0,16n} \right)\left( m \right)$

b. Độ cao của sàn tầng hai so với mặt sân ứng với $n = 25$ là:

${h_{25}} = 0,5 + 0,16 \times 25 = 4,5\left( {\;m} \right)$

Câu 28: Một hình vuông màu vàng có cạnh 1 đơn vị dài được chia thành chín hình vuông nhỏ hơn và hình vuông ở chính giữa được tô màu xanh như Hình 2.1 Mỗi hình vuông màu vàng nhỏ hơn lại được chia thành chín hình vuông con, và mỗi hình vuông con ở chính giữa lại được tô màu xanh. Nếu quá trình này được tiếp tục lặp lại năm lần, thì tồng diện tích các hình vuông được tô màu xanh bao nhiêu?

Lời giải

Diện tích ô vuông màu xanh sau lần phân chia thứ nhất là: $\frac{1}{9}$, số ô vuông màu xanh được tạo thêm là ${8^0}$

Diện tích ô vuông màu xanh sau lần phân chia thứ hai là: $\frac{1}{{{9^2}}}$, số ô vuông màu xanh được tạo thêm là ${8^1}$

Diện tích ô vuông màu xanh sau lần phân chia thứ năm là: $\frac{1}{{{9^5}}}$, số ô vuông màu xanh được tạo thêm là ${8^4}$

Tổng diện tích các ô vuông màu xanh là: $\frac{1}{9} + \frac{1}{{{9^2}}} \times {8^1} + \ldots + \frac{1}{{{9^5}}} \times {8^4} = 0,445$

Câu 29: Một tháp 10 tầng có diện tích sàn của tầng dưới cùng là $6144{m^2}$ . Tính diện tích mặt sàn tầng trên cùng,biết rằng diện tích mặt sàn mỗi tầng bằng nửa diện tích mặt sàn tầng ngay bên dưới.

Lời giải

${u_{10}} = {u_1} \cdot {q^9} = 6144 \cdot {\left( {\frac{1}{2}} \right)^9} = 12\left( {{m^2}} \right)$

Câu 30: Một khay nước có nhiệt độ ${25^0}C$được đặt vào ngăn đá của tủ lạnh. Cho biết sau mỗi giờ, nhiệt độ của nước đá giảm đi $25\% $. Tính nhiệt độ khay nước đó sau 4 giờ.

Lời giải

${u_5} = {u_1} \cdot {q^4} = 20 \cdot 0,{75^4} \approx 6,{33^ \circ }C$.

Câu 31: Một công ty mua một chiếc máy với giá 1 tỉ 200 triệu đồng. Công ty nhận thấy, trong vòng 5 năm đầu, tốc độ khấu hao là $25\% $/năm (tức là sau mổi một năm, giá trị còn lại của chiếc máy bằng $75\% $ giá trị của năm trước đó)

a) Viết công thức tính giá trị của chiếc máy đó sau 1 năm, 2 năm.

b) Sau 5 năm, giá trị của chiếc máy đó còn khoảng bao nhiêu triệu đồng (làm tròn kết quả đến hàng đơn vị)?

Lời giải

a) Giá trị của chiếc máy đó sau 1 năm là:

1200. $0,75 = 900$ (triệu đồng).

Giá trị của chiếc máy đó sau 2 năm là:

$1200 \cdot 0,75 \cdot 0,75 = 1200 \cdot 0,{75^2} = 675$ (triệu đồng).

b) Sau 5 năm, giá trị chiếc máy đó còn là:

$1200 \cdot 0,{75^5} \approx 285$ (triệu đồng).

Câu 32: Một con chó con nặng $0,4kg$ mới sinh và sau mỗi tuần tuổi khối lượng của nó tăng thêm $24\% $. Giả sử ${u_n}\,\,(kg)$ là khối lượng của con chó vào cuối tuần tuổi thứ .

a) Viết lần lượt các công thức tính ${u_2},{u_3}$. Từ đó dự đoán công thức của ${u_n}$.

b) Con chó nặng bao nhiêu kilôgam khi được sáu tuần tuổi?

Lời giải

a) Giả sử ${u_n}\left( {\;kg} \right)$ là khối lượng của con chó vào cuối tuần tuổi thứ $n$.

Ta có ${u_1} = 0,4;{u_2} = {u_1} + {u_1}24\% = {u_1}\left( {1 + 24\% } \right);{u_3} = {u_2} + {u_2}24\% = {u_1}{(1 + 24\% )^2}$.

Tương tự, ta có ${u_n} = {u_1}{(1 + 24\% )^{n – 1}}\forall n \geqslant 1$.

b) Sau sáu tuần tuổi thì con chó nặng là

${u_6} = 0,4 \cdot {(1 + 24\% )^5} = 1,17\left( {\;kg} \right)$.

Câu 33: Anh Nam là một cầu thủ bóng đá chuyên nghiệp. Anh vừa kí hợp đồng 5 năm với một câu lạc bộ với mức lương năm khởi điểm là 300 triệu đồng. Chủ tịch câu lạc bộ đưa ra cho anh Nam ba phương án về lương như sau:

Phương án 1: Mỗi năm ngoài mức lương cố định như trên, sẽ được thưởng thêm 50 triệu đồng.

Phương án 2: Mỗi năm lương sẽ tăng thêm 10% so với lương năm trước đó, bắt đầu kể từ năm thứ hai.

Phương án 3: Mỗi năm lương sẽ tăng thêm 30 triệu so với lương năm trước đó, bắt đầu kể từ năm thứ hai.

Em hãy tính giúp anh Nam xem với phương án lương nào thì tổng lương sau 5 năm của anh Nam là lớn nhât?

Lời giải

Ta tính tổng tiền lương của anh Nam theo từng phương án:

Phương án 1: Mỗi năm ngoài mức lương cố định như trên, sẽ được thưởng thêm 50 triệu đồng thì sau 5 năm tổng số tiền lương của anh Nam là

$5 \cdot 300 + 5 \cdot 50 = 1750\;$(triệu đồng)

Phương án 2: Mỗi năm lương sẽ tăng thêm $10\% $ so với lương năm trước đó, bắt đầu kể từ năm thứ hai thì sau 5 năm tổng số tiền lương của anh Nam là

$00 + 300 \cdot \left( {1 + 10\% } \right) + 300 \cdot {(1 + 10\% )^2} + 300 \cdot {(1 + 10\% )^3} + 300{(1 + 10\% )^4}:1831,53$ (triệu đồng)

Phương án 3: Mỗi năm lương sẽ tăng thêm 30 triệu so với lương năm trước đó, bắt đầu kể từ năm thứ hai thì sau 5 năm tổng số tiền lương của anh Nam là

$300 + 330 + 360 + 390 + 420 = 1800$ ( triệu đồng)

Vậy anh Nam nên sử dụng Phương án 2 để nhận được tổng lương sau 5 năm là cao nhất.