Các Dạng Bài Toán Thực Tế Về Dãy Số Lớp 11 Có Lời Giải

Các dạng bài toán thực tế về dãy số lớp 11 có lời giải được soạn dưới dạng file word và PDF gồm 2 trang. Các bạn xem và tải về ở dưới.

A. KIẾN THỨC CƠ BẢN

1. Mỗi hàm số $u$ xác định trên tập các số nguyên dương ${N^*}$ được gọi là một dãy số vô hạn (gọi tắt là dãy số), kí hiệu là $u = u\left( n \right)$.

Ta thường viết ${u_n}$ thay cho $u\left( n \right)$ và kí hiệu dãy số $u = u\left( n \right)$ bởi $\left( {{u_n}} \right)$, do đó dãy số $\left( {{u_n}} \right)$ được viết dưới dạng khai triển ${u_1},{u_2}, \ldots ,{u_n}, \cdots $ Số ${u_1}$ gọi là số hạng đầu, ${u_n}$ là số hạng thứ $n$ và gọi là số hạng tổng quát của dãy số.

2. Mỗi hàm số $u$ xác định trên tập $M = \left\{ {1;2;3; \ldots ;m} \right\}$ với $m \in {N^*}$ được gọi là một dãy số hữu hạn.

Dạng khai triển của dãy số hữu hạn là ${u_1},{u_2}, \ldots ,{u_m}$. Số ${u_1}$ gọi là số hạng đầu, ${u_m}$ là số hạng cuối.

3. Một dãy số có thể cho bằng:

Liệt kê các số hạng (chỉ dùng cho các dãy hữu hạn và có ít số hạng);

Công thức của số hạng tổng quát;

Phương pháp mô tả;

Phương pháp truy hồi.

4. Dãy số $\left( {{u_n}} \right)$ được gọi là dãy số tăng nếu ta có ${u_{n + 1}} > {u_n}$ với mọi $n \in {N^*}$.

Dãy số $\left( {{u_n}} \right)$ được gọi là dãy số giảm nếu ta có ${u_{n + 1}} < {u_n}$ với mọi $n \in {N^*}$.

5. Dãy số $\left( {{u_n}} \right)$ được gọi là bị chặn trên nếu tồn tại một số $M$ sao cho ${u_n} \leqslant M\forall n \in {N^*}$.

Dãy số $\left( {{u_n}} \right)$ được gọi là bị chặn dưới nếu tồn tại một số $m$ sao cho ${u_n} \geqslant m\forall n \in {{\mathbf{N}}^*}$.

Dãy số $\left( {{u_n}} \right)$ được gọi là bị chặn nếu nó vừa bị chặn trên vừa bị chặn dưới, tức là tồn tại các số $m,M$ sao cho $m \leqslant {u_n} \leqslant M\forall n \in {N^*}$.

B. BÀI TẬP VẬN DỤNG

Câu 1:

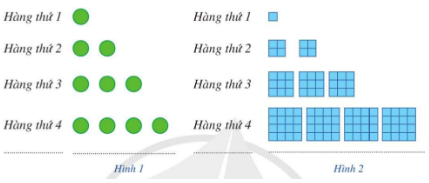
a) Gọi ${u_n}$ là số chấm ở hàng thứ $n$ trong Hình 1. Dự đoán công thức của số hạng tổng quát cho dãy số $({u_n})$.

b) Gọi ${v_n}$ là tổng diện tích của các hình tô màu ở hàng thứ $n$ trong Hình 2 (mỗi ô vuông nhỏ là một đơn vị diện tích). Dự đoán công thức của số hạng tổng quát cho dãy số $\left( {{v_n}} \right)$.

Lời giải

a) Số chấm ở hàng thứ nhất là: ${u_1} = 1$;

Số chấm ở hàng thứ hai là: ${u_2} = 2$;

Số chấm ở hàng thứ ba là: ${u_3} = 3$;

Số chấm ở hàng thứ tư là: ${u_4} = 4$;

Vậy số chấm ở hàng thứ $n$ là: ${u_n} = n$.

b) Diện tích của các ô màu ở hàng thứ nhất là: ${v_1} = 1 = {1^3}$;

Diện tích của các ô màu ở hàng thứ hai là: ${v_2} = 8 = {2^3}$;

Diện tích của các ô màu ở hàng thứ ba là: ${v_3} = 27 = {3^3}$;

Diện tích của các ô màu ở hàng thứ tư là: ${v_4} = 64 = {4^3}$;

Vậy diện tích của các ô màu ở hàng thứ $n$ là: ${v_n} = {n^3}$.

Câu 2: Chị Mai gửi tiền tiết kiệm vào ngân hàng theo thể thức lãi kép như sau: Lần đầu chị gửi 100 triệu đồng. Sau đó, cứ hết 1 tháng chị lại gửi thêm vào ngân hàng 6 triệu đồng. Biết lãi suất của ngân hàng là $0,5\% $một tháng. Gọi ${P_n}$ (triệu đồng) là số tiền chị có trong ngân hàng sau $n$ tháng.

a) Tính số tiền chị có trong ngân hàng sau 1 tháng.

b) Tính số tiền chị có trong ngân hàng sau 3 tháng.

c) Dự đoán công thức của ${P_n}$ tính theo $n$.

Lời giải

a) Số tiền chị có trong ngân hàng sau 1 tháng là:

${P_1} = 100 + 100 \cdot 0,5\% + 6 = 100,5 + 6$ (triệu đồng).

b) Số tiền chị có trong ngân hàng sau 2 tháng là:

${P_2} = 100,5 + 6 + \left( {100,5 + 6} \right) \cdot 0,5\% + 6$

$ = \left( {100,5 + 6} \right)\left( {1 + 0,5\% } \right) + 6$

$ = 100,5\left( {1 + 0,5\% } \right) + 6.\left( {1 + 0,5\% } \right) + 6$ (triệu đồng).

Số tiền chị có trong ngân hàng sau 3 tháng là:

${P_3} = \left( {100,5 + 6} \right)\left( {1 + 0,5\% } \right) + 6 + \left[ {\left( {100,5 + 6} \right)\left( {1 + 0,5\% } \right) + 6} \right] \cdot 0,5\% + 6$

$ = 100,5 \cdot {(1 + 0,5\% )^2} + 6{(1 + 0,5\% )^2} + 6 \cdot \left( {1 + 0,5\% } \right) + 6$ (triệu đồng).

c) Số tiền chị có trong ngân hàng sau 4 tháng là:

${P_4} = \left( {100,5 + 6} \right){(1 + 0,5\% )^2} + 6 \cdot \left( {1 + 0,5\% } \right) + 6$$ + \left[ {\left( {100,5 + 6} \right){{(1 + 0,5\% )}^2} + 6 \cdot \left( {1 + 0,5\% } \right) + 6} \right]0,5\% + 6$$ = 100,5 \cdot {(1 + 0,5\% )^3} + 6 \cdot {(1 + 0,5\% )^3} + 6{(1 + 0,5\% )^2} + 6 \cdot \left( {1 + 0,5\% } \right) + 6$

Số tiền chị có trong ngân hàng sau $n$ tháng là:

${P_n} = 100,5 \cdot {(1 + 0,5\% )^{n – 1}} + 6{(1 + 0,5\% )^{n – 1}} + 6{(1 + 0,5\% )^{n – 2}} + 6 \cdot {(1 + 0,5\% )^{n – 3}} + \ldots + 6\;\;$với mọi $n \in {N^*}.$

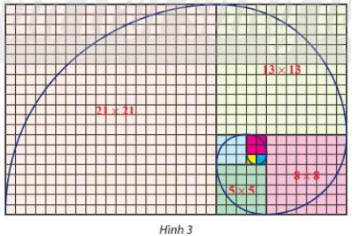
Câu 3: Trên lưới ô vuông, mỗi ô cạnh 1 đơn vị, người ta vẽ 8 hình vuông và tô màu khác nhau như Hình 3 . Tìm dãy số biểu diển độ dài cạnh của 8 hình vuông đó từ nhỏ đến lớn. Có nhận xét gì về dãy số trên?

Lời giải

${u_1} = 1;{u_2} = 1;{u_3} = 2;{u_4} = 3;{u_5} = 5;{u_6} = 8;{u_7} = 13;{u_8} = 21$

Ta có dãy số: $\left( {{u_n}} \right):\left\{ {\begin{array}{*{20}{c}}
{{u_1} = 1} \\
{{u_2} = 1} \\
{{u_n} = {u_{n – 1}} + {u_{n – 2}}}
\end{array}} \right.$

Câu 4: Ông An gửi tiết kiệm 100 triệu đồng kì hạn 1 tháng với lãi suất một năm theo hình thức tính lãi kép. Số tiền (triệu đồng) của ông An thu được sau tháng được cho bởi công thức ${A_n} = {\left( {1 + \frac{{0,06}}{{12}}} \right)^n}$.

a) Tìm số tiền ông An nhận được sau tháng thứ nhất, sau tháng thứ hai.

b) Tìm số tiền ông An nhận được sau 1 năm.

Lời giải

a) Số tiền ông An nhận được sau 1 tháng: ${A_1} = 100{\left( {1 + \frac{{0.06}}{{12}}} \right)^1} = 100,5$ (triệu đồng)

Số tiền ông An nhận được sau 2 tháng: ${A_2} = 100{\left( {1 + \frac{{0,06}}{{12}}} \right)^2} = 101,0025$

(triệu đồng)

b) Số tiền ông An nhận được sau 1 năm: ${A_{12}} = 100{\left( {1 + \frac{{0,06}}{{12}}} \right)^{12}} = 106,1678$ (triệu đồng)

Câu 5: Chị Hương vay trả góp một khoản tiền 100 triệu đồng và đồng ý trả dần 2 triệu đồng mỗi tháng với lãi suất $0,8\% $ số tiền còn lại của mỗi tháng.

Gọi ${A_n}\left( {n \in N} \right)$ là số tiền còn nọ̣ (triệu đồng) của chị Hương sau $n$ tháng.

a) Tìm lần lượt ${A_0},{A_1},{A_2},{A_3},{A_4},{A_5},{A_6}$ để tính số tiền còn nợ của chị Hương sau 6 tháng.

b) Dự đoán hệ thức truy hồi đối với dãy số $\left( {{A_n}} \right)$.

Lời giải

a) Ta có:

${A_0} = 100$

${A_1} = 100 + 100 \times 0,008 – 2 = 98,8$

${A_2} = 98,8 + 98,8 \times 0,008 – 2 = 97,59$

${A_3} = 97,59 + 97,59 \times 0,008 – 2 = 96,37$

${A_4} = 96,37 + 96,37 \times 0,008 – 2 = 95,14$

${A_5} = 95,14 + 95,14 \times 0,008 – 2 = 93,90$

${A_6} = 93,90 + 93,90 \times 0,008 – 2 = 92,65$

Vậy sau 6 tháng số tiền chị Hương còn nợ là 92, 65 triệu đồng.

b) Hệ thức truy hồ: ${A_n} = {A_{n – 1}} + {A_{n – 1}} \times 0.008 – 2 = 1.008{A_{n – 1}} – 2$ (triệu đồng)

Câu 6: Chị Mai gửi tiền tiết kiệm vào ngân hàng theo hình thức lãi kép như sau: Lần đầu chị gửi 100 triệu đồng. Sau đó, cứ hết 1 tháng chị lại gửi thêm vào ngân hàng 6 triệu đồng. Biết lãi suất của ngân hảng là $0,5\% $ một tháng. Gọi ${P_n}$ (triệu đồng) là số tiền chị có trong ngân hàng sau $n$ tháng.

a) Tính số tiền chị có trong ngân hàng sau 1 tháng.

b) Tính số tiền chị có trong ngân hàng sau 3 tháng.

c) Dự đoán công thức của ${P_n}$.

Lời giải

a) Số tiền cả gốc và lãi chị Mai có được sau 1 tháng (khi chưa gửi thêm 6 triệu đồng) là:

$100 + 100 \cdot \frac{{0,5}}{{100}} = 100 \cdot 1,005 = 100,5\;\;$(triệu đồng).

Số tiền chị có trong ngân hàng sau 1 tháng là: 100,5 + 6 = 106,5 (triệu đồng).

b) Số tiền chị Mai có trong ngân hàng sau 2 tháng là:

$106,5 \cdot 1,005 + 6 = 113,0325\;$(triệu đồng)

Số tiền chị Mai có trong ngân hàng sau 3 tháng là:

$113,0325 \cdot 1,005 + 6 = 119,5976625$ (triệu đồng).

c) Ta có:

${P_1} = 100 \cdot 1,005 + 6$;

${P_2} = {P_1} \cdot 1,005 + 6 = \left( {100 \cdot 1,005 + 6} \right) \cdot 1,005 + 6$

$ = 100 \cdot 1,{005^2} + 6 \cdot 1,005 + 6;$

${P_3} = {P_2} \cdot 1,005 + 6 = \left( {100 \cdot 1,{{005}^2} + 6 \cdot 1,005 + 6} \right) \cdot 1,005 + 6$

$ = 100 \cdot 1,{005^3} + 6 \cdot 1,{005^2} + 6 \cdot 1,005 + 6; \ldots ;$

Cứ như thế, ta dự đoán được công thức của ${P_n}$ :

${P_n} = 100 \cdot 1,{005^n} + 6 \cdot 1,{005^{n – 1}} + 6 \cdot 1,{005^{n – 2}} + \ldots + 6$

$ = 100 \cdot 1,{005^n} + 6 \cdot \left( {1,{{005}^{n – 1}} + 1,{{005}^{n – 2}} + \ldots . + 1} \right)$.

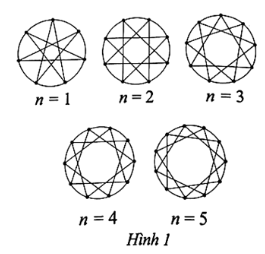
Câu 7: Với mỗi số nguyên dương , lấy điểm cách đều nhau trên đường tròn. Nối mỗi điểm với điểm cách nó hai điểm trên đường tròn đó để tạo thành các ngôi sao như Hình 1. Gọi là số đo góc ở đỉnh tính theo đơn vị độ của mỗi ngôi sao thì ta được dãy số . Tìm công thức của số hạng tổng quát

Lời giải

Ta thấy đường tròn được chia thành $n + 6$ cung bằng nhau và mỗi cung có số đo bằng ${\left( {\frac{{360}}{{n + 6}}} \right)^\natural }$. Do mỗi điểm được nối với điểm cách nó hai điểm trên đường tròn nên góc ở đỉnh của mỗi ngôi sao là góc nội tiếp chắn $n + 6 – 2.3 = n$ cung bằng nhau đó. Suy ra số đo góc ở đỉnh tính theo đơn vị độ của mỗi ngôi sao là ${u_n} = \frac{1}{2} \cdot \frac{{360}}{{n + 6}} \cdot n = \frac{{180n}}{{n + 6}}$.

Câu 8: Bác Hưng để 10 triệu đồng trong tài khoản ngân hàng. Vào cuối mỗi năm, ngân hàng trả lãi vào tài khoản của bác ấy, nhưng sau đó sẽ tính phí duy trì tài khoản hằng năm là 120 nghìn đồng.

a) Gọi ${A_0}$ là số tiền bác Hưng đã gửi. Viết công thức tính lần lượt ${A_1},{A_2},{A_3}$. Từ đó dự đoán hệ thức truy hồi cho số dư ${A_n}$ (tính theo đơn vị đồng) trong tài khoản của bác Hưng vào cuối năm thứ $n$.

b) Tìm số dư trong tài khoản của bác Hưng sau 4 năm.

Lời giải

a) Vào cuối năm thứ nhất, số tiền trong tài khoản của bác Hưng là

${A_1} = {A_0}\left( {1 + 3\% } \right) – 120000 = 1,03{A_0} – 120000\;$(đồng)

Vào cuối năm thứ hai, số tiền trong tài khoản của bác Hưng là

${A_2} = {A_1}\left( {1 + 3\% } \right) – 120000 = 1,03{A_1} – 120000\;$(đồng)

Vào cuối năm thứ ba, số tiền trong tài khoản của bác Hưng là

${A_3} = {A_2}\left( {1 + 3\% } \right) – 120000 = 1,03{A_2} – 120000\;$(đồng)

Tương tự, vào cuối năm thứ $n\left( {n \geqslant 1} \right)$, số tiền trong tài khoản của bác Hưng là

${A_n} = {A_{n – 1}}\left( {1 + 3\% } \right) – 120000 = 1,03{A_{n – 1}} – 120000\;$(đồng)

b) Ta tính lần lượt ${A_1},{A_2},{A_3},{A_4}$ :

${A_1} = 10180000$; ${A_2} = 10365400;$${A_3} = 10556362$; ${A_4} = 10753053.$

Như vậy, số dư trong tài khoản của bác Hưng sau 4 năm là 10753053 đồng.

Câu 9: Giá của một chiếc máy photocopy lúc mới mua là 50 triệu đồng. Biết rằng giá trị của nó sau mỗi năm sử dụng chỉ còn $75\% $ giá trị trong năm liền trước đó. Tính giá trị còn lại của chiếc máy photocopy đó sau mỗi năm, trong khoảng thời gian 5 năm kể từ khi mua.

Lời giải

Giá trị của máy photocopy sau 1 năm sử dụng là

${T_1} = 50 \cdot 75\% = 37,5$ ( triệu đồng )

Giá trị của máy photocopy sau 2 năm sử dụng là

${T_2} = {T_1} \cdot 75\% = 28,125$ ( triệu đồng )

Giá trị của máy photocopy sau 3 năm sử dụng là

${T_3} = {T_2} \cdot 75\% = 21,0938$ ( triệu đồng )

Giá trị của máy photocopy sau 4 năm sử dụng là

${T_4} = {T_3} \cdot 75\% = 15,8203$ ( triệu đồng )

Giá trị của máy photocopy sau 5 năm sử dụng là

${T_5} = {T_4} \cdot 75\% = 11,8652$ ( triệu đồng )

Chú ý. Tổng quát, giá trị của máy photocopy sau $n$ năm sử dụng là

${T_n} = {T_1} \cdot {(0,75)^{n – 1}}\;$ ( triệu đồng )

Câu 10: Nếu tỉ lệ lạm phát là $3,5\% $mỗi năm và giá trung bình của một căn hộ chung cư mới tại thời điểm hiện tại là 2,5 tỉ đồng thì giá trung bình của một căn hộ chung cư mới sau $n$ năm được cho bởi công thức ${A_n} = 2,5.{(1,035)^n}$ ( tỉ đồng). Tìm giá trung bình của một căn hộ chung cư mới sau 5 năm nữa.

Lời giải

Giá trung bình của một căn hộ chung cư mới sau 5 năm là

${A_5} = 2,5 \cdot {(1,035)^5} = 2,9692\;$( tỉ đồng)

Câu 11: Bác An gửi tiết kiệm 200 triệu đồng kì hạn 3 tháng, với lãi suất một năm. Số tiền (triệu đồng) cả vốn lẫn lãi mà bác An nhận được sau quý (mỗi quý là 3 tháng) sẽ là

${A_n} = 200{\left( {1 + \frac{{0,03}}{4}} \right)^n},n = 0,1,2, \ldots $

a) Viết ba số hạng đầu của dãy số.

b) Tìm số tiền bác An nhận được sau 2 năm.

Lời giải

a) Ba số hạng đầu của dãy số là ${A_1} = 201,5;{A_2} = 203,0113;{A_3} = 204,5338$.

b) Chú ý rằng 2 năm bằng 8 quý, tức là $n = 8$. Do đó, sau 2 năm só tiền bác An nhận được là ${A_8} = 212,3198$ triệu đồng.

Câu 12: Vi khuẩn E.Coli sinh sản thông qua một quá trình gọi là quá trình phân đôi. Vi khuẩn E.Coli phân chia làm đôi cứ sau 20 phút. Giả sử tốc độ phân chia này được duy trì trong 12 giờ kể tử khi vi khuẩn ban đầu xâm nhập vào cơ thể. Hỏi sau 12 giờ sẽ có bao nhiêu vi khuẩn E.Coli trong cơ thể? Giả sử có một nguồn dinh dưỡng vô hạn để vi khuẩn E.Coli duy trì tốc độ phân chia như cũ trong 48 giờ kể từ khi vi khuẩn ban đầu xâm nhập vào cơ thẻ. Hỏi sau 48 giờ sẽ có bao nhiêu vi khuẩn E.Coli trong cơ thể?

Lời giải

Giả sử ban đầu có 1 vi khuẩn E.Coli.

Sau 20 phút lần một, số vi khuẩn là $1 \cdot 2 = 2$.

Sau 20 phút lần hai, số vi khuẩn là $2 \cdot 2 = {2^2}$.

Sau 20 phút lần ba, số vi khuẩn là ${2^2} \cdot 2 = {2^3}$.

Sau 20 phút lần bốn, số vi khuẩn là ${2^3} \cdot 2 = {2^4}$.

Tương tự như vậy sau 12 giờ (bằng $3 \cdot 12$ lần 20 phút) thì số vi khuẩn là ${2^{3 \cdot 12}} = {2^{36}} \approx 6,87 \cdot {10^{10}}$ (con)

Sau 48 giờ (bằng $3 \cdot 48 = 144$ lần 20 phút) thì số vi khuẩn là:

${2^{144}} \approx 2,23 \cdot {10^{43}}$ (con).

Câu 13: Một công ty dược phẩm đang thử nghiệm một loại thuốc mới. Một thí nghiệm bắt đầu với $1,{0.10^9}$vi khuẩn. Một liều thuốc được sử dụng sau mỗi bốn giờ có thể tiêu diệt $4,{0.10^8}$ vi khuẩn. Giữa các liều thuốc, số lượng vi khuẩn tăng lên $25\% $.

a) Viết hệ thức truy hồi cho số lượng vi khuẩn sống trước mỗi lần sử dụng thuốc.

b) Tìm số vi khuẩn còn sống trước lần sử dụng thuốc thứ năm.

Lời giải

a) Gọi ${u_0} = 1,0 \cdot {10^9}$ là số vi khuẩn tại thời điểm ban đầu và ${u_n}$ là số vi khuẩn trước lần dùng thuốc thứ $n$.

Do mỗi liều thuốc được sử dụng sau bốn giờ có thể tiêu diệt $4,0 \cdot {10^8}$ vi khuẩn và giữa các liều thuốc, số lượng vi khuẩn tăng lên $25\% $ nên ta có

${u_{n + 1}} = \left( {{u_n} – 4,0 \cdot {{10}^8}} \right) + 25\% \cdot {u_n} = 1,25{u_n} – 4,0 \cdot {10^8}$.

b) Ta tính $\;{u_5}$ như sau:

${u_1} = 1,0 \cdot {10^9};$

${u_2} = 1,25{u_1} – 4,0 \cdot {10^8} = 8,5 \cdot {10^8};$

${u_3} = 1,25{u_2} – 4,0 \cdot {10^8} = 6,625 \cdot {10^8};$

${u_4} = 1,25{u_3} – 4,0 \cdot {10^8} = 4,28125 \cdot {10^8};$

${u_5} = 1,25{u_4} – 4,0 \cdot {10^8} = 1,3515625 \cdot {10^8}$

Vậy số vi khuẩn còn sống trước lần sử dụng thuốc thứ năm là 135156250 con.

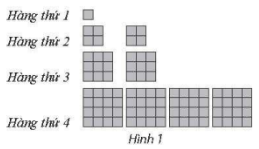
Câu 14: Gọi là tổng diện tích các hình vuông có ở hàng thứ trog Hinh 1 (mỗi ô vuông nhỏ là 1 đơn vị diện tích).

a) Tính ${u_1};{u_2};{u_3};{u_4}$.

b) Dự đoán công thức tính số hạng tổng quát của dãy số $\left( {{u_n}} \right)$.

Lời giải

a) ${u_1} = 1;{u_2} = 8;{u_3} = 27;{u_4} = 64$.

b) Ta có: ${u_1} = {1^3};{u_2} = {2^3};{u_3} = {3^3};{u_4} = {4^3}$.

Do đó, dự đoán ${u_n} = {n^3}$.