Giải Toán 12 Chân Trời Sáng Tạo Bài 2 Chương 2 Toạ Độ Của Vectơ Trong Không Gian

Câu 1. Trong không gian $Oxyz$, biết:

a) $\vec a = 5\vec i + 7\vec j – 3\vec k,\vec b = 2\vec i + 4\vec k$. Tìm tọa độ các vectơ $\vec a,\vec b$.

b) $\overrightarrow {OM} = 4\vec i – \vec j + 3\vec k,\overrightarrow {ON} = 8\vec i – 5\vec j$. Tìm toạ độ các điểm $M,N$.

Lời giải

a)

Phương pháp: $\overrightarrow a = {a_1}\overrightarrow i + {a_2}\overrightarrow j + {a_3}\overrightarrow k \Rightarrow \overrightarrow a = \left( {{a_1};\,{a_2};\,{a_3}} \right)$

$\vec a = 5\vec i + 7\vec j – 3\vec k \Rightarrow \overrightarrow a = \left( {5;7; – 3} \right)$

$\vec b = 2\vec i + 4\vec k = 2\vec i + 0\overrightarrow j + 4\vec k \Rightarrow \overrightarrow b = \left( {2;0;4} \right)$

b)

Phương pháp: $\overrightarrow {OM} = x\overrightarrow i + y\overrightarrow j + z\overrightarrow k \Rightarrow M\left( {x;\,y;\,z} \right)$

$\overrightarrow {OM} = 4\vec i – \vec j + 3\vec k \Rightarrow M\left( {4; – 1;3} \right)$

$\overrightarrow {ON} = 8\vec i – 5\vec j = 8\vec i – 5\vec j + 0\overrightarrow k \Rightarrow N\left( {8;5;0} \right)$

Câu 2. Trong không gian $Oxyz$, biết:

a) $\vec a = \left( { – 2;5; – 7} \right),\vec b = \left( {4;0;1} \right)$. Tính $\vec a,\vec b$ theo các vectơ $\vec i,\vec j,\vec k$.

b) $A\left( {7; – 2;1} \right),B\left( {0;5;0} \right)$. Tính $\overrightarrow {OA} ,\overrightarrow {OB} $ theo các vectơ $\vec i,\vec j,\vec k$.

Lời giải

a)

Phương pháp: $\overrightarrow a = \left( {{a_1};\,{a_2};\,{a_3}} \right) \Rightarrow \overrightarrow a = {a_1}\overrightarrow i + {a_2}\overrightarrow j + {a_3}\overrightarrow k $

$\vec a = \left( { – 2;5; – 7} \right) \Rightarrow \vec a = – 2\vec i + 5\vec j – 7\vec k$;

$\vec b = \left( {4;0;1} \right) \Rightarrow \overrightarrow b = 4\vec i + 0\overrightarrow j + 1\vec k = 4\vec i + \vec k$
b)

Phương pháp: $M\left( {x;\,y;\,z} \right) \Rightarrow \overrightarrow {OM} = x\overrightarrow i + y\overrightarrow j + z\overrightarrow k $

$A\left( {7; – 2;1} \right) \Rightarrow \overrightarrow {OA} = 7\vec i – 2\vec j + \vec k$;

$B\left( {0;5;0} \right) \Rightarrow \overrightarrow {OB} = 0\overrightarrow i + 5\vec j + 0\overrightarrow k = 5\vec j$

Câu 3. Cho tứ diện $SABC$ có $ABC$ là tam giác vuông tại $B$, $BC = 3,BA = 2,SA$ vuông góc với mặt phẳng $\left( {ABC} \right)$ và có độ dài bằng 2 (Hình 13).

a) Xác định một hệ toạ độ dựa trên gợi ý của hình vẽ và chỉ ra các vectơ đơn vị trên các trục toạ độ.

b) Tìm toạ độ các điểm $A,B,C,S$.

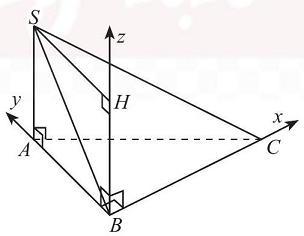
Hình 13

Lời giải

a)

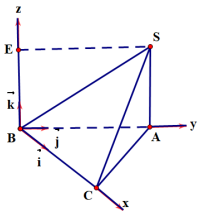
Các vecto đơn vị trên ba trục $Ox,Oy,Oz$ lần lượt là $\vec i;\vec j;\vec k$ với độ dài $\vec i;\vec j;\vec k$ lần lượt bằng $\frac{1}{3}BC;\frac{1}{2}BA;\frac{1}{2}SA$

b) Vì $B$ trùng với gốc tọa độ nên $B\left( {0;0;0} \right)$.

Vì $\vec j$ và $\overrightarrow {BA} $ cùng hướng và $BA = 2$ nên $\overrightarrow {BA} = 2\vec j$. Suy ra $A\left( {0;2;0} \right)$.

Vî $\vec i$ và $\overrightarrow {BC} $ cùng hướng và $BC = 3$ nên $\overrightarrow {BC} = 3\vec i$. Suy ra $C\left( {3;0;0} \right)$.

Gọi $E$ là hình chiếu của $S$ lên trục $Oz$.

Ta có $BE = AS = 2$. Vì $\vec k$ và $\overrightarrow {BE} $ cùng hướng và $BE = 2$ nên $\overrightarrow {BE} = 2\vec k$.

Theo quy tắc hình bình hành ta có $\overrightarrow {BS} = \overrightarrow {BA} + \overrightarrow {BE} = 2\vec j + 2\vec k$.

Suy ra $S\left( {0;2;2} \right)$.

Câu 4. Cho hình chóp $S \cdot ABC$ có đáy $ABC$ là tam giác đều cạnh bằng $2,SA$ vuông góc với đáy và $SA$ bằng 1 (Hình 14). Thiết lập hệ toạ độ như hình vẽ, hãy vẽ các vectơ đơn vị trên các trục $Ox,Oy,Oz$ và tìm toạ độ các điểm $A,B,C,S$.

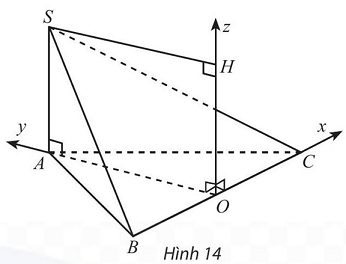
Lời giải

 

Các vecto đơn vị trên ba trục $Ox,Oy,Oz$ lần lượt là $\vec i = \overrightarrow {OC} ;\vec j = \overrightarrow {OE} ;\vec k = \overrightarrow {OH} $ với $E$ là điểm thuộc tia $Oy$ sao cho $OE = 1$ và $H$ là điểm thuộc tia $Oz$ sao cho $OH = 1$.

Vì $\vartriangle ABC$ đều và $AO \bot BC$ nên $O$ là trung điểm của $BC$. Mà $BC = 2$ nên $OB = OC = 1$ và $OA = \sqrt 3 $.

Vì $\vec j$ và $\overrightarrow {OA} $ cùng hướng và $OA = \sqrt 3 $ nên $\overline {OA} = \sqrt 3 \vec j$. Suy ra $A\left( {0;\sqrt 3 ;0} \right)$.

Vì $\vec i$ và $\overrightarrow {OC} $ cùng hướng và $OC = 1$ nên $\overrightarrow {OC} = \vec i$. Suy ra $C\left( {1;0;0} \right)$.

Vì $\vec i$ và $\overrightarrow {OB} $ ngược hướng và $OB = 1$ nên $OB = – \vec i$. Suy ra $B\left( { – 1;0;0} \right)$.

Theo quy tắc hình bình hành ta có $\overrightarrow {OS} = \overrightarrow {OA} + \overrightarrow {OH} = \sqrt 3 \vec j + \vec k$. Suy ra $S\left( {0;\sqrt 3 ;1} \right)$.

Câu 5. Trong không gian $Oxyz$, cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi cạnh bằng 5 , giao điểm hai đường chéo $AC$ và $BD$ trùng với gốc $O$. Các vectơ $\overrightarrow {OB} ,\overrightarrow {OC} ,\overrightarrow {OS} $ lần lượt cùng hướng với $\vec i$, $\vec j,\vec k$ và $OA = OS = 4$ (Hình 15). Tìm tọa độ các vectơ $\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {AS} $ và $\overrightarrow {AM} $ với $M$ là trung điểm của cạnh $SC$.

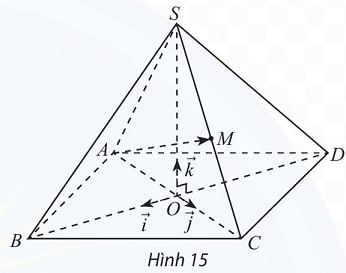
Lời giải

 

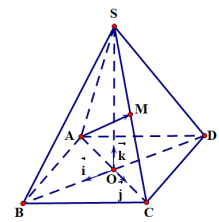
Vì $ABCD$ là hình thoi cạnh bằng $5,O$ là giao điểm của $AC$ và $BD$ nên $O$ là trung điểm của $AC$ và $BD$.

Xét $\vartriangle OAB$ vuông tại $O$, có $OB = \sqrt {A{B^2} – O{A^2}} = \sqrt {25 – 16} = 3$

Vì $\overrightarrow {OA} $ và $\vec i$ cùng hướng và $OB = 3$ nên $\overrightarrow {OB} = 3\vec i$. Vì $\overrightarrow {OA} $ và $\vec j$ cùng hướng và $OA = 4$ nên $\overrightarrow {OA} = – 4\vec j$.

Ta có $\overrightarrow {AB} = \overrightarrow {OB} – \overrightarrow {OA} = 3\vec i + 4\vec j$.

Do đó $\overrightarrow {AB} = \left( {3;4;0} \right)$.

Có $AC = 2OA = 8$ và $\overrightarrow {AC} $ và $\vec j$ cùng hướng nên $\overrightarrow {AC} = 8\vec j$.

Do đó $\overrightarrow {AC} = \left( {0;8;0} \right)$.

Có $\overrightarrow {OS} $ và $\vec k$ cùng hướng và $OS = 4$ nên $\overrightarrow {OS} = 4\vec k$. Có $\overrightarrow {SB} = \overrightarrow {OB} – \overrightarrow {OS} = 3\vec i – 4\vec k$. Do đó $\overrightarrow {SB} = \left( {3;0; – 4} \right)$ Lại có $\overrightarrow {AS} = \overrightarrow {AB} + \overrightarrow {BS} = \left( {3\vec i + 4\vec j} \right) – \left( {3\vec i – 4\vec k} \right) = 4\vec j + 4\vec k$. Do đó $\overrightarrow {AS} = \left( {0;4;4} \right)$. Vi $M$ là trung điềm của $SC$ nên $\overrightarrow {AM} = \frac{1}{2}\left( {\overrightarrow {AS} + \overrightarrow {AC} } \right) = \frac{1}{2}\left( {4\vec j + 4\vec k + 8\vec j} \right) = 6\vec j + 2\vec k$. Do đó $\overrightarrow {AM} = \left( {0;6;2} \right)$.

Câu 6. Một chiếc xe đang kéo căng sợi dây cáp $AB$ trong công trường xây dựng, trên đó đã thiết lập hệ toạ độ $Oxyz$ như Hình 16 với độ dài đơn vị trên các trục toạ độ bằng $1\;m$. Tìm tọa độ của vectơ $\overrightarrow {AB} $.

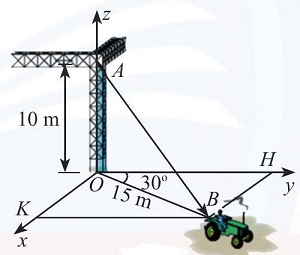
Hình 16

Lời giải

Vì $\overrightarrow {OA} $ và $\vec k$ cùng hướng và $OA = 10$ nên $\overrightarrow {OA} = 10\vec k$.

Xét $\vartriangle OBH$ vuông tại $H$ có $BH = OB \cdot sin{30^ \circ } = 7,5\;m;OH = OB \cdot cos{30^ \circ } = \frac{{15\sqrt 3 }}{2}\;m$.

Vì $\overrightarrow {OH} $ và $\vec j$ cùng hướng và $OH = \frac{{15\sqrt 3 }}{2}$ nên $\overrightarrow {OH} = \frac{{15\sqrt 3 }}{2}\vec j$.

Có $BH = OK = 7,5$.

Vì $\overrightarrow {OK} $ và $\vec i$ cùng hướng và $OK = 7,5$ nên $\overrightarrow {OK} = 7,5\vec i$.

Vi $\overrightarrow {AB} = \overrightarrow {OB} – \overrightarrow {OA} = \overrightarrow {OH} + \overrightarrow {OK} – \overline {OA} = 7,5\vec i + \frac{{15\sqrt 3 }}{2}\vec j – 10\vec k$.

Vậy $\overrightarrow {AB} = \left( {7,5;\frac{{15\sqrt 3 }}{2}; – 10} \right)$.

Câu 7. Ở một sân bay, ví trí của máy bay được xác định bởi điểm $M$ trong không gian $Oxyz$ như Hình 17. Gọi $H$ là hình chiếu vuông góc của $M$ xuống mặt phẳng $\left( {Oxy} \right)$. Cho biết $OM = 50,\left( {\vec i,\overrightarrow {OH} } \right) = {64^ \circ },\left( {\overrightarrow {OH} ,\overrightarrow {OM} } \right) = {48^ \circ }$.

Tìm toạ độ của điểm $M$.

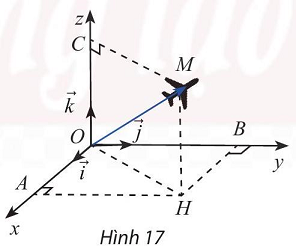
Lời giải

Giả sử $M\left( {x;y;z} \right).H \in \left( {Oxy} \right) \Rightarrow H\left( {x;y;0} \right)$.

Vì $OBHA$ là hình bình hành nên $BH = OA$.

Vì $OCMH$ là hình bình hành nên $OC = MH$.

Xét $\vartriangle MHO$ vuông tại $H$ có $OH = OM \cdot cos{48^ \circ } = 50 \cdot cos{48^ \circ } \approx 33,46$;

$MH = OM \cdot sin{48^ \circ } = 50 \cdot sin{48^ \circ } \approx 37,16$.

Xét $\vartriangle OAH$ vuông tại $A$ có $BH = OA = OH \cdot cos{64^ \circ } = 33,46 \cdot cos{64^ \circ } \approx 14,67$

Xét $\vartriangle OBH$ vuông tại $B$ có $OB = \sqrt {O{H^2} – B{H^2}} = \sqrt {33,{{46}^2} – 14,{{67}^2}} \approx 30,07$

Vì $\overrightarrow {OA} $ và $\vec i$ cùng hướng và $OA = 14,46$ nên $\overrightarrow {OA} = 14,67\vec i$.

Vì $\overrightarrow {OB} $ và $\vec j$ cùng hướng và $OB = 30,07$ nên $\overrightarrow {OB} = 30,07\vec j$.

Vì $\overrightarrow {OC} $ và $\vec k$ cùng hướng và $OC = 37,16$ nên $\overrightarrow {OC} = 37,16\vec k$.

Áp dụng quy tắc hình bình hành ta có: $\overrightarrow {OM} = \overrightarrow {OH} + \overrightarrow {OC} = \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} $ $ = 14,67\vec i + 30,07\vec j + 26,16\vec k$

Vậy $M\left( {14,67;30,07;26,16} \right)$.