- Phương pháp Xác Định Các Đặc Trưng Của Sóng Cơ Vật Lí 11
- 35 Câu Trắc Nghiệm Các Đặc Trưng Của Sóng Cơ Vật Lí 11 Có Đáp Án
- Phương pháp Xác Định Cường Độ Sóng Vật Lí 11
- Phương pháp Xác Định Độ Lệch Pha Giữa Hai Điểm Trên Cùng Phương Truyền Sóng Vật Lí 11
- 20 Câu Trắc Nghiệm Độ Lệch Pha Giữa Hai Điểm Trên Cùng Phương Truyền Sóng Vật Lí 11
- Các Dạng Bài Tập Liên Quan Đến Phương Trình Sóng Vật Lí 11
- 30 Câu Trắc Nghiệm Liên Quan Đến Phương Trình Sóng Vật Lí 11 Có Đáp Án
- Trắc nghiệm lý thuyết Sóng ngang-Sóng dọc-Sự truyền năng lượng của sóng cơ Vật lí 11
- Phương Pháp Giải Sóng ngang-Sóng dọc-Sự truyền năng lượng của sóng cơ Vật lí 11
- Các Dạng Bài Tập Về Sóng Điện Từ Vật Lí 11 Giải Chi Tiết
- Các Dạng Bài Tập Về Giao Thoa Sóng Cơ Vật Lí 11 Giải Chi Tiết
- Các Dạng Bài Tập Trắc Nghiệm Giao Thoa Sóng Cơ Vật Lí 11 Có Đáp Án
- 10 Câu Trắc Nghiệm Lý Thuyết Giao Thoa Sóng Cơ Vật Lí 11 Có Đáp Án
- Các Dạng Bài Tập Về Giao Thoa Ánh Sáng Vật Lí 11 Giải Chi Tiết
- 40 Câu Trắc Nghiệm Lý Thuyết Giao Thoa Ánh Sáng Vật Lí 11 Có Đáp Án
Các dạng bài tập về giao thoa ánh sáng vật lí 11 giải chi tiết được soạn dưới dạng file word và PDF gồm 6 trang. Các bạn xem và tải về ở dưới.
DẠNG 1. VỊ TRÍ VÂN SÁNG, VÂN TỐI-KHOẢNG VÂN
A. Phương pháp giải
a. Điều kiện để tại $A$ có vân sáng, vân tối
• Tại $A$ có vân sáng khi ${d_2} – {d_1} = k\lambda $ với $k = 0, \pm 1; \pm 2; \ldots $
• Tại A có vân tối khi ${d_2} – {d_1} = \left( {k + \frac{1}{2}} \right)\lambda $ với $k = 0, \pm 1; \pm 2; \ldots $
b. Vị trí các vân sáng, các vân tối
• Khoảng cách giữa 2 vân sáng hoặc 2 vân tối liên tiếp được gọi là khoảng vân, kí hiệu là i.
$i = \frac{{\lambda D}}{a}$
• Vị trí các vân sáng: ${x_S} = ki = k\frac{{\lambda D}}{a}$
Với $k = 0$, vân sáng trung tâm, vân sáng bậc 1 , ứng với $k = \pm 1$; vân sáng bậc 2 , ứng với $k = \pm 2 \ldots $
• Vị trí các vân tối: ${x_t} = \left( {k + \frac{1}{2}} \right)i = \left( {k + \frac{1}{2}} \right)\frac{{\lambda D}}{a}$
Vân tối thứ nhất ứng với $k = 0,k = – 1$; vân tối thứ hai ứng với $k = 1,k = – 2 \ldots $
Trong đó a là khoảng cách giữa hai nguồn kết hợp, $D$ là khoảng cách từ hai nguồn kết hợp đến màn quan sát, $i$ là khoảng vân, $\lambda $ là bước sóng ánh sáng
B. Bài tập tự luận
Bài 1: (SBT – KNTT) Trong một thí nghiệm Y-âng về giao thoa ánh sáng với $a = 0,2\;mm,D = $ $1,2\;m$, người ta đo được $i = 0,36\;mm$. Tính bước sóng $\lambda $ và tần số $f$ của bức xạ.
Lời giải:
Công thức khoảng vân: $i = \frac{{\lambda .D}}{a}$
$ \Rightarrow \lambda = \frac{{a \cdot i}}{D} = \frac{{0,2 \cdot {{10}^{ – 3}} \cdot 0,36 \cdot {{10}^{ – 3}}}}{{1,2}} = 0,06 \cdot {10^{ – 6}}\;m$
Tần số: $f = \frac{c}{\lambda } = \frac{{3 \cdot {{10}^B}}}{{0,06 \cdot {{10}^{ – 6}}}} = {5.10^{15}}\;Hz$
Bài 2: (SBT – KNTT) Trong một thí nghiệm Y-âng, biết $a = 0,15\;mm,D = 1,20\;m$, khoảng cách giữa 12 vân sáng liên tiếp là $5,2\;mm$. Tính bước sóng ánh sáng.
Lời giải:
Khoảng cách giữa 12 vân sáng liên tiếp tương ứng với 11 khoảng vân.
Khoảng vân $i = 5,2/11 = 0,473\;mm$
Bước sóng $\lambda = \frac{{a.i}}{D} = \frac{{0,15 \cdot {{10}^{ – 3}} \cdot 0,473 \cdot {{10}^{ – 3}}}}{{1,2}} = 5,9 \cdot {10^{ – 8}}\;m$
Bài 3: (SBT – KNTT) Trong một thí nghiệm Y-âng về giao thoa ánh sáng, hai khe được chiếu bằng ánh sáng đơn sắc. Khoảng cách giữa hai khe là $0,6\;mm$. Khoảng vân trên màn quan sát đo được là $1\;mm$. Từ vị trí ban đầu, nếu tịnh tiến màn quan sát một đoạn $25\;cm$ lại gần mặt phẳng chứa hai khe thì khoảng vân mới trên màn là $0,8\;mm$. Tính bước sóng của ánh sáng dùng trong thí nghiệm.
Lời giải:
Khoảng vân ban đầu: $i = \frac{{\lambda D}}{a}$
Khoảng vân sau khi dịch chuyển màn quan sát: $i’ = \frac{{\lambda D’}}{a} = \frac{{\lambda \left( {D – 0,25} \right)}}{a}$
Ta có: $\frac{i}{{i’}} = \frac{D}{{D – 0,25}}$
$ \Rightarrow \frac{1}{{0,8}} = \frac{D}{{D – 0,25}} \Rightarrow D = 1,25\;m$
Bước sóng $\lambda = \frac{{\frac{{a.i}}{D}}}{D} = \frac{{0,6 \cdot {{10}^{ – 3}} \cdot 1 \cdot {{10}^{ – 3}}}}{{1,25}} = 4,8 \cdot {10^{ – 7}}\;m$
Bài 4: (SGK – CTST) Trong một thí nghiệm Young về giao thoa ánh sáng, khi nguồn sáng là ánh sáng đơn sắc có bước sóng $\lambda $, người ta đo khoảng cách giữa 9 vân sáng liên tiếp là 25,3 mm. Cho biết khoảng cách giữa hai khe là $0,200\;mm$ và khoảng cách từ hai khe đến màn là $1\;m$.
a. Tính bước sóng $\lambda $.
b. Tính khoảng cách từ vân sáng bậc hai đến vân tối thứ tư ở cùng bên so với vân sáng trung tâm( vân sáng cách đều hai khe sáng).
Lời giải
a. Ta có $8i = 25,3\;mm$, suy ra $I = 3,16\;mm$.
Bước sóng $\lambda = \frac{{a.i}}{D} = \frac{{0,200 \cdot {{10}^{ – 3}} \cdot 3,16 \cdot {{10}^{ – 3}}}}{1} = 0,632.10 – 6\;m = 632\;nm$
b. Khoảng cách từ vân sáng bậc hai đến vân tối thứ tư ở cùng bên so với vân sáng trung tâm là: $3,5i$ $ – 2i = 1,5i = 1,5 \cdot 3,16 = 4,74\;mm$
Bài 5: (SGK – CTST) Thí nghiệm Young về giao thoa ánh sáng thường được sử dụng để đo bước sóng của ánh sáng đơn sắc. Khi chiếu hai khe bằng một nguồn phát ánh sáng đơn sắc, ta thấy vân sáng thứ năm cách vân trung tâm là $2,8\;cm$. Biết hai khe đặt cách nhau $0,2\;mm$ và cách màn một khoảng 1,5m. Xác định bước sóng của ánh sáng được dùng trong thí nghiệm.
Lời giải:
Khoảng cách từ vân sáng thứ 5 đến vân sáng trung tâm:
$5i = 2,8\;cm = > i = 0,56\;cm$
Khoảng vân $i = \frac{{\lambda D}}{a} \Leftrightarrow 0,56 \cdot {10^{ – 2}} = \frac{{\lambda \cdot 1,5}}{{0,2 \cdot {{10}^{ – 3}}}}$$ \Leftrightarrow \lambda = 0,75 \cdot {10^{ – 6}}\;m$
Bài 6: Trong thí nghiệm Y-âng về giao thoa của ánh sáng đơn sắc, hai khe hẹp cách nhau 1 $mm$, mặt phẳng chứa hai khe cách màn quan sát $1,5\;m$. Khoảng cách giữa 5 vân sáng liên tiếp là 3,6 $mm$. Bước sóng của ánh sáng dùng trong thí nghiệm này bằng bao nhiêu?
Lời giải:
Biên độ 5 vân sáng liên tiếp có 4 khoảng vân: $4i = 3,6 = > i = 0,9\;mm$.
Bước sóng $\lambda = \frac{{ai}}{D} = \frac{{{{10}^{ – 3}} \cdot 0,9 \cdot {{10}^{ – 3}}}}{{1,5}} = 0,6 \cdot {10^{ – 6}}\;m$
Bài 7: (SBT – KNTT) Trong thí nghiệm Young về giao thoa với ánh sáng đơn sắc có bước sóng $\lambda $, khoảng cách giữa 2 khe là $0,15\;mm$, khoảng cách giữa mặt phẳng chứa 2 khe và màn quan sát là $1\;m$. Hai điểm $M$ và $N$ trên màn quan sát đối xứng nhau qua vân sáng trung tâm. Trên đoạn $MN$ có 11 vân sáng, tại $M$ và $N$ là hai vân sáng, Biết khoảng cách $MN$ là $30\;mm$. Tính bước sóng của ánh sáng dùng trong thí nghiệm này.
Lời giải:
$i = \frac{{MN}}{{11 – 1}} = \frac{{30 \cdot {{10}^{ – 3}}}}{{11 – 1}} = 3 \cdot {10^{ – 3}}\;m = \lambda $
$ = \frac{{ai}}{D} = \frac{{0,15 \cdot {{10}^{ – 3}} \cdot 0,3 \cdot {{10}^{ – 3}}}}{1} = 0,45 \cdot {10^{ – 6}}\;m$
Bài 8: (SBT – CTST) Trong thí nghiệm Young về giao thoa của ánh sáng đơn sắc, hai khe hẹp cách nhau $1,2\;mm$, mặt phẳng chứa 2 khe cách màn quan sát là $1,5\;m$. Khoảng cách giữa 5 vân sáng liên tiếp là $3,6\;mm$. Bước sóng của ánh sáng dùng trong thí nghiệm này bằng bao nhiêu?
Lời giải:
Ta có $4i = 4\frac{{\lambda D}}{a} = 4\frac{{\lambda .1,5}}{{1,2 \cdot {{10}^{ – 3}}}} = 3,6 \cdot {10^{ – 3}}$ suy ra $\lambda = 720\;nm$
Bài 9: (SBT – CTST) Khi thực hiện thí nghiệm Young về giao thoa ánh sáng với ánh sáng đơn sắc có bước sóng $560\;nm$, ta thấy khoảng cách giữa vân sáng bậc hai và vân tối thứ 5 kể từ vân trung tâm và cùng phía với vân trung tâm là $3\;mm$. Cho biết khoảng cách từ mặt phẳng chứa $2khe$ đến màn quan sát là 1,2 m. Tính khoảng cách giữa hai khe.
Lời giải:
Ta có $4,5i – 2i = 2,{5^{\frac{{\lambda D}}{a}}} = 2,5\frac{{560 \cdot {{10}^{ – 9}} \cdot 1,2}}{a} = 3 \cdot {10^{ – 3}}$$ = > a = 0,56\;mm$
Bài 10: (SBT – KNTT) Trong thí nghiệm Young về giao thoa với ánh sáng, nguồn $S$ phát ánh sáng đơn sắc có bước sóng $\lambda $. Màn quan sát cách 2 khe một khoảng không đổi $D$, khoảng cách giữa 2 khe ${S_1}\;{S_2} = a$ có thể thay đổi (nhưng ${S_1},\;{S_2}$ luôn cách đều $S$ ). Xét điểm $P$ trên màn quan sát, lúc đầu là vân sáng bậc 4 , nếu lần lượt giảm hoặc tăng khoảng cách ${S_1}\;{S_2}$ một lượng $\Delta a$ thì tại đó là vân sáng bậc $k$ và $3k$. Nếu tăng khoảng cách ${S_1}\;{S_2}$ một lượng $2\Delta a$ thì tại đó là vân sáng hay vân tối, bậc hoặc thứ bao nhiêu?
Lời giải:
Lúc đầu : ${x_M} = k \cdot \frac{{\lambda D}}{{a – \Delta a}}$ và ${x_M} = 3k \cdot \frac{{\lambda D}}{{a + \Delta a}}$
$ \Rightarrow \frac{{3\left( {a – \Delta a} \right)}}{{a + \Delta a}} = 1 \Rightarrow \Delta a = 0,5\;m$
Lúc sau: ${x_M} = 4 \cdot \frac{{\lambda D}}{a}$ và ${x_M} = k.\frac{{\lambda D}}{{a + 2\Delta a}}$
$ \Rightarrow \frac{{{k^n}}}{{4.2}} = 1 \Rightarrow k’ = 8$
Khi đó tại $M$ là vân sáng bậc 8 .
Bài 11: (SBT – CTST) Trong thí nghiệm Young về giao thoa ánh sáng, hai khe được chiếu bằng ánh sáng trắng có bước sóng trong khoảng từ $400\;nm$ đến $760\;nm$. Biết khoảng cách giữa 2 khe là $0,3\;mm$; khoảng cách từ mặt phẳng chứa 2 khe đến màn quan sát là $2,00\;m$
a. Tính khoảng cách từ vân sáng bậc 1 màu đỏ đến vân sáng bậc một màu tím ở cùng phía so với vân trung tâm. Khoảng cách giữa hai vân sáng này có màu gì?
b. Tính khoảng cách từ vân sáng bậc 2 màu đỏ đến vân sáng bậc 2 màu tím ở cùng phía so với vân trung tâm. Trong khoảng giữa hai vân sáng này có xuất hiện dải màu cầu vồng không?
Lời giải:
a. ${x_{d1}} – {x_{t1}} = 1 \cdot \frac{{{\lambda _d}D}}{a} – 1 \cdot \frac{{{\lambda _t}D}}{a} = 2,4\;mm$ : trong khoảng giữa vân sáng bậc 1 màu đỏ và vân sáng bậc một màu tím là dải màu biến thiên liên tục từ đỏ đến tím như màu cầu vồng (quang phổ bậc một của ánh sáng trắng).
b. ${x_{d2}} – {x_{t2}} = 2 \cdot \frac{{{\lambda _d}D}}{a} – 2 \cdot \frac{{{\lambda _i}D}}{a} = 2\left( {{x_{d1}} – {x_{t1}}} \right) = 4,8\;mm$
${x_{t3}} = 3 \cdot \frac{{{\lambda _t}D}}{a} = 8,0\;mm;$${x_{d2}} = 2 \cdot \frac{{{\lambda _d}D}}{a} = 10,13\;mm:\;{x_{t3}} > {x_{d2}}$
$ \Rightarrow $vân sáng bậc ba màu tím nằm trong vùng quang phổ bậc hai nên vùng quang phổ bậc hai này không có dải màu biến thiên liên tục từ đỏ đến tím như màu cầu vồng.
Bài 12: Trong thí nghiệm Y-âng về giao thoa với ánh sáng đơn sắc có bước sóng, khoảng cách giữa hai khe hẹp là $a$, khoảng cách từ mặt phẳng chứa hai khe hẹp đến màn quan sát là $2\;m$. Trên màn quan sát, tại điểm $M$ cách vân sáng trung tâm $6\;mm$, có vân sáng bậc 5 . Khi thay đổi khoảng cách giữa hai khe hẹp một đoạn bằng $0,2\;mm$ sao cho vị trí vân sáng trung tâm không thay đổi thì tại $M$ có vân sáng bậc 6 . Giá trị của $\lambda $ bằng bao nhiêu?
Lời giải
Vì bậc vân tăng lên nên a tăng thêm:
${x_M} = 5\frac{{\lambda D}}{a} = 6\frac{{\lambda D}}{{a + 0,2}} \Rightarrow \frac{5}{a} = \frac{6}{{a + 0,2}}$
$ \Rightarrow a = 1\left( {\;mm} \right) \Rightarrow \lambda = \frac{{a{x_M}}}{{5D}} = 0,{6.10^{ – 6}}\left( {\;m} \right)$
Bài 13: Trong thí nghiệm Y-âng về giao thoa với ánh sáng đơn sắc xác định, thì tại điểm $M$ trên màn quan sát là vân sáng bậc 5 . Sau đó giảm khoảng cách giữa hai khe một đoạn bằng $0,2\;mm$
thì tại $M$ trở thành vân tối thứ 5 so với vân sáng trung tâm. Ban đầu khoảng cách giữa hai khe là bao nhiêu?
Lời giải
${x_M} = 5\frac{{\lambda D}}{a} = 4,5\frac{{\lambda D}}{{a – 0,2}} \Rightarrow \frac{5}{a} = \frac{{4,5}}{{a – 0,2}} \Rightarrow a = 2\left( {mm} \right)$
Bài 14: Trong thí nghiệm giao thoa Y-âng, khoảng cách hai khe là $1\;mm$. Giao thoa thực hiện với ánh sáng đơn sắc có bước sóng $\lambda $ thì tại điểm $M$ có tọa độ $1,2\;mm$ là vị trí vân sáng bậc 4 . Nếu dịch màn xa thêm một đoạn $25\;cm$ theo phương vuông góc với mặt phẳng hai khe thì tại $M$ là vị trí vân sáng bậc 3 . Xác định bước sóng.
Lời giải
$\left\{ {\begin{array}{*{20}{l}}
{{x_M} = 4\frac{{\lambda D}}{a} \Rightarrow \frac{{\lambda D}}{a} = \frac{{{x_M}}}{4}}\\
{{x_M} = 3\frac{{\lambda \left( {D + 0,25} \right)}}{a} = 3\frac{{\lambda D}}{a} + 0,75 \cdot \frac{\lambda }{a}}
\end{array}} \right.$
$ \Rightarrow \lambda = 0,4 \cdot {10^{ – 6}}\left( {\;m} \right)$
Bài 15: Thực hiện thí nghiệm Y-âng về giao thoa với ánh sáng có bước sóng. Khoảng cách giữa hai khe hẹp là $1\;mm$. Trên màn quan sát, tại điểm $M$ cách vân trung tâm 4,2 $mm$ có vân sáng bậc 5. Giữ cố định các điều kiện khác, di chuyển dần màn quan sát dọc theo đường thẳng vuông góc với mặt phẳng chứa hai khe ra xa cho đến khi vân giao thoa tại $M$ chuyển thành vân tối thứ hai thì khoảng dịch màn là $0,6\;m$. Bước sóng $\lambda $ bằng bao nhiêu?
Lời giải
Vị trí điểm M: ${x_M} = 5i = 5\frac{{\lambda D}}{a} = 4,2 \cdot {10^{ – 3}}\left( {\;m} \right)$
Ban đầu, các vân tối tính từ vân trung tâm đến $M$ lần lượt có tọa độ là $0,5i;1,5i;2,5i;3,5i$ và 4,5i.
Khi dịch màn ra xa $0,6\;mM$ trở thành vân tối thứ 2 thì ${x_M} = 3,5i’$ hay
${x_M} = 3,5\frac{{\lambda \left( {D + 0,6} \right)}}{a} = 4,{2.10^{ – 3}}\left( {\;m} \right)$
Từ (1) và (2) tính ra: $D = 1,4m,\lambda = 0,6\mu m$.
DẠNG 2. BÀI TOÁN TÌM SỐ VÂN SÁNG, VÂN TỐI CÓ TRÊN MỘT MIỀN
A. Phương pháp giải
• Gọi L: bề rộng của trường giao thoa
$ \Rightarrow $ Số vân sáng quan sát được trên màn: $ – \frac{L}{{2i}} \leqslant k \leqslant \frac{L}{{2i}}$
hoặc ${N_s} = 1 + 2\left[ {\frac{L}{{2i}}} \right]\;$ (chỉ lấy phần nguyên của $\frac{L}{{2i}}$ )
$ \Rightarrow $ Số vân tối quan sát được trên màn: $ – \frac{L}{{2i}} – \frac{1}{2} \leqslant k \leqslant \frac{L}{{2i}} – \frac{1}{2}$
hoặc $\;{N_t} = 2\mid $ (thương được làm tròn)
$ \Rightarrow $ Số vân sáng, vân tối giữa hai điểm $M,N$ có tọa độ ${x_1},{x_2}\left( {{x_1} < {x_2}} \right)$ :
• Vân sáng: ${x_1} < ki < {x_2} \Rightarrow k\; + $ Vân tối: ${x_1} < \left( {k + 0,5} \right)i < {x_2} \Rightarrow k$
Lưu ý: $M,N$ cùng phía thì ${x_1},{x_2}$ cùng dấu; khác phía thì ${x_1},{x_2}$ trái dấu
B. BÀi TẬP TỰ LUẬN
Bài 1: (SBT – CTST) Trong thí nghiệm Young về giao thoa ánh sáng, hai khe được chiếu bởi ánh sáng đơn sắc có bước sóng là $600\;nm$. Biết khoảng cách giữa 2 khe là $1,20\;mm$ và khoảng cách từ mặt phẳng chứa 2 khe đến màn quan sát là $2,00\;m$.
a. Tại các điểm $M$ và $N$ trên màn, $M,N$ cùng phía so với vân trung tâm cách vân trung tâm các khoảng lần lượt là $6,00\;mm$ và $9,5\;mm$ có vân sáng hay vân tối?
b. Không kể các vân tại $M$ và $N$, trong khoảng giữa $M,N$ có bao nhiêu vân sáng và bao nhiêu vân tối?
Lời giải:
a. Ta có $i = \frac{{600 \cdot {{10}^{ – 9}}.2}}{{1,2 \cdot {{10}^{ – 3}}}} = 1,00\;mm$
$\frac{{{x_y}}}{i} = 6$ : tại $M$ có vân sáng bậc sáu.
$\frac{{{x_N}}}{i} = 9,5$ : tại $N$ có vân tối thứ mười.
b. Không kể các vân tại $M$ và $N$, trong khoảng giữa $M,N$ có 3 vân sáng (bậc bảy, bậc tám và bậc chín) và ba vân tối ( thứ bảy, thứ tám và thứ chín).
Bài 2: Trong thí nghiệm Young về giao thoa ánh sáng, hai khe được chiếu bằng ánh sáng đơn sắc có bước sóng 0,6 . Khoảng cách giữa hai khe là $1\;mm$, khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát là $2,5\;m$, bề rộng miền giao thoa là $1,25\;cm$. Tổng số vân sáng và vân tối có trong miền giao thoa là bao nhiêu?
Lời giải:
$i = \frac{{\lambda D}}{a} = 1,5\left( {\;mm} \right)$
$ \Rightarrow \left\{ {\begin{array}{*{20}{c}}
{{N_s} = 2\left[ {\frac{L}{{2i}}} \right] + 1 = 2\left[ {\frac{{12,5}}{{2 \cdot 1,5}}} \right] + 1 = 2\left[ {4,17} \right] + 1} \\
{{N_t} = {N_s} – 1 = 8}
\end{array}} \right.$
$ \Rightarrow {N_t} + {N_s}$ vân.
Bài 3: Trong thí nghiệm Young về giao thoa ánh sáng, các khe hẹp được chiếu sáng bởi ánh sáng đơn sắc. Khoảng vân trên màn là $1,2\;mm$. Trong khoảng giữa hai điểm $M$ và $N$ trên màn ở cùng một phía so với vân sáng trung tâm, cách vân trung tâm lần lượt $2\;mm$ và $4,5\;mm$, quan sát được bao nhiêu vân sáng, vân tối?
Lời giải:
Tại M: ${k_M} = \frac{2}{{1,2}} = $ Tại N: $\;{k_N} = \frac{{4,5}}{{1,2}} = 3$
Một điểm bất kỳ nằm trong đoạn $MN$ sẽ có: $\;1,7 \leqslant k \leqslant 3,75$
Nếu $k$ nguyên thì cho vân sáng Có 2 vân sáng ứng với $k = 2,3$.
Nếu $k$ bán nguyên thì cho vân tối Có 2 vân tối ứng với $k = 2,5;3,5$
Bài 4: Trong một thí nghiệm giao thoa ánh sáng với khe $Y$-âng, hai khe cách nhau $2\;mm$, khoảng cách từ hai khe tới màn quan sát là $2\;m$. Ánh sáng đơn sắc có bước sóng $ = 0,5$. Cho $M$ và $N$ là hai điểm nằm trong trường giao thoa, chúng nằm khác phía nhau so với vân chính giữa, có $OM = 12,3\;mm,ON = 5,2$ $mm$. Số vân sáng và số vân tối trong đoạn $MN$ là bao nhiêu?
Lời giải:
Khoảng vân: $i = \frac{{\lambda D}}{a} = 0,5\;mm$
Vì hai điểm $M$ và $N$ trên màn ở khác phía so với vân sáng trung tâm nên có thể chọn
${x_M} = – 12,3\;$ và ${x_N} = 5,2$
*${x_M} \leqslant ki = k.0,5 \leqslant {x_N} \Rightarrow – 24,6 \leqslant k \leqslant 10,4$
$ \Rightarrow k = – 24; \ldots ;10$ (có 35 giá trị k)
*${x_M} \leqslant \left( {m + 0,5} \right)i = \left( {m + 0,5} \right)0,5 \leqslant {x_N}$
$ \Rightarrow – 25,1 \leqslant m \leqslant 9,9 \Rightarrow m = – 25;…$(có 35 giá trị k)
DẠNG 3. BÀI TOÁN TRÙNG VÂN
A. Phương pháp giải
Vị trí vân sáng trùng nhau ${x_1} = {x_2}:{k_1}{\lambda _1} = {k_2}{\lambda _2}$
B. Bài tập tự luận
Bài 1: (SBT – CTST) Trong thí nghiệm Young về giao thoa ánh sáng, biết khoảng cách giữa 2 khe là $0,4\;mm$ và khoảng cách từ hai khe đến màn quan sát là $1,00\;m$. Khi ta dùng ánh sáng đơn sắc có bước sóng ${\lambda _1}$ thì quan sát thấy trên một khoảng trong vùng giao thoa có chứa 7 vân sáng với khoảng cách giữa 2 vân sáng ngoài cùng bằng $9,00\;m$.
a. Tính bước sóng ${\lambda _1}$
b. Sử dụng nguồn sáng gồm 2 ánh sáng đơn sắc có bước sóng ${\lambda _1}$ và ${\lambda _2}$ với ${\lambda _2} = 400\;nm$. Xác định vị trí trên màn có vân sáng cùng màu với vân sáng trung tâm và gần vân trung tâm nhất.
Lời giải:
a. Ta có $6{\mathbf{i}} = \frac{{6{\lambda _1}D}}{a} = > 6\frac{{{\lambda _1} \cdot 1,0}}{{0,4,{{10}^{ – 3}}}} = 9 \cdot {10^{ – 3}} = > {\lambda _1} = 600\;mm$
b. Tại vân trung tâm hai ánh sáng đơn sắc ${\lambda _1}$ và ${\lambda _2}$ cho vân sáng trùng nhau nên vân trung tâm có màu hỗn hợp của hai ánh sáng đơn sắc. Vị trí vân cùng màu với vân trung tâm là vị trí hai vân sáng tương ứng vủa ${\lambda _1}$ và ${\lambda _2}$ trùng nhau:
${k_1}\frac{{{\lambda _1}D}}{a} = {k_2}\frac{{{\lambda _2}D}}{a} = > {k_1}{\lambda _1} = {k_2}{\lambda _2} \Rightarrow {k_1} = 400/600.{k_2}$
Vì ${k_1}$ và ${k_2}$ là số nguyên nên suy ra giá trị tương ứng của ${k_1},{k_2}$ là: ${k_1} = \pm 2; \pm 4; \pm 6 \ldots $ và ${k_2} = $ $ \pm 3; \pm 6; \pm 9 \ldots $
Vị trí vân cùng màu và gần vân trung tâm nhất tương ứng với ${k_1} = \pm 2$ và ${k_2} = \pm 3$ :
${x_1} = {x_2} \Leftrightarrow {k_1}{i_1} = {k_2}{i_2} = 3\;mm$ (ở hai phía so với vân trung tâm).
Bài 2: (SBT – KNTT) Trong một thí nghiệm về giao thoa ánh sáng với 2 khe Y-âng, khoảng cách giữa hai khe hẹp là $a = 2\;mm$, khoảng cách giữa 2 mặt phẳng chứa hai khe với màn quan sát là $D = 1,2\;m$. Khe sáng hẹp phát đồng thời hai bức xạ đơn sắc màu đỏ ${\lambda _1} = 0,66\mu m$ và màu lục ${\lambda _2} = $ $0,55\mu m$.
a. Tính khoảng vân của hai ánh sáng màu đỏ và màu lục.
b. Tính khoảng cách ngắn nhất giữa hai vân sáng cùng màu với vân sáng trung tâm.
Lời giải:
a. Với ánh sáng đỏ ${\lambda _1} = 0,66\mu m$
${i_1} = \frac{{{\lambda _1} \cdot D}}{a} = \frac{{0,66 \cdot {{10}^{ – 3}} \cdot 1,2 \cdot {{10}^3}}}{2} = 0,44\;mm$
Với ánh sáng lục ${\lambda _2} = 0,55\mu m$
${i_2} = \frac{{{\lambda _2} \cdot D}}{a} = \frac{{0,55 \cdot {{10}^{ – 3}} \cdot 1,2 \cdot {{10}^3}}}{2} = 0,35\;mm$
b. Vân chính giữa ứng với $k = 0$ là chung cho cả hai bức xạ, tức là tại đó cả hai bức xạ đều cho vân sáng và vân có màu là màu hỗn hợp của màu đỏ và màu lục, tức là màu vàng – da cam.
Vân đầu tiên cùng màu với vân này ở tại điểm $A$ và cách tâm $O$ của vân chính giữa một khoảng $x = $ OA sao cho: ${k_1}{i_1} = \;{k_2}{i_2}$ với $k \in Z$.
Ta nhận thấy $6{k_1} = 5{k_2}$
Do vậy, giá trị nhỏ nhất của $\;1$ là 5 và của $\;{k_2}$ là 6 , tức là: $OA = 0,33.6 = 1,98\;mm$
Bài 3: Trong thí nghiệm giao thoa ánh sáng với khe Y-âng khoảng cách giữa hai khe là $2\;mm$, khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát là $1,2\;m$. Chiếu sáng hai khe bằng ánh sáng hỗn hợp gồm hai ánh sáng đơn sắc có bước sóng $500\;nm$ và $660\;nm$ thì thu được hệ vân giao thoa trên màn. Biết vân sáng chính giữa (trung tâm) ứng với hai bức xạ trên trùng nhau. Khoảng cách từ vân chính giữa đến vân gần nhất cùng màu với vân chính giữa là bao nhiêu?
Lời giải:
Khoảng vân của bước sóng $500\;nm$ là
${i_1} = \frac{{{\lambda _1}D}}{a} = 0,3\;mm$
Điều kiện để 2 vân sáng trùng nhau: $\frac{{{k_1}}}{{{k_2}}} = \frac{{{\lambda _2}}}{{{\lambda _1}}} = \frac{{660}}{{500}} = \frac{{33}}{{25}}$
$ \Rightarrow $ Khoảng vân trùng: ${i_ \equiv } = 33{i_1} = 33.0,3 = 9,9\;mm$
Vậy khoảng cách từ vân chính giữa đến vân gần nhất cùng màu với vân chính giữa là $9,9\;mm$.
Bài 4: Trong thí nghiệm Y-âng về giao thoa ánh sáng, khoảng cách giữa hai khe là $0,5\;mm$, khoảng cách từ hai khe đến màn quan sát là $2\;m$. Nguồn sáng dùng trong thí nghiệm gồm hai bức xạ có bước sóng ${\lambda _1} = 450\;nm$ và ${\lambda _2} = 600\;nm$. Trên màn quan sát, gọi $M,N$ là hai điểm ở cùng một phía so với vân trung tâm và cách vân trung tâm lần lượt là $5,5\;mm$ và $22\;mm$. Trên đoạn $MN$, số vị trí vân sáng trùng nhau của hai bức xạ là:
Lời giải:
Ta có
${i_1} = \frac{{D{\lambda _1}}}{a} = 1,8\;mm;\frac{{{k_1}}}{{{k_2}}} = \frac{{{\lambda _2}}}{{{\lambda _1}}} = \frac{4}{3} \Rightarrow {i_ \equiv } = 4{i_1} = 7,2\;mm$
$ \Rightarrow $ Tọa độ các vị trí trùng: ${x_ \equiv } = 7,2n$ với $n \in Z$
$M,N$ nằm cùng phía so với vân trung tâm nên ${x_M},{x_N}$ cùng dấu.
Ta có: ${x_M} \leqslant {x_ \equiv } \leqslant {x_N} \Leftrightarrow 5,5 \leqslant 3,36n \leqslant 33,6 \Leftrightarrow 1,6 \leqslant n \leqslant 10$
$5,5 \leqslant {x_ \equiv } = 7,2n \leqslant 22\left( {n \in \mathbb{Z}} \right) \Rightarrow n = \left\{ {1,2,3} \right\}$
Vậy có 3 vị trí vân sáng trùng nhau của 2 bức xạ.
Bài 5: Trong thí nghiệm Y-âng về giao thoa ánh sáng, nguồn sáng phát đồng thời hai ánh sáng đơn sắc gồm ánh sáng đỏ có bước sóng $684\;nm$ và ánh sáng lam có bước sóng $456\;nm$. Trong khoảng giữa hai vân sáng có màu cùng màu với vân sáng trung tâm, nếu đếm được 6 vân sáng màu lam thì số vân sáng màu đỏ là bao nhiêu?
Lời giải:
$\frac{{{k_1}}}{{{k_2}}} = \frac{{{\lambda _2}}}{{\lambda 1}} = \frac{{456}}{{684}} = \frac{2}{3}$
Điều kiện để cho sự trùng nhau của hệ hai vân sáng .
$ \Rightarrow $ Cứ giữa hai vân sáng liên tiếp cùng màu với vân trung tâm sẽ có 2 vị trí cho vân sáng lam và 1 vị trí cho vân sáng đỏ.
$ \Rightarrow $ Nếu giữa hai vân trùng màu với vân trung tâm không liên tiếp ta đếm được 6 vân sáng lam thì có tương ứng 3 vân đỏ (ứng với 2 khoảng vân trùng đôi).
$\frac{{{k_1}}}{{{k_2}}} = \frac{{{\lambda _2}}}{{{\lambda _1}}} \Leftrightarrow \frac{6}{9} = \frac{{{\lambda _2}}}{{0,6}} \Rightarrow {\lambda _2} = 0,4\mu m$
Bài 6: Trong thí nghiệm Y-âng về giao thoa ánh sáng, nguồn sáng phát đồng thời hai bức xạ đơn sắc, trong đó bức xạ màu đỏ có bước sóng ${\lambda _D} = 720\;nm$ và bức xạ màu lục có bước sóng ${\lambda _{luc\;}}$ (có giá trị trong khoảng từ $500\;nm$ đến $575\;nm$ ). Trên màn quan sát, giữa hai vân sáng gần nhau nhất và cùng màu với vân sáng trung tâm có 8 vân sáng màu lục. Giá trị của ${\lambda _{luc\;}}$ là
Lời giải:
Tọa độ 2 vân sáng trùng nhau khi: $x_{luc}^s = x_d^s \Leftrightarrow \frac{{k \cdot D{\lambda _{luc}}}}{a} = \frac{{k’ \cdot D{\lambda _d}}}{a} \Leftrightarrow {\lambda _{luc\;}} = \frac{{k’}}{k}{\lambda _d}$
Do trên màn quan sát, giữa hai vân sáng gần nhau nhất và cùng màu với vân sáng trung tâm có 8 vân sáng màu lục nên
$k = 9 \Rightarrow {\lambda _{luc}} = \frac{{k’ \cdot 0,72}}{9}$
Do $\;0,5 \leqslant {\lambda _{luc}} \leqslant 0,575 \Rightarrow 6,25 \leqslant k’ \leqslant 7,18 \Rightarrow k’ = 7 \Rightarrow {\lambda _{luc}} = \frac{{7 \cdot 0,72}}{9} = 0,56\mu m$.
Bài 7: Trong thí nghiệm Y-âng về giao thoa ánh sáng, khe hẹp $S$ phát ra đồng thời hai bức xạ đơn sắc có bước sóng là ${\lambda _1} = 0,42\mu m$ (màu tím), ${\lambda _2} = 0,56\mu m$ (màu lục). Biết $a = 1\;mm,D = 2\;m$
a) Khoảng cách gần nhất từ vị trí trên màn có hai vân sáng trùng nhau đến vân trung tâm là bao nhiêu?
b) Xét một vùng giao thoa rộng $3\;cm$ trên màn quan sát đối xứng với vân trung tâm, có mấy vạch sáng là kết quả trùng nhau của hai hệ vân, số vân sáng màu tím trong vùng này là bao nhiêu?
c) Trên màn quan sát, gọi $M,N$ là hai điểm khác phía so với vân trung tâm và cách vân trung tâm lần lượt là $5,5\;mm$ và $16,8\;mm$. Trên đoạn $MN$, số vị trí vân sáng trùng nhau của hai bức xạ là bao nhiêu?
Lời giải:
Khoảng vân giao thoa của ánh sáng tím:
${i_1} = \frac{{D{\lambda _1}}}{a} = \frac{{2 \cdot 0,42}}{1} = 0,84$
a) Điều kiện để 2 vân sáng trùng nhau:
${x_{s1}} = {x_{s2}} \Leftrightarrow {k_1}{i_1} = {k_2}{i_2} \Rightarrow \frac{{{k_1}}}{{{k_2}}} = \frac{{{i_2}}}{{{i_1}}} = \frac{{{\lambda _2}}}{{{\lambda _1}}} = \frac{{0,56}}{{0,42}}$
$ \Rightarrow $ Khoảng vân trùng: $\;{i_ \equiv } = 4{i_1} = 4.0,84 = 3,36$
Vậy khoảng cách gần nhất từ vị trí có hai vân sáng trùng nhau đến vân trung tâm là 3,36 mm.
b) Do vùng giao thoa đối xứng vân trung tâm nên ta có số vị trí trùng nhau của hai hệ vân giao thoa;
${N_ \equiv } = 2\left[ {\frac{L}{{2{i_ \equiv }}}} \right] + 1 = 2\left[ {\frac{{30}}{{2 \cdot 3,36}}} \right] + 1\;vân\;$
Số vị trí cho vân sáng của ánh sáng tím
${N_1} = 2\left[ {\frac{L}{{2{i_1}}}} \right] + 1 = 2\left[ {\frac{{30}}{{2.0,84}}} \right] + 1\;:\;vân\;$
Vậy số vân sáng màu tím quan sát thấy là $\;35 – 9$ : vân.
c) Tọa độ các vị trí trùng $\;{x_ \equiv } = n{i_ \equiv } = 3$, với $n$
$M,N$ là hai điểm nằm khác phía so với vân trung tâm nên $\;{x_M}$ trái dấu
Ta có:
$ – {x_M} \leqslant {x_ \equiv } \leqslant {x_N} \Leftrightarrow – 5,5 \leqslant 3,36n \leqslant 16,8 \Leftrightarrow – 1,6 \leqslant n$
Có 7 giá trị $n$ nguyên ứng với 7 vạch trùng nhau của hai bức xạ trong đoạn $MN$, tại $N$ là một vân trùng.
Bài 8: Trong thí nghiệm giao thoa khe Y-âng, cho giao thoa đồng thời ba ánh sáng đơn sắc có bước sóng ${\lambda _1} = 0,4\mu m;{\lambda _2} = 0,5\mu m;{\lambda _3} = 0,6\mu m$. Biết khoảng cách giữa hai khe là $0,8\;mm$ và khoảng cách từ mặt phẳng chứa hai khe tới màn bằng $1,2\;m$. Khoảng cách giữa hai vân sáng gần nhau nhất có cùng màu với vân sáng trung tâm là bao nhiêu?
Lời giải:
Khoảng vân của bức xạ
${i_1} = \frac{{{\lambda _1}D}}{a} = \frac{{0,4 \cdot {{10}^{ – 6}}1,2}}{{0,8 \cdot {{10}^{ – 3}}}} = 0,6 \cdot {10^{ – 3}}\;m = 0,6\;mm$
Điều kiện trùng ba: ${x_{ \equiv 3}} = {k_1} \cdot {i_1} = {k_2} \cdot {i_2} = {k_3} \cdot {i_3}\left( {{k_1},{k_2},{k_3} \in Z} \right)$
$ \Leftrightarrow {k_1} \cdot {\lambda _1} = {k_2} \cdot {\lambda _2} = {k_3} \cdot {\lambda _3}$
$ \Leftrightarrow 0,4{k_1} = 0,5{k_2} = 0,6{k_3}$
$ \Leftrightarrow {k_1} = \frac{5}{4}{k_2} = \frac{6}{4}{k_3}$
(nguyên hóa chia cả 3 vế cho 0,4 )
$ \Leftrightarrow 4{k_1} = 5{k_2} = 6{k_3}$
$BSCNNX\left( {4,5,6} \right) = 60$
Khoảng cách giữa hai vân sáng gần nhau nhất cùng màu với vân trung tâm là khoảng vân trùng ba:
${i_{ \equiv 3}} = \frac{X}{a}{i_1} = \frac{{60}}{4} \cdot 0,6 = 9\;mm$
Bài 9: Trong thí nghiệm khe Y-âng về giao thoa ánh sáng, nguồn $S$ phát ra đồng thời ba ánh sáng đơn sắc có bước sóng lần lượt: $0,4\mu m$ (màu tím), $0,48\mu m$ (màu lam) và $0,72\mu m$ (màu đỏ). Giữa 2 vân sáng liên tiếp có màu giống như màu của vân trung tâm có số vân có màu đơn sắc lam và vân có màu đơn sắc đỏ là bao nhiêu?
Lời giải:
Vị trí 3 vân trùng nhau (có màu giống vân trung tâm) ${x_{ \equiv 3}} = {k_t}{\lambda _t}\frac{D}{a} = {k_l}{\lambda _l}\frac{D}{a} = {k_d}{\lambda _d}\frac{D}{a}$
$ \Rightarrow {k_t}{\lambda _t} = {k_\ell }{\lambda _l} = {k_d}{\lambda _d} \Leftrightarrow 0,4{k_t} = 0,48{k_l} = 0,72{k_d}$$ \Leftrightarrow 5{k_t} = 6{k_l} = 9{k_d}$
$BSCNN\left( {5,6,9} \right) = 90 \Rightarrow {k_t} = 18,{k_\ell } = 15;{k_d} = 10$ (3 bộ số trùng nhau đầu tiên)
Lại có:
${k_l}{\lambda _l} = {k_d}{\lambda _d} \Leftrightarrow 0,48{k_l} = 0,72{k_d}$$ \Leftrightarrow \frac{{{k_l}}}{{{k_d}}} = \frac{3}{2};\frac{6}{4};\frac{9}{6};\frac{{12}}{8};\frac{{15}}{{10}}$
${k_\ell }{\lambda _l} = {k_t}{\lambda _t} \Leftrightarrow 0,48{k_l} = 0,4{k_t}$$ \Leftrightarrow \frac{{{k_\ell }}}{{{k_t}}} = \frac{5}{6};\frac{{10}}{{12}};\frac{{15}}{{18}}$
${k_t}{\lambda _t} = {k_d}{\lambda _d} \Leftrightarrow 0,4{k_t} = 0,72{k_d}$$ \Leftrightarrow \frac{{{k_t}}}{{{k_d}}} = \frac{9}{5};\frac{{18}}{{10}}$
$ \Rightarrow $ Giữa hai cặp vân trùng ba liên tiếp $\;(0;0;0)$ và $\left( {18,15,10} \right)$ có:
4 cặp lam đỏ trùng nhau; 2 cặp lam tím trùng nhau; 1 cặp tím đỏ trùng nhau
$ \Rightarrow $ Vân màu lam $ = 14 – 4 – 2 = 8$
Vân màu đỏ $ = 9 – 4 – 1 = 4$.
Bài 10: Trong thí nghiệm Y-âng, cho 3 bức xạ ${\lambda _1} = 400\;nm,{\lambda _2} = 500\;nm,{\lambda _3} = 600\;nm$. Trên màn quan sát ta hứng được hệ vân giao thoa trong khoảng giữa 3 vân sáng gần nhau nhất cùng màu với vân sáng trung tâm, ta quan sát được số vân sáng là bao nhiêu?
Lời giải:
Ta có $\frac{{{k_1}}}{{{k_2}}} = \frac{{{i_2}}}{{{i_1}}} = \frac{5}{4} = \frac{{15}}{{12}},\frac{{{k_1}}}{{{k_3}}} = \frac{{{i_3}}}{{{i_1}}} = \frac{3}{2} = \frac{{15}}{{10}}$
$ \Rightarrow {i_{123}} = 15{i_1} = 12{i_2} = 10{i_3}$
Trong khoảng giữa 3 vân sáng cùng màu với vân trung tâm
Số vân sáng của bức xạ 1 là:
${N_1} = \frac{{2{i_{123}}}}{{{i_1}}} – 1 = \frac{{30{i_1}}}{{{i_1}}} – 1 = 29$
Số vân sáng của bức xạ 2 là:
${N_2} = \frac{{2{i_{123}}}}{{{i_2}}} – 1 = \frac{{24{i_2}}}{{{i_2}}} – 1 = 23$
Số vân sáng của bức xạ 3 là:
${N_3} = \frac{{2{i_{123}}}}{{{i_3}}} – 1 = \frac{{20{i_3}}}{{{i_3}}} – 1 = 19$
Số vân trùng của bức xạ 1,2 là
${N_{12}} = \frac{{2{i_{123}}}}{{{i_{12}}}} – 1 = \frac{{30{i_1}}}{{5{i_1}}} – 1 = 5$
Số vân trùng của bức xạ 1,3 là
${N_{13}} = \frac{{2{i_{123}}}}{{{i_{13}}}} = \frac{{30{i_1}}}{{3{i_1}}} – 1 = 9$
Số vân trùng của bức xạ 2, 3 là $\frac{{{k_2}}}{{{k_3}}} = \frac{{{i_3}}}{{{i_2}}} = \frac{6}{5} \Rightarrow {i_{23}} = 6{i_2}$$ \Rightarrow {N_{23}} = \frac{{2{i_{123}}}}{{{i_{23}}}} – 1 = \frac{{24{i_2}}}{{6{i_2}}} – 1 = 3$
Số vân trùng của bức xạ $1,2,3$ là ${N_{123}} = 1$
Số vân sáng quan sát được $N = {N_1} + {N_2} + {N_3} – {N_{12}} – {N_{13}} – {N_{23}} + {N_{123}} = 55$.
DẠNG 4. GIAO THOA VỚI ÁNH SÁNG TRẮNG
A. Phương pháp giải
Điều kiện ánh sáng trắng: $0,38\mu m$ (tím) $ \leqslant \lambda \leqslant 0,76\mu m$ (đỏ)
B. Bài tập tự luận
Bài 1: (SBT – KNTT) Thực hiện thí nghiệm Young về giao thoa với ánh sáng, khoảng cách giữa 2 khe là $2\;mm$, khoảng cách giữa mặt phẳng chứa 2 khe và màn quan sát là $2\;m$. Người ta chiếu sáng hai khe bằng ánh sáng trắng có bước sóng nằm trong khoảng từ $0,4\mu m$ đến $0,76\mu m$. Hỏi tại điểm $M$ trên màn ảnh cách vân trung tâm 3,3mm sẽ cho vân tối có bước sóng ngắn nhất bằng bao nhiêu?
Lời giải:
Vị trí tại $M$ cho vân tối:
${x_M} = \left( {k + 0,5} \right) \cdot \frac{{\lambda D}}{{{\;^a}}}$$ \Rightarrow \lambda = \frac{{a{x_N}}}{{\left( {k + 0,5} \right)D}} = \frac{{2 \cdot {{10}^{ – 3}} \cdot 3,3,{{10}^{ – 3}}}}{{k + 0,5}}\left( {\;m} \right)$
Theo đề bài:
$,4 \cdot {10^{ – 6}}\;m \leqslant \lambda \leqslant 0,75 \cdot {10^{ – 6}}\;m$
$ \Rightarrow 0,4 \cdot {10^{ – 6}} \leqslant \frac{{\frac{{2 \cdot {{10}^{ – 3}} \cdot 3,3 \cdot {{10}^{ – 3}}}}{{k + 0,5}}}}{\;} \leqslant 0,75 \cdot {10^{ – 6}}$
$8,3 \leqslant k \leqslant 16 \Rightarrow {\lambda _{min}} = \frac{{\frac{{2 \cdot {{10}^{ – 3}} \cdot 3,3 \cdot {{10}^{ – 3}}}}{{16 + 0,5}}}}{\;} = 0,4 \cdot {10^{ – 6}}\;m = 0,4\mu m$
Bài 2: (SBT – CTST) Trong thí nghiệm Young về giao thoa ánh sáng, hai khe được chiếu bằng ánh sáng trắng có bước sóng trong khoảng từ $400\;nm$ đến $750\;nm$. Những ánh sáng đơn sắc nào cho vân sáng tại vị trí vân sáng bậc bốn của ánh sáng đỏ?
Lời giải:
Ta có: $\;{x_{d4}} = 4 \cdot \frac{{{\lambda _d}D}}{a};\;{x_s} = k \cdot \frac{{\lambda D}}{a}$; các ánh sáng đơn sắc khác cho vân sáng tại vị trí này khi $4{\lambda _d} = k\lambda $.
Mà $400 \leqslant \lambda \leqslant 750$. Suy ra: $4 < k \leqslant 7,5 \Rightarrow k = 5,6,7$
$Ba$ ánh sáng đơn sắc khác cho vân sáng trùng lên vân sáng bậc bốn của ánh sáng đỏ, có bước sóng lần lượt là $429\;nm;500\;nm;600\;nm$
Bài 3: Trong thí nghiệm giao thoa Y-âng, khoảng cách giữa hai khe là $1\;mm$, khoảng cách từ mặt phẳng chứa hai khe đến màn $1\;m$. Nguồn sáng $S$ phát ánh sáng trắng có bước sóng nằm trong khoảng từ $0,38\mu m$ đến $0,76\mu m$. Thí nghiệm thực hiện trong không khí.
a) Tính độ rộng của quang phổ bậc 4 quan sát được trên màn.
b) Tính bề rộng khoảng chồng chập của quang phổ bậc 3 và bậc 5 .
c) Hỏi tại điểm $M$ trên màn cách vân sáng trung tâm $3,5\;mm$ những bức xạ nào cho vân sáng? Cho vân tối?
d) Trên màn $M$ là vị trí gần vân trung tâm nhất có đúng 3 bức xạ cho vân sáng. Tìm khoảng cách từ $M$ đến vân trung tâm.
Lời giải:
a) Bề rộng quang phổ bậc 4 trên màn tính theo công thức:
${\delta _4} = x_4^D – x_4^T = 4\frac{{\left( {{\lambda _D} – {\lambda _T}} \right)D}}{a} = 4\frac{{\left( {0,76 – 0,38} \right) \cdot 1}}{1} = 1,52\;mm.\;$
b) Bề rộng khoảng chồng chập của quang phổ bậc 3 và bậc 5 là:
$\Delta x = x_{thap\;}^D – x_{cao\;}^T = x_3^D – x_5^T = \left( {3{\lambda _D} – 5{\lambda _T}} \right) \cdot \frac{D}{a}$
$ = \left( {3 \cdot 0,76 – 5 \cdot 0,38} \right)\frac{1}{1} = 0,38\;mm$
c) Tai điểm M bức xạ $\lambda $ cho vân sáng thì ${x_M} = k\frac{{\lambda D}}{a} \Rightarrow \lambda = \frac{{a{x_M}}}{{kD}} = \frac{{3,5}}{k}\mu m$
Do $0,38 \leqslant \lambda \leqslant 0,76 \Rightarrow 4,6 \leqslant k \leqslant 9,2 \Rightarrow k = \left\{ {5,6,7,8,9} \right\}$
Thay các giá trị $k$ vào ${\;^{\left( 1 \right)}}$ ta tìm được bước sóng của các bức xạ cho vân sáng tại $M$:
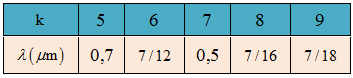
Tại điểm M bức xạ $\lambda $ cho vân tối thì ${x_M} = \left( {m + 0,5} \right)\frac{{\lambda D}}{a}$
$ \Rightarrow \lambda = \frac{{a{x_M}}}{{\left( {m + 0,5} \right)D}} = \frac{{3,5}}{{m + 0,5}}\mu m$
Do $0,38 \leqslant \frac{{3,5}}{{m + 0,5}} \leqslant 0,76 \Rightarrow 4,1 \leqslant m \leqslant 8,7 \Rightarrow m = \left\{ {5,6,7,8} \right\}$
Thay các giá trị $k$ vào (2) ta tìm được bước sóng của các bức xạ cho vân tối tại $M$:
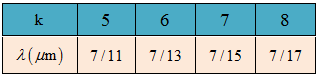
d) Vị trí có 3 bức xạ cho vân sáng: $n + 1 = 3 \Rightarrow n = 2$
Để tại $M$ có đúng 3 bức xạ chồng nhau thì vân màu tím quang phổ bậc $k$ phải chồng lên vân màu đỏ quang phổ bậc $\left( {k – 2} \right)$ tức là:
$\begin{array}{*{20}{c}}
{x_T^k \leqslant x_D^{k – 2} \Rightarrow k\frac{{{\lambda _T}D}}{a} \leqslant \left( {k – 2} \right)\frac{{{\lambda _D}D}}{a}} \\
{ \Rightarrow k \geqslant 2\frac{{{\lambda _D}}}{{{\lambda _D} – {\lambda _T}}} = 2\frac{{0,76}}{{0,76 – 0,38}} = 4 \Rightarrow k = 4,5,6, \ldots }
\end{array}$
Vị trí $M$ gần nhất để tại đó có đúng 3 bức xạ cho vân sáng là ${x_{Mmin}} = 4\frac{{{\lambda _T}D}}{a} = \frac{{4 \cdot 0,38 \cdot 1}}{1} = 1,52\;mm$.
Bài 4: Trong thí nghiệm Y-âng về giao thoa ánh sáng, hai khe được chiếu bằng ánh sáng trắng có bước sóng từ $0,38\mu m$ đến $0,76\mu m$. Khoảng cách giữa hai khe là $0,8\;mm$, khoảng cách từ mặt phẳng chứ hai khe đến màn quan sát là $1,2\;m$. Độ rộng quang phổ bậc 3 (nằm về một phía so với vân sáng trung tâm) là bao nhiêu?
Lời giải:
Độ rộng quang phổ bậc 3 (nằm về một phía so với vân sáng trung tâm) là
${\delta _3} = x_3^D – x_3^T = 3\frac{{{\lambda _D}D}}{a} – 3\frac{{{\lambda _T}D}}{a}$
$ = 3\frac{{\left( {{\lambda _D} – {\lambda _T}} \right)D}}{a} = 3\frac{{\left( {0,76 \cdot {{10}^{ – 6}} – 0,38 \cdot {{10}^{ – 6}}} \right) \cdot 1,2}}{{0,8 \cdot {{10}^{ – 3}}}}$
$ = 1,71 \cdot {10^{ – 3}}\;m = 1,71\;mm$
Bài 5: Trong thí nghiệm Y-âng dùng ánh sáng trắng có bước sóng từ $0,4\mu m$ đến $0,75\mu m$. Bề rộng quang phổ bậc 1 là $0,7\;mm$. Khi dịch màn ra xa khe thêm $40\;cm$ thì bề rộng quang phổ bậc 1 là $0,84\;mm$. Khoảng cách giữa hai khe ${S_1},\;{S_2}$ là bao nhiêu?
Lời giải:
Độ rộng quang phổ bậc 1 là: ${\delta _1} = x_1^D – x_1^T = \left( {{\lambda _D} – {\lambda _T}} \right)\frac{D}{a}$
Khi chưa dịch màn: ${\delta _1} = \left( {{\lambda _D} – {\lambda _T}} \right)\frac{D}{a} \Leftrightarrow 0,7 = \left( {0,75 – 0,4} \right)\frac{D}{a}$
Khi dịch màn: ${\delta _1} = \left( {{\lambda _D} – {\lambda _T}} \right)\frac{{D + 0,4}}{a}$$ \Leftrightarrow 0,84 = \left( {0,75 – 0,4} \right)\frac{{D + 0,4}}{a}$
Chia vế cho vế của (1) cho (2) ta được: $\frac{{0,7}}{{0,84}} = \frac{D}{{D + 0,4}} \Rightarrow D = 2\;m$
Thay $D = 2\;m$ lên ${\;^{\left( 1 \right)}}$, ta được: $0,7 = \left( {0.75 – 0,4} \right) \cdot \frac{2}{a} \Rightarrow a = 1\;mm$.
Bài 6: Trong thí nghiệm Y-âng về giao thoa ánh sáng, hai khe được chiếu bằng ánh sáng trắng có bước sóng từ $380\;nm$ đến $760\;nm$ Khoảng cách giữa hai khe là $0,8\;mm$, khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát là $2\;m$. Trên màn, tại vị trí cách vân trung tâm $3\;mm$ có vân sáng của các bức xạ với bước sóng bao nhiêu?
Lời giải:
Giả sử tại vị trí có tọa độ $x = 3\;mm$ trùng với vân sáng bậc $k$ của bức xạ có bước sóng $\lambda $, ta có:
$x = k\frac{{\lambda D}}{a} \Rightarrow k = \frac{{ax}}{{\lambda D}}$
Do ${\lambda _{min\;}} = 0,38\mu m \leqslant \lambda \leqslant 0,76\mu m = {\lambda _{max}}$ nên $\frac{{ax}}{{{\lambda _{max}}D}} \leqslant k \leqslant \frac{{ax}}{{{\lambda _{min\;}}D}}$
$ \Leftrightarrow \frac{{0,8 \cdot {{10}^{ – 3}} \cdot 3 \cdot {{10}^{ – 3}}}}{{0,76 \cdot {{10}^{ – 6}} \cdot 2}} \leqslant k \leqslant \frac{{0,8 \cdot {{10}^{ – 3}} \cdot 3 \cdot {{10}^{ – 3}}}}{{0,38 \cdot {{10}^{ – 6}} \cdot 2}} \Leftrightarrow 1,6 \leqslant k \leqslant 3,2$
Do $k \in Z$ nên có 2 bức xạ cho vân sáng trùng nhau tại vị trí có $x = 3\;mm$ và bước sóng tương ứng là
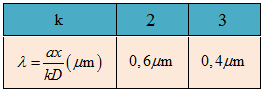
Bài 7: Trong thí nghiệm Y-âng về giao thoa ánh sáng, hai khe được chiếu bằng ánh sáng trắng có bước sóng từ $0,38\mu m$ đến $0,76\mu m$ Tại vị trí vân sáng bậc 4 của ánh sáng đơn sắc có bước sóng $0,76\mu m$ còn có bao nhiêu vân sáng nữa của các ánh sáng đơn sắc khác?
Lời giải:
Tại vị trí ${x_M}$ là sự trùng nhau của vân sáng bậc 4 màu đỏ $0,76\mu m$ và bậc $k$ của các màu khác, ta có:
${x_M} = 4{i_d} = ki$
$ \Leftrightarrow 4{\lambda _{\dot d}} = k\lambda \Rightarrow k = \frac{{4{\lambda _{\dot d}}}}{\lambda } = \frac{{4 \cdot 0,76}}{\lambda }$
$Do\;\;{\lambda _{min\;}} = 0,38\mu m \leqslant \lambda \leqslant 0,76\mu m = {\lambda _{max}}$
$ \Rightarrow \frac{{4.0,76}}{{0,76}} < k \leqslant \frac{{4.0,76}}{{0,38}} \Leftrightarrow 4 < k \leqslant 8$
Do $k \in Z$ nên có 4 giá trị của $k = 5,6,7,8$ ứng với ứng với 4 vân sáng khác màu đỏ tại $M$.
Bài 8: Thí nghiệm Y-âng về giao thoa ánh sáng. Khoảng cách giữa hai khe là $1\;mm$, màn quan sát đặt song song với mặt phẳng chứa hai khe và cách hai khe $2\;m$. Chiếu sáng hai khe bằng ánh sáng trắng có bước sóng $0,400\mu m \leqslant \lambda \geqslant 0,750\mu m$. Bước sóng lớn nhất của các bức xạ cho vân tối tại điểm $N$ trên màn, cách vân trung tâm $12\;mm$ là bao nhiêu?
Lời giải:
Bước sóng của bức xạ cho vân tối tại vị trí x:
$x = \left( {k + 0,5} \right) \cdot \frac{{\lambda D}}{a}$
$ \Rightarrow \lambda = \frac{{ax}}{{\left( {k + 0,5} \right) \cdot D}} = \frac{{1 \cdot 12}}{{\left( {k + 0,5} \right) \cdot 2}} = \frac{6}{{k + 0,5}}\left( {\mu m} \right)$
Cho $\lambda $ vào điều kiện bước sóng của ánh sáng trắng:
${\lambda _d} \leqslant \lambda \leqslant {\lambda _4} \Rightarrow 0,4 \leqslant \frac{6}{{k + 0,5}} \geqslant 0,75$
$ \Rightarrow 7,5 \leqslant k \leqslant 14,5 \Rightarrow k = \left\{ {8; \ldots 14} \right\}$
Trong các bước sóng của các bức xạ cho vân tối tại $M$, bước sóng ứng với $k = 8$ là bước sóng dài nhất ( $\lambda $ càng lớn khi $k$ càng nhỏ) là:
${\lambda _{max}} = \frac{6}{{8 + 0,5}} = 0,705\mu m$






