Các Dạng Bài Tập Về Giao Thoa Sóng Cơ Vật Lí 11 Giải Chi Tiết

Các dạng bài tập về giao thoa sóng cơ vật lí 11 giải chi tiết được soạn dưới dạng file word và PDF gồm 6 trang. Các bạn xem và tải về ở dưới.

DẠNG 1. Điều kiện cực đại – cực tiểu

A. PHƯƠNG PHÁP GIẢI

• Những điểm dao động với biên độ cực đại: ${d_2} – {d_1} = k\lambda $ với $k = 0, \pm 1, \pm 2 \ldots $

• Những điểm dao động với biên độ cực tiểu: ${d_2} – {d_1} = \left( {k + \frac{1}{2}} \right)\lambda $ với $k = 0, \pm 1, \pm 2 \ldots $

B. BÀI TẬP TỰ LUẬN

Bài 1: (SGK – KNTT) Trong thí nghiệm ở hình 12.1, tốc độ truyền sóng trên mặt nước là 20 $cm/s$, cần rung có tần số $40\;Hz$. Tính khoảng cách giữa hai điểm cực đại giao thoa cạnh nhau trên đoạn thẳng ${S_1}\;{S_2}$.

Lời giải:

Khoảng cách giữa hai điểm cực đại giao thoa cạnh nhau có độ dài bằng nửa bước sóng nên có giá trị bằng $\frac{\lambda }{2} = \frac{v}{{2f}} = \frac{{0,2}}{{2,40}} = 2,5 \cdot {10^{ – 3}}\;cm$.

Bài 2: (SGK – CTST) Trong thí nghiệm giao thoa sóng trên mặt nước với hai nguồn kết hợp cùng pha, ta thấy tại một điểm cách hai nguồn các khoảng lần lượt là $20\;cm$ và $12\;cm$, sóng có biên độ cực đại, đồng thời giữa điểm này và đường trung trực của hai nguồn có 4 dãy gồm những điểm dao động với biên độ cực đại. Biết tốc độ truyền sóng là $40\;cm/s$. Tính tần số của sóng.

Lời giải:

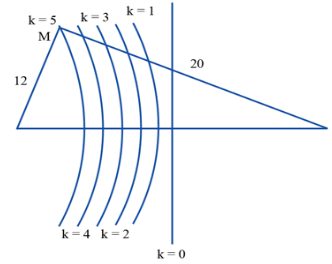
Hai nguồn dao động cùng pha nên những điểm thuộc đường trung trực của đoạn nối hai nguồn là những điểm có biên độ cực đại.

Gọi điểm $M$ là điểm cách hai nguồn các khoảng lần lượt là $20\;cm$ và $12\;cm$, sóng có biên độ cực đại: ${d_2} – {d_1} = 20 – 12 = 8 = k\lambda $

Do giữa điểm $M$ và đường trung trực của hai nguồn có 4 dãy gồm những điểm dao động với biên độ cực đại nên $M$ thuộc dãy cực đại bậc 5 .

$ \Rightarrow k = 5 \Rightarrow \lambda = \frac{8}{5} = 1,6\;cm \Rightarrow f = \frac{v}{\lambda } = \frac{{40}}{{1,6}} = 25\;Hz$

DẠNG 2. Phương trình giao thoa – Biên độ giao thoa

A. PHƯƠNG PHÁP GIẢI

Xét 2 nguồn kết hợp cùng pha ${u_1} = {u_2} = Acos\left( {\omega t} \right)$

Xét điểm $M$ trong vùng giao thoa có khoảng cách tới các nguồn là ${d_1},\;{d_2}$

Phương trình sóng do ${u_1},\,{u_2}$ truyền tới M là:

${u_{1M}} = Acos\left( {\omega t – 2\pi \frac{{{d_1}}}{\lambda }} \right)$; ${u_{2M}} = Acos\left( {\omega t – 2\pi \frac{{{d_2}}}{\lambda }} \right)$

Phương trình sóng tổng hợp tại M:

${u_M} = {u_{1M}} + {u_{2M}} = 2Acos\left[ {\pi \frac{{{d_2} – {d_1}}}{\lambda }} \right]cos\left[ {2\omega t – \pi \frac{{{d_1} + {d_2}}}{\lambda }} \right]$

Độ lệch pha của hai sóng từ hai nguồn đến M: $\Delta {\varphi _M} = \frac{{2\pi }}{\lambda }\left( {{d_1} – {d_2}} \right)$

Biên độ dao động tổng hợp tại M: ${A_M} = 2A\left| {cos\left[ {\pi \frac{{\left( {{d_2} – {d_1}} \right)}}{\lambda }} \right]} \right|$

B. BÀI TẬP TỰ LUẬN

Bài 1: Cho phương trình dao động của hai nguồn $A$ và $B$ trên mặt nước đều là $u = acos\omega t$. Biên độ sóng do $A$ và $B$ truyền đi đều bằng $1\;mm$. Vận tốc truyền sóng là $3\;m/s$. Điểm $M$ cách $A$ và $B$ lần lượt là ${d_1} = 2\;m$ và ${d_2} = 2,5\;m$. Tần số dao động là $40\;Hz$. Viết phương trình dao động tại $M$ do hai nguồn $A$ và $B$ truyền tới.

Lời giải:

Ta có $\omega = 2\pi f = 80\pi \left( {rad/s} \right);\lambda = \frac{v}{f} = 7,5\;cm$

Hai nguồn cùng pha nên ta có:

${u_M} = {u_{1M}} + {u_{2M}}$$ = 2\;Acos\left( {\omega t + \varphi – \frac{{\pi \left( {{d_1} + {d_2}} \right)}}{\lambda }} \right)cos\left( {\frac{{\pi \left( {{d_2} – {d_1}} \right)}}{\lambda }} \right)$

$ = 2cos\left( {80\pi t – \frac{{\pi \cdot 450}}{{7,5}}} \right)cos\left( {\frac{{50\pi }}{{7,5}}} \right)$

$ = – cos\left( {80\pi t} \right) = x = cos\left( {80\pi t – \pi } \right)\left( {mm} \right)$

Phương trình truyền sóng là $x = cos\left( {80\pi t – \pi } \right)\left( {mm} \right)$

Bài 2: Tại ${S_1},\;{S_2}$ trên mặt chất lỏng ta tạo ra hai dao động điều hòa giống nhau với phương trình ${u_1} = {u_2} = 2cos\left( {100\pi t} \right)cm$. Cho rằng sóng truyền đi với biên độ không đổi và bước sóng là $12\;cm$. M là một điểm trên mặt chất lỏng ấy cách ${S_1},\;{S_2}$ lần lượt ${S_1}M = 14\;cm$ và ${S_2}M = 16\;cm$. Biên độ sóng tổng hợp tại $M$ do hai sóng truyền tới là bao nhiêu?

Lời giải:

Độ lệch pha của hai sóng tại $M$ là: $\Delta \varphi = \frac{{2\pi }}{\lambda }\left( {{d_2} – {d_1}} \right) = \frac{\pi }{3}$

Biên độ dao động tổng hợp tại $M$ là:

${A_M} = \left| {2\;Acos\frac{{\Delta \varphi }}{2}} \right| = 2\sqrt 3 \left( {\;cm} \right)$

Bài 3: Trên mặt thoáng chất lỏng có hai nguồn kết hớp $A,B$ có phương trình dao động là ${u_A} = {u_B} = 2cos10\pi \left( {cm} \right)$. Vận tốc truyền sóng là $3\;m/s$. Xác định biên độ và pha ban đầu của sóng tại điểm $N$ cách $A45\;cm$ và cách $B60\;cm$.

Lời giải:

Ta có $f = 5\;Hz,\lambda = 60\;cm$

Hai nguồn cùng pha nên ta có:

${u_M} = {u_{1M}} + {u_{2M}}$$ = 2\;Acos\left( {\omega t + \varphi – \frac{{\pi \left( {{d_1} + {d_2}} \right)}}{\lambda }} \right)cos\left( {\frac{{\pi \left( {{d_2} – {d_1}} \right)}}{\lambda }} \right)$

$ = 4cos\left( {10\pi t – \frac{{105\pi }}{{60}}} \right)cos\frac{{\pi \cdot 15}}{{60}}$$ = 2\sqrt 2 cos\left( {10\pi t – \frac{{7\pi }}{4}} \right)\left( {cm} \right)$

Vậy biên độ là $2\sqrt 2 \;cm$; pha ban đầu là $\frac{{ – 7\pi }}{4}$

Bài 4: Tại mặt chất lỏng có hai nguồn phát sóng kết hợp và dao động theo phương vuông góc với mặt chất lỏng có cùng phương trình (trong đó $u$ tính bằng $cm,t$ tính bằng $s$ ). Tốc độ truyền sóng trên mặt chất lỏng là $80\;cm/s$. Gọi $M$ là điểm trên mặt chất lỏng cách, lần lượt là $12\;cm$ và $9\;cm$. Coi biên độ của sóng truyền từ hai nguồn trên đến điểm $M$ là không đổi. Phần tử chất lỏng tại $M$ dao động với biên độ là bao nhiêu?

Lời giải:

Bước sóng $\lambda = \frac{v}{f} = 4\;cm$

${A_M} = 2A\left| {cos\left[ {\pi \frac{{\left( {{d_2} – {d_1}} \right)}}{\lambda }} \right]} \right|\;$

Thay số ta được

${A_M}\; = 2\sqrt 2 \;cm$

DẠNG 3. Số điểm cực đại và cực tiểu

A. PHƯƠNG PHÁP GIẢI

• Trên đoạn ${S_1}\;{S_2}:\; – {S_1}{S_2} \leqslant {d_2} – {d_1} \leqslant {S_1}{S_2}$

• Số cực đại: $\; – \frac{{{S_1}{S_2}}}{\lambda } \leqslant k \leqslant – $

• Số cực tiểu : $\; – \frac{{{S_1}{S_2}}}{\lambda } – \frac{1}{2} \leqslant k \leqslant \frac{{{S_1}S}}{\lambda }$

• Trên đoạn MN bất kì: ${d_{2M}} – {d_{1M}} \leqslant {d_2} – {d_1} \leqslant {d_{2N}} – {d_{1N}}$

• Số cực đại:

$\frac{{{d_{2M}} – {d_{1M}}}}{\lambda } \leqslant k \leqslant \frac{{{d_{2N}} – {d_{1N}}}}{\lambda }$

• Số cực tiểu :

$\frac{{{d_{2M}} – {d_{1M}}}}{\lambda } – \frac{1}{2} \leqslant k \leqslant \frac{{{d_{2N}} – {d_{1N}}}}{\lambda }$

B. BÀI TẬP TỰ LUẬN

Bài 1: (SBT – CTST) Trong hiện tượng giao thoa sóng nước do hai nguồn kết hợp $A$ và $B$ dao động cùng pha tạo ra, trên cùng một dây gồm những điểm dao động với biên độ cực đại, xét điểm $M$ cách $A$ và $B$ các khoảng bằng $21\;cm;19\;cm$ và điểm $N$ cách $A$ một khoảng $24\;cm$. Tính khoảng cách từ $N$ đến $B$.

Lời giải:

Ta có điều kiện cực đại giao thoa: $MA – MB = k\lambda = NA – NB$

Suy ra $NB = 24 – 2 = 22\;cm$

Bài 2: (SBT – CTST) Trên mặt nước có sự giao thoa của hai sóng do hai nguồn kết hợp $A$ và $B$ dao động cùng pha, cùng biên độ tạo ra. Gọi $\lambda $ là bước sóng của sóng do hai nguồn phát ra. Xét một điểm nằm trong vùng giao thoa trên dây đứng yên thứ ba kể từ đường trung trực của đoạn $AB$, xác định hiệu khoảng cách từ điểm này đến hai nguồn $A$ và $B$.

Lời giải:

$M$ cách $A$ và $B$ các khoảng $MA$ và $MB$ sao cho thỏa mãn điều kiện cực tiểu giao thoa:

$MA – MB = \left( {k + 1/2} \right)\lambda $

Vân đứng yên thứ ba tương ứng với $k = 2$ nên $MA – MB = 5\lambda /2$

Bài 3: (SBT – CTST) Trong hiện tượng giao thoa sóng trên mặt nước do hai nguồn kết hợp $A$ và $B$ cùng pha, cùng tần số bằng $24\;Hz$ gây ra. Tại một điểm $M$ trong vùng giao thoa trên mặt nước, ta quan sát thấy sóng có biên độ cực đại và là dãy cực đại thứ ba kể từ cực đại trung tâm. Phải thay đổi tần số sóng bằng bao nhiêu để tại $M$ có

a. dãy cực đại bậc bốn kể từ cực đại trung tâm?

b. dãy đứng yên thứ ba kể từ cực đại trung tâm?

Luu ý: Bài tập này có thể giải mà không cần dữ liệu về giá trị của tốc độ truyền sóng.

Lời giải:

a. Để thay đổi từ dãy cực đại bậc ba thành dãy cực đại bậc bốn kể từ đường trung trực của $AB$ thì MA- MB $ = 3{\lambda _1} = 4{\lambda _2} = > {3^{\frac{v}{{{f_1}}}}} = {4^{\frac{v}{{{f_2}}}}}$

Từ đó suy ra: ${f_2} = \frac{4}{3}{f_1} = 32\;Hz$

b. Để thay đổi từ dãy cực đại bậc ba thành dãy đứng yên thứ ba kể từ đường trung trực của $AB$ thì $MA – MB = 3{\lambda _1} = 2,5{\lambda _3} \Rightarrow 3\frac{v}{{{f_1}}} = 2,5 \cdot \frac{v}{{{f_3}}}$

Từ đó suy ra: ${f_3} = \frac{{2,5}}{3}{f_1} = 20\;Hz$

Bài 4: (SBT – CTST) Trong thí nghiệm giao thoa sóng trên mặt nước, hai nguồn sóng A và $B$ dao động với phương trình ${u_A} = {u_B} = 5cos10t\left( {cm} \right)$. Biết tốc độ truyền sóng là $20\;cm/s$.

a. Viết phương trình dao động của điểm $M$ trên mặt nước cách $A,B$ lần lượt là $7,2\;cm$ và $8,2\;cm$. b. Một điểm $N$ trên mặt nước có $AN – BN = 10\;cm$. Điểm $N$ nằm trên dãy gồm những điểm dao động với biên độ cực đại hay đứng yên?

Lời giải:

a. Ta có $\lambda = 20/5 = 4\;cm$

${u_M} = {u_1} + {u_2} = Acos\left( {\omega t – \frac{{2\pi {x_1}}}{\lambda }} \right) + Acos\left( {\omega t – \frac{{2\pi {x_2}}}{\lambda }} \right)$

Suy ra ${u_M} = 2\;Acos\left( {\pi \frac{{{x_1} – {x_2}}}{\lambda }} \right)cos\left( {\omega t – \pi \frac{{{x_1} + {x_2}}}{\lambda }} \right)$$ = 5\sqrt 2 cos\left( {10\pi t – 3,85\pi } \right)cm$

b. $AN – BN = 10\;cm – 2,5\lambda :N$ nằm trên dãy đứng yên thứ 3 kể từ cực đại trung tâm, gần phía A hơn.

Bài 5: (SBT – CTST)

Trong thí nghiệm giao thoa sóng trên mặt nước, hai nguồn sóng kết hợp cùng pha đặt tại hai điểm $A$ và $B$ cách nhau $30\;cm$. Xét điểm $M$ nằm trên đoạn $AB$ và cách $A20\;cm$; điểm $N$ nằm trên mặt nước và cách $M40\;cm,MN$ vuông góc với $AB$ (hình 8.2)

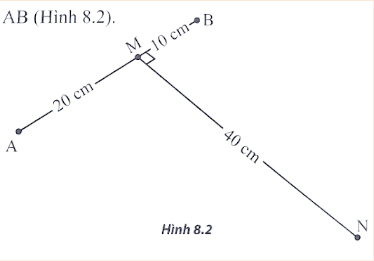
a. Với tần số của hai nguồn bằng $10\;Hz$ thì tại $N$ có sóng với biên độ cực đại và giữa $N$ với đường trung trực của $AB$ không có dãy cực đại. Tính tốc độ truyền sóng.

b. Với tốc độ truyền sóng tính được ở câu a, để điểm $N$ đứng yên thì tần số của hai nguồn phải bằng bao nhiêu?

Lời giải:

a. Theo đề bài, $N$ nằm ở dãy cực đại bậc 1 kể từ cực đại trung tâm.

Do đó, $NA – NB = k\lambda \Rightarrow \sqrt {{{20}^2} + {{40}^2}} – \sqrt {{{10}^2} + {{40}^2}} $

$ = 1.v/10 \Rightarrow v \approx 35\;cm/s$

b. Để điểm $N$ đứng yên thì $N$ phải nằm trên dãy cực tiểu.

Ta có: $NA – NB = \left( {k + 1/2} \right)\lambda = \left( {k + 1/2} \right).\frac{{35}}{f}$

$ \Rightarrow f = 10\left( {k + 1/2} \right) = > f = 5\;Hz;15\;Hz;25\;Hz \ldots $.

Bài 6: (SBT – CTST) Trong thí nghiệm giao thoa sóng trên mặt nước với hai nguồn kết hợp $A$ và $B$ dao động cùng pha, tốc độ truyền sóng là $0,5\;m/s$ với tần số sóng là $25\;Hz$.

a. Trong vùng không gian giữa 2 nguồn, có bao nhiêu dãy gồm những điểm dao động với biên độ cực đại và bao nhiêu dãy gồm những điểm đứng yên? Cho biết 2 nguồn cách nhau $13\;cm$.

b. Tính khoảng cách giữa 2 điểm liên tiếp trên đoạn $AB$ dao động với biên độ cực đại và khoảng cách giữa 2 điểm liên tiếp đứng yên.

c. Khoảng cách giữa một điểm dao động với biên độ cực đại và một điểm đứng yên kế cận trên đoạn $AB$ bằng bao nhiêu?

Lời giải:

a. Ta có: Bước sóng $\lambda = \frac{v}{f} = \frac{{50}}{{25}} = 2\;cm$

Gọi $M$ là một điểm dao động với biên độ cực đại nằm trên $AB$.

Ta có: $\{ MA – MB = k\lambda MA + MB = AB = > MA = \left( {k\lambda + AB} \right)/2$

Vì $0 < MA < AB \Rightarrow – \frac{{AB}}{\lambda } < k < \frac{{AB}}{\lambda }$

$ \Rightarrow – 6,5 < k < 6,5$

$ \Rightarrow k = 0; \pm 1; \ldots .. – 6$ nên có 12 dãy gồm những điểm đứng yên.

b. Gọi ${M_1}$ và ${M_2}$ là hai điểm liên tiếp trên $AB$ dao động với biên độ cực đại, với ${M_1}A > {M_2}A$ :

${M_1}\;A – {M_2}\;A = k\frac{\lambda }{2} + \frac{{AB}}{2} – \left( {\frac{{\left( {k – 1} \right)\lambda }}{2} + \frac{{AB}}{2}} \right)$$ = \lambda /2 = 1,0\;cm$

Tương tự, khoảng cách giữa hai điểm liên tiếp đứng yên trên $AB$ cũng bằng $1,0\;cm$.

c. Khoảng cách giữa 1 điểm dao động với biên độ cực đại và một điểm đứng yên kế cần là $\lambda /4 = $ $0,5\;cm$

Bài 7: Hai nguồn sóng cơ $AB$ cách nhau dao động chạm nhẹ trên mặt chất lỏng, cùng tần số $80\;Hz$, cùng pha theo phương vuông góc với mặt chất lỏng. Vận tốc truyền sóng $16\;m/s$. Số điểm không dao động trên đoạn $AB = 90\;cm$ là bao nhiêu?

Lời giải:

Ta có: Bước sóng $\lambda = \frac{v}{f} = \frac{{20}}{{100}} = 0,2m = 20\;cm$

Do 2 nguồn cùng pha nên số điểm không dao động trên $AB$ là số giá trị k nguyên thỏa mãn

$\frac{{ – AB}}{\lambda } – 0,5 < k < \frac{{AB}}{\lambda } – 0,5$$ \Leftrightarrow – 5 < k < 4$$ \Rightarrow k = 4, \pm 3, \pm 2, \pm 1,0$

Có 8 giá trị của $k$ thỏa mãn yêu cầu nên có 8 điểm trên $AB$ không dao động.

Vậy số điểm không dao động trên đoạn $AB$ là 8 điểm.

Bài 8: Trong một thí nghiệm về giao thoa sóng nước, hai nguồn sóng kết hợp dao động cùng pha đặt tại hai điểm $A$ và $B$ cách nhau $16\;cm$. Sóng truyền trên mặt nước với bước sóng $3\;cm$. Trên đoạn $AB$, số điểm mà tại đó phần tử nước dao động với biên độ cực đại là bao nhiêu?

Lời giải:

Do 2 nguồn cùng pha nên số điểm cực đại trên $AB$ là số giá trị k nguyên thỏa mãn $\frac{{ – AB}}{\lambda } < k < \frac{{AB}}{\lambda }$$ \Leftrightarrow – 5,33 < k < 5,33$$ \Rightarrow k = \pm 5, \pm 4, \ldots \pm 1,0$

có 11 giá trị của $k$ thỏa mãn yêu cầu nên có 11 điểm trên $AB$ dao động cực đại.

Bài 9: Trên mặt nước nằm ngang, tại hai điểm ${S_1},\;{S_2}$ cách nhau $9,6\;cm$, người ta đặt hai nguồn sóng cơ kết hợp, dao động điều hòa theo phương thẳng đứng có tần số $15\;Hz$ và luôn dao động cùng pha. Biết tốc độ truyền sóng trên mặt nước là $45\;cm/s$ và coi biên độ sóng không đổi khi truyền đi. Số điểm dao động với biên độ cực đại trên đoạn ${S_1}\;{S_2}$ là bao nhiêu?

Lời giải:

Ta có : Bước sóng

$\lambda = \frac{v}{f} = \frac{{45}}{{15}} = 3\;cm$

Do 2 nguồn cùng pha nên số điểm dao động cực đại trên $AB$ là số giá trị $k$ nguyên thỏa mãn $\frac{{ – AB}}{\lambda } < k < \frac{{AB}}{\lambda } \Leftrightarrow – 3,2 < k < 3,2$$ \Rightarrow k = \pm 3, \pm 2, \pm 1,0$

có 7 giá trị của $k$ thỏa mãn yêu cầu nên có 7 điểm trên $AB$ dao động cực đại.

Bài 10: Hai nguồn ${S_1}$ và ${S_2}$ trên mặt nước khác nhau $24\;cm$ cùng dao động theo phương trình $u = 4cos\left( {40\pi t} \right)\left( {mm} \right)$. Biết tốc độ truyền sóng trên mặt chất lỏng là $1\;m/s$. Biên độ sóng không đổi. Số điểm dao động với biên độ $8\;mm$ trên đoạn ${S_1}{S_2}$ là bao nhiêu?

Lời giải:

Ta có $:f = 20\;Hz$. Bước sóng

$\lambda = \frac{v}{f} = \frac{{100}}{{20}} = 5\;cm$

Điểm dao động với biên độ $8\;mm$ là điểm dao động cực đại.

Do 2 nguồn cùng pha nên số điểm dao động cực đại trên $AB$ là số giá trị $k$ nguyên thỏa mãn $\frac{{ – AB}}{\lambda } < k < \frac{{AB}}{\lambda } \Leftrightarrow – 4,8 < k < 4,8$$ \Rightarrow k = \pm 4, \pm 3, \pm 2, \pm 1,0$

$ \Rightarrow $có 9 giá trị của $k$ thỏa mãn yêu cầu nên có 9 điểm trên $AB$ dao động cực đại.

Bài 11: Hai nguồn sóng cơ ${S_1}$ và ${S_2}$ trên mặt chất lỏng khác nhau $24\;cm$ dao động theo phương trình ${u_1} = {u_2} = 5cos\left( {30\pi t} \right)$, lan truyền trong môi trường với tốc độ $v = 75\;cm/s$. Xét điểm $M$ cách ${S_1}$ khoảng $18\;cm$ và vuông góc ${S_1}\;{S_2}$ với tại ${S_1}$. Xác định số đường cực đại đi qua ${S_2}M$.

Lời giải:

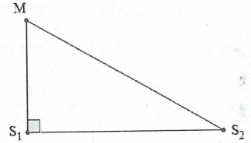
Ta có $:f = 15\;Hz$. Bước sóng $\lambda = \frac{v}{f} = \frac{{75}}{{15}} = 5\;cm$

$M{S_2} = \sqrt {MS_1^2 + {S_1}S_1^2} = 30\;cm$

Tại $M$ ta có: ${d_2} – {d_1} = M{S_2} – M{S_1} = 14\;cm$

Tại ${S_2}$ ta có: ${d_2} – {d_1} = – {S_1}{S_2} = – 24\;cm$

Do 2 nguồn cùng pha nên số cực đại qua ${S_2}M$ là số giá trị $k$ thỏa mãn.

$ – 24 < k\lambda < 14 \Leftrightarrow – 4,8 < k < 2,8$

$ \Rightarrow k = – 4, – 3, \pm 2, \pm 1,0 \Rightarrow $có 7 giá trị của $k$ thỏa mãn yêu cầu.

Bài 12: Trong thí nghiệm giao thoa sóng trên mặt nước. Hai nguồn kết hợp $A$ và $B$ cùng pha cách nhau $10\;cm$. Tại điểm $M$ mặt nước cách $A$ và $B$ lần lượt là ${d_1} = 40\;cm$ và ${d_2} = 34\;cm$ dao động có biên độ cực đại. Giữa $M$ và đường trung trực của $AB$ có một cực đại khác. Trên khoảng MA số điểm dao động không dao động là bao nhiêu?

Lời giải:

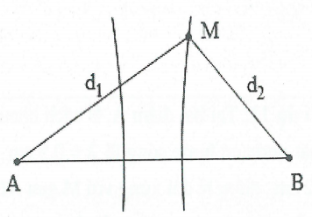
Do giữa $M$ và trung trực của $AB$ có 1 dãy cực đại nên $M$ thuộc cực đại số 2 .

Khi đó ${d_1} – {d_2} = 2\lambda \Rightarrow \lambda = 3\;cm$

Tại $M$ ta có ${d_1} – {d_2} = 6\;cm$

Tại A ta có ${d_1} – {d_2} = – AB = – 10\;cm$

Điều kiện cực tiểu ${d_1} – {d_2} = \left( {k + 0,5} \right)\lambda $

$ – 10 < \left( {k + 0,5} \right)\lambda < 6 \Rightarrow – 3,88 < k < 1,5 \Rightarrow k = – 3, – 2, \pm 1,0$

có 5 giá trị của $k$ thỏa mãn yêu cầu nên có 5 điểm trên $AM$ không dao động.

Bài 13: Trên mặt nước, hai nguồn kết hợp $A,B$ cách nhau $24\;cm$ luôn dao động với phương trình ${u_1} = {u_2} = 4cos\left( {40\pi t + \frac{\pi }{6}} \right)\left( {cm} \right)$

Hai điểm $CD$ nằm trên mặt nước mà $ABCD$ là một hình chữ nhật với $AD = 18\;cm$. Biết vận tốc truyền sóng trên mặt nước là $v = 40\;cm/s$. Số điếm cực đại và đứng yên trên đoạn $CD$ lần lượt là bao nhiêu?

Lời giải:

Ta có $:f = 20\;Hz$. Bước sóng $\lambda = \frac{v}{f} = 2\;cm$

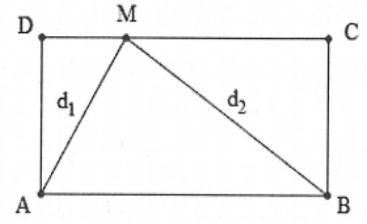
$AC = BD = \sqrt {{{18}^2} + {{24}^2}} = 30\;cm$

Tại $D$ ta có ${d_1} – {d_2} = – 12\;cm$

Tại $C$ ta có ${d_1} – {d_2} = 12\;cm$

Số cực đại trên $CD$ là số giá trị $k$ nguyên thỏa mãn:

$\frac{{ – 12}}{\lambda } \leqslant k \leqslant \frac{{12}}{\lambda } \Leftrightarrow – 6 \leqslant k \leqslant 6$ suy ra có 13 cực đại.

Số cực tiểu $\frac{{ – 12}}{\lambda } – 0,5 \leqslant k \leqslant \frac{{12}}{\lambda } – 0,5$ $ \Leftrightarrow – 6,5 \leqslant k \leqslant 5,5 \Rightarrow $có 12 cực tiểu.

Bài 14: Trên mặt nước có hai nguồn sóng nước $A,B$ giống hệt nhau cách nhau một khoảng . Trên đường tròn nằm trên mặt nước có tâm là trung điểm của $O$ của đoạn $AB$ có bán kính sẽ có số điểm dao động với biên độ cực đại là bao nhiêu?

Lời giải:

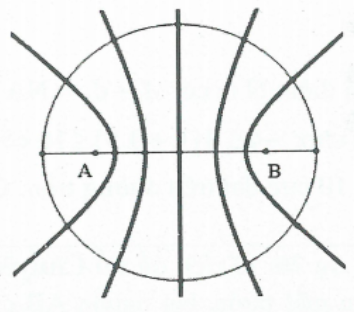
Do đường tròn tâm $O$ có bán kính $R = 12\lambda $ còn $AB = 9,6\lambda $ nên đoạn $AB$ thuộc đường tròn.

Vì hai nguồn $A,B$ giống hệt nhau nên dao động cùng pha. Số điểm dao động với biên độ cực đại trên $AB$ là: $\frac{{ – Ab}}{\lambda } < k < \frac{{AB}}{\lambda }$

Thay số: $ – 9,6 < k < 9,6 \Rightarrow $ có 19 giá trị của $k$

Vậy nên đoạn $AB$ có 19 điểm dao động với biên độ cực đại hay trên đường tròn tâm $O$ có 2.19 $ = 38$ điểm.

Bài 15: Hai nguồn kết hợp giống hệt nhau được đặt cách nhau một khoảng $x$ trên đường kính của một vòng tròn bán kính $R(x < 2R)$ và đối xứng qua tâm của vòng tròn. Biết rằng mỗi nguồn đều phát sóng có bước sóng $\lambda $ và $x = 4\lambda $. Số điểm dao động cực đại trên vòng tròn là bao nhiêu?

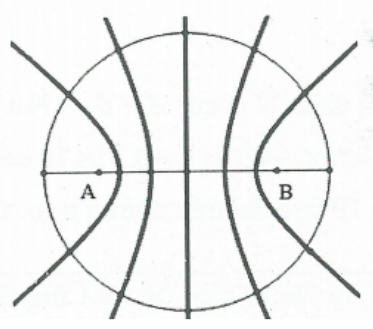
Lời giải:

Do đường tròn tâm $O$ có bán kính $2R > x$ nên đoạn $AB$ thuộc đường tròn.

Vì hai nguồn $A,B$ giống hệt nhau nên dao động cùng pha. Số điểm dao động với biên độ cực đại trên $AB$ là: $\frac{{ – AB}}{\lambda } < k < \frac{{AB}}{\lambda }$

Thay số: $ – 4 < k < 4 \Rightarrow $ có 7 giá trị của $k$

Vậy nên đoạn $AB$ có 7 điểm dao động với biên độ cực đại hay trên đường tròn tâm $O$ có $2.7 = 14$ điểm.