Các Dạng Toán Bài Các Khái Niệm Mở Đầu VecTơ Giải Chi Tiết

Các dạng toán bài các khái niệm mở đầu vectơ giải chi tiết được soạn dưới dạng file word và PDF gồm 4 trang. Các bạn xem và tải về ở dưới.

DẠNG 1: XÁC ĐỊNH VECTƠ- TÍNH ĐỘ DÀI VECTƠ

• Xác định một vectơ và xác định sự cùng phương, cùng hướng của hai vectơ theo định nghĩa.

• Dựa vào các tính chất hình học của các hình đã cho biết để tính độ dài của một vectơ.

Bài 1. Với hai điểm phân biệt $A,B$ có thể xác định được bao nhiêu vectơ khác vectơ-không có điểm đầu và điểm cuối được lấy từ hai điểm trên?

Lời giải

Hai vectơ $\overrightarrow {AB} $ và $\overrightarrow {BA} $.

Bài 2. Với hai điểm phân biệt $A,B,\,C$ có thể xác định được bao nhiêu vectơ khác vectơ-không có điểm đầu và điểm cuối được lấy từ bai điểm trên?

Lời giải

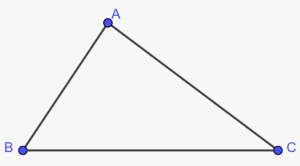
Các vectơ là: $\overrightarrow {AB} $, $\overrightarrow {BA} $, $\overrightarrow {AC} $, $\overrightarrow {CA} $, $\overrightarrow {BC} $, $\overrightarrow {CB} $.

Bài 3. Có bao nhiêu vectơ khác vectơ không có điểm đầu và cuối là các đỉnh của tứ giác $ABCD$ ?

Lời giải

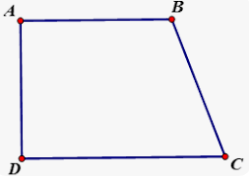
Cách 1:

Các vectơ là: $\overrightarrow {AB} $, $\overrightarrow {BA} $, $\overrightarrow {BC} $, $\overrightarrow {CB} $,$\overrightarrow {CD} $, $\overrightarrow {DC} $, $\overrightarrow {DA} $, $\overrightarrow {AD} $, $\overrightarrow {BD} $, $\overrightarrow {DB} $,$\overrightarrow {AC} $, $\overrightarrow {CA} $ .

Cách 2:

Một vectơ khác vectơ không được xác định bởi 2 điểm phân biệt. Khi có 4 điểm $A,B,C,D$ ta có 4 cách chọn điểm đầu và 3 cách chọn điểm cuối. Nên ta sẽ có $3.4 = 12$ cách xác định số vectơ khác $\vec 0$ thuộc 4 điểm trên.

Bài 4. Trên mặt phẳng cho 6 điểm phân biệt $A,B,C,D,E;F$. Hỏi có bao nhiêu vectơ khác vectơ không, mà có điểm đầu và điểm cuối là các điểm đã cho?

Lời giải

Xét tập $X = \left\{ {A,B,C,D,E;F} \right\}$. Với mỗi cách chọn hai phần tử của tập $X$ và sắp xếp theo một thứ tự ta được một vectơ thỏa mãn yêu cầu.

Mỗi vectơ thỏa mãn yêu cầu tương ứng cho ta 30 phần tử thuộc tập $X$.

Vậy số các vectơ thỏa mãn yêu cầu bằng 30 .

Bài 5. Số vectơ (khác vectơ $\vec 0)$ có điểm đầu và điểm cuối lấy từ 2024 điểm phân biệt cho trước?

Lời giải

Một vectơ khác vectơ không được xác định bởi 2 điểm phân biệt. Khi có 2024 điểm ta có 2024 cách chọn điểm đầu và 2023cách chọn điểm cuối. Nên ta sẽ có $2024.2023 = 4094552$ cách xác định số vectơ khác $\vec 0$ thuộc 2024 điểm trên.

Một cách tổng quát:

Số vectơ (khác vectơ $\vec 0)$ có điểm đầu và điểm cuối lấy từ $n$ điểm phân biệt cho trước là:

$N = n.(n – 1)$.

Bài 6. Cho ba điểm $M,N,P$ thẳng hàng, trong đó điểm $N$ nằm giữa hai điểm $M$ và $P$. Tìm các cặp vectơ cùng hướng?

Lời giải

Các vec tơ cùng hướng là : $\overrightarrow {MN} $ và $\overrightarrow {MP} ,\overrightarrow {MN} $ và $\overrightarrow {NP} ,\overrightarrow {PM} $ và $\overrightarrow {PN} ,\overrightarrow {PN} $ và $\overrightarrow {NM} $.

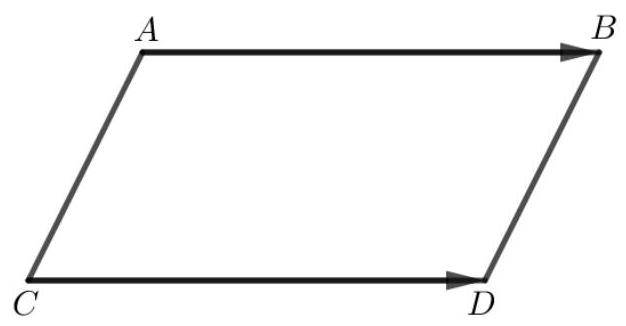
Bài 7. Cho hình bình hành $ABCD$. Tìm vectơ khác $\vec 0$, cùng phương với vectơ $\overrightarrow {AB} $ và có điểm đầu, điểm cuối là đỉnh của hình bình hành $ABCD$.

Lời giải

Các vectơ cùng phương với $\overrightarrow {AB} $ mà thỏa mãn đề bài là: $\overrightarrow {BA} ,\overrightarrow {CD} ,\overrightarrow {DC} $.

Bài 8. Cho hình lục giác đều $ABCDEF$ tâm $O$.

a) Tìm số các vectơ khác vectơ – không, cùng phương với vectơ $\overrightarrow {OB} $ có điểm đầu và điểm cuối là các đỉnh của lục giác?

b) Tìm số các vectơ bằng $\overrightarrow {OC} $ có điểm đầu và điểm cuối là các đỉnh của lục giác?

Lời giải

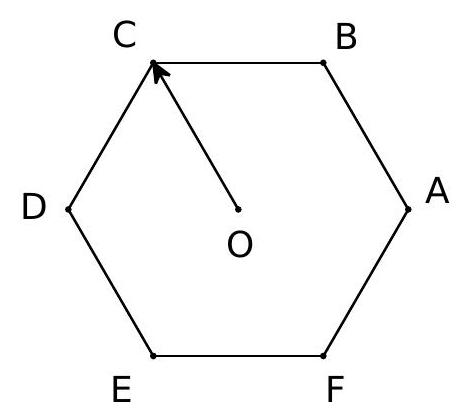
a) Các vectơ cùng phương với vectơ $\overrightarrow {OB} $ là: $\overrightarrow {BE} ,\overrightarrow {EB} ,\overrightarrow {DC} ,\overrightarrow {CD} ,\overrightarrow {FA} ,\overrightarrow {AF} $.
b) Đó là các vectơ: $\overrightarrow {AB} ,\overrightarrow {ED} $.

Bài 9. Cho điểm $A$ và véctơ $\vec a$ khác $\vec 0$. Tìm điểm $M$ sao cho:
a) $\overrightarrow {AM} $ cùng phương với $\vec a$.
b) $\overrightarrow {AM} $ cùng hướng với $\vec a$.

Lời giải

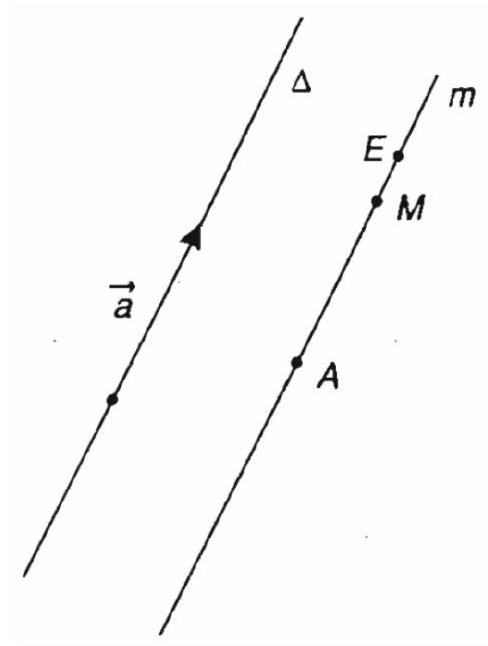
Gọi $\Delta $ là giá của $\vec a$.

a) Nếu $\overrightarrow {AM} $ cùng phương với $\vec a$ thì đường thẳng $AM$ song song với $\Delta $. Do đó $M$ thuộc đường thẳng $m$ đi qua $A$ và song song với $\Delta $. Ngược lại, mọi điểm $M$ thuộc đường thẳng $m$ thì $\overrightarrow {AM} $ cùng phương với $\vec a$. Chú ý rằng nếu $A$ thuộc đường thẳng $\Delta $ thì $m$ trùng với $\Delta $.

b) Lập luận tương tự như trên, ta thấy các điểm $M$ thuộc một nửa đường thẳng gốc $A$ của đường thẳng $m$. Cụ thể, đó là nửa đường thẳng chưa điểm $E$ sao cho $\overrightarrow {AE} $ và $\vec a$ cùng hướng.

Bài 10. Cho tam giác $ABC$ vuông cân tại $A$, có $AB = AC = 4$. Gọi $M$ là trung điểm của $BC$.
a) Tính $\left| {\overrightarrow {BC} } \right|$
b) Tính $\left| {\overrightarrow {AM} } \right|$

Lời giải

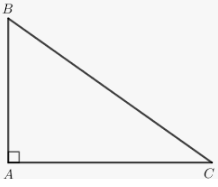
a) Ta có: $\left| {\overrightarrow {BC} } \right| = BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {16 + 16} = 4\sqrt 2 \Rightarrow \left| {\overrightarrow {BC} } \right| = 4\sqrt 2 $

b) $AM$ là trung tuyến tam giác vuông $ABC$ nên ta có: $AM = \frac{{BC}}{2} = \frac{{4\sqrt 2 }}{2} = 2\sqrt 2 \Rightarrow \left| {\overrightarrow {AM} } \right| = 2\sqrt 2 $

Bài 11. Gọi $G$ là trọng tâm tam giác vuông $ABC$ với cạnh huyền $BC = 18$. Tính $\left| {\overrightarrow {GM} } \right|$ (với M là trung điểm của BC)

Lời giải

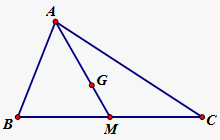
Ta có: $GM = \frac{1}{3} \cdot AM = \frac{1}{3} \cdot \frac{{BC}}{2} = \frac{1}{3} \cdot \frac{{18}}{2} = 3 \Rightarrow \left| {\overrightarrow {GM} } \right| = 3$

Bài 12. Cho hình vuông $ABCD$ có độ dài cạnh 3. Gọi G là trọng tâm tam giác $ABC$.
a) Giá trị của $\left| {\overrightarrow {AC} } \right|$ là bao nhiêu?
b) Tính $\left| {\overrightarrow {AG} } \right|$

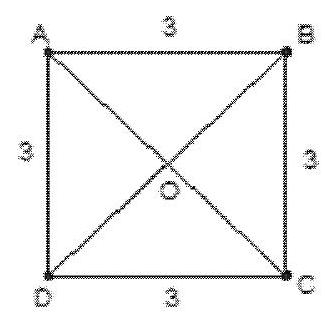
a) vì $AC$ là đường chéo hình vuông nên $AC = 3\sqrt 2 \Rightarrow \left| {\overrightarrow {AC} } \right| = AC = 3\sqrt 2 $

b) Gọi $M$ là trung điểm của $BC:AM = \sqrt {A{B^2} + B{M^2}} = \sqrt {{3^2} + {{\left( {\frac{3}{2}} \right)}^2}} = \frac{{3\sqrt 5 }}{2}$

G là trọng tâm tam giác $ABC$ nên: $AG = \frac{2}{3}AM = \frac{2}{3} \cdot \frac{{3\sqrt 5 }}{2} = \sqrt 5 \Rightarrow \left| {\overrightarrow {AG} } \right| = \sqrt 5 $

DẠNG 2: HAI VECTƠ BẰNG NHAU VÀ CÁC BÀI TOÁN LIÊN QUAN

Để chứng minh hai vectơ bằng nhau ta chứng minh

Cách 1: chúng có cùng độ dài và cùng hướng

Cách 2: tứ giác $ABCD$ là hình bình hành thì $\overrightarrow {AB} = \overrightarrow {CD} $.

Bài 1. Cho vectơ $\overrightarrow {AB} $ và một điểm $C$. Có bao nhiêu điểm $D$ thỏa mãn $\overrightarrow {AB} = \overrightarrow {CD} $.

Lời giải

Nếu $C$ nằm trên đường thẳng $AB$ thì $D$ cũng nằm trên đường thẳng $AB$.

Nếu $C$ không nằm trên đường thẳng $AB$ thì tứ giác $ABDC$ là hình bình hành. Khi đó $D$ nằm trên đường thẳng đi qua $C$ và song song với đường thẳng $AB$.

Do vậy, có vô số điểm $D$ thỏa mãn $\overrightarrow {AB} = \overrightarrow {CD} $.

Bài 2. Cho hai điểm phân biệt $A,B$. Xác định điều kiện để điểm $I$ là trung điểm $AB$.

Lời giải

Vì $I$ là trung điểm $AB$ nên ta có $\overrightarrow {IA} + \overrightarrow {IB} = \vec 0 \Leftrightarrow \overrightarrow {IA} = – \overrightarrow {IB} \Leftrightarrow \overrightarrow {IA} = \overrightarrow {BI} $.

Vậy điều kiện để điểm $I$ là trung điểm $AB$ là: $\overrightarrow {IA} = \overrightarrow {BI} $.

Bài 3. Cho tam giác $ABC$. Gọi $D,E,F$ lần lượt là trung điểm các cạnh $BC,CA,AB$.

Chứng minh $\overrightarrow {EF} = \overrightarrow {CD} $.

Lời giải

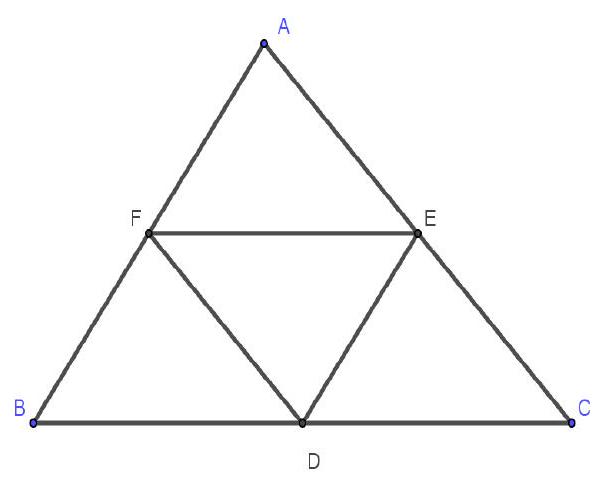
Cách 1: Vì $EF$ là đường trung bình của tam giác $ABC$ nên $EF//CD$ nên

$EF = \frac{1}{2}CB \Rightarrow EF = CD \Rightarrow \left| {EF} \right| = \left| {CD} \right|\left( 1 \right)$.

Mặt khác: $\overrightarrow {EF} $ cùng hướng $\overrightarrow {CD} \left( 2 \right)$.

Từ (1) và (2) ta có: $\overrightarrow {EF} = \overrightarrow {CD} $.

Cách 2: Chứng minh EFCD là hình bình hành

Dễ chứng minh được $EF = \frac{1}{2}BC = CD$ và $EF//CD \Rightarrow EFCD$ là hình bình hành $ \Rightarrow \overrightarrow {EF} = \overrightarrow {CD} $.

Bài 4. Cho $\vartriangle ABC$ có $M,N,P$ lần lượt là trung điểm của các cạnh $AB,BC,CA$. Tìm điểm $I$ sao cho $\overrightarrow {NP} = \overrightarrow {MI} $.

Lời giải

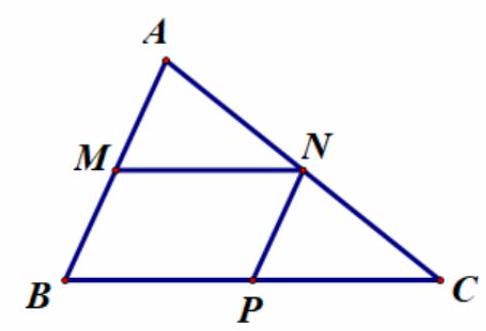
Vì $\overrightarrow {NP} = \overrightarrow {MI} $ mà $\overrightarrow {NP} = \overrightarrow {MB} $ nên $I \equiv B$.

Bài 5. Cho tứ giác $ABCD$. Gọi $M,N,P,Q$ lần lượt là trung điểm $AB,BC,CD,DA$. Chứng minh $\overrightarrow {MN} = \overrightarrow {QP} ;\overrightarrow {NP} = \overrightarrow {MQ} $.

Lời giải

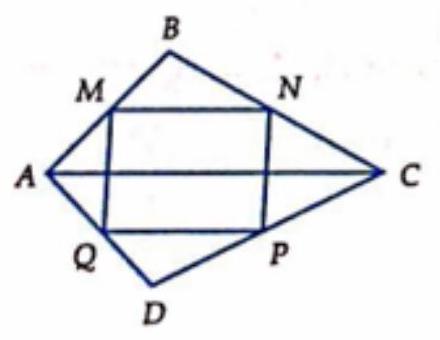
Ta có $MN$ là đường trung bình tam giác $ABC \Rightarrow MN\parallel = \frac{1}{2}AC$ và $PQ$ là đường trung bình tam giác $DAC \Rightarrow PQ\parallel = \frac{1}{2}AC$. Do đó $MN\parallel = PQ \Rightarrow MNPQ$ là hình bình hành nên suy ra $\overrightarrow {MN} = \overrightarrow {QP} ;\overrightarrow {NP} = \overrightarrow {MQ} $.

Bài 6. Cho hình vuông $ABCD$ tâm $O$. Hãy liệt kê tất cả các vectơ bằng nhau nhận đỉnh và tâm của hình vuông làm điểm đầu và điểm cuối.

Lời giải

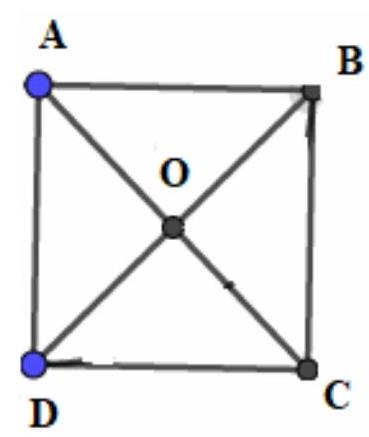
Các vectơ bằng nhau nhận đỉnh và tâm của hình vuông làm điểm đầu và điểm cuối là:

$\overrightarrow {AB} = \overrightarrow {DC} ,\overrightarrow {AD} = \overrightarrow {BC} ,\overrightarrow {BA} = \overrightarrow {CD} ,\overrightarrow {DA} = \overrightarrow {CB} ,\overrightarrow {AO} = \overrightarrow {OC} ,\overrightarrow {OA} = \overrightarrow {CO} ,\overrightarrow {BO} = \overrightarrow {OD} ,\overrightarrow {OB} = \overrightarrow {DO} $

Bài 7. Cho hình bình hành $ABCD$. Gọi $E$ là điểm đối xứng $C$ của qua $D$.

Chứng minh rằng $\overrightarrow {AE} = \overrightarrow {BD} $.

Lời giải

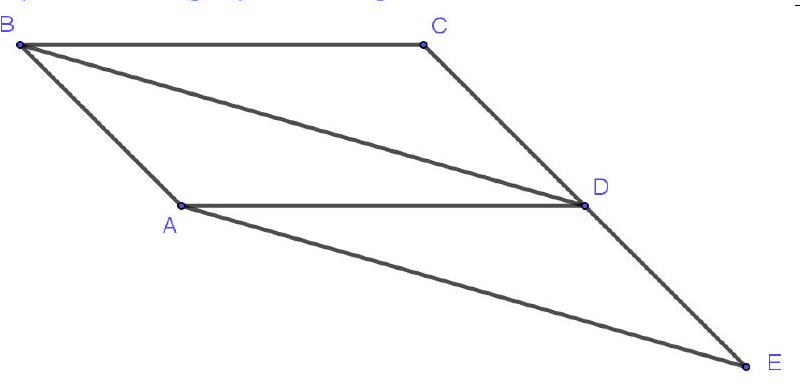
Vì $ABCD$ là hình bình hành nên ta có: $\overrightarrow {BA} = \overrightarrow {CD} $ (1).

Ta có: $E$ là điểm đối xứng $C$ của qua $D$ nên $D$ là trung điểm cuả $CE \Leftrightarrow \overrightarrow {CD} = \overrightarrow {DE} $ (2).

Từ (1) và (2) ta có: $\overrightarrow {BA} = \overrightarrow {DE} \Leftrightarrow ABDE$ là hình bình hành nên $\overrightarrow {AE} = \overrightarrow {BD} $.

Bài 8. Cho hình bình hành $ABCD$. Goi $M,N$ lần lượt là trung điểm của $AB,DC$. $AN$ và $CM$ lần lượt cắt $BD$ tại $E,F$. Chứng minh rằng $\overrightarrow {DE} = \overrightarrow {EF} = \overrightarrow {FB} $

Lời giải

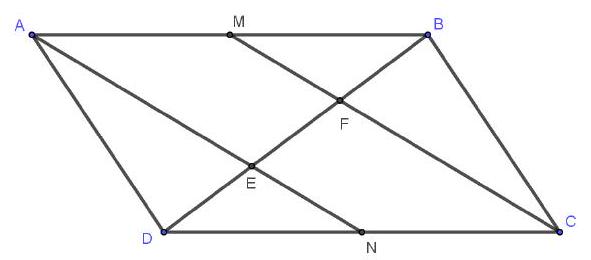
Ta có : $\left\{ {\begin{array}{*{20}{l}}
{AM = CN} \\
{AM//CN}
\end{array} \Leftrightarrow AMCN} \right.$ là hình bình hành.

Theo gt ta có : $N$ là trung điểm $DC$ và $NE//CF \Rightarrow NE$ là đường trung bình của $\vartriangle DFC$

$ \Rightarrow E$ là trung điểm của $DF \Rightarrow \overrightarrow {DE} = \overrightarrow {EF} $

Tương tự ta cũng có : $F$ là trung điểm của $BE$ nên $\overrightarrow {EF} = \overrightarrow {FB} \left( 2 \right)$.

Từ (1) và (2) ta có: $\overrightarrow {DE} = \overrightarrow {EF} = \overrightarrow {FB} $.

Bài 9. Cho hình vuông $ABCD$ tâm $O$ cạnh $a$. Gọi $M$ là trung điểm của $AB,N$ là điểm đối xứng với $C$ qua $D$. Hãy tính độ dài của vectơ $\overrightarrow {MN} $.

Lời giải

Áp dụng định lý Pytago trong tam giác vuông $MAD$ ta có:

$D{M^2} = A{M^2} + A{D^2} = {\left( {\frac{a}{2}} \right)^2} + {a^2} = \frac{{5{a^2}}}{4} \Rightarrow DM = \frac{{a\sqrt 5 }}{2}$

Qua $N$ kẻ đường thẳng song song với $AD$ cắt $AB$ tại $P$. Khi đó tứ giác $ADNP$ là hình vuông và $PM = PA + AM = a + \frac{a}{2} = \frac{{3a}}{2}$

Áp dụng định lý Pytago trong tam giác vuông NPM ta có:

$M{N^2} = N{P^2} + P{M^2} = {a^2} + {\left( {\frac{{3a}}{2}} \right)^2} = \frac{{13{a^2}}}{4} \Rightarrow MN = \frac{{a\sqrt {13} }}{2}$

Suy ra $\left| {\overrightarrow {MN} } \right| = MN = \frac{{a\sqrt {13} }}{2}$

Bài 10. Trên mặt phẳng tọa độ $Oxy$, hãy vẽ các vectơ $\overrightarrow {OA} ,\overrightarrow {MN} $ với $A\left( {1;2} \right),M\left( {0; – 1} \right),N\left( {3;5} \right)$.

a) Chỉ ra mối liên hệ giữa hai vectơ trên.

b) Một vật thể khởi hành từ $M$ và chuyển động thẳng đều với vận tốc (tính theo giờ) được biểu diễn bởi vectơ $\vec v = \overrightarrow {OA} $. Hỏi vật thể đó có đi qua $N$ hay không ? Nếu có thì sau bao lâu vật sẽ tới $N$ ?

Lời giải

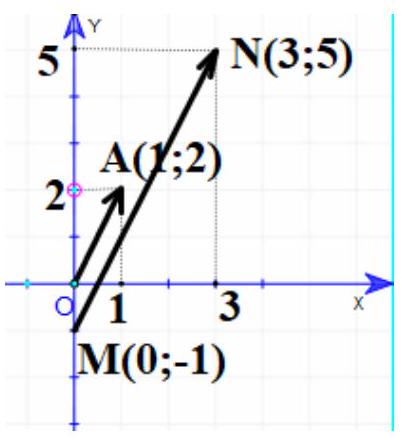
a) Dựa vào hình vẽ , nhận thấy giá của vectơ $\overrightarrow {OA} $ song song với giá của vectơ $\overrightarrow {MN} $ và độ dài đoạn $\left| {\overrightarrow {MN} \left| { = 3} \right|\overrightarrow {OA} } \right|$, chiều đi từ $O$ đến $A$ cùng chiều đi từ $M$ đến $N$.

b) Một vật thể khởi hành từ $M$ và chuyển động thẳng đều với vận tốc (tính theo giờ) được biểu diễn bởi vectơ $\vec v = \overrightarrow {OA} $.

Vật thể gặp $N$ và thời gian gấp 3 lần thời gian đi từ $O$ đến $A$.