Đề Kiểm Tra HK2 Toán 11 Cánh Diều Form Mới Giải Chi Tiết-Đề 5

Đề kiểm tra HK2 Toán 11 Cánh diều form mới giải chi tiết-Đề 5 được soạn dưới dạng file word và PDF gồm 4 trang. Các bạn xem và tải về ở dưới.
Phần 1. Câu trắc nghiệm nhiều phương án chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thi sinh chỉ chọn một phuơng án đúng nhất.

Câu 1. Rút gọn biểu thức $P = {x^{\frac{1}{3}}} \cdot \sqrt[4]{x}$, với $x$ là số thực dương.

A. $P = {x^{\frac{1}{{12}}}}$. B. $P = {x^{\frac{7}{{12}}}}$. C. $P = {x^{\frac{2}{3}}}$. D. $P = {x^{\frac{2}{7}}}$.

Câu 2. Đồ thị (hình bên) là đồ thị của hàm số nào ?

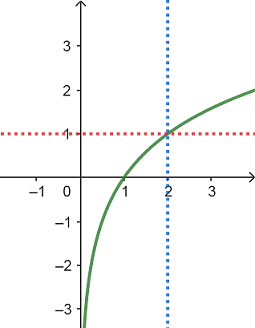
A. $y = {log_{\frac{1}{2}}}x$. B. $y = {log_{\frac{1}{3}}}x$. C. $y = {log_3}x$. D. $y = {log_2}x$.

Câu 3. Trong không gian, cho các mệnh đề sau, mệnh đề nào là mệnh đề đúng?

A. Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song với nhau.

B. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng còn lại.

C. Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì vuông góc với nhau.

D. Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc thì song song với đường thẳng còn lại.

Câu 4. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, cạnh bên $SA$ vuông góc với mặt đáy và $SA = a\sqrt 2 $. Tìm số đo của góc giữa đường thẳng $SC$ và mặt phẳng $\left( {SAB} \right)$.

A. ${45^ \circ }$. B. ${30^ \circ }$. C. ${90^ \circ }$. D. ${60^ \circ }$.

Câu 5. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi, $SA = SC$. Khẳng định nào sau đây đúng?

A. Mặt phẳng $\left( {SBD} \right)$ vuông góc với mặt phẳng $\left( {ABCD} \right)$.

B. Mặt phẳng $\left( {SBC} \right)$ vuông góc với mặt phẳng $\left( {ABCD} \right)$.

C. Mặt phẳng $\left( {SAD} \right)$ vuông góc với mặt phẳng $\left( {ABCD} \right)$.

D. Mặt phẳng $\left( {SAB} \right)$ vuông góc với mặt phẳng $\left( {ABCD} \right)$.

Câu 6. Cho hình lập phương $ABCD \cdot A’B’C’D’$ có độ dài cạnh bằng 10 . Tính khoảng cách giữa hai mặt phẳng $\left( {ADD’A’} \right)$ và $\left( {BCC’B’} \right)$.

A. $\sqrt {10} $. B. 100 . C. 10 . D. 5 .

Câu 7. Cho hình chóp $S.ABC$ có tam giác $ABC$ vuông tại $A,AB = a,AC = 2a,SA$ vuông góc với đáy và $SA = 3a$. Thể tích khối chóp $S.ABC$ bằng

A. $6{a^3}$. B. ${a^3}$. C. $3{a^3}$. D. $2{a^3}$.

Câu 8. Minh và Hùng cùng thực hiện hai thí nghiệm độc lập với nhau, xác suất thành công của Minh là 0,45 , xác suất thành công của Hùng là 0,68 . Đề được tham gia cuộc thi nghiên cứu khoa học toàn quốc, học sinh đó phải thành công tạo ra sản phẩm hoàn chỉnh. Vậy khả năng cả hai bạn được tham gia cuộc thi là bao nhiêu?

A. $P\left( X \right) = 0,306$. B. $P\left( X \right) = 0,176$. C. $P\left( X \right) = 0,144$. D. $P\left( X \right) = 0,374$.

Câu 9. Gieo hai con súc xắc cân đối và đồng chất. Xác suất để tổng số chấm trên mặt xuất hiện của hai con súc xắc bằng 7 là:

A. $P = \frac{7}{{36}}$. B. $P = \frac{7}{{23}}$. C. $P = \frac{1}{6}$. D. $P = \frac{5}{{36}}$.

Câu 10. Cho hàm số $y = {3^{x + 1}}$. Đẳng thức nào sau đây đúng?

A. $y’\left( 1 \right) = \frac{9}{{ln3}}$. B. $y’\left( 1 \right) = 3 \cdot ln3$. C. $y’\left( 1 \right) = 9 \cdot ln3$. D. $y’\left( 1 \right) = \frac{3}{{ln3}}$.

Câu 11. Cho hàm số $f\left( x \right) = \frac{1}{{2x – 1}}$. Tính $f”\left( { – 1} \right)$.

A. $ – \frac{8}{{27}}$ B. $\frac{2}{9}$. C. $\frac{8}{{27}}$ D. $ – \frac{4}{{27}}$.

Câu 12. Phương trình tiếp tuyến của đồ thị hàm số $y = {x^2} – x – 2$ tại điểm có hoành độ $x = 1$ là

A. $2x – y = 0$ B. $2x – y – 4 = 0$. C. $x – y – 1 = 0$. D. $x – y – 3 = 0$.

Phần 2. Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai

Câu 1. Một trường học có tỉ lệ học sinh nam và nữ là $5:3$. Trong đó, tỉ lệ số học sinh nam thuận tay trái là $11\% $, tỉ lệ số học sinh nữ thuận tay trái là $9\% $. Khi đó:

a) Xác suất để chọn được 1 học sinh nam ở trường không thuận tay trái là: $\frac{{273}}{{800}}$.

b) Xác suất để chọn được 1 học sinh nữ ở trường không thuận tay trái là: $\frac{{89}}{{160}}$.

c) Xác suất để chọn được 1 học sinh nam, 1 học sinh nữ ở trường thuận tay trái lần lượt là:

$\frac{{11}}{{160}}$ và $\frac{{27}}{{800}}$.

d) Xác suất để chọn ngẫu nhiên 5 học sinh ở trường trong đó có đúng 1 học sinh nam và 1 học sinh nữ thuận tay trái là: $\frac{{297}}{{128000}}$

Câu 2. Cho hình chóp $S \cdot ABCD$ có đáy $ABCD$ là hình thoi tâm $O$, cạnh $a,\widehat {ABC} = {60^ \circ }$, $SO \bot \left( {ABCD} \right)$ và $SO = \frac{{3a}}{4}$, đặt $x = d\left( {O,\left( {SAB} \right)} \right),\;y = d\left( {D,\left( {SAB} \right)} \right),\;z = d\left( {CD,SA} \right)$. Các mệnh đề sau đúng hay sai?

a) $x = \frac{{3a}}{4}$.

b) $y = 2x$.

c) $y = z + x$.

d) $x + y + z = \frac{{15a}}{8}$.

Câu 3. Cho hàm số $f\left( x \right) = {3^{2x}} – {2.3^x}$ có đồ thị như hình vẽ sau

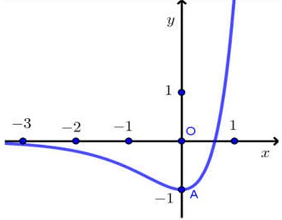
Các mệnh đề sau đúng hay sai?

a) Đường thẳng $y = 0$ cắt đồ thị hàm số $\left( C \right)$ tại điểm có hoành độ là $x = {log_3}2$.

b) Bất phương trình $f\left( x \right) \geqslant – 1$ có nghiệm duy nhất.

c) Bất phương trình $f\left( x \right) \geqslant 0$ có tập nghiệm là: $\left( { – \infty ;{log_3}2} \right)$.

d) Đường thẳng $y = 0$ cắt đồ thị hàm số $\left( C \right)$ tại 2 điểm phân biệt.

Câu 4. Cho hàm số $f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}
{\frac{{{x^2} – 1}}{{x – 1}}}&{\;khi\;x \ne 1} \\
a&{\;khi\;x = 1}
\end{array}} \right.$

a) Ta có $\mathop {\lim }\limits_{x \to 1} \frac{{{x^2} – 1}}{{x – 1}} = 2$

b) Với $a = – 2$ thì hàm số có đạo hàm tại $x = 1$

c) Với $a = 2$ thì hàm số có đạo hàm tại $x = 1$

d) Với $a = {m_0}$ thì hàm số có đạo hàm tại $x = 1$, khi đó :$\mathop {\lim }\limits_{x \to {m_0}} ({x^2} + 2x – 3) = 5$

Phần 3. Câu trả lời ngắn.
Thi sinh trả lời đáp án từ câu 1 đến câu 6.

Câu 1. Bình và Minh cùng thi bắn đĩa bay. Xác suất bắn trúng đĩa của mỗi người lần lượt là 0,7 và 0,8 . Nếu một người bắn trước và trượt thì tỉ lệ bắn trúng của người sau sẽ tăng thêm 0,1 và ngược lại nếu người đó bắn trúng thì tỉ lệ bắn trúng của người sau sẽ giảm đi 0,1 . Thứ tự bắn giữa hai người là ngẫu nhiên và cuộc thi dừng lại khi người này trúng, người kia trượt. Tính xác suất để không có ai thắng sau 1 lượt bắn.

Câu 2. Cho hình hộp chữ nhật $ABCD \cdot A’B’C’D’$ có $AB = a,AD = 2a,AA’ = 3a$. Tính góc phẳng nhị diện $\left[ {A’,BD,A} \right]$ ?

Câu 3. Cho hình chóp $S \cdot ABC$ có đáy là tam giác đều cạnh $a,SA \bot \left( {ABC} \right)$ và $SB = 2a$. Gọi $G$ là trọng tâm tam giác $ABC$. Tính khoảng cách từ $G$ đến mặt phẳng $\left( {SBC} \right)$.

Câu 4. Các khí thải ra gây hiệu ứng nhà kính là nguyên nhân chủ yếu làm trái đất nóng lên. Theo OECD (Tổ chức Hợp tác và Phát triển kinh tế thế giới), khi nhiệt độ trái đất tăng thì tổng giá trị kinh tế toàn cầu giảm. Người ta ước tính được rằng, khi nhiệt độ trái đất tăng ${2^ \circ }C$ thì tổng giá trị kinh tế toàn cầu giảm $3\% $; còn nhiệt độ trái đất tăng thêm ${5^ \circ }C$ thì tổng kinh tế toàn cầu giảm $10\% $. Biết rằng, nếu nhiệt độ trái đất tăng thêm ${t^ \circ }C$, tổng giá trị kinh tế toàn cầu giảm $f\left( t \right)\% $ thì $f\left( t \right) = k{a^t}$, trong đó $k,a$ là hằng số dương. Khi nhiệt độ trái đất tăng thêm bao nhiêu ${\;^ \circ }C$ thì tổng giá trị kinh tế toàn cầu giảm đến $20\% $ ?

Câu 5. Cho một vật chuyển động theo phương trình $s\left( t \right) = – {t^2} + 40t + 10$ trong đó $s$ là quãng đường vật đi được (đơn vị $m$ ), $t$ là thời gian chuyển động (đơn vị $s$ ). Tại thời điểm vật dừng lại thì vật đi được quãng đường bằng bao nhiêu?

Câu 6. Cho hàm số $f\left( x \right) = ln\left( {\frac{{x + 1}}{x}} \right)$. Tính tổng $S = f’\left( 1 \right) + f’\left( 2 \right) + \ldots f’\left( {2024} \right)$.

ĐÁP ÁN VÀ LỜI GIẢI THAM KHẢO

Phần 1. Câu trắc nghiệm nhiều phương án chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án đúng nhất.

1B	2D	3B	4B	5D	6C
7B	8A	9C	10C	11A	12D

Câu 1. Rút gọn biểu thức $P = {x^{\frac{1}{3}}} \cdot \sqrt[4]{x}$, với $x$ là số thực dương.

A. $P = {x^{\frac{1}{{12}}}}$.

B. $P = {x^{\frac{7}{{12}}}}$.

C. $P = {x^{\frac{2}{3}}}$.

D. $P = {x^{\frac{2}{7}}}$.

Lời giải

$P = {x^{\frac{1}{3}}} \cdot \sqrt[4]{x} = {x^{\frac{1}{3}}} \cdot {x^{\frac{1}{4}}} = {x^{\frac{7}{{12}}}}$

Câu 2. Đồ thị (hình bên) là đồ thị của hàm số nào ?

A. $y = {log_{\frac{1}{2}}}x$.

B. $y = {log_{\frac{1}{3}}}x$.

C. $y = {log_3}x$.

D. $y = {log_2}x$.

Lời giải

Dựa vào đồ thị hàm số ta thấy đồ thị hàm số đồng biến trên $\left( {0; + \infty } \right)$ nên $a > 1$ do đó ta loại đáp án A và B.

Lại có $A\left( {2;1} \right)$ thuộc đồ thị hàm số nên loại phương án C.

Câu 3. Trong không gian, cho các mệnh đề sau, mệnh đề nào là mệnh đề đúng?

A. Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song với nhau.

B. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng còn lại.

C. Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì vuông góc với nhau.

D. Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc thì song song với đường thẳng còn lại.

Lời giải

Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng còn lại.

Câu 4. Cho hình chóp $S \cdot ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, cạnh bên $SA$ vuông góc với mặt đáy và $SA = a\sqrt 2 $. Tìm số đo của góc giữa đường thẳng $SC$ và mặt phẳng $\left( {SAB} \right)$.

A. ${45^ \circ }$.

B. ${30^ \circ }$.

C. ${90^ \circ }$.

D. ${60^ \circ }$.

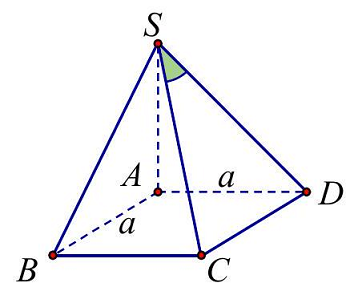
Lời giải

Dễ thấy $CB \bot \left( {SAB} \right) \Rightarrow SB$ là hình chiếu vuông góc của $SC$ lên $\left( {SAB} \right)$.

Vậy góc giữa đường thẳng $SC$ và mặt phẳng $\left( {SAB} \right)$ là $\widehat {CSB}$.

Tam giác $CSB$ có $\hat B = {90^ \circ };CB = a;SB = a\sqrt 3 $$ \Rightarrow tan\widehat {CSB} = \frac{{CB}}{{SB}} = \frac{a}{{a\sqrt 3 }} = \frac{1}{{\sqrt 3 }}$.

Vậy $\widehat {CSB} = {30^ \circ }$.

Câu 5. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi, $SA = SC$. Khẳng định nào sau đây đúng?

A. Mặt phẳng $\left( {SBD} \right)$ vuông góc với mặt phẳng $\left( {ABCD} \right)$.

B. Mặt phẳng $\left( {SBC} \right)$ vuông góc với mặt phẳng $\left( {ABCD} \right)$.

C. Mặt phẳng $\left( {SAD} \right)$ vuông góc với mặt phẳng $\left( {ABCD} \right)$.

D. Mặt phẳng $\left( {SAB} \right)$ vuông góc với mặt phẳng $\left( {ABCD} \right)$.

Lời giải

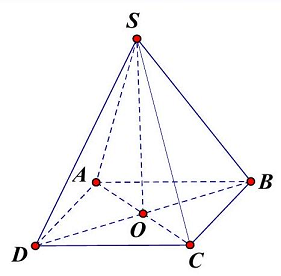
Gọi $O = AC \cap BD$.

Tứ giác $ABCD$ là hình thoi nên $AC \bot BD$ (1).

Mặt khác tam giác $SAC$ cân tại $S$ nên $SO \bot AC$ (2).

Từ (1) và (2) suy ra $AC \bot \left( {SBD} \right)$ nên $\left( {SBD} \right) \bot \left( {ABCD} \right)$.

Câu 6. Cho hình lập phương $ABCD \cdot A’B’C’D’$ có độ dài cạnh bằng 10 . Tính khoảng cách giữa hai mặt phẳng $\left( {ADD’A’} \right)$ và $\left( {BCC’B’} \right)$.

A. $\sqrt {10} $.

B. 100 .

C. 10 .

D. 5 .

Lời giải

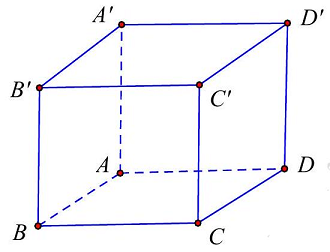
Ta có $\left( {ADD’A’} \right)//\left( {BCC’B’} \right)$$ \Rightarrow d\left( {\left( {ADD’A’} \right);\left( {BCC’B’} \right)} \right) = d\left( {A;\left( {\left( {BCC’B’} \right)} \right)} \right) = AB = 10$.

Câu 7. Cho hình chóp $S.ABC$ có tam giác $ABC$ vuông tại $A,AB = a,AC = 2a,SA$ vuông góc với đáy và $SA = 3a$. Thể tích khối chóp $S.ABC$ bằng

A. $6{a^3}$.

B. ${a^3}$.

C. $3{a^3}$.

D. $2{a^3}$.

Lời giải

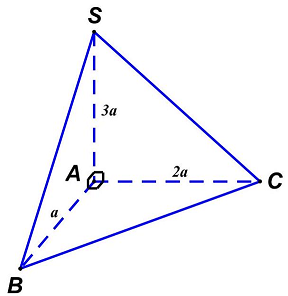
Ta có: ${V_{S.ABC}} = \frac{1}{3}{S_{ABC}} \cdot SA = \frac{1}{3} \cdot \frac{1}{2} \cdot AB \cdot AC \cdot SA = \frac{1}{6}a \cdot 2a \cdot 3a = {a^3}$.

Câu 8. Minh và Hùng cùng thực hiện hai thí nghiệm độc lập với nhau, xác suất thành công của Minh là 0,45 , xác suất thành công của Hùng là 0,68 . Đề được tham gia cuộc thi nghiên cứu khoa học toàn quốc, học sinh đó phải thành công tạo ra sản phẩm hoàn chỉnh. Vậy khả năng cả hai bạn được tham gia cuộc thi là bao nhiêu?

A. $P\left( X \right) = 0,306$.

B. $P\left( X \right) = 0,176$.

C. $P\left( X \right) = 0,144$.

D. $P\left( X \right) = 0,374$.

Lời giải

Gọi $A$ là biến cố “Minh được tham gia”; $B$ là biến cố “Hùng được tham gia cuộc thi”; $X$ là biển cố “Cả hai bạn được tham gia cuộc thi”.

Vì $A$ và $B$ là hai biến cố độc lập và $P\left( X \right) = P\left( A \right) \cdot P\left( B \right) = 0,45 \cdot 0,68 = 0,306$.

Chọn A

Câu 9. Gieo hai con súc xắc cân đối và đồng chất. Xác suất để tổng số chấm trên mặt xuất hiện của hai con súc xắc bằng 7 là:

A. $P = \frac{7}{{36}}$.

B. $P = \frac{7}{{23}}$.

C. $P = \frac{1}{6}$.

D. $P = \frac{5}{{36}}$.

Số phần tử của không gian mẫu là: $\left| \Omega \right| = 6.6 = 36$.

Lời giải

Gọi biến cố $A$ : “Tổng số chấm trên mặt xuất hiện của hai con xúc xắc bằng 7 “.

Các kết quả thuận lợi cho A là: $A = \left\{ {\left( {1;6} \right);\left( {2;5} \right);\left( {3;4} \right);\left( {4;3} \right);\left( {5;2} \right);\left( {6;1} \right)} \right\}$.

Do đó, ${n_A} = 6$. Vậy $P\left( A \right) = \frac{6}{{36}} = \frac{1}{6}$.

Chọn C

Câu 10. Cho hàm số $y = {3^{x + 1}}$. Đẳng thức nào sau đây đúng?

A. $y’\left( 1 \right) = \frac{9}{{ln3}}$.

B. $y’\left( 1 \right) = 3 \cdot ln3$.

C. $y’\left( 1 \right) = 9 \cdot ln3$.

D. $y’\left( 1 \right) = \frac{3}{{ln3}}$.

Ta có $y’ = {3^{x + 1}} \cdot ln3 \Rightarrow y’\left( 1 \right) = 9ln3$.

Lời giải

Câu 11. Cho hàm số $f\left( x \right) = \frac{1}{{2x – 1}}$. Tính $f”\left( { – 1} \right)$.

A. $ – \frac{8}{{27}}$

B. $\frac{2}{9}$.

C. $\frac{8}{{27}}$

D. $ – \frac{4}{{27}}$.

Lời giải

Tập xác định $D = \mathbb{R} \setminus \left\{ {\frac{1}{2}} \right\}$.

$f’\left( x \right) = \frac{{ – 2}}{{{{(2x – 1)}^2}}},f”\left( x \right) = \frac{8}{{{{(2x – 1)}^3}}}$.

Khi đó $f”\left( { – 1} \right) = – \frac{8}{{27}}$.

Câu 12. Phương trình tiếp tuyến của đồ thị hàm số $y = {x^2} – x – 2$ tại điểm có hoành độ $x = 1$ là

A. $2x – y = 0$

B. $2x – y – 4 = 0$.

C. $x – y – 1 = 0$.

D. $x – y – 3 = 0$.

Lời giải

Gọi $M$ là tiếp điểm của tiếp tuyến và đồ thị hàm số. Theo giả thiết: $M\left( {1; – 2} \right)$

Gọi $k$ là hệ số góc của tiếp tuyến với đồ thị hàm số tại $M$.

Ta có $y’ = 2x – 1,k = y’\left( 1 \right) = 1$

Phương trình tiếp tuyến cần tìm là $y = 1\left( {x – 1} \right) – 2 \Leftrightarrow x – y – 3 = 0$

Phần 2. Câu trắc nghiệm đúng sai.

Thí sinh trả lời từ câu 1 đến câu 4. Trong mối ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoăc sai

Câu 1. Một trường học có tỉ lệ học sinh nam và nữ là $5:3$. Trong đó, tỉ lệ số học sinh nam thuận tay trái là $11\% $, tỉ lệ số học sinh nữ thuận tay trái là $9\% $. Khi đó:

a) Xác suất để chọn được 1 học sinh nam ở trường không thuận tay trái là: $\frac{{273}}{{800}}$.

b) Xác suất để chọn được 1 học sinh nữ ở trường không thuận tay trái là: $\frac{{89}}{{160}}$.

c) Xác suất để chọn được 1 học sinh nam, 1 học sinh nữ ở trường thuận tay trái lần lượt là:

$\frac{{11}}{{160}}$ và $\frac{{27}}{{800}}$.

d) Xác suất để chọn ngẫu nhiên 5 học sinh ở trường trong đó có đúng 1 học sinh nam và 1 học sinh nữ thuận tay trái là: $\frac{{297}}{{128000}}$

Lời giải

a) Sai

b) Sai

c) Đúng

d) Sai

a) Xác suất để chọn được 1 học sinh nam ở trường không thuận tay trái là:

$\frac{5}{8}.0,89 = \frac{{89}}{{160}}$.

b) Xác suất để chọn được 1 học sinh nữ ở trường không thuận tay trái là:

$\frac{3}{8}.0,91 = \frac{{273}}{{800}}$.

-Xác suất để chọn được 1 học sinh ở trường không thuận tay trái là:

$\frac{{89}}{{160}} + \frac{{273}}{{800}} = \frac{{359}}{{400}}$.

c) Xác suất để chọn được 1 học sinh nam, 1 học sinh nữ ở trường không thuận tay trái lần lượt là:

$\frac{5}{8} \cdot 0,11 = \frac{{11}}{{160}}$ và $\frac{3}{8} \cdot 0,09 = \frac{{27}}{{800}}$.

d) Xác suất để chọn ngẫu nhiên 5 học sinh ở trường trong đó có đúng 1 học sinh nam và 1 học sinh nữ thuận tay trái là:

$\frac{{11}}{{160}} \cdot \frac{{27}}{{800}} \cdot {\left( {\frac{{359}}{{400}}} \right)^3} \approx 1,68 \cdot {10^{ – 3}}$.

Câu 2. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi tâm $O$, cạnh $a,\widehat {ABC} = {60^ \circ }$, $SO \bot \left( {ABCD} \right)$ và $SO = \frac{{3a}}{4}$, đặt $x = d\left( {O,\left( {SAB} \right)} \right),\;y = d\left( {D,\left( {SAB} \right)} \right),\;z = d\left( {CD,SA} \right)$. Các mệnh đề sau đúng hay sai?

a) $x = \frac{{3a}}{4}$.

b) $y = 2x$.

c) $y = z + x$.

d) $x + y + z = \frac{{15a}}{8}$.

Lời giải

a) Sai

b) Đúng

c) Sai

d) Đúng

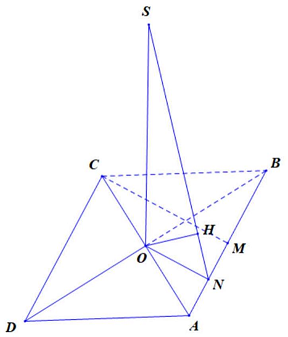
Tam giác $ABC$ đều cạnh $a$ nên đường cao $CM = \frac{{a\sqrt 3 }}{2}$. Gọi $N$ là trung điểm của $AM$ $ \Rightarrow ON \bot AB;ON = \frac{{a\sqrt 3 }}{4}$.

Kẻ $OH \bot SN \Rightarrow d\left( {O,\left( {SAB} \right)} \right) = OH$.

$\frac{1}{{O{H^2}}} = \frac{1}{{S{O^2}}} + \frac{1}{{O{N^2}}};ON = \frac{1}{2}CM = \frac{{a\sqrt 3 }}{4};SO = \frac{{3a}}{4} \Rightarrow OH = \frac{{3a}}{8}$.

$x = d\left( {O,\left( {SAB} \right)} \right) = \frac{{3a}}{8}$,

$y = d\left( {D,\left( {SAB} \right)} \right) = 2 \cdot d\left( {O,\left( {SAB} \right)} \right) = 2x$,

$z = d\left( {CD,SA} \right) = d\left( {D,\left( {SAB} \right)} \right) = 2x$.

Vậy $x + y + z = 5x = \frac{{15a}}{8}$.

Câu 3. Cho hàm số $f\left( x \right) = {3^{2x}} – {2.3^x}$ có đồ thị như hình vẽ sau

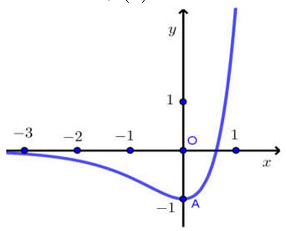
Các mệnh đề sau đúng hay sai?

a) Đường thẳng $y = 0$ cắt đồ thị hàm số $\left( C \right)$ tại điểm có hoành độ là $x = {log_3}2$.

b) Bất phương trình $f\left( x \right) \geqslant – 1$ có nghiệm duy nhất.

c) Bất phương trình $f\left( x \right) \geqslant 0$ có tập nghiệm là: $\left( { – \infty ;{log_3}2} \right)$.

d) Đường thẳng $y = 0$ cắt đồ thị hàm số $\left( C \right)$ tại 2 điểm phân biệt.

Lời giải

a) Đúng

b) Sai

c) Sai

d) Sai

a: ${3^{2x}} – 2 \cdot {3^x} = 0 \Leftrightarrow {3^x} – 2 = 0 \Leftrightarrow x = {log_3}2$ nên a đúng.

$b$ Bất phương trình $f\left( x \right) \geqslant – 1$ có nghiệm duy nhất: b sai.

$c$ Bất phương trình $f\left( x \right) \geqslant 0$ có tập nghiệm là: $\left( {{log_3}2; + \infty } \right)$ nên c sai.

$d$ Đường thẳng $y = 0$ cắt đồ thị hàm số $\left( C \right)$ tại 2 điểm phân biệt: $d$ sai.

Câu 4. Cho hàm số $f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}
{\frac{{{x^2} – 1}}{{x – 1}}}&{\;khi\;x \ne 1} \\
a&{\;khi\;x = 1}
\end{array}} \right.$

a) Ta có $\mathop {\lim }\limits_{x \to 1} \frac{{{x^2} – 1}}{{x – 1}} = 2$

b) Với $a = – 2$ thì hàm số có đạo hàm tại $x = 1$

c) Với $a = 2$ thì hàm số có đạo hàm tại $x = 1$

d) Với $a = {m_0}$ thì hàm số có đạo hàm tại $x = 1$, khi đó :$\mathop {\lim }\limits_{x \to {m_0}} ({x^2} + 2x – 3) = 5$

Lời giải

a) Đúng

b) Sai

c) Đúng

d) Đúng

a) $\mathop {\lim }\limits_{x \to 1} \frac{{{x^2} – 1}}{{x – 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{(x – 1)(x + 1)}}{{x – 1}} = \mathop {\lim }\limits_{x \to 1} (x + 1) = 2$

b) Để hàm số có đạo hàm tại $x = 1$ thì trước hết $f\left( x \right)$ phải liên tục tại $x = 1$

Hay $\mathop {\lim }\limits_{x \to 1} \frac{{{x^2} – 1}}{{x – 1}} = 2 = f(1) = a$

Khi đó, ta có: $\mathop {\lim }\limits_{x \to 1} \frac{{f(x) – f(1)}}{{x – 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{\frac{{{x^2} – 1}}{{x – 1}} – 2}}{{x – 1}}$ $ = \mathop {\lim }\limits_{x \to 1} \frac{{\frac{{{x^2} – 2x + 1}}{{x – 1}}}}{{x – 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{{x^2} – 2x + 1}}{{{{\left( {x – 1} \right)}^2}}} = \mathop {\lim }\limits_{x \to 1} 1 = 1$.

Vậy $a = 2$ là giá trị cần tìm.

Do vậy b) sai và c) đúng.

d) $\mathop {\lim }\limits_{x \to {m_0}} ({x^2} + 2x – 3) = \mathop {\lim }\limits_{x \to 2} ({x^2} + 2x – 3) = {2^2} + 2.2 – 3 = 5$

Do vậy d) đúng.

Phần 3. Câu trả lời ngắn.
Thí sinh trả lời đáp án từ câu 1 đến câu 6.

Câu 1. Bình và Minh cùng thi bắn đĩa bay. Xác suất bắn trúng đĩa của mỗi người lần lượt là 0,7 và 0,8 . Nếu một người bắn trước và trượt thì tỉ lệ bắn trúng của người sau sẽ tăng thêm 0,1 và ngược lại nếu người đó bắn trúng thì tỉ lệ bắn trúng của người sau sẽ giảm đi 0,1 . Thứ tự bắn giữa hai người là ngẫu nhiên và cuộc thi dừng lại khi người này trúng, người kia trượt. Tính xác suất để không có ai thắng sau 1 lượt bắn.

Trả lời: 0,52 .

Lời giải

Xác suất để hai người cùng trúng sau 1 lượt bắn là: $\frac{1}{2} \cdot 0,7 \cdot 0,7 + \frac{1}{2} \cdot 0,8 \cdot 0,6 = 0,485$.

Xác suất để hai người cùng trượt sau 1 lượt bắn là: $\frac{1}{2} \cdot 0,3 \cdot 0,1 + \frac{1}{2} \cdot 0,2 \cdot 0,2 = 0,035$.

Xác suất để không có ai thắng sau 1 lượt bắn là: 0,52 .

Câu 2. Cho hình hộp chữ nhật $ABCD \cdot A’B’C’D’$ có $AB = a,AD = 2a,AA’ = 3a$. Tính góc phẳng nhị diện $\left[ {A’,BD,A} \right]$ ?

Trả lời: $ \approx 73,{4^ \circ }$

Lời giải

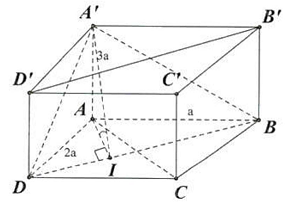
Kẻ $AI \bot BD$. Mà $BD \bot A’A \Rightarrow BD \bot \left( {AA’I} \right)$

Ta có: $\left\{ {\begin{array}{*{20}{l}}
{\left( {A’BD} \right) \cap \left( {ABD} \right) = BD} \\
{Trong\left( {ABD} \right),AI \bot BD} \\
{Trong\left( {A’BD} \right),A’I \bot BD}
\end{array}} \right.$

$ \Rightarrow \left[ {A’,BD,A} \right] = \widehat {A’IA}$

Ta có: $AI = \frac{1}{{\sqrt {\frac{1}{{A{B^2}}} + \frac{1}{{A{D^2}}}} }} = \frac{1}{{\sqrt {\frac{1}{{{a^2}}} + \frac{1}{{{{(2a)}^2}}}} }} = \frac{{2\sqrt 5 }}{5}a$

Xét $\vartriangle AA’I$ vuông tại $A:tan\widehat {A’IA} = \frac{{A’A}}{{AI}} = \frac{{a\sqrt 3 }}{{\frac{{2\sqrt 5 }}{5}a}} = \frac{{3\sqrt 5 }}{2} \Rightarrow \widehat {A’IA} \approx 73,{4^ \circ }$

Câu 3. Cho hình chóp $S \cdot ABC$ có đáy là tam giác đều cạnh $a,SA \bot \left( {ABC} \right)$ và $SB = 2a$. Gọi $G$ là trọng tâm tam giác $ABC$. Tính khoảng cách từ $G$ dến mặt phẳng $\left( {SBC} \right)$.

Trả lời: $\frac{{\sqrt {15} }}{{15}}a$

Lời giải

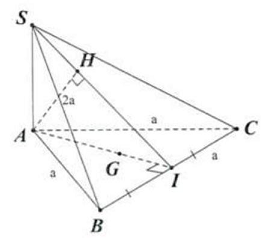
Kẻ $AI \bot BC$, kẻ $AH \bot SI$ tại $H$

Ta có: $\left\{ {\begin{array}{*{20}{l}}
{BC \bot SA} \\
{BC \bot AI}
\end{array} \Rightarrow BC \bot \left( {SAI} \right) \Rightarrow BC \bot AH} \right.$.

Ta lại có: $AH \bot SI \Rightarrow AH \bot \left( {SBC} \right) \Rightarrow d\left( {A,\left( {SBC} \right)} \right) = AH$

Ta có: $SA = \sqrt {S{B^2} – B{A^2}} = \sqrt {{{(2a)}^2} – {a^2}} = \sqrt 3 a$

Ta có: $AH = \frac{1}{{\sqrt {\frac{1}{{S{A^2}}} + \frac{1}{{A{I^2}}}} }} = \frac{1}{{\sqrt {\frac{1}{{{{(\sqrt 3 a)}^2}}} + \frac{1}{{{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2}}}} }} = \frac{{\sqrt {15} }}{5}a$

Vậy $d\left( {A,\left( {SBC} \right)} \right) = \frac{{\sqrt {15} }}{5}a$.

Ta có: $GA$ cắt $\left( {SBC} \right)$ tại $I$

$ \Rightarrow \frac{{d\left( {G,\left( {SBC} \right)} \right)}}{{d\left( {A,\left( {SBC} \right)} \right)}} = \frac{{GI}}{{AI}} = \frac{1}{3}$$ \Rightarrow d\left( {G,\left( {SBC} \right)} \right) = \frac{1}{3}d\left( {A,\left( {SBC} \right)} \right) = \frac{{\sqrt {15} }}{{15}}a$.

Câu 4. Các khí thải ra gây hiệu ứng nhà kính là nguyên nhân chủ yếu làm trái đất nóng lên. Theo OECD (Tổ chức Hợp tác và Phát triển kinh tế thế giới), khi nhiệt độ trái đất tăng thì tổng giá trị kinh tế toàn cầu giảm. Người ta ước tính được rằng, khi nhiệt độ trái đất tăng ${2^ \circ }C$ thì tổng giá trị kinh tế toàn cầu giảm $3\% $; còn nhiệt độ trái đất tăng thêm ${5^ \circ }C$ thì tổng kinh tế toàn cầu giảm $10\% $. Biết rằng, nếu nhiệt độ trái đất tăng thêm ${t^ \circ }C$, tổng giá trị kinh tế toàn cầu giảm $f\left( t \right)\% $ thì $f\left( t \right) = k{a^t}$, trong đó $k,a$ là hằng số dương. Khi nhiệt độ trái đất tăng thêm bao nhiêu ${\;^ \circ }C$ thì tổng giá trị kinh tế toàn cầu giảm đến $20\% $ ?

Trả lời: 6,7

Lời giải

Theo bài ra ta có $\left\{ {\begin{array}{*{20}{l}}
{k \cdot {a^2} = 3} \\
{k \cdot {a^5} = 10}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{a = \sqrt[3]{{\frac{{10}}{3}}}} \\
{k = 3 \cdot \sqrt[3]{{\frac{9}{{100}}}}}
\end{array}} \right.} \right.$.

Do đó $f\left( t \right) = 3 \cdot \sqrt[3]{{\frac{9}{{100}}}} \cdot {\left( {\sqrt[3]{{\frac{{10}}{3}}}} \right)^t}$.

Khi kinh tế toàn cầu giảm đến $20\% $ thì nhiệt độ trái đất tăng lên số nhiệt độ $t$ thỏa mãn

$20 = 3 \cdot \sqrt[3]{{\frac{9}{{100}}}} \cdot {\left( {\sqrt[3]{{\frac{{10}}{3}}}} \right)^t}$$ \Leftrightarrow t = {log_{\sqrt[3]{{\frac{{10}}{3}}}}}\left( {\frac{{20}}{{3 \cdot \sqrt[3]{{\frac{9}{{100}}}}}}} \right) \approx 6,7$.

Câu 5. Cho một vật chuyển động theo phương trình $s\left( t \right) = – {t^2} + 40t + 10$ trong đó $s$ là quãng đường vật đi được (đơn vị $m$ ), $t$ là thời gian chuyển động (đơn vị $s$ ). Tại thời điểm vật dừng lại thì vật đi được quãng đường bằng bao nhiêu?

Trả lời: $410\left( m \right)$

Lời giải

Ta có phương trình vận tốc của vật: $v\left( t \right) = s’\left( t \right) = – 2t + 40$.

Thời gian vật chuyển động cho đến khi dừng lại: $v\left( t \right) = 0 \Leftrightarrow – 2t + 40 = 0 \Leftrightarrow t = 20\left( s \right)$.

Quãng đường vật đi được là: $s = s\left( {20} \right) = 410\left( m \right)$.

Câu 6. Cho hàm số $f\left( x \right) = ln\left( {\frac{{x + 1}}{x}} \right)$. Tính tổng $S = f’\left( 1 \right) + f’\left( 2 \right) + \ldots f’\left( {2024} \right)$.

Trả lời: $ – \frac{{2024}}{{2025}}$

Lời giải

Ta có: $f’\left( x \right) = \frac{{{{\left( {\frac{{x + 1}}{x}} \right)}’}}}{{\frac{{x + 1}}{x}}} = \frac{{\frac{{ – 1}}{{{x^2}}}}}{{\frac{{x + 1}}{x}}} = – \frac{1}{{x\left( {x + 1} \right)}} = \frac{1}{{x + 1}} – \frac{1}{x}$.

Khi đó $S = \frac{1}{2} – 1 + \frac{1}{3} – \frac{1}{2} + \ldots + \frac{1}{{2024}} – \frac{1}{{2023}} + \frac{1}{{2025}} – \frac{1}{{2024}} = \frac{1}{{2025}} – 1 = – \frac{{2024}}{{2025}}$.