Đề Thi Học Kỳ 2 Toán 11 Chân Trời Sáng Tạo Giải Chi Tiết-Đề 1

Đề thi học kỳ 2 Toán 11 Chân trời sáng tạo giải chi tiết-Đề 1 được soạn dưới dạng file word và PDF gồm 5 trang. Các bạn xem và tải về ở dưới.
I. TRẮC NGHIỆM (7 điểm)

Câu 1. Cho $a$ là số thực dương tùy ý, $\frac{{{a^{\frac{2}{3}}}.{a^{\frac{3}{4}}}}}{{\sqrt[6]{a}}}$ bằng

A. ${a^{\frac{1}{3}}}$. B. ${a^{\frac{5}{4}}}$. C. ${a^{\frac{3}{4}}}$. D. ${a^{\frac{4}{5}}}$.

Câu 2. Cho hai số dương $a,b\left( {a \ne 1} \right)$. Mệnh đề nào dưới đây SAI?

A. $lo{g_a}{a^\alpha } = \alpha $. B. $lo{g_a}1 = 0$. C. $lo{g_a}a = 2a$. D. $lo{g_{{a^\alpha }}}b = \frac{1}{\alpha }lo{g_a}b$.

Câu 3. Với $a$ là số thực dương tùy, $lo{g_5}{a^2}$ bằng

A. $2lo{g_5}a$. B. $2 + lo{g_5}a$. C. $\frac{1}{2} + lo{g_5}a$. D. $\frac{1}{2}lo{g_5}a$.

Câu 4. Nếu $lo{g_a}x = \frac{1}{2}lo{g_a}9 – lo{g_a}5 + lo{g_a}2(a > 0,a \ne 1)$ thì $x$ bằng:

A. $\frac{2}{5}$. B. $\frac{3}{5}$ C. $\frac{6}{5}$. D. 3 .

Câu 5. Hàm số nào dưới đây đồng biến trên tập xác định của nó?

A. $y = lo{g_{\frac{2}{3}}}x$. B. $y = lo{g_{0,9}}x$. C. $y = lo{g_{\sqrt {0,9} }}x$. D. $y = lo{g_{\sqrt 2 }}x$.

Câu 6. Sự tăng trưởng của một loại vi khuẩn tuân theo công thức $S = A \cdot {e^{rt}}$, trong đó $A$ là số lượng vi khuẩn ban đầu, $r$ là tỉ lệ tăng trưởng $(r > 0),t$ là thời gian tăng trưởng. Biết rằng số lượng vi khuẩn ban đầu là 100 con và sau 5 giờ có 300 con. Để số lượng vi khuẩn ban đầu sẽ tăng gấp đôi thì thời gian tăng trưởng $t$ gần với kết quả nào sau đây nhất.

A. 3 giờ 9 phút. B. 3 giờ 2 phút. C. 3 giờ 16 phút. D. 3 giờ 30 phút.

Câu 7. Nghiệm của phương trình $lo{g_{2023}}\left( {2024x} \right) = 0$ là:

A. $x = \frac{1}{{2024}}$. B. $x = 2024$. C. $x = {2023^{2024}}$. D. $x = 1$.

Câu 8. Số nghiệm của phương trình ${3^{{x^2} – x}} = 9$ là

A. 2 . B. 0 . C. 1. D. 3 .

Câu 9. Bất phương trình ${\left( {\frac{1}{3}} \right)^{{x^2} – 4x – 12}} > 1$ có tất cả bao nhiêu nghiệm nguyên?

A. 3 . B. 5 . C. 7 . D. Vô số.

Câu 10. Cho hàm số $y = f\left( x \right)$ xác định trên $\mathbb{R}$ thỏa mãn $\mathop {\lim }\limits_{x \to 4} \frac{{f(x) – f(4)}}{{x – 4}} = 5$. Kết quả đúng là:

A. $f’\left( 5 \right) = 4$. B. $f’\left( x \right) = 4$. C. $f’\left( 4 \right) = 5$. D. $f’\left( x \right) = 5$.

Câu 11. Hệ số góc của tiếp tuyến của đồ thị hàm số $y = f\left( x \right)$ tại điểm ${M_0}\left( {{x_0};f\left( {{x_0}} \right)} \right)$ là

A. $f\left( {{x_0}} \right)$. B. $f’\left( {{x_0}} \right)$. C. $f\left( x \right)$. D. ${x_0}$.

Câu 12. Phương trình tiếp tuyến với đồ thị hàm số $y = {x^2} + 2x$ tại điểm ${x_0} = 1$ là :

A. $y = 4x + 2$. B. $y = 4x$. C. $y = 4x – 4$. D. $y = 4x – 1$.

Câu 13. Cho chuyển động thẳng xác định bởi phương trình $s = {t^3} – 3{t^2} – 9t + 2$ ( $t$ tính bằng giây, $s$ tính bằng mét). Khẳng định nào sau đây đúng?

A. Vận tốc của chuyển động bằng 0 khi $t = 0$ hoặc $t = 2$.

B. Vận tốc của chuyển động tại thời điểm $t = 2$ là $v = 18\;m/s$.

C. Gia tốc của chuyển động tại thời điểm $t = 3$ là $a = 12\;m/{s^2}$.

D. Gia tốc của chuyển động bằng 0 khi $t = 0$.

Câu 14. Hàm số $y = {x^n}\left( {n \in \mathbb{N}{\;^*}} \right)$ có đạo hàm trên $\mathbb{R}$ đạo hàm của hàm số $y = {x^n}$ là

A. ${\left( {{x^n}} \right)’} = n{x^{n – 1}}$. B. ${\left( {{x^n}} \right)’} = n{x^{n + 1}}$. C. $y’ = {x^{n – 1}}$. D. $y = {x^n}$.

Câu 15. Quy tắc tính đạo hàm nào sau đây là đúng?

A. ${(u + v)’} = u’ + v’$. B. ${(u + v)’} = u’v + uv’$. C. ${(u + v)’} = u’ – v’$. D. ${(u + v)’} = u’v – uv’$.

Câu 16. Đạo hàm của hàm số $y = {11^x}$ là

A. $y’ = {11^x}ln11$. B. $y’ = \frac{{{{11}^x}}}{{ln11}}$. C. $y’ = x{.11^{x – 1}}$. D. $y’ = {11^x}$.

Câu 17. Hàm số $y = cosx$ có đạo hàm cấp 2 là:

A. $y” = – sinx$. B. $y” = – cosx$. C. $y” = sinx$. D. $y” = \frac{1}{{cosx}}$.

Câu 18. Hàm số $y = 2{x^5}$ có đạo hàm là

A. $y’ = 5{x^6}$. B. $y’ = 10{x^5}$. C. $y’ = 5x$. D. $y’ = 10{x^4}$.

Câu 19. Cho hàm số $f\left( x \right) = {x^3} + 2x$, giá trị của $f”\left( 1 \right)$ bằng:

A. 8 . B. 2 . C. 6 . D. 3 .

Câu 20. Bạn Minh gieo một con xúc xắc cân đối, đồng nhất. Cho biết không gian mẫu $\Omega $ ?

A. $\Omega = \left\{ {1;2;3;4;5;6} \right\}$. B. $\Omega = \left\{ {1;6} \right\}$. C. $\Omega = \left\{ 1 \right\}$. D. $\Omega = \left\{ 6 \right\}$.

Câu 21. Xét phép thử gieo một con xúc xắc cân đối và đồng chất hai lần liên tiếp. Gọi $A$ là biến cố “Lần đầu xuất hiện mặt 6 chấm” và $B$ là biến cố “Lần thứ hai xuất hiện mặt 6 chấm”. Khẳng định nào sau đây $SAI$ ?

A. $A$ và $B$ là hai biến cố độc lập.

B. $A \cap B$ là biến cố “Tổng số chấm xuất hiện của hai lần gieo bằng 12 ”

C. $A \cup B$ là biến cố “Ít nhất một lần xuất hiện mặt 6 chấm”

D. $A$ và $B$ là hai biến cố xung khắc.

Câu 22. Gieo hai con xúc xắc cân đối đồng chất. Gọi X là biến cố “Tích số chấm xuất hiện trên hai mặt con súc sắc là số lẻ”. Tính xác suất của $X$.

A. $\frac{1}{3}$. B. $\frac{1}{5}$. C. $\frac{1}{4}$. D. $\frac{1}{2}$.

Câu 23. Cho hai biến cố $A$ và $B$ độc lập với nhau. Biết suất của biến cố $A \cup B$.

A. 0,65 . B. 0,3 . C. 0,15 . D. 0,45 .

Câu 24. Bạn Toàn gieo một con xúc xắc cân đối, đồng nhất. Gọi biến cố $A$ “Số chấm trên mặt xuất hiện nhỏ hơn 3” và biến cố $B$ “Số chấm trên mặt xuất hiện lớn hơn 3”. Chọn mệnh đề đúng?

A. $P\left( {A \cup B} \right) = \frac{5}{6}$. B. $P\left( {A \cup B} \right) = 1$. C. $P\left( {A \cup B} \right) = 1$. D. $P\left( {A \cup B} \right) = \frac{2}{3}$.

Câu 25. Trong một lớp học có 15 học sinh nam và 10 học sinh nữ. Giáo viên gọi 4 học sinh lên bảng làm bài tập. Tính xác suất để 4 học sinh lên bảng có cả nam và nữ.

A. $\frac{{400}}{{501}}$. B. $\frac{{307}}{{506}}$. C. $\frac{{443}}{{501}}$. D. $\frac{{443}}{{506}}$.

Câu 26. Trong các mệnh đề sau mệnh đề nào đúng?

A. Góc giữa hai đường thẳng $m$ và $n$ bằng góc giữa hai đường thẳng $a$ và $b$ cùng đi qua một điểm và tương ứng song song với $m$ và $n$.

B. Góc giữa hai đường thẳng $a$ và $b$ bất kì luôn là góc tù.

C. Góc giữa hai đường thẳng $a$ và $b$ bất kì luôn là góc nhọn.

D. Góc giữa hai đường thẳng $m$ và $n$ bằng góc giữa hai đường thẳng $a$ và $b$ tương ứng song song với $m$ và $n$.

Câu 27. Cho hình chóp $S.ABC$ có $SA \bot \left( {ABC} \right)$ và $H$ là hình chiếu vuông góc $S$ của lên $BC$.

Hãy chọn khẳng định đúng?

A. $BC \bot AC$. B. $BC \bot AB$. C. $BC \bot SC$. D. $BC \bot AH$.

Câu 28. Cho hình chóp $S \cdot ABCD$ có đáy là hình vuông, cạnh bên $SA$ vuông góc với mặt phẳng $\left( {ABCD} \right)$ (như hình vẽ minh hoạ). Hãy chọn khẳng định đúng.

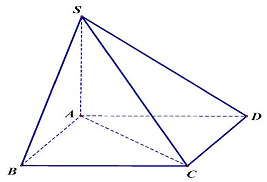
A. $CD \bot \left( {SAB} \right)$. B. $BC \bot \left( {SAC} \right)$. C. $AC \bot \left( {SBD} \right)$. D. $BC \bot \left( {SAB} \right)$.

Câu 29. Cho hình hộp chữ nhật $ABCD \cdot A’B’C’D’$. Mặt phẳng nào sau đây vuông góc với mặt phẳng $\left( {ABCD} \right)$ ?

A. ${{\left( {BCD’A’} \right).\;}}$ B. $\left( {ADC’B’} \right)$. C. $\left( {A’B’C’D’} \right)$. D. ${\;^{\left( {ADD’A’} \right).\;}}$

Câu 30. Cho hai mặt phẳng $\left( P \right),\left( Q \right)$ vuông góc với nhau. Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?

(1) Góc giữa hai mặt phẳng là ${90^ \circ }$.

(2) Mọi đường thẳng trong $\left( P \right)$ đều vuông góc với $\left( Q \right)$.

(3) Tồn tại đường thẳng trong $(Q)$ vuông góc với $(P)$.

(4) Nếu $(R)$ vuông góc với $(Q)$ thì $(R)$ song song với $(P)$.

(5) Nếu mặt phẳng $(R)$ vuông góc với $(P),(R)$ vuông góc với $(Q)$ thì $(R)$ vuông góc với giao tuyến của $(P)$ và $(Q)$.

A. 3 . B. 4 . C. 1 . D. 5 .

Câu 31. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, $SA \bot \left( {ABCD} \right),AB = a$ và $SB = \sqrt 2 a$. Khoảng cách từ điểm $S$ đến mặt phẳng $\left( {ABCD} \right)$ bằng

A. $a$. B. $\sqrt 2 a$. C. $2a$. D. $\sqrt 3 a$.

Câu 32. Cho tứ diện đều $ABCD$ có cạnh bằng $a$. Khoảng cách giữa hai đường thẳng $AB$ và $CD$ bằng:

A. $\frac{a}{2}$ . B. $\frac{{\sqrt 2 a}}{2}$ C. $\frac{{\sqrt 3 a}}{2}$ D. $a$.

Câu 33. Cho hình chóp $S \cdot ABC$ có $SC$ vuông góc với $\left( {ABC} \right)$. Góc giữa $SA$ với $\left( {ABC} \right)$ là góc giữa:

A. $SA$ và $AB$. B. $SA$ và $SC$. C. $SB$ và $BC$. D. $SA$ và $AC$.

Câu 34. Cho hình chóp $S.ABCD$ có $ABCD$ là hình vuông cạnh a. $SA = a\sqrt 2 $ và $SA \bot \left( {ABCD} \right)$. Tính góc giữa $SC$ và mặt phẳng $\left( {ABCD} \right)$.

A. ${30^ \circ }$. B. ${45^ \circ }$. C. ${60^ \circ }$. D. ${90^ \circ }$.

Câu 35. Cho hình chóp $S.ABC$ có $SA \bot \left( {ABC} \right)$, đáy $ABC$ là tam giác đều cạnh $a$ và $SA = \frac{{3a}}{2}$ . Tính số đo góc phẳng nhị diện $\left[ {S,BC,A} \right]$.

A. ${30^ \circ }$. B. ${45^ \circ }$. C. ${60^ \circ }$. D. ${90^ \circ }$.

II. TỰ LUẬN (3 điểm)

Bài 1. (1 điểm) a) Tính đạo hàm của hàm số $y = \sqrt {2x + 3} $.

b) Một con lắc lò xo dao động điều hoà theo phương ngang trên mặt phẳng không ma sát, có phương trình chuyển động $x = 4cos\left( {\pi t – \frac{{2\pi }}{3}} \right) + 3$ centimét. Tìm thời điểm mà vận tốc tức thời của con lắc bằng 0 .

Bài 2. (1 điểm) Một hộp đựng 11 tấm thẻ cùng loại được ghi số từ 1 đến 11. Rút ngẫu đồng thời hai thẻ từ trong hộp. Tính xác suất để tích hai số ghi trên hai thẻ là một số chẵn.

Bài 3. (1 điểm) Cho hình chóp $S \cdot ABC$ có $SA$ vuông góc với đáy; $SA = a\sqrt 3 $. Tam giác $ABC$ đều cạnh $a$.

a) Tính thể tích khối chóp $S \cdot ABC$.

b) Gọi $G$ là trọng tâm $\Delta SAC$. Tính khoảng cách từ điểm $G$ đến mặt phẳng $(SBC)$.

ĐÁP ÁN VÀ LỜI GIẢI CHI TIẾT

I. Bảng đáp án trắc nghiệm

1. B	2. C	3. A	4. C	5. D	6. A	7. A
8. A	9. C	10. C	11. B	12. D	13. C	14. A
15. A	16. A	17. B	18. D	19. C	20. A	21. D
22. C	23. A	24. A	25. D	26. A	27. D	28. D
29. D	30. A	31. A	32. B	33. D	34. B	35. C

II. Lời giải chi tiết trắc nghiệm

Câu 1. Cho là số thực dương tùy ý, bằng
A. ${a^{\frac{1}{3}}}$.
B. ${a^{\frac{5}{4}}}$.
C. ${a^{\frac{3}{4}}}$.
D. ${a^{\frac{4}{5}}}$.

Lời giải

Đáp án đúng là: B

$\frac{{{a^{\frac{2}{3}}} \cdot {a^{\frac{3}{4}}}}}{{\sqrt[6]{a}}} = \frac{{{a^{\frac{{17}}{{12}}}}}}{{{a^{\frac{1}{6}}}}} = {a^{\frac{5}{4}}}$.

Câu 2. Cho hai số dương $a,b\left( {a \ne 1} \right)$. Mệnh đề nào dưới đây SAI?
A. $lo{g_a}{a^\alpha } = \alpha $.
B. $lo{g_a}1 = 0$.
C. $lo{g_a}a = 2a$.
D. $lo{g_{{a^\alpha }}}b = \frac{1}{\alpha }lo{g_a}b$.

Lời giải

Đáp án đúng là: C

$lo{g_a}a = 1$.

Câu 3. Với $a$ là số thực dương tùy, $lo{g_5}{a^2}$ bằng
A. $2lo{g_5}a$.
B. $2 + lo{g_5}a$.
C. $\frac{1}{2} + lo{g_5}a$.
D. $\frac{1}{2}lo{g_5}a$.

Lời giải

Đáp án đúng là: A

Ta có $lo{g_5}{a^2} = 2lo{g_5}a$.

Câu 4. Nếu $lo{g_a}x = \frac{1}{2}lo{g_a}9 – lo{g_a}5 + lo{g_a}2(a > 0,a \ne 1)$ thì $x$ bằng:
A. $\frac{2}{5}$.
B. $\frac{3}{5}$.
C. $\frac{6}{5}$.
D. 3 .

Lời giải

Đáp án đúng là: C

$lo{g_a}x = \frac{1}{2}lo{g_a}9 – lo{g_a}5 + lo{g_a}2 = lo{g_a}3 – lo{g_a}5 + lo{g_a}2 = lo{g_a}\frac{3}{5} + lo{g_a}2 = lo{g_a}\frac{6}{5}$.

$ \Rightarrow x = \frac{6}{5}$.

Câu 5. Hàm số nào dưới đây đồng biến trên tập xác định của nó?
A. $y = lo{g_{\frac{2}{3}}}x$.
B. $y = lo{g_{0,9}}x$.
C. $y = lo{g_{\sqrt {0,9} }}x$.
D. $y = lo{g_{\sqrt 2 }}x$.

Lời giải

Đáp án đúng là: D

Hàm số $y = lo{g_a}x$ đồng biến khi $a > 1$. Do đó chọn đáp án D.

Câu 6. Sự tăng trưởng của một loại vi khuẩn tuân theo công thức $S = A \cdot {e^{rt}}$, trong đó $A$ là số lượng vi khuẩn ban đầu, $r$ là tỉ lệ tăng trưởng $(r > 0),t$ là thời gian tăng trưởng. Biết rằng số lượng vi khuẩn ban đầu là 100 con và sau 5 giờ có 300 con. Để số lượng vi khuẩn ban đầu sẽ tăng gấp đôi thì thời gian tăng trưởng $t$ gần với kết quả nào sau đây nhất.
A. 3 giờ 9 phút.
B. 3 giờ 2 phút.
C. 3 giờ 16 phút.
D. 3 giờ 30 phút.

Lời giải

Đáp án đúng là: A

Trước tiên, ta tìm tỉ lệ tăng trưởng mỗi giờ của loài vi khuẩn này.

Từ giả thiết, ta có:

$300 = 100.{e^{5r}} \Leftrightarrow {e^{5r}} = 3 \Leftrightarrow 5r = ln3 \Leftrightarrow r = \frac{{ln3}}{5} \approx 0,2197$

Tức là tỉ lệ tăng trưởng của loại vi khuẩn này là $21,97\% $ mỗi giờ.

Từ 100 con để có 200 con thì thời gian cần thiết là bao nhiêu?

$200 = 100.{e^{rt}} \Leftrightarrow rt = ln2 \Leftrightarrow t = \frac{{ln2}}{r} = \frac{{ln2}}{{\frac{{ln3}}{5}}} \approx 3,15$

Ta có (giờ) $ = 3$ giờ 9 phút.

Câu 7. Nghiệm của phương trình $lo{g_{2023}}\left( {2024x} \right) = 0$ 1à:
A. $x = \frac{1}{{2024}}$.
B. $x = 2024$.
C. $x = {2023^{2024}}$.
D. $x = 1$.

Lời giải

Đáp án đúng là: A

$lo{g_{2023}}\left( {2024x} \right) = 0 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x > 0} \\
{2024x = 1}
\end{array} \Leftrightarrow x = \frac{1}{{2024}}} \right.$.

Câu 8. Số nghiệm của phương trình ${3^{{x^2} – x}} = 9$ là
A. 2 .
B. 0 .
C. 1 .
D. 3 .

Lời giải

Đáp án đúng là: A

${3^{{x^2} – x}} = 9 \Leftrightarrow {3^{{x^2} – x}} = {3^2} \Leftrightarrow {x^2} – x = 2 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 2} \\
{x = – 1}
\end{array}} \right.$.

Vậy phương trình có 2 nghiệm.

Câu 9. Bất phương trình ${\left( {\frac{1}{3}} \right)^{{x^2} – 4x – 12}} > 1$ có tất cả bao nhiêu nghiệm nguyên?
A. 3 .
B. 5 .
C. 7 .
D. Vô số.

Lời giải

Đáp án đúng là: C

${\left( {\frac{1}{3}} \right)^{{x^2} – 4x – 12}} > 1 \Leftrightarrow {\left( {\frac{1}{3}} \right)^{{x^2} – 4x – 12}} > {\left( {\frac{1}{3}} \right)^0} \Leftrightarrow {x^2} – 4x – 12 < 0 \Leftrightarrow – 2 < x < 6$.

Vì $x \in \mathbb{Z}$ nên $x \in \left\{ { – 1;0;1;2;3;4;5} \right\}$.

Câu 10. Cho hàm số $y = f\left( x \right)$ xác định trên $\mathbb{R}$ thỏa mãn $\mathop {\lim }\limits_{x \to 4} \frac{{f(x) – f(4)}}{{x – 4}} = 5$. Kết quả đúng là:
A. $f’\left( 5 \right) = 4$.
B. $f’\left( x \right) = 4$.
C. $f’\left( 4 \right) = 5$.
D. $f’\left( x \right) = 5$

Lời giải

Đáp án đúng là: C

$f'(4) = \mathop {\lim }\limits_{x \to 4} \frac{{f(x) – f(4)}}{{x – 4}} = 5$.

Câu 11. Hệ số góc của tiếp tuyến của đồ thị hàm số $y = f\left( x \right)$ tại điểm ${M_0}\left( {{x_0};f\left( {{x_0}} \right)} \right)$ là
A. $f\left( {{x_0}} \right)$.
B. $f’\left( {{x_0}} \right)$.
C. $f\left( x \right)$.
D. ${x_0}$.

Lời giải

Đáp án đúng là: B

Hệ số góc của tiếp tuyến của đồ thị hàm số $y = f\left( x \right)$ tại điểm ${M_0}\left( {{x_0};f\left( {{x_0}} \right)} \right)$ là $f’\left( {{x_0}} \right)$.

Câu 12. Phương trình tiếp tuyến với đồ thị hàm số $y = {x^2} + 2x$ tại điểm ${x_0} = 1$ là :
A. $y = 4x + 2$.
B. $y = 4x$.
C. $y = 4x – 4$.
D. $y = 4x – 1$.

Lời giải

Đáp án đúng là: D

Có $y’ = 2x + 2 \Rightarrow y’\left( 1 \right) = 4$.

Với ${x_0} = 1 \Rightarrow {y_0} = 3$.

Phương trình tiếp tuyến của đồ thị hàm số là: $y = 4\left( {x – 1} \right) + 3 = 4x – 1$.

Câu 13. Cho chuyển động thẳng xác định bởi phương trình $s = {t^3} – 3{t^2} – 9t + 2$ ( $t$ tính bằng giây, $s$ tính bằng mét). Khẳng định nào sau đây đúng?

A. Vận tốc của chuyển động bằng 0 khi $t = 0$ hoặc $t = 2$.

B. Vận tốc của chuyển động tại thời điểm $t = 2$ là $v = 18\;m/s$.

C. Gia tốc của chuyển động tại thời điểm $t = 3$ là $a = 12\;m/{s^2}$.

D. Gia tốc của chuyển động bằng 0 khi $t = 0$.

Lời giải

Đáp án đúng là: C

Có $v\left( t \right) = s’\left( t \right) = 3{t^2} – 6t – 9;a\left( t \right) = v’\left( t \right) = 6t – 6$.

Vận tốc của chuyển động bằng 0 thì $3{t^2} – 6t – 9 = 0 \Leftrightarrow t = 3$.

$\begin{array}{*{20}{r}}
{}&{v\left( 2 \right) = {{3.2}^2} – 6.2 – 9 = – 9\;m/s} \\
{}&{a\left( 3 \right) = 6.3 – 6 = 12\;m/{s^2}.}
\end{array}$

Gia tốc bằng 0 khi $6t – 6 = 0 \Leftrightarrow t = 1$.

Câu 14. Hàm số $y = {x^n}\left( {n \in \mathbb{N}{\;^*}} \right)$ có đạo hàm trên $\mathbb{R}$ đạo hàm của hàm số $y = {x^n}$ là
A. ${\left( {{x^n}} \right)’} = n{x^{n – 1}}$.
B. ${\left( {{x^n}} \right)’} = n{x^{n + 1}}$.
C. $y’ = {x^{n – 1}}$.
D. $y = {x^n}$.

Lời giải

Đáp án đúng là: A

$y’ = {\left( {{x^n}} \right)’} = n{x^{n – 1}}$.

Câu 15. Quy tắc tính đạo hàm nào sau đây là đúng?
A. ${(u + v)’} = u’ + v’$.
B. ${(u + v)’} = u’v + uv’$.
C. ${(u + v)’} = u’ – v’$.
D. ${(u + v)’} = u’v – uv’$.

Lời giải

Đáp án đúng là: A

Ta có ${(u + v)’} = u’ + v’$.

Câu 16. Đạo hàm của hàm số $y = {11^x}$ là
A. $y’ = {11^x}ln11$.
B. $y’ = \frac{{{{11}^x}}}{{ln11}}$.
C. $y’ = x{.11^{x – 1}}$.
D. $y’ = {11^x}$.

Lời giải

Đáp án đúng là: A

$y’ = {\left( {{{11}^x}} \right)’} = {11^x}ln11$.

Câu 17. Hàm số $y = cosx$ có đạo hàm cấp 2 là:
A. $y” = – sinx$.
B. $y” = – cosx$.
C. $y” = sinx$.
D. $y” = \frac{1}{{cosx}}$.

Lời giải

Đáp án đúng là: B

$y’ = {(cosx)’} = – sinx;y” = {( – sinx)”} = – cosx$.

Câu 18. Hàm số $y = 2{x^5}$ có đạo hàm là
A. $y’ = 5{x^6}$.
B. $y’ = 10{x^5}$.
C. $y’ = 5x$.
D. $y’ = 10{x^4}$.

Lời giải

Đáp án đúng là: D

Có $y’ = {\left( {2{x^5}} \right)’} = 10{x^4}$.

Câu 19. Cho hàm số $f\left( x \right) = {x^3} + 2x$, giá trị của $f”\left( 1 \right)$ bằng:
A. 8 .
B. 2 .
C. 6 .
D. 3 .

Lời giải

Đáp án đúng là: C

Có $f’\left( x \right) = {\left( {{x^3} + 2x} \right)’} = 3{x^2} + 2;f”\left( x \right) = 6x$.

Do đó $f”\left( 1 \right) = 6.1 = 6$.

Câu 20. Bạn Minh gieo một con xúc xắc cân đối, đồng nhất. Cho biết không gian mẫu $\Omega $ ?
A. $\Omega = \left\{ {1;2;3;4;5;6} \right\}$.
B. $\Omega = \left\{ {1;6} \right\}$.
C. $\Omega = \left\{ 1 \right\}$.
D. $\Omega = \left\{ 6 \right\}$.

Lời giải

Đáp án đúng là: A

$\Omega = \left\{ {1;2;3;4;5;6} \right\}$.

Câu 21. Xét phép thử gieo một con xúc xắc cân đối và đồng chất hai lần liên tiếp. Gọi $A$ là biến cố “Lần đầu xuất hiện mặt 6 chấm” và $B$ là biến cố “Lần thứ hai xuất hiện mặt 6 chấm”.

Khẳng định nào sau đây SAI?

A. $A$ và $B$ là hai biến cố độc lập.

B. $A \cap B$ là biến cố “Tổng số chấm xuất hiện của hai lần gieo bằng 12 ”

C. $A \cup B$ là biến cố “Ít nhất một lần xuất hiện mặt 6 chấm”

D. $A$ và $B$ là hai biến cố xung khắc.

Lời giải

Đáp án đúng là: D

Đáp án sai là D : $A$ và $B$ là hai biến cố xung khắc.

Câu 22. Gieo hai con xúc xắc cân đối đồng chất. Gọi $X$ là biến cố “Tích số chấm xuất hiện trên hai mặt con súc sắc là số lẻ”. Tính xác suất của X.
A. $\frac{1}{3}$.
B. $\frac{1}{5}$.
C. $\frac{1}{4}$.
D. $\frac{1}{2}$.

Lời giải

Đáp án đúng là: C

Gọi A là biến cố: “Con xúc xắc thứ nhất xuất hiện mặt lẻ” $ \Rightarrow P\left( A \right) = \frac{1}{2}$.

B là biến cố: “Con xúc xắc thứ hai xuất hiện mặt lẻ” $ \Rightarrow P\left( B \right) = \frac{1}{2}$.

C là biến cố: “Tích số chấm xuất hiện trên hai mặt con súc sắc là số lẻ”.

Có $C = A \cdot B$ mà $A,B$ là hai biến cố độc lập nên

$P\left( C \right) = P\left( {AB} \right) = P\left( A \right) \cdot P\left( B \right) = \frac{1}{4}$.

Câu 23. Cho hai biến cố $A$ và $B$ độc lập với nhau. Biết suất của biến cố $A \cup B$.
A. 0,65 .
B. 0,3 .
C. 0,15 .
D. 0,45 .

Lời giải

Đáp án đúng là: A

Vì $A$ và $B$ là hai biến cố độc lập nên $P\left( {AB} \right) = P\left( A \right)P\left( B \right) \Rightarrow P\left( B \right) = 0,3$.

Có $P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) – P\left( {AB} \right) = 0,5 + 0,3 – 0,15 = 0,65$.

Câu 24. Bạn Toàn gieo một con xúc xắc cân đối, đồng nhất. Gọi biến cố $A$ “Số chấm trên mặt xuất hiện nhỏ hơn 3” và biến cố $B$ “Số chấm trên mặt xuất hiện lớn hơn 3”. Chọn mệnh đề đúng?
A. $P\left( {A \cup B} \right) = \frac{5}{6}$.
B. $P\left( {A \cup B} \right) = 1$.
C. $P\left( {A \cup B} \right) = 1$.
D. $P\left( {A \cup B} \right) = \frac{2}{3}$.

Lời giải

Đáp án đúng là: A

Có $A = \left\{ {1;2} \right\} \Rightarrow P\left( A \right) = \frac{1}{3}$;

$B = \left\{ {4;5;6} \right\} \Rightarrow P\left( B \right) = \frac{1}{2}$.

Vì $A,B$ là hai biến cố xung khắc nên $P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) = \frac{1}{3} + \frac{1}{2} = \frac{5}{6}$.

Câu 25. Trong một lớp học có 15 học sinh nam và 10 học sinh nữ. Giáo viên gọi 4 học sinh lên bảng làm bài tập. Tính xác suất để 4 học sinh lên bảng có cả nam và nữ.
A. $\frac{{400}}{{501}}$.
B. $\frac{{307}}{{506}}$.
C. $\frac{{443}}{{501}}$.
D. $\frac{{443}}{{506}}$.

Lời giải

Đáp án đúng là: D

Số phần tử của không gian mẫu là $n\left( \Omega \right) = C_{25}^4 = 12650$.

Gọi $A$ là biến cố: ” 4 học sinh lên bảng có cả nam và nữ”.

TH1: Có 1 nam 3 nữ $ \Rightarrow C_{15}^1 \cdot C_{10}^3 = 1800$ cách

TH2: Có 2 nam 2 nữ $ \Rightarrow C_{15}^2 \cdot C_{10}^2 = 4725$ cách

TH3: Có 3 nam 1 nữ $ \Rightarrow C_{15}^3 \cdot C_{10}^1 = 4550$ cách.

Do đó $n\left( A \right) = 11075$ cách.

Vậy $P\left( A \right) = \frac{{11075}}{{12650}} = \frac{{443}}{{506}}$

Câu 26. Trong các mệnh đề sau mệnh đề nào đúng?

A. Góc giữa hai đường thẳng $m$ và $n$ bằng góc giữa hai đường thẳng $a$ và $b$ cùng đi qua một điểm và tương ứng song song với $m$ và $n$.

B. Góc giữa hai đường thẳng $a$ và $b$ bất kì luôn là góc tù.

C. Góc giữa hai đường thẳng $a$ và $b$ bất kì luôn là góc nhọn.

D. Góc giữa hai đường thẳng $m$ và $n$ bằng góc giữa hai đường thẳng $a$ và $b$ tương ứng song song với $m$ và $n$.

Lời giải

Đáp án đúng là: A

Góc giữa hai đường thẳng $m$ và $n$ bằng góc giữa hai đường thẳng $a$ và $b$ cùng đi qua một điểm và tương ứng song song với $m$ và $n$.

Câu 27. Cho hình chóp $S.ABC$ có $SA \bot \left( {ABC} \right)$ và $H$ là hình chiếu vuông góc $S$ của lên $BC$. Hãy chọn khẳng định đúng?
A. $BC \bot AC$.
B. $BC \bot AB$.
C. $BC \bot SC$.
D. $BC \bot AH$.

Lời giải

Đáp án đúng là: D

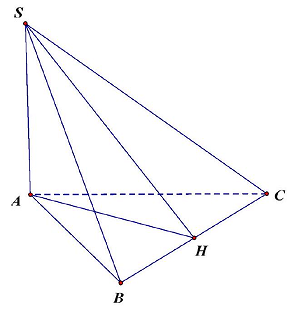
Vì H là hình chiếu vuông góc $S$ của lên $BC$ nên $SH \bot BC$ (1).

Mà $SA \bot \left( {ABC} \right) \Rightarrow SA \bot BC$ (2).

Từ (1) và (2), suy ra $BC \bot \left( {SAH} \right) \Rightarrow BC \bot AH$.

Câu 28. Cho hình chóp $S \cdot ABCD$ có đáy là hình vuông, cạnh bên $SA$ vuông góc với mặt phẳng $\left( {ABCD} \right)$ (như hình vẽ minh hoạ). Hãy chọn khẳng định đúng.

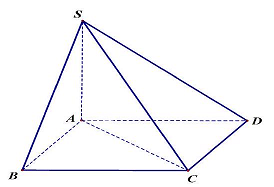
A. $CD \bot \left( {SAB} \right)$.
B. $BC \bot \left( {SAC} \right)$.
C. $AC \bot \left( {SBD} \right)$.
D. $BC \bot \left( {SAB} \right)$.

Lời giải

Đáp án đúng là: D

Vì $ABCD$ là hình vuông nên $BC \bot AB\left( 1 \right)$.

Vì $SA \bot \left( {ABCD} \right) \Rightarrow SA \bot BC$ (2).

Từ (1) và (2) $ \Rightarrow BC \bot \left( {SAB} \right)$.

Câu 29. Cho hình hộp chữ nhật $ABCD \cdot A’B’C’D’$. Mặt phẳng nào sau đây vuông góc với mặt phẳng $\left( {ABCD} \right)$ ?
A. $\left( {BCD’A’} \right)$.
B. $\left( {ADC’B’} \right)$.
C. $\left( {A’B’C’D’} \right)$.
D. $\left( {ADD’A’} \right)$.

Lời giải

Đáp án đúng là: D

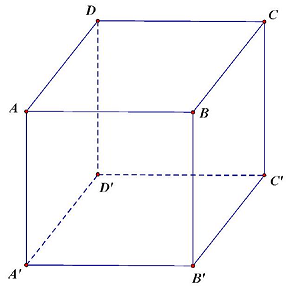
Vì $ABCD \cdot A’B’C’D’$ là hình hộp chữ nhật nên $\left( {ADD’A’} \right) \bot \left( {ABCD} \right)$.

Câu 30. Cho hai mặt phẳng $\left( P \right),\left( Q \right)$ vuông góc với nhau. Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?

(1) Góc giữa hai mặt phẳng là ${90^ \circ }$.

(2) Mọi đường thẳng trong $\left( P \right)$ đều vuông góc với $\left( Q \right)$.

(3) Tồn tại đường thẳng trong $(Q)$ vuông góc với $(P)$.

(4) Nếu $(R)$ vuông góc với $(Q)$ thì $(R)$ song song với $(P)$.

(5) Nếu mặt phẳng $(R)$ vuông góc với $(P),(R)$ vuông góc với $(Q)$ thì $(R)$ vuông góc với giao tuyến của $(P)$ và $(Q)$.

A. 3 .
B. 4 .
C. 1 .
D. 5 .

Lời giải

Đáp án đúng là: A

Mệnh đề thứ nhất đúng theo định nghĩa về góc.

Mệnh đề thứ hai sai và mệnh đề thứ ba đúng theo định nghĩa hai mặt phẳng vuông góc.

Mệnh đề thứ tư sai vì $\left( R \right)$ có thể trùng với $\left( Q \right)$.

Mệnh đề thứ năm đúng theo tính chất hai mặt phẳng cắt nhau cùng vuông góc với mặt phẳng thứ 3 thì giao tuyến của chúng sẽ vuông góc với mặt phẳng ấy.

Câu 31. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, $SA \bot \left( {ABCD} \right),AB = a$ và $SB = \sqrt 2 a$. Khoảng cách từ điểm $S$ đến mặt phẳng $\left( {ABCD} \right)$ bằng
A. $a$.
B. $\sqrt 2 a$.
C. $2a$.
D. $\sqrt 3 a$.

Lời giải

Đáp án đúng là: A

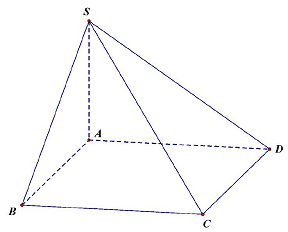
Vì $SA \bot \left( {ABCD} \right)$ nên $d\left( {S,\left( {ABCD} \right)} \right) = SA$.

Xét $\vartriangle SAB$ vuông tại $A$, có $SA = \sqrt {S{B^2} – A{B^2}} = \sqrt {2{a^2} – {a^2}} = a$.

Câu 32. Cho tứ diện đều $ABCD$ có cạnh bằng $a$. Khoảng cách giữa hai đường thẳng $AB$ và $CD$ bằng:
A. $\frac{a}{2}$ .
B. $\frac{{\sqrt 2 a}}{2}$
C. $\frac{{\sqrt 3 a}}{2}$
D. $a$.

Lời giải

Đáp án đúng là: B

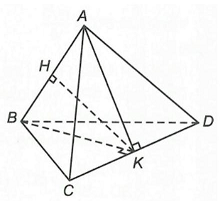
Gọi $K$ là trung điểm $CD$. Suy ra $\left\{ {\begin{array}{*{20}{l}}
{CD \bot AK} \\
{CD \bot BK}
\end{array} \Rightarrow CD \bot \left( {ABK} \right)} \right.$.

Dựng $HK \bot AB \Rightarrow HK = d\left( {AB;CD} \right)$.

Xét tam giác $BHK$ vuông tại $H$, ta có

$HK = \sqrt {B{K^2} – B{H^2}} = \sqrt {{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2} – {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 2 }}{2}.\;d\left( {AB,CD} \right) = \frac{{a\sqrt 2 }}{2}$.

Câu 33. Cho hình chóp $S \cdot ABC$ có $SC$ vuông góc với ${{\left( {ABC} \right)}}$. Góc giữa $SA$ với $\left( {ABC} \right)$ là góc giữa:
A. $SA$ và $AB$.
B. $SA$ và $SC$.
C. $SB$ và $BC$.
D. $SA$ và $AC$.

Lời giải

Đáp án đúng là: D

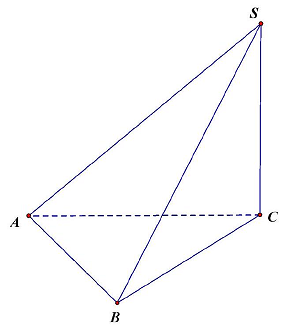
Vì $SC \bot \left( {ABC} \right)$ nên $CA$ là hình chiếu của $SA$ trên mặt phẳng $\left( {ABC} \right)$.

Do đó góc giữa $SA$ với $\left( {ABC} \right)$ là góc giữa hai đường thẳng $SA$ và $AC$.

Câu 34. Cho hình chóp $S.ABCD$ có $ABCD$ là hình vuông cạnh a. $SA = a\sqrt 2 $ và

$SA \bot \left( {ABCD} \right)$. Tính góc giữa $SC$ và mặt phẳng $\left( {ABCD} \right)$.
A. ${30^ \circ }$.
B. ${45^ \circ }$.
C. ${60^ \circ }$.
D. ${90^ \circ }$.

Lời giải

Đáp án đúng là: B

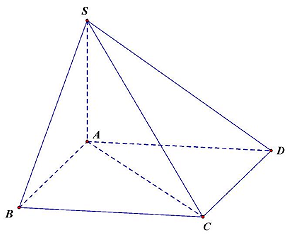
Vì $SA \bot \left( {ABCD} \right)$ nên $AC$ là hình chiếu của $SC$ trên mặt phẳng $\left( {ABCD} \right)$.

Do đó góc giữa $SC$ và mặt phẳng $\left( {ABCD} \right)$ là $SCA$.

Vì $ABCD$ là hình vuông cạnh a nên $AC = a\sqrt 2 $.

Xét $\vartriangle SAC$ vuông tại , có $tanSCA = \frac{{SA}}{{AC}} = 1 \Rightarrow SCA = {45^ \circ }$.

Câu 35. Cho hình chóp $S \cdot ABC$ có $SA \bot \left( {ABC} \right)$, đáy $ABC$ là tam giác đều cạnh $a$ và $SA = \frac{{3a}}{2}$. Tính số đo góc phẳng nhị diện $\left[ {S,BC,A} \right]$.
A. ${30^ \circ }$.
B. ${45^ \circ }$.
C. ${60^ \circ }$.
D. ${90^ \circ }$.

Lời giải

Đáp án đúng là: C

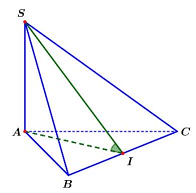
Gọi $I$ là trung điểm $BC \Rightarrow AI \bot BC$ (vì $ABC$ là tam giác đều).

Ta có: $\left\{ {\begin{array}{*{20}{l}}
{BC \bot AI} \\
{BC \bot SA}
\end{array} \Rightarrow BC \bot \left( {SAI} \right) \Rightarrow BC \bot SI} \right.$

Khi đó:

$\left\{ {\begin{array}{*{20}{l}}
{\left( {SBC} \right) \cap \left( {ABC} \right) = BC} \\
{SI \bot BC} \\
{AI \bot BC}
\end{array} \Rightarrow \left[ {S,BC,A} \right] = SIA} \right.$

Mà $\vartriangle ABC$ đều cạnh $a \Rightarrow AI = \frac{{a\sqrt 3 }}{2}$.

Xét $\vartriangle SAI$ vuông tại $A$, ta có:

$tanSIA = \frac{{SA}}{{AI}} = \sqrt 3 \Rightarrow SIA = {60^ \circ }$

III. Lời giải tự luận

Bài 1. (1 điểm) a) Tính đạo hàm của hàm số $y = \sqrt {2x + 3} $.

b) Một con lắc lò xo dao động điều hoà theo phương ngang trên mặt phẳng không ma sát, có phương trình chuyển động $x = 4cos\left( {\pi t – \frac{{2\pi }}{3}} \right) + 3$, trong đó $t$ tính bằng giây và $x$ tính bằng centimét. Tìm thời điểm mà vận tốc tức thời của con lắc bằng 0 .

Lời giải

a) $y’ = \frac{{{{(2x + 3)}’}}}{{2\sqrt {2x + 3} }} = \frac{1}{{\sqrt {2x + 3} }}$.

b) Vận tốc tức thời của con lắc là $v\left( t \right) = x’\left( t \right) = – 4\pi sin\left( {\pi t – \frac{{2\pi }}{3}} \right)\left( {m/s} \right)$.

Khi vận tốc tức thời của con lắc bằng 0 thì

$ – 4\pi sin\left( {\pi t – \frac{{2\pi }}{3}} \right) = 0 \Leftrightarrow \pi t – \frac{{2\pi }}{3} = k\pi \left( {k \in \mathbb{Z}} \right)$

$ \Leftrightarrow \pi t = \frac{{2\pi }}{3} + k\pi \left( {k \in \mathbb{Z}} \right) \Leftrightarrow t = \frac{2}{3} + k\left( {k \in \mathbb{Z}} \right)$

Vậy khi $t = \frac{2}{3} + k\left( {k \in \mathbb{Z}} \right)$ vận tốc tức thời của con lắc bằng 0 .

Bài 2. (1 điểm) Một hộp đựng 11 tấm thẻ cùng loại được ghi số từ 1 đến 11. Rút ngẫu đồng thời hai thẻ từ trong hộp. Tính xác suất để tích hai số ghi trên hai thẻ là một số chẵn.

Lời giải

Gọi $A$ là biến cố “tích hai số ghi trên hai thẻ là một số chẵn”.

Số phần tử không gian mẫu: $n(\Omega ) = C_{11}^2 = 55$

Trường hợp 1: Rút được 1 thẻ ghi số chẵn và 1 thẻ ghi số lẻ có $C_5^1.C_6^1 = 30$ khả năng.

Trường hợp 2: Rút được 2 thẻ ghi số chẵn có $C_5^2 = 10$ khả năng.

$ \Rightarrow n(A) = 30 + 10 = 40$.

Vậy, $P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{{40}}{{55}} = \frac{8}{{11}}$

Bài 3. (1 điểm) Cho hình chóp $S \cdot ABC$ có $SA$ vuông góc với đáy; $SA = a\sqrt 3 $. Tam giác $ABC$ đều cạnh $a$.

a) Tính thể tích khối chóp $S \cdot ABC$.

b) Gọi $G$ là trọng tâm $\Delta SAC$. Tính khoảng cách từ điểm $G$ đến mặt phẳng $(SBC)$.

Lời giải

a) Ta có: $SA \bot (ABC)$

$ \Rightarrow {V_{S.ABC}} = \frac{1}{3}{S_{ABC}}.SA$

Tam giác $ABC$ đều cạnh $a$$ \Rightarrow {S_{ABC}} = \frac{{{a^2}\sqrt 3 }}{4}$.

Vậy ${V_{S.ABC}} = \frac{1}{3}{S_{ABC}}.SA = \frac{1}{3}.\frac{{{a^2}\sqrt 3 }}{4}.a\sqrt 3 = \frac{{{a^3}}}{4}$.

b) Gọi $I$ là trung điểm $SC.$

Ta có: $AG$ cắt $(SBC)$ tại $I$ nên $\frac{{d\left( {G;(SBC)} \right)}}{{d\left( {A;(SBC)} \right)}} = \frac{{GI}}{{AI}} = \frac{1}{3}$

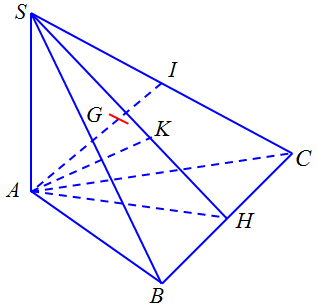
$ \Rightarrow d\left( {G;(SBC)} \right) = \frac{1}{3}d\left( {A;(SBC)} \right)$

Trong $\left( {ABC} \right)$ kẻ $AH \bot BC$ tại $H$. (1)

Lại có, $SA \bot BC\,$ (Do ($SA \bot (ABC)$) (2)

Từ (1) và (2) $ \Rightarrow (SAH) \bot BC$

$ \Rightarrow (SAH) \bot (SBC$ (3)

Trong $\left( {SAH} \right)$ kẻ $AK \bot SH$ tại $K$ (4)

Từ (3) và (4) $ \Rightarrow AK \bot (SBC)$

$ \Rightarrow d\left( {A;(SBC)} \right) = AK$

Ta có $AH = \frac{{a\sqrt 3 }}{2}$ (Đường cao tam giác đều)

Tam giác $SAH$ vuông tại $A$ có $AK$ là đường cao nên $\frac{1}{{A{K^2}}} = \frac{1}{{A{S^2}}} + \frac{1}{{A{H^2}}} = \frac{1}{{{{\left( {a\sqrt 3 } \right)}^2}}} + \frac{1}{{{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2}}}$

$ = \frac{1}{{3{a^2}}} + \frac{4}{{3{a^2}}} = \frac{5}{{3{a^2}}}$

$ \Rightarrow A{K^2} = \frac{{3{a^2}}}{5} \Rightarrow AK = \frac{{a\sqrt {15} }}{5}$

Vậy $d\left( {G;(SBC)} \right) = \frac{1}{3}d\left( {A;(SBC)} \right)$

$ = \frac{1}{3}AK = \frac{1}{3}.\frac{{a\sqrt {15} }}{5} = \frac{{a\sqrt {15} }}{{15}}$