Đề Kiểm Tra Học Kỳ 2 Toán 11 Chân Trời Sáng Tạo Giải Chi Tiết-Đề 2

Đề kiểm tra học kỳ 2 Toán 11 Chân trời sáng tạo giải chi tiết-Đề 2 được soạn dưới dạng file word và PDF gồm 5 trang. Các bạn xem và tải về ở dưới.
I. PHẦN TRẮC NGHIỆM (7 điểm)

Câu 1. Biểu thức nào là luỹ thừa với số mũ thực

A. ${3^{\frac{1}{3}}}$. B. ${2^{ – x}}$. C. ${x^{ – 2}}$. D. ${2^x}$.

Câu 2. Cho $a$ là số thực dương. Giá trị rút gọn của biểu thức $P = \frac{{{a^{\frac{1}{4}}} – {a^{\frac{9}{4}}}}}{{{a^{\frac{1}{4}}} – {a^{\frac{5}{4}}}}}$ là:

A. $2a$. B. $a$. C. $1 – a$. D. $1 + a$.

Câu 3. Cho hai số dương $a,b$ với $a \ne 1$. Số $\alpha $ thoả mãn ${a^\alpha } = b$, khi đó $\alpha $ bằng

A. $\alpha = lo{g_a}b$. B. $\alpha = lo{g_b}a$. C. $\alpha = lo{g_a}a$. D. $\alpha = lo{g_b}b$.

Câu 4. Hàm số nào sau đây là hàm số mũ

A. $y = {2^{\frac{x}{2}}}$. B. $y = – {2^x}$. C. $y = {x^{ – 2}}$. D. $y = {x^2}$.

Câu 5. Trong các hình sau, hình nào là dạng đồ thị của hàm số $y = lo{g_a}x,a > 1$

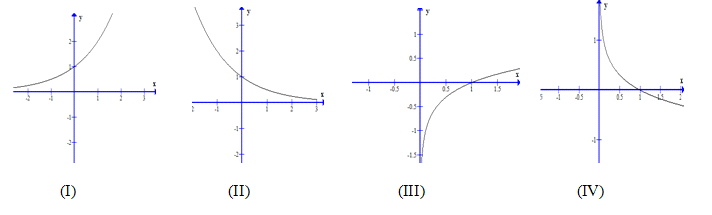
A. (I). B. (II). C. (IV). D. (III).

Câu 6. Một sinh viên gửi tiết kiệm ngân hàng lãi suất $13\% $ / năm với hình thức lãi kép. Hỏi sau bao nhiêu năm sinh viên đó thu được gấp ba lần số tiền ban đầu, biết lãi suất cố định trong các năm.

A. 8 năm 9 tháng. B. 15 năm 5 tháng. C. 8 năm. D. 9 năm.

Câu 7. Tổng các nghiệm thực của phương trình ${3^{{x^2} – 3x + 8}} = {9^{2x – 1}}$ bằng

A. $ – 7$ . B. $5$ . C. $6$ . D. $7$ .

Câu 8. Tổng các giá trị nghiệm của phương trình $\log _{\frac{1}{2}}^2x – 5{\log _2}x + 6 = 0$ bằng

A. 10 . B. $\frac{{65}}{{64}}$. C. 5 . D. $\frac{{129}}{{64}}$

Câu 9. Cho hàm số $y = f\left( x \right)$ có đồ thị $\left( C \right)$ và đạo hàm $f’\left( 2 \right) = 6$. Hệ số góc của tiếp tuyến của (C) tại điểm $M\left( {2;f\left( 2 \right)} \right)$ bằng

A. 2 . B. 3 . C. 6 . D. 12 .

Câu 10. Hàm số $f\left( x \right) = {x^2} + 2x + 1$. Khi đó với $a \in \mathbb{R}$ thì khẳng định nào đúng ?

A. $f’\left( a \right) = 2a + 3$. B. $f’\left( a \right) = {a^2} + 1$. C. $f’\left( a \right) = 2a + 2$. D. $f’\left( a \right) = 2a$.

Câu 11. Đạo hàm của hàm số $y = {3^x}$ là

A. $y’ = x \cdot {3^{x – 1}}$. B. $y’ = {3^x} \cdot ln3$. C. $y’ = {3^x}$. D. $y’ = \frac{{{3^x}}}{{ln3}}$.

Câu 12. Một chất điểm chuyển động có phương trình $s\left( t \right) = t + 1$ ( $t$ tính bằng giây, $s$ tính bằng mét). Vận tốc tức thời của chất điểm tại thời điểm $t = 3\;s$ bằng

A. $1\;m/s$. B. $15\;m/s$. C. $4\;m/s$. D. $0\;m/s$.

Câu 13. Hàm số $y = {x^5}$ có đạo hàm cấp 2 là

A. $5{x^4}$. B. $20x$. C. $20{x^3}$. D. $5{x^3}$.

Câu 14. Cho $f\left( x \right) = 201$. Tính $f”\left( x \right)$.

A. $f”\left( x \right) = 2$. B. $f”\left( x \right) = x$. C. $f”\left( x \right) = 0$ D. $f”\left( x \right) = 1$.

Câu 15. Hàm số $y = \frac{1}{{x + 1}}$ có đạo hàm cấp hai tại $x = 1$ là

A. $y”\left( 1 \right) = \frac{1}{2}$. B. $y”\left( 1 \right) = – \frac{1}{4}$. C. $y”\left( 1 \right) = 4$. D. $y”\left( 1 \right) = \frac{1}{4}$.

Câu 16. Hàm số $y = cotx$ có đạo hàm là:

A. $y’ = – \frac{1}{{co{s^2}x}}$. B. $y’ = – \frac{1}{{si{n^2}x}}$. C. $y’ = \frac{1}{{si{n^2}x}}$ D. $y’ = – tanx$.

Câu 17. Đạo hàm của hàm số là

A. $y’ = x \cdot {3^{x – 1}}$. B. $y’ = {3^x} \cdot ln3$. C. $y’ = {3^x}$. D. $y’ = \frac{{{3^x}}}{{ln3}}$.

Câu 18. Cho $f(x) = {({x^2} – 3x + 3)^2}$. Biểu thức $f’\left( 1 \right)$ có giá trị là bao nhiêu?

A. -1 . B. -2 . C. $ – 12$. D. 1.

Câu 19. Đạo hàm của hàm số $y = {x^4} – 3{x^2} + 2x – 1$ bằng biểu thức nào sau đây?

A. $y’ = 4{x^3} – 6x + 3$. B. $y’ = 4{x^4} – 6x + 2$. C. $y’ = 4{x^3} – 3x + 2$. D. $y’ = 4{x^3} – 6x + 2$.

Câu 20. Tung một con xúc xắc, gọi A là biến cố: “Xuất hiện mặt có số chấm lớn hơn hoặc bằng 4 “, $B$ là biến cố: ” Xuất hiện mặt có số chấm nhỏ hơn hoặc bằng 2 “. Khẳng định nào sau đây là đúng?

A. $A$ và $B$ là hai biến cố xung khắc. B. A và $B$ là hai biến cố đối.

C. Cả $A$ và $B$ đều đúng. D. Không đủ thông tin để kết luận.

Câu 21. Cho $A,B$ là hai biến cố độc lập. Biết $P\left( A \right) = \frac{1}{3},P\left( B \right) = \frac{1}{4}$. Tính $P\left( {AB} \right)$.

A. $\frac{7}{{12}}$. B. $\frac{1}{{12}}$ . C. $\frac{1}{7}$. D. $\frac{1}{2}$ .

Câu 22. Hai xạ thủ $M$ và $N$ cùng bắn súng vào một tấm bia. Biết rằng xác suất bắn trúng của xạ thủ $M$ là 0,3 , của xạ thủ $N$ là 0,2 . Khả năng bắn trúng của hai xạ thủ là độc lập. Xác suất của biến cố “Cả hai xạ thủ đều bắn trúng” là

A. 0,05 . B. 0,06 . C. 0,07 . D. 0,08 .

Câu 23. Gọi $S$ là tập các số tự nhiên có 4 chữ số khác nhau được tạo từ tập $E = \left\{ {1;2;3;4;5} \right\}$. Chọn ngẫu nhiên một số từ tập $S$. Tính xác suất để số được chọn là một số chẵn?

A. $\frac{3}{4}$. B. $\frac{2}{5}$. C. $\frac{3}{5}$. D. $\frac{1}{2}$.

Câu 24. Gieo một đồng xu cân đối và đồng chất liên tiếp ba lần. Gọi $A$ là biến cố “Có ít nhất hai mặt sấp xuất hiện liên tiếp” và $B$ là biến cố “Kết quả ba lần gieo là như nhau”. Xác định biến cố $A \cup B$.

A. $A \cup B = \left\{ {SSS,SSN,NSS,SNS,NNN} \right\}$. B. $A \cup B = \left\{ {SSS,NNN} \right\}$.

C. $A \cup B = \left\{ {SSS,SSN,NSS,NNN} \right\}$. D. $A \cup B = \Omega $.

Câu 25. Cho $A,B$ là hai biến cố độc lập. Biết $P\left( A \right) = 0,5;P\left( {A \cap B} \right) = 0,2$. Tính $P\left( {A \cup B} \right)$.

A. 0,3 . B. 0,5 . C. 0,6 . D. 0,7 .

Câu 26. Cho hình lập phương $ABCD \cdot A’B’C’D’$. Góc giữa hai đường thẳng $A’C’$ và $BD$ bằng.

A. ${60^ \circ }$. B. ${30^ \circ }$. C. ${45^ \circ }$. D. ${90^ \circ }$.

Câu 27. Cho hình lập phương $ABCD \cdot A’B’C’D’$ như hình vẽ

Khẳng định nào sau đây đúng

A. $AA’ \bot \left( {ABB’A’} \right)$. B. $CA’ \bot \left( {ABC’D’} \right)$. C. $AA’ \bot \left( {ABCD} \right)$. D. $CA’ \bot \left( {ABCD} \right)$.

Câu 28. Thể tích của khối lăng trụ có diện tích đáy $S$ và chiều cao $h$ là:

A. $\frac{1}{3}Sh$. B. $Sh$. C. $\frac{1}{2}Sh$. D. $3Sh$.

Câu 29. Cho hình chóp $S.ABCD$ có $ABCD$ là hình chữ nhật và $SA \bot \left( {ABCD} \right)$. Mệnh đề nào dưới đây đúng ?

A. $AB \bot \left( {SAD} \right)$. B. $BC \bot \left( {SAD} \right)$. C. $AC \bot \left( {SAD} \right)$. D. $BD \bot \left( {SAD} \right)$.

Câu 30. Cho khối chóp tứ giác đều $S \cdot ABCD$ có cạnh đáy bằng $\sqrt 2 a$ và tam giác $SAC$ đều. Thể tích của khối chóp đã cho bằng

A. $\frac{{\sqrt 3 {a^3}}}{2}$. B. $\frac{{\sqrt 3 {a^3}}}{3}$. C. $\frac{{2\sqrt 3 {a^3}}}{3}$. D. $\frac{{3\sqrt 3 {a^3}}}{2}$.

Câu 31. Cho hai mặt phẳng $\left( P \right)$ và $\left( Q \right)$ cắt nhau và một điểm $M$ không thuộc $\left( P \right)$ và $\left( Q \right)$. Qua $M$ có bao nhiêu mặt phẳng vuông góc với $\left( P \right)$ và $(Q)$ ?

A. 1 . B. 2 . C. 3 . D. Vô số.

Câu 32. Cho hình chóp $S.ABCD$ có $ABCD$ là hình vuông, $SA$ vuông góc với mặt phẳng đáy. Mặt phẳng $\left( {ABCD} \right)$ vuông góc với mặt phẳng nào dưới đây?

A. $\left( {SAC} \right)$. B. $\left( {SBD} \right)$. C. $\left( {SCD} \right)$. D. $\left( {SBC} \right)$.

Câu 33. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, $SA \bot \left( {ABCD} \right)$. Tính khoảng cách từ điểm $B$ đến mặt phẳng $(SAC)$.

A. $\frac{a}{2}$. B. $\frac{{a\sqrt 2 }}{2}$. C. $\frac{{a\sqrt 2 }}{3}$. D. $\frac{{a\sqrt 2 }}{4}$.

Câu 34. Trong các mệnh đề sau, mệnh đề nào đúng?

A. Góc giữa đường thẳng và mặt phẳng bằng góc giữa đường thẳng đó và hình chiếu của nó trên mặt phẳng đã cho.

B. Góc giữa đường thẳng a và mặt phẳng $\left( P \right)$ bằng góc giữa đường thẳng $b$ và mặt phẳng $\left( P \right)$ khi và $b$ song song (hoặc $a$ trùng với $b$ ).

C. Góc giữa đường thẳng a và mặt phẳng $\left( P \right)$ bằng góc giữa đường thẳng $a$ và mặt phẳng $\left( Q \right)$ thì mặt phẳng $\left( P \right)$ song song với mặt phẳng $\left( Q \right)$.

D. Góc giữa đường thẳng a và mặt phẳng $\left( P \right)$ bằng góc giữa đường thẳng $b$ và mặt phẳng $\left( P \right)$ thì $a$ song song với $b$.

Câu 35. Cho hình chóp $S \cdot ABC$ có $SA$ vuông góc với mặt phẳng $\left( {ABC} \right),SA = 2a$, tam giác $ABC$ vuông tại $B,AB = a\sqrt 3 $ và $BC = a$ (minh họa như hình vẽ bên). Góc giữa đường thẳng $SC$ và mặt phẳng $\left( {ABC} \right)$ bằng

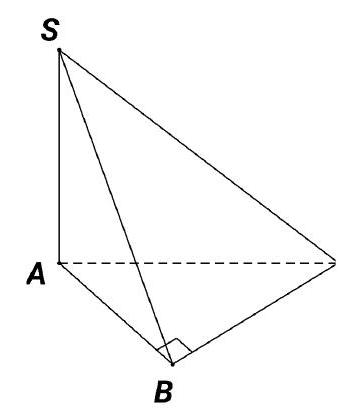
A. ${90^ \circ }$. B. ${45^ \circ }$. C. ${30^ \circ }$. D. ${60^ \circ }$.

II. TỰ LUẬN (3 điểm)

Bài 1. (1 điểm) a) Tính đạo hàm cấp hai của hàm số $y = sinax$ ( $a$ là hằng số).

b) Một chất điểm chuyển động có quãng đường được cho bởi phương trình $s\left( t \right) = \frac{1}{4}{t^4} – {t^3} + \frac{5}{2}{t^2} + 10t$, trong đó $t > 0$ với $t$ tính bằng giây (s) và $s$ tính bằng mét $\left( m \right)$. Tính vận tốc chuyển động của chất điểm tại thời điểm chất điểm có gia tốc chuyển động nhỏ nhất.

Bài 2. (1 điểm) Cho hình chóp có đáy là tam giác vuông cân tại $A,SA \bot \left( {ABC} \right)$ và ; $SA = \frac{{a\sqrt 6 }}{2}$. Gọi $H$ là trung điểm cạnh $BC$.

a) Chứng minh: $BC \bot \left( {SAH} \right)$.

b) Tính góc giữa đường thẳng $SH$ và mặt phẳng $\left( {ABC} \right)$.

Bài 3. (1 điểm) Gọi $A$ là tập hợp tất cả các số tự nhiên có chữ số đôi một khác nhau. Chọn ngẫu nhiên một số thuộc $A$. Tính xác suất để số tự nhiên được chọn chia hết cho 25.

ĐÁP ÁN VÀ LỜI GIẢI CHI TIẾT

I. Bảng đáp án trắc nghiệm

1. A	2. D	3. A	4. A	5. D	6. D	7. D
8. D	9. C	10. C	11. B	12. A	13. C	14. C
15. D	16. B	17. B	18. B	19. D	20. A	21. B
22. B	23. B	24. C	25. D	26. D	27. C	28. B
29. A	30. C	31. A	32. A	33. B	34. B	35. B

II. Lời giải chi tiết trắc nghiệm

Câu 1. Biểu thức nào là luỹ thừa với số mũ thực

A. ${3^{\frac{1}{3}}}$.

B. ${2^{ – x}}$.

C. ${x^{ – 2}}$.

D. ${2^x}$.

Lời giải

Đáp án đúng là: A

Biểu thức lũy thừa của số mũ thực là ${3^{\frac{1}{3}}}$.

Câu 2. Cho $a$ là số thực dương. Giá trị rút gọn của biểu thức $P = \frac{{{a^{\frac{1}{4}}} – {a^{\frac{9}{4}}}}}{{{a^{\frac{1}{4}}} – {a^{\frac{5}{4}}}}}$ là:

A. $2a$.

B. $a$.

C. $1 – a$.

D. $1 + a$.

Lời giải

Đáp án đúng là: D

$P = \frac{{{a^{\frac{1}{4}}} – {a^{\frac{9}{4}}}}}{{{a^{\frac{1}{4}}} – {a^{\frac{5}{4}}}}} = \frac{{{a^{\frac{1}{4}}}\left( {1 – {a^2}} \right)}}{{{a^{\frac{1}{4}}}\left( {1 – a} \right)}} = \frac{{{a^{\frac{1}{4}}}\left( {1 – a} \right)\left( {1 + a} \right)}}{{{a^{\frac{1}{4}}}\left( {1 – a} \right)}} = 1 + a$

Câu 3. Cho hai số dương $a,b$ với $a \ne 1$. Số $\alpha $ thoả mãn ${a^\alpha } = b$, khi đó $\alpha $ bằng

A. $\alpha = lo{g_a}b$.

B. $\alpha = lo{g_b}a$.

C. $\alpha = lo{g_a}a$.

D. $\alpha = lo{g_b}b$.

Lời giải

Đáp án đúng là: A

${a^\alpha } = b$ với $a,b$ là hai số dương, $a \ne 1$.

Câu 4. Hàm số nào sau đây là hàm số mũ

A. $y = {2^{\frac{x}{2}}}$.

B. $y = – {2^x}$.

C. $y = {x^{ – 2}}$.

D. $y = {x^2}$.

Lời giải

Đáp án đúng là: A

Hàm số mũ là $y = {2^{\frac{x}{2}}}$.

Câu 5. Trong các hình sau, hình nào là dạng đồ thị của hàm số $y = lo{g_a}x,a > 1$

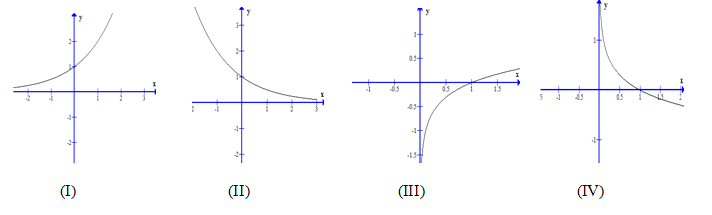
A. (I).

B. (II).

C. (IV).

D. (III).

Lời giải

Đáp án đúng là: D

Đồ thị của hàm số $y = lo{g_a}x,a > 1$ là hình III.

Câu 6. Một sinh viên gửi tiết kiệm ngân hàng lãi suất $13\% $ / năm với hình thức lãi kép. Hỏi sau bao nhiêu năm sinh viên đó thu được gấp ba lần số tiền ban đầu, biết lãi suất cố định trong các năm.

A. 8 năm 9 tháng.

B. 15 năm 5 tháng.

C. 8 năm.

D. 9 năm.

Lời giải

Đáp án đúng là: D

Giả sử sinh viên đó gửi vào ngân hàng $A$ đồng với lãi kép $13\% $ /năm thì số tiền bạn sinh viên đó nhận được cả vốn lần lãi sau n kì hạn là: ${S_n} = A{(1 + 13\% )^n}$.

Theo đề có ${S_n} = 3A$ nên $3A = A{(1 + 13\% )^n} \Rightarrow 3 = {(1 + 13\% )^n} \Rightarrow n = lo{g_{1 + 13\% }}3 \approx 9$.

Vậy sau khoảng 9 năm sinh viên đó thu được gấp ba lần số tiền ban đầu.

Câu 7. Tổng các nghiệm thực của phương trình ${3^{{x^2} – 3x + 8}} = {9^{2x – 1}}$ bằng

A. $ – 7$ .

B. $5$ .

C. $6$ .

D. $7$ .

Lời giải

Đáp án đúng là: D

${3^{{x^2} – 3x + 8}} = {9^{2x – 1}}$$ \Leftrightarrow {3^{{x^2} – 3x + 8}} = {3^{2\left( {2x – 1} \right)}}$

$ \Leftrightarrow {x^2} – 3x + 8 = 4x – 2$$ \Leftrightarrow {x^2} – 7x + 10 = 0$

$ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{x = 2} \\
{x = 5}
\end{array}} \right.$

Vậy tổng hai nghiệm của phương trình là 7 .

Câu 8. Tổng các giá trị nghiệm của phương trình $\log _{\frac{1}{2}}^2x – 5{\log _2}x + 6 = 0$ bằng

A. 10 .

B. $\frac{{65}}{{64}}$.

C. 5 .

D. $\frac{{129}}{{64}}$.

Lời giải

Đáp án đúng là: $D$

Điều kiện: $x > 0$.

$log_{\frac{1}{2}}^2x – 5lo{g_2}x + 6 = 0$

$ \Leftrightarrow – log_2^2x – 5lo{g_2}x + 6 = 0$

$ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{lo{g_2}x = – 6} \\
{lo{g_2}x = 1}
\end{array}} \right.$

$ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = \frac{1}{{64}}} \\
{x = 2}
\end{array}} \right.$ (thỏa mãn).

Tổng các nghiệm là: $2 + \frac{1}{{64}} = \frac{{129}}{{64}}$.

Câu 9. Cho hàm số $y = f\left( x \right)$ có đồ thị $\left( C \right)$ và đạo hàm $f’\left( 2 \right) = 6$. Hệ số góc của tiếp tuyến của (C) tại điểm $M\left( {2;f\left( 2 \right)} \right)$ bằng

A. 2 .

B. 3 .

C. 6 .

D. 12 .

Lời giải

Đáp án đúng là: ${\mathbf{C}}$

Hệ số góc của tiếp tuyến của $\left( C \right)$ tại điểm $M\left( {2;f\left( 2 \right)} \right)$ bằng $f’\left( 2 \right) = 6$.

Câu 10. Hàm số $f\left( x \right) = {x^2} + 2x + 1$. Khi đó với $a \in \mathbb{R}$ thì khẳng định nào đúng ?

A. $f’\left( a \right) = 2a + 3$.

B. $f’\left( a \right) = {a^2} + 1$.

C. $f’\left( a \right) = 2a + 2$.

D. $f’\left( a \right) = 2a$.

Lời giải

Đáp án đúng là: C

$f’\left( x \right) = 2x + 2 \Rightarrow f’\left( a \right) = 2a + 2$.

Câu 11. Đạo hàm của hàm số $y = {3^x}$ là

A. $y’ = x \cdot {3^{x – 1}}$.

B. $y’ = {3^x} \cdot ln3$.

C. $y’ = {3^x}$.

D. $y’ = \frac{{{3^x}}}{{ln3}}$.

Lời giải

Đáp án đúng là: B

$y’ = {\left( {{3^x}} \right)’} = {3^x}ln3$.

Câu 12. Một chất điểm chuyển động có phương trình $s\left( t \right) = t + 1$ ( $t$ tính bằng giây, $s$ tính bằng mét). Vận tốc tức thời của chất điểm tại thời điểm $t = 3\;s$ bằng

A. $1\;m/s$.

B. $15\;m/s$.

C. $4\;m/s$.

D. $0\;m/s$.

Lời giải

Đáp án đúng là: A

Ta có $v\left( t \right) = s’\left( t \right) = 1$.

Do đó vận tốc tức thời của chất điểm tại thời điểm $t = 3\;s$ bằng $1\;m/s$.

Câu 13. Hàm số $y = {x^5}$ có đạo hàm cấp 2 là

A. $5{x^4}$.

B. $20x$.

C. $20{x^3}$.

D. $5{x^3}$.

Lời giải

Đáp án đúng là: C

Có $y’ = {\left( {{x^5}} \right)’} = 5{x^4};y” = 20{x^3}$.

Câu 14. Cho $f\left( x \right) = 201$. Tính $f”\left( x \right)$.

A. $f”\left( x \right) = 2$.

B. $f”\left( x \right) = x$.

C. $f”\left( x \right) = 0$

D. $f”\left( x \right) = 1$.

Lời giải

Đáp án đúng là: $C$

Câu 15. Hàm số $y = \frac{1}{{x + 1}}$ có đạo hàm cấp hai tại $x = 1$ là

A. $y”\left( 1 \right) = \frac{1}{2}$.

B. $y”\left( 1 \right) = – \frac{1}{4}$.

C. $y”\left( 1 \right) = 4$.

D. $y”\left( 1 \right) = \frac{1}{4}$.

Lời giải

Đáp án đúng là: D

$y’ = {\left( {\frac{1}{{x + 1}}} \right)’} = – \frac{1}{{{{(x + 1)}^2}}};\;y” = \frac{2}{{{{(x + 1)}^3}}}$.

Do đó $y”\left( 1 \right) = \frac{2}{{{{(1 + 1)}^3}}} = \frac{1}{4}.$

Câu 16. Hàm số $y = cotx$ có đạo hàm là:

A. $y’ = – \frac{1}{{co{s^2}x}}$.

B. $y’ = – \frac{1}{{si{n^2}x}}$.

C. $y’ = \frac{1}{{si{n^2}x}}$

D. $y’ = – tanx$.

Lời giải

Đáp án đúng là: B

$y’ = {(cotx)’} = – \frac{1}{{si{n^2}x}}$.

Câu 17. Đạo hàm của hàm số là

A. $y’ = x \cdot {3^{x – 1}}$.

B. $y’ = {3^x} \cdot ln3$.

C. $y’ = {3^x}$.

D. $y’ = \frac{{{3^x}}}{{ln3}}$.

Lời giải

Đáp án đúng là: B

$y’ = {\left( {{3^x}} \right)’} = {3^x}ln3$.

Câu 18. Cho $f(x) = {({x^2} – 3x + 3)^2}$. Biểu thức $f’\left( 1 \right)$ có giá trị là bao nhiêu?

A. -1 .

B. -2 .

C. $ – 12$.

D. 1.

Lời giải

Đáp án đúng là: B

Có $f’\left( x \right) = 2\left( {2x – 3} \right)\left( {{x^2} – 3x + 3} \right)$.

Có $f’\left( 1 \right) = 2\left( {2.1 – 3} \right)\left( {{1^2} – 3.1 + 3} \right) = – 2$.

Câu 19. Đạo hàm của hàm số $y = {x^4} – 3{x^2} + 2x – 1$ bằng biểu thức nào sau đây?

A. $y’ = 4{x^3} – 6x + 3$.

B. $y’ = 4{x^4} – 6x + 2$.

C. $y’ = 4{x^3} – 3x + 2$.

D. $y’ = 4{x^3} – 6x + 2$.

Lời giải

Đáp án đúng là: D

$y’ = 4{x^3} – 6x + 2$.

Câu 20. Tung một con xúc xắc, gọi A là biến cố: “Xuất hiện mặt có số chấm lớn hơn hoặc bằng 4″, B là biến cố: ” Xuất hiện mặt có số chấm nhỏ hơn hoặc bằng 2″. Khẳng định nào sau đây là đúng?

A. $A$ và $B$ là hai biến cố xung khắc.

B. $A$ và $B$ là hai biến cố đối.

C. Cả $A$ và $B$ đều đúng.

D. Không đủ thông tin để kết luận.

Đáp án đúng là: A

Hai biến cố $A$ và $B$ là hai biến cố xung khắc.

Câu 21. Cho $A,B$ là hai biến cố độc lập. Biết $P\left( A \right) = \frac{1}{3},P\left( B \right) = \frac{1}{4}$. Tính $P\left( {AB} \right)$.

A. $\frac{7}{{12}}$.

B. $\frac{1}{{12}}$.

C. $\frac{1}{7}$.

D. $\frac{1}{2}$.

Lời giải

Đáp án đúng là: B

$P\left( {AB} \right) = P\left( A \right) \cdot P\left( B \right) = \frac{1}{{12}}$.

Câu 22. Hai xạ thủ $M$ và $N$ cùng bắn súng vào một tấm bia. Biết rằng xác suất bắn trúng của xạ thủ $M$ là 0,3, của xạ thủ $N$ là 0,2 . Khả năng bắn trúng của hai xạ thủ là độc lập. Xác suất của biến cố “Cả hai xạ thủ đều bắn trúng” là

A. 0,05 .

B. 0,06 .

C. 0,07 .

D. 0,08 .

Lời giải

Đáp án đúng là: B

Gọi $A$ là biến cố: “Xạ thủ $M$ bắn trúng bia”.

$B$ là biến cố: “Xạ thủ $N$ bắn trúng bia”.

C là biến cố: “Cả hai xạ thủ đều bắn trúng bia”.

Khi đó $C = A.B$.

Theo đề có $P\left( A \right) = 0,3;P\left( B \right) = 0,2$.

Vì $A,B$ là hai biến cố độc lập nên $P\left( C \right) = P\left( {A \cdot B} \right) = P\left( A \right) \cdot P\left( B \right) = 0,3 \cdot 0,2 = 0,06$.

Câu 23. Gọi $S$ là tập các số tự nhiên có 4 chữ số khác nhau được tạo từ tập $E = \left\{ {1;2;3;4;5} \right\}$. Chọn ngẫu nhiên một số từ tập $S$. Tính xác suất để số được chọn là một số chẵn?

A. $\frac{3}{4}$.

B. $\frac{2}{5}$.

C. $\frac{3}{5}$.

D. $\frac{1}{2}$.

Lời giải

Đáp án đúng là: B

Từ tập $E = \left\{ {1;2;3;4;5} \right\}$ ta lập được $A_5^4 = 120$ số tự nhiên có 4 chư số khác nhau.

Gọi số chẵn có 4 chữ số khác nhau có dạng $\overline {abcd} ;\left( {a,b,c,d \in E} \right)$.

Ta có $d = \left\{ {2;4} \right\} \Rightarrow d$ có 2 cách chọn.

Chọn 3 số xếp vào vị trí $a,b,c$ có $A_4^3$ cách chọn.

Do đó có $2.A_4^3 = 48$ cách chọn.

Vậy xác suất để số được chọn là một số chã̃n là $\frac{{48}}{{120}} = \frac{2}{5}$.

Câu 24. Gieo một đồng xu cân đối và đồng chất liên tiếp ba lần. Gọi $A$ là biến cố “Có ít nhất hai mặt sấp xuất hiện liên tiếp” và $B$ là biến cố “Kết quả ba lần gieo là như nhau”. Xác định biến cố $A \cup B$.

A. $A \cup B = \left\{ {SSS,SSN,NSS,SNS,NNN} \right\}$.

B. $A \cup B = \left\{ {SSS,NNN} \right\}$.

C. $A \cup B = \left\{ {SSS,SSN,NSS,NNN} \right\}$.

D. $A \cup B = \Omega $.

Lời giải

Đáp án đúng là: C

Ta có $A = \left\{ {SSS,SSN,NSS} \right\};B = \left\{ {SSS,NNN} \right\}$.

Khi đó $A \cup B = \left\{ {SSS,SSN,NSS,NNN} \right\}$.

Câu 25. Cho $A,B$ là hai biến cố độc lập. Biết $P\left( A \right) = 0,5;P\left( {A \cap B} \right) = 0,2$. Tính $P\left( {A \cup B} \right)$.

A. 0,3 .

B. 0,5 .

C. 0,6 .

D. 0,7 .

Lời giải

Đáp án đúng là: D

Vì $A,B$ là hai biến cố độc lập nên $P\left( {A \cap B} \right) = P\left( A \right) \cdot P\left( B \right) \Rightarrow P\left( B \right) = 0,2:0,5 = 0,4$.

Do đó $P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) – P\left( {AB} \right) = 0,5 + 0,4 – 0,2 = 0,7$.

Câu 26. Cho hình lập phương $ABCD \cdot A’B’C’D’$. Góc giữa hai đường thẳng $A’C’$ và $BD$ bằng.

A. ${60^ \circ }$.

B. ${30^ \circ }$.

C. ${45^ \circ }$.

D. ${90^ \circ }$.

Lời giải

Đáp án đúng là: D

Có $AC//A’C’$ nên $\left( {A’C’,BD} \right) = \left( {AC,BD} \right) = {90^ \circ }$.

Câu 27. Cho hình lập phương $ABCD \cdot A’B’C’D’$ như hình vẽ

Khẳng định nào sau đây đúng

A. $AA’ \bot \left( {ABB’A’} \right)$.

B. $CA’ \bot \left( {ABC’D’} \right)$.

C. $AA’ \bot \left( {ABCD} \right)$.

D. $CA’ \bot \left( {ABCD} \right)$.

Lời giải

Đáp án đúng là: C

Có $ABCD \cdot A’B’C’D’$ là hình lập phương nên $AA’ \bot \left( {ABCD} \right)$.

Câu 28. Thể tích của khối lăng trụ có diện tích đáy $S$ và chiều cao $h$ là:

A. $\frac{1}{3}Sh$.

B. $Sh$.

C. $\frac{1}{2}Sh$.

D. $3Sh$.

Lời giải

Đáp án đúng là: B

Thể tích của khối lăng trụ có diện tích đáy $S$ và chiều cao $h$ là: $V = S.h$.

Câu 29. Cho hình chóp $S.ABCD$ có $ABCD$ là hình chữ nhật và $SA \bot \left( {ABCD} \right)$. Mệnh đề nào dưới đây đúng ?

A. $AB \bot \left( {SAD} \right)$.

B. $BC \bot \left( {SAD} \right)$.

C. $AC \bot \left( {SAD} \right)$.

D. $BD \bot \left( {SAD} \right)$.

Lời giải

Đáp án đúng là: A

Vì $SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AB$ mà $AB \bot AD$ (do $ABCD$ là hình chữ nhật).

Do đó $AB \bot \left( {SAD} \right)$.

Câu 30. Cho khối chóp tứ giác đều $S \cdot ABCD$ có cạnh đáy bằng $\sqrt 2 a$ và tam giác $SAC$ đều. Thể tích của khối chóp đã cho bằng

A. $\frac{{\sqrt 3 {a^3}}}{2}$.

B. $\frac{{\sqrt 3 {a^3}}}{3}$.

C. $\frac{{2\sqrt 3 {a^3}}}{3}$.

D. $\frac{{3\sqrt 3 {a^3}}}{2}$.

Lời giải

Đáp án đúng là: C

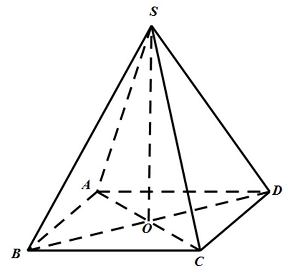
${S_{ABCD}} = {(\sqrt 2 a)^2} = 2{a^2}$

Gọi $O = AC \cap BD \Rightarrow SO \bot \left( {ABCD} \right)$

$ \Rightarrow \;$ là đường cao của chóp và

$SO$ là đường cao của tam giác đều $SAC \Rightarrow SO = \frac{{2a \cdot \sqrt 3 }}{2} = a\sqrt 3 $

Vậy $V = \frac{1}{3} \cdot 2{a^2} \cdot a\sqrt 3 = \frac{{2\sqrt 3 a}}{3}$.

Câu 31. Cho hai mặt phẳng $\left( P \right)$ và $\left( Q \right)$ cắt nhau và một điểm $M$ không thuộc $\left( P \right)$ và $\left( Q \right)$. Qua $M$ có bao nhiêu mặt phẳng vuông góc với $P$ và $Q$?

A. 1 .

B. 2 .

C. 3 .

D. Vô số.

Lời giải

Đáp án đúng là: A

Cho hai mặt phẳng $\left( P \right)$ và $\left( Q \right)$ cắt nhau và một điểm $M$ không thuộc $\left( P \right)$ và $\left( Q \right)$. Qua $M$ có 1 mặt phẳng vuông góc với $\left( P \right)$ và $\left( Q \right)$.

Câu 32. Cho hình chóp $S \cdot ABCD$ có $ABCD$ là hình vuông, $SA$ vuông góc với mặt phẳng đáy. Mặt phẳng $\left( {ABCD} \right)$ vuông góc với mặt phẳng nào dưới đây?

A. $\left( {SAC} \right)$.

B. $\left( {SBD} \right)$.

C. $\left( {SCD} \right)$.

D. $\left( {SBC} \right)$.

Lời giải

Đáp án đúng là: A

Vì $ABCD$ là hình vuông nên $AC \bot BD$ mà $SA \bot BD$ (do $SA \bot \left( {ABCD} \right)$ ).

Do đó $BD \bot \left( {SAC} \right) \Rightarrow \left( {SAC} \right) \bot \left( {ABCD} \right)$.

Câu 33. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a,SA \bot \left( {ABCD} \right)$. Tính khoảng cách từ điểm $B$ đến mặt phẳng

A. $\frac{a}{2}$.

B. $\frac{{a\sqrt 2 }}{2}$.

C. $\frac{{a\sqrt 2 }}{3}$.

D. $\frac{{a\sqrt 2 }}{4}$.

Lời giải

Đáp án đúng là: B

Gọi $O$ là tâm của hình vuông $ABCD$.

Vì $ABCD$ là hình vuông nên $AC \bot BO$ mà $BO \bot SA\left( {SA \bot \left( {ABCD} \right)} \right)$.

Suy ra $BO \bot \left( {SAC} \right)$

Do đó $d\left( {B,\left( {SAC} \right)} \right) = BO$.

Vì $ABCD$ là hình vuông cạnh a nên $BD = a\sqrt 2 \Rightarrow BO = \frac{{a\sqrt 2 }}{2}$.

Câu 34. Trong các mệnh đề sau, mệnh đề nào đúng?

A. Góc giữa đường thẳng và mặt phẳng bằng góc giữa đường thẳng đó và hình chiếu của nó trên mặt phẳng đã cho.

B. Góc giữa đường thẳng a và mặt phẳng $\left( P \right)$ bằng góc giữa đường thẳng $b$ và mặt phẳng $\left( P \right)$ khi và $b$ song song (hoặc $a$ trùng với $b$ ).

C. Góc giữa đường thẳng a và mặt phẳng $\left( P \right)$ bằng góc giữa đường thẳng $a$ và mặt phẳng $\left( Q \right)$ thì mặt phẳng $\left( P \right)$ song song với mặt phẳng $\left( Q \right)$.

D. Góc giữa đường thẳng a và mặt phẳng $\left( P \right)$ bằng góc giữa đường thẳng $b$ và mặt phẳng $\left( P \right)$ thì $a$ song song với $b$.

Lời giải

Đáp án đúng là: B

Góc giữa đường thẳng a và mặt phẳng $\left( P \right)$ bằng góc giữa đường thẳng $b$ và mặt phẳng $\left( P \right)$ khi $a$ và $b$ song song (hoặc $a$ trùng với $b$ ).

Câu 35. Cho hình chóp $S.ABC$ có $SA$ vuông góc với mặt phẳng $\left( {ABC} \right),SA = 2a$, tam giác $ABC$ vuông tại $B,AB = a\sqrt 3 $ và $BC = a$ (minh họa như hình vẽ bên). Góc giữa đường thẳng $SC$ và mặt phẳng $\left( {ABC} \right)$ bằng

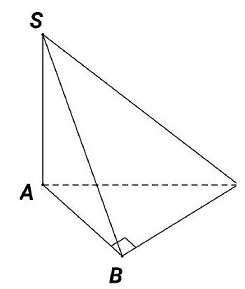
A. ${90^ \circ }$.

B. ${45^ \circ }$.

C. ${30^ \circ }$.

D. ${60^ \circ }$.

Lời giải

Đáp án đúng là: B

Vì $SA \bot \left( {ABC} \right)$ nên $AC$ là hình chiếu của $SC$ trên mặt phẳng $\left( {ABC} \right)$.

Do đó góc giữa $SC$ và mặt phẳng $\left( {ABC} \right)$ bằng $SCA$.

Vì $\vartriangle ABC$ vuông tại B nên $AC = \sqrt {A{B^2} + B{C^2}} = 2a$.

Xét $\vartriangle SAC$ vuông tại $A$, có $tanSCA = \frac{{SA}}{{AC}} = \frac{{2a}}{{2a}} = 1 \Rightarrow SCA = {45^ \circ }$.

III. Lời giải tự luận

Bài 1. (1 điểm) a) Tính đạo hàm cấp hai của hàm số $y = sinax$ ( $a$ là hằng số).

b) Một chất điểm chuyển động có quãng đường được cho bởi phương trình $s\left( t \right) = \frac{1}{4}{t^4} – {t^3} + \frac{5}{2}{t^2} + 10t$, trong đó $t > 0$ với $t$ tính bằng giây (s) và $s$ tính bằng mét (m). Tính vận tốc chuyển động của chất điểm tại thời điểm chất điểm có gia tốc chuyển động nhỏ nhất.

Lời giải.

a) $y’ = {(sinax)’} = acosax$

$y” = {(acosax)’} = – {a^2}sinax$.

b) Gọi $v\left( t \right),a\left( t \right)$ lần lượt là vận tốc và gia tốc của chất điểm.

Ta có $\left\{ {\begin{array}{*{20}{l}}
{v\left( t \right) = s’\left( t \right) = {t^3} – 3{t^2} + 5t + 10} \\
{a\left( t \right) = v’\left( t \right) = 3{t^2} – 6t + 5}
\end{array}} \right.$.

Mà $a\left( t \right) = 3{t^2} – 6t + 5 = 3{(t – 1)^2} + 2 \geqslant 2$ với mọi $t$, dấu ” $ = $ ” xảy ra khi chỉ khi

Suy ra gia tốc chuyển động của chất điểm nhỏ nhất bằng $2\;m/{s^2}$ khi $t = 1$.

Vận tốc chuyển động của chất điểm tại thời điểm gia tốc nhỏ nhất là

$v\left( 1 \right) = {(1)^3} – 3 \cdot {1^2} + 5 \cdot 1 + 10 = 13\left( {\;m/s} \right).$

Bài 2. (1 điểm) Cho hình chóp có đáy là tam giác vuông cân tại $A,SA \bot \left( {ABC} \right)$ và $;SA = \frac{{a\sqrt 6 }}{2}$. Gọi $H$ là trung điểm cạnh $BC$.

a) Chứng minh: $BC \bot \left( {SAH} \right)$.

b) Tính góc giữa đường thẳng $SH$ và mặt phẳng $\left( {ABC} \right)$.

Lời giải

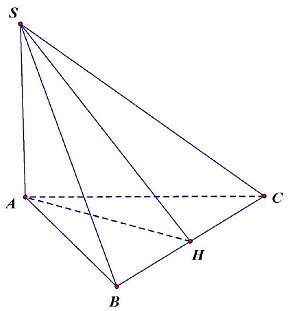
a) Ta có: $SA \bot \left( {ABC} \right) \Rightarrow SA \bot BC$

Do $\vartriangle ABC$ cân tại $A,H$ là trung điểm của $BC$ nên $AH \bot BC$

Suy ra $BC \bot \left( {SAH} \right)$.

b) Vì $SA \bot \left( {ABC} \right)$ nên $AH$ là hình chiếu của $SH$ trên mặt phẳng $\left( {ABC} \right)$.

Do đó $\left( {SH,\left( {ABC} \right)} \right) = \widehat {SHA}$.

Có $BC = \sqrt {A{B^2} + A{C^2}} = a\sqrt 2 $ mà $AH$ là đường trung tuyến ứng với cạnh $BC$ của tam giác vuông $ABC$ nên $AH = \frac{{BC}}{2} = \frac{{a\sqrt 2 }}{2}$.

$tanSHA = \frac{{SA}}{{AH}} = \frac{{\frac{{a\sqrt 6 }}{2}}}{{\frac{{a\sqrt 2 }}{2}}} = \sqrt 3 $

Xét $\vartriangle SAH$ vuông tại $A$, ta có

Vậy $\left( {SH,\left( {ABC} \right)} \right) = \widehat {SHA} = {60^ \circ }$.

Bài 3. (1 điểm) Gọi $A$ là tập hợp tất cả các số tự nhiên có chữ số đôi một khác nhau. Chọn ngẫu nhiên một số thuộc $A$. Tính xác suất để số tự nhiên được chọn chia hết cho 25 .

Lời giải

Số phần tử không gian mẫu $n\left( \Omega \right) = 9 \cdot A_9^7$.

Gọi $A$ là biến cố chọn được số chia hết cho 25 .

Số $\overline {{a_1}{a_2}{a_3}{a_4}{a_5}{a_6}{a_7}{a_8}} \vdots 25$ khi $\overline {{a_7}{a_8}} \vdots 25$, nên số $\overline {{a_7}{a_8}} $ là $25,50,75$.

TH 1: số $\overline {{a_1}{a_2}{a_3}{a_4}{a_5}{a_6}25} $ có 7 . $A_7^5$ số.

TH 2: số $\overline {{a_1}{a_2}{a_3}{a_4}{a_5}{a_6}75} $ có 7 . $A_7^5$ số.

TH 3: số có số

$ \Rightarrow n\left( A \right) = 7 \cdot A_7^5 + 7 \cdot A_7^5 + A_8^6$

$P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{11}}{{324}}$.