Đề Thi HK2 Toán 11 Chân Trời Sáng Tạo Theo Form Mới Giải Chi Tiết-Đề 5

Đề thi HK2 Toán 11 Chân trời sáng tạo theo form mới giải chi tiết-Đề 5 được soạn dưới dạng file word và PDF gồm 4 trang. Các bạn xem và tải về ở dưới.

Phần 1. Câu trắc nghiệm nhiều phương án chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thi sinh chỉ chọn một phưong án đúng nhất.

Câu 1. Với mọi số thực dương $a,b,x,y$ và $a,b$ khác 1 , mệnh đề nào sau đây sai?

A. $lo{g_b}a \cdot lo{g_a}x = lo{g_b}x$. B. $lo{g_a}\left( {xy} \right) = lo{g_a}x + lo{g_b}x$.

C. $lo{g_a}\frac{x}{y} = lo{g_a}x – lo{g_a}y$. D. $lo{g_a}\frac{1}{x} = \frac{1}{{lo{g_a}x}}$.

Câu 2. Hàm số nào sau đây đồng biến trên $\mathbb{R}$ ?

A. $y = {\left( {\frac{e}{\pi }} \right)^x}$. B. $y = {\left( {\frac{2}{e}} \right)^x}$. C. $y = {(\sqrt 2 )^x}$. D. $y = {(0,5)^x}$.

Câu 3. Giải phương trình $lo{g_{\frac{1}{2}}}\left( {x – 1} \right) = – 2$.

A. $x = 2$. B. $x = \frac{5}{2}$. C. $x = \frac{3}{2}$. D. $x = 5$.

Câu 4. Cho hình lập phương $ABCD \cdot A’B’C’D’$, góc giữa hai đường thẳng $A’B$ và $B’C$ là

A. ${90^ \circ }$. B. ${60^ \circ }$. C. ${30^ \circ }$. D. ${45^ \circ }$.

Câu 5. Cho hình chóp $S \cdot ABCD$ có đáy là hình vuông cạnh $a$. $SA$ vuông góc với mặt phẳng $\left( {ABCD} \right)$ và $SA = a\sqrt 6 $ (hình vẽ). Gọi $\alpha $ là góc giữa đường thẳng $SB$ và mặt phẳng $\left( {SAC} \right)$. Tính $sin\alpha $ ta được kết quả là:

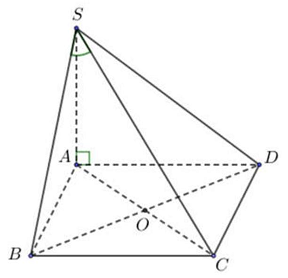
A. $\frac{1}{{\sqrt {14} }}$. B. $\frac{{\sqrt 2 }}{2}$. C. $\frac{{\sqrt 3 }}{2}$. D. $\frac{1}{5}$.

Câu 6. Cho hình chóp $S \cdot ABCD$ có đáy $ABCD$ là hình vuông tâm $O,SA \bot \left( {ABCD} \right)$. Khẳng định nào sau đây sai?

A. $\left( {SBC} \right) \bot \left( {SAB} \right)$. B. $\left( {SAB} \right) \bot \left( {ABCD} \right)$. C. $\left( {SAC} \right) \bot \left( {ABCD} \right)$. D. $\left( {SAC} \right) \bot \left( {SAD} \right)$.

Câu 7. Cho hình chóp $S \cdot ABCD$ có $ABCD$ là hình vuông tâm $O$ cạnh $a$. Tính khoảng cách giữa $SC$ và $AB$ biết rằng $SO = a$ và vuông góc với mặt đáy của hình chóp.

A. $a$. B. $\frac{{a\sqrt 5 }}{5}$. C. $\frac{{2a}}{5}$. D. $\frac{{2a}}{{\sqrt 5 }}$.

Câu 8. Cho một hình chóp $S \cdot ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, cạnh bên $SA$ vuông góc với đáy, $SA = 2a$, thể tích của khối chóp là $V$. Khẳng định nào sau đây đúng ?

A. $V = \frac{2}{3}{a^3}$. B. $V = 2{a^3}$. C. $V = \frac{1}{3}{a^3}$. D. $V = {a^3}$.

Câu 9. Cho hai biến cố $A$ và $B$ độc lập. Khi đó $P\left( {AB} \right)$ bằng:

A. $P\left( A \right) – P\left( B \right)$. B. $P\left( A \right) + P\left( B \right)$. C. $P\left( A \right) \cdot P\left( B \right)$. D. $\left[ {1 – P\left( A \right)} \right]\left[ {1 – P\left( B \right)} \right]$.

Câu 10. Một hộp có 5 viên bi màu đen, 4 viên bi màu trắng. Chọn ngẫu nhiên 2 viên bi từ chiếc hộp đó. Tìm xác suất để chọn được 2 viên bi cùng màu.

A. $\frac{1}{4}$. B. $\frac{4}{9}$. C. $\frac{1}{9}$. D. $\frac{5}{4}$.

Câu 11. Tính đạo hàm của hàm số $f\left( x \right) = {e^{2x – 3}}$.

A. $f’\left( x \right) = 2 \cdot {e^{2x – 3}}$. B. $f’\left( x \right) = – 2 \cdot {e^{2x – 3}}$. C. $f’\left( x \right) = 2 \cdot {e^{x – 3}}$. D. $f’\left( x \right) = {e^{2x – 3}}$.

Câu 12. Phương trình tiếp tuyến của đồ thị hàm số $y = {x^2} – x – 2$ tại điểm có hoành độ $x = 1$ là

A. $2x – y = 0$ B. $2x – y – 4 = 0$. C. $x – y – 1 = 0$. D. $x – y – 3 = 0$.

Phần 2. Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗ ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai

Câu 1. An và Huy lần lượt lấy ngẫu nhiên các mảnh giấy có kích thước giống nhau được đánh số từ 1 đến 9 trong một hộp kín. Gọi biến cố $A$ : “An lấy được mảnh giấy đánh số chẵn”. Biến cố $B$ : “Huy lấy được mảnh giấy đánh số chẵn”. Biến cố $C$ : “An lấy được mảnh giấy đánh số 8 “. Khi đó:

a) $P\left( A \right) = \frac{4}{9}$

b) $P\left( C \right) = \frac{1}{9}$

c) $P\left( B \right) = \frac{4}{9}$

d) Hai biến cố $A$ và $C$ không độc lập.

Câu 2. Cho ba tia $Ox,Oy,Oz$ vuông góc nhau từng đôi một. Trên $Ox,Oy,Oz$ lần lượt lấy các điểm $A,B,C$ sao cho $OA = OB = OC = a$. Các mệnh đề sau đúng hay sai?

a) $O.ABC$ là hình chóp đều.

b) Tam giác $ABC$ có diện tích $S = \frac{{{a^2}\sqrt 3 }}{2}$.

c) Tam giác $ABC$ có chu vi $2p = \frac{{3a\sqrt 2 }}{2}$.

d) Ba mặt phẳng $\left( {OAB} \right),\left( {OBC} \right),\left( {OCA} \right)$ vuông góc với nhau từng đôi một.

Câu 3. Cho phương trình ${3^x} = m + 1$. Các mệnh đề sau đúng hay sai?

a) Phương trình có nghiệm dương nếu $m > 0$.

b) Phương trình luôn có nghiệm với mọi $m$.

c) Phương trình luôn có nghiệm duy nhất $x = lo{g_3}\left( {m + 1} \right)$.

d) Phương trình có nghiệm với $m \geqslant – 1$.

Câu 4. Một chuyển động xác định bởi phương trình $S\left( t \right) = {t^3} – 3{t^2} – 9t + 2$. Trong đó $t$ được tính bằng giây, $S$ được tính bằng mét. Các mệnh đề sau đúng hay sai?

a) Vận tốc của chuyển động bằng $0khit = 0\;s$ hoặc $t = 2\;s$.

b) Gia tốc của chuyển động tại thời điểm $t = 3\;s$ là $12\;m/{s^2}$.

c) Gia tốc của chuyển động bằng $0\;m/{s^2}$ khi $t = 0\;s$.

d) Vận tốc của chuyển động tại thời điểm $t = 2\;s$ là $v = 18\;m/s$.

Phần 3. Câu trả lời ngắn.
Thí sinh trả lời đáp án từ câu 1 đến câu 6.

Câu 1. Một chiếc hộp chứa 8 viên bi màu xanh, 5 viên bi màu đỏ có cùng kích thước và khối lượng. Lấy lần lượt một viên bi từ hộp và không trả lại, thực hiện hai lần liêp tiếp. Tính xác suất để lấy được ít nhất 1 viên bi màu đỏ.

Câu 2. Khi tung một đồng xu không cân đối thì người ta thấy rằng xác suất để đồng xu xuất hiện mặt sấp bằng $\frac{2}{3}$. Tung đồng xu này ba lần liên tiếp. Tính xác suất để chỉ xuất hiện mặt sấp;

Câu 3. Cho hình chóp $S.ABC$ có đáy là tam giác đều cạnh $a,SA \bot \left( {ABC} \right)$ và $SB = a\sqrt 5 $. Gọi $M$ là trung điểm $BC$. Tính góc giữa đường thẳng $SM$ và mặt phẳng $\left( {SAC} \right)$ ?

Câu 4. Cho hình chóp $S.ABCD$ có $SA \bot \left( {ABCD} \right),SA = 3a,ABCD$ là hình vuông cạnh bằng $a$. Tính khoảng cách giữa hai đường thẳng $AC$ và $SB$.

Câu 5. Số lượng tế bào còn sống trong khoảng thời gian $t$ (phút) kể từ lúc tiến hành thí nghiệm được xác định bởi $f\left( t \right) = a \cdot {e^{bt}}$ trong đó $a,b$ là các hằng số cho trước. Nếu bắt đầu một thí nghiệm sinh học với 5.000 .000 tế bào thì có $45\% $ các tế bào sẽ chết sau mỗi phút, hỏi sau ít nhất bao lâu nó sẽ còn ít hơn 1.000 tế bào?

Câu 6. Một vật rơi tự do theo phương thẳng đứng có quãng đường dịch chuyển $S\left( t \right) = \frac{1}{2}g{t^2}$ với $t$ là thời gian tính bằng giây $\left( s \right)$ kể từ lúc vật bắt đầu rơi, $S$ là quãng đường tính bằng mét $\left( m \right),g = 9,8\;m/{s^2}$. Vận tốc tức thời của vật tại thời điểm $t = 4s$ ?

ĐÁP ÁN VÀ LỜI GIẢI THAM KHẢO

Phần 1. Câu trắc nghiệm nhiều phương án chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phuơng án đúng nhất.

1D	2C	3D	4B	5A	6D
7D	8A	9C	10B	11A	12D

Câu 1. Với mọi số thực dương $a,b,x,y$ và $a,b$ khác 1 , mệnh đề nào sau đây sai?

A. $lo{g_b}a \cdot lo{g_a}x = lo{g_b}x$.

B. $lo{g_a}\left( {xy} \right) = lo{g_a}x + lo{g_b}x$.

C. $lo{g_a}\frac{x}{y} = lo{g_a}x – lo{g_a}y$.

D. $lo{g_a}\frac{1}{x} = \frac{1}{{lo{g_a}x}}$.

$lo{g_a}\frac{1}{x} = \frac{1}{{lo{g_a}x}}$

Lời giải

Câu 2. Hàm số nào sau đây đồng biến trên $\mathbb{R}$ ?

A. $y = {\left( {\frac{e}{\pi }} \right)^x}$.

B. $y = {\left( {\frac{2}{e}} \right)^x}$.

C. $y = {(\sqrt 2 )^x}$.

D. $y = {(0,5)^x}$.

Lời giải

Hàm số $y = {a^x}$ đồng biến khi $a > 1$ và nghịch biến khi $0 < a < 1$.

Suy ra hàm số $y = {(\sqrt 2 )^x}$ đồng biến trên $\mathbb{R}$.

Câu 3. Giải phương trình $lo{g_{\frac{1}{2}}}\left( {x – 1} \right) = – 2$.

A. $x = 2$.

B. $x = \frac{5}{2}$.

C. $x = \frac{3}{2}$.

D. $x = 5$.

Lời giải

Ta có $lo{g_{\frac{1}{2}}}\left( {x – 1} \right) = – 2 \Leftrightarrow x – 1 = {\left( {\frac{1}{2}} \right)^{ – 2}} \Leftrightarrow x = 5$.

Câu 4. Cho hình lập phương $ABCD \cdot A’B’C’D’$, góc giữa hai đường thẳng $A’B$ và $B’C$ là

A. ${90^ \circ }$.

B. ${60^ \circ }$.

C. ${30^ \circ }$.

D. ${45^ \circ }$.

Lời giải

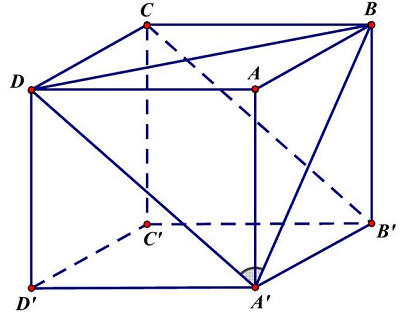
Ta có $B’C//A’D \Rightarrow \widehat {\left( {A’B;B’C} \right)} = \widehat {\left( {A’B;A’D} \right)} = \widehat {DA’B}$.

Xét $\vartriangle DA’B$ có $A’D = A’B = BD$ nên $\vartriangle DA’B$ là tam giác đều.

Vậy $\widehat {DA’B} = {60^ \circ }$.

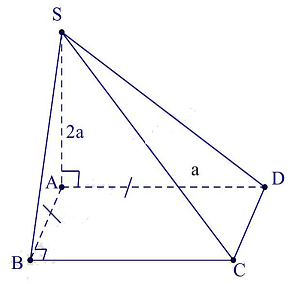
Câu 5. Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh $a$. $SA$ vuông góc với mặt phẳng $\left( {ABCD} \right)$ và $SA = a\sqrt 6 $ (hình vẽ). Gọi $\alpha $ là góc giữa đường thẳng $SB$ và mặt phẳng $\left( {SAC} \right)$. Tính $sin\alpha $ ta được kết quả là:

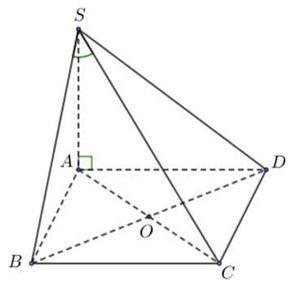
A. $\frac{1}{{\sqrt {14} }}$.

B. $\frac{{\sqrt 2 }}{2}$.

C. $\frac{{\sqrt 3 }}{2}$.

D. $\frac{1}{5}$.

Lời giải

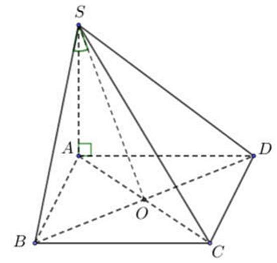
Gọi $O$ là tâm hình vuông $ABCD$ thì $BO \bot \left( {SAC} \right) \Rightarrow \alpha = \widehat {\left( {SB,\left( {SAC} \right)} \right)} = \widehat {BSO}$.

Ta có $SB = a\sqrt 7 ,sin\alpha = \frac{{BO}}{{SB}} = \frac{{\frac{{a\sqrt 2 }}{2}}}{{a\sqrt 7 }} = \frac{1}{{\sqrt {14} }}$.

Câu 6. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông tâm $O,SA \bot \left( {ABCD} \right)$. Khẳng định nào sau đây sai?

A. $\left( {SBC} \right) \bot \left( {SAB} \right)$.

B. $\left( {SAB} \right) \bot \left( {ABCD} \right)$.

C. $\left( {SAC} \right) \bot \left( {ABCD} \right)$.

D. $\left( {SAC} \right) \bot \left( {SAD} \right)$.

Chọn D

Lời giải

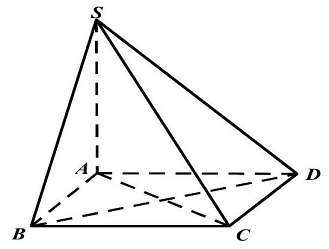
Ta có $\left\{ {\begin{array}{*{20}{l}}
{BC \bot AB} \\
{BC \bot SA}
\end{array} \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow \left( {SBC} \right) \bot \left( {SAB} \right)} \right.$.

Ta có $SA \bot \left( {ABCD} \right) \Rightarrow \left( {SAB} \right) \bot \left( {ABCD} \right)$ và $\left( {SAC} \right) \bot \left( {ABCD} \right)$.

Vậy đáp án ${\mathbf{D}}$ sai.

Câu 7. Cho hình chóp $S \cdot ABCD$ có $ABCD$ là hình vuông tâm $O$ cạnh $a$. Tính khoảng cách giữa $SC$ và $AB$ biết rằng $SO = a$ và vuông góc với mặt đáy của hình chóp.

A. $a$.

B. $\frac{{a\sqrt 5 }}{5}$.

C. $\frac{{2a}}{5}$.

D. $\frac{{2a}}{{\sqrt 5 }}$.

Lời giải

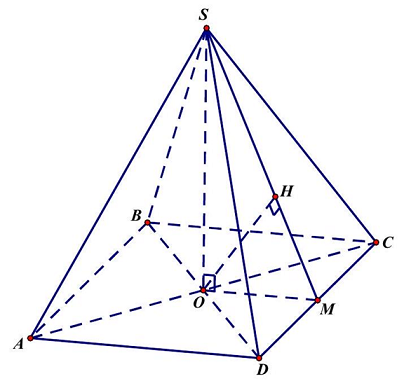
Từ giả thiết suy ra hình chóp $S.ABCD$ là hình chóp tứ giác đều.

Ta có $AB//CD \Rightarrow AB//\left( {SCD} \right)$ nên $d\left( {SC;AB} \right) = d\left( {AB;mp\left( {SCD} \right)} \right) = d\left( {A;mp\left( {SCD} \right)} \right)$.

Mặt khác $O$ là trung điểm $AC$ nên $d\left( {A;mp\left( {SCD} \right)} \right) = 2d\left( {O;mp\left( {SCD} \right)} \right)$.

Như vậy $d\left( {SC;AB} \right) = 2d\left( {O;mp\left( {SCD} \right)} \right)$.

Gọi $M$ là trung điểm $CD$, ta có $OM \bot CD$ và $OM = \frac{a}{2}$. Kẻ $OH \bot SM$, với $H \in SM$, thì $OH \bot mp\left( {SCD} \right)$.

Xét tam giác $SOM$ vuông tại $O$, ta có $\frac{1}{{O{H^2}}} = \frac{1}{{S{O^2}}} + \frac{1}{{O{M^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{{{\left( {\frac{a}{2}} \right)}^2}}} = \frac{5}{{{a^2}}}$.

Từ đó $OH = \frac{a}{{\sqrt 5 }}$.

Vậy $d\left( {SC;AB} \right) = 2d\left( {O;mp\left( {SCD} \right)} \right) = 2.OH = \frac{{2a}}{{\sqrt 5 }}$.

Câu 8. Cho một hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, cạnh bên $SA$ vuông góc với đáy, $SA = 2a$, thể tích của khối chóp là $V$. Khẳng định nào sau đây đúng ?

A. $V = \frac{2}{3}{a^3}$.

B. $V = 2{a^3}$.

C. $V = \frac{1}{3}{a^3}$.

D. $V = {a^3}$.

Lời giải

Ta có: $V = \frac{1}{3} \cdot {S_{ABCD}} \cdot SA = \frac{2}{3}{a^3}$.

Câu 9. Cho hai biến cố $A$ và $B$ độc lập. Khi đó $P\left( {AB} \right)$ bằng:

A. $P\left( A \right) – P\left( B \right)$.

B. $P\left( A \right) + P\left( B \right)$.

C. $P\left( A \right) \cdot P\left( B \right)$.

D. $\left[ {1 – P\left( A \right)} \right]\left[ {1 – P\left( B \right)} \right]$.

Lời giải

Chọn C

Câu 10. Một hộp có 5 viên bi màu đen, 4 viên bi màu trắng. Chọn ngẫu nhiên 2 viên bi từ chiếc hộp đó. Tìm xác suất để chọn được 2 viên bi cùng màu.

A. $\frac{1}{4}$.

B. $\frac{4}{9}$.

C. $\frac{1}{9}$.

D. $\frac{5}{4}$.

Lời giải

Chọn B.

Gọi $A$ là biến cố: “Lấy được 2 viên bi màu trắng”, suy ra $P\left( A \right) = \frac{{C_4^2}}{{C_9^2}} = \frac{1}{6}$.

Gọi $B$ là biến cố: “Lấy được 2 viên bi màu đen”, suy ra $P\left( B \right) = \frac{{C_5^2}}{{C_9^2}} = \frac{5}{{18}}$.

Gọi $C$ là biến cố: “Lấy được 2 viên bi cùng màu”.

Ta có $C = A \cup B$ và $A,B$ là hai biến cố xung khắc.

Vì vậy: $P\left( C \right) = P\left( A \right) + P\left( B \right) = \frac{4}{9}$.

Câu 11. Tính đạo hàm của hàm số $f\left( x \right) = {e^{2x – 3}}$.

A. $f’\left( x \right) = 2 \cdot {e^{2x – 3}}$.

B. $f’\left( x \right) = – 2 \cdot {e^{2x – 3}}$.

C. $f’\left( x \right) = 2 \cdot {e^{x – 3}}$.

D. $f’\left( x \right) = {e^{2x – 3}}$.

Lời giải

Ta có $f’\left( x \right) = {(2x – 3)’}.{e^{2x – 3}} = 2 \cdot {e^{2x – 3}}$.

Câu 12. Phương trình tiếp tuyến của đồ thị hàm số $y = {x^2} – x – 2$ tại điểm có hoành độ $x = 1$ là

A. $2x – y = 0$

B. $2x – y – 4 = 0$.

C. $x – y – 1 = 0$.

D. $x – y – 3 = 0$.

Lời giải

Gọi $M$ là tiếp điểm của tiếp tuyến và đồ thị hàm số. Theo giả thiết: $M\left( {1; – 2} \right)$

Gọi $k$ là hệ số góc của tiếp tuyến với đồ thị hàm số tại $M$.

Ta có $y’ = 2x – 1,k = y’\left( 1 \right) = 1$

Phương trình tiếp tuyến cần tìm là $y = 1\left( {x – 1} \right) – 2 \Leftrightarrow x – y – 3 = 0$

Phần 2. Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗ ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai

Câu 1. An và Huy lần lượt lấy ngẫu nhiên các mảnh giấy có kích thước giống nhau được đánh số từ 1 đến 9 trong một hộp kín. Gọi biến cố $A$ : “An lấy được mảnh giấy đánh số chẵn”. Biến cố $B$ : “Huy lấy được mảnh giấy đánh số chẵn”. Biến cố $C$ : “An lấy được mảnh giấy đánh số 8 “. Khi đó:

a) $P\left( A \right) = \frac{4}{9}$

b) $P\left( C \right) = \frac{1}{9}$

c) $P\left( B \right) = \frac{4}{9}$

d) Hai biến cố $A$ và $C$ không độc lập.

Lời giải

a) Đúng

b) Đúng

c) Đúng

d) Sai

Ta có $P\left( A \right) = \frac{4}{9},P\left( C \right) = \frac{1}{9}$.

Nếu $A$ xảy ra thì xác suất để Huy lấy được mảnh giấy đánh số chã̃n là $\frac{3}{8}$, nếu $A$ không xảy ra thì xác suất để Huy lấy ra được mảnh giấy đánh số chẵn là $\frac{4}{8}$. Do đó $P\left( B \right) = \frac{4}{9} \cdot \frac{3}{8} + \frac{5}{9} \cdot \frac{4}{8} = \frac{4}{9}$.

Rõ ràng hai biến cố $A$ và $B$ không độc lập, hai biến cố $C$ và $B$ không độc lập, hai biến cố $A$ và $C$ độc lập.

Câu 2. Cho ba tia $Ox,Oy,Oz$ vuông góc nhau từng đôi một. Trên $Ox,Oy,Oz$ lần lượt lấy các điểm $A,B,C$ sao cho $OA = OB = OC = a$. Các mệnh đề sau đúng hay sai?

a) $O.ABC$ là hình chóp đều.

b) Tam giác $ABC$ có diện tích $S = \frac{{{a^2}\sqrt 3 }}{2}$.

c) Tam giác $ABC$ có chu vi $2p = \frac{{3a\sqrt 2 }}{2}$.

d) Ba mặt phẳng $\left( {OAB} \right),\left( {OBC} \right),\left( {OCA} \right)$ vuông góc với nhau từng đôi một.

Lời giải

a) Đúng

b) Đúng

c) Sai

d) Đúng

Áp dụng định lý Pytago trong tam giác $OAB$ vuông tại $O$ ta có:

$A{B^2} = O{A^2} + O{B^2} = {a^2} + {a^2} = 2{a^2} \Rightarrow AB = a\sqrt 2 .\;$

Hoàn toàn tương tự ta tính được $BC = AC = a\sqrt 2 $.

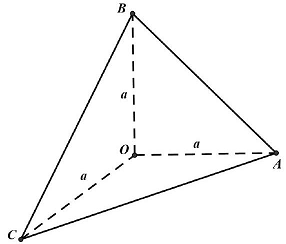
$ \Rightarrow \vartriangle ABC$ là tam giác đều. Mặt khác theo giả thiết $OA = OB = OC = a \Rightarrow $ các mặt bên của hình chóp

$O \cdot ABC$ là các tam giác cân tại $O \Rightarrow O \cdot ABC$ là hình chóp đều $ \Rightarrow $ đáp án a đúng.

Chu vi $\vartriangle ABC$ là: $2p = AB + AC + BC = a\sqrt 2 + a\sqrt 2 + a\sqrt 2 = 3a\sqrt 2 \Rightarrow $ đáp án c sai.

Nửa chu vi Diện tích $\vartriangle ABC$ là: $p = \frac{{3a\sqrt 2 }}{2}$. Diện tích $\vartriangle ABC$ là:

$S = \sqrt {\frac{{3a\sqrt 2 }}{2}{{\left( {\frac{{3a\sqrt 2 }}{2} – a\sqrt 2 } \right)}^3}} = \sqrt {\frac{{3a\sqrt 2 }}{2}{{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^3}} $

$ = \sqrt {\frac{{3a\sqrt 2 }}{2} \cdot \frac{{2{a^3}\sqrt 2 }}{8}} = \sqrt {\frac{{3{a^4}}}{4}} = \frac{{{a^2}\sqrt 3 }}{2}$ (đvdt).

$ \Rightarrow $ đáp án b đúng.

Dễ chứng minh được $\left\{ {\begin{array}{*{20}{l}}
{OA \bot \left( {OBC} \right)} \\
{OA \subset \left( {OAB} \right)} \\
{OA \subset \left( {OAC} \right)}
\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{\left( {OAB} \right) \bot \left( {OBC} \right)} \\
{\left( {OAC} \right) \bot \left( {OBC} \right)}
\end{array},\left\{ {\begin{array}{*{20}{l}}
{OB \bot \left( {OAC} \right)} \\
{OB \subset \left( {OAB} \right)}
\end{array} \Rightarrow \left( {OAB} \right) \bot \left( {OAC} \right)} \right.} \right.} \right.$.

$ \Rightarrow $ đáp án d đúng.

Câu 3. Cho phương trình ${3^x} = m + 1$. Các mệnh đề sau đúng hay sai?

a) Phương trình có nghiệm dương nếu $m > 0$.

b) Phương trình luôn có nghiệm với mọi $m$.

c) Phương trình luôn có nghiệm duy nhất $x = lo{g_3}\left( {m + 1} \right)$.

d) Phương trình có nghiệm với $m \geqslant – 1$.

Lời giải

a) Đúng

b) Sai

c) Sai

d) Sai

Ta có ${3^x} > 0,\forall x \in \mathbb{R}$ nên ${3^x} = m + 1$ có nghiệm $ \Leftrightarrow m + 1 > 0 \Leftrightarrow m > – 1$.

Từ đó ta loại được đáp án b và d

Xét đáp án a, phương trình có nghiệm dương thì ${3^x} > {3^0} = 1$ nên $m + 1 > 1 \Leftrightarrow m > 0$.

Từ đó đáp án a đúng.

Xét đáp án c, ta thấy sai vì ở đây thiếu điều kiện $m > – 1$.

Câu 4. Một chuyển động xác định bởi phương trình $S\left( t \right) = {t^3} – 3{t^2} – 9t + 2$. Trong đó $t$ được tính bằng giây, $S$ được tính bằng mét. Các mệnh đề sau đúng hay sai?

a) Vận tốc của chuyển động bằng 0 khi $t = 0\;s$ hoặc $t = 2\;s$.

b) Gia tốc của chuyển động tại thời điểm $t = 3\;s$ là $12\;m/{s^2}$.

c) Gia tốc của chuyển động bằng $0\;m/{s^2}$ khi $t = 0\;s$.

d) Vận tốc của chuyển động tại thời điểm $t = 2\;s$ là $v = 18\;m/s$.

Lời giải

a) Sai

b) Đúng

c) Sai

d) Sai

Vận tốc của chuyển động tại thời điểm $t$ có phương trình là $v\left( t \right) = S’\left( t \right) = 3{t^2} – 6t – 9$.

Gia tốc của chuyển động tại thời điểm $t$ có phương trình là $a\left( t \right) = v’\left( t \right) = 6t – 6$.

Tại thời điểm $t = 3\;s$ ta có $a\left( 3 \right) = 6.3 – 6 = 12\;m/{s^2}$.

Phần 3. Câu trả lời ngắn.

Thí sinh trả lời đáp án từ câu 1 đến câu 6.

Câu 1. Một chiếc hộp chứa 8 viên bi màu xanh, 5 viên bi màu đỏ có cùng kích thước và khối lượng. Lấy lần lượt một viên bi từ hộp và không trả lại, thực hiện hai lần liêp tiếp. Tính xác suất để lấy được ít nhất 1 viên bi màu đỏ.

Trả lời: $\frac{{25}}{{39}}$

Ta có sơ đồ cây như sau:

Lời giải

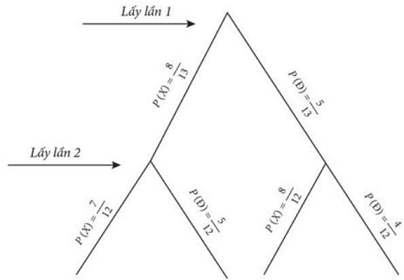
Trong đó: $X$ là biến cố “Lấy được 1 viên bi màu xanh”, Đ là biến cố “Lấy được 1 viên bi màu đỏ”.

Xác suất lấy được ít nhất một viên bi đỏ: $\frac{{25}}{{39}}$.

Câu 2. Khi tung một đồng xu không cân đối thì người ta thây rằng xác suất để đồng xu xuất hiện mặt sấp bằng $\frac{2}{3}$. Tung đồng xu này ba lần liên tiếp. Tính xác suất để chỉ xuất hiện mặt sấp;

Trả lời: $\frac{8}{{27}}$

Lời giải

Xác suất chỉ xuất hiện mặt sấp là: ${\left( {\frac{2}{3}} \right)^3} = \frac{8}{{27}}$.

Câu 3. Cho hình chóp $S.ABC$ có đáy là tam giác đều cạnh $a,SA \bot \left( {ABC} \right)$ và $SB = a\sqrt 5 $. Gọi $M$ là trung điểm $BC$. Tính góc giữa đường thẳng $SM$ và mặt phẳng $\left( {SAC} \right)$ ?

Trả lời: $ \approx 11,{5^0}$

Lời giải

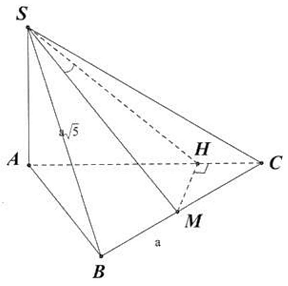
Kẻ $MH \bot AC$

Ta có: $MH \bot SA \Rightarrow MH \bot \left( {SAC} \right)$ tại $H$ và $SM$ cắt mp $\left( {SAC} \right)$ tại $S$

$ \Rightarrow SH$ là hình chiếu của $SM$ trên $mp\left( {SAC} \right)$

$ \Rightarrow \left( {SM,\left( {SAC} \right)} \right) = \left( {SM,SH} \right) = \widehat {MSH}$

Ta có: $HM = MC \cdot sin{60^ \circ } = \frac{a}{2} \cdot sin{60^ \circ } = \frac{{a\sqrt 3 }}{4}$;

$HC = MC \cdot cos{60^ \circ } = \frac{a}{4} \Rightarrow AH = AC – HC = a – \frac{a}{4} = \frac{{3a}}{4}$

Ta có: $SH = \sqrt {S{A^2} + A{H^2}} = \sqrt {{{(a\sqrt 5 )}^2} – {a^2} + {{\left( {\frac{{3a}}{4}} \right)}^2}} = \frac{{\sqrt {73} }}{4}a$

Xét $\vartriangle SHM$ vuông tại $H:tan\widehat {MSH} = \frac{{HM}}{{SH}} = \frac{{\frac{{a\sqrt 3 }}{4}}}{{\frac{{\sqrt {73} a}}{4}}} = \frac{{\sqrt {219} }}{{73}} \Rightarrow \widehat {MSH} \approx 11,{5^0}$

Câu 4. Cho hình chóp $S.ABCD$ có $SA \bot \left( {ABCD} \right),SA = 3a,ABCD$ là hình vuông cạnh bằng $a$. Tính khoảng cách giữa hai đường thẳng $AC$ và $SB$.

Trả lời: $d\left( {AC,SB} \right) = \frac{{3\sqrt {19} }}{{19}}a$

Lời giải

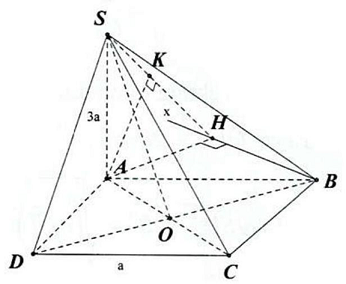
Dựng $Bx//AC \Rightarrow AC//\left( {SBx} \right)$

Suy ra $d\left( {AC,SB} \right) = d\left( {AC,\left( {SBx} \right)} \right) = d\left( {A,\left( {SBx} \right)} \right)$

Dựng và chứng minh được $d\left( {A,\left( {SBx} \right)} \right) = AK$

Ta có: $\vartriangle AHB$ vuông cân tại $H$ nên $AH = \frac{{AB}}{{\sqrt 2 }} = \frac{a}{{\sqrt 2 }}$

Ta có:

$AK = \frac{1}{{\sqrt {\frac{1}{{S{A^2}}} + \frac{1}{{A{H^2}}}} }} = \frac{1}{{\sqrt {\frac{1}{{{{(3a)}^2}}} + \frac{1}{{{{\left( {\frac{a}{{\sqrt 2 }}} \right)}^2}}}} }} = \frac{{3\sqrt {19} }}{{19}}a$

Vậy $d\left( {AC,SB} \right) = \frac{{3\sqrt {19} }}{{19}}a$.

Câu 5. Số lượng tế bào còn sống trong khoảng thời gian $t$ (phút) kể từ lúc tiến hành thí nghiệm được xác định bởi $f\left( t \right) = a \cdot {e^{bt}}$ trong đó $a,b$ là các hằng số cho trước. Nếu bắt đầu một thí nghiệm sinh học với 5.000 .000 tế bào thì có $45\% $ các tế bào sẽ chết sau mỗi phút, hỏi sau ít nhất bao lâu nó sẽ còn ít hơn 1.000 tế bào?

Trả lời: 14,245 phút

Ta có $f\left( t \right) = a.{e^{bt}}$

Lời giải

Khi $t = 0 \Rightarrow f\left( 0 \right) = 5.000.000 \Leftrightarrow a.{e^0} = 5.000.000 \Leftrightarrow a = 5.000.000$

Khi $t = 1 \Rightarrow f\left( 1 \right) = \frac{{100 – 45}}{{100}}a = \frac{{55}}{{100}}a$$ \Leftrightarrow a \cdot {e^b} = \frac{{55}}{{100}}a \Leftrightarrow b = ln\left( {\frac{{55}}{{100}}} \right)$.

Theo đề ta có bất phương trình $f\left( t \right) = a \cdot {e^{bt}} < 1000$$ \Leftrightarrow t > \frac{{ln\left( {\frac{{1000}}{a}} \right)}}{b} \approx 14,245$

Câu 6. Một vật rơi tự do theo phương thẳng đứng có quãng đường dịch chuyển $S\left( t \right) = \frac{1}{2}g{t^2}$ với $t$ là thời gian tính bằng giây $\left( s \right)$ kể từ lúc vật bắt đầu rơi, $S$ là quãng đường tính bằng mét $\left( m \right),g = 9,8\;m/{s^2}$. Vận tốc tức thời của vật tại thời điểm $t = 4s$ ?

Trả lời: 19,6 (m/s)

Lời giải

Quãng đường vật dịch chuyển trong 4 giây là: $S\left( 4 \right) = \frac{1}{2} \cdot 9,8 \cdot {4^2} = 78,4\left( {\;m} \right)$.

Vận tốc tức thời tại thời điểm $t = 4s$ là: $v = \frac{{78,4}}{4} = 19,6\left( {\;m/s} \right)$