Đề Thi HK 2 Toán 11 Kết Nối Tri Thức Cấu Trúc Mới Giải Chi Tiết-Đề 4

Đề thi HK 2 Toán 11 Kết nối tri thức cấu trúc mới giải chi tiết-Đề 4 được soạn dưới dạng file word và PDF gồm 3 trang. Các bạn xem và tải về ở dưới.
Phần 1. Câu trắc nghiệm nhiều phương án chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phuơng án đúng nhất.

Câu 1. Với $a$ và $b$ là các số thực dương. Biểu thức $lo{g_a}\left( {{a^2}b} \right)$ bằng

A. $2 – lo{g_a}b$. B. $2 + lo{g_a}b$. C. $1 + 2lo{g_a}b$. D. $2lo{g_a}b$.

Câu 2. Tập nghiệm của bất phương trình $lo{g_{\frac{1}{2}}}\left( {{x^2} – x + 7} \right) > 0$ là

A. $\left( { – \infty ;2} \right) \cup \left( {3; + \infty } \right)$. B. $\left( { – \infty ;2} \right)$. C. $\left( {2;3} \right)$. D. $\left( {3; + \infty } \right)$.

Câu 3. Cho hình chóp $S \cdot ABCD$ có đáy $ABCD$ là hình thoi tâm $O,SA \bot \left( {ABCD} \right)$. Tìm khẳng định sai?

A. $AD \bot SC$. B. $SC \bot BD$. C. $SA \bot BD$. D. $SO \bot BD$.

Câu 4. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, $AB = 2a,AD = a$. $SA$ vuông góc với mặt phẳng đáy. $SA = a\sqrt 3 $. Cosin của góc giữa $SC$ và mặt đáy bằng:

A. $\frac{{\sqrt 5 }}{4}$. B. $\frac{{\sqrt 7 }}{4}$. C. $\frac{{\sqrt 6 }}{4}$. D. $\frac{{\sqrt {10} }}{4}$.

Câu 5. Cho hình chóp $S \cdot ABCD$ có đáy $ABCD$ là hình chữ nhật, $AB = a,AD = a\sqrt 2 $, $SA \bot \left( {ABCD} \right)$. Gọi $M$ là trung điểm của $AD,I$ là giao điểm của $AC$ và $BM$. Khẳng định nào sau đây đúng?

A. $\left( {SAC} \right) \bot \left( {SMB} \right)$. B. $\left( {SAC} \right) \bot \left( {SBD} \right)$. C. $\left( {SBC} \right) \bot \left( {SMB} \right)$. D. $\left( {SAB} \right) \bot \left( {SBD} \right)$.

Câu 6. Cho hình lập phương $ABCD.A’B’C’D’$ có cạnh là $a > 0$. Khi đó, khoảng cách giữa hai đường thẳng chéo nhau $AB’$ và $BC’$ là

A. $\frac{{a\sqrt 3 }}{2}$. B. $\frac{{a\sqrt 3 }}{3}$. C. $\frac{{a\sqrt 2 }}{3}$. D. $\frac{{a\sqrt 6 }}{3}$.

Câu 7. Lăng trụ tam giác đều có độ dài tất cả các cạnh bằng 3 . Thể tích khối lăng trụ đã cho bằng

c. $\frac{{27\sqrt 3 }}{2}$.

A. $\frac{{9\sqrt 3 }}{4}$. B. $\frac{{27\sqrt 3 }}{4}$. C. $\frac{{9\sqrt 3 }}{2}$.

Câu 8. Một hộp có 20 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số $1,2,3, \ldots ,19,20$; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một chiếc thẻ trong hộp. Xét các biến cố: $A$ : “Số xuất hiện trên thẻ được rút ra là số chia hết cho 2”;

$B$ : “Số xuất hiện trên thẻ được rút ra là số chia hết cho 5 “;

$C$ : “Số xuất hiện trên thẻ được rút ra là số chia hết cho 2 hoặc chia hết cho 5”;

$D$ : “Số xuất hiện trên thẻ được rút ra là số vừa chia hết cho 2 vừa chia hết cho 5 “.

Biến cố $C$ là biển cố hợp của:

A. Biến cố $B$ và biến cố $D$.

B. Biến cố $A$ và biến cố $D$.

C. Biến cố $A$ và biến cố $B$.

D. Biến cố $A$ và biến cố $D$ hoặc biến cố $B$ và biến cố $D$.

Câu 9. Ba xạ thủ bắn vào mục tiêu một cách độc lập với nhau. Xác suất bắn trúng của xạ thủ thứ nhất, thứ hai và thứ ba lần lượt là 0,$6;0,7;0,8$. Xác suất để có ít nhất một xạ thủ bắn trúng là:

A. 0,188 . B. 0,024 . C. 0,976 . D. 0,812 .

Câu 10. Gieo một con xúc xắc cân đối và đồng chất hai lần. Xác suất sao cho tổng số chấm trong hai lần gieo là số chẵn bằng:

A. $\frac{1}{2}$. B. $\frac{1}{4}$. C. $\frac{3}{4}$. D. $\frac{1}{3}$.

Câu 11. Cho hàm số $f\left( x \right) = sin2x$. Tính $f’\left( x \right)$.

A. $f’\left( x \right) = 2sin2x$. B. $f’\left( x \right) = cos2x$. C. $f’\left( x \right) = 2cos2x$. D. $f’\left( x \right) = – \frac{1}{2}cos2x$.

Câu 12. Cho hàm số $y = {x^3} – 3{x^2} – 2$. Hệ số góc của tiếp tuyến với đồ thị hàm số tại điểm có hoành độ $x = 2$ là

A. 6 . B. 0 . C. -6 . D. -2 .

Phần 2. Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai

Câu 1. Một chiếc hộp có chín thẻ giống nhau được đánh số từ 1 đến 20 . Rút ngẫu nhiên hai thẻ rồi nhân hai số ghi trên hai thẻ với nhau. Gọi $A$ là biến cố “Rút được một thẻ đánh số chẵn và một thẻ đánh số lẻ”, $B$ là biến cố “Rút được hai thẻ đều đánh số chẵn”. Khi đó:

a) Biến cố “Tích hai số ghi trên hai thẻ là một số chẵn” là $A \cup B$.

b) $P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right)$

c) $P\left( A \right) < P\left( B \right)$

d) Xác suất để kết quả nhận được là một số chẵn là: $\frac{{461}}{{722}}$

Câu 2. Cho hình chóp $S \cdot ABCD$ có $SA \bot \left( {ABCD} \right)$ và đáy $ABCD$ là hình vuông tâm $O$. Các mệnh đề sau đúng hay sai?

a) $\left( {\left( {SBC} \right),\left( {ABCD} \right)} \right) = \widehat {SBA}$.

b) $d\left( {D,\left( {SAC} \right)} \right) = DO$.

c) $\left( {SC,\left( {SAD} \right)} \right) = \widehat {CSD}$.

d) $d\left( {CD,SB} \right) = BD$.

Câu 3. Gọi $S$ là tập nghiệm của bất phương trình $lo{g_{0,3}}\left( {4{x^2}} \right) \geqslant lo{g_{0,3}}\left( {12x – 5} \right)$. Kí hiệu $m,M$ lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của tập $S$. Các mệnh đề sau đúng hay sai?

a) $M – m = 3$.

b) $M – m = 1$.

c) $m + M = 3$.

d) $m + M = 2$.

Câu 4. Cho hai hàm số $f\left( x \right)$ và $g\left( x \right)$ đều có đạo hàm trên $\mathbb{R}$ và thỏa mãn ${f^3}\left( {2 – x} \right) – 2 \cdot {f^2}\left( {2 + 3x} \right) + {x^2} \cdot g\left( x \right) + 36x = 0,\forall x \in \mathbb{R}$. Các mệnh đề sau đúng hay sai?

a) $f’\left( 2 \right) = 2$

b) $f\left( 2 \right) = 2$

c) $f\left( 2 \right) + f’\left( 2 \right) = 4$

d) $3 \cdot f\left( 2 \right) + 4 \cdot f’\left( 2 \right) = 10$.

Phần 3. Câu trả lời ngắn.
Thí sinh trả lời đáp án từ câu 1 đến câu 6.

Câu 1. Ở thành phố $X$, xác suất để một ngày là nắng ráo là 0,8 . Nếu trời nắng thì xác suất để Minh đi ra biển chơi là 0,7 . Nếu trời mưa thì xác suất để Minh ra biển chơi là 0,1 . Xác định xác suất mà Minh sẽ đi biển chơi vào một ngày bất kì.

Câu 2. An và Bình, mỗi bạn cùng gieo hai con xúc xắc cân đối và đồng chất. Tính xác suất để hai bạn tung được số điểm như nhau.

Câu 3. Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh $a,SA \bot \left( {ABCD} \right)$. Biết góc giữa $SC$ và mặt phẳng $\left( {ABCD} \right)$ là ${60^ \circ }$. Tính góc phẳng nhị diện $\left[ {S,BD,C} \right]$ ?

Câu 4. Một hình chóp cụt đều $ABC \cdot A’B’C’$ có cạnh đáy lớn bằng $4a$, cạnh đáy nhỏ bằng $2a$ và chiều cao của nó bằng $\frac{{3a}}{2}$. Tìm thể tích của khối chóp cụt đều đó.

Câu 5. Cường độ một trận động dất $M$ (Richter) tính theo thang Richter được xác định theo công thức $M = logA – log{A_0}$. Với $A$ là cường độ tối đa đo được bằng địa chấn kế (biên độ của những sóng địa chấn đo ở $100\;km$ cách chấn tâm của cơn động đất) và ${A_0}$ là một biên độ chuẩn. Năng lượng được phát ra bởi một trận động đất có cường độ $M$ được xác định bởi ${E_M} = {E_0} \cdot {10^{1,5M}}$ trong đó ${E_0}$ là một hằng số dương. Hỏi với hai trận động đất có biên độ ${A_1},{A_2}$ thỏa mãn ${A_1} = 4{A_2}$, thì tỉ lệ năng lượng được phát ra bởi hai trận động đất này là?

Câu 6. Cho hàm số $y = {x^3} – 3{x^2} + 2$. Có bao nhiêu tiếp tuyến với đồ thị hàm số đi qua điểm $A\left( {1;0} \right)$ ?

ĐÁP ÁN VÀ LỜI GIẢI THAM KHẢO

Phần 1. Câu trắc nghiệm nhiều phương án chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án đúng nhất.

1B	2C	3A	4D	5A	6B
7B	8C	9C	10A	11C	12B

Câu 1. Với $a$ và $b$ là các số thực dương. Biểu thức $lo{g_a}\left( {{a^2}b} \right)$ bằng

A. $2 – lo{g_a}b$.

B. $2 + lo{g_a}b$.

C. $1 + 2lo{g_a}b$.

D. $2lo{g_a}b$.

Lời giải

Ta có: $lo{g_a}\left( {{a^2}b} \right) = lo{g_a}{a^2} + lo{g_a}b = 2 + lo{g_a}b$.

Câu 2. Tập nghiệm của bất phương trình $lo{g_{\frac{1}{2}}}\left( {{x^2} – x + 7} \right) > 0$ là

A. $\left( { – \infty ;2} \right) \cup \left( {3; + \infty } \right)$.

B. $\left( { – \infty ;2} \right)$.

C. $\left( {2;3} \right)$.

D. $\left( {3; + \infty } \right)$.

Lời giải

$lo{g_{\frac{1}{2}}}\left( {{x^2} – x + 7} \right) > 0 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{{x^2} – 5x + 7 > 0} \\
{{x^2} – 5x + 7 < 1}
\end{array}} \right.$ $ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{{{\left( {x – \frac{5}{2}} \right)}^2} + \frac{3}{4} > 0,\forall x \in \mathbb{R}} \\
{{x^2} – 5x + 6 < 0}
\end{array} \Rightarrow x \in \left( {2;3} \right)} \right.$.

Câu 3. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi tâm $O,SA \bot \left( {ABCD} \right)$. Tìm khẳng định sai?

A. $AD \bot SC$.

B. $SC \bot BD$.

C. $SA \bot BD$.

D. $SO \bot BD$.

Lời giải

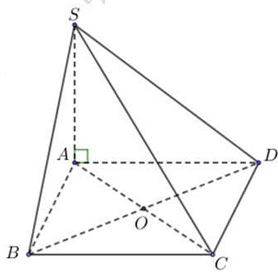
Ta có $\left\{ {\begin{array}{*{20}{l}}
{BD \bot AC} \\
{BD \bot SA}
\end{array} \Rightarrow BD \bot SC} \right.$.

Ta có $\left\{ {\begin{array}{*{20}{l}}
{SA \bot \left( {ABCD} \right)} \\
{BD \subset \left( {ABCD} \right)}
\end{array} \Rightarrow SA \bot BD} \right.$.

Ta có $\left\{ {\begin{array}{*{20}{l}}
{BD \bot AC} \\
{BD \bot SA}
\end{array} \Rightarrow BD \bot \left( {SAC} \right) \Rightarrow BD \bot SO} \right.$.

Vậy khẳng định $AD \bot SC$ là khẳng định sai.

Câu 4. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, $AB = 2a,AD = a.SA$ vuông góc với mặt phẳng đáy. $SA = a\sqrt 3 $. Cosin của góc giữa $SC$ và mặt đáy bằng:

A. $\frac{{\sqrt 5 }}{4}$.

B. $\frac{{\sqrt 7 }}{4}$.

C. $\frac{{\sqrt 6 }}{4}$.

D. $\frac{{\sqrt {10} }}{4}$.

Lời giải

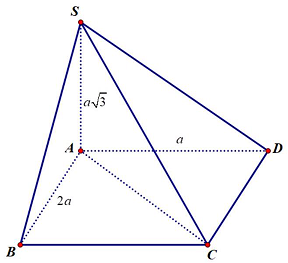
Hình chiếu của $SC$ lên $\left( {ABCD} \right)$ là $AC$

Do đó $\left[ {\widehat {SC,\left( {ABCD} \right)}} \right] = \widehat {SCA}$

$AC = \sqrt {A{B^2} + A{D^2}} = \sqrt {4{a^2} + {a^2}} = a\sqrt 5 \Rightarrow SC = 2a\sqrt 2 $

Trong tam giác vuông $SAC:cos\widehat {SCA} = \frac{{AC}}{{SC}} = \frac{{a\sqrt 5 }}{{2a\sqrt 2 }} = \frac{{\sqrt {10} }}{4}$.

Câu 5. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật, $AB = a,AD = a\sqrt 2 $, $SA \bot \left( {ABCD} \right)$. Gọi $M$ là trung điểm của $AD,I$ là giao điểm của $AC$ và $BM$. Khẳng định nào sau đây đúng?

A. $\left( {SAC} \right) \bot \left( {SMB} \right)$.

B. $\left( {SAC} \right) \bot \left( {SBD} \right)$.

C. $\left( {SBC} \right) \bot \left( {SMB} \right)$.

D. $\left( {SAB} \right) \bot \left( {SBD} \right)$.

Lời giải

Chọn A

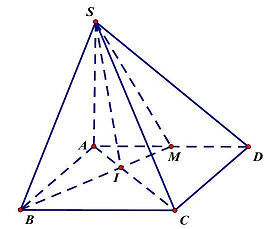
Ta có: $SA \bot \left( {ABCD} \right) \Rightarrow SA \bot BM$ (1).

Xét tam giác vuông $ABM$ có: $tan\widehat {AMB} = \frac{{AB}}{{AM}} = \sqrt 2 $.

Xét tam giác vuông $ACD$ có: $tan\widehat {CAD} = \frac{{CD}}{{AD}} = \frac{1}{{\sqrt 2 }}$. Ta có:

$cot\widehat {AIM} = cot\left( {{{180}^ \circ } – \left( {\widehat {AMB} + \widehat {CAD}} \right)} \right)$$ = – cot\left( {\widehat {AMB} + \widehat {CAD}} \right) = – \frac{{1 – tan\widehat {AMB} \cdot tan\widehat {CAD}}}{{tan\widehat {AMB} + tan\widehat {CAD}}} = 0$

$ \Rightarrow \widehat {AIM} = {90^ \circ } \Rightarrow BM \bot AC\left( 2 \right)$.

Từ (1) và (2) suy ra: $BM \bot \left( {SAC} \right)$ mà $BM \subset \left( {SAC} \right)$ nên $\left( {SAC} \right) \bot \left( {SMB} \right)$

Câu 6. Cho hình lập phương $ABCD \cdot A’B’C’D’$ có cạnh là $a > 0$. Khi đó, khoảng cách giữa hai đường thẳng chéo nhau $AB’$ và $BC’$ là

A. $\frac{{a\sqrt 3 }}{2}$.

B. $\frac{{a\sqrt 3 }}{3}$.

C. $\frac{{a\sqrt 2 }}{3}$.

D. $\frac{{a\sqrt 6 }}{3}$.

Lời giải

Gọi $O$ là tâm hình vuông $ABCD$. Trong mặt phẳng $\left( {ACC’A’} \right)$, kẻ $CH \bot C’O$ tại $H$, mà $CH \bot BD$ (do $\left. {BD \bot \left( {ACC’A’} \right)} \right)$ nên $CH \bot \left( {C’BD} \right) \Rightarrow d\left( {C;C’BD} \right) = CH$

Ta có: $AB’//\left( {C’BD} \right) \Rightarrow d\left( {AB’,BC’} \right) = d\left( {AB’,\left( {C’BD} \right)} \right) = d\left( {A,\left( {C’BD} \right)} \right) = d\left( {C,\left( {C’BD} \right)} \right) = CH$ Xét $\vartriangle C’CO$ vuông tại $C$, đường cao $CH$ :

$\frac{1}{{C{H^2}}} = \frac{1}{{C{O^2}}} + \frac{1}{{C{C^{22}}}} = \frac{3}{{{a^2}}} \Rightarrow CH = \frac{{a\sqrt 3 }}{3}$.

Câu 7. Lăng trụ tam giác đều có độ dài tất cả các cạnh bằng 3 . Thể tích khối lăng trụ đã cho bằng

A. $\frac{{9\sqrt 3 }}{4}$.

B. $\frac{{27\sqrt 3 }}{4}$.

c. $\frac{{27\sqrt 3 }}{2}$.

D. $\frac{{9\sqrt 3 }}{2}$.

Lời giải

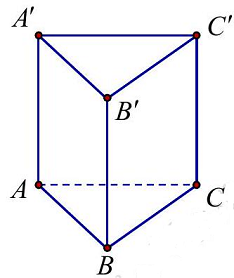
Diện tích đáy: ${S_{\vartriangle ABC}} = \frac{1}{2} \cdot 3 \cdot 3 \cdot sin{60^ \circ } = \frac{{9\sqrt 3 }}{4}$. Thể tích ${V_{lt}} = {S_{\vartriangle ABC}} \cdot AA’ = \frac{{27\sqrt 3 }}{4}$.

Câu 8. Một hộp có 20 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số $1,2,3, \ldots ,19,20$; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một chiếc thẻ trong hộp. Xét các biến cố:

$A$ : “Số xuất hiện trên thẻ được rút ra là số chia hết cho 2”;

$B$ : “Số xuất hiện trên thẻ được rút ra là số chia hết cho 5 “;

$C$ : “Số xuất hiện trên thẻ được rút ra là số chia hết cho 2 hoặc chia hết cho 5”;

$D$ : “Số xuất hiện trên thẻ được rút ra là số vừa chia hết cho 2 vừa chia hết cho 5 “.

Biến cố $C$ là biến cố hợp của:

A. Biến cố $B$ và biến cố $D$.

B. Biến cố $A$ và biến cố $D$.

C. Biến cố $A$ và biến cố $B$.

D. Biến cố $A$ và biến cố $D$ hoặc biến cố $B$ và biến cố $D$.

Chọn C

Lời giải

Câu 9. Ba xạ thủ bắn vào mục tiêu một cách độc lập với nhau. Xác suất bắn trúng của xạ thủ thứ nhất, thứ hai và thứ ba lần lượt là 0,$6;0,7;0,8$. Xác suất để có ít nhất một xạ thủ bắn trúng là:

A. 0,188 .

B. 0,024 .

C. 0,976 .

D. 0,812 .

Lời giải

Chọn C.

Gọi ${A_i}$ là biến cố: “Người thứ $i$ bắn trúng mục tiêu” với $1 \leqslant i \leqslant 3,i \in \mathbb{N}$.

Xác suất để cả ba xạ thủ cùng bắn không trúng mục tiêu là:

$P\left( {\overline {{A_1}} \overline {{A_2}} \overline {{A_3}} } \right) = P\left( {\overline {{A_1}} } \right) \cdot P\left( {\overline {{A_2}} } \right) \cdot P\left( {\overline {{A_3}} } \right)$$ = 0,4 \cdot 0,3 \cdot 0,2 = 0,024$.

Xác suất để có ít nhất một xạ thủ bắn trúng mục tiêu là:

$P\left( {{A_1} \cup {A_2} \cup {A_3}} \right) = 1 – 0,024 = 0,976$.

Câu 10. Gieo một con xúc xắc cân đối và đồng chất hai lần. Xác suất sao cho tổng số chấm trong hai lần gieo là số chẵn bằng:

A. $\frac{1}{2}$.

B. $\frac{1}{4}$.

C. $\frac{3}{4}$.

D. $\frac{1}{3}$.

Lời giải

Chọn A.

Gọi ${A_1}$ là biến cố: “Lần gieo đầu tiên xuất hiện mặt có số chấm chẵn”; gọi ${A_2}$ là biến cố: “Lần gieo thứ hai xuất hiện mặt có số chấm chẵn”.

Ta có: $P\left( {{A_1}} \right) = \frac{1}{2},P\left( {{A_2}} \right) = \frac{1}{2}$.

Gọi $C$ là biến cố: “Tổng số chấm trong hai lần gieo là số chẵn”.

Ta có $C = \left( {AB} \right) \cup \left( {\overline A \overline B } \right)$, đồng thời $AB$ và $\overline A \overline B $ là hai biến cố xung khắc.

Suy ra:

$P\left( C \right) = P\left( {{A_1}{A_2}} \right) + P\left( {\overline {{A_1}} \overline {{A_2}} } \right)$$ = P\left( {{A_1}} \right) \cdot P\left( {{A_2}} \right) + P\left( {\overline {{A_1}} } \right) \cdot P\left( {\overline {{A_2}} } \right)$$ = \frac{1}{2} \cdot \frac{1}{2} + \frac{1}{2} \cdot \frac{1}{2} = \frac{1}{2}$

Câu 11. Cho hàm số $f\left( x \right) = sin2x$. Tính $f’\left( x \right)$.

A. $f’\left( x \right) = 2sin2x$.

B. $f’\left( x \right) = cos2x$.

C. $f’\left( x \right) = 2cos2x$.

D. $f’\left( x \right) = – \frac{1}{2}cos2x$.

Lời giải

Ta có $f\left( x \right) = sin2x$, suy ra $f’\left( x \right) = 2cos2x$.

Câu 12. Cho hàm số $y = {x^3} – 3{x^2} – 2$. Hệ số góc của tiếp tuyến với đồ thị hàm số tại điểm có hoành độ $x = 2$ là

A. 6 .

B. 0 .

C. -6 .

D. -2 .

Lời giải

Tập xác định $D = \mathbb{R}$.

Đạo hàm: $y’ = 3{x^2} – 6x$.

Hệ số góc của tiếp tuyến với đồ thị hàm số tại điểm có hoành độ $x = 2$ là $k = y’\left( 2 \right) = {3.2^2} – 6.2 = 0$.

Phần 2. Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai

Câu 1. Một chiếc hộp có chín thẻ giống nhau được đánh số từ 1 đến 20. Rút ngẫu nhiên hai thẻ rồi nhân hai số ghi trên hai thẻ với nhau. Gọi $A$ là biến cố “Rút được một thẻ đánh số chẵn và một thẻ đánh số lẻ”, $B$ là biến cố “Rút được hai thẻ đều đánh số chẵn”. Khi đó:

a) Biến cố “Tích hai số ghi trên hai thẻ là một số chẵn” là $A \cup B$.

b) $P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right)$

c) $P\left( A \right) < P\left( B \right)$

d) Xác suất để kết quả nhận được là một số chẵn là: $\frac{{461}}{{722}}$

Lời giải

a) Đúng

b) Đúng

c) Sai

d) Sai

Gọi $A$ là biến cố “Rút được một thẻ đánh số chẵn và một thẻ đánh số lẻ”, $B$ là biến cố “Rút được hai thẻ đều đánh số chẵn”.

Khi đó biến cố “Tích hai số ghi trên hai thẻ là một số chẵn” là $A \cup B$.

Do hai biến cố xung khắc nên $P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right)$.

Vì có 10 số chẵn và 10 số lẻ nên ta có:

$P\left( A \right) = \frac{{C_{10}^1 \cdot C_{10}^1}}{{C_{20}^2}} = \frac{{10}}{{19}},P\left( B \right) = \frac{{C_{10}^2}}{{C_{20}^2}} = \frac{9}{{38}}$.

Do đó, $P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) = \frac{{10}}{{19}} + \frac{9}{{38}} = \frac{{29}}{{38}}$.

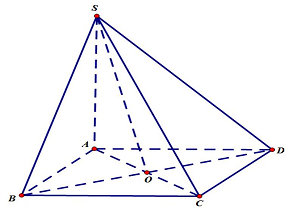
Câu 2. Cho hình chóp $S.ABCD$ có $SA \bot \left( {ABCD} \right)$ và đáy $ABCD$ là hình vuông tâm $O$. Các mệnh đề sau đúng hay sai?

a) $\left( {\left( {SBC} \right),\left( {ABCD} \right)} \right) = \widehat {SBA}$.

b) $d\left( {D,\left( {SAC} \right)} \right) = DO$.

c) $\left( {SC,\left( {SAD} \right)} \right) = \widehat {CSD}$.

d) $d\left( {CD,SB} \right) = BD$.

Lời giải

a) Đúng

b) Đúng

c) Đúng

d) Sai

d: sai vì $BD$ không vuông góc với $CD$.

Câu 3. Gọi $S$ là tập nghiệm của bất phương trình $lo{g_{0,3}}\left( {4{x^2}} \right) \geqslant lo{g_{0,3}}\left( {12x – 5} \right)$. Kí hiệu $m,M$ lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của tập $S$. Các mệnh đề sau đúng hay sai?

a) $M – m = 3$.

b) $M – m = 1$.

c) $m + M = 3$.

d) $m + M = 2$.

Lời giải

a) Sai

b) Sai

c) Đúng

d) $Sai$

Ta có: $lo{g_{0,3}}\left( {4{x^2}} \right) \geqslant lo{g_{0,3}}\left( {12x – 5} \right)$$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{12x – 5 > 0} \\
{4{x^2} \leqslant 12x – 5}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x > \frac{5}{{12}}} \\
{4{x^2} – 12x + 5 \leqslant 0}
\end{array}} \right.} \right.$

$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x > \frac{5}{{12}}} \\
{\frac{1}{2} \leqslant x \leqslant \frac{5}{2}}
\end{array} \Leftrightarrow \frac{1}{2} \leqslant x \leqslant \frac{5}{2}} \right.$.

Tập nghiệm của bất phương trình đã cho $S = \left[ {\frac{1}{2};\frac{5}{2}} \right]$.

Khi đó: $M = \frac{5}{2};m = \frac{1}{2}$ và $m + M = \frac{5}{2} + \frac{1}{2} = 3$.

Câu 4. Cho hai hàm số $f\left( x \right)$ và $g\left( x \right)$ đều có đạo hàm trên $\mathbb{R}$ và thỏa mãn ${f^3}\left( {2 – x} \right) – 2 \cdot {f^2}\left( {2 + 3x} \right) + {x^2} \cdot g\left( x \right) + 36x = 0,\forall x \in \mathbb{R}$. Các mệnh đề sau đúng hay sai?

a) $f’\left( 2 \right) = 2$

b) $f\left( 2 \right) = 2$

c) $f\left( 2 \right) + f’\left( 2 \right) = 4$

d) $3 \cdot f\left( 2 \right) + 4 \cdot f’\left( 2 \right) = 10$.

Lời giải

a) Sai

b) Đúng

c) Sai

d) Đúng

${f^3}\left( {2 – x} \right) – 2{f^2}\left( {2 + 3x} \right) + {x^2} \cdot g\left( x \right) + 36x = 0,\;\forall x \in \mathbb{R}\left( 1 \right)$.

Vì (1) đúng $\forall x \in \mathbb{R}$ nên cũng đúng với $x = 0 \Rightarrow {f^3}\left( 2 \right) – 2{f^2}\left( 2 \right) = 0 \Rightarrow \left[ {\begin{array}{*{20}{l}}
{f\left( 2 \right) = 0} \\
{f\left( 2 \right) = 2}
\end{array}} \right.$

Lấy đạo hàm hai vế của (1) ta có:

$ – 3{f^2}\left( {2 – x} \right) \cdot f’\left( {2 – x} \right) – 12f\left( {2 + 3x} \right) \cdot f’\left( {2 + 3x} \right) + 2x \cdot g\left( x \right) + {x^2} \cdot g’\left( x \right) + 36 = 0,\forall x \in \mathbb{R}$

Cho $x = 0 \Rightarrow – 3{f^2}\left( 2 \right) \cdot f’\left( 2 \right) – 12f\left( 2 \right).f’\left( 2 \right) + 36 = 0$ (2).

Ta thấy $f\left( 2 \right) = 0$ không thỏa mãn $\left( 2 \right)$ nên $f\left( 2 \right) = 2$, khi đó $f’\left( 2 \right) = 1 \Rightarrow 3f\left( 2 \right) + 4f’\left( 2 \right) = 10$.

Vậy $A = 3 \cdot f\left( 2 \right) + 4 \cdot f’\left( 2 \right) = 10$.

Phần 3. Câu trả lời ngắn.

Thí sinh trả lời đáp án từ câu 1 đến câu 6.

Câu 1. Ở thành phố $X$, xác suất để một ngày là nắng ráo là 0,8 . Nếu trời nắng thì xác suất để Minh đi ra biển chơi là 0,7 . Nếu trời mưa thì xác suất để Minh ra biển chơi là 0,1 . Xác định xác suất mà Minh sẽ đi biển chơi vào một ngày bất kì.

Trả lời: 0,58

Lời giải

Rõ ràng việc Minh đi biển hay không hoàn toàn phụ thuộc vào thời tiết.

Ta có sơ đồ cây như sau:

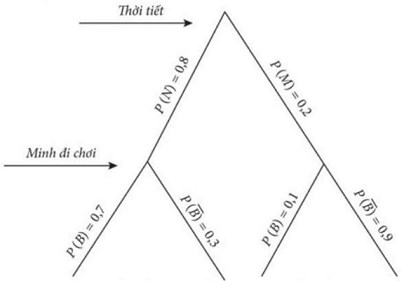
Trong đó: $N$ là biến cố “Trời nắng”, $M$ là biến cố “Trời mưa”, $B$ là biến cố “Đi biển”.

Xác suất Minh đi biển chơi là: $0,8 \cdot 0,7 + 0,2 \cdot 0,1 = 0,58$.

Câu 2. An và Bình, mỗi bạn cùng gieo hai con xúc xắc cân đối và đồng chất. Tính xác suất để hai bạn tung được số điểm như nhau.

Trả lời: $\frac{1}{6}$

Lời giải

Vì hai bạn An và Bình tung xúc xắc ra kết quả độc lập. Do đó xác suất để hai bạn ra cùng số điểm là $6 \cdot {\left( {\frac{1}{6}} \right)^2} = \frac{1}{6}$.

Câu 3. Cho hình chóp $S \cdot ABCD$ có đáy là hình vuông cạnh $a,SA \bot \left( {ABCD} \right)$. Biết góc giữa $SC$ và mặt phẳng $\left( {ABCD} \right)$ là ${60^ \circ }$. Tính góc phẳng nhị diện $\left[ {S,BD,C} \right]$ ?

Trả lời: $\widehat {SOC} = 106,{1^0}$

Lời giải

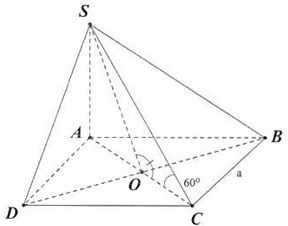
Ta có: $SA \bot \left( {ABCD} \right)$ tại $A$ và $SC$ cắt $mp\left( {ABCD} \right)$ tại $C$

$ \Rightarrow AC$ là hình chiếu của $SC$ trên $mp\left( {ABCD} \right)$

$ \Rightarrow \left( {SC,\left( {ABCD} \right)} \right) = \left( {SC,AC} \right) = \widehat {SCA} = {60^ \circ }$

Ta có: $ \Rightarrow SA = AC \cdot tan{60^ \circ } = a\sqrt 2 \cdot \sqrt 3 = \sqrt 6 a$

Ta có: $\left\{ {\begin{array}{*{20}{l}}
{BD \bot SA} \\
{BD \bot AC}
\end{array} \Rightarrow BD \bot \left( {SAC} \right)} \right.$

Ta có: $\left\{ {\begin{array}{*{20}{l}}
{\left( {SBD} \right) \cap \left( {CBD} \right) = BD} \\
{Trong\left( {CBD} \right),CO \bot BD \Rightarrow \left[ {S,BD,C} \right] = \widehat {SOC}} \\
{Trong\left( {SBC} \right),SO \bot BD}
\end{array}} \right.$

Xét $\vartriangle SAO$ vuông tại $A:tan\widehat {SOA} = \frac{{SA}}{{AO}} = \frac{{a\sqrt 6 }}{{\frac{{a\sqrt 2 }}{2}}} = 2\sqrt 3 \Rightarrow \widehat {SOA} = 73,{9^0}$

$ \Rightarrow \widehat {SOC} = 106,{1^0}$

Câu 4. Một hình chóp cụt đều $ABC \cdot A’B’C’$ có cạnh đáy lớn bằng $4a$, cạnh đáy nhỏ bằng $2a$ và chiều cao của nó bằng $\frac{{3a}}{2}$. Tìm thể tích của khối chóp cụt đều đó.

Trả lời: $\frac{{7{a^3}\sqrt 3 }}{2}$

Lời giải

Gọi $O,I$ theo thứ tự là tâm của đáy lớn $ABC$ và đáy bé $A’B’C’;K,J$ theo thứ tự là trung điểm của $BC$ và $B’C’$.

Ta có $h = IO = \frac{{3a}}{2}$ là chiều cao của hình chóp cụt đều $ABC \cdot A’B’C’$.

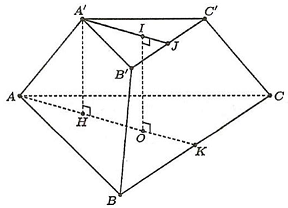
Diện tích hai đáy hình chóp cụt đều là:

${S_1} = {S_{\vartriangle ABC}} = \frac{{{{(4a)}^2}\sqrt 3 }}{4} = 4{a^2}\sqrt 3 ;{S_2} = {S_{\vartriangle A’B’C’}} = \frac{{{{(2a)}^2}\sqrt 3 }}{4} = {a^2}\sqrt 3 $

Thể tích khối chóp cụt đều là:

$V = \frac{1}{3}h\left( {{S_1} + \sqrt {{S_1}{S_2}} + {S_2}} \right)$

$ = \frac{1}{3} \cdot \frac{{3a}}{2}\left( {4{a^2}\sqrt 3 + \sqrt {4{a^2}\sqrt 3 \cdot {a^2}\sqrt 3 } + {a^2}\sqrt 3 } \right) = \frac{{7{a^3}\sqrt 3 }}{2}$ (đơn vị thể tích)

Câu 5. Cường độ một trận động đất $M$ (Richter) tính theo thang Richter được xác định theo công thức $M = logA – log{A_0}$. Với $A$ là cường độ tối đa đo được bằng địa chấn kế (biên độ của những sóng địa chấn đo ở $100\;km$ cách chấn tâm của cơn động đất) và ${A_0}$ là một biên độ chuẩn. Năng lượng được phát ra bởi một trận động đất có cường độ $M$ được xác định bởi ${E_M} = {E_0} \cdot {10^{1,5M}}$ trong đó ${E_0}$ là một hằng số dương. Hỏi với hai trận động đất có biên độ ${A_1},{A_2}$ thỏa mãn ${A_1} = 4{A_2}$, thì tỉ lệ năng lượng được phát ra bởi hai trận động đất này là?

Trả lời: 8.

Lời giải

Theo công thức ${E_M} = {E_0} \cdot {10^{1,5M}}$ ta có $\left\{ {\begin{array}{*{20}{l}}
{{E_1} = {{10}^{1,5{M_1}}}} \\
{{E_2} = {{10}^{1,5{M_2}}}}
\end{array}} \right.$.

Suy ra $\frac{{{E_2}}}{{{E_1}}} = \frac{{{{10}^{1,5{M_2}}}}}{{{{10}^{1,5{M_1}}}}} = {10^{1,5\left( {{M_2} – {M_1}} \right)}}$$ = {10^{1,5\left( {log{A_1} – log{A_2}} \right)}} = {10^{1,5log\frac{{{A_1}}}{{{A_2}}}}} = {10^{1,5log4}} = 8$.

Câu 6. Cho hàm số $y = {x^3} – 3{x^2} + 2$. Có bao nhiêu tiếp tuyến với đồ thị hàm số đi qua điểm $A\left( {1;0} \right)$ ?

Trả lời: 1 .

Lời giải

Gọi đồ thị hàm số $y = {x^3} – 3{x^2} + 2$ là $\left( C \right)$.

Ta có $y’ = 3{x^2} – 6x$

Gọi $M\left( {{x_0};{y_0}} \right) \in \left( C \right)$ là tiếp điểm. Suy ra phương trình tiếp tuyến với $\left( C \right)$ tại $M$ là $y = \left( {3x_0^2 – 6{x_0}} \right)\left( {x – {x_0}} \right) + x_0^3 – 3x_0^2 + 2\left( {\;d} \right)$.

Vì $\left( d \right)$ đi qua điểm $A\left( {1;0} \right)$ nên $\left( {3x_0^2 – 6{x_0}} \right)\left( {1 – {x_0}} \right) + x_0^3 – 3x_0^2 + 2 = 0$

$\left( {3x_0^2 – 6{x_0}} \right)\left( {1 – {x_0}} \right) + x_0^3 – 3x_0^2 + 2 = 0$$ \Leftrightarrow \left( {3x_0^2 – 6{x_0}} \right)\left( {1 – {x_0}} \right) + \left( {{x_0} – 1} \right)\left( {x_0^2 – 2{x_0} – 2} \right) = 0$

$ \Leftrightarrow \left( {{x_0} – 1} \right)\left( { – 2x_0^2 + 4{x_0} – 2} \right) = 0$

$ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{{x_0} = 1} \\
{ – 2x_0^2 + 4{x_0} – 2 = 0}
\end{array} \Leftrightarrow {x_0} = 1.} \right.$

Suy ra có 1 tiếp tuyến với $\left( C \right)$ đi qua điểm $A$.