Đề Ôn Tập HK2 Toán 11 Cánh Diều Cấu Trúc Mới Giải Chi Tiết-Đề 4

Đề ôn tập HK2 Toán 11 Cánh diều cấu trúc mới giải chi tiết-Đề 4 được soạn dưới dạng file word và PDF gồm 4 trang. Các bạn xem và tải về ở dưới.
Phần 1. Câu trắc nghiệm nhiều phương án chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thi sinh chỉ chọn một phuơng án đúng nhất.

Câu 1. Cho $a$ là một số dương, biểu thức ${a^{\frac{2}{3}}}\sqrt a $ viết dưới dạng lũy thừa với số mũ hữu tỉ là ?

A. ${a^{\frac{5}{6}}}$. B. ${a^{\frac{7}{6}}}$. C. ${a^{\frac{4}{3}}}$. D. ${a^{\frac{6}{7}}}$.

Câu 2. Hàm số nào có đồ thị như hình vẽ ở dưới đây?

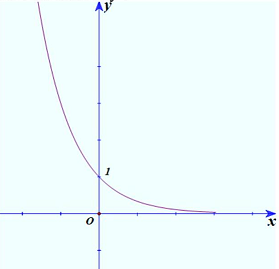
A. $y = {\left( {\frac{1}{{\sqrt 2 }}} \right)^2}$. B. $y = {(\sqrt 2 )^x}$. C. $y = {\left( {\frac{1}{3}} \right)^x}$. D. $y = {3^x}$.

Câu 3. Cho tứ diện $ABCD$ có $AB = AC$ và $DB = DC$. Khẳng định nào sau đây đúng?

A. $CD \bot AB$. B. $AC \bot BD$. C. $BC \bot AD$. D. $BC \bot CD$.

Câu 4. Cho hình chóp tứ giác đều $S.ABCD$ có tất cả các cạnh bằng nhau. Gọi $E,M$ lần lượt là trung điểm của các cạnh $BC$ và $SA,\alpha $ là góc tạo bởi đường thẳng $EM$ và mặt phẳng $\left( {SBD} \right)$. Giá trị của $tan\alpha $ bằng

A. 2 . B. $\sqrt 3 $. C. 1 . D. $\sqrt 2 $.

Câu 5. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông, hai mặt bên $\left( {SAB} \right)$ và $\left( {SAD} \right)$ vuông góc với mặt đáy. $AH,AK$ lần lượt là đường cao của tam giác $SAB,SAD$. Mệnh đề nào sau đây là sai?

A. $BC \bot AH$. B. $SA \bot AC$. C. $HK \bot SC$. D. $AK \bot BD$.

Câu 6. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông tâm $O,SA \bot \left( {ABCD} \right)$. Gọi $I$ là trung điểm của $SC$. Khoảng cách từ $I$ đến mặt phẳng $\left( {ABCD} \right)$ bằng độ dài đoạn thẳng nào?

A. $IO$. B. $IA$. C. IC . D. $IB$.

Câu 7. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a,SD = \frac{{3a}}{2}$, hình chiếu vuông góc của $S$ trên mặt phẳng $\left( {ABCD} \right)$ là trung điểm của cạnh $AB$. Tính theo $a$ thể tích khối chóp $S.ABCD$.

A. $\frac{{{a^3}}}{2}$. B. $\frac{{{a^3}}}{3}$. C. $\frac{{{a^3}}}{4}$. D. $\frac{{2{a^3}}}{3}$.

Câu 8. Hai cầu thủ sút phạt đền. Mỗi người đá 1 lần với xác suất ghi bàn tương ứng là 0,8 và 0,7 . Tính xác suất để có ít nhất 1 cầu thủ ghi bàn.

A. $P\left( X \right) = 0,42$. B. $P\left( X \right) = 0,94$. C. $P\left( X \right) = 0,234$. D. $P\left( X \right) = 0,9$.

Câu 9. Các chữ số $1,6,9$ được sắp theo thứ tự ngẫu nhiên để tạo ra một số có 3 chữ số. Tìm xác suất để số này là số chính phương.

A. $\frac{2}{3}$. B. $\frac{1}{6}$. C. $\frac{1}{3}$. D. $\frac{1}{2}$.

Câu 10. Tính đạo hàm của hàm số $y = {17^{ – x}}$

A. $y’ = {17^{ – x}}ln17$. B. $y’ = – x \cdot {17^{ – x – 1}}$. C. $y’ = – {17^{ – x}}$. D. $y’ = – {17^{ – x}}ln17$.

Câu 11. Đạo hàm cấp hai của hàm số $y = lnx$ là.

A. $y” = \frac{1}{{{x^2}}}$. B. $y” = – \frac{1}{{{x^2}}}$. C. $y” = \frac{1}{x}$. D. $y” = – \frac{1}{x}$.

Câu 12. Cho hàm số $y = \frac{{{x^3}}}{3} + 3{x^2} – 2$ có đồ thị là $\left( C \right)$. Viết phương trình tiếp tuyến với đồ thị $\left( C \right)$ biết tiếp tuyến có hệ số góc $k = – 9$.

A. $y + 16 = – 9\left( {x + 3} \right)$. B. $y – 16 = – 9\left( {x – 3} \right)$. C. $y = – 9\left( {x + 3} \right)$. D. $y – 16 = – 9\left( {x + 3} \right)$.

Phần 2. Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoạc sai

Câu 1. Theo kết quả khảo sát ở một trường học về số học sinh yêu thích một loại nước giải khát $A$ được cho bởi bảng sau:

Lớp	Thích		Không thích
	Số học sinh nam	Số học sinh nữ	Số học sinhnam	Số học sinhnữ
11A	23	12	5	10
11B	25	15	6	12
11C	20	15	8	15

a) Xác suất để chọn được một học sinh nam và một học sinh nữ ở khối lớp 11 mà thích uống nước giải khát $A$ là $\frac{{952}}{{4565}}$.

b) Xác suất để chọn được một học sinh nam ở lớp $11A$ và một học sinh nam ở lớp $11B$ không thích nước giải khát $A$ là $\frac{1}{{2739}}$.

c) Gọi $A$ là biến cố: “Học sinh nam thích nước giải khát $A$ “. Tính được $P\left( A \right) = \frac{{42}}{{79}}$.

d) Việc thích uống nước giải khát $A$ có phụ thuộc vào giới tính.

Câu 2. Cho hình chóp $S.ABC$ có $SA \bot \left( {ABC} \right)$, tam giác $ABC$ vuông tại $B$ (tham khảo hình vẽ).

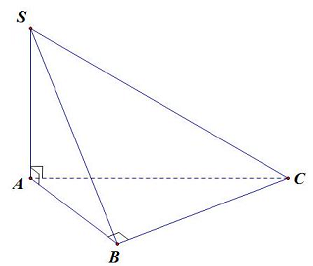
Các mệnh đề sau đúng hay sai?

a) Khoảng cách từ $C$ đến mặt phẳng $\left( {SAB} \right)$ là đoạn $BC$.

b) $BC \bot \left( {SAB} \right)$.

c) Khoảng cách từ $B$ đến mặt phẳng $\left( {SAC} \right)$ là đoạn $AB$.

d) $SB \bot BC$.

Câu 3. Cho hai hàm số $f\left( x \right) = lo{g_{0,5}}x$ và $g\left( x \right) = {2^{ – x}}$. Các mệnh đề sau đúng hay sai?

a) Đồ thị hai hàm số đối xứng nhau qua đường thẳng $y = – x$.

b) Tập xác định của hai hàm số trên là $\mathbb{R}$.

c) Đồ thị của hai hàm số cắt nhau tại đúng một điểm.

d) Hai hàm số trên đều nghịch biến trên tập xác định của nó.

Câu 4. Cho hàm số $f\left( x \right) = \left| {x + 1} \right|$. Khẳng định nào sau đây là sai?

a) $f\left( x \right)$ liên tục tại $x = – 1$.

b) $f\left( x \right)$ có đạo hàm tại $x = – 1$.

c) $f\left( { – 1} \right) = 0$.

d) $f\left( x \right)$ đạt giá trị nhỏ nhất tại $x = – 1$.

Phần 3. Câu trả lời ngắn.
Thí sinh trả lời đáp án từ câu 1 đến câu 6.

Câu 1. Một chiếc túi chứa 5 quả bóng màu đỏ và 6 quả bóng màu xanh có cùng kích thước và khối lượng. Lần lượt lấy ngẫu nhiên một quả bóng rồi trả lại vào túi. Tính xác suất lấy được hai quả bóng màu xanh sau 2 lượt lấy

Câu 2. Cho hình chóp $S \cdot ABC$ có đáy là tam giác đều cạnh $a,SB \bot \left( {ABC} \right)$ và $SB = 4a$. Tính góc giữa đường thẳng $SC$ và mặt phẳng $\left( {SAB} \right)$ ?

Câu 3. Cho hình chóp $S.ABCD$ có đáy là hình vuông cạnh $a$, tam giác $SAB$ đều và nằm trong mặt phẳng vuông góc với đáy. Tìm thể tích khối chóp $S.ABCD$.

Câu 4. Trong tin học, độ hiệu quả của một thuật toán tỉ lệ với tốc độ thực thi chương trình và được tính bởi $E\left( n \right) = \frac{n}{{P\left( n \right)}}$, trong đó $n$ là số lượng dữ liệu đầu vào và $P\left( n \right)$ là độ phức tạp của thuật toán. Biết rằng một thuật toán có $P\left( n \right) = lo{g_2}n$ và khi $n = 300$ thì để chạy nó, máy tính mất 0,02 giây. Hỏi khi $n = 90000$ thì phải mất bao lâu để chạy chương trình tương ứng?

Câu 5. Có bao nhiêu giá trị nguyên thuộc khoảng $\left( { – 30;30} \right)$ của tham số $m$ để mọi tiếp tuyến của đồ thị hàm số $y = {x^3} – m{x^2} + \left( {2m – 3} \right)x – 1$ đều có hệ số góc dương?

Câu 6. Tính đạo hàm cấp hai của hàm số $y = lnx$

ĐÁP ÁN VÀ LỜI GIẢI THAM KHẢO

Phần 1. Câu trắc nghiệm nhiều phương án chọn.
Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phuơng án đúng nhất.

1B	2C	3C	4D	5D	6A
7B	8B	9D	10D	11B	12D

Câu 1. Cho $a$ là một số dương, biểu thức ${a^{\frac{2}{3}}}\sqrt a $ viết dưới dạng lũy thừa với số mũ hữu tỉ là?

A. ${a^{\frac{5}{6}}}$.

B. ${a^{\frac{7}{6}}}$.

C. ${a^{\frac{4}{3}}}$.

D. ${a^{\frac{6}{7}}}$.

Lời giải

Với $a > 0$, ta có ${a^{\frac{2}{3}}}\sqrt a = {a^{\frac{2}{3}}} \cdot {a^{\frac{1}{2}}} = {a^{\frac{2}{3} + \frac{1}{2}}} = {a^{\frac{7}{6}}}$.

Câu 2. Hàm số nào có đồ thị như hình vẽ ở dưới đây?

A. $y = {\left( {\frac{1}{{\sqrt 2 }}} \right)^2}$.

B. $y = {(\sqrt 2 )^x}$.

C. $y = {\left( {\frac{1}{3}} \right)^x}$.

D. $y = {3^x}$.

Lời giải

Đồ thị hàm số ở hình vẽ là đồ thị của hàm số mũ có dạng $y = {a^x}$. Loại đáp án $A$

Dựa vào đồ thị ta thấy hàm số nghịch biến trên $\mathbb{R}$ nên $0 < a < 1$. Loại đáp án $B,D$

Vậy đồ thị trong hình vẽ là đồ thị hàm số $y = {\left( {\frac{1}{3}} \right)^x}$.

Câu 3. Cho tứ diện $ABCD$ có $AB = AC$ và $DB = DC$. Khẳng định nào sau đây đúng?

A. $CD \bot AB$.

B. $AC \bot BD$.

C. $BC \bot AD$.

D. $BC \bot CD$.

Lời giải

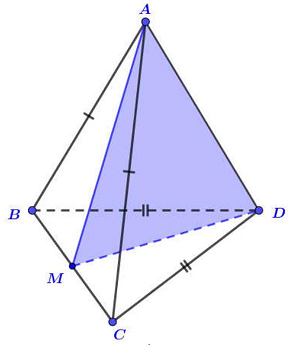
Gọi $M$ là trung điểm $BC$. Do tam giác $ABC$ cân tại $A$ và tam giác $DBC$ cân tại $D$ nên, có: $\left\{ {\begin{array}{*{20}{l}}
{BC \bot DM} \\
{BC \bot AM}
\end{array} \Rightarrow BC \bot AD} \right.$.

Câu 4. Cho hình chóp tứ giác đều $S \cdot ABCD$ có tất cả các cạnh bằng nhau. Gọi $E,M$ lần lượt là trung điểm của các cạnh $BC$ và $SA,\alpha $ là góc tạo bởi đường thẳng $EM$ và mặt phẳng $\left( {SBD} \right)$. Giá trị của $tan\alpha $ bằng

A. 2 .

B. $\sqrt 3 $.

C. 1 .

D. $\sqrt 2 $.

Lời giải

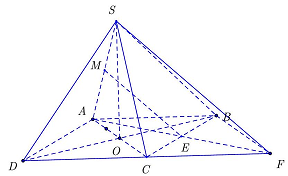
Dựng hình bình hành $ABFC$.

Ta có $EM//SF$ nên góc giữa $EM$ và $\left( {SBD} \right)$ bằng góc giữa $SF$ và $\left( {SBD} \right)$.

$FB//AC \Rightarrow FB \bot \left( {SBD} \right)$ do đó góc giữa $SF$ và $\left( {SBD} \right)$ bằng góc $\widehat {FSB}$.

Ta có $tan\widehat {FSB} = \frac{{BF}}{{SB}} = \frac{{AC}}{{SB}} = \sqrt 2 $. Vậy chọn D.

Câu 5. Cho hình chóp $S \cdot ABCD$ có đáy $ABCD$ là hình vuông, hai mặt bên $\left( {SAB} \right)$ và $\left( {SAD} \right)$ vuông góc với mặt đáy. $AH,AK$ lần lượt là đường cao của tam giác $SAB,SAD$. Mệnh đề nào sau đây là sai?

A. $BC \bot AH$.

B. $SA \bot AC$.

C. $HK \bot SC$.

D. $AK \bot BD$.

Lời giải

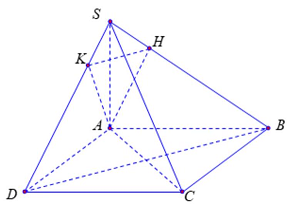
Ta có $\left\{ {\begin{array}{*{20}{l}}
{\left( {SAB} \right) \bot \left( {ABCD} \right)} \\
{\left( {SAD} \right) \bot \left( {ABCD} \right)}
\end{array}} \right.$ nên $SA \bot \left( {ABCD} \right)$

Suy ra $SA \bot AC$ (B đúng); $SA \bot BC;SA \bot BD$.

Mặt khác $BC \bot AB$ nên $BC \bot \left( {SAB} \right)$ suy ra $BC \bot AH$ (A đúng).

và $BD \bot AC$ nên $BD \bot \left( {SAC} \right)$ suy ra $BD \bot SC$;

Đồng thời $HK//BD$ nên $HK \bot SC$ (C đúng).

Vậy mệnh đề sai là $AK \bot BD$ (vì không đủ điều kiện chứng minh).

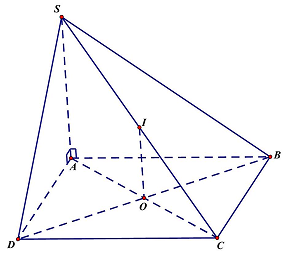
Câu 6. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông tâm $O,SA \bot \left( {ABCD} \right)$. Gọi $I$ là trung điểm của $SC$. Khoảng cách từ $I$ đến mặt phẳng $\left( {ABCD} \right)$ bằng độ dài đoạn thẳng nào?

A. $IO$.

B. $IA$.

C. $IC$.

D. $IB$.

Lời giải

Do $I$ là trung điểm của $SC$ và $O$ là trung điểm $AC$ nên $IO//SA$. Do $SA \bot \left( {ABCD} \right)$ nên $IO \bot \left( {ABCD} \right)$, hay khoảng cách từ $I$ đến mặt phẳng $\left( {ABCD} \right)$ bằng độ dài đoạn thẳng $IO$.

Câu 7. Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a,SD = \frac{{3a}}{2}$, hình chiếu vuông góc của $S$ trên mặt phẳng $\left( {ABCD} \right)$ là trung điểm của cạnh $AB$. Tính theo $a$ thể tích khối chóp $S.ABCD$.

A. $\frac{{{a^3}}}{2}$.

B. $\frac{{{a^3}}}{3}$.

C. $\frac{{{a^3}}}{4}$.

D. $\frac{{2{a^3}}}{3}$.

Lời giải

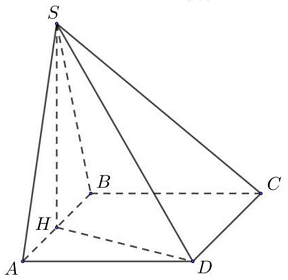
Gọi $H$ là trung điểm $AB \Rightarrow SH \bot \left( {ABCD} \right)$.

Ta có: $SH = \sqrt {S{D^2} – H{D^2}} = \sqrt {S{D^2} – \left( {A{H^2} + A{D^2}} \right)} = \sqrt {\frac{{9{a^2}}}{4} – \left( {\frac{{{a^2}}}{4} + {a^2}} \right)} = a$.

Vậy: ${V_{S.ABCD}} = \frac{1}{3}{S_{ABCD}} \cdot SH = \frac{{{a^3}}}{3}$.

Câu 8. Hai cầu thủ sút phạt đền. Mỗi người đá 1 lần với xác suất ghi bàn tương ứng là 0,8 và 0,7 . Tính xác suất để có ít nhất 1 cầu thủ ghi bàn.

A. $P\left( X \right) = 0,42$.

B. $P\left( X \right) = 0,94$.

C. $P\left( X \right) = 0,234$.

D. $P\left( X \right) = 0,9$.

Lời giải

Gọi $A$ là biến cố “Cầu thủ thứ nhất ghi bàn”; $B$ là biến cố “Cầu thủ thứ hai ghi bàn”; $X$ là biến cố “Ít nhất một trong hai cầu thủ ghi bàn”.

• Cầu thủ thứ nhất ghi bàn và cầu thủ hai không ghi bàn là $A\overline B $, ta có:

$P\left( {A\overline B } \right) = P\left( A \right) \cdot P\left( {\overline B } \right) = 0,8 \cdot 0,3 = 0,24$.

• Cầu thủ thứ nhất không ghi bàn và cầu thủ hai ghi bàn là $\overline A B$, ta có:

$P\left( {\overline A B} \right) = P\overline A \cdot P\left( B \right) = 0,2 \cdot 0,7 = 0,14$.

• Cả hai cầu thủ ghi bàn là $AB$, ta có: $P\left( {AB} \right) = P\left( A \right) \cdot P\left( B \right) = 0,8 \cdot 0,7 = 0,56$.

Biến cố để có ít nhất một cầu thủ ghi bàn là $X = A\overline B \cup \overline A B \cup AB$.

Xác suất để có ít nhất một cầu thủ ghi bàn là:

$P\left( X \right) = P\left( {A\overline B } \right) + P\left( {\overline A B} \right) + P\left( {AB} \right) = 0,24 + 0,14 + 0,56 = 0,94$.

Chọn B

Câu 9. Các chữ số $1,6,9$ được sắp theo thứ tự ngẫu nhiên để tạo ra một số có 3 chữ số. Tìm xác suất để số này là số chính phương.

A. $\frac{2}{3}$.

B. $\frac{1}{6}$.

C. $\frac{1}{3}$.

D. $\frac{1}{2}$.

Lời giải

Ta có thể tạo được 6 số từ ba chữ số 1,6, 9. Các số đó là: 169,196,619,691,916,961.

Các số chính phương là $169,196,961$. Vậy xác suất để số này là số chính phương là $\frac{1}{2}$.

Chọn D

Câu 10. Tính đạo hàm của hàm số $y = {17^{ – x}}$

A. $y’ = {17^{ – x}}ln17$.

B. $y’ = – x \cdot {17^{ – x – 1}}$.

C. $y’ = – {17^{ – x}}$.

D. $y’ = – {17^{ – x}}ln17$.

Lời giải

Áp dụng công thức: ${\left( {{a^u}} \right)’} = u’ \cdot {a^u}lna$ ta có: $y’ = {\left( {{{17}^{ – x}}} \right)’} = – {17^{ – x}} \cdot ln17$.

Câu 11. Đạo hàm cấp hai của hàm số $y = lnx$ là.

A. $y” = \frac{1}{{{x^2}}}$.

B. $y” = – \frac{1}{{{x^2}}}$.

C. $y” = \frac{1}{x}$.

D. $y” = – \frac{1}{x}$.

Lời giải

$y’ = \frac{1}{x},y” = – \frac{1}{{{x^2}}}$

Câu 12. Cho hàm số $y = \frac{{{x^3}}}{3} + 3{x^2} – 2$ có đồ thị là $\left( C \right)$. Viết phương trình tiếp tuyến với đồ thị $\left( C \right)$ biết tiếp tuyến có hệ số góc $k = – 9$.

A. $y + 16 = – 9\left( {x + 3} \right)$.

B. $y – 16 = – 9\left( {x – 3} \right)$.

C. $y = – 9\left( {x + 3} \right)$.

D. $y – 16 = – 9\left( {x + 3} \right)$.

Lời giải

Gọi $M\left( {{x_0};\frac{{x_0^3}}{3} + 3x_0^2 – 2} \right)$ là tiếp điểm.

Ta có: $k = f’\left( {{x_0}} \right) \Leftrightarrow {x_0}{\;^2} + 6{x_0} = – 9 \Leftrightarrow {x_0} = – 3 \Rightarrow {y_0} = f\left( {{x_0}} \right) = 16$

Phương trình tiếp tuyến với đồ thị $\left( C \right)$ thỏa mãn đầu bài là: $y – 16 = – 9\left( {x + 3} \right)$.

Phần 2. Câu trắc nghiệm đúng sai.
Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai

Câu 1. Theo kết quả khảo sát ở một trường học về số học sinh yêu thích một loại nước giải khát $A$ được cho bởi bảng sau:

Lớp	Thích		Không thích
	Số học sinh nam	Số học sinh nữ	Số học sinhnam	Số học sinhnữ
11A	23	12	5	10
11B	25	15	6	12
11C	20	15	8	15

a) Xác suất để chọn được một học sinh nam và một học sinh nữ ở khối lớp 11 mà thích uống nước giải khát $A$ là $\frac{{952}}{{4565}}$.

b) Xác suất để chọn được một học sinh nam ở lớp $11A$ và một học sinh nam ở lớp $11B$ không thích nước giải khát $A$ là $\frac{1}{{2739}}$.

c) Gọi $A$ là biến cố: “Học sinh nam thích nước giải khát $A$ “. Tính được $P\left( A \right) = \frac{{42}}{{79}}$.

d) Việc thích uống nước giải khát $A$ có phụ thuộc vào giới tính.

Lời giải

a) Đúng

b) Sai

c) Sai

d) Đúng

a) Xác suất để chọn được một học sinh nam và một học sinh nữ ở khối lớp 11 mà thích uống nước giải khát $A$ là $\frac{{C_{68}^1C_{42}^1}}{{C_{166}^2}} = \frac{{952}}{{4565}}$.

b) Xác suất để chọn được một học sinh nam ở lớp $11\;A$ và một học sinh nam ở lớp $11\;B$ không thích nước giải khát $A$ là $\frac{{C_5^1C_6^1}}{{C_{166}^2}} = \frac{2}{{913}}$.

c) Gọi $A$ là biến cố: “Học sinh nam thích nước giải khát $A$ “. Tính được $P\left( A \right) = \frac{{68}}{{87}}$.

Gọi $B$ là biến cố: “Học sinh nữ thích nước giải khát $A$ “. Tính được $P\left( B \right) = \frac{{42}}{{79}}$.

Ta có $P\left( {A \cup B} \right) = \frac{{110}}{{166}} = P\left( A \right) + P\left( B \right) – P\left( {AB} \right)$, từ đó tính được $P\left( {AB} \right) \approx 0,6506$.

Trong khi đó $P\left( A \right) \cdot P\left( B \right) \approx 0,4155$ nên hai biến cố $A$ và $B$ không độc lập hay việc thích uống nước giải khát $A$ có phụ thuộc vào giới tính.

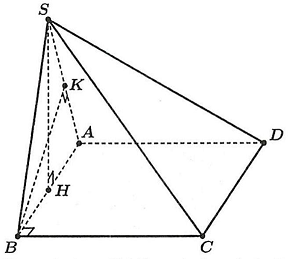
Câu 2. Cho hình chóp $S.ABC$ có $SA \bot \left( {ABC} \right)$, tam giác $ABC$ vuông tại $B$ (tham khảo hình vẽ).

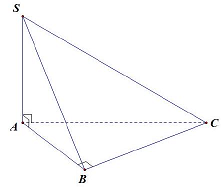
Các mệnh đề sau đúng hay sai?

a) Khoảng cách từ $C$ đến mặt phẳng $\left( {SAB} \right)$ là đoạn $BC$.

b) $BC \bot \left( {SAB} \right)$.

c) Khoảng cách từ $B$ đến mặt phẳng $\left( {SAC} \right)$ là đoạn $AB$.

d) $SB \bot BC$.

Lời giải

a) Đúng

b) Đúng

c) Sai

d) Đúng

Suy ra khoảng cách từ $C$ đến mặt phẳng $\left( {SAB} \right)$ là đoạn $BC$. Đáp án $A$ đúng.

$\vartriangle ABC$ vuông tại $B$ nên $AB$ không vuông góc với $\left( {SAC} \right)$. Vậy đáp án sai là $C$.

Câu 3. Cho hai hàm số $f\left( x \right) = lo{g_{0,5}}x$ và $g\left( x \right) = {2^{ – x}}$. Các mệnh đề sau đúng hay sai?

a) Đồ thị hai hàm số đối xứng nhau qua đường thẳng $y = – x$.

b) Tập xác định của hai hàm số trên là $\mathbb{R}$.

c) Đồ thị của hai hàm số cắt nhau tại đúng một điểm.

d) Hai hàm số trên đều nghịch biến trên tập xác định của nó.

Lời giải

a) Sai

b) Sai

c) Đúng

d) Đúng

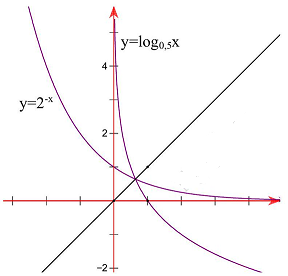
Đồ thị hai hàm số như hình vẽ suy ra a sai, b sai, c đúng, d đúng.

Câu 4. Cho hàm số $f\left( x \right) = \left| {x + 1} \right|$. Khẳng định nào sau đây là sai?

a) $f\left( x \right)$ liên tục tại $x = – 1$.

b) $f\left( x \right)$ có đạo hàm tại $x = – 1$.

c) $f\left( { – 1} \right) = 0$.

d) $f\left( x \right)$ đạt giá trị nhỏ nhất tại $x = – 1$.

Lời giải

a) Đúng

b) Sai

c) Đúng

d) Đúng

$f(x) = |x + 1| = \,\left\{ \begin{gathered}
(x + 1)\,\,\,khi\,x \geqslant – 1 \hfill \\
– (x + 1)\,\,khi\,\,x \geqslant – 1\, \hfill \\
\end{gathered} \right.$

* $f( – 1) = 0 \Rightarrow $ Phương án $C$ đúng.

$f(x) \geqslant 0,\forall x.\quad f(x) = 0 \Leftrightarrow x = – 1 \Rightarrow $ Phương án $D$ dủng.

* $\mathop {\lim }\limits_{x \to – {1^ + }} f(x) = \mathop {\lim }\limits_{x \to – {1^ + }} (x + 1) = 0$.

$\mathop {\lim }\limits_{x \to – {1^ – }} f(x) = \mathop {\lim }\limits_{x \to – {1^ – }} ( – x – 1) = 0. \Rightarrow $ Phương án A đúng.

* $\mathop {\lim }\limits_{x \to – {1^ – }} \frac{{f(x) – f( – 1)}}{{x – ( – 1)}} = \mathop {\lim }\limits_{x \to – {1^ – }} \frac{{ – x – 1}}{{x + 1}} = – 1$

$\mathop {\lim }\limits_{x \to – {1^ + }} \frac{{f(x) – f( – 1)}}{{x – ( – 1)}} = \mathop {\lim }\limits_{x \to – {1^ + }} \frac{{x + 1}}{{x + 1}} = 1$

Suy ra không tồn tại giới hạn của tỷ số $\frac{{f\left( x \right) – f\left( { – 1} \right)}}{{x – \left( { – 1} \right)}}$ khi $x \to – 1$.

Do đó hàm số đã cho không có đạo hàm tại $x = – 1$.

Phần 3. Câu trả lời ngắn.
Thí sinh trả lời đáp án từ câu 1 đến câu 6.

Câu 1. Một chiếc túi chứa 5 quả bóng màu đỏ và 6 quả bóng màu xanh có cùng kích thước và khối lượng. Lần lượt lấy ngẫu nhiên một quả bóng rồi trả lại vào túi. Tính xác suất lấy được hai quả bóng màu xanh sau 2 lượt lấy

Trả lời: $\frac{{36}}{{121}}$

Ta có sơ đồ cây như sau:

Lời giải

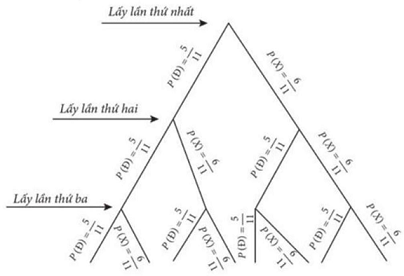
Trong đó: là biến cố “Lấy được quả bóng màu đỏ”, $X$ là biến cố “Lấy được quả bóng màu xanh”.

Dựa vào sơ đồ cây, xác suất lấy 2 bóng xanh sau 2 lượt là ${\left( {\frac{6}{{11}}} \right)^2} = \frac{{36}}{{121}}$.

Câu 2. Cho hình chóp $S.ABC$ có đáy là tam giác đều cạnh $a,SB \bot \left( {ABC} \right)$ và $SB = 4a$. Tính góc giữa đường thẳng $SC$ và mặt phẳng $\left( {SAB} \right)$ ?

Trả lời: $\left( {SC,\left( {SAB} \right)} \right) \approx 12,{1^0}$

Lời giải

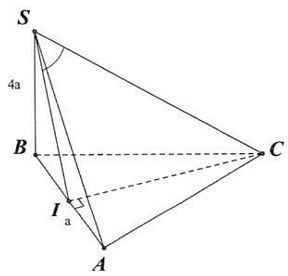
Kẻ $CI \bot AB \Rightarrow I$ là trung điểm $AB$

Ta có: $\left\{ {\begin{array}{*{20}{l}}
{CI \bot AB} \\
{CI \bot SB}
\end{array} \Rightarrow CI \bot \left( {SAB} \right)} \right.$ tại $I$ và $SC$ cắt mp $\left( {SAB} \right)$ tại $S$

$ \Rightarrow SI$ là hình chiếu của $SC$ trên $mp\left( {SAB} \right)$

$ \Rightarrow \left( {SC,\left( {SAB} \right)} \right) = \left( {SC,SI} \right) = \widehat {CSI}$

Ta có: $IC = \frac{{a\sqrt 3 }}{2}$

Ta có: $SC = \sqrt {S{B^2} + B{C^2}} = \sqrt {{{(4a)}^2} + {a^2}} = \sqrt {17} a$

Xét $\vartriangle SCI$ vuông tại $I:sin\widehat {CSI} = \frac{{CI}}{{SC}} = \frac{{\frac{{a\sqrt 3 }}{2}}}{{\sqrt {17} a}} = \frac{{\sqrt {51} }}{{34}} \Rightarrow \widehat {CSI} \approx 12,{1^0}$

Vậy $\left( {SC,\left( {SAB} \right)} \right) \approx 12,{1^0}$.

Câu 3. Cho hình chóp $S \cdot ABCD$ có đáy là hình vuông cạnh $a$, tam giác $SAB$ đều và nằm trong mặt phẳng vuông góc với đáy. Tìm thể tích khối chóp $S.ABCD$.

Trả lò̀i: $\frac{{{a^3}\sqrt 3 }}{6}$

Lời giải

Gọi $H$ là trung điểm $AB$, suy ra $SH \bot AB$ (do tam giác $SAB$ dều).

Mặt khác $\left( {SAB} \right) \bot \left( {ABCD} \right)$ nên $SH \bot \left( {ABCD} \right)$.

Đường cao hình chóp là $SH = \frac{{a\sqrt 3 }}{2}$; diện tích đáy hình chóp ${S_{ABCD}} = {a^2}$.

Thể tích khối chóp là:

${V_{S.ABCD}} = \frac{1}{3}SH \cdot {S_{ABCD}} = \frac{1}{3} \cdot \frac{{a\sqrt 3 }}{2} \cdot {a^2} = \frac{{{a^3}\sqrt 3 }}{6}$ (đơn vị thể tích).

Câu 4. Trong tin học, độ hiệu quả của một thuật toán tỉ lệ với tốc độ thực thi chương trình và được tính bởi $E\left( n \right) = \frac{n}{{P\left( n \right)}}$, trong đó $n$ là số lượng dữ liệu đầu vào và $P\left( n \right)$ là độ phức tạp của thuật toán. Biết rằng một thuật toán có $P\left( n \right) = lo{g_2}n$ và khi $n = 300$ thì để chạy nó, máy tính mất 0,02 giây. Hỏi khi $n = 90000$ thì phải mất bao lâu để chạy chương trình tương ứng?

Trả lời: 3 giây

Lời giải

Ta có $E\left( {300} \right) = \frac{{300}}{{lo{g_2}300}}$ máy tính phải chạy mất 0,02 giây.

Suy ra $E\left( {90000} \right) = \frac{{90000}}{{lo{g_2}90000}}$ máy tính phải mất thời gian để chạy là: $\frac{{E\left( {90000} \right) \cdot 0,02}}{{E\left( {300} \right)}} = 3$ giây.

Câu 5. Có bao nhiêu giá trị nguyên thuộc khoảng $\left( { – 30;30} \right)$ của tham số $m$ để mọi tiếp tuyến của đồ thị hàm số $y = {x^3} – m{x^2} + \left( {2m – 3} \right)x – 1$ đều có hệ số góc dương?

Trả lời: không có giá trị của tham số $m$

Lời giải

$y = {x^3} – m{x^2} + \left( {2m – 3} \right)x – 1 \Rightarrow y’ = 3{x^2} – 2mx + 2m – 3$.

Mọi tiếp tuyến của đồ thị hàm số $y = {x^3} – m{x^2} + \left( {2m – 3} \right)x – 1$ đều có hệ số góc dương $ \Leftrightarrow y’ = 3{x^2} – 2mx + 2m – 3 > 0,\forall x \in \mathbb{R}$

$ \Leftrightarrow \Delta ‘ = {m^2} – 3\left( {2m – 3} \right) < 0 \Leftrightarrow {m^2} – 6m + 9 < 0\left( {VN} \right)$.

Vậy không có giá trị của tham số $m$ thỏa mãn yêu cầu bài toán.

Câu 6. Tính đạo hàm cấp hai của hàm số $y = lnx$

Trả lời: $y” = – \frac{1}{{{x^2}}}$

Lời giải

$y’ = \frac{1}{x},y” = – \frac{1}{{{x^2}}}$