Đề Kiểm Tra HK1 Toán 11 Cánh Diều Giải Chi Tiết-Đề 5

Đề kiểm tra HK1 Toán 11 Cánh diều giải chi tiết-Đề 5 được soạn dưới dạng file word và PDF gồm 5 trang. Các bạn xem và tải về ở dưới.

I. PHẦN TRẮC NGHIỆM

Câu 1: Giá trị của $\cot {30^ \circ }$ là

A. $\sqrt 3 $. B. 0 . C. -1 . D. $ – \sqrt 3 $.

Câu 2: Đẳng thức nào sau đây là đúng?

A. $cos\left( {a + \frac{\pi }{3}} \right) = \frac{{\sqrt 3 }}{2}sina – \frac{1}{2}cosa$. B. $cos\left( {a + \frac{\pi }{3}} \right) = \frac{1}{2}sina – \frac{{\sqrt 3 }}{2}cosa$.

C. $cos\left( {a + \frac{\pi }{3}} \right) = \frac{1}{2}cosa – \frac{{\sqrt 3 }}{2}sina$. D. $cos\left( {a + \frac{\pi }{3}} \right) = cosa + \frac{1}{2}$.

Câu 3: Nghiệm của phương trình $cosx = – \frac{1}{2}$ là

Ta có: $cosx = – \frac{1}{2} \Leftrightarrow cosx = cos\frac{{2\pi }}{3} \Leftrightarrow x = \pm \frac{{2\pi }}{3} + k2\pi ,k \in \mathbb{Z}$.

A. $x = \pm \frac{\pi }{3} + k2\pi $. B. $x = \pm \frac{\pi }{6} + k2\pi $. C. $x = \pm \frac{{2\pi }}{3} + k2\pi $. D. $x = \pm \frac{\pi }{6} + k\pi $

Câu 4: Phương trình $sin2x = 1$ có nghiệm là

A. $x = \frac{\pi }{4} + k3\pi $. B. $x = \frac{\pi }{4} + k\pi $. C. $x = \frac{\pi }{4} + k\frac{\pi }{2}$. D. $x = \frac{\pi }{4} + k2\pi $.

Câu 5: Tìm tập xác định của hàm số $y = tanx$.

A. $\mathbb{R} \setminus \left\{ {k2\pi \mid k \in \mathbb{Z}} \right\}$. B. $\mathbb{R} \setminus \left\{ {\frac{\pi }{2} + k\pi \mid k \in \mathbb{Z}} \right\}$.

C. $\mathbb{R} \setminus \left\{ {k\pi \mid k \in \mathbb{Z}} \right\}$. D. $\mathbb{R} \setminus \left\{ {\frac{\pi }{2} + k2\pi \mid k \in \mathbb{Z}} \right\}$.

Câu 6: Hàm số nào sau đây nghịch biến trên $\left( {\frac{\pi }{2};\pi } \right)$ ?

A. $y = – cotx$. B. $y = tanx$. C. $y = – sinx$. D. $y = cosx$.

Câu 7: Trong các công thức sau, công thức nào đúng?

A. $sin2a = 2sina$. B. $sin2a = sina + cosa$. C. $sin2a = 2sinacosa$. D. $sin2a = co{s^2}a – si{n^2}a$.

Câu 8: Hàm số $y = tanx + cotx + \frac{1}{{sinx}} + \frac{1}{{cosx}}$ không xác định trong khoảng nào trong các khoảng sau đây?

A. $\left( {k2\pi ;\frac{\pi }{2} + k2\pi } \right)$ với $k \in \mathbb{Z}$. B. $\left( {\pi + k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right)$ với $k \in \mathbb{Z}$.

C. $\left( {\frac{\pi }{2} + k2\pi ;\pi + k2\pi } \right)$ với $k \in \mathbb{Z}$. D. $\left( {\pi + k2\pi ;2\pi + k2\pi } \right)$ với $k \in \mathbb{Z}$.

Câu 9: Nếu $\alpha $ là góc nhọn và $sin2\alpha = a$. Tính $sin\alpha + cos\alpha $.

A. $\sqrt {a + 1} – \sqrt {{a^2} – a} $. B. $\sqrt {a + 1} $. C. $\sqrt {a + 1} + \sqrt {{a^2} – a} $. D. $\left( {\sqrt 2 – 1} \right)a + 1$

Câu 10: Cho cấp số cộng $\left( {{u_n}} \right)$ có số hạng tổng quát là ${u_n} = 3n – 2$. Tìm công sai $d$ của cấp số cộng.

A. $d = – 3$. B. $d = 3$. C. $d = 2$. D. $d = – 2$.

Câu 11: Cho cấp số cộng $\left( {{u_n}} \right)$ có ${u_1} = – 3$ và $d = \frac{1}{2}$. Khẳng định nào sau đây đúng?

A. ${u_n} = – 3 + \frac{1}{2}\left( {n + 1} \right)$. B. ${u_n} = – 3 + \frac{1}{2}n – 1$. C. ${u_n} = – 3 + \frac{1}{2}\left( {n – 1} \right)$. D. ${u_n} = – 3 + \frac{1}{4}\left( {n – 1} \right)$.

Câu 12: Cho dãy số $\left( {{u_n}} \right)$ với ${u_n} = \frac{{a{n^2}}}{{n + 1}}$ ( $a$ hằng số). Hỏi ${u_{n + 1}}$ là số hạng nào sau đây?

Ta có: ${u_{n + 1}} = \frac{{a \cdot {{(n + 1)}^2}}}{{\left( {n + 1} \right) + 1}} = \frac{{a \cdot {{(n + 1)}^2}}}{{n + 2}}$.

A. ${u_{n + 1}} = \frac{{a \cdot {{(n + 1)}^2}}}{{n + 2}}$. B. ${u_{n + 1}} = \frac{{a \cdot {{(n + 1)}^2}}}{{n + 1}}$. C. ${u_{n + 1}} = \frac{{a \cdot {n^2} + 1}}{{n + 1}}$. D. ${u_{n + 1}} = \frac{{a{n^2}}}{{n + 2}}$.

Câu 13: Dãy số $\left( {{u_n}} \right)$ nào sau đây là cấp số nhân?

A. $\left\{ {\begin{array}{*{20}{l}}
{{u_1} = 5} \\
{{u_{n + 1}} = 3{u_n},\forall n \in {\mathbb{N}^*}}
\end{array}} \right.$ B. ${u_n} = 2n + 1$. C. ${u_n} = {n^2}$. D. ${u_n} = {3^{{n^2} + 1}}$.

Câu 14: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành tâm $I$. Khi đó giao tuyến của hai mặt phẳng $\left( {SAB} \right)$ và $\left( {SCD} \right)$ là

A. Đường thẳng đi qua $S$ và song song với $AD$ và $BC$.

B. Đường thẳng $SI$.

C. Đường thẳng đi qua $I$ và song song với $AB$ và $CD$.

D. Đường thẳng đi qua $S$ và song song với $AB$ và $CD$.

Câu 15: Cho $\lim \frac{{2{n^2} – n + 1}}{{4{n^2} – 4}} = \frac{a}{b}$ với $\frac{a}{b}$ là phân số tối giản. Mệnh đề đúng là

A. $a + b = 6$. B. $2a + b = 6$. C. $2a + b = 0$. D. $2a – b = 0$.

Câu 16: Xác định $\mathop {\lim }\limits_{x \to 0} \frac{{|x|}}{{{x^2}}}$.

A. $ + \infty $. B. 0 . C. $ – \infty $. D. Không tồn tại.

Câu 17: Cho các mệnh đề sau:

(I). Có duy nhất một mặt phẳng đi qua ba điểm.

(II). Nếu một đường thẳng có hai điểm phân biệt thuộc một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phằng đó.

(III). Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng còn có một điểm chung khác nữ (IV). Tồn tại bốn điểm không cùng thuộc một mặt phẳng.

Số mệnh đề đúng là

A. 1 . B. 2 . C. 3 . D. 4 .

Câu 18: Cho tứ diện $ABCD,G$ là trọng tâm tam giác $\vartriangle BCD$. Giao tuyến của $\left( {ACD} \right)$ và $\left( {GAB} \right)$ là

A. $AN$ (với $N$ là trung điểm $CD$ ).

B. $AK$ (với $K$ là hình chiếu của $C$ trên $BD$ ).

C. $AH$ (với $H$ là hình chiếu của $B$ trên $CD$ ).

D. $AM$ (với $M$ là trung điểm $AB$ ).

Câu 19: Khẳng định nào sau đây sai?

A. Phép chiếu song song có thể biến đường tròn thành một điểm.

B. Phép chiếu song song có thể biến đường tròn thành đoạn thẳng.

C. Phép chiếu song song có thể biến đường tròn thành đường elip.

D. Phép chiếu song song có thể biến đường tròn thành đường tròn.

Câu 20: Cho tam giác $ABC$ có ba góc $A,B,C$ thỏa mãn đẳng thức $sinA = cosB + cosC$. Khẳng định nào sau đây là khẳng định đúng?

A. Tam giác $ABC$ là tam giác đều. B. Tam giác $ABC$ vuông tại $B$ hoặc $C$.

C. Tam giác $ABC$ vuông cân tại $A$. D. Tam giác $ABC$ vuông tại $B$.

Câu 21: Kết quả của giới hạn $lim{\left( {\frac{1}{2}} \right)^n}$ bằng

A. 0 . B. $ + \infty $. C. $\frac{1}{2}$. D. $ – \infty $.

Câu 22: Cho hàm số $f\left( x \right)$ có đồ thị như hình vẽ. Hỏi hàm số $f\left( x \right)$ không liên tục tại điểm nào sau đây?

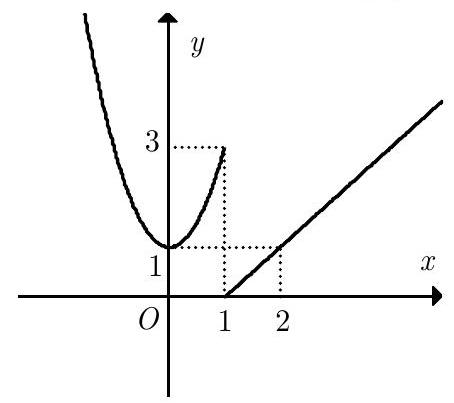
A. ${x_0} = 3$. B. ${x_0} = 0$. C. ${x_0} = 1$. D. ${x_0} = 2$.

Câu 23: Giá trị của $\mathop {\lim }\limits_{x \to 2} \frac{{x + 2}}{x}$ bằng

A. 2 . B. 0 . C. 1 . D. 3 .

Câu 24: Cho hình chóp $S.ABCD$. Gọi $M$ và $N$ lần lượt là trung điểm của $SA$ và $SC$. Khẳng định nào sau đây đúng?

A. $MN//\left( {SBC} \right)$. B. $MN//\left( {SAB} \right)$. C. $MN//\left( {SCD} \right)$. D. $MN//\left( {ABCD} \right)$.

Câu 25: Cho tứ diện $ABCD$ có ${G_1}$ và ${G_2}$ lần lượt là trọng tâm của tam giác $ABC$ và $ACD.H$ là điểm bất kỳ thuộc miền trong tam giác $BCD$. Tìm giao tuyến của hai mặt phẳng $\left( {H{G_1}{G_2}} \right)$ và $\left( {BCD} \right)$

A. Là đường thẳng qua $H$ và song song song với $BD$.

B. Là đường thẳng $AH$.

C. Là đường thẳng qua $H$ và song song song với $BC$.

D. Là đường thẳng qua $H$ và song song song với $CD$.

Câu 26: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang $\left( {AB\parallel CD} \right)$. Gọi $I,J$ lần lượt là trung điểm của $AD$ và $BC,G$ là trọng tâm $\vartriangle SAB$. Giao tuyến của hai mặt phẳng $\left( {SAB} \right)$ và $\left( {IJG} \right)$ là

A. Đường thẳng qua $G$ và cắt $BC$.

B. Đường thẳng qua $S$ và song song với $AB$.

C. Đường thẳng qua $G$ và song song với $DC$.

D. $SC$.

Câu 27: Hàm số nào sau đây gián đoạn tại $x = – 2$ ?

A. $y = \frac{{x + 2}}{{{x^2} + 1}}$. B. $y = {x^3} + 3x + 1$. C. $y = \frac{{3x + 5}}{{{x^2} – 4}}$. D. $y = \sqrt {{x^2} + 4} $.

Câu 28: Giới hạn $\mathop {\lim }\limits_{x \to 1} \frac{{{x^2} – 3x + 2}}{{{x^3} – {x^2} + x – 1}}$ bằng

A. -1 . B. $ – \frac{1}{2}$. C. $\frac{1}{2}$. D. -2 .

Câu 29: Cho hình hộp $ABCD \cdot A’B’C’D’$. Gọi $O,O’$ lần lượt là tâm của hai đáy $ABCD$ và $A’B’C’D’$. Mệnh đề nào sau đây sai?

A. $\left( {ABO’} \right)//\left( {OC’D’} \right)$. B. $\left( {ABB’} \right)//\left( {CDD’} \right)$. C. $\left( {B’AC} \right)//\left( {DA’C’} \right)$. D. $\left( {BA’D’} \right)//\left( {ADC’} \right)$.

Câu 30: Cho hình chóp $S.ABCD$ có đáy là hình bình hành. $M$ là trung điểm của $SC$. Gọi $I$ là giao điểm của đường thẳng $AM$ với mặt phẳng $\left( {SBD} \right)$. Chọn khẳng định đúng trong các khẳng định sau đây.

A. $IM = 2IA$. B. $IA = 2IM$. C. $IA = 3IM$. D. $IM = 3IA$.

Câu 31: Cho hàm số $f(x) = \sqrt {\frac{1}{{x – 1}}} $. Chọn mệnh đề sai.

A. $\mathop {\lim }\limits_{x \to 3} f(x) = \frac{{\sqrt 2 }}{2}$.

B. Hàm số liên tục tại mọi điểm $x \ne 1$.

C. Hàm số liên tục tại mọi điểm $x \in (1; + \infty )$.

D. $\mathop {\lim }\limits_{x \to 2} f(x) = 1$.

Câu 32: Giá trị $\mathop {\lim }\limits_{x \to 3} \frac{{\sqrt {x + 1} – 2}}{{x – 3}}$ bằng

A. $\frac{1}{4}$. B. $\frac{1}{2}$. C. $ – \frac{1}{4}$. D. $ – \frac{1}{2}$.

Câu 33: Cho hình chóp $S.ABCD$ có đáy là hình bình hành, gọi $M$ là trung điểm của $SC$ (như hình vẽ).

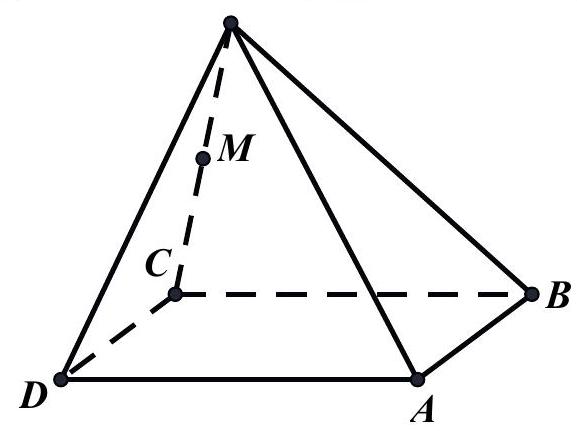
Hình chiếu song song của điểm $M$ theo phương $AC$ lên mặt phẳng $\left( {SAD} \right)$ là điểm nào sau đây?

A. Trung điểm của $SB$. B. Trung điểm của $SD$.

C. Điểm $D$. D. Trung điểm của $SA$.

Câu 34: Cho hình hộp $ABCD \cdot A’B’C’D’$. Gọi $M$ là trung điểm của $AB$. Mặt phẳng $\left( {MA’C’} \right)$ cắt hình hộp $ABCD \cdot A’B’C’D’$ theo thiết diện là hình gì?

A. Hình lục giác. B. Hình thang. C. Hình tam giác. D. Hình ngũ giác.

Câu 35: Cho tứ diện $ABCD$, gọi ${G_1},{G_2}$ lần lượt là trọng tâm các tam giác $BCD$ và $ACD$. Mệnh đề nào sau đây sai?

A. ${G_1}{G_2}//\left( {ABC} \right)$. B. ${G_1}{G_2} = \frac{2}{3}AB$.

C. Ba đường thẳng $B{G_1},A{G_2}$ và $CD$ đồng quy. D. ${G_1}{G_2}//\left( {ABD} \right)$.

II. PHẦN TỰ LUẬN

Câu 1: Giải phương trình $si{n^2}x + 2sinx – cosx + 1 = 0$.

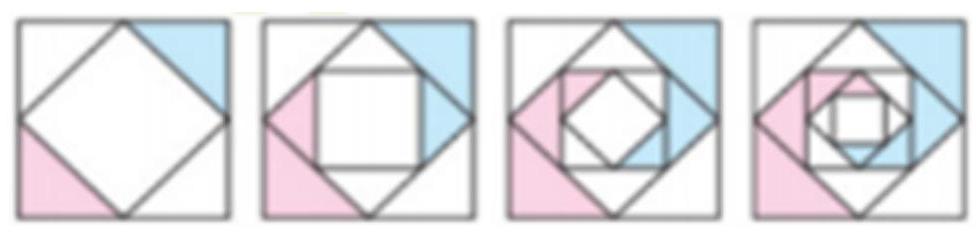
Câu 2: Một thợ thủ công muốn vẽ trang trí một hình vuông kích thước $4m \times 4m$ bằng cách vẽ một hình vuông mới với các đỉnh là trung điểm các cạnh của hình vuông ban đầu và tô kín màu lên hai tam giác đối diện (như hình vẽ). Quá trình vẽ và tô theo quy luật đó được lặp lại 5 lần. Tính số tiền nước sơn để người thợ đó hoàn thành trang trí hình vuông như trên? Biết tiền nước sơn $1{m^2}$ là 60000 đ.

Câu 3:  Cho hàm số $f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}
{\frac{{3 – \sqrt {x + 9} }}{{\sqrt {2x + 4} – 2}}}&{khi\,x > 0} \\
{5x – \frac{1}{3}{m^2}}&{khi\,x \leqslant 0}
\end{array}} \right.$. Tìm các giá trị của tham số $m$ để hàm số $f\left( x \right)$ liên tục tại $x = 0$.

Câu 4: Cho tứ diện đều $ABCD$ cạnh $a$. Gọi $G$ là trọng tâm tam giác $ABD$, điểm $M,H$ lần lượt thuộc cạnh $CD,AD$ sao cho $DM = 2MC$ và $DH = 2HA$. Gọi $E$ là giao điểm $DG$ cắt $BH$. Mặt phẳng $\left( \alpha \right)$ đi qua $E$ song song $\left( {ABC} \right)$ cắt $BM$ tại $F$. Tính độ dài đoạn thẳng $EF$.

ĐÁP ÁN VÀ LỜI GIẢI

I. PHẦN TRẮC NGHIỆM

1.A	2.C	3.C	4.B	5.B
6.D	7.C	8.D	9.B	10.B
11.C	12.A	13.A	14.D	15.D
16.D	17.C	18.A	19.A	20.C
21.A	22.C	23.A	24.D	25.A
26.C	27.C	28.B	29.D	30.B
31.C	32.A	33.D	34.B	35.B

HƯỚNG DẪN GIẢI CHI TIẾT

Câu 1: Giá trị của $\cot {30^ \circ }$ là

A. $\sqrt 3 $.

B. 0 .

C. -1 .

D. $ – \sqrt 3 $.

Lời giải

Ta có: $cot3{0^ \circ } = \sqrt 3 $.

Câu 2: Đẳng thức nào sau đây là đúng?

A. $cos\left( {a + \frac{\pi }{3}} \right) = \frac{{\sqrt 3 }}{2}sina – \frac{1}{2}cosa$.

B. $cos\left( {a + \frac{\pi }{3}} \right) = \frac{1}{2}sina – \frac{{\sqrt 3 }}{2}cosa$.

C. $cos\left( {a + \frac{\pi }{3}} \right) = \frac{1}{2}cosa – \frac{{\sqrt 3 }}{2}sina$.

D. $cos\left( {a + \frac{\pi }{3}} \right) = cosa + \frac{1}{2}$.

Lời giải

Ta có: $cos\left( {a + \frac{\pi }{3}} \right) = cosa \cdot cos\frac{\pi }{3} – sina \cdot sin\frac{\pi }{3} = \frac{1}{2}cosa \cdot – \frac{{\sqrt 3 }}{2}sina$.

Câu 3: Nghiệm của phương trình $cosx = – \frac{1}{2}$ là

A. $x = \pm \frac{\pi }{3} + k2\pi $.

B. $x = \pm \frac{\pi }{6} + k2\pi $.

C. $x = \pm \frac{{2\pi }}{3} + k2\pi $.

D. $x = \pm \frac{\pi }{6} + k\pi $.

Lời giải

Ta có: $cosx = – \frac{1}{2} \Leftrightarrow cosx = cos\frac{{2\pi }}{3} \Leftrightarrow x = \pm \frac{{2\pi }}{3} + k2\pi ,k \in \mathbb{Z}$.

Câu 4: Phương trình $sin2x = 1$ có nghiệm là

A. $x = \frac{\pi }{4} + k3\pi $.

B. $x = \frac{\pi }{4} + k\pi $.

C. $x = \frac{\pi }{4} + k\frac{\pi }{2}$.

D. $x = \frac{\pi }{4} + k2\pi $.

Lời giải

Ta có: $sin2x = 1 \Leftrightarrow 2x = \frac{\pi }{2} + k2\pi \Leftrightarrow x = \frac{\pi }{4} + k\pi ,\left( {k \in \mathbb{Z}} \right)$.

Câu 5: Tìm tập xác định của hàm số $y = tanx$.

A. $\mathbb{R} \setminus \left\{ {k2\pi \mid k \in \mathbb{Z}} \right\}$.

B. $\mathbb{R} \setminus \left\{ {\frac{\pi }{2} + k\pi \mid k \in \mathbb{Z}} \right\}$.

C. $\mathbb{R} \setminus \left\{ {k\pi \mid k \in \mathbb{Z}} \right\}$.

D. $\mathbb{R} \setminus \left\{ {\frac{\pi }{2} + k2\pi \mid k \in \mathbb{Z}} \right\}$.

Lời giải

Hàm số xác định khi và chỉ khi $cosx \ne 0 \Leftrightarrow x \ne \frac{\pi }{2} + k\pi ,\left( {k \in \mathbb{Z}} \right)$.

Câu 6: Hàm số nào sau đây nghịch biến trên $\left( {\frac{\pi }{2};\pi } \right)$ ?

A. $y = – cotx$.

B. $y = tanx$.

C. $y = – sinx$.

D. $y = cosx$.

Lời giải

Với $x \in \left( {\frac{\pi }{2};\pi } \right):$ Khi giá trị của $x$ tăng thì giá trị tương ứng của hàm số $y = cosx$ giảm

$ \Rightarrow $ Hàm số $y = cosx$ nghịch biến trên $\left( {\frac{\pi }{2};\pi } \right)$.

Câu 7: Trong các công thức sau, công thức nào đúng?

A. $sin2a = 2sina$.

B. $sin2a = sina + cosa$.

C. $sin2a = 2sinacosa$.

D. $sin2a = co{s^2}a – si{n^2}a$.

Ta có $sin2a = 2sinacosa$.

Lời giải

Câu 8: Hàm số $y = tanx + cotx + \frac{1}{{sinx}} + \frac{1}{{cosx}}$ không xác định trong khoảng nào trong các khoảng sau đây?

A. $\left( {k2\pi ;\frac{\pi }{2} + k2\pi } \right)$ với $k \in \mathbb{Z}$.

B. $\left( {\pi + k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right)$ với $k \in \mathbb{Z}$.

C. $\left( {\frac{\pi }{2} + k2\pi ;\pi + k2\pi } \right)$ với $k \in \mathbb{Z}$.

D. $\left( {\pi + k2\pi ;2\pi + k2\pi } \right)$ với $k \in \mathbb{Z}$.

Lời giải

Điều kiện xác định của hàm số là $\left\{ {\begin{array}{*{20}{l}}
{sinx \ne 0} \\
{cosx \ne 0}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x \ne k\pi } \\
{x \ne \frac{\pi }{2} + k\pi }
\end{array},k \in \mathbb{Z}} \right.} \right.$

Khi đó, hàm số không xác định tại $x = \frac{{3\pi }}{2} + k2\pi $ với $k \in \mathbb{Z}$.

Suy ra, hàm số không xác định trên khoảng $\left( {\pi + k2\pi ;2\pi + k2\pi } \right)$ với $k \in \mathbb{Z}$.

Câu 9: Nếu $\alpha $ là góc nhọn và $sin2\alpha = a$. Tính $sin\alpha + cos\alpha $.

A. $\sqrt {a + 1} – \sqrt {{a^2} – a} $.

B. $\sqrt {a + 1} $.

C. $\sqrt {a + 1} + \sqrt {{a^2} – a} $.

D. $\left( {\sqrt 2 – 1} \right)a + 1$.

Lời giải

Do $\alpha $ là góc nhọn nên $sin\alpha > 0;cos\alpha > 0 \Rightarrow sin\alpha + cos\alpha > 0$.

Ta có ${(sin\alpha + cos\alpha )^2} = si{n^2}\alpha + cos{\alpha ^2} + 2sin\alpha cos\alpha = 1 + sin2\alpha = 1 + a$.

Suy ra $sin\alpha + cos\alpha = \sqrt {a + 1} $.

Câu 10: Cho cấp số cộng $\left( {{u_n}} \right)$ có số hạng tổng quát là ${u_n} = 3n – 2$. Tìm công sai $d$ của cấp số cộng.

A. $d = – 3$.

B. $d = 3$.

C. $d = 2$.

D. $d = – 2$.

Lời giải

Ta có ${u_{n + 1}} – {u_n} = 3\left( {n + 1} \right) – 2 – 3n + 2 = 3$

Suy ra $d = 3$ là công sai của cấp số cộng.

Câu 11: Cho cấp số cộng $\left( {{u_n}} \right)$ có ${u_1} = – 3$ và $d = \frac{1}{2}$. Khẳng định nào sau đây đúng?

A. ${u_n} = – 3 + \frac{1}{2}\left( {n + 1} \right)$.

B. ${u_n} = – 3 + \frac{1}{2}n – 1$.

C. ${u_n} = – 3 + \frac{1}{2}\left( {n – 1} \right)$.

D. ${u_n} = – 3 + \frac{1}{4}\left( {n – 1} \right)$.

Lời giải

Áp dụng công thức số hạng tổng quát của cấp số cộng $\left( {{u_n}} \right)$, ta có:

${u_n} = {u_1} + \left( {n – 1} \right)d \Leftrightarrow {u_n} = – 3 + \frac{1}{2}\left( {n – 1} \right).$

Câu 12: Cho dãy số $\left( {{u_n}} \right)$ với ${u_n} = \frac{{a{n^2}}}{{n + 1}}$ ( $a$ hằng số). Hỏi ${u_{n + 1}}$ là số hạng nào sau đây?

A. ${u_{n + 1}} = \frac{{a \cdot {{(n + 1)}^2}}}{{n + 2}}$.

B. ${u_{n + 1}} = \frac{{a \cdot {{(n + 1)}^2}}}{{n + 1}}$.

C. ${u_{n + 1}} = \frac{{a \cdot {n^2} + 1}}{{n + 1}}$.

D. ${u_{n + 1}} = \frac{{a{n^2}}}{{n + 2}}$.

Ta có: ${u_{n + 1}} = \frac{{a \cdot {{(n + 1)}^2}}}{{\left( {n + 1} \right) + 1}} = \frac{{a \cdot {{(n + 1)}^2}}}{{n + 2}}$.

Lời giải

Câu 13: Dãy số $\left( {{u_n}} \right)$ nào sau đây là cấp số nhân?

A. $\left\{ {\begin{array}{*{20}{l}}
{{u_1} = 5} \\
{{u_{n + 1}} = 3{u_n},\forall n \in {\mathbb{N}^*}}
\end{array}} \right.$

B. ${u_n} = 2n + 1$.

C. ${u_n} = {n^2}$.

D. ${u_n} = {3^{{n^2} + 1}}$.

Lời giải

Xét dãy số $\left\{ {\begin{array}{*{20}{l}}
{{u_1} = 5} \\
{{u_{n + 1}} = 3{u_n},\forall n \in {\mathbb{N}^*}}
\end{array}} \right.$ có $\frac{{{u_{n + 1}}}}{{{u_n}}} = 3,\forall n \in {\mathbb{N}^*}$ nên dãy số này là cấp số nhân.

Câu 14: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành tâm $I$. Khi đó giao tuyến của hai mặt phẳng $\left( {SAB} \right)$ và $\left( {SCD} \right)$ là

A. Đường thẳng đi qua $S$ và song song với $AD$ và $BC$.

B. Đường thẳng $SI$.

C. Đường thẳng đi qua $I$ và song song với $AB$ và $CD$.

D. Đường thẳng đi qua $S$ và song song với $AB$ và $CD$.

Lời giải

Ta có $AB//CD$.

Hai mặt phẳng $\left( {SAB} \right)$ và $\left( {SCD} \right)$ có $S$ là một điểm chung và lần lượt chứa hai đường thẳng song song là $AB$ và $CD$.

Vậy giao tuyến của hai mặt phẳng $\left( {SAB} \right)$ và $\left( {SCD} \right)$ là đường thẳng đi qua $S$ và song song với $AB$ và $CD$.

Câu 15: Cho $\lim \frac{{2{n^2} – n + 1}}{{4{n^2} – 4}} = \frac{a}{b}$ với $\frac{a}{b}$ là phân số tối giản. Mệnh đề đúng là

A. $a + b = 6$.

B. $2a + b = 6$.

C. $2a + b = 0$.

D. $2a – b = 0$.

Lời giải

Ta có: $\lim \frac{{2{n^2} – n + 1}}{{4{n^2} – 4}} = \lim \frac{{2 – \frac{1}{n} + \frac{1}{{{n^2}}}}}{{4 – \frac{4}{{{n^2}}}}} = \frac{1}{2} \Rightarrow a = 1,b = 2$.

Câu 16: Xác định $\mathop {\lim }\limits_{x \to 0} \frac{{|x|}}{{{x^2}}}$.

A. $ + \infty $.

B. 0 .

C. $ – \infty $.

D. Không tồn tại.

Lời giải

Ta có $\mathop {\lim }\limits_{x \to {0^ + }} \frac{{|x|}}{{{x^2}}} = \mathop {\lim }\limits_{x \to {0^ + }} \frac{x}{{{x^2}}} = \mathop {\lim }\limits_{x \to {0^ + }} \frac{1}{x} = + \infty$

$ \Rightarrow \mathop {\lim }\limits_{x \to {0^ – }} \frac{{|x|}}{{{x^2}}} = \mathop {\lim }\limits_{x \to {0^ – }} \frac{{ – x}}{{{x^2}}} = \mathop {\lim }\limits_{x \to {0^ – }} \frac{{ – 1}}{x} = + \infty $.

Vậy không tồn tại $\mathop {\lim }\limits_{x \to 0} \frac{{|x|}}{{{x^2}}}$.

Câu 17: Cho các mệnh đề sau:

(I). Có duy nhất một mặt phẳng đi qua ba điểm.

(II). Nếu một đường thẳng có hai điểm phân biệt thuộc một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phằng đó.

(III). Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng còn có một điểm chung khác nữ (IV). Tồn tại bốn điểm không cùng thuộc một mặt phẳng.

Số mệnh đề đúng là

A. 1 .

B. 2 .

C. 3 .

D. 4 .

Lời giải

Có duy nhất một mặt phẳng đi qua ba điểm không thẳng hàng nên mệnh đề (I) sai.

Mệnh đề (II), (III) và (IV) đúng.

Vậy số mệnh đề đúng là 3 .

Câu 18: Cho tứ diện $ABCD,G$ là trọng tâm tam giác $\vartriangle BCD$. Giao tuyến của $\left( {ACD} \right)$ và $\left( {GAB} \right)$ là

A. $AN$ (với $N$ là trung điểm $CD$ ).

B. $AK$ (với $K$ là hình chiếu của $C$ trên $BD$ ).

C. $AH$ (với $H$ là hình chiếu của $B$ trên $CD$ ).

D. $AM$ (với $M$ là trung điểm $AB$ ).

Lời giải

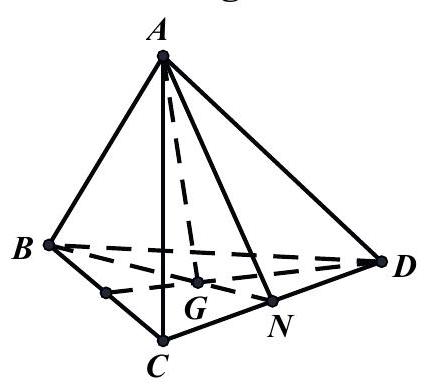
Ta thấy $\left( {GAB} \right)$ chính là mặt phẳng $\left( {ANB} \right)$. Suy ra giao tuyến của $\left( {GAB} \right)$ với $\left( {ACD} \right)$ chính là $AN$.

Câu 19: Khẳng định nào sau đây sai?

A. Phép chiếu song song có thể biến đường tròn thành một điểm.

B. Phép chiếu song song có thể biến đường tròn thành đoạn thẳng.

C. Phép chiếu song song có thể biến đường tròn thành đường elip.

D. Phép chiếu song song có thể biến đường tròn thành đường tròn.

Lời giải

Phương chiếu vuông góc với mặt phẳng chứa đường tròn biến đường tròn thành đường tròn. Phương chiếu nằm trong mặt phẳng chứa đường tròn biến đường tròn thành đoạn thẳng. Phương chiếu cắt (không vuông góc) với mặt phẳng chứa đường tròn biến đường tròn thành đường elip.

Câu 20: Cho tam giác $ABC$ có ba góc $A,B,C$ thỏa mãn đẳng thức $sinA = cosB + cosC$. Khẳng định nào sau đây là khẳng định đúng?

A. Tam giác $ABC$ là tam giác đều.

B. Tam giác $ABC$ vuông tại $B$ hoặc $C$.

C. Tam giác $ABC$ vuông cân tại $A$.

D. Tam giác $ABC$ vuông tại $B$.

Lời giải

Nếu tam giác $ABC$ vuông cân tại $A$, thì $sinA = cosB + cosC$ là đẳng thức đúng.

Câu 21: Kết quả của giới hạn $lim{\left( {\frac{1}{2}} \right)^n}$ bằng

A. 0 .

B. $ + \infty $.

C. $\frac{1}{2}$.

D. $ – \infty $.

Lời giải

Có $lim{q^n} = 0$ nếu $\left| q \right| < 1$.

Vì $\left| {\frac{1}{2}} \right| < 1$ nên $lim{\left( {\frac{1}{2}} \right)^n} = 0$.

Câu 22: Cho hàm số $f\left( x \right)$ có đồ thị như hình vẽ. Hỏi hàm số $f\left( x \right)$ không liên tục tại điểm nào sau đây?

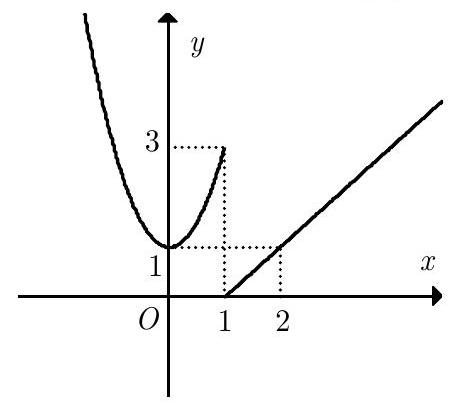
A. ${x_0} = 3$.

B. ${x_0} = 0$.

C. ${x_0} = 1$.

D. ${x_0} = 2$.

Lời giải

Dựa vào đồ thị ta thấy hàm số $f\left( x \right)$ không liên tục tại điểm ${x_0} = 1$.

Câu 23: Giá trị của $\mathop {\lim }\limits_{x \to 2} \frac{{x + 2}}{x}$ bằng

A. 2 .

B. 0 .

C. 1 .

D. 3 .

Lời giải

Ta có: $\mathop {\lim }\limits_{x \to 2} \frac{{x + 2}}{x} = \mathop {\lim }\limits_{x \to 2} \left( {1 + \frac{2}{x}} \right) = 1 + \frac{2}{2} = 2$.

Câu 24: Cho hình chóp $S.ABCD$. Gọi $M$ và $N$ lần lượt là trung điểm của $SA$ và $SC$. Khẳng định nào sau đây đúng?

A. $MN//\left( {SBC} \right)$.

B. $MN//\left( {SAB} \right)$.

C. $MN//\left( {SCD} \right)$.

D. $MN//\left( {ABCD} \right)$.

Lời giải

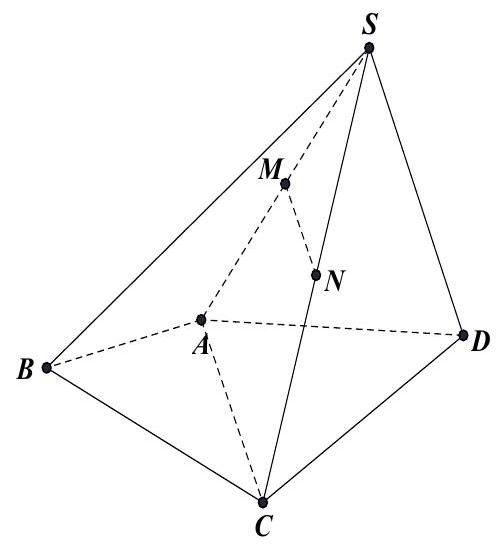
$MN$ là đường trung bình của tam giác $SAC$ nên $MN//AC$ mà $AC \in \left( {ABCD} \right)$ $ \Rightarrow MN//\left( {ABCD} \right)$.

Câu 25: Cho tứ diện $ABCD$ có ${G_1}$ và ${G_2}$ lần lượt là trọng tâm của tam giác $ABC$ và $ACD.H$ là điểm bất kỳ thuộc miền trong tam giác $BCD$. Tìm giao tuyến của hai mặt phẳng $\left( {H{G_1}{G_2}} \right)$ và $\left( {BCD} \right)$

A. Là đường thẳng qua $H$ và song song song với $BD$.

B. Là đường thẳng $AH$.

C. Là đường thẳng qua $H$ và song song song với $BC$.

D. Là đường thẳng qua $H$ và song song song với $CD$.

Lời giải

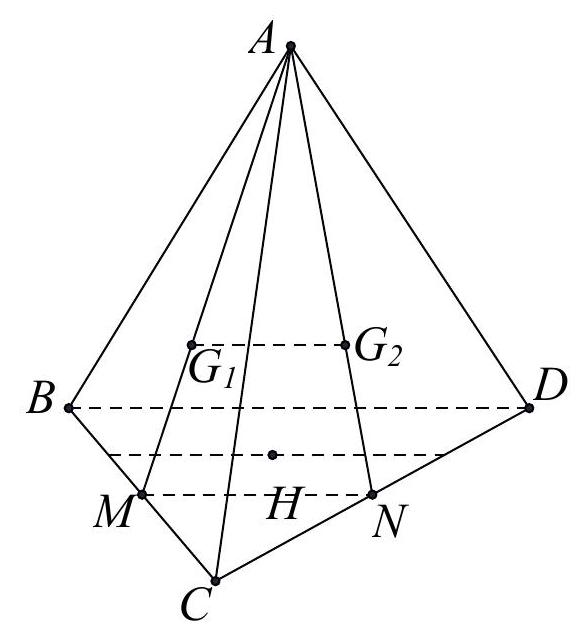
Gọi $M,N$ lần lượt là trung điểm của $CB,CD$. Khi đó ta có $\frac{{A{G_1}}}{{AM}} = \frac{{A{G_2}}}{{AN}} = \frac{2}{3}$.

Do đó ${G_1}{G_2}//MN$.

Mà ${G_1}{G_2} \subset \left( {H{G_1}{G_2}} \right),MN \subset \left( {BCD} \right),H \in \left( {H{G_1}{G_2}} \right) \cap \left( {BCD} \right)$ nên giao tuyến của hai mặt phẳng $\left( {H{G_1}{G_2}} \right)$ và $\left( {BCD} \right)$ là đường thẳng qua $H$, song song với $BD$.

Câu 26: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thang $\left( {AB\parallel CD} \right)$. Gọi $I,J$ lần lượt là trung điểm của $AD$ và $BC,G$ là trọng tâm $\vartriangle SAB$. Giao tuyến của hai mặt phẳng $\left( {SAB} \right)$ và $\left( {IJG} \right)$ là

A. Đường thẳng qua $G$ và cắt $BC$.

B. Đường thẳng qua $S$ và song song với $AB$.

C. Đường thẳng qua $G$ và song song với $DC$.

D. $SC$.

Lời giải

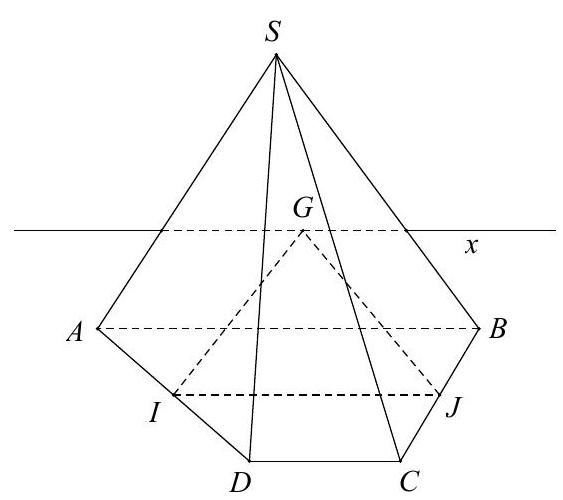
Ta có $IJ\parallel AB\left( 1 \right)$ (đường trung bình hình thang ).

$G \in \left( {GIJ} \right) \cap \left( {SAB} \right)\left( 2 \right)$.

$IJ \subset \left( {GIJ} \right),AB \subset \left( {SAB} \right)\left( 3 \right)$.

Từ (1), (2),(3) $ \Rightarrow Gx = \left( {GIJ} \right) \cap \left( {SAB} \right),Gx\parallel AB,Gx\parallel CD$.

Câu 27: Hàm số nào sau đây gián đoạn tại $x = – 2$ ?

A. $y = \frac{{x + 2}}{{{x^2} + 1}}$.

B. $y = {x^3} + 3x + 1$.

C. $y = \frac{{3x + 5}}{{{x^2} – 4}}$.

D. $y = \sqrt {{x^2} + 4} $.

Lời giải

Xét hàm số $y = \frac{{3x + 5}}{{{x^2} – 4}}$, hàm số này không xác định tại $x = – 2$. Do đó hàm số gián đoạn tại $x = – 2$.

Câu 28: Giới hạn $\mathop {\lim }\limits_{x \to 1} \frac{{{x^2} – 3x + 2}}{{{x^3} – {x^2} + x – 1}}$ bằng

A. -1 .

B. $ – \frac{1}{2}$.

C. $\frac{1}{2}$.

D. -2 .

Lời giải

Ta có $\mathop {\lim }\limits_{x \to 1} \frac{{{x^2} – 3x + 2}}{{{x^3} – {x^2} + x – 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{(x – 1)(x – 2)}}{{(x – 1)\left( {{x^2} + 1} \right)}} = \mathop {\lim }\limits_{x \to 1} \frac{{x – 2}}{{{x^2} + 1}} = – \frac{1}{2}$.

Câu 29: Cho hình hộp $ABCD \cdot A’B’C’D’$. Gọi $O,O’$ lần lượt là tâm của hai đáy $ABCD$ và $A’B’C’D’$. Mệnh đề nào sau đây sai?

A. $\left( {ABO’} \right)//\left( {OC’D’} \right)$.

B. $\left( {ABB’} \right)//\left( {CDD’} \right)$.

C. $\left( {B’AC} \right)//\left( {DA’C’} \right)$.

D. $\left( {BA’D’} \right)//\left( {ADC’} \right)$.

Lời giải

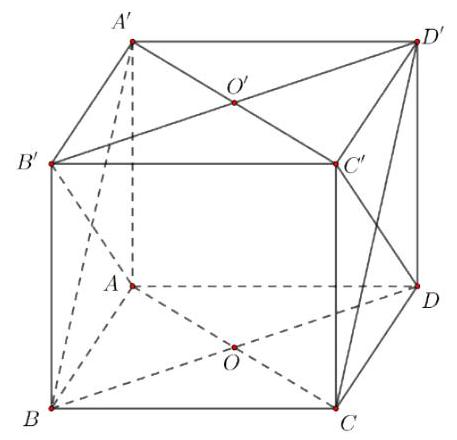
Ta thấy $AB’ \cap A’B$, mà $\left( {BA’D’} \right) \equiv \left( {CBA’D’} \right)$ và $\left( {ADC’} \right) \equiv \left( {ADC’B’} \right)$ nên hai mặt này cắt nhau.

Câu 30: Cho hình chóp $S.ABCD$ có đáy là hình bình hành. $M$ là trung điểm của $SC$. Gọi $I$ là giao điểm của đường thẳng $AM$ với mặt phẳng $\left( {SBD} \right)$. Chọn khẳng định đúng trong các khẳng định sau đây.

A. $IM = 2IA$.

B. $IA = 2IM$.

C. $IA = 3IM$.

D. $IM = 3IA$.

Lời giải

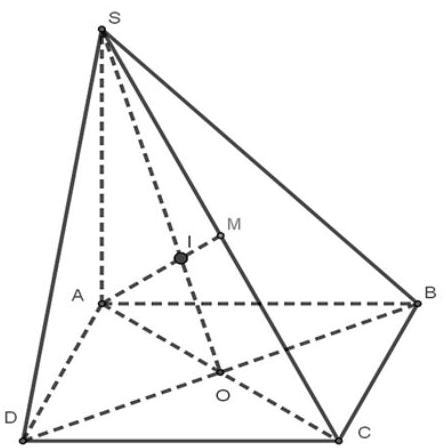
Gọi $AC \cap BD = O$ thì $\left( {SAC} \right) \cap \left( {SBD} \right) = SO$.

Trong mặt phẳng $\left( {SAC} \right)$, lấy $AM \cap SO = I \Rightarrow I = AM \cap \left( {SBD} \right)$.

Do trong $\vartriangle SAC,AM$ và $SO$ là hai đường trung tuyến, nên $I$ là trọng tâm $\vartriangle SAC$.

Vậy $IA = 2IM$.

Câu 31: Cho hàm số $f(x) = \sqrt {\frac{1}{{x – 1}}} $. Chọn mệnh đề sai.

A. $\mathop {\lim }\limits_{x \to 3} f(x) = \frac{{\sqrt 2 }}{2}$.

B. Hàm số liên tục tại mọi điểm $x \ne 1$.

C. Hàm số liên tục tại mọi điểm $x \in (1; + \infty )$.

D. $\mathop {\lim }\limits_{x \to 2} f(x) = 1$.

Lời giải

Hàm số xác định khi $\frac{1}{{x – 1}} > 0 \Leftrightarrow x \in (1; + \infty ) \Rightarrow $ Hàm số liên tục tại mọi điểm $x \in (1; + \infty )$.

Câu 32: Giá trị $\mathop {\lim }\limits_{x \to 3} \frac{{\sqrt {x + 1} – 2}}{{x – 3}}$ bằng

A. $\frac{1}{4}$.

B. $\frac{1}{2}$.

C. $ – \frac{1}{4}$.

D. $ – \frac{1}{2}$.

Lời giải

Ta có $\mathop {\lim }\limits_{x \to 3} \frac{{\sqrt {x + 1} – 2}}{{x – 3}} = \mathop {\lim }\limits_{x \to 3} \frac{{x – 3}}{{(\sqrt {x + 1} + 2)(x – 3)}} = \mathop {\lim }\limits_{x \to 3} \frac{1}{{\sqrt {x + 1} + 2}} = \frac{1}{4}$.

Câu 33: Cho hình chóp $S.ABCD$ có đáy là hình bình hành, gọi $M$ là trung điểm của $SC$ (như hình vẽ).

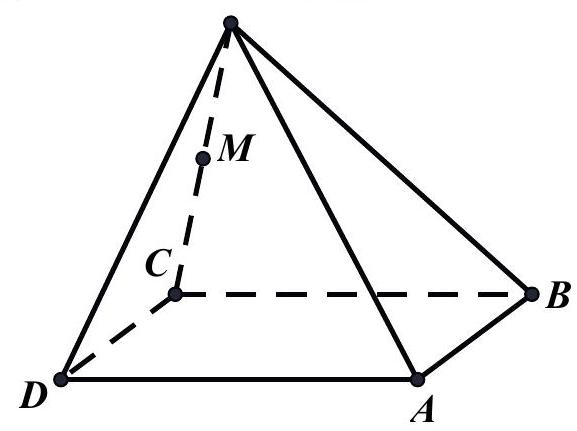
Hình chiếu song song của điểm $M$ theo phương $AC$ lên mặt phẳng $\left( {SAD} \right)$ là điểm nào sau đây?

A. Trung điểm của $SB$.

B. Trung điểm của $SD$.

C. Điểm $D$.

D. Trung điểm của $SA$.

Lời giải

Gọi $N$ là trung điểm $SA$.

Khi đó $MN//AC$ nên hình chiếu song song của điểm $M$ lên mặt phẳng $\left( {SAD} \right)$ là trung điểm $SA$

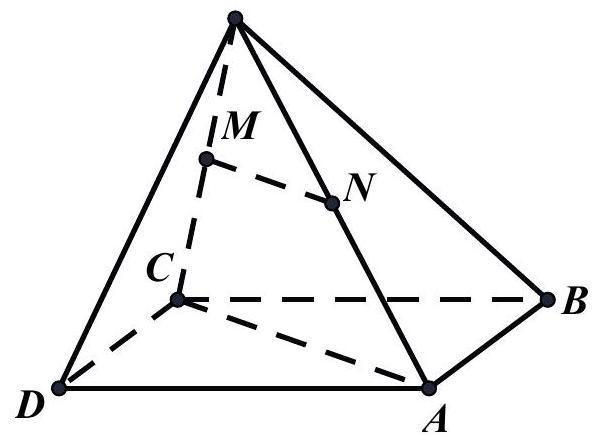
Câu 34: Cho hình hộp $ABCD \cdot A’B’C’D’$. Gọi $M$ là trung điểm của $AB$. Mặt phẳng $\left( {MA’C’} \right)$ cắt hình hộp $ABCD \cdot A’B’C’D’$ theo thiết diện là hình gì?

A. Hình lục giác.

B. Hình thang.

C. Hình tam giác.

D. Hình ngũ giác.

Lời giải

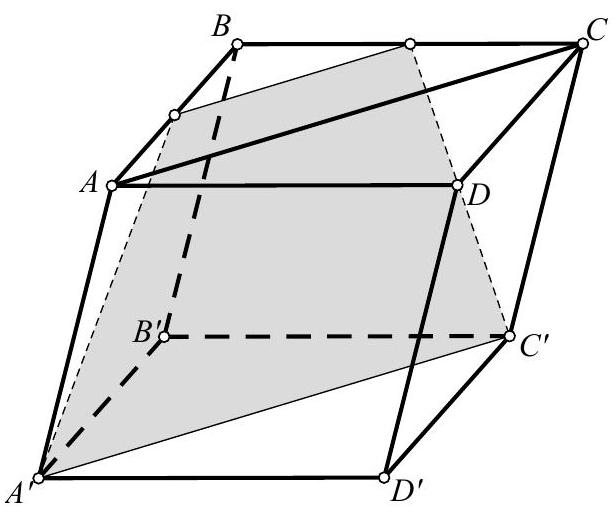
Gọi $N$ là trung điểm của $BC$, ta có $MN//AC//A’C’$ nên $MN \subset \left( {MA’C’} \right)$.

$\left( {MA’C’} \right) \cap \left( {ABB’A’} \right) = MA’;\left( {MA’C’} \right) \cap \left( {ABCD} \right) = MN$

$\left( {MA’C’} \right) \cap \left( {BCC’B’} \right) = NC’;\left( {MA’C’} \right) \cap \left( {A’B’C’D’} \right) = A’C’$

Thiết diện thu được là tứ giác $MNC’A’$. Do $MN//A’C’$ nên $MNC’A’$ là hình thang.

Câu 35: Cho tứ diện $ABCD$, gọi ${G_1},{G_2}$ lần lượt là trọng tâm các tam giác $BCD$ và $ACD$. Mệnh đề nào sau đây sai?

A. ${G_1}{G_2}//\left( {ABC} \right)$.

B. ${G_1}{G_2} = \frac{2}{3}AB$.

C. Ba đường thẳng $B{G_1},A{G_2}$ và $CD$ đồng quy.

D. ${G_1}{G_2}//\left( {ABD} \right)$.

Lời giải

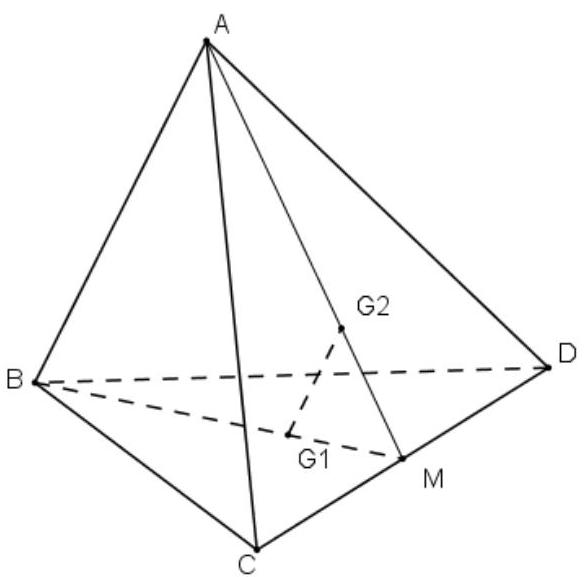
Gọi $M$ là trung điểm của $CD$ nên ba đường thẳng $B{G_1},A{G_2}$ và $CD$ đồng quy tại $M$, mặt khác:

$\frac{{M{G_1}}}{{MB}} = \frac{{M{G_2}}}{{MA}} = \frac{1}{3}$, suy ra ${G_1}{G_2}//AB$ và $\frac{{{G_1}{G_2}}}{{AB}} = \frac{1}{3}$.

Vậy ${G_1}{G_2}//\left( {ABD} \right),{G_1}{G_2}//\left( {ABC} \right)$ và ${G_1}{G_2} = \frac{1}{3}AB$.

II. PHẦN TỰ LUẬN

Câu 1: Giải phương trình $si{n^2}x + 2sinx – cosx + 1 = 0$.

Lời giải

Ta có : $si{n^2}x + 2sinx – cosx + 1 = 0. \Leftrightarrow {(1 + sinx)^2} = cosx$

Điều kiện: $cosx \geqslant 0$.

$\left( 1 \right) \Leftrightarrow {(1 + sinx)^4} = co{s^2}x $$\Leftrightarrow {(1 + sinx)^4} = 1 – si{n^2}x $$\Leftrightarrow {(1 + sinx)^4} = \left( {1 – sinx} \right)\left( {1 + sinx} \right)$.

$ \Leftrightarrow \left( {1 + sinx} \right)\left[ {{{(1 + sinx)}^3} – \left( {1 – sinx} \right)} \right] = 0$

$ \Leftrightarrow \left( {1 + sinx} \right)\left[ {si{n^3}x + 3si{n^2}x + 4sinx} \right] = 0 $

$\Leftrightarrow \left( {1 + sinx} \right)sinx\left( {si{n^2}x + 3sinx + 4} \right) = 0$

$ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{1 + {\text{sin}}x = 0} \\
{{\text{sin}}x = 0} \\
{{\text{si}}{{\text{n}}^2}x + 3{\text{sin}}x + 4 = 0}
\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{{\text{sin}}x = – 1} \\
{{\text{sin}}x = 0}
\end{array}} \right.} \right.$.
$ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = – \frac{\pi }{2} + k2\pi } \\
{x = k2\pi }
\end{array},k \in \mathbb{Z}} \right.$

Vậy họ nghiệm của phương trình là $\left[ {\begin{array}{*{20}{l}}
{x = – \frac{\pi }{2} + k2\pi } \\
{x = k2\pi }
\end{array},k \in \mathbb{Z}} \right.$.

Câu 2: Một thợ thủ công muốn vẽ trang trí một hình vuông kích thước $4m \times 4m$ bằng cách vẽ một hình vuông mới với các đỉnh là trung điểm các cạnh của hình vuông ban đầu và tô kín màu lên hai tam giác đối diện (như hình vẽ). Quá trình vẽ và tô theo quy luật đó được lặp lại 5 lần. Tính số tiền nước sơn để người thợ đó hoàn thành trang trí hình vuông như trên? Biết tiền nước sơn $1{m^2}$ là 60000 đ.

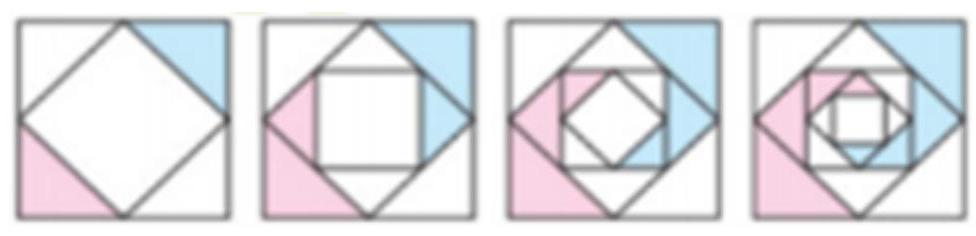
Lời giải

Gọi ${S_i}$ là tổng diện tích tam giác được tô sơn màu ở lần vẽ hình vuông thứ $i\;\left( {1 \leqslant i \leqslant 5;i \in \mathbb{N}} \right)$ và $S$ là diện tích hình vuông ban đầu.

Ta có: ${S_1} = \frac{1}{2}\left( {\frac{1}{2}S} \right);{S_2} = \frac{1}{{{2^2}}}\left( {\frac{1}{2}S} \right);{S_3} = \frac{1}{{{2^3}}}\left( {\frac{1}{2}S} \right);$

${S_4} = \frac{1}{{{2^4}}}\left( {\frac{1}{2}S} \right);{S_5} = \frac{1}{{{2^5}}}\left( {\frac{1}{2}S} \right)$.

Tổng diện tích các tam giác được tô sơn sau 5 lần là

$\sum_{i=1}^{5} S_{i}=\frac{1}{2} S \sum_{i=1}^{5} \frac{1}{2^{i}}=\frac{1}{2} \cdot 16 \cdot \frac{1}{2} \cdot \frac{1-\left(\frac{1}{2}\right)^{5}}{1-\frac{1}{2}}=\frac{31}{4}$.

Số tiền nước sơn để người thợ đó hoàn thành trang trí là $\frac{{31}}{4} \cdot 60000 = 465000$ đ.

Câu 3: Cho hàm số $f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}
{\frac{{3 – \sqrt {x + 9} }}{{\sqrt {2x + 4} – 2}}}&{khi\,x > 0} \\
{5x – \frac{1}{3}{m^2}}&{khi\,x \leqslant 0}
\end{array}} \right.$. Tìm các giá trị của tham số $m$ để hàm số $f\left( x \right)$ liên tục tại $x = 0$.

Lời giải

Tập xác định: $D = \mathbb{R}$.

Ta có: $\mathop {\lim }\limits_{x \to {0^ + }} f(x) = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{3 – \sqrt {x + 9} }}{{\sqrt {2x + 4} – 2}}$

$ = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{(3 – \sqrt {x + 9} )(3 + \sqrt {x + 9} )(\sqrt {2x + 4} + 2)}}{{(\sqrt {2x + 4} – 2)(\sqrt {2x + 4} + 2)(3 + \sqrt {x + 9} )}}$

$ = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{ – x(\sqrt {2x + 4} + 2)}}{{2x(3 + \sqrt {x + 9} )}} = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{ – (\sqrt {2x + 4} + 2)}}{{2(3 + \sqrt {x + 9} )}} = – \frac{1}{3}$

Mặt khác: $\mathop {\lim }\limits_{x \to {0^ – }} f(x) = \mathop {\lim }\limits_{x \to {0^ – }} \left( {5x – \frac{1}{3}{m^2}} \right) = – \frac{1}{3}{m^2}$ và $f(0) = – \frac{1}{3}{m^2}$

Hàm số liên tục tại $x = 0 \Leftrightarrow \mathop {\lim }\limits_{x \to 0} f(x) = f(0)$$ \Leftrightarrow \mathop {\lim }\limits_{x \to {0^ + }} f(x) = \mathop {\lim }\limits_{x \to {0^ – }} f(x) = f(0)$

$ \Leftrightarrow \frac{{ – 1}}{3}{m^2} = – \frac{1}{3} \Leftrightarrow {m^2} = 1 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{m = 1} \\
{m = – 1}
\end{array}} \right.$

Vậy với $\left[ {\begin{array}{*{20}{l}}
{m = 1} \\
{m = – 1}
\end{array}} \right.$ thì hàm số liên tục tại $x = 0$.

Câu 4: Cho tứ diện đều $ABCD$ cạnh $a$. Gọi $G$ là trọng tâm tam giác $ABD$, điểm $M,H$ lần lượt thuộc cạnh $CD,AD$ sao cho $DM = 2MC$ và $DH = 2HA$. Gọi $E$ là giao điểm $DG$ cắt $BH$. Mặt phẳng $\left( \alpha \right)$ đi qua $E$ song song $\left( {ABC} \right)$ cắt $BM$ tại $F$. Tính độ dài đoạn thẳng $EF$.

Lời giải

Mặt phẳng $\left( \alpha \right)$ đi qua $E$ song song $\left( {ABC} \right)$ cắt $BM$ tại $F$ suy ra $EF//\left( {ABC} \right)$ Giả thiết có $\frac{{DM}}{{DC}} = \frac{2}{3} = \frac{{DH}}{{DA}} \Rightarrow MH//AC$ mà $EF//\left( {ABC} \right)$ nên $EF//MH$

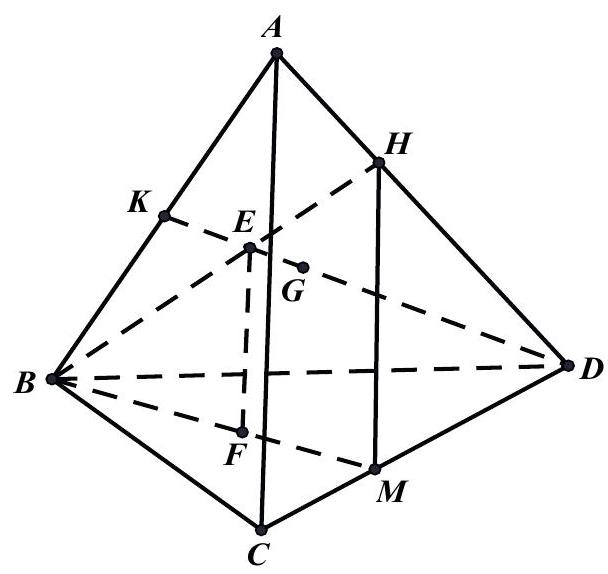
Khi đó: $\frac{{MH}}{{AC}} = \frac{{DM}}{{DC}} = \frac{2}{3} \Rightarrow MH = \frac{2}{3}DC = \frac{2}{3}a$

Gọi $K = DG \cap AB$

Ta có: $\frac{{DG}}{{DK}} = \frac{{DH}}{{DA}} = \frac{2}{3} \Rightarrow HG//AK $

$\Rightarrow \frac{{HG}}{{AK}} = \frac{{DH}}{{DA}} = \frac{2}{3} $

$\Rightarrow HG = \frac{2}{3}AK = \frac{2}{3}BK$

$ \Rightarrow \frac{{HE}}{{BE}} = \frac{{HG}}{{BK}} = \frac{2}{3} $

$\Rightarrow \frac{{EF}}{{MH}} = \frac{{BE}}{{BH}} = \frac{3}{5} $

$\Leftrightarrow EF = \frac{3}{5}HM = \frac{3}{5} \cdot \frac{2}{3}a = \frac{2}{5}a$.

Vậy độ dài của đường thẳng $EF$ bằng $\frac{2}{5}a$.