Đề Thi Học Kỳ 1 Môn Toán 11 Kết Nối Tri Thức Giải Chi Tiết-Đề 8

Đề thi học kỳ 1 môn Toán 11 Kết nối tri thức giải chi tiết-Đề 8 được soạn dưới dạng file word và PDF gồm 6 trang. Các bạn xem và tải về ở dưới.

I. PHẦN TRẮC NGHIỆM (7,0 điểm)

Câu 1: Số nào dưới đây là một nghiệm của phương trình $sinx = \frac{{\sqrt 2 }}{2}$ ?

A. $\frac{\pi }{2}$. B. $\frac{\pi }{4}$. C. $ – \frac{{3\pi }}{4}$. D. $ – \frac{\pi }{4}$.

Câu 2: Đồ thị của một hàm số $y = cosx$ có tính chất nào dưới đây?

A. Đối xứng qua gốc tọa độ. B. Đối xứng qua trục hoành.

C. Đối xứng qua trục tung. D. Đối xứng qua điểm $I\left( {0;1} \right)$.

Câu 3: Phương trình nào sau đây là phương trình bậc nhất đối với $sinx;cosx$ ?

A. $\sqrt 3 sin3x – cos3x = 2$. B. $si{n^2}x + \sqrt 3 cosx = 2$. C. $si{n^2}x + \sqrt 3 co{s^2}x = 2$. D. $\sqrt 3 sinx – cosx = 2$.

Câu 4: Cho dãy số vô hạn $\left( {{u_n}} \right)$, biết $\left\{ {\begin{array}{*{20}{l}}
{{u_1} = 1} \\
{{u_{n + 1}} = 2{u_n} + 3,n \in {\mathbb{N}^*}}
\end{array}} \right.$. Tính số hạng thứ 4 của dãy số.

A. 21 . B. 29 . C. 11 . D. 13 .

Câu 5: Cho dãy số hữu hạn gồm 5 số hạng $\frac{1}{3};\frac{1}{5};\frac{1}{7};\frac{1}{9};\frac{1}{{11}}$. Số hạng thứ 3 của dãy số bằng

A. $\frac{1}{5}$. B. $\frac{1}{3}$. C. $\frac{1}{7}$. D. $\frac{1}{9}$.

Câu 6: Trong các dãy số sau, dãy số nào có giới hạn bằng 0 ?

A. dãy $\left( {{v_n}} \right)$ với ${v_n} = \frac{{n + 1}}{n}$. B. dãy $\left( {{v_n}} \right)$ với ${v_n} = \frac{1}{n}$.

C. dãy $\left( {{v_n}} \right)$ với ${v_n} = 2023$. D. dãy $\left( {{v_n}} \right)$ với ${v_n} = \frac{{2n + 3}}{n}$.

Câu 7: Cho và $\left( {{v_n}} \right)$ là các dãy số thỏa mãn $\mathop {lim}\limits_{n \to + \infty } {u_n} = a,\mathop {lim}\limits_{n \to + \infty } {v_n} = b,\left( {a;b \in \mathbb{R}} \right)$. Khẳng định nào sau đây sai?
A. $\mathop {lim}\limits_{n \to + \infty } \left( {{u_n} + {v_n}} \right) = a + b$. B. $\mathop {lim}\limits_{n \to + \infty } \left( {2{u_n} – 3{v_n}} \right) = 2a – 3b$.
C. $\mathop {lim}\limits_{n \to + \infty } \frac{{{u_n}}}{{{v_n}}} = \frac{a}{b}$. D. $\mathop {lim}\limits_{n \to + \infty } \left( {{u_n}{v_n}} \right) = ab$.

Câu 8: Cho $\mathop {\lim }\limits_{x \to 1} f(x) = 2,\mathop {\lim }\limits_{x \to 1} g(x) = 3$. Tính $\mathop {\lim }\limits_{x \to 1} [f(x) + g(x)]$.

A. 5 . B. -5 . C. -1 . D. 1 .

Câu 9: Cho hàm số $f\left( x \right) = \frac{{x – 3}}{{x – 2}}$. Khẳng định nào sau đây sai?

A. $f\left( x \right)$ liên tục tại ${x_0} = 3$. B. $f\left( x \right)$ liên tục tại ${x_0} = – 2$.

C. $f\left( x \right)$ liên tục tại ${x_0} = 2$. D. $f\left( x \right)$ liên tục tại ${x_0} = – 3$.

Câu 10: Hàm số nào dưới đây gián đoạn tại điểm ${x_0} = – 4$ ?

A. $y = \left( {2x – 3} \right)\left( {{x^2} + 5} \right)$. B. $y = \frac{{2x – 1}}{{x + 4}}$. C. $y = \frac{x}{{x – 4}}$. D. $y = \frac{{x + 1}}{{{x^2} + 4}}$.

Câu 11: Hàm số nào sau đây liên tục trên $\mathbb{R}$

A. $y = {x^3} + 2{x^2} – 4$. B. $y = \frac{{x + 1}}{{x – 3}}$. C. $y = tanx$. D. $y = \sqrt {2 + x} $.

Câu 12: Điều kiện để hai đường thẳng trong không gian song song với nhau là

A. Không có điểm chung.

B. Đồng phẳng hoặc không có điểm chung.

C. Đồng phẳng.

D. Đồng phẳng và không có điểm chung.

Câu 13: Cho tứ diện $ABCD$. Gọi $M,N$ lần lượt là trung điểm của các cạnh $AB$ và $AC$. Chọn khẳng định đúng?

A. $MN//\left( {BCD} \right)$. B. $MN//\left( {ACD} \right)$. C. $MN//\left( {ABD} \right)$. D. $MN//\left( {ABC} \right)$.

Câu 14: Cho tứ diện $ABCD$ với $M,N$ lần lượt là trọng tâm các tam giác $ABD,ACD$. Khi đó $MN$ song song với mặt phẳng nào?

A. Mặt phẳng $\left( {ABD} \right)$.

B. Mặt phẳng $\left( {ACD} \right)$.

C. Mặt phẳng $\left( {ABC} \right)$.

D. Mặt phẳng $\left( {IBC} \right)$ với $I$ là trung điểm của $AD$.

Câu 15: Trong các mệnh đề sau, mệnh đề nào đúng?

A. Nếu hai mặt phẳng $\left( \alpha \right)$ và $\left( \beta \right)$ song song với nhau thì mọi đường thẳng nằm trong $\left( \alpha \right)$ đều song song với mọi đường thẳng nằm trong $\left( \beta \right)$.

B. Nếu hai đường thẳng song song lần lượt nằm trong hai mặt phẳng phân biệt $\left( \alpha \right)$ và $\left( \beta \right)$ thì $\left( \alpha \right)$ song song với $\left( \beta \right)$.

C. Qua một điểm nằm ngoài mặt phẳng cho trước ta vẽ được vô số mặt phẳng song song với mặt phẳng đó.

D. Nếu hai mặt phẳng $\left( \alpha \right)$ và $\left( \beta \right)$ song song với nhau thì mọi đường thẳng nằm trong $\left( \alpha \right)$ đều song song với $\left( \beta \right)$.

Câu 16: Trong không gian, mệnh đề nào sau đây đúng?

A. Phép chiếu song song biến hai đường thẳng cắt nhau thành hai đường thẳng song song.

B. Phép chiếu song song biến hai đường thẳng cắt nhau thành hai đường thẳng trùng nhau.

C. Phép chiếu song song biến hai đường thẳng cắt nhau thành hai đường thẳng cắt nhau hoặc trùng nhau.

D. Phép chiếu song song biến hai đường thẳng cắt nhau thành hai đường thẳng cắt nhau.

Câu 17: Một cuộc khảo sát đã tiến hành xác định tuổi (tính theo năm) của 120 chiếc ô tô. Kết quả điều tra được cho trong bảng số liệu dưới đây:

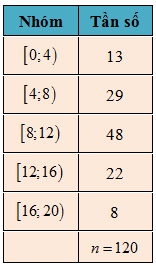
Trong các mệnh đề dưới đây, đâu là mệnh đề đúng?

A. Có 29 ô tô ở độ tuổi là 4 . B. Có 48 ô tô ở độ tuổi dưới 12.

C. Có 8 ô tô từ độ tuổi 16 đến 20. D. Có 13 ô tô có độ tuổi dưới 4.

Câu 18: Tìm hiểu thời gian xem YouTube trong tuần trước (đơn vị: giờ) của một số học sinh thu được kết quả sau:

Tính thời gian xem YouTube trung bình trong tuần trước của các bạn học sinh này (đơn vị: giờ).

A. $\bar x = 8.4375$. B. $\bar x = 7.4375$ C. $\bar x = 6.4375$ D. $\bar x = 9.4375$

Câu 19: Thống kê chiều cao của học sinh lớp $11A$ ta có bảng số liệu sau:

Hỏi lớp có bao nhiêu học sinh có chiều cao từ $168\;cm$ trở lên?

A. 11 . B. 20 . C. 31 . D. 8 .

Câu 20: Cho mẫu số liệu về điểm thi học kỳ I của các học sinh trong khối 11 của một trường THPT Chuyên T như sau:

Mẫu số liệu trên có bao nhiêu số liệu, bao nhiêu nhóm?

A. 150 số liệu; 5 nhóm. B. 45 số liệu; 6 nhóm.

C. 6 số liệu; 150 nhóm. D. 5 số liệu; 30 nhóm.

Câu 21: Rút gọn biểu thức $A = cos\left( {7\pi – x} \right) – sin\left( {\frac{{3\pi }}{2} + x} \right) + 2tan\left( {\frac{{5\pi }}{2} – x} \right) + cot\left( {23\pi – x} \right)$ ta được

A. $A = 3cotx$. B. $A = 2cosx$. C. $A = cosx$. D. $A = cotx$.

Câu 22: Tập giá trị của hàm số: $y = 5si{n^2}x + 4sin2xcos2x + 5co{s^2}x$ có tất cả bao nhiêu giá trị nguyên?

A. 6 . B. 4 . C. 3 . D. 5 .

Câu 23: Cho dãy số $\left( {{u_n}} \right)$ có ${u_1} = – 3$ và ${u_{n + 1}} = {u_n} + n$ với $n \geqslant 1,n \in \mathbb{N}$. Số hạng thứ 3 của dãy số đã cho là

A. ${u_3} = – 1$. B. ${u_3} = 3$. C. ${u_3} = – 2$. D. ${u_3} = 0$.

Câu 24: Cho cấp số cộng $\left( {{u_n}} \right)$ có ${u_1} = 2023$ và ${u_n} = {u_{n – 1}} – 3$ với $n \geqslant 2,n \in \mathbb{N}$. Số hạng tổng quát của cấp số cộng đã cho là

A. ${u_n} = – 3n + 2020\left( {n \geqslant 2,n \in \mathbb{N}} \right)$. B. ${u_n} = 3n + 2014\left( {n \geqslant 2,n \in \mathbb{N}} \right)$.

C. ${u_n} = – 3n + 2026\left( {n \geqslant 2,n \in \mathbb{N}} \right)$. D. ${u_n} = 3n + 2026\left( {n \geqslant 2,n \in \mathbb{N}} \right)$.

Câu 25: Cho cấp số nhân $\left( {{u_n}} \right)$ có số hạng đầu ${u_1} = 2$ và công bội $q = 3$. Số hạng tổng quát của cấp số nhân là:

A. ${u_n} = {2.3^n}$. B. ${u_n} = 3 \cdot {2^n}$. C. ${u_n} = 3 \cdot {2^{n – 1}}$. D. ${u_n} = 2 \cdot {3^{n – 1}}$.

Câu 26: Kết quả của giới hạn $\mathop {\lim }\limits_{x \to + \infty } \frac{{2{n^2} – n + 1}}{{3{n^2} + 2}}$ bằng:

A. $\frac{3}{2}$. B. 2 . C. $\frac{2}{3}$. D. 3 .

Câu 27: Kết quả của giới hạn $\mathop {\lim }\limits_{x \to – \infty } \frac{{2{x^2} + 5x – 3}}{{{x^2} + 6x + 3}}$ là:

A. -2 . B. $ + \infty $. C. 3 . D. 2 .

Câu 28: Giá trị của giới hạn $\mathop {\lim }\limits_{x \to {3^ – }} \frac{{3 – x}}{{\sqrt {27 – {x^3}} }}$ là:

A. $\frac{1}{3}$. B. 0 . C. $\frac{5}{3}$. D. $\frac{3}{5}$.

Câu 29: Biết $\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt[3]{{x + 7}} – 2}}{{{x^2} – 1}} = \frac{a}{b}$ với $a,b \in \mathbb{N},b \ne 0,\frac{a}{b}$ là phân số tối giản. giá trị của ${a^2} + {b^2}$ bằng

A. 25 . B. 575 . C. 23 . D. 577 .

Câu 30: Cho hàm số $f(x) = \left\{ {\begin{array}{*{20}{l}}
{x + {m^2}}&{khix < – 1} \\
0&{khi – 1 \leqslant x < 1} \\
{x + m}&{khix \geqslant 1}
\end{array}} \right.$ Tìm $m$ để hàm số liên tục trên $\mathbb{R}$.

A. $m = 1$. B. $\left[ {\begin{array}{*{20}{l}}
{m = 1} \\
{m = – 1}
\end{array}} \right.$. C. $\left\{ {\begin{array}{*{20}{l}}
{m \ne 1} \\
{m \ne – 1}
\end{array}} \right.$. D. $m = – 1$.

Câu 31: Trong các tính chất sau, tính chất nào không đúng?

A. Có hai đường thẳng phân biệt cùng đi qua hai điểm phân biệt cho trước.

B. Tồn tại bốn điểm không cùng thuộc một mặt phẳng.

C. Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng.

D. Nếu một đường thẳng đi qua hai điểm phân biệt thuộc một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó.

Câu 32: Cho tứ diện $ABCD$. Gọi $M,N$ lần lượt là trung điểm $AD$ và $AC$. Gọi $G$ là trọng tâm tam giác $BCD$. Giao tuyến của hai mặt phẳng $\left( {GMN} \right)$ và $\left( {BCD} \right)$ là đường thẳng

A. Qua $M$ và song song với $AB$. B. Qua $N$ và song song với $BD$.

C. Qua $G$ và song song với $CD$. D. Qua $G$ và song song với $BC$.

Câu 33: Xét hình tứ diện $ABCD$.

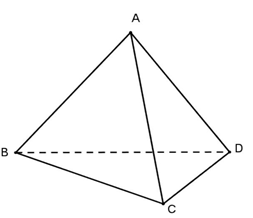
Hai đường thẳng $AC;BD$ có vị trí tương đối là

A. song song. B. trùng nhau. C. chéo nhau. D. cắt nhau.

Câu 34: Cho tứ diện $ABCD$ có $M,N,P$ lần lượt là trung điểm của các cạnh $AD,BC$ và $BD$ (tham khảo hình vẽ bên).

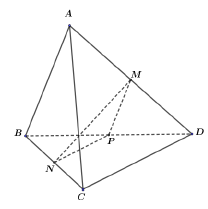
Gọi đường thẳng $d$ là giao tuyến của mặt phẳng $\left( {MNP} \right)$ và mặt phẳng $\left( {ACD} \right)$.

Khẳng định nào sau đây đúng?

A. $d$ song song với $AB$. B. $d$ song song với $CD$.

C. $d$ song song với $AC$. D. $d$ song song với $BC$.

Câu 35: Cho hình chóp tam giác $S.ABC$. Gọi $M,N$ lần lượt là trung điểm của các cạnh $SA,SB$. Gọi điểm $E$ thuộc cạnh $SC$ sao cho $SE = \frac{1}{4}SC$.

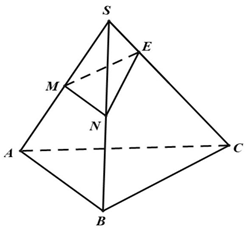
Mệnh đề nào dưới đây là mệnh đề sai?

A. Các đường thẳng $MN,AB$ song song. B. Các đường thẳng $NE,BC$ chéo nhau.

C. Các đường thẳng $MN,SC$ chéo nhau. D. Các đường thẳng $ME,AC$ cắt nhau.

II. PHẦN TỰ LUẬN (3,0 điểm)

Câu 1: (0,5 điểm) Cho phương trình $2co{s^2}2x + cos2x – 1 = 0$. Tìm các nghiệm của phương trình nằm trong khoảng $x \in \left( { – \pi ;3\pi } \right)$.

Câu 2: (1,0 điểm) Cho hàm số $f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}
{\frac{{\sqrt {3 – 2x} + x}}{{3 + x}}}&{\;khi\;x < – 3} \\
{2mx + 5}&{\;khi\;x \geqslant – 3}
\end{array}} \right.$. Tìm $m$ để hàm số có giới hạn tại $x = – 3$.

Câu 3: (1,0 điểm) Để tiết kiệm năng lượng, một công ty điện lực đề xuất bán điện sinh hoạt cho dân với theo hình thức lũy tiến (bậc thang) như sau: Mỗi bậc gồm 10 số; bậc 1 từ số thứ 1 đến số thứ 10 , bậc 2 từ số thứ 11 đến số 20 , bậc 3 từ số thứ 21 đến số thứ $30, \ldots $ Bậc 1 có giá là 800 đồng/ 1 số, giá của mỗi số ở bậc thứ $n + 1$ tăng so với giá của mỗi số ở bậc thứ $n$ là $2,5\% $. Gia đình ông A sử dụng hết 347 số trong tháng 1. Hỏi tháng 1 ông A phải đóng bao nhiêu tiền? (đơn vị là đồng, kết quả được làm tròn đến hàng phần trăm).

Câu 4: (0,5 điểm) Cho tứ diện $ABCD,G$ là trọng tâm tam giác $ABD$ và $M$ là điểm trên cạnh $BC$ sao cho $BM = 2MC$. Chứng minh đường thẳng $MG$ song song với mặt phẳng $\left( {ACD} \right)$.

ĐÁP ÁN VÀ LỜI GIẢI

BẢNG ĐÁP ÁN

1.B	2.C	3.D	4.B	5.C
6.B	7.C	8.A	9.C	10.B
11.A	12.D	13.A	14.C	15.D
16.C	17.D	18.A	19.A	20.A
21.D	22.D	23.D	24.C	25.D
26.C	27.D	28.B	29.D	30.D
31.A	32.C	33.C	34.B	35.B

HƯỚNG DÃ̃N GIẢI CHI TIẾT

I. PHẦN TRẮC NGHIỆM (7,0 điểm)

Câu 1: Số nào dưới đây là một nghiệm của phương trình $sinx = \frac{{\sqrt 2 }}{2}$ ?

A. $\frac{\pi }{2}$.

B. $\frac{\pi }{4}$.

C. $ – \frac{{3\pi }}{4}$.

D. $ – \frac{\pi }{4}$.

Lời giải

Ta có $sin\frac{\pi }{4} = \frac{{\sqrt 2 }}{2}$.

Câu 2: Đồ thị của một hàm số $y = cosx$ có tính chất nào dưới đây?

A. Đối xứng qua gốc tọa độ.

B. Đối xứng qua trục hoành.

C. Đối xứng qua trục tung.

D. Đối xứng qua điểm $I\left( {0;1} \right)$.

Lời giải

Hàm số $y = cosx$ là hàm số chẵn nên đồ thị đối xứng qua trục tung.

Câu 3: Phương trình nào sau đây là phương trình bậc nhất đối với $sinx;cosx$ ?

A. $\sqrt 3 sin3x – cos3x = 2$.

B. $si{n^2}x + \sqrt 3 cosx = 2$.

C. $si{n^2}x + \sqrt 3 co{s^2}x = 2$.

D. $\sqrt 3 sinx – cosx = 2$.

Lời giải

Phương trình $\sqrt 3 sinx – cosx = 2$ là phương trình bậc nhất đối với $sinx;cosx$

Câu 4: Cho dãy số vô hạn $\left( {{u_n}} \right)$, biết $\left\{ {\begin{array}{*{20}{l}}
{{u_1} = 1} \\
{{u_{n + 1}} = 2{u_n} + 3,n \in {\mathbb{N}^*}}
\end{array}} \right.$. Tính số hạng thứ 4 của dãy số.

A. 21 .

B. 29 .

C. 11 .

D. 13 .

Lời giải

Ta có: ${u_1} = 1;{u_2} = 2.1 + 3 = 5;{u_3} = 2.5 + 3 = 13;{u_4} = 2.13 + 3 = 29$.

Câu 5: Cho dãy số hữu hạn gồm 5 số hạng $\frac{1}{3};\frac{1}{5};\frac{1}{7};\frac{1}{9};\frac{1}{{11}}$. Số hạng thứ 3 của dãy số bằng

A. $\frac{1}{5}$.

B. $\frac{1}{3}$.

C. $\frac{1}{7}$.

D. $\frac{1}{9}$.

Lời giải

Số hạng thứ 3 của dãy số là $\frac{1}{7}$.

Câu 6: Trong các dãy số sau, dãy số nào có giới hạn bằng 0 ?

A. dãy $\left( {{v_n}} \right)$ với ${v_n} = \frac{{n + 1}}{n}$.

B. dãy $\left( {{v_n}} \right)$ với ${v_n} = \frac{1}{n}$.

C. dãy $\left( {{v_n}} \right)$ với ${v_n} = 2023$.

D. dãy $\left( {{v_n}} \right)$ với ${v_n} = \frac{{2n + 3}}{n}$.

Lời giải

Theo định nghĩa dãy số $\left( {{v_n}} \right)$ có giới hạn là 0 thì chỉ có ${v_n} = \frac{1}{n}$ là dãy số có giới hạn bằng 0 .

Câu 7: Cho và $\left( {{v_n}} \right)$ là các dãy số thỏa mãn $\mathop {lim}\limits_{n \to + \infty } {u_n} = a,\mathop {lim}\limits_{n \to + \infty } {v_n} = b,\left( {a;b \in \mathbb{R}} \right)$. Khẳng định nào sau đây sai?
A. $\mathop {lim}\limits_{n \to + \infty } \left( {{u_n} + {v_n}} \right) = a + b$.

B. $\mathop {lim}\limits_{n \to + \infty } \left( {2{u_n} – 3{v_n}} \right) = 2a – 3b$.

C. $\mathop {lim}\limits_{n \to + \infty } \frac{{{u_n}}}{{{v_n}}} = \frac{a}{b}$.

D. $\mathop {lim}\limits_{n \to + \infty } \left( {{u_n}{v_n}} \right) = ab$.
Lời giải

Chọn ý C vì thiếu điều kiện mẫu số khác 0 .

Câu 8: Cho $\mathop {\lim }\limits_{x \to 1} f(x) = 2,\mathop {\lim }\limits_{x \to 1} g(x) = 3$. Tính $\mathop {\lim }\limits_{x \to 1} [f(x) + g(x)]$.

A. 5 .

B. -5 .

C. -1 .

D. 1 .

Lời giải

Có $\mathop {\lim }\limits_{x \to 1} [f(x) + g(x)] = \mathop {\lim }\limits_{x \to 1} f(x) + \mathop {\lim }\limits_{x \to 1} g(x) = 2 + 3 = 5$.

Câu 9: Cho hàm số $f\left( x \right) = \frac{{x – 3}}{{x – 2}}$. Khẳng định nào sau đây sai?

A. $f\left( x \right)$ liên tục tại ${x_0} = 3$.

B. $f\left( x \right)$ liên tục tại ${x_0} = – 2$.

C. $f\left( x \right)$ liên tục tại ${x_0} = 2$.

D. $f\left( x \right)$ liên tục tại ${x_0} = – 3$.

Lời giải

Ta có hàm số $f\left( x \right) = \frac{{x – 3}}{{x – 2}}$ liên tục tại mọi điểm $x \ne 2$

Tại $x = 2$ thì $f\left( x \right)$ không xác định, do đó $f\left( x \right)$ không liên tục tại ${x_0} = 2$.

Câu 10: Hàm số nào dưới đây gián đoạn tại điểm ${x_0} = – 4$ ?

A. $y = \left( {2x – 3} \right)\left( {{x^2} + 5} \right)$.

B. $y = \frac{{2x – 1}}{{x + 4}}$.

C. $y = \frac{x}{{x – 4}}$.

D. $y = \frac{{x + 1}}{{{x^2} + 4}}$.

Lời giải

Ta có: hàm số $y = \frac{{2x – 1}}{{x + 4}}$ là hàm phân thức hữu tỷ không xác định tại $x = – 4$ nên hàm số bị gián đoạn tại $x = – 4$.

Câu 11: Hàm số nào sau đây liên tục trên $\mathbb{R}$

A. $y = {x^3} + 2{x^2} – 4$.

B. $y = \frac{{x + 1}}{{x – 3}}$.

C. $y = tanx$.

D. $y = \sqrt {2 + x} $.

Lời giải

Hàm đa thức liên tục trên $\mathbb{R}$.

Câu 12: Điều kiện để hai đường thẳng trong không gian song song với nhau là

A. Không có điểm chung.

B. Đồng phẳng hoặc không có điểm chung.

C. Đồng phẳng.

D. Đồng phẳng và không có điểm chung.

Lời giải

Điều kiện để hai đường thẳng trong không gian song song với nhau là đồng phẳng và không có điểm chung.

Câu 13: Cho tứ diện $ABCD$. Gọi $M,N$ lần lượt là trung điểm của các cạnh $AB$ và $AC$. Chọn khẳng định đúng?

A. $MN//\left( {BCD} \right)$.

B. $MN//\left( {ACD} \right)$.

C. $MN//\left( {ABD} \right)$.

D. $MN//\left( {ABC} \right)$.

Lời giải

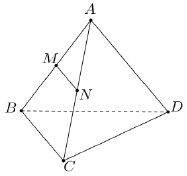
Theo giả thiết, ta có $MN$ là đường trunng bình của tam giác $ABC$, suy ra $MN//BC$.

$\left\{ {\begin{array}{*{20}{l}}
{MN//BC} \\
{MN \not\subset \left( {BCD} \right) \Rightarrow MN//\left( {BCD} \right)} \\
{BC \subset \left( {BCD} \right)}
\end{array}} \right.$.

Câu 14: Cho tứ diện $ABCD$ với $M,N$ lần lượt là trọng tâm các tam giác $ABD,ACD$. Khi đó $MN$ song song với mặt phẳng nào?

A. Mặt phẳng $\left( {ABD} \right)$.

B. Mặt phẳng $\left( {ACD} \right)$.

C. Mặt phẳng $\left( {ABC} \right)$.

D. Mặt phẳng $\left( {IBC} \right)$ với $I$ là trung điểm của $AD$.

Lời giải

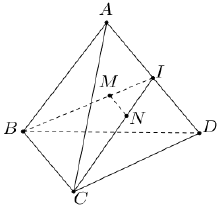
Gọi $I$ là trung điểm của $AD$.

Do $M,N$ lần lượt là trọng tâm các tam giác $ABD$ và $ACD$, theo tính chất trọng tâm của tam giác nên ta có $\frac{{IM}}{{IB}} = \frac{{IN}}{{IC}} = \frac{1}{3}$ và $M,N$ nằm trong mặt phẳng $\left( {IBC} \right)$.

Trong mặt phẳng $\left( {IBC} \right)$, theo định lý Ta – lét ta có $MN//BC$.

Mà $BC \subset \left( {ABC} \right)$ và $MN \not\subset \left( {ABC} \right)$ suy ra $MN//\left( {ABC} \right)$.

Câu 15: Trong các mệnh đề sau, mệnh đề nào đúng?

A. Nếu hai mặt phẳng $\left( \alpha \right)$ và $\left( \beta \right)$ song song với nhau thì mọi đường thẳng nằm trong $\left( \alpha \right)$ đều song song với mọi đường thẳng nằm trong $\left( \beta \right)$.

B. Nếu hai đường thẳng song song lần lượt nằm trong hai mặt phẳng phân biệt $\left( \alpha \right)$ và $\left( \beta \right)$ thì $\left( \alpha \right)$ song song với $\left( \beta \right)$.

C. Qua một điểm nằm ngoài mặt phẳng cho trước ta vẽ được vô số mặt phẳng song song với mặt phẳng đó.

D. Nếu hai mặt phẳng $\left( \alpha \right)$ và $\left( \beta \right)$ song song với nhau thì mọi đường thẳng nằm trong $\left( \alpha \right)$ đều song song với $\left( \beta \right)$.

Lời giải

Mệnh đề đúng là:

‘Nếu hai mặt phẳng $\left( \alpha \right)$ và $\left( \beta \right)$ song song với nhau thì mọi đường thẳng nằm trong $\left( \alpha \right)$ đều song song với $\left( \beta \right)$ ‘’.

Câu 16: Trong không gian, mệnh đề nào sau đây đúng?

A. Phép chiếu song song biến hai đường thẳng cắt nhau thành hai đường thẳng song song.

B. Phép chiếu song song biến hai đường thẳng cắt nhau thành hai đường thẳng trùng nhau.

C. Phép chiếu song song biến hai đường thẳng cắt nhau thành hai đường thẳng cắt nhau hoặc trùng nhau.

D. Phép chiếu song song biến hai đường thẳng cắt nhau thành hai đường thẳng cắt nhau.

Lời giải

Theo tính chất của phép chiếu song song, mệnh đề đúng là:

‘Phép chiếu song song biến hai đường thẳng cắt nhau thành hai đường thẳng cắt nhau hoặc trùng nhau’,

Câu 17: Một cuộc khảo sát đã tiến hành xác định tuổi (tính theo năm) của 120 chiếc ô tô. Kết quả điều tra được cho trong bảng số liệu dưới đây:

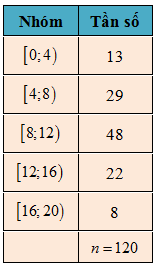
Trong các mệnh đề dưới đây, đâu là mệnh đề đúng?

A. Có 29 ô tô ở độ tuổi là 4 .

B. Có 48 ô tô ở độ tuổi dưới 12.

C. Có 8 ô tô từ độ tuổi 16 đến 20.

D. Có 13 ô tô có độ tuổi dưới 4.

Lời giải

Trong bảng 1 ta thấy:

Có 13 ô tô có độ tuổi dưới 4;

Có 29 ô tô có độ tuổi từ 4 đến dưới 8;

Có 48 ô tô có độ tuổi từ 8 đến dưới 12;

Có 22 ô tô có độ tuổi từ 12 đến dưới 16 ;

Có 8 ô tô có độ tuổi từ 16 đến dưới 20.

Câu 18: Tìm hiểu thời gian xem YouTube trong tuần trước (đơn vị: giờ) của một số học sinh thu được kết quả sau:

Tính thời gian xem YouTube trung bình trong tuần trước của các bạn học sinh này (đơn vị: giờ).

A. $\bar x = 8.4375$.

B. $\bar x = 7.4375$

C. $\bar x = 6.4375$

D. $\bar x = 9.4375$

Lời giải

Ta có:

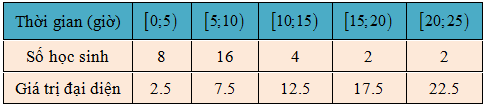
Thời gian xem YouTube trung bình trong tuần trước của các bạn học sinh này là:

$\overline x = \frac{{8 \times 2.5 + 16 \times 7.5 + 4 \times 12.5 + 2 \times 17.5 + 2 \times 22.5}}{{8 + 16 + 4 + 2 + 2}} = 8.4375\;\;$(giờ)

Câu 19: Thống kê chiều cao của học sinh lớp $11A$ ta có bảng số liệu sau:

Hỏi lớp có bao nhiêu học sinh có chiều cao từ $168\;cm$ trở lên?

A. 11 .

B. 20 .

C. 31 .

D. 8 .

Lời giải

Số học sinh có chiều cao từ $168\;cm$ trở lên là $8 + 3 = 11$.

Câu 20: Cho mẫu số liệu về điểm thi học kỳ I của các học sinh trong khối 11 của một trường THPT Chuyên T như sau:

Mẫu số liệu trên có bao nhiêu số liệu, bao nhiêu nhóm?

A. 150 số liệu; 5 nhóm.

B. 45 số liệu; 6 nhóm.

C. 6 số liệu; 150 nhóm.

D. 5 số liệu; 30 nhóm.

Lời giải

Mẫu số liệu $\left( T \right)$ có: $20 + 45 + 35 + 40 + 10 = 150$ (số liệu).

5 nhóm: $\left[ {5;6} \right);\left[ {6;7} \right);\left[ {7;8} \right);\left[ {8;9} \right);\left[ {9;10} \right]$.

Câu 21: Rút gọn biểu thức $A = cos\left( {7\pi – x} \right) – sin\left( {\frac{{3\pi }}{2} + x} \right) + 2tan\left( {\frac{{5\pi }}{2} – x} \right) + cot\left( {23\pi – x} \right)$ ta được

A. $A = 3cotx$.

B. $A = 2cosx$.

C. $A = cosx$.

D. $A = cotx$.

Lời giải

Ta có: $cos\left( {7\pi – x} \right) = cos\left( {\pi – x + 3.2\pi } \right) = cos\left( {\pi – x} \right) = – cosx$.

$sin\left( {\frac{{3\pi }}{2} + x} \right) = sin\left( {\pi + \frac{\pi }{2} + x} \right) = – sin\left( {\frac{\pi }{2} + x} \right) = – cosx$

$tan\left( {\frac{{5\pi }}{2} – x} \right) = tan\left( {2\pi + \frac{\pi }{2} – x} \right) = tan\left( {\frac{\pi }{2} – x} \right) = cotx$

$cot\left( {23\pi – x} \right) = cot\left( { – x} \right) = – cotx$.

Suy ra $A = – cosx – \left( { – cosx} \right) + 2cotx + \left( { – cotx} \right) = cotx$.

Câu 22: Tập giá trị của hàm số: $y = 5si{n^2}x + 4sin2xcos2x + 5co{s^2}x$ có tất cả bao nhiêu giá trị nguyên?

A. 6 .

B. 4 .

C. 3 .

D. 5 .

Lời giải

Ta có: $y = 5si{n^2}x + 4sin2xcos2x + 5co{s^2}x = 5\left( {si{n^2}x + co{s^2}x} \right) + 2sin4x = 5 + 2sin4x$.

Vì $ – 1 \leqslant sin4x \leqslant 1 \Leftrightarrow – 2 \leqslant 2sin4x \leqslant 2 \Leftrightarrow 3 \leqslant 5 + 2sin4x \leqslant 7 \Leftrightarrow 3 \leqslant y \leqslant 7$

Do $y \in \mathbb{Z}$ nên $y \in \left\{ {3;4;5;6;7} \right\}$. Vậy $y$ có 5 giá trị nguyên.

Câu 23: Cho dãy số $\left( {{u_n}} \right)$ có ${u_1} = – 3$ và ${u_{n + 1}} = {u_n} + n$ với $n \geqslant 1,n \in \mathbb{N}$. Số hạng thứ 3 của dãy số đã cho là

A. ${u_3} = – 1$.

B. ${u_3} = 3$.

C. ${u_3} = – 2$.

D. ${u_3} = 0$.

Lời giải

Ta có $:{u_1} = – 3$ và ${u_{n + 1}} = {u_n} + n$ với $n \geqslant 1,n \in \mathbb{N}$.

Suy ra: ${u_2} = {u_1} + 1 = – 3 + 1 = – 2;{u_3} = {u_2} + 2 = – 2 + 2 = 0$.

Câu 24: Cho cấp số cộng $\left( {{u_n}} \right)$ có ${u_1} = 2023$ và ${u_n} = {u_{n – 1}} – 3$ với $n \geqslant 2,n \in \mathbb{N}$. Số hạng tổng quát của cấp số cộng đã cho là

A. ${u_n} = – 3n + 2020\left( {n \geqslant 2,n \in \mathbb{N}} \right)$.

B. ${u_n} = 3n + 2014\left( {n \geqslant 2,n \in \mathbb{N}} \right)$.

C. ${u_n} = – 3n + 2026\left( {n \geqslant 2,n \in \mathbb{N}} \right)$.

D. ${u_n} = 3n + 2026\left( {n \geqslant 2,n \in \mathbb{N}} \right)$.

Lời giải

Ta có ${u_1} = 2023$ và ${u_n} = {u_{n – 1}} – 3$ với $n \geqslant 2,n \in \mathbb{N}$ nên suy ra :

$d = {u_n} – {u_{n – 1}} = \left( {{u_{n – 1}} – 3} \right) – {u_{n – 1}} = – 3$.

Vậy số hạng tổng quát của cấp số cộng đã cho là :

${u_n} = {u_1} + \left( {n – 1} \right)d = 2023 + \left( {n – 1} \right)\left( { – 3} \right) = – 3n + 2026$ với $n \geqslant 2,n \in \mathbb{N}$.

Câu 25: Cho cấp số nhân $\left( {{u_n}} \right)$ có số hạng đầu ${u_1} = 2$ và công bội $q = 3$. Số hạng tổng quát của cấp số nhân là:

A. ${u_n} = {2.3^n}$.

B. ${u_n} = 3 \cdot {2^n}$.

C. ${u_n} = 3 \cdot {2^{n – 1}}$.

D. ${u_n} = 2 \cdot {3^{n – 1}}$.

Lời giải

Theo công thức số hạng tổng quát của cấp số nhân ta có ${u_n} = {u_1} \cdot {q^{n – 1}} = {2.3^{n – 1}}$.

Câu 26: Kết quả của giới hạn $\mathop {\lim }\limits_{x \to + \infty } \frac{{2{n^2} – n + 1}}{{3{n^2} + 2}}$ bằng:

A. $\frac{3}{2}$.

B. 2 .

C. $\frac{2}{3}$.

D. 3 .

Lời giải

Ta có $\mathop {\lim }\limits_{x \to + \infty } \frac{{2{n^2} – n + 1}}{{3{n^2} + 2}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{2 – \frac{1}{n} + \frac{1}{{{n^2}}}}}{{3 + \frac{2}{{{n^2}}}}} = \frac{2}{3}$.

Câu 27: Kết quả của giới hạn $\mathop {\lim }\limits_{x \to – \infty } \frac{{2{x^2} + 5x – 3}}{{{x^2} + 6x + 3}}$ là:

A. -2 .

B. $ + \infty $.

C. 3 .

D. 2 .

Lời giải

Ta có $\mathop {\lim }\limits_{x \to – \infty } \frac{{2{x^2} + 5x – 3}}{{{x^2} + 6x + 3}} = \mathop {\lim }\limits_{x \to – \infty } \frac{{2 + \frac{5}{x} – \frac{3}{{{x^2}}}}}{{1 + \frac{6}{x} + \frac{3}{{{x^2}}}}} = 2$.

Câu 28: Giá trị của giới hạn $\mathop {\lim }\limits_{x \to {3^ – }} \frac{{3 – x}}{{\sqrt {27 – {x^3}} }}$ là:

A. $\frac{1}{3}$.

B. 0 .

C. $\frac{5}{3}$.

D. $\frac{3}{5}$.

Lời giải

Ta có $3 – x > 0$ với mọi $x < 3$, do đó: $\mathop {\lim }\limits_{x \to {3^ – }} \frac{{3 – x}}{{\sqrt {27 – {x^3}} }} = \mathop {\lim }\limits_{x \to {3^ – }} \frac{{3 – x}}{{\sqrt {(3 – x)\left( {9 + 3x + {x^2}} \right)} }}$

$ = \mathop {\lim }\limits_{x \to {3^ – }} \frac{{\sqrt {3 – x} }}{{\sqrt {9 + 3x + {x^2}} }} = \frac{{\sqrt {3 – 3} }}{{\sqrt {9 + 3.3 + {3^2}} }} = 0$

Câu 29: Biết $\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt[3]{{x + 7}} – 2}}{{{x^2} – 1}} = \frac{a}{b}$ với $a,b \in \mathbb{N},b \ne 0,\frac{a}{b}$ là phân số tối giản. giá trị của ${a^2} + {b^2}$ bằng

A. 25 .

B. 575 .

C. 23 .

D. 577 .

Lời giải

Ta có $\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt[3]{{x + 7}} – 2}}{{{x^2} – 1}}$$ = \mathop {\lim }\limits_{x \to 1} \frac{{(\sqrt[3]{{x + 7}} – 2)\left( {\sqrt[3]{{{{(x + 7)}^2}}} + 2\sqrt[3]{{x + 7}} + 4} \right)}}{{\left( {{x^2} – 1} \right)\left( {\sqrt[3]{{{{(x + 7)}^2}}} + 2\sqrt[3]{{x + 7}} + 4} \right)}}$

$ = \mathop {\lim }\limits_{x \to 1} \frac{{x + 7 – 8}}{{\left( {{x^2} – 1} \right)\left( {\sqrt[3]{{{{(x + 7)}^2}}} + 2\sqrt[3]{{x + 7}} + 4} \right)}}$$ = \mathop {\lim }\limits_{x \to 1} \frac{{x – 1}}{{(x – 1)(x + 1)\left( {\sqrt[3]{{{{(x + 7)}^2}}} + 2\sqrt[3]{{x + 7}} + 4} \right)}}$

$ = \mathop {\lim }\limits_{x \to 1} \frac{1}{{(x + 1)\left( {\sqrt[3]{{{{(x + 7)}^2}}} + 2\sqrt[3]{{x + 7}} + 4} \right)}} = \frac{1}{{24}}$.

Suy ra $\left\{ {\begin{array}{*{20}{l}}
{a = 1} \\
{b = 24}
\end{array} \Rightarrow {a^2} + {b^2} = 577} \right.$.

Câu 30: Cho hàm số $f(x) = \left\{ {\begin{array}{*{20}{l}}
{x + {m^2}}&{khix < – 1} \\
0&{khi – 1 \leqslant x < 1} \\
{x + m}&{khix \geqslant 1}
\end{array}} \right.$ Tìm $m$ để hàm số liên tục trên $\mathbb{R}$.

A. $m = 1$.

B. $\left[ {\begin{array}{*{20}{l}}
{m = 1} \\
{m = – 1}
\end{array}} \right.$.

C. $\left\{ {\begin{array}{*{20}{l}}
{m \ne 1} \\
{m \ne – 1}
\end{array}} \right.$.

D. $m = – 1$.

Lời giải

Xét $x \in ( – \infty ; – 1)$ ta có $f(x) = x + {m^2}$ nên hàm số liên tục trên khoảng $( – \infty ; – 1)$.

Xét $x \in ( – 1;1)$ ta có $f(x) = 0$ nên hàm số liên tục trên khoảng $( – 1;1)$.

Xét $x \in (1; + \infty )$ ta có $f(x) = x + m$ nên hàm số liên tục trên khoảng $(1; + \infty )$.

Để hàm số liên tục trên $\mathbb{R}$ thì hàm số phải liên tục tại $x = – 1$ và $x = 1$ nên điều kiện cần tìm là

$\left\{ \begin{gathered}
\mathop {\lim }\limits_{x \to – {1^ – }} f(x) = \mathop {\lim }\limits_{x \to – {1^ + }} f(x) = f( – 1) \hfill \\
\mathop {\lim }\limits_{x \to {1^ – }} f(x) = \mathop {\lim }\limits_{x \to {1^ + }} f(x) = f(1) \hfill \\
\end{gathered} \right.$

$ \Leftrightarrow \left\{ \begin{gathered}
\mathop {\lim }\limits_{x \to – {1^ – }} (x + {m^2}) = \mathop {\lim }\limits_{x \to – {1^ + }} 0 = 0 \hfill \\
\mathop {\lim }\limits_{x \to {1^ – }} 0 = \mathop {\lim }\limits_{x \to {1^ + }} (x + m) = 1 + m \hfill \\
\end{gathered} \right.$

$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{{m^2} – 1 = 0} \\
{m + 1 = 0}
\end{array} \Leftrightarrow m = – 1.} \right.$

Vậy $m=-1$ là giá trị cần tìm.

Câu 31: Trong các tính chất sau, tính chất nào không đúng?

A. Có hai đường thẳng phân biệt cùng đi qua hai điểm phân biệt cho trước.

B. Tồn tại bốn điểm không cùng thuộc một mặt phẳng.

C. Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng.

D. Nếu một đường thẳng đi qua hai điểm phân biệt thuộc một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó.

Lời giải

Chỉ có duy nhất một đường thẳng đi qua hai điểm phân biệt cho trước.

Câu 32: Cho tứ diện $ABCD$. Gọi $M,N$ lần lượt là trung điểm $AD$ và $AC$. Gọi $G$ là trọng tâm tam giác $BCD$. Giao tuyến của hai mặt phẳng $\left( {GMN} \right)$ và $\left( {BCD} \right)$ là đường thẳng

A. Qua $M$ và song song với $AB$.

B. Qua $N$ và song song với $BD$.

C. Qua $G$ và song song với $CD$.

D. Qua $G$ và song song với $BC$.

Lời giải

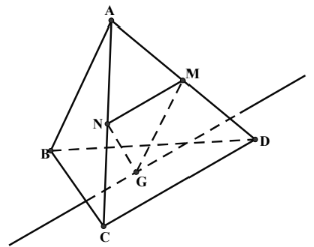
Ta có $MN$ là đường trung bình tam giác $ACD$ nên $MN//CD$.

Mặt khác $G \in \left( {GMN} \right) \cap \left( {BCD} \right)$. Hai mặt phẳng $\left( {ACD} \right)$ và $\left( {BCD} \right)$ lần lượt chứa $DC$ và $MN$ nên giao tuyến của hai mặt phẳng $\left( {GMN} \right)$ và $\left( {BCD} \right)$ là đường thẳng đi qua $G$ và song song với $CD$.

Câu 33: Xét hình tứ diện $ABCD$.

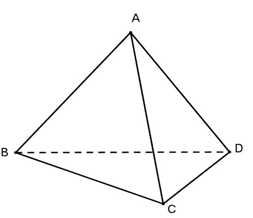
Hai đường thẳng $AC;BD$ có vị trí tương đối là

A. song song.

B. trùng nhau.

C. chéo nhau.

D. cắt nhau.

Lời giải

Vì $ABCD$ là hình tứ diện nên bốn điểm $A,B,C,D$ không đồng phẳng. Suy ra hai đường thẳng $AC;BD$ không đồng phẳng. Do đó hai đường thẳng $AC;BD$ chéo nhau.

Câu 34: Cho tứ diện $ABCD$ có $M,N,P$ lần lượt là trung điểm của các cạnh $AD,BC$ và $BD$ (tham khảo hình vẽ bên).

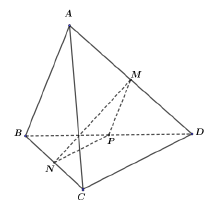
Gọi đường thẳng $d$ là giao tuyến của mặt phẳng $\left( {MNP} \right)$ và mặt phẳng $\left( {ACD} \right)$.

Khẳng định nào sau đây đúng?

A. $d$ song song với $AB$.

B. $d$ song song với $CD$.

C. $d$ song song với $AC$.

D. $d$ song song với $BC$.

Lời giải

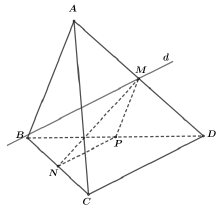
Ta có điểm $M \in AD,AD \subset \left( {ACD} \right) \Rightarrow M \in \left( {ACD} \right)$ và điểm $M \in \left( {MNP} \right)$.

$ \Rightarrow M \in \left( {MNP} \right) \cap \left( {ACD} \right)$.

Mà $NP//CD$ (theo tính chất đường trung bình trong tam giác), $NP \subset \left( {MNP} \right),CD \subset \left( {ACD} \right)$.

Suy ra $\left( {MNP} \right) \cap \left( {ACD} \right) = d$, với $d$ đi qua điểm $M$ và song song với $CD$.

Câu 35: Cho hình chóp tam giác $S.ABC$. Gọi $M,N$ lần lượt là trung điểm của các cạnh $SA,SB$. Gọi điểm $E$ thuộc cạnh $SC$ sao cho $SE = \frac{1}{4}SC$.

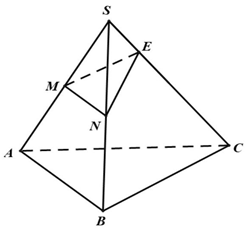
Mệnh đề nào dưới đây là mệnh đề sai?

A. Các đường thẳng $MN,AB$ song song.

B. Các đường thẳng $NE,BC$ chéo nhau.

C. Các đường thẳng $MN,SC$ chéo nhau.

D. Các đường thẳng $ME,AC$ cắt nhau.

Lời giải

Hai đường thẳng $NE,BC$ cùng nằm trong mặt phẳng $\left( {SBC} \right)$ nên mệnh đề $B$ sai.

II. PHẦN TỰ LUẬN (3,0 điểm)

Câu 1: (0,5 điểm) Cho phương trình $2co{s^2}2x + cos2x – 1 = 0$. Tìm các nghiệm của phương trình nằm trong khoảng $x \in \left( { – \pi ;3\pi } \right)$.

Lời giải

Ta có: $2co{s^2}2x + cos2x – 1 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{cos2x = – 1} \\
{cos2x = \frac{1}{2}}
\end{array}} \right.$.

Xét phương trình: $cos2x = \frac{1}{2} \Leftrightarrow 2x = \pm \frac{\pi }{3} + k2\pi \Leftrightarrow x = \pm \frac{\pi }{6} + k\pi \left( {k \in \mathbb{Z}} \right)$.

$ \Leftrightarrow cos2x = – 1 \Leftrightarrow 2x = \pi + l2\pi \Leftrightarrow x = \frac{\pi }{2} + l\pi \left( {l \in \mathbb{Z}} \right)$

Phương trình có nghiệm $x \in \left( { – \pi ;3\pi } \right)$ nên ta có:

Với $x = \frac{\pi }{6} + k\pi : – \pi < \frac{\pi }{6} + k\pi < 3\pi $

$ \Leftrightarrow – 1 < \frac{1}{6} + k < 3 \Leftrightarrow – \frac{7}{6} < k < \frac{{17}}{6}$

Vì $k \in \mathbb{Z}$ nên $k \in \left\{ { – 1;0;1;2} \right\}$ do đó có 4 nghiệm thoả mãn là: $\left\{ { – \frac{{5\pi }}{6};\frac{\pi }{6};\frac{{7\pi }}{6};\frac{{13\pi }}{6}} \right\}$.

Với $x = – \frac{\pi }{6} + k\pi : – \pi < – \frac{\pi }{6} + k\pi < 3\pi $$ \Leftrightarrow – 1 < – \frac{1}{6} + k < 3 \Leftrightarrow – \frac{5}{6} < k < \frac{{19}}{6}$

Vì $k \in \mathbb{Z}$ nên $k \in \left\{ {0;1;2;3} \right\}$ do đó có 4 nghiệm thoả mãn là: $\left\{ { – \frac{\pi }{6};\frac{{5\pi }}{6};\frac{{11\pi }}{6};\frac{{17\pi }}{6}} \right\}$.

Với $x = \frac{\pi }{2} + l\pi : – \pi < \frac{\pi }{2} + l\pi < 3\pi \Leftrightarrow – 1 < \frac{1}{2} + l < 3 \Leftrightarrow – \frac{3}{2} < l < \frac{5}{2}$.

Vì $l \in \mathbb{Z}$ nên $l \in \left\{ { – 1;0;1;2} \right\}$ do đó có 4 nghiệm thoả mãn là: $\left\{ { – \frac{\pi }{2};\frac{\pi }{2};\frac{{3\pi }}{2};\frac{{5\pi }}{2}} \right\}$.

Vậy, phương trình đã cho có 12 nghiệm trong khoảng $\left( { – \pi ;3\pi } \right)$ là :

$\left\{ { – \frac{{5\pi }}{6};\frac{\pi }{6};\frac{{7\pi }}{6};\frac{{13\pi }}{6}; – \frac{\pi }{6};\frac{{5\pi }}{6};\frac{{11\pi }}{6};\frac{{17\pi }}{6}; – \frac{\pi }{2};\frac{\pi }{2};\frac{{3\pi }}{2};\frac{{5\pi }}{2}} \right\}$.

Câu 2: (1,0 điểm) Cho hàm số $f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}
{\frac{{\sqrt {3 – 2x} + x}}{{3 + x}}}&{\;khi\;x < – 3} \\
{2mx + 5}&{\;khi\;x \geqslant – 3}
\end{array}} \right.$. Tìm $m$ để hàm số có giới hạn tại $x = – 3$.

Lời giải

Ta có: $\mathop {\lim }\limits_{x \to {3^ – }} f(x) = \mathop {\lim }\limits_{x \to {3^ – }} \frac{{ – (x – 1)(x + 3)}}{{(3 + x)(\sqrt {3 – 2x} – x)}}$$ = \mathop {\lim }\limits_{x \to – {3^ – }} \frac{{( – x + 1)}}{{(\sqrt {3 – 2x} – x)}} = \frac{2}{3}$

Mặt khác: $\mathop {\lim }\limits_{x \to {3^ + }} f(x) = \mathop {\lim }\limits_{x \to {3^ + }} (2mx + 5) = – 6m + 5$

Để hàm số có giới hạn tại $x = – 3$ khi và chi khi: $\mathop {\lim }\limits_{x \to – {3^ + }} f(x) = \mathop {\lim }\limits_{x \to – {3^ – }} f(x)$

$ \Leftrightarrow – 6m + 5 = \frac{2}{3} \Leftrightarrow m = \frac{{13}}{{18}}$

Vậy khi $m = \frac{{13}}{{18}}$ thì hàm số có giới hạn tại $x = – 3$.

Câu 3: (1,0 điểm) Để tiết kiệm năng lượng, một công ty điện lực đề xuất bán điện sinh hoạt cho dân với theo hình thức lũy tiến (bậc thang) như sau: Mỗi bậc gồm 10 số; bậc 1 từ số thứ 1 đến số thứ 10 , bậc 2 từ số thứ 11 đến số 20 , bậc 3 từ số thứ 21 đến số thứ $30, \ldots $ Bậc 1 có giá là 800 đồng/ 1 số, giá của mỗi số ở bậc thứ $n + 1$ tăng so với giá của mỗi số ở bậc thứ $n$ là $2,5\% $. Gia đình ông A sử dụng hết 347 số trong tháng 1. Hỏi tháng 1 ông A phải đóng bao nhiêu tiền? (đơn vị là đồng, kết quả được làm tròn đến hàng phần trăm).

Lời giải

Gọi ${u_1}$ là số tiền phải trả cho 10 số điện đầu tiên. ${u_1} = 10.800 = 8000$ (đồng)

${u_2}$ là số tiền phải trả cho các số điện từ 11 đến $20:{u_2} = {u_1}\left( {1 + 0,025} \right)$

${u_{34}}$ là số tiền phải trả cho các số điện từ 331 đến $340:{u_{34}} = {u_1}{(1 + 0,025)^{33}}$

Số tiền phải trả cho 340 số điện đầu tiên là: ${S_1} = {u_1} \cdot \frac{{1 – {{(1 + 0,025)}^{34}}}}{{1 – \left( {1 + 0,025} \right)}} = 420903,08$

Số tiền phỉ trả cho các số điện từ 341 đến 347 là: ${S_2} = 7.800{(1 + 0,025)^{34}} = 12965,80$

Vậy tháng 1 gia đình ông A phải trả số tiền là: $S = {S_1} + {S_2} = 433868,89$ (đồng).

Câu 4: (0,5 điểm) Cho tứ diện $ABCD$, $G$ là trọng tâm tam giác $ABD$ và $M$ là điểm trên cạnh $BC$ sao cho $BM = 2MC$. Chứng minh đường thẳng $MG$ song song với mặt phẳng $\left( {ACD} \right)$.

Lời giải

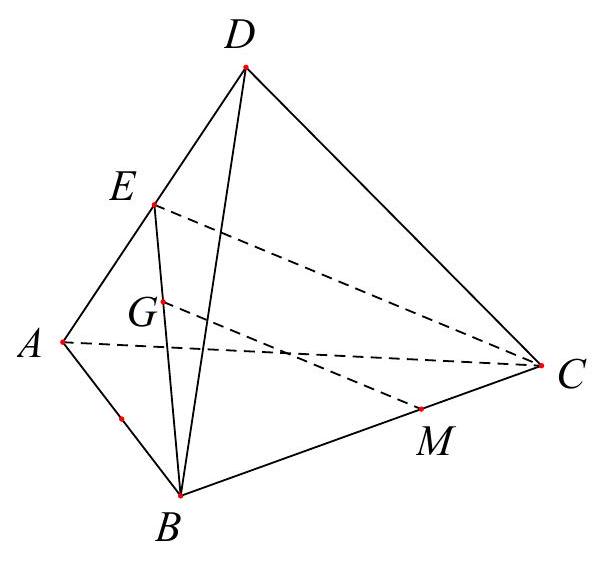
Gọi $E$ là trung điểm $AD$.

Do $G$ là trọng tâm $\vartriangle ABD$ nên: $\frac{{BG}}{{BE}} = \frac{2}{3}$ (1)

Mặt khác do $BM = 2MC \Rightarrow \frac{{BM}}{{BC}} = \frac{2}{3}$ (2)

Từ (1) và (2) $ \Rightarrow GM//EC$, mà $EC \subset \left( {ACD} \right)$ nên $MG//\left( {ACD} \right)$.