- Trắc Nghiệm Bài 15 Giới Hạn Của Dãy Số Mức Thông Hiểu Giải Chi Tiết
- Trắc Nghiệm Bài 16 Giới Hạn Của Hàm Số Mức Thông Hiểu Giải Chi Tiết
- Trắc Nghiệm Bài 17 Hàm Số Liên Tục Mức Thông Hiểu Giải Chi Tiết
- Các Dạng Toán Về Giới Hạn Của Dãy Số Giải Chi Tiết
- 70 Câu Trắc Nghiệm Về Giới Hạn Của Dãy Số Giải Chi Tiết
- Các Dạng Toán Về Giới Hạn Của Hàm Số Có Lời Giải Chi Tiết
- 60 Câu Trắc Nghiệm Về Giới Hạn Của Hàm Số Giải Chi Tiết
- Các Dạng Bài Tập Về Hàm Số Liên Tục Giải Chi Tiết
- 30 Câu Trắc Nghiệm Về Hàm Số Liên Tục Có Lời Giải Chi Tiết
30 câu trắc nghiệm về hàm số liên tục có lời giải chi tiết được soạn dưới dạng file word và PDF gồm 4 trang. Các bạn xem và tải về ở dưới.
Câu 1: Tìm giá trị thực của tham số $m$ để hàm số $f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}
{\frac{{{x^2} – x – 2}}{{x – 2}}}&{khi x \ne 2} \\
m&{khi x = 2}
\end{array}} \right.$ liên tục tại $x = 2.$
A. $m = 0.$ B. $m = 1.$ C. $m = 2.$ D. $m = 3.$
Xem đáp án và lời giải
Chọn D
Tập xác định: $D = \mathbb{R}$, chứa $x = 2$. Theo giả thiết thì ta phải có
$m = f\left( 2 \right) = \mathop {\lim }\limits_{x \to 2} f\left( x \right)$$ = \mathop {\lim }\limits_{x \to 2} \frac{{{x^2} – x – 2}}{{x – 2}} = \mathop {\lim }\limits_{x \to 2} \left( {x + 1} \right) = 3$
Câu 2: Tìm giá trị thực của tham số $m$ để hàm số $f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}
{\frac{{{x^3} – {x^2} + 2x – 2}}{{x – 1}}}&{khi x \ne 1} \\
{3x + m}&{khi x = 1}
\end{array}} \right.$ liên tục tại $x = 1.$
A. $m = 0.$ B. $m = 2.$ C. $m = 4.$ D. $m = 6.$
Xem đáp án và lời giải
Chọn A
. Hàm số xác định với mọi $x \in \mathbb{R}$. Theo giả thiết ta phải có
$3 + m = f\left( 1 \right) = \mathop {\lim }\limits_{x \to 1} f\left( x \right)$
$ = \mathop {\lim }\limits_{x \to 1} \frac{{{x^3} – {x^2} + 2x – 2}}{{x – 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{\left( {x – 1} \right)\left( {{x^2} + 2} \right)}}{{x – 1}}$
$ = \mathop {\lim }\limits_{x \to 1} \left( {{x^2} + 2} \right) = 3 \Leftrightarrow m = 0$
Câu 3: Tìm giá trị thực của tham số $k$ để hàm số $y = f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}
{\frac{{\sqrt x – 1}}{{x – 1}}}&{khi x \ne 1} \\
{k + 1}&{khi x = 1}
\end{array}} \right.$ liên tục tại $x = 1.$
A. $k = \frac{1}{2}.$ B. $k = 2.$ C. $k = – \frac{1}{2}.$ D. $k = 0.$
Xem đáp án và lời giải
Chọn C
Hàm số $f\left( x \right)$ có TXĐ: $D = \left[ {0; + \infty } \right).$ Điều kiện bài toán tương đương với
Ta có: $k + 1 = y\left( 1 \right) = \mathop {\lim }\limits_{x \to 1} {\mkern 1mu} y = \mathop {\lim }\limits_{x \to 1} {\mkern 1mu} \frac{{\sqrt x – 1}}{{x – 1}}$$ = \mathop {\lim }\limits_{x \to 1} {\mkern 1mu} \frac{1}{{\sqrt x + 1}} = \frac{1}{2} \Leftrightarrow k = – \frac{1}{2}.$
Câu 4: Biết rằng hàm số $f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}
{\frac{{3 – x}}{{\sqrt {x + 1} – 2}}}&{khi x \ne 3} \\
m&{khi x = 3}
\end{array}} \right.$ liên tục tại $x = 3$ (với $m$ là tham số). Khẳng định nào dưới đây đúng?
A. $m \in \left( { – 3;0} \right).$ B. $m \leqslant – 3.$ C. $m \in \left[ {0;5} \right).$ D. $m \in \left[ {5; + \infty } \right).$
Xem đáp án và lời giải
Chọn B
Hàm số $f\left( x \right)$ có tập xác định là $\left( { – 1; + \infty } \right).$ Theo giả thiết ta phải có
$m = f\left( 3 \right) = \mathop {\lim }\limits_{x \to 3} {\mkern 1mu} f\left( x \right) = \mathop {\lim }\limits_{x \to 3} {\mkern 1mu} \frac{{3 – x}}{{\sqrt {x + 1} – 2}}$$ = \mathop {\lim }\limits_{x \to 3} {\mkern 1mu} \frac{{\left( {3 – x} \right)\left( {\sqrt {x + 1} + 2} \right)}}{{x – 3}} = – \mathop {\lim }\limits_{x \to 3} {\mkern 1mu} \left( {\sqrt {x + 1} + 2} \right) = – 4$
Câu 5: Hàm số $f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}
3&{khi{\mkern 1mu} {\mkern 1mu} x = – 1} \\
{\frac{{{x^4} + x}}{{{x^2} + x}}}&{khi{\mkern 1mu} {\mkern 1mu} x \ne – 1,{\mkern 1mu} {\mkern 1mu} x \ne 0} \\
1&{khi{\mkern 1mu} {\mkern 1mu} x = 0}
\end{array}} \right.$ liên tục tại:
A. mọi điểm trừ $x = 0,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} x = 1.$ B. mọi điểm $x \in \mathbb{R}.$
C. mọi điểm trừ $x = – 1.$ D. mọi điểm trừ $x = 0.$
Xem đáp án và lời giải
Chọn B
Hàm số $y = f\left( x \right)$ có TXĐ: $D = \mathbb{R}$.
Dễ thấy hàm số $y = f\left( x \right)$ liên tục trên mỗi khoảng $\left( { – \infty ; – 1} \right),\left( { – 1;0} \right)$ và $\left( {0; + \infty } \right)$.
(i) Xét tại $x = – 1$, ta có
$\mathop {\lim }\limits_{x \to – 1} {\mkern 1mu} f\left( x \right) = \mathop {\lim }\limits_{x \to – 1} {\mkern 1mu} \frac{{{x^4} + x}}{{{x^2} + x}}$$ = \mathop {\lim }\limits_{x \to – 1} {\mkern 1mu} \frac{{x\left( {x + 1} \right)\left( {{x^2} – x + 1} \right)}}{{x\left( {x + 1} \right)}} = \mathop {\lim }\limits_{x \to – 1} {\mkern 1mu} \left( {{x^2} – x + 1} \right)$$ = 3 = f\left( { – 1} \right).$
$\xrightarrow[{}]{{}}$ hàm số $y = f\left( x \right)$ liên tục tại $x = – 1$.
(ii) Xét tại $x = 0$, ta có
$\mathop {\lim }\limits_{x \to 0} {\mkern 1mu} f\left( x \right) = \mathop {\lim }\limits_{x \to 0} {\mkern 1mu} \frac{{{x^4} + x}}{{{x^2} + x}}$$ = \mathop {\lim }\limits_{x \to 0} {\mkern 1mu} \frac{{x\left( {x + 1} \right)\left( {{x^2} – x + 1} \right)}}{{x\left( {x + 1} \right)}}$$ = \mathop {\lim }\limits_{x \to 0} {\mkern 1mu} \left( {{x^2} – x + 1} \right) = 1 = f\left( 0 \right).$
$\xrightarrow[{}]{{}}$ hàm số $y = f\left( x \right)$ liên tục tại $x = 0$.
Câu 6: Số điểm gián đoạn của hàm số $f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}
{0,5}&{khi{\mkern 1mu} {\mkern 1mu} x = – 1} \\
{\frac{{x\left( {x + 1} \right)}}{{{x^2} – 1}}}&{khi{\mkern 1mu} {\mkern 1mu} x \ne – 1,{\mkern 1mu} {\mkern 1mu} x \ne 1} \\
1&{khi{\mkern 1mu} {\mkern 1mu} x = 1}
\end{array}} \right.$ là:
A. $0.$ B. $1.$ C. $2.$ D. $3.$
Xem đáp án và lời giải
Chọn B
Hàm số $y = f\left( x \right)$ có TXĐ $D = \mathbb{R}$.
Hàm số $f\left( x \right) = \frac{{x\left( {x + 1} \right)}}{{{x^2} – 1}}$ liên tục trên mỗi khoảng $\left( { – \infty ; – 1} \right)$, $\left( { – 1;1} \right)$ và $\left( {1; + \infty } \right)$.
(i) Xét tại $x = – 1$, ta có $\mathop {\lim }\limits_{x \to – 1} {\mkern 1mu} f\left( x \right) = \mathop {\lim }\limits_{x \to – 1} {\mkern 1mu} \frac{{x\left( {x + 1} \right)}}{{{x^2} – 1}} = \mathop {\lim }\limits_{x \to – 1} {\mkern 1mu} \frac{x}{{x – 1}} = \frac{1}{2} = f\left( { – 1} \right)$$\xrightarrow[{}]{{}}$ Hàm số liên tục tại $x = – 1$.
(ii) Xét tại $x = 1$, ta có $\left\{ \begin{gathered}
\mathop {\lim }\limits_{x \to {1^ + }} {\mkern 1mu} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} {\mkern 1mu} \frac{{x\left( {x + 1} \right)}}{{{x^2} – 1}} = \mathop {\lim }\limits_{x \to {1^ + }} {\mkern 1mu} \frac{x}{{x – 1}} = + \infty \hfill \\
\mathop {\lim }\limits_{x \to {1^ – }} {\mkern 1mu} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ – }} {\mkern 1mu} \frac{{x\left( {x + 1} \right)}}{{{x^2} – 1}} = \mathop {\lim }\limits_{x \to {1^ – }} {\mkern 1mu} \frac{x}{{x – 1}} = – \infty \hfill \\
\end{gathered} \right.$
$\xrightarrow[{}]{{}}$Hàm số $y = f\left( x \right)$ gián đoạn tại $x = 1$.
Câu 7: Có bao nhiêu giá trị thực của tham số $m$ để hàm số $f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}
{{m^2}{x^2}}&{khi x \leqslant 2} \\
{\left( {1 – m} \right)x}&{khi x > 2}
\end{array}} \right.$ liên tục trên $\mathbb{R}$?
A. 2. B. 1. C. 0. D. 3.
Xem đáp án và lời giải
Chọn A
TXĐ: $D = \mathbb{R}$. Hàm số liên tục trên mỗi khoảng $\left( { – \infty ;2} \right)$; $\left( {2; + \infty } \right)$.
Khi đó $f\left( x \right)$ liên tục trên $\mathbb{R} \Leftrightarrow $$f\left( x \right)$ liên tục tại $x = 2$
$ \Leftrightarrow \mathop {\lim }\limits_{x \to 2} {\mkern 1mu} f\left( x \right) = f\left( 2 \right) \Leftrightarrow \mathop {\lim }\limits_{x \to {2^ + }} {\mkern 1mu} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ – }} {\mkern 1mu} f\left( x \right) = f\left( 2 \right){\mkern 1mu} .$ $\left( * \right)$
Ta có $\left\{ \begin{gathered}
f\left( 2 \right) = 4{m^2} \hfill \\
\mathop {\lim }\limits_{x \to {2^ + }} {\mkern 1mu} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} {\mkern 1mu} \left[ {\left( {1 – m} \right)x} \right] = 2\left( {1 – m} \right) \hfill \\
\mathop {\lim }\limits_{x \to {2^ – }} {\mkern 1mu} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ – }} {\mkern 1mu} {m^2}{x^2}{\mkern 1mu} = 4{m^2} \hfill \\
\end{gathered} \right.$
$\xrightarrow[{}]{{}}\left( * \right) \Leftrightarrow 4{m^2} = 2\left( {1 – m} \right) \Leftrightarrow \left[ \begin{gathered}
m = – 1 \hfill \\
m = \frac{1}{2} \hfill \\
\end{gathered} \right..$
Câu 8: Biết rằng hàm số $f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}
{\sqrt x }&{khi x \in \left[ {0;4} \right]} \\
{1 + m}&{khi x \in \left( {4;6} \right]}
\end{array}} \right.$ tục trên $\left[ {0;6} \right].$ Khẳng định nào sau đây đúng?
A. $m < 2.$ B. $2 \leqslant m < 3.$ C. $3 < m < 5.$ D. $m \geqslant 5.$
Xem đáp án và lời giải
Chọn A
Dễ thấy $f\left( x \right)$ liên tục trên mỗi khoảng $\left( {0;4} \right)$ và $\left( {4;6} \right)$. Khi đó hàm số liên tục trên đoạn $\left[ {0;6} \right]$ khi và chỉ khi hàm số liên tục tại $x = 4,{\mkern 1mu} {\mkern 1mu} x = 0,{\mkern 1mu} {\mkern 1mu} x = 6$.
Tức là ta cần có $\left\{ \begin{gathered}
\mathop {\lim }\limits_{x \to {0^ + }} {\mkern 1mu} f\left( x \right) = f\left( 0 \right) \hfill \\
\mathop {\lim }\limits_{x \to {6^ – }} {\mkern 1mu} f\left( x \right) = f\left( 6 \right) \hfill \\
\mathop {\lim }\limits_{x \to {4^ – }} {\mkern 1mu} f\left( x \right) = \mathop {\lim }\limits_{x \to {4^ + }} {\mkern 1mu} f\left( x \right) = f\left( 4 \right) \hfill \\
\end{gathered} \right. \left( * \right)$
$ \bullet \left\{ \begin{gathered}
\mathop {\lim }\limits_{x \to {0^ + }} {\mkern 1mu} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} {\mkern 1mu} \sqrt x = 0 \hfill \\
f\left( 0 \right) = \sqrt 0 = 0 \hfill \\
\end{gathered} \right.;$
$ \bullet \left\{ \begin{gathered}
\mathop {\lim }\limits_{x \to {6^ – }} {\mkern 1mu} f\left( x \right) = \mathop {\lim }\limits_{x \to {6^ – }} {\mkern 1mu} \left( {1 + m} \right) = 1 + m \hfill \\
f\left( 6 \right) = 1 + m \hfill \\
\end{gathered} \right.;$
$ \bullet \left\{ \begin{gathered}
\mathop {\lim }\limits_{x \to {4^ – }} {\mkern 1mu} f\left( x \right) = \mathop {\lim \sqrt x = 2}\limits_{x \to {4^ – }} {\mkern 1mu} \hfill \\
\mathop {\lim }\limits_{x \to {4^ + }} {\mkern 1mu} f\left( x \right) = \mathop {\lim }\limits_{x \to {4^ + }} {\mkern 1mu} \left( {1 + m} \right) = 1 + m \hfill \\
f\left( 4 \right) = 1 + m \hfill \\
\end{gathered} \right.;$Khi đó $\left( * \right)$ trở thành $1 + m = 2 \Leftrightarrow m = 1 < 2.$
Câu 9: Có bao nhiêu giá trị của tham số $a$ để hàm số $f\left( x \right) = \left\{ \begin{gathered}
\frac{{{x^2} – 3x + 2}}{{\left| {x – 1} \right|}}\,\,khi\,\,x \ne 1 \hfill \\
a\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x = 1 \hfill \\
\end{gathered} \right.\,$ liên tục trên $\mathbb{R}.$
A. 1. B. 2. C. 0. D. 3.
Xem đáp án và lời giải
Chọn C
Hàm số $f\left( x \right)$ liên tục trên $\left( { – \infty ;1} \right)$ và $\left( {1; + \infty } \right).$ Khi đó hàm số đã cho liên tục trên $\mathbb{R}$ khi và chỉ khi nó liê tục tại $x = 1,$ tức là ta cần có
$\mathop {\lim }\limits_{x \to 1} f\left( x \right) = f\left( 1 \right) \Leftrightarrow \mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ – }} f\left( x \right) = f\left( 1 \right). \left( * \right)$
Ta có $f\left( x \right) = \,\left\{ {\begin{array}{*{20}{l}}
{x – 2}&{khi x > 1} \\
a&{khi x = 1} \\
{2 – x}&{khi x < 1}
\end{array}} \right.$
$\xrightarrow[{}]{}\left\{ \begin{gathered}
\mathop {\lim }\limits_{x \to {1^ – }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ – }} \left( {2 – x} \right) = 1 \hfill \\
\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \left( {x – 2} \right) = – 1 \hfill \\
\end{gathered} \right.\xrightarrow[{}]{}\left( * \right)$
không tỏa mãn với mọi $a \in \mathbb{R}.$
Vậy không tồn tại giá trị $a$ thỏa yêu cầu.
Câu 10: Biết rằng $f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}
{\frac{{{x^2} – 1}}{{\sqrt x – 1}}}&{khi x \ne 1} \\
a&{khi x = 1}
\end{array}} \right.$ liên tục trên đoạn $\left[ {0;1} \right]$ (với $a$ là tham số). Khẳng định nào dưới đây về giá trị $a$ là đúng?
A. $a$ là một số nguyên. B. $a$ là một số vô tỉ. C. $a > 5.$ D. $a < 0.$
Xem đáp án và lời giải
Chọn A
Hàm số xác định và liên tục trên $\left[ {0;1} \right)$. Khi đó $f\left( x \right)$ liên tục trên $\left[ {0;1} \right]$ khi và chỉ khi $\mathop {\lim }\limits_{x \to {1^ – }} f\left( x \right) = f\left( 1 \right). \left( * \right)$
Ta có $\left\{ \begin{gathered}
f\left( 1 \right) = a \hfill \\
\mathop {\lim }\limits_{x \to {1^ – }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ – }} \frac{{{x^2} – 1}}{{\sqrt x – 1}} = \mathop {\lim }\limits_{x \to {1^ – }} \left[ {\left( {x + 1} \right)\left( {\sqrt x + 1} \right)} \right] = 4 \hfill \\
\end{gathered} \right.$$\xrightarrow[{}]{}\left( * \right) \Leftrightarrow a = 4$
Câu 11: Xét tính liên tục của hàm số $f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}
{\frac{{x – 1}}{{\sqrt {2 – x} – 1}}}&{khi x < 1} \\
{ – 2x}&{khi x \geqslant 1}
\end{array}} \right..$ Khẳng định nào dưới đây đúng?
A. $f\left( x \right)$ không liên tục trên $\mathbb{R}.$ B. $f\left( x \right)$ không liên tục trên $\left( {0;2} \right).$
C. $f\left( x \right)$ gián đoạn tại $x = 1.$ D. $f\left( x \right)$ liên tục trên $\mathbb{R}.$
Xem đáp án và lời giải
Chọn D
Ta có $\left\{ \begin{gathered}
f\left( 1 \right) = – 2 \hfill \\
\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \left( { – 2x} \right) = – 2 \hfill \\
\mathop {\lim }\limits_{x \to {1^ – }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ – }} \frac{{x – 1}}{{\sqrt {2 – x} – 1}} = \mathop {\lim }\limits_{x \to {1^ – }} \left[ { – \left( {\sqrt {2 – x} + 1} \right)} \right] = – 2 \hfill \\
\end{gathered} \right.$ $\xrightarrow[{}]{}f\left( x \right)$liên tục tại $x = 1.$
Vậy hàm số $f\left( x \right)$ liên tục trên $\mathbb{R}.$
Câu 12: Tìm giá trị nhỏ nhất của $a$ để hàm số $f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}
{\frac{{{x^2} – 5x + 6}}{{\sqrt {4x – 3} – x}}}&{khi x > 3} \\
{1 – {a^2}x}&{khi x \leqslant 3}
\end{array}} \right.$ liên tục tại $x = 3$.
A. $ – \frac{2}{{\sqrt 3 }}$. B. $\frac{2}{{\sqrt 3 }}.$ C. $ – \frac{4}{3}.$ D. $\frac{4}{3}.$
Xem đáp án và lời giải
Chọn A
Điều kiện bài toán trở thành: $\mathop {\lim }\limits_{x \to {3^ + }} f(x) = \mathop {\lim }\limits_{x \to {3^ – }} f(x) = f(3)$ $ \bullet $
Ta có
$f\left( 3 \right) = 1 – 3{a^2}$
$\mathop {\lim }\limits_{x \to {3^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {3^ + }} \frac{{{x^2} – 5x + 6}}{{\sqrt {4x – 3} – x}}$$ = \mathop {\lim }\limits_{x \to {3^ + }} \frac{{\left( {x – 2} \right)\left( {\sqrt {4x – 3} + x} \right)}}{{1 – x}} = – 3$
$\mathop {\lim }\limits_{x \to {3^ – }} f\left( x \right) = \mathop {\lim }\limits_{x \to {3^ – }} \left( {1 – {a^2}x} \right) = 1 – 3{a^3}.$
$\xrightarrow[{}]{}\left( * \right) \Leftrightarrow a = \pm \frac{2}{{\sqrt 3 }}\xrightarrow[{}]{}{a_{\min }} = – \frac{2}{{\sqrt 3 }}.$
Câu 13: Tìm giá trị lớn nhất của $a$ để hàm số $f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}
{\frac{{\sqrt[3]{{3x + 2}} – 2}}{{x – 2}}}&{khi x > 2} \\
{{a^2}x + \frac{1}{4}}&{khi x \leqslant 2}
\end{array}} \right.$ liên tục tại $x = 2.$
A. ${a_{\max }} = 3.$ B. ${a_{\max }} = 0.$ C. ${a_{\max }} = 1.$ D. ${a_{\max }} = 2.$
Xem đáp án và lời giải
Chọn C
Ta cần có $\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ – }} f\left( x \right) = f\left( 2 \right). \left( * \right)$
Ta có $\left\{ \begin{gathered}
f\left( 2 \right) = 2{a^2} – \frac{7}{4} \hfill \\
\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} \frac{{\sqrt[3]{{3x + 2}} – 2}}{{x – 2}} = \frac{1}{4} \hfill \\
\mathop {\lim }\limits_{x \to {2^ – }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ – }} \left( {{a^2}x + \frac{1}{4}} \right) = 2{a^2} – \frac{7}{4} \hfill \\
\end{gathered} \right.$
$\xrightarrow[{}]{}\left( * \right) \Leftrightarrow a = \pm 1\xrightarrow[{}]{}{a_{\max }} = 1$
Câu 14: Xét tính liên tục của hàm số $f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}
{1 – \cos x}&{khi x \leqslant 0} \\
{\sqrt {x + 1} }&{khi x > 0}
\end{array}} \right..$ Khẳng định nào sau đây đúng?
A. $f\left( x \right)$ liên tục tại $x = 0.$ B. $f\left( x \right)$ liên tục trên $\left( { – \infty ;1} \right).$
C. $f\left( x \right)$ không liên tục trên $\mathbb{R}.$ D. $f\left( x \right)$ gián đoạn tại $x = 1.$
Xem đáp án và lời giải
Chọn C
Hàm số xác định với mọi $x \in \mathbb{R}$.
Ta có $f\left( x \right)$ liên tục trên $\left( { – \infty ;0} \right)$ và $\left( {0; + \infty } \right).$
Mặt khác $\left\{ \begin{gathered}
f\left( 0 \right) = 1 \hfill \\
\mathop {\lim }\limits_{x \to {0^ – }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ – }} \left( {1 – \cos x} \right) = 1 – \cos 0 = 0 \hfill \\
\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} \sqrt {x + 1} = \sqrt {0 + 1} = 1 \hfill \\
\end{gathered} \right.$ $\xrightarrow[{}]{}f\left( x \right)$gián đoạn tại $x = 0.$
Câu 15: Tìm các khoảng liên tục của hàm số $f\left( x \right) = \left\{ {\begin{array}{*{20}{l}}
{\cos \frac{{\pi x}}{2}}&{khi \left| x \right| \leqslant 1} \\
{x – 1}&{khi \left| x \right| > 1}
\end{array}} \right..$ Mệnh đề nào sau đây là sai?
A. Hàm số liên tục tại $x = – 1$.
B. Hàm số liên tục trên các khoảng $\left( { – \infty , – 1} \right);\,\,\left( {1; + \infty } \right).$
C. Hàm số liên tục tại $x = 1$.
D. Hàm số liên tục trên khoảng $\left( { – 1,1} \right)$.
Xem đáp án và lời giải
Chọn A
Ta có $f\left( x \right)$ liên tục trên $\left( { – \infty ; – 1} \right),\,\,\left( { – 1;1} \right),\,\,\left( {1; + \infty } \right).$
$ \bullet $ Ta có $\left\{ \begin{gathered}
f\left( { – 1} \right) = \cos \left( { – \frac{\pi }{2}} \right) = 0 \hfill \\
\mathop {\lim }\limits_{x \to {{\left( { – 1} \right)}^ – }} f\left( x \right) = \mathop {\lim }\limits_{x \to {{\left( { – 1} \right)}^ – }} \left( {x – 1} \right) = – 2 \hfill \\
\end{gathered} \right.$ $\xrightarrow[{}]{}f\left( x \right)$gián đoạn tại $x = – 1.$
$ \bullet $ Ta có $\left\{ \begin{gathered}
f\left( 1 \right) = \cos \frac{\pi }{2} = 0 \hfill \\
\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \left( {x – 1} \right) = 0 \hfill \\
\mathop {\lim }\limits_{x \to {1^ – }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ – }} \cos \frac{{\pi x}}{2} = 0 \hfill \\
\end{gathered} \right.$ $\xrightarrow[{}]{}f\left( x \right)$liên tục tại $x = 1.$
Câu 16: Hàm số $f\left( x \right)$ có đồ thị như hình bên không liên tục tại điểm có hoành độ là bao nhiêu?
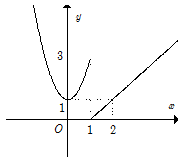
A. $x = 0.$ B. $x = 1.$ C. $x = 2.$ D. $x = 3.$
Xem đáp án và lời giải
Chọn B
Dễ thấy tại điểm có hoành độ $x = 1$ đồ thị của hàm số bị $”$đứt$”$ nên hàm số không liên tục tại đó.
Cụ thể: $\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = 0\not = 3 = \mathop {\lim }\limits_{x \to {1^ – }} f\left( x \right)$ nên $f\left( x \right)$ gián đoạn tại $x = 1.$
Câu 17: Cho hàm số $f\left( x \right) = \left\{ \begin{gathered}
\frac{{{x^2}}}{x} & khi x < 1, x \ne 0 \hfill \\
0 & khi x = 0 \hfill \\
\sqrt x & khi x \geqslant 1 \hfill \\
\end{gathered} \right..$ Hàm số $f\left( x \right)$ liên tục tại:
A. mọi điểm thuộc $\mathbb{R}$. B. mọi điểm trừ $x = 0$.
C. mọi điểm trừ $x = 1$. D. mọi điểm trừ $x = 0$ và $x = 1$.
Xem đáp án và lời giải
Chọn A
Hàm số $y = f\left( x \right)$ có TXĐ: $D = \mathbb{R}$.
Dễ thấy hàm số $y = f\left( x \right)$ liên tục trên mỗi khoảng $\left( { – \infty ;0} \right),\left( {0;1} \right)$ và $\left( {1; + \infty } \right)$.
Ta có $\left\{ \begin{gathered}
f\left( 0 \right) = 0 \hfill \\
\mathop {\lim }\limits_{x \to {0^ – }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ – }} \frac{{{x^2}}}{x} = \mathop {\lim }\limits_{x \to {0^ – }} x = 0 \hfill \\
\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{{x^2}}}{x} = \mathop {\lim }\limits_{x \to {0^ + }} x = 0 \hfill \\
\end{gathered} \right.$ $\xrightarrow[{}]{}f\left( x \right)$ liên tục tại $x = 0.$
Ta có $\left\{ \begin{gathered}
f\left( 1 \right) = 1 \hfill \\
\mathop {\lim }\limits_{x \to {1^ – }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ – }} \frac{{{x^2}}}{x} = \mathop {\lim }\limits_{x \to {1^ – }} x = 1 \hfill \\
\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \sqrt x = 1 \hfill \\
\end{gathered} \right.$$\xrightarrow[{}]{}f\left( x \right)$ liên tục tại $x = 1.$
Vậy hàm số $y = f\left( x \right)$ liên tục trên $\mathbb{R}$.
Câu 18: Cho hàm số $f\left( x \right) = \left\{ \begin{gathered}
\frac{{{x^2} – 1}}{{x – 1}} & khi\,\,x < 3,\,\,x \ne 1 \hfill \\
4 & khi\,\,x = 1 \hfill \\
\sqrt {x + 1} & khi\,\,x \geqslant 3 \hfill \\
\end{gathered} \right.$. Hàm số $f\left( x \right)$ liên tục tại:
A. mọi điểm thuộc $\mathbb{R}$. B. mọi điểm trừ $x = 1$.
C. mọi điểm trừ $x = 3$. D. mọi điểm trừ $x = 1$ và $x = 3$.
Xem đáp án và lời giải
Chọn D
Hàm số $y = f\left( x \right)$ có TXĐ: $D = \mathbb{R}$.
Dễ thấy hàm số $y = f\left( x \right)$ liên tục trên mỗi khoảng $\left( { – \infty ;1} \right),\left( {1;3} \right)$ và $\left( {3; + \infty } \right)$.
Ta có $\left\{ \begin{gathered}
f\left( 1 \right) = 4 \hfill \\
\mathop {\lim }\limits_{x \to 1} f\left( x \right) = \mathop {\lim }\limits_{x \to 1} \frac{{{x^2} – 1}}{{x – 1}} = \mathop {\lim }\limits_{x \to 1} \left( {x + 1} \right) = 2 \hfill \\
\end{gathered} \right.$ $\xrightarrow[{}]{}f\left( x \right)$ gián đoạn tại $x = 1.$
Ta có $\left\{ \begin{gathered}
f\left( 3 \right) = 2 \hfill \\
\mathop {\lim }\limits_{x \to {3^ – }} f\left( x \right) = \mathop {\lim }\limits_{x \to {3^ – }} \frac{{{x^2} – 1}}{{x – 1}} = \mathop {\lim }\limits_{x \to {3^ – }} \left( {x + 1} \right) = 4 \hfill \\
\end{gathered} \right.$ $\xrightarrow[{}]{}f\left( x \right)$gián đoạn tại $x = 3.$
Câu 19: Số điểm gián đoạn của hàm số $h\left( x \right) = \left\{ \begin{gathered}
2x khi x < 0 \hfill \\
{x^2} + 1 khi 0 \leqslant x \leqslant 2 \hfill \\
3x – 1 khi x > 2 \hfill \\
\end{gathered} \right.$ là:
A. 1. B. 2. C. 3. D. 0.
Xem đáp án và lời giải
Chọn A
Hàm số $y = h\left( x \right)$ có TXĐ: $D = \mathbb{R}$.
Dễ thấy hàm số $y = h\left( x \right)$ liên tục trên mỗi khoảng $\left( { – \infty ;0} \right),\left( {0;2} \right)$ và $\left( {2; + \infty } \right)$.
Ta có $\left\{ \begin{gathered}
h\left( 0 \right) = 1 \hfill \\
\mathop {\lim }\limits_{x \to {0^ – }} h\left( x \right) = \mathop {\lim }\limits_{x \to {0^ – }} 2x = 0 \hfill \\
\end{gathered} \right.$ $\xrightarrow[{}]{}f\left( x \right)$không liên tục tại $x = 0$.
Ta có $\left\{ \begin{gathered}
h\left( 2 \right) = 5 \hfill \\
\mathop {\lim }\limits_{x \to {2^ – }} h\left( x \right) = \mathop {\lim }\limits_{x \to {2^ – }} \left( {{x^2} + 1} \right) = 5 \hfill \\
\mathop {\lim }\limits_{x \to {2^ + }} h\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} \left( {3x – 1} \right) = 5 \hfill \\
\end{gathered} \right.$ $\xrightarrow[{}]{}f\left( x \right)$liên tục tại $x = 2$.
Câu 20: Tính tổng $S$ gồm tất cả các giá trị $m$ để hàm số $f\left( x \right) = \left\{ \begin{gathered}
{x^2} + x\,\,\,\,\,khi x < 1 \hfill \\
2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, khi x = 1 \hfill \\
{m^2}x + 1\,\,\,khi x > 1 \hfill \\
\end{gathered} \right.$ liên tục tại $x = 1$.
A. $S = – 1.$ B. $S = 0.$ C. $S = 1.$ D. $S = 2.$
Xem đáp án và lời giải
Chọn B
Hàm số xác định với mọi $x \in \mathbb{R}$.
Điều kiện bài toán trở thành $\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ – }} f\left( x \right) = f\left( 1 \right). \left( * \right)$
Ta có $\left\{ \begin{gathered}
f\left( 1 \right) = 2 \hfill \\
\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \left( {{m^2}x + 1} \right) = {m^2} + 1 \hfill \\
\mathop {\lim }\limits_{x \to {1^ – }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ – }} \left( {{x^2} + x} \right) = 2 \hfill \\
\end{gathered} \right.$
$\xrightarrow[{}]{}\left( * \right) \Leftrightarrow {m^2} + 1 = 2$
$ \Leftrightarrow m = \pm 1\xrightarrow[{}]{}S = 0.$
Câu 21: Cho hàm số $f\left( x \right) = \left\{ \begin{gathered}
– x\cos x khi\,\,x < 0 \hfill \\
\frac{{{x^2}}}{{1 + x}} & khi\,\,0 \leqslant x < 1 \hfill \\
{x^3} & khi\,\,x \geqslant 1 \hfill \\
\end{gathered} \right..$ Hàm số $f\left( x \right)$ liên tục tại:
A. mọi điểm thuộc $x \in \mathbb{R}.$ B. mọi điểm trừ $x = 0.$
C. mọi điểm trừ $x = 1.$ D. mọi điểm trừ $x = 0; x = 1.$
Xem đáp án và lời giải
Chọn C
Hàm số $y = f\left( x \right)$ có TXĐ: $D = \mathbb{R}$.
Dễ thấy $f\left( x \right)$ liên tục trên mỗi khoảng $\left( { – \infty ;0} \right),\left( {0;1} \right)$ và $\left( {1; + \infty } \right)$.
Ta có $\left\{ \begin{gathered}
f\left( 0 \right) = 0 \hfill \\
\mathop {\lim }\limits_{x \to {0^ – }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ – }} \left( { – x\cos x} \right) = 0 \hfill \\
\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{{x^2}}}{{1 + x}} = 0 \hfill \\
\end{gathered} \right.$
$\xrightarrow[{}]{}f\left( x \right)$liên tục tại $x = 0$.
Ta có $\left\{ \begin{array}{l}
f\left( 1 \right) = 1\\
\mathop {\lim }\limits_{x \to {1^ – }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ – }} \frac{{{x^2}}}{{1 + x}} = \frac{1}{2}\\
\mathop {\,\,\lim }\limits_{x \to {1^ + }} f\left( x \right) = \,\mathop {\lim {x^3} = 1}\limits_{x \to {1^ + }}
\end{array} \right.$
$\xrightarrow[{}]{}f\left( x \right)$ không liên tục tại $x = 1$.
Câu 22: Cho hàm số $f\left( x \right) = – 4{x^3} + 4x – 1.$ Mệnh đề nào sau đây là sai?
A. Hàm số đã cho liên tục trên $\mathbb{R}.$
B. Phương trình $f\left( x \right) = 0$ không có nghiệm trên khoảng $\left( { – \infty ;1} \right).$
C. Phương trình $f\left( x \right) = 0$ có nghiệm trên khoảng $\left( { – 2;0} \right).$
D. Phương trình $f\left( x \right) = 0$ có ít nhất hai nghiệm trên khoảng $\left( { – 3;\frac{1}{2}} \right).$
Xem đáp án và lời giải
Chọn B
(i) Hàm $f\left( x \right)$ là hàm đa thức nên liên tục trên $\mathbb{R}\xrightarrow[{}]{}$ A đúng.
(ii) Ta có $\left\{ \begin{gathered}
f\left( { – 1} \right) = – 1 < 0 \hfill \\
f\left( { – 2} \right) = 23 > 0 \hfill \\
\end{gathered} \right.$ $\xrightarrow[{}]{}f\left( x \right) = 0$ có nghiệm ${x_1}$ trên $\left( { – 2;1} \right)$, mà
$\left( { – 2; – 1} \right) \subset \left( { – 2;0} \right) \subset \left( { – \infty ;1} \right)\xrightarrow[{}]{}$ B sai và C đúng
(iii) Ta có $\left\{ \begin{gathered}
f\left( 0 \right) = – 1 < 0 \hfill \\
f\left( {\frac{1}{2}} \right) = \frac{1}{2} > 0 \hfill \\
\end{gathered} \right.$ $\xrightarrow[{}]{}f\left( x \right) = 0$ có nghiệm ${x_2}$ thuộc $\left( {0;\frac{1}{2}} \right).$ Kết hợp với (1) suy ra $f\left( x \right) = 0$ có các nghiệm ${x_1},\,\,{x_2}$ thỏa: $ – 3 < {x_1} < – 1 < 0 < {x_2} < \frac{1}{2}\xrightarrow[{}]{}$ D đúng.
Câu 23: Cho phương trình $2{x^4} – 5{x^2} + x + 1 = 0.$ Mệnh đề nào sau đây là đúng?
A. Phương trình không có nghiệm trong khoảng $\left( { – 1;1} \right).$
B. Phương trình không có nghiệm trong khoảng $\left( { – 2;0} \right).$
C. Phương trình chỉ có một nghiệm trong khoảng $\left( { – 2;1} \right).$
D. Phương trình có ít nhất hai nghiệm trong khoảng $\left( {0;2} \right).$
Xem đáp án và lời giải
Chọn D
Hàm số $f\left( x \right) = 2{x^4} – 5{x^2} + x + 1$ là hàm đa thức có tập xác định là $\mathbb{R}$ nên liên tục trên $\mathbb{R}$.
Ta có
(i) $\left\{ \begin{gathered}
f\left( 0 \right) = 1 \hfill \\
f\left( { – 1} \right) = – 3 \hfill \\
\end{gathered} \right. \Rightarrow f\left( { – 1} \right).f\left( 0 \right) < 0$ $\xrightarrow{{}}f\left( x \right) = 0$có ít nhất một nghiệm ${x_1}$ thuộc $\left( { – 1;0} \right)$.
(ii) $\left\{ \begin{gathered}
f\left( 0 \right) = 1 \hfill \\
f\left( 1 \right) = – 1 \hfill \\
\end{gathered} \right. \Rightarrow f\left( 0 \right).f\left( 1 \right) < 0$ $\xrightarrow{{}}f\left( x \right) = 0$ có ít nhất một nghiệm ${x_2}$ thuộc $\left( {0;1} \right).$
(iii) $\left\{ \begin{gathered}
f\left( 1 \right) = – 1 \hfill \\
f\left( 2 \right) = 15 \hfill \\
\end{gathered} \right. \Rightarrow f\left( 1 \right).f\left( 2 \right) < 0$ $\xrightarrow{{}}f\left( x \right) = 0$có ít nhất một nghiệm ${x_3}$ thuộc $\left( {1;2} \right).$
Vậy phương trình $f\left( x \right) = 0$ đã cho có các nghiệm${x_1},{\mkern 1mu} {\mkern 1mu} {x_2},{\mkern 1mu} {\mkern 1mu} {x_3}$ thỏa
$ – 1 < {x_1} < 0 < {x_2} < 1 < {x_3} < 2$
Câu 24: Cho hàm số $f(x) = {x^3} – 3x – 1$. Số nghiệm của phương trình $f\left( x \right) = 0$ trên $\mathbb{R}$ là:
A. $0.$ B. $1.$ C. $2.$ D. $3.$
Xem đáp án và lời giải
Chọn D
Hàm số $f\left( x \right) = {x^3} – 3x – 1$ là hàm đa thức có tập xác định là $\mathbb{R}$ nên liên tục trên $\mathbb{R}$. Do đó hàm số liên tục trên mỗi khoảng $\left( { – 2; – 1} \right), \left( { – 1;0} \right), \left( {0;2} \right).$
Ta có
$ \bullet $ $\left\{ \begin{gathered}
f\left( { – 2} \right) = – 3 \hfill \\
f\left( { – 1} \right) = 1 \hfill \\
\end{gathered} \right.$ $ \Rightarrow f\left( { – 2} \right)f\left( { – 1} \right) < 0\xrightarrow{{}}\left( 1 \right)$ có ít nhất một nghiệm thuộc $\left( { – 2; – 1} \right).$
$ \bullet $ $\left\{ \begin{gathered}
f\left( { – 1} \right) = 1 \hfill \\
f\left( 0 \right) = – 1 \hfill \\
\end{gathered} \right.$ $ \Rightarrow f\left( { – 1} \right)f\left( 0 \right) < 0\xrightarrow{{}}\left( 1 \right)$có ít nhất một nghiệm thuộc $\left( { – 1;0} \right).$
$ \bullet $ $\left\{ \begin{gathered}
f\left( 2 \right) = 1 \hfill \\
f\left( 0 \right) = – 1 \hfill \\
\end{gathered} \right.$ $ \Rightarrow f\left( 2 \right)f\left( 0 \right) < 0\xrightarrow{{}}\left( 1 \right)$ có ít nhất một nghiệm thuộc $\left( {0;2} \right).$
Như vậy phương trình $\left( 1 \right)$ có ít nhất ba thuộc khoảng $\left( { – 2;2} \right)$. Tuy nhiên phương trình $f\left( x \right) = 0$ là phương trình bậc ba có nhiều nhất ba nghiệm. Vậy phương trình $f\left( x \right) = 0$ có đúng nghiệm trên $\mathbb{R}.$
Câu 25: Cho hàm số $f\left( x \right)$ liên tục trên đoạn $\left[ { – 1;4} \right]$ sao cho $f\left( { – 1} \right) = 2$, $f\left( 4 \right) = 7$. Có thể nói gì về số nghiệm của phương trình $f\left( x \right) = 5$ trên đoạn $[ – 1;4]$:
A. Vô nghiệm. B. Có ít nhất một nghiệm.
C. Có đúng một nghiệm. D. Có đúng hai nghiệm.
Xem đáp án và lời giải
Chọn B
Ta có $f\left( x \right) = 5 \Leftrightarrow f\left( x \right) – 5 = 0$. Đặt $g\left( x \right) = f\left( x \right) – 5.$ Khi đó
$\left\{ \begin{gathered}
g\left( { – 1} \right) = f\left( { – 1} \right) – 5 = 2 – 5 = – 3 \hfill \\
g\left( 4 \right) = f\left( 4 \right) – 5 = 7 – 5 = 2 \hfill \\
\end{gathered} \right.$$ \Rightarrow g\left( { – 1} \right)g\left( 4 \right) < 0$
Vậy phương trình $g\left( x \right) = 0$ có ít nhất một nghiệm thuộc khoảng $\left( {1;4} \right)$ hay phương trình $f\left( x \right) = 5$ có ít nhất một nghiệm thuộc khoảng $\left( {1;4} \right)$.
Câu 26: Có tất cả bao nhiêu giá trị nguyên của tham số $m$ thuộc khoảng $\left( { – 10;10} \right)$ để phương trình ${x^3} – 3{x^2} + \left( {2m – 2} \right)x + m – 3 = 0$ có ba nghiệm phân biệt ${x_1}, {x_2}, {x_3}$ thỏa mãn ${x_1} < – 1 < {x_2} < {x_3}$?
A. $19.$ B. $18.$ C. $4.$ D. $3.$
Xem đáp án và lời giải
Chọn C
Xét hàm số $f\left( x \right) = {x^3} – 3{x^2} + \left( {2m – 2} \right)x + m – 3$ liên tục trên $\mathbb{R}$.
● Giả sử phương trình có ba nghiệm phân biệt ${x_1}, {x_2}, {x_3}$ sao cho ${x_1} < – 1 < {x_2} < {x_3}$. Khi đó $f\left( x \right) = \left( {x – {x_1}} \right)\left( {x – {x_2}} \right)\left( {x – {x_3}} \right)$.
Ta có $f\left( { – 1} \right) = \left( { – 1 – {x_1}} \right)\left( { – 1 – {x_2}} \right)\left( { – 1 – {x_3}} \right) > 0$ (do ${x_1} < – 1 < {x_2} < {x_3}$).
Mà $f\left( { – 1} \right) = – m – 5$ nên suy ra $ – m – 5 > 0 \Leftrightarrow m < – 5.$
● Thử lại: Với $m < – 5$, ta có
▪ $\mathop {\lim }\limits_{x \to – \infty } f\left( x \right) = – \infty $ nên tồn tại $a < – 1$ sao cho $f\left( a \right) < 0$. $\left( 1 \right)$
▪ Do $m < – 5$ nên $f\left( { – 1} \right) = – m – 5 > 0$. $\left( 2 \right)$
▪ $f\left( 0 \right) = m – 3 < 0$. $\left( 3 \right)$
▪ $\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = + \infty $ nên tồn tại $b > 0$ sao cho $f\left( b \right) > 0$. $\left( 4 \right)$
Từ $\left( 1 \right)$ và $\left( 2 \right)$, suy ra phương trình có nghiệm thuộc khoảng $\left( { – \infty ; – 1} \right)$;
Từ $\left( 2 \right)$ và $\left( 3 \right)$, suy ra phương trình có nghiệm thuộc khoảng $\left( { – 1;0} \right)$;
Từ $\left( 3 \right)$ và $\left( 4 \right)$, suy ra phương trình có nghiệm thuộc khoảng $\left( {0; + \infty } \right).$
Vậy khi $m < – 5$ thỏa mãn $\xrightarrow[{m \in \left( { – 10;10} \right)}]{{m \in \mathbb{Z}}}m \in \left\{ { – 9; – 8; – 7; – 6} \right\}.$









