Các Dạng Toán Về Giới Hạn Của Hàm Số Có Lời Giải Chi Tiết

Các dạng toán về giới hạn của hàm số có lời giải chi tiết được soạn dưới dạng file word và PDF gồm 4 trang. Các bạn xem và tải về ở dưới.

Dạng 1: Dãy số có giới hạn hữu hạn
1. Phương pháp

Nếu hàm số $f\left( x \right)$ xác định trên $K \supset {x_0}$ thì $\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right).$

2. Các ví dụ

Ví dụ 1: Tính $\mathop {\lim }\limits_{x \to – 1} \left( {{x^2} – x + 7} \right).$

Lời giải

$\mathop {\lim }\limits_{x \to – 1} \left( {{x^2} – x + 7} \right) = 1 + 1 + 7 = 9.$

Ví dụ 2: Tính $\mathop {\lim }\limits_{x \to 1} \frac{{3{x^4} – 2{x^5}}}{{5{x^4} + 3{x^6} + 1}}$

Lời giải

$\mathop {\lim }\limits_{x \to 1} \frac{{3{x^4} – 2{x^5}}}{{5{x^4} + 3{x^6} + 1}} = \frac{{3 – 2}}{{5 + 3 + 1}} = \frac{1}{9}.$

Ví dụ 3: Tính $\mathop {\lim }\limits_{x \to – 1} \left| {4{x^3} – 2x – 3} \right|$

Lời giải

$\mathop {\lim }\limits_{x \to – 1} \left| {4{x^3} – 2x – 3} \right| = \left| { – 4 + 2 – 3} \right| = 5.$

Ví dụ 4: Tính $\mathop {\lim }\limits_{x \to – 1} \frac{{\sqrt[3]{x} + 1}}{{\sqrt[3]{{{x^2} + 3}} – 2}}$

Lời giải

$\mathop {\lim }\limits_{x \to – 1} \frac{{\sqrt[3]{x} + 1}}{{\sqrt[3]{{{x^2} + 3}} – 2}} = \frac{{ – 1 + 1}}{{\sqrt[3]{4} – 2}} = 0.$

Ví dụ 5: Tính $\mathop {\lim }\limits_{x \to – 2} \sqrt {\frac{{{x^4} – 4{x^2} + 3}}{{7{x^2} + 9x – 1}}} $

Lời giải

$\mathop {\lim }\limits_{x \to – 2} \sqrt {\frac{{{x^4} – 4{x^2} + 3}}{{7{x^2} + 9x – 1}}} = \sqrt {\frac{{16 – 16 + 3}}{{28 – 18 – 1}}} = \sqrt {\frac{1}{3}} .$
Dạng 2. Giới hạn tại vô cực
1. Phương pháp

Một số giới hạn đặc biệt

$\mathop {\lim }\limits_{x \to \pm \infty } \frac{C}{{{x^k}}} = 0$ ($C$ là hằng số, $k$ nguyên dương ).

$\mathop {\lim }\limits_{x \to + \infty } {x^k} = + \infty $ với $k$ nguyên dương;

$\mathop {\lim }\limits_{x \to – \infty } {x^k} = – \infty $ nếu $k$ là số nguyên lẻ;

$\mathop {\lim }\limits_{x \to – \infty } {x^k} = – \infty $ nếu $k$ là số nguyên chẵn.

Nhận xét: $\mathop {\lim }\limits_{x \to + \infty } f(x) = + \infty \Leftrightarrow \mathop {\lim }\limits_{x \to + \infty } \left[ { – f(x)} \right] = – \infty $.

2. Các ví dụ

Ví dụ 1: Tính $\mathop {\lim }\limits_{x \to – \infty } \left( { – 2{x^3} + 5x} \right)$

Lời giải

Cách 1: Sử dụng MTCT tính giá trị của $f(x) = – 2{x^3} + 5x$ tại một điểm có giá trị âm rất nhỏ (do ta đang xét giới hạn của hàm số khi $x \to – \infty $), chẳng hạn tại $ – {10^{20}}$. Máy hiển thị kết quả như hình:

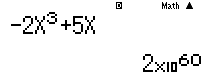Đó là một giá trị dương rất lớn.

Vậy chọn đáp án C , tức $\mathop {\lim }\limits_{x \to – \infty } \left( { – 2{x^3} + 5x} \right) = + \infty $.

Cách 2: Ta có $ – 2{x^3} + 5x = {x^3}\left( { – 2 + \frac{5}{{{x^2}}}} \right)$.

Vì $\mathop {\lim }\limits_{x \to – \infty } {x^3} = – \infty $ và $\mathop {\lim }\limits_{x \to – \infty } \left( { – 2 + \frac{5}{{{x^2}}}} \right) = – 2 < 0$ nên $\mathop {\lim }\limits_{x \to – \infty } {x^3}\left( { – 2 + \frac{5}{{{x^2}}}} \right) = + \infty $.

Vậy theo Quy tắc 1, $\mathop {\lim }\limits_{x \to – \infty } \left( { – 2{x^3} + 5x} \right) = \mathop {\lim }\limits_{x \to – \infty } {x^3}\left( { – 2 + \frac{5}{{{x^2}}}} \right) = + \infty $.

Ví dụ 2: Tính $\mathop {\lim }\limits_{x \to – \infty } \left( {3{x^4} – 2{x^2} + 1} \right)$

Lời giải

Cách 1: Theo nhận xét trên thì $\mathop {\lim }\limits_{x \to – \infty } \left( {3{x^4} – 2{x^2} + 1} \right) = + \infty \quad \left( {x \to – \infty ,k} \right.$ chẵn và ${a_k} > 0$)

Thật vậy, ta có $3{x^4} – 2{x^2} + 1 = {x^4}\left( {3 – \frac{2}{{{x^2}}} + \frac{1}{{{x^4}}}} \right)$.

Vì $\mathop {\lim }\limits_{x \to – \infty } {x^4} = + \infty $ và $\mathop {\lim }\limits_{x \to \infty } \left( {3 – \frac{2}{{{x^2}}} + \frac{1}{{{x^4}}}} \right) = 3 > 0$ nên $\mathop {\lim }\limits_{x \to – \infty } \left( {3{x^4} – 2{x^2} + 1} \right) = + \infty $.

Nhận xét:

– Giới hạn tại vô cực của hàm đa thức là vô cực, chỉ phụ thuộc vào số hạng chứa lũy thừa bậc cao nhất.

– Giới hạn của hàm đa thức tại $ + \infty $ phụ thuộc vào hệ số của lũy thừa bậc cao nhất. (Giống với giới hạn của dãy số dạng đa thức).

– Giới hạn của hàm đa thức tại $ – \infty $ phụ thuộc vào bậc và hệ số của lũy thừa bậc cao nhất.

Cách 2: Sử dụng MTCT tính giá trị hàm số $f(x) = 3{x^4} – 2{x^2} + 1$ tại $x = – {10^{20}}$, ta được kết quả như hình :

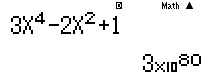Kết quả là một số dương rất lớn. Do đó chọn đáp án A,

Ví dụ 3: Cho hàm số $f(x) = \sqrt {{x^2} – 2x + 5} $ . Tính $\mathop {\lim }\limits_{x \to – \infty } f\left( x \right)$

Lời giải

Hàm số xác định trên.

Có thể giải nhanh như sau : Vì ${x^2} – 2x + 5$ là một hàm đa thức của $x$ nên có giới hạn tại vô cực. Mà $\sqrt {{x^2} – 2x + 5} > 0$ với mọi $x$ nên giới hạn của $f(x) = \sqrt {{x^2} – 2x + 5} $ tại $ – \infty $ chắc chắn là +o .

Thật vậy, ta có $\sqrt {{x^2} – 2x + 5} = \sqrt {{x^2}\left( {1 – \frac{2}{x} + \frac{5}{{{x^2}}}} \right)} = |x|\sqrt {1 – \frac{2}{x} + \frac{5}{{{x^2}}}} $.

Vì $\mathop {\lim }\limits_{x \to – \infty } |x| = + \infty $ và $\mathop {\lim }\limits_{x \to – \infty } \sqrt {1 – \frac{2}{x} + \frac{5}{{{x^2}}}} = 1 > 0$ nên $\mathop {\lim }\limits_{x \to – \infty } \sqrt {{x^2} – 2x + 5} = + \infty $.

Hoặc ta có thể sử dụng MTCT để tính giá trị của $f(x)$ tại một giá trị âm rất nhỏ của $x$, chẳng hạn tại $x = – {10^{20}}$ ta được kết quả như hình:

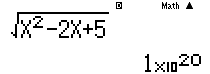Kết quả này là một số dương rất lớn. Do đó ta chọn đáp án B. (Dễ thâý kết quả hiển thị trên máy tính như trên chỉ là kết quả gần đúng do khả năng tính toán hạn chế của MTCT. Tuy nhiên kết quả đó cũng giúp ta lựa chọn được đáp án chính xác).

Lưu ý:

Ta có $\mathop {\lim }\limits_{x \to \pm \infty } |x| = + \infty $.

Khi $x \to – \infty $ thì $x > 0$.

Với $x < 0$ ta có $\sqrt {{x^2}} = – x$.

Cần đặc biệt lưu ý các điều trên khi tính giới hạn tại $ – \infty $ của hàm chứa căn thức.

Ví dụ 4: $\mathop {\lim }\limits_{x \to – \infty } \left( {\sqrt {{x^2} – x} – \sqrt {4{x^2} + 1} } \right)$

Lời giải

Cách 1: Ta có:

$\sqrt {{x^2} – x} – \sqrt {4{x^2} + 1} = \sqrt {{x^2}\left( {1 – \frac{1}{x}} \right)} – \sqrt {{x^2}\left( {4 + \frac{1}{{{x^2}}}} \right)} $

$ = |x|\sqrt {1 – \frac{1}{x}} – |x|\sqrt {4 + \frac{1}{{{x^2}}}} = |x|\left( {\sqrt {1 – \frac{1}{x}} – \sqrt {4 + \frac{1}{{{x^2}}}} } \right)$

Mà $\mathop {\lim }\limits_{x \to – \infty } |x| = + \infty $ và $\mathop {\lim }\limits_{x \to \infty } \left( {\sqrt {1 – \frac{1}{x}} – \sqrt {4 + \frac{1}{{{x^2}}}} } \right) = 1 – 2 = – 1 < 0$.

Vậy $\mathop {\lim }\limits_{x \to – \infty } \left( {\sqrt {{x^2} – x} – \sqrt {4{x^2} + 1} } \right) = \mathop {\lim }\limits_{x \to – \infty } \left[ {|x|\left( {\sqrt {1 – \frac{1}{x}} – \sqrt {4 + \frac{1}{{{x^2}}}} } \right)} \right] = – \infty $.

Lưu ý:

– Độc giả nên đọc lại phần giới hạn dãy số có chứa căn thức để hiểu hơn tại sao lại có định hướng giải như vậy (mà không đi nhân chia với biểu thức liên hợp).

– Có thể thấy như sau: Vì $\mathop {\lim }\limits_{x \to – \infty } \sqrt {{x^2} – x} = + \infty ;\mathop {\lim }\limits_{x \to – \infty } \sqrt {4{x^2} + 1} = + \infty $.

Mà hệ số của ${x^2}$ trong $4{x^2} + 1$ lớn hơn hệ số của ${x^2}$ trong ${x^2} – x$ nên suy ra

$$\mathop {\lim }\limits_{x \to – \infty } \left( {\sqrt {{x^2} – x} – \sqrt {4{x^2} + 1} } \right) = – \infty $

Cách 2: Sử dụng MTCT tính giá trị hàm số tại $x = – {10^{10}}$ta được kết quả như hình.

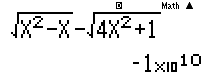Dạng 3. giới hạn một bên
1. Phương pháp

Ta cần nắm các tính chất sau

$\mathop {\lim }\limits_{x \to x_0^ + } f(x) = L \Leftrightarrow \forall \left( {{x_n}} \right),{x_0} < {x_n} < b,\,\mathop {\lim }\limits_{n \to + \infty } {x_n} = {x_0} \Rightarrow \mathop {\lim }\limits_{n \to + \infty } f({x_n}) = L$

$\begin{gathered}
\mathop {\lim }\limits_{x \to x_0^ – } f(x) = L \Leftrightarrow \forall \left( {{x_n}} \right),a < {x_n} < {x_0},\,\mathop {\lim }\limits_{n \to + \infty } {x_n} = {x_0} \Rightarrow \mathop {\lim }\limits_{n \to + \infty } f({x_n}) = L \hfill \\
\mathop {\lim }\limits_{x \to x_0^ – } f(x) = \mathop {\lim }\limits_{x \to x_0^ + } f(x) = L \Rightarrow \mathop {\lim }\limits_{x \to {x_0}} f(x) = L \hfill \\
\end{gathered} $

2. Các ví dụ

Ví dụ 1: Tính$\mathop {\lim }\limits_{x \to {3^ + }} \frac{{\left| {x – 3} \right|}}{{2x – 6}}$

Lời giải

Cách 1: Giải bằng tự luận

$\mathop {\lim }\limits_{x \to {3^ + }} \frac{{\left| {x – 3} \right|}}{{2x – 6}} = \mathop {\lim }\limits_{x \to {3^ + }} \frac{{x – 3}}{{2\left( {x – 3} \right)}} = \frac{1}{2}.$

Cách 2: Giải nhanh bằng máy tính

Nhập vào màn hình $\frac{{\left| {x – 3} \right|}}{{2x – 6}}$ và ấn $\boxed{CALC}\,\,\,\,3 + {10^{ – 5}}\,\boxed = $ ta được kết quả

Ví dụ 2: Tính $\mathop {\lim }\limits_{x \to {1^ – }} \sqrt {\frac{{1 – {x^3}}}{{3{x^2} + x}}} $

Lời giải

$\mathop {\lim }\limits_{x \to {1^ – }} \sqrt {\frac{{1 – {x^3}}}{{3{x^2} + x}}} = \sqrt {\frac{0}{4}} = 0.$

Ví dụ 3: Tính $\mathop {\lim }\limits_{x \to – {2^ – }} \frac{{{x^3} – 2x + 3}}{{{x^2} + 2x}}$

Lời giải

Tử số có giới hạn là $ – 1$, mẫu số có giới hạn 0 và khi $x < – 2$ thì ${x^2} + 2x > 0.$

Do đó $\mathop {\lim }\limits_{x \to – {2^ – }} \frac{{{x^3} – 2x + 3}}{{{x^2} + 2x}} = – \infty .$

Ví dụ 4: Tính $\mathop {\lim }\limits_{x \to {0^ + }} \frac{{2x + \sqrt x }}{{5x – \sqrt x }}$

Lời giải

$\mathop {\lim }\limits_{x \to {0^ + }} \frac{{2x + \sqrt x }}{{5x – \sqrt x }} = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{\sqrt x \left( {2\sqrt x + 1} \right)}}{{\sqrt x \left( {5\sqrt x – 1} \right)}} = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{\left( {2\sqrt x + 1} \right)}}{{\left( {5\sqrt x – 1} \right)}} = \frac{{ – 1}}{1} = – 1.$

Ví dụ 5: Tính $\mathop {\lim }\limits_{x \to {{\left( { – 1} \right)}^ + }} \frac{{{x^2} + 4x + 3}}{{\sqrt {{x^3} + {x^2}} }}$

Lời giải

$\mathop {\lim }\limits_{x \to {{\left( { – 1} \right)}^ + }} \frac{{{x^2} + 4x + 3}}{{\sqrt {{x^3} + {x^2}} }} = \mathop {\lim }\limits_{x \to {{\left( { – 1} \right)}^ + }} \frac{{\left( {x + 1} \right)\left( {x + 3} \right)}}{{\sqrt {{x^2}\left( {x + 1} \right)} }} = \mathop {\lim }\limits_{x \to {{\left( { – 1} \right)}^ + }} \frac{{\sqrt {x + 1} \left( {x + 3} \right)}}{{\sqrt {{x^2}} }} = \frac{0}{1} = 0.$

Ví dụ 6: Cho hàm số $f\left( x \right) = \left\{ \begin{gathered}
\frac{{{x^2} + 1}}{{1 – x}} & khi x < 1 \hfill \\
\sqrt {2x – 2} & khi x \geqslant 1 \hfill \\
\end{gathered} \right..$ Khi đó $\mathop {\lim }\limits_{x \to {1^ – }} f\left( x \right)$ bằng bao nhiêu?

Lời giải

$\mathop {\lim }\limits_{x \to {1^ – }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ – }} \frac{{{x^2} + 1}}{{1 – x}} = + \infty $ vì tử số có giới hạn là 2, mẫu số có giới hạn 0 và $1 – x > 0$ với $x < 1.$
Dạng 4. Dạng vô định $\frac{0}{0}$
1. Phương pháp

• Nhận dạng vô định $\frac{0}{0}$: $\mathop {\lim }\limits_{x \to {x_0}} \frac{{u(x)}}{{v(x)}} khi \mathop {\lim }\limits_{x \to {x_0}} u(x) = \mathop {\lim }\limits_{x \to {x_0}} u(x) = 0.$

• Phân tích tử và mẫu thành các nhân tử và giản ước

$\mathop {\lim }\limits_{x \to {x_o}} \frac{{u(x)}}{{v(x)}} = \mathop {\lim }\limits_{x \to {x_o}} \frac{{(x – {x_0})A(x)}}{{(x – {x_0})B(x)}} = \mathop {\lim }\limits_{x \to {x_o}} \frac{{A(x)}}{{B(x)}}$ và tính $ \mathop {\lim }\limits_{x \to {x_o}} \frac{{A(x)}}{{B(x)}}.$

Nếu phương trình $f\left( x \right) = 0$ có nghiệm là ${x_0}$ thì $f\left( x \right) = \left( {x – {x_0}} \right).g\left( x \right)$

Đặc biệt:

• Nếu tam thức bậc hai $f(x) = a{x^2} + bx + c$ có hai nghiệm phân biệt ${x_1},{x_2}$ thì $f(x)$ được phân tích thành $f(x) = a\left( {x – {x_1}} \right)\left( {x – {x_2}} \right)$
• Cho phương trình bậc $3:a{x^3} + b{x^2} + cx + d = 0\left( {a \ne 0} \right)$
+ Nếu ${\text{a}} + {\text{b}} + {\text{c}} + {\text{d}} = 0$ thì pt có một nghiệm là ${{\text{x}}_1} = 1$, để phân tích thành nhân tử ta dùng phép chia đa thức hoặc dùng sơ đồ Hooc-ner
+ Nếu ${\text{a}} – {\text{b}} + {\text{c}} – {\text{d}} = 0$ thì pt có một nghiệm là ${{\text{x}}_1} = – 1$, để phân tích thành nhân tử ta dùng phép chia đa thức hoặc dùng sơ đồ Hooc-ner

• Nếu $u\left( x \right)$ và $v\left( x \right)$ có chứa dấu căn thì có thể nhân tử và mẫu với biểu thức liên hiệp, sau đó phân tích chúng thành tích để giản ước.

• $A – B\,$ lượng liên hợp là $A + B$
• $\sqrt A – B$ lượng liên hợp là $\sqrt A + B$
• $\sqrt A – \sqrt B \,$ lượng liên hợp là $\sqrt A + \sqrt B \,$
• $\sqrt[3]{A} – B$ lượng liên hợp là $\left( {\sqrt[3]{{{A^2}}} + B\sqrt[3]{A} + {B^2}} \right)$
• $\sqrt[3]{A} + B\,\,$ lượng liên hợp là $\left( {\sqrt[3]{{{A^2}}} – B\sqrt[3]{A} + {B^2}} \right)$

2. Các ví dụ

Ví dụ 1: Tính $\mathop {\lim }\limits_{x \to 1} \frac{{{x^2} – 3x + 2}}{{x – 1}}$

Lời giải

Cách 1: Giải bằng tự luận

$\mathop {\lim }\limits_{x \to 1} \frac{{{x^2} – 3x + 2}}{{x – 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{\left( {x – 1} \right)\left( {x – 2} \right)}}{{x – 1}} = \mathop {\lim }\limits_{x \to } \left( {x – 2} \right) = – 1.$

Cách 2: Giải nhanh bằng máy tính

Nhập vào màn hình $\frac{{{X^2} – 3X + 2}}{{X – 1}}$ ấn $\boxed{CALC}\,\,\,\,1 + {10^{ – 10}}\,\boxed = $ ta được kết quả

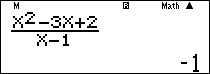
Ví dụ 2: Tính $L = \mathop {\lim }\limits_{x \to 1} \frac{{2{x^2} – 3x + 1}}{{1 – {x^2}}}.$

Lời giải

Cách 1: Giải bằng tự luận

$\mathop {\lim }\limits_{x \to 1} \frac{{2{x^2} – 3x + 1}}{{1 – {x^2}}} = \mathop {\lim }\limits_{x \to 1} \frac{{\left( {2x – 1} \right)\left( {x – 1} \right)}}{{\left( {1 – x} \right)\left( {1 + x} \right)}} = \mathop {\lim }\limits_{x \to 1} \frac{{ – \left( {2x – 1} \right)}}{{\left( {1 + x} \right)}} = \frac{{ – 1}}{2}.$

Cách 2: Giải nhanh bằng máy tính

Nhập vào màn hình $\frac{{2{X^2} – 3X + 1}}{{1 – {X^2}}}$ ấn $\boxed{CALC}\,\,\,\,1 + {10^{ – 10}}\,\boxed = $ ta được kết quả

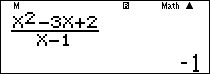
Ví dụ 3: Tính $\mathop {\lim }\limits_{x \to 1} \frac{{{x^2} – 3x + 2}}{{{x^3} – 1}}$

Lời giải

Cách 1: Giải bằng tự luận

$\mathop {\lim }\limits_{x \to 1} \frac{{{x^2} – 3x + 2}}{{{x^3} – 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{\left( {x – 1} \right)\left( {x – 2} \right)}}{{\left( {x – 1} \right)\left( {{x^2} + x + 1} \right)}} = \mathop {\lim }\limits_{x \to 1} \frac{{x – 2}}{{{x^2} + x + 1}} = \frac{{ – 1}}{3}.$

Cách 2: Giải nhanh bằng máy tính

Nhập vào màn hình $\frac{{{x^2} – 3x + 2}}{{{x^3} – 1}}$ ấn $\boxed{CALC}\,\,\,\,1 + {10^{ – 10}}\,\boxed = $ ta được kết quả

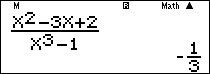
Ví dụ 4: Tính $\mathop {\lim }\limits_{t \to a} \frac{{{t^4} – {a^4}}}{{t – a}}$

Lời giải

$\mathop {\lim }\limits_{t \to a} \frac{{{t^4} – {a^4}}}{{t – a}} = \mathop {\lim }\limits_{t \to a} \left( {{t^3} + {t^2}a + t{a^2} + {a^3}} \right) = 4{a^3}.$

Ví dụ 5: Tính $\mathop {\lim }\limits_{y \to 1} \frac{{{y^4} – 1}}{{{y^3} – 1}}$

Lời giải

Cách 1: Giải bằng tự luận

$\mathop {\lim }\limits_{y \to 1} \frac{{{y^4} – 1}}{{{y^3} – 1}} = \mathop {\lim }\limits_{y \to 1} \frac{{\left( {y – 1} \right)\left( {{y^3} + {y^2} + y + 1} \right)}}{{\left( {y – 1} \right)\left( {{y^2} + y + 1} \right)}} = \mathop {\lim }\limits_{y \to 1} \frac{{{y^3} + {y^2} + y + 1}}{{{y^2} + y + 1}} = \frac{4}{3}.$

Cách 2: Giải nhanh bằng máy tính

Nhập vào màn hình $\frac{{{Y^4} – 1}}{{{Y^3} – 1}}$ ấn $\boxed{CALC}\,\,\,\,1 + {10^{ – 10}}\,\boxed = $ ta được kết quả

Ví dụ 6: Tính $\mathop {\lim }\limits_{x \to 2} \frac{{4 – {x^2}}}{{\sqrt {x + 7} – 3}}$

Lời giải

Cách 1: Giải bằng tự luận

$\mathop {\lim }\limits_{x \to 2} \frac{{4 – {x^2}}}{{\sqrt {x + 7} – 3}}$

$\begin{gathered}
& = \mathop {\lim }\limits_{x \to 2} \frac{{ – \left( {{x^2} – 4} \right)\left( {\sqrt {x + 7} + 3} \right)}}{{\left( {\sqrt {x + 7} – 3} \right)\left( {\sqrt {x + 7} + 3} \right)}} = \mathop {\lim }\limits_{x \to 2} \frac{{ – \left( {x – 2} \right)\left( {x + 2} \right)\left( {\sqrt {x + 7} + 3} \right)}}{{x + 7 – 9}} \hfill \\
& = \mathop {\lim }\limits_{x \to 2} \left[ {\left( {x + 2} \right)\left( {\sqrt {x + 7} + 3} \right)} \right] = – 24. \hfill \\
\end{gathered} $

Cách 2: Giải nhanh bằng máy tính

Nhập vào màn hình $\frac{{4 – {X^2}}}{{\sqrt {X + 7} – 3}}$ ấn $\boxed{CALC}\,\,\,\,1 + {10^{ – 5}}\,\boxed = $ ta được kết quả $ \approx – 24.$

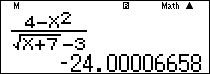
Lưu ý: Để ra kết quả chính xác $ – 24$ ta có thể tính theo quy tắc Lô-pi-tan như sau:

Nhập $\frac{{{{\left. {\frac{d}{{dx}}\left( {4 – {X^2}} \right)} \right|}_{x = 2}}}}{{{{\left. {\frac{d}{{dx}}\left( {\sqrt {X + 7} – 3} \right)} \right|}_{x = 2}}}}$ rồi ấn phím $\boxed = $ ta được kết quả chính xác $ – 24.$

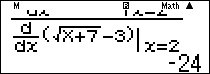
Ví dụ 7: Tính $\mathop {\lim }\limits_{x \to 0} \frac{{\sqrt {1 + x} – 1}}{x}$

Lời giải

Cách 1: Giải bằng tự luận

$\mathop {\lim }\limits_{x \to 0} \frac{{\sqrt {1 + x} – 1}}{x} = \mathop {\lim }\limits_{x \to 0} \frac{{1 + x – 1}}{{x\left( {\sqrt {1 + x} + 1} \right)}} = \mathop {\lim }\limits_{x \to 0} \frac{1}{{\sqrt {1 + x} + 1}} = \frac{1}{2}.$

Cách 2: Giải nhanh bằng máy tính

Nhập vào màn hình $\frac{{\sqrt {1 + x} – 1}}{x}$ ấn $\boxed{CALC}\,\,\,\,0 + {10^{ – 5}}\,\boxed = $ ta được kết quả $ \approx \frac{1}{2}.$

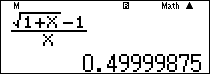
Lưu ý: Để ra kết quả chính xác $\frac{1}{2}$ ta có thể tính theo quy tắc Lô-pi-tan như sau:

Nhập $\frac{{{{\left. {\frac{d}{{dx}}\left( {\sqrt {1 + X} – 1} \right)} \right|}_{x = 0}}}}{{{{\left. {\frac{d}{{dx}}\left( X \right)} \right|}_{x = 0}}}}$ rồi ấn phím $\boxed = $ ta được kết quả chính xác $0,5 = \frac{1}{2}.$

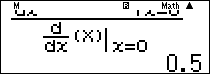
Ví dụ 8: Tính $\mathop {\lim }\limits_{x \to 4} \frac{{{x^2} – 6x + 8}}{{\sqrt x – 2}}$

Lời giải

Cách 1: Giải bằng tự luận

$\mathop {\lim }\limits_{x \to 4} \frac{{{x^2} – 6x + 8}}{{\sqrt x – 2}} = \mathop {\lim }\limits_{x \to 4} \frac{{\left( {x – 2} \right)\left( {x – 4} \right)\left( {\sqrt x + 2} \right)}}{{x – 4}} = \mathop {\lim }\limits_{x \to 4} \left( {x – 2} \right)\left( {\sqrt x + 2} \right) = 2 \times 4 = 8.$

Cách 2: Giải nhanh bằng máy tính

Nhập vào màn hình $\frac{{{x^2} – 6x + 8}}{{\sqrt x – 2}}$ ấn $\boxed{CALC}\,\,\,\,4 + {10^{ – 5}}\,\boxed = $ ta được kết quả $ \approx 8.$

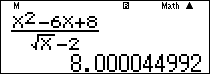
Lưu ý: Để ra kết quả chính xác $8$ ta có thể tính theo quy tắc Lô-pi-tan như sau:

Nhập $\frac{{{{\left. {\frac{d}{{dx}}\left( {{X^2} – 6X + 8} \right)} \right|}_{x = 4}}}}{{{{\left. {\frac{d}{{dx}}\left( {\sqrt X – 2} \right)} \right|}_{x = 4}}}}$ rồi ấn phím $\boxed = $ ta được kết quả chính xác $8.$

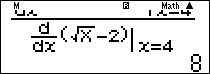
Ví dụ 9: Tính $\mathop {\lim }\limits_{x \to 2} \frac{{\sqrt[3]{{{x^2} + 4}} – 2}}{{4 – \sqrt {2{x^2} + 8} }}$

Lời giải

Cách 1: Giải bằng tự luận

$E = \mathop {\lim }\limits_{x \to 2} \frac{{\sqrt[3]{{{x^2} + 4}} – 2}}{{4 – \sqrt {2{x^2} + 8} }}$

Nhân tử và mẫu hai lượng liên hợp:

$\left[ {{{\left( {\sqrt[3]{{{x^2} + 4}}} \right)}^2} + 2\sqrt[3]{{{x^2} + 4}} + 4} \right]\left[ {4 + \sqrt {2{x^2} + 8} } \right]$

$E = \mathop {\lim }\limits_{x \to 2} \frac{{\left( {\sqrt[3]{{{x^2} + 4}} – 2} \right)\left[ {{{\left( {\sqrt[3]{{{x^2} + 4}}} \right)}^2} + 2\sqrt[3]{{{x^2} + 4}} + 4} \right]\left( {4 + \sqrt {2{x^2} + 8} } \right)}}{{\left( {4 – \sqrt {2{x^2} + 8} } \right)\left( {4 + \sqrt {2{x^2} + 8} } \right)\left[ {{{\left( {\sqrt[3]{{{x^2} + 4}}} \right)}^2} + 2\sqrt[3]{{{x^2} + 4}} + 4} \right]}}$

$\begin{gathered}
& = \mathop {\lim }\limits_{x \to 2} \frac{{\left( {{x^2} + 4 – 8} \right)\left( {4 + \sqrt {2{x^2} + 8} } \right)}}{{\left( {16 – 2{x^2} – 8} \right)\left[ {{{\left( {\sqrt[3]{{{x^2} + 4}}} \right)}^2} + 2\sqrt[3]{{{x^2} + 4}} + 4} \right]}} \hfill \\
& = \mathop {\lim }\limits_{x \to 2} \frac{{\left( {{x^2} – 4} \right)\left( {4 + \sqrt {2{x^2} + 8} } \right)}}{{\left[ { – 2\left( {{x^2} – 4} \right)} \right]\left[ {{{\left( {\sqrt[3]{{{x^2} + 4}}} \right)}^2} + 2\sqrt[3]{{{x^2} + 4}} + 4} \right]}} \hfill \\
& = \mathop {\lim }\limits_{x \to 2} \frac{{4 + \sqrt {2{x^2} + 8} }}{{ – 2\left[ {{{\left( {\sqrt[3]{{{x^2} + 4}}} \right)}^2} + 2\sqrt[3]{{{x^2} + 4}} + 4} \right]}} = \frac{8}{{ – 24}} = – \frac{1}{3}. \hfill \\
\end{gathered} $

Cách 2: Giải nhanh bằng máy tính

Nhập vào màn hình $\frac{{\sqrt[3]{{{x^2} + 4}} – 2}}{{4 – \sqrt {2{x^2} + 8} }}$ ấn $\boxed{CALC}\,\,\,\,4 + {10^{ – 5}}\,\boxed = $ ta được kết quả $ \approx – \frac{1}{3}.$

Lời bình: Nếu ta dùng quy tắc Lô-pi-tan

Nhập $\frac{{{{\left. {\frac{d}{{dx}}\left( {\sqrt[3]{{{x^2} + 4}} – 2} \right)} \right|}_{x = 2}}}}{{{{\left. {\frac{d}{{dx}}\left( {4 – \sqrt {2{x^2} + 8} } \right)} \right|}_{x = 2}}}}$ rồi ấn phím $\boxed = $ ta được kết quả $ – 0,\left( 3 \right) = – \frac{1}{3}.$

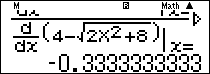
Ví dụ 10: Tính $\mathop {\lim }\limits_{x \to – 2} \frac{{\sqrt[4]{{{x^2} + 12}} – 2}}{{{x^2} – 4}}$

Lời giải

Cách 1: Giải bằng tự luận

$E = \mathop {\lim }\limits_{x \to – 2} \frac{{\sqrt[4]{{{x^2} + 12}} – 2}}{{{x^2} – 4}}$

$ = \mathop {\lim }\limits_{x \to – 2} \frac{{\left( {\sqrt[4]{{{x^2} + 12}} – 2} \right)\left( {\sqrt[4]{{{x^2} + 12}} + 2} \right)}}{{\left( {{x^2} – 4} \right)\left( {\sqrt[4]{{{x^2} + 12}} + 2} \right)}}$

$ = \mathop {\lim }\limits_{x \to – 2} \frac{{\sqrt {{x^2} + 12} – 4}}{{\left( {{x^2} – 4} \right)\left( {\sqrt[4]{{{x^2} + 12}} + 2} \right)}}$ (vẫn còn dạng vô định $\frac{0}{0}$)

$\begin{gathered}
& = \mathop {\lim }\limits_{x \to – 2} \frac{{\left( {\sqrt {{x^2} + 12} – 4} \right)\left( {\sqrt {{x^2} + 12} + 4} \right)}}{{\left( {{x^2} – 4} \right)\left( {\sqrt[4]{{{x^2} + 12}} + 2} \right)\left( {\sqrt {{x^2} + 12} + 4} \right)}} \hfill \\
& = \mathop {\lim }\limits_{x \to – 2} \frac{{{x^2} + 12 – 16}}{{\left( {{x^2} – 4} \right)\left( {\sqrt[4]{{{x^2} + 12}} + 2} \right)\left( {\sqrt {{x^2} + 12} + 4} \right)}} \hfill \\
& = \mathop {\lim }\limits_{x \to – 2} \frac{1}{{\left( {\sqrt[4]{{{x^2} + 12}} + 2} \right)\left( {\sqrt {{x^2} + 12} + 4} \right)}} = \frac{1}{{32}}. \hfill \\
\end{gathered} $

Cách 2: Giải nhanh bằng máy tính

Ta dùng quy tắc Lô-pi-tan

Nhập $\frac{{{{\left. {\frac{d}{{dx}}\left( {\sqrt[4]{{{x^2} + 12}} – 2} \right)} \right|}_{x = – 2}}}}{{{{\left. {\frac{d}{{dx}}\left( {{x^2} – 4} \right)} \right|}_{x = – 2}}}}$ rồi ấn phím $\boxed = $ ta được kết quả $0,03125 = \frac{1}{{32}}.$

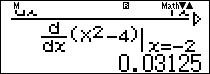
Ví dụ 11: Tính $\mathop {\lim }\limits_{x \to 1} \frac{{\sqrt[6]{x} – 1}}{{{x^2} – 1}}$

Lời giải

Cách 1: Giải bằng tự luận

$E = \mathop {\lim }\limits_{x \to 1} \frac{{\sqrt[6]{x} – 1}}{{{x^2} – 1}}$

$ = \mathop {\lim }\limits_{x \to 1} \frac{{\left( {\sqrt[6]{x} – 1} \right)\left( {\sqrt[6]{{{x^2}}} + \sqrt[6]{x} + 1} \right)}}{{\left( {{x^2} – 1} \right)\left( {\sqrt[6]{{{x^2}}} + \sqrt[6]{x} + 1} \right)}}$

$ = \mathop {\lim }\limits_{x \to 1} \frac{{\sqrt x – 1}}{{\left( {{x^2} – 1} \right)\left( {\sqrt[6]{{{x^2}}} + \sqrt[6]{x} + 1} \right)}}$ (Vẫn dạng vô định $\frac{0}{0}$)

$\begin{gathered}
& = \mathop {\lim }\limits_{x \to 1} \frac{{\left( {\sqrt x – 1} \right)\left( {\sqrt x + 1} \right)}}{{\left( {x – 1} \right)\left( {x + 1} \right)\left( {\sqrt[6]{{{x^2}}} + \sqrt[6]{x} + 1} \right)\left( {\sqrt x + 1} \right)}} \hfill \\
& = \mathop {\lim }\limits_{x \to 1} \frac{1}{{\left( {x + 1} \right)\left( {\sqrt[6]{{{x^2}}} + \sqrt[6]{x} + 1} \right)\left( {\sqrt x + 1} \right)}} = \frac{1}{{12}}. \hfill \\
\end{gathered} $

Cách 2: Giải nhanh bằng máy tính

Ta dùng quy tắc Lô-pi-tan

Nhập $\frac{{{{\left. {\frac{d}{{dx}}\left( {\sqrt[6]{X} – 1} \right)} \right|}_{x = 1}}}}{{{{\left. {\frac{d}{{dx}}\left( {{x^2} – 1} \right)} \right|}_{x = 1}}}}$ rồi ấn phím $\boxed = $ ta được kết quả $0,08\left( 3 \right) = \frac{1}{{12}}.$

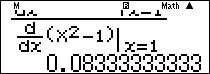
Để chuyển $0,08\left( 3 \right) = \frac{1}{{12}}$ ta bấm như sau 0.08Qs3=

Dạng 5. Dạng vô định $\frac{\infty }{\infty }$
1. Phương pháp

• Nhận biết dạng vô định $\frac{\infty }{\infty }$

$\begin{gathered}
\mathop {\lim }\limits_{x \to {x_0}} \frac{{u(x)}}{{v(x)}} khi \mathop {\lim }\limits_{x \to {x_0}} u(x) = \pm \infty ,\,\mathop {\lim }\limits_{x \to {x_0}} v(x) = \pm \infty . \hfill \\
\mathop {\lim }\limits_{x \to \pm \infty } \frac{{u(x)}}{{v(x)}} khi \mathop {\lim }\limits_{x \to {x_0}} u(x) = \pm \infty ,\,\mathop {\lim }\limits_{x \to {x_0}} v(x) = \pm \infty . \hfill \\
\end{gathered} $

• Chia tử và mẫu cho ${x^n}$ với n là số mũ cao nhất của biến ở mẫu ( Hoặc phân tích thành tích chứa nhân tử ${x^n}$ rồi giản ước)

• Nếu u(x) hoặc v(x) có chứa biến x trong dấu căn thì đưa x^k ra ngoài dấu căn (Với k là mũ cao nhất của biến x trong dấu căn), sau đó chia tử và mẫu cho luỹ thừa cao nhất của x (thường là bậc cao nhất ở mẫu).

• Cách tính giới hạn dạng này hoàn toàn tương tự giới hạn dãy số.

2. Các ví dụ

Ví dụ 1: Tính $\mathop {\lim }\limits_{x \to + \infty } \frac{{2{x^4} + {x^3} – 2{x^2} – 3}}{{x – 2{x^4}}}$

Lời giải

Cách 1: Giải bằng tự luận

$\mathop {\lim }\limits_{x \to + \infty } \frac{{2{x^4} + {x^3} – 2{x^2} – 3}}{{x – 2{x^4}}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{2 + \frac{1}{x} – \frac{2}{{{x^2}}} – \frac{3}{{{x^4}}}}}{{\frac{1}{{{x^3}}} – 2}} = – 1.$

Cách 2: Mẹo giải nhanh

$\frac{{2{x^4} + {x^3} – 2{x^2} – 3}}{{x – 2{x^4}}} \sim \frac{{2{x^4}}}{{ – 2{x^4}}} = – 1.$

Cách 3: Giải nhanh bằng máy tính

Nhập vào màn hình $\frac{{2{x^4} + {x^3} – 2{x^2} – 3}}{{x – 2{x^4}}}$ ấn $\boxed{CALC}\,\,\,\,{10^{15}}\,\boxed = $ ta được kết quả $ – 1.$

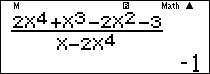
Lời bình: “Bậc tử bằng bậc mẫu” nên kết quả $\frac{2}{{ – 2}} = – 1.$

Ví dụ 2: Tính $\mathop {\lim }\limits_{x \to + \infty } \frac{{3{x^4} – 2{x^5}}}{{5{x^4} + 3x + 2}}$

Lời giải

Cách 1: Giải bằng tự luận

$\begin{gathered}
\mathop {\lim }\limits_{x \to + \infty } \frac{{3{x^4} – 2{x^5}}}{{5{x^4} + 3x + 2}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{3 – 2x}}{{5 + \frac{3}{{{x^3}}} + \frac{2}{{{x^4}}}}} \hfill \\
\mathop {\lim }\limits_{x \to + \infty } \left( {5 + \frac{3}{{{x^3}}} + \frac{2}{{{x^4}}}} \right) = 5 > 0;\,\,\mathop {\lim }\limits_{x \to + \infty } \left( {3 – 2x} \right) = – \infty . \hfill \\
\end{gathered} $

Do đó: $\mathop {\lim }\limits_{x \to + \infty } \frac{{3{x^4} – 2{x^5}}}{{5{x^4} + 3x + 2}} = – \infty .$

Cách 2: Mẹo giải nhanh

$\frac{{3{x^4} – 2{x^5}}}{{5{x^4} + 3x + 2}} \sim \frac{{ – 2{x^5}}}{{5{x^4}}} = – \frac{2}{5}x = – \infty .$

Cách 3: Giải nhanh bằng máy tính

Nhập vào màn hình $\frac{{3{x^4} – 2{x^5}}}{{5{x^4} + 3x + 2}}$ ấn $\boxed{CALC}\,\,\,\,{10^{15}}\,\boxed = $ ta được kết quả $ \approx – \infty .$

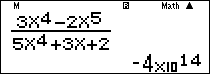
Lời bình: Bậc tử lớn hơn bậc mẫu nên kết quả là $\infty .$

Ví dụ 3: Tính $\mathop {\lim }\limits_{x \to + \infty } \frac{{3{x^4} – 2{x^5}}}{{5{x^4} + 3{x^6} + 2}}$

Lời giải

Cách 1: Giải bằng tự luận

$\mathop {\lim }\limits_{x \to + \infty } \frac{{3{x^4} – 2{x^5}}}{{5{x^4} + 3{x^6} + 2}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\frac{3}{{{x^2}}} – \frac{2}{x}}}{{\frac{5}{{{x^2}}} + 3 + \frac{2}{{{x^6}}}}} = \frac{0}{3} = 0.$

Cách 2: Mẹo giải nhanh

$\frac{{3{x^4} – 2{x^5}}}{{5{x^4} + 3{x^6} + 2}} \sim \frac{{ – 2{x^5}}}{{3{x^6}}} = – \frac{2}{3}.\frac{1}{x} = 0.$

Cách 3: Giải nhanh bằng máy tính

Nhập vào màn hình $\frac{{3{x^4} – 2{x^5}}}{{5{x^4} + 3{x^6} + 2}}$ ấn $\boxed{CALC}\,\,\,\,{10^{15}}\,\boxed = $ ta được kết quả $ \approx 0.$

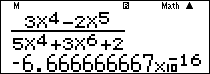
Lời bình: “Bậc tử bé hơn bậc mẫu” nên kết quả là $0.$

Ví dụ 4: Tính $\mathop {\lim }\limits_{x \to + \infty } \sqrt {\frac{{3{x^4} + 4{x^5} + 2}}{{9{x^5} + 5{x^4} + 4}}} $

Lời giải

Cách 1: Giải bằng tự luận

$\mathop {\lim }\limits_{x \to + \infty } \sqrt {\frac{{3{x^4} + 4{x^5} + 2}}{{9{x^5} + 5{x^4} + 4}}} = \mathop {\lim }\limits_{x \to + \infty } \sqrt {\frac{{\frac{3}{x} + 4 + \frac{2}{{{x^5}}}}}{{9 + \frac{5}{x} + \frac{4}{{{x^5}}}}}} = \frac{2}{3}.$

Cách 2: Mẹo giải nhanh

$\sqrt {\frac{{3{x^4} + 4{x^5} + 2}}{{9{x^5} + 5{x^4} + 4}}} \sim \sqrt {\frac{{4{x^5}}}{{9{x^5}}}} = \sqrt {\frac{4}{9}} = \frac{2}{3}.$

Cách 3: Giải nhanh bằng máy tính

Nhập vào màn hình $\sqrt {\frac{{3{x^4} + 4{x^5} + 2}}{{9{x^5} + 5{x^4} + 4}}} $ ấn $\boxed{CALC}\,\,\,\,{10^{15}}\,\boxed = $ ta được kết quả $ \approx 0.$

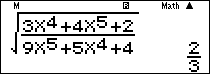
Ví dụ 5: Tính $L = \mathop {\lim }\limits_{x \to – \infty } \frac{{\sqrt {{x^2} + 2x} + 3x}}{{\sqrt {4{x^2} + 1} – x + 2}}.$

Lời giải

Cách 1: Giải bằng tự luận

$\mathop {\lim }\limits_{x \to – \infty } \frac{{\sqrt {{x^2} + 2x} + 3x}}{{\sqrt {4{x^2} + 1} – x + 2}} = \mathop {\lim }\limits_{x \to – \infty } \frac{{\left| x \right|\sqrt {1 + \frac{2}{x}} + 3x}}{{\left| x \right|\sqrt {4 + \frac{1}{{{x^2}}}} – x + 2}} = \mathop {\lim }\limits_{x \to – \infty } \frac{{ – \sqrt {1 + \frac{2}{x}} + 3}}{{ – \sqrt {4 + \frac{1}{{{x^2}}}} – 1 + \frac{2}{x}}} = \frac{2}{{ – 3}}.$

Cách 2: Giải nhanh bằng máy tính

Nhập vào màn hình $\frac{{\sqrt {{x^2} + 2x} + 3x}}{{\sqrt {4{x^2} + 1} – x + 2}}$ ấn $\boxed{CALC}\,\,\,\, – {10^{15}}\,\boxed = $ ta được kết quả $\frac{2}{3}.$

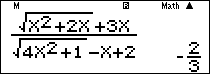
Ví dụ 6: Tính $\mathop {\lim }\limits_{x \to + \infty } \frac{{\sqrt {4{x^2} + 1} – \sqrt {x + 5} }}{{2x – 7}}$

Lời giải

Cách 1: Giải bằng tự luận

$\mathop {\lim }\limits_{x \to + \infty } \frac{{\sqrt {4{x^2} + 1} – \sqrt {x + 5} }}{{2x – 7}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\sqrt {4 + \frac{1}{{{x^2}}}} – \sqrt {\frac{1}{x} + \frac{5}{{{x^2}}}} }}{{2 – \frac{7}{x}}} = \frac{{2 – 0}}{{2 – 0}} = 1.$

Cách 2: Giải nhanh bằng máy tính

Nhập vào màn hình $\frac{{\sqrt {4{x^2} + 1} – \sqrt {x + 5} }}{{2x – 7}}$ ấn $\boxed{CALC}\,\,\,\,{10^{25}}\,\boxed = $ ta được kết quả

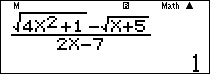
Ví dụ 7: Tính $\mathop {\lim }\limits_{x \to + \infty } \left( {x + 5} \right)\sqrt {\frac{x}{{{x^3} – 1}}} $

Lời giải

Cách 1: Giải bằng tự luận

$\mathop {\lim }\limits_{x \to + \infty } \left( {x + 5} \right)\sqrt {\frac{x}{{{x^3} – 1}}} = \mathop {\lim }\limits_{x \to + \infty } \sqrt {\frac{{x{{\left( {x + 5} \right)}^2}}}{{{x^3} – 1}}} = \mathop {\lim }\limits_{x \to + \infty } \sqrt {\frac{{{{\left( {1 + \frac{5}{x}} \right)}^2}}}{{1 – \frac{1}{{{x^3}}}}}} = 1.$

Cách 2: Giải nhanh bằng máy tính

Nhập vào màn hình $\left( {x + 5} \right)\sqrt {\frac{x}{{{x^3} – 1}}} $ ấn $\boxed{CALC}\,\,\,\,{10^{25}}\,\boxed = $ ta được kết quả

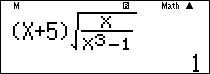
Ví dụ 8: Tính $\mathop {\lim }\limits_{x \to – \infty } \frac{{{{\left( { – {x^2} + 1} \right)}^3}{{\left( {1 – 2x} \right)}^{94}}}}{{2{x^{100}} + 3}}$

Lời giải

$E = \mathop {\lim }\limits_{x \to – \infty } \frac{{{{\left( { – {x^2} + 1} \right)}^3}{{\left( {1 – 2x} \right)}^{94}}}}{{2{x^{100}} + 3}}$
$ = \mathop {\lim }\limits_{x \to – \infty } \frac{{{{\left[ {{x^2}\left( { – 1 + \frac{1}{{{x^2}}}} \right)} \right]}^3}{{\left[ {x\left( {\frac{1}{x} – 2} \right)} \right]}^{94}}}}{{{x^{100}}\left( {2 + \frac{3}{{{x^{100}}}}} \right)}}$
$ = \mathop {\lim }\limits_{x \to – \infty } \frac{{{x^6}{{\left( { – 1 + \frac{1}{{{x^2}}}} \right)}^3}{x^{94}}{{\left( {\frac{1}{x} – 2} \right)}^{^{94}}}}}{{{x^{100}}\left( {2 + \frac{3}{{{x^{100}}}}} \right)}}$
$ = \mathop {\lim }\limits_{x \to – \infty } \frac{{{{\left( { – 1 + \frac{1}{{{x^2}}}} \right)}^3}{{\left( {\frac{1}{x} – 2} \right)}^{94}}}}{{2 + \frac{3}{{{x^{100}}}}}} = \frac{{{{\left( { – 1} \right)}^3}.{{\left( { – 2} \right)}^{94}}}}{2} = – {2^{93}}$

Dạng 6. Dạng vô định $\infty – \infty $,$0.\infty $
1. Phương pháp

• Nếu biểu thức chứa biến số dưới dấu căn thì nhân và chia với biểu thức liên hợp

• Nếu biểu thức chứa nhiều phân thức thì quy đồng mẫu và đưa về cùng một biểu thức.

• Thông thường, các phép biến đổi này có thể cho ta khử ngay dạng vô định $\infty – \infty ;0.\infty $ hoặc chuyển về dạng vô định $\frac{\infty }{\infty };\,\frac{0}{0}$

2. Các ví dụ

Ví dụ 1: Tính $\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {x + 1} – \sqrt {x – 3} } \right)$

Lời giải

$\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {x + 1} – \sqrt {x – 3} } \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{{x + 1 – x + 3}}{{\sqrt {x + 1} + \sqrt {x – 3} }} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\frac{4}{{\sqrt x }}}}{{\left( {\sqrt {1 + \frac{1}{x}} + \sqrt {1 – \frac{3}{x}} } \right)}} = 0.$

Ví dụ 2: Tính $\mathop {\lim }\limits_{x \to + \infty } x\left( {\sqrt {{x^2} + 5} – x} \right)$

Lời giải

$\mathop {\lim }\limits_{x \to + \infty } x\left( {\sqrt {{x^2} + 5} – x} \right) = \mathop {\lim }\limits_{x \to + \infty } x\frac{{{x^2} + 5 – {x^2}}}{{\sqrt {{x^2} + 5} + x}} = \mathop {\lim }\limits_{x \to + \infty } \frac{5}{{\sqrt {1 + \frac{5}{{{x^2}}}} + 1}} = \frac{5}{2}.$

Ví dụ 3: Tính $\mathop {\lim }\limits_{x \to + \infty } \left( {x – \sqrt {{x^2} + 5x} } \right)$

Lời giải

$E = \mathop {\lim }\limits_{x \to + \infty } \left( {x – \sqrt {{x^2} + 5x} } \right)$

Nhân và chia liên hợp $x + \sqrt {{x^2} + 5x} $

$E = \mathop {\lim }\limits_{x \to + \infty } \frac{{\left( {x – \sqrt {{x^2} + 5x} } \right)\left( {x + \sqrt {{x^2} + 5x} } \right)}}{{x + \sqrt {{x^2} + 5x} }} = \mathop {\lim }\limits_{x \to + \infty } \frac{{{x^2} – {x^2} – 5x}}{{x + \left| x \right|\sqrt {1 + \frac{5}{x}} }}$

$ = \mathop {\lim }\limits_{x \to + \infty } \frac{{ – 5x}}{{x + x\sqrt {1 + \frac{5}{x}} }}$ (Vì $ = \mathop {\lim }\limits_{x \to + \infty } \left| x \right| = \mathop {\lim }\limits_{x \to + \infty } x$)

$ = \mathop {\lim }\limits_{x \to + \infty } \frac{{ – 5}}{{1 + \sqrt {1 + \frac{5}{x}} }} = \frac{{ – 5}}{{1 + \sqrt {1 + 0} }} = – \frac{5}{2}.$

Ví dụ 4: Tính$\mathop {\lim }\limits_{x \to {0^ – }} \frac{1}{x}\left( {\frac{1}{{x + 1}} – 1} \right)$

Lời giải

$E = \mathop {\lim }\limits_{x \to {0^ – }} \frac{1}{x}\left( {\frac{1}{{x + 1}} – 1} \right)$ (Dạng vô định $0.\infty $)

$ = \mathop {\lim }\limits_{x \to {0^ – }} \frac{{1 – x – 1}}{{x\left( {x + 1} \right)}} = \mathop {\lim }\limits_{x \to {0^ – }} \frac{{ – 1}}{{x + 1}} = – 1.$

Ví dụ 5: Tính $\mathop {\lim }\limits_{x \to + \infty } \frac{1}{x}\sqrt {{x^2} + 5} = 0.$

Lời giải

$\mathop {\lim }\limits_{x \to + \infty } \frac{1}{x}\sqrt {{x^2} + 5} = \mathop {\lim }\limits_{x \to + \infty } \sqrt {1 + \frac{5}{x}} = 1.$

Ví dụ 6: Tính$\mathop {\lim }\limits_{x \to + \infty } x\left( {\sqrt {{x^2} + 2} – x} \right)$

Lời giải

$\mathop {\lim }\limits_{x \to + \infty } x\left( {\sqrt {{x^2} + 2} – x} \right) = \mathop {\lim }\limits_{x \to + \infty } x\frac{{{x^2} + 2 – {x^2}}}{{\sqrt {{x^2} + 2} + x}} = \mathop {\lim }\limits_{x \to + \infty } \frac{2}{{\sqrt {1 + \frac{2}{{{x^2}}}} + 1}} = \frac{2}{2} = 1$.

Ví dụ 7: Tính $\mathop {\lim }\limits_{x \to 0} \frac{{\sqrt {x + 1} – \sqrt {{x^2} + x + 1} }}{x}$

Lời giải

$\mathop {\lim }\limits_{x \to 0} \frac{{\sqrt {x + 1} – \sqrt {{x^2} + x + 1} }}{x} = \mathop {\lim }\limits_{x \to 0} \frac{{x + 1 – {x^2} – x – 1}}{{\sqrt {x + 1} + \sqrt {{x^2} + x + 1} }}$
$ = \mathop {\lim }\limits_{x \to 0} \frac{{ – x}}{{\sqrt {x + 1} + \sqrt {{x^2} + x + 1} }} = \frac{0}{2} = 0$

Ví dụ 8: Tính $\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {x + 5} – \sqrt {x – 7} } \right)$

Lời giải

$\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {x + 5} – \sqrt {x – 7} } \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{{x + 5 – x + 7}}{{\sqrt {x + 5} + \sqrt {x – 7} }}$
$ = \mathop {\lim }\limits_{x \to + \infty } \frac{{12}}{{\sqrt {x + 5} + \sqrt {x – 7} }}$
$ = \mathop {\lim }\limits_{x \to + \infty } \frac{{\frac{{12}}{{\sqrt x }}}}{{\sqrt {1 + \frac{5}{x}} + \sqrt {1 – \frac{7}{x}} }} = \frac{0}{2} = 0.$

Ví dụ 9: Tính $\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} – 5x} – x} \right)$.

Lời giải

$\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} – 5x} – x} \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{{{x^2} – x – {x^2}}}{{\sqrt {{x^2} – 5x} + x}}$
$ = \mathop {\lim }\limits_{x \to + \infty } \frac{{ – 5x}}{{\sqrt {{x^2} – 5x} + x}}$
$ = \mathop {\lim }\limits_{x \to + \infty } \frac{{ – 5}}{{\sqrt {1 – \frac{5}{x}} + 1}} = – \frac{5}{2}.$

Ví dụ 10: Tính $\mathop {\lim }\limits_{x \to – \infty } \frac{1}{x}\sqrt {{x^2} + 5} = 1$.

Lời giải

$\mathop {\lim }\limits_{x \to – \infty } \frac{{\sqrt {{x^2} + 5} }}{x} = \mathop {\lim }\limits_{x \to – \infty } \frac{{\left| x \right|.\sqrt {1 + \frac{5}{{{x^2}}}} }}{x} = \mathop {\lim }\limits_{x \to – \infty } \frac{{ – x\sqrt {1 + \frac{5}{{{x^2}}}} }}{x} = \mathop {\lim }\limits_{x \to – \infty } – \sqrt {1 + \frac{5}{{{x^2}}}} = – 1.$