Các Dạng Toán Bài VecTơ Trong Mặt Phẳng Tọa Độ Giải Chi Tiết

Các dạng toán bài Vectơ trong mặt phẳng tọa độ giải chi tiết được soạn dưới dạng file word và PDF gồm 4 trang. Các bạn xem và tải về ở dưới.

DẠNG 1: TỌA ĐỘ ĐIỂM-TỌA ĐỘ CỦA VECTƠ

A. Phương pháp

1) Cho hai vectơ $\vec u\left( {x;y} \right)$ và $\vec v\left( {x’;y’} \right)$. Khi đó:

• $\vec u + \vec v = \left( {x + x’;y + y’} \right)$

• $\vec u – \vec v = \left( {x – x’;y – y’} \right)$

• $k\vec u = \left( {kx;ky} \right)$ với $k \in \mathbb{R}$

• $\vec u = \vec v \Leftrightarrow \left\{ \begin{array}{l}
x = x’\\
y = y’
\end{array} \right.$.

Nhận xét: Vectơ $\vec v\left( {x’;y’} \right)$ cùng phương với vectơ $\vec u\left( {x;y} \right) \ne \vec 0$ khi và chỉ khai tồn tại số $k$ sao cho $x’ = kx,y’ = ky$ hay là $\frac{{x’}}{x} = \frac{{y’}}{y}$ nếu $xy \ne 0$.

2) Với hai điểm $M\left( {x;y} \right)$ và $N\left( {x’;y’} \right)$ thì

• $\overrightarrow {MN} = \left( {x’ – x;y’ – y} \right)$

• $MN = \left| {\overrightarrow {MN} } \right| = \sqrt {{{\left( {x’ – x} \right)}^2} + {{\left( {y’ – y} \right)}^2}} $

3) Chú ý:

• Trung điểm $M$ của đoạn thẳng $AB$ có tọa độ là $\left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)$

• Trọng tâm $G$ của tam giác $ABC$ có tọa độ là $\left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3}} \right)$

B. Trắc nghiệm

Bài 1. Xác định tọa độ của vectơ $\vec c = \vec a + 3\vec b$ biết $\vec a = \left( {2; – 1} \right),\vec b = \left( {3;4} \right)$

Lời giải

$\vec c = \vec a + 3\vec b = \left( {2; – 1} \right) + \left( {9;12} \right) = \left( {11;11} \right)$

Bài 2. Cho $\vec a = \left( {2;1} \right),\vec b = \left( {3;4} \right),\vec c = \left( { – 7;2} \right)$. Tìm vectơ $\vec x$ sao cho $\vec x – 2\vec a = \vec b – 3\vec c$.

Lời giải

$\vec x – 2\vec a = \vec b – 3\vec c \Leftrightarrow \vec x = 2\vec a + \vec b – 3\vec c = \left( {28;0} \right)$

Bài 3. Trong hệ tọa độ $Oxy$, cho 3 điểm $A\left( {2;1} \right);B\left( {0; – 3} \right);C\left( {3;1} \right)$. Tìm tọa độ điểm $D$ để $ABCD$ là hình bình hành.

Lời giải

Gọi $D\left( {x;y} \right)$. Ta có: $\overrightarrow {AD} = \overrightarrow {BC} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x – 2 = 3} \\
{y – 1 = 4}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x = 5} \\
{y = 5}
\end{array} \Rightarrow D\left( {5;5} \right)} \right.} \right.$

Bài 4. Trong hệ tọa độ $Oxy$, cho $A\left( { – 4;1} \right);B\left( {2;4} \right);C\left( {2; – 2} \right)$. Tìm tọa độ điểm $D$ sao cho $C$ là trọng tâm $\vartriangle ABD$

Lời giải

Gọi $D\left( {x;y} \right)$. C là trọng tâm $\vartriangle ABD$ khi đó:

$\left\{ {\begin{array}{*{20}{l}}
{2 = \frac{{ – 4 + 2 + x}}{3}} \\
{ – 2 = \frac{{1 + 4 + y}}{3}}
\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{x = 8} \\
{y = – 11}
\end{array} \Rightarrow D\left( {8; – 11} \right)} \right.} \right.$

Bài 5. Trong hệ tọa độ $Oxy$, cho $M\left( {2;0} \right);N\left( {2;2} \right);P\left( { – 1;3} \right)$ lần lượt là trung điểm các cạnh $BC,CA,AB$ của $\vartriangle ABC$.Tọa độ điểm $B$ là:

Lời giải

Ta có $BPMN$ là hình bình hành nên

$\left\{ {\begin{array}{*{20}{l}}
{{x_B} + {x_N} = {x_P} + {x_M}} \\
{{y_B} + {y_N} = {y_P} + {y_M}}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{{x_B} + 2 = \left( { – 1} \right) + 2} \\
{{y_B} + 2 = 3 + 0}
\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{{x_B} = – 1} \\
{{y_B} = 1}
\end{array}} \right.} \right.} \right.$

Bài 6. Trong hệ tọa độ $Oxy$, cho 3 điểm $A\left( {2;5} \right);B\left( {1;1} \right);C\left( {3;3} \right)$. Tìm điểm $E$ thuộc mặt phẳng tọa độ thỏa mãn $\overrightarrow {AE} = 3\overrightarrow {AB} – 2\overrightarrow {AC} $ ?

Lời giải

Gọi $E\left( {x;y} \right) \Rightarrow \overrightarrow {AE} = \left( {x – 2;y – 5} \right),\overrightarrow {AB} = \left( { – 1; – 4} \right),\overrightarrow {AC} = \left( {1; – 2} \right)$

$\overrightarrow {AE} = 3\overrightarrow {AB} – 2\overrightarrow {AC} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x – 2 = – 5} \\
{y – 5 = – 8}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x = – 3} \\
{y = – 3}
\end{array} \Rightarrow E\left( { – 3; – 3} \right)} \right.} \right.$

Bài 7. Trong mặt phẳng $Oxy$, cho các điểm $A\left( { – 4;2} \right),B\left( {2;4} \right)$. Tính độ dài $AB$.

Lời giải

Ta có: $\overrightarrow {AB} = \left( {6;2} \right)$ nên $AB = \sqrt {36 + 4} \Leftrightarrow AB = 2\sqrt {10} $.

Bài 8. Cho hình bình hành $ABCD$ có tọa độ tâm $I\left( {3;2} \right)$ và hai đỉnh $B\left( { – 1;3} \right);C\left( {8; – 1} \right)$. Tìm tọa độ hai đỉnh $A,D$.

Lời giải

Ta có:

$I$ là trung điểm $BD \Rightarrow D = \left( {2{x_I} – {x_B};2{y_I} – {y_B}} \right) \Rightarrow D\left( {7;1} \right)$.

$I$ là trung điểm $AC \Rightarrow C = \left( {2{x_I} – {x_C};2{y_I} – {y_C}} \right) \Rightarrow A\left( { – 2;5} \right)$.

Bài 9. Trong mặt phẳng tọa độ $Oxy$, cho ba điểm $M\left( {2; – 3} \right),N\left( { – 1;2} \right),P\left( {3; – 2} \right)$. Gọi $Q$ là điểm thoả $\overrightarrow {QP} + \overrightarrow {QN} – 4\overrightarrow {MQ} = \vec 0$. Tìm tọa độ điểm $Q$.

Lời giải

Giả sử $Q\left( {x;y} \right)$. Khi đó: $\overrightarrow {QP} + \overrightarrow {QN} – 4\overrightarrow {MQ} = \vec 0$

$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{3 – x – 1 – x – 4\left( {x – 2} \right) = 0} \\
{ – 2 – y + 2 – y – 4\left( {y + 3} \right) = 0}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x = \frac{5}{3}} \\
{y = – 2}
\end{array}} \right.} \right.$.

Vậy $Q\left( {\frac{5}{3}; – 2} \right)$.

DẠNG 2: HAI VECTƠ CÙNG PHƯONG-BA ĐIỂM THẲNG HÀNG-BIỂU DIỄN MỘT THEO HAI KHÔNG CÙNG PHƯƠNG

A. Phương pháp

• Cho $\overrightarrow a = ({a_1};{a_2}),\,\overrightarrow b = ({b_1};{b_2})$, ta có:

$\vec a$ và $\vec b$ cùng phương $ \Leftrightarrow {a_1} \cdot {b_1} – {a_2} \cdot {b_2} = 0$

• Cho $A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right),C\left( {{x_C};{y_C}} \right)$. Ba điểm $A,B,C$ thẳng hàng khi vectơ $\overrightarrow {AB} $ không cùng phương vectơ $\overrightarrow {AC} $.

• Để phân tích $\vec c\left( {{c_1};{c_2}} \right)$ qua hai vectơ $\vec a = \left( {{a_1};{a_2}} \right),\vec b = \left( {{b_1};{b_2}} \right)$ không cùng phương, ta giả sử $\vec c = n \cdot \vec a + m \cdot \vec b$. Khi đó ta quy về giải hệ phương trình: $\left\{ {\begin{array}{*{20}{l}}
{{a_1}n + {b_1}m = {c_1}} \\
{{a_2}n + {b_2}m = {c_2}}
\end{array}} \right.$ tìm $n,m$.

Dựa vào tính chất của hình và sử dụng công thức

• $M$ là trung điểm đoạn thẳng $AB$ suy ra ${x_M} = \frac{{{x_A} + {x_B}}}{2},{y_M} = \frac{{{y_A} + {y_B}}}{2}$

• Tọa độ điểm $M$ chia đoạn $AB$ theo tỉ lệ $k \ne 1:\overrightarrow {MA} = k\overrightarrow {MB} \Leftrightarrow {x_M} = \frac{{{x_A} – k{x_B}}}{{1 – k}};{y_A} = \frac{{{y_A} – k{y_B}}}{{1 – k}}$

• G trọng tâm tam giác $ABC$ suy ra ${x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3},{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{2}$

$\vec a\left( {x;y} \right) = \vec b\left( {x’;y’} \right) \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x = x’} \\
{y = y’}
\end{array}} \right.$

• Cho $A\left( {{x_A};{y_A}} \right),B\left( {{x_B};{y_B}} \right),C\left( {{x_C};{y_C}} \right),D\left( {{x_D};{y_D}} \right)$. Nếu $\overrightarrow {AB} = \overrightarrow {CD} $ thì $\left\{ {\begin{array}{*{20}{l}}
{{x_B} – {x_A} = {x_D} – {x_C}} \\
{{y_B} – {y_A} = {y_D} – {y_C}}
\end{array}} \right.$

• $ABCD$ là hình bình hành khi $\overrightarrow {AB} = \overrightarrow {CD} $

B. Trắc nghiệm

Bài 1. Cho 2 vectơ $\vec u = \left( {2m – 1} \right)\vec i + \left( {3 – m} \right)\vec j$ và $\vec v = 2\vec i + 3\vec j$. Tìm $m$ để hai vectơ cùng phương.

Lời giải

Để 2 vectơ cùng phương thì $\frac{{2m – 1}}{2} = \frac{{3 – m}}{3} \Leftrightarrow m = \frac{9}{8}$.

Bài 2. Trong mặt phẳng $Oxy$, cho $A\left( {m – 1;2} \right);B\left( {2;5 – 2m} \right);C\left( {m – 3;4} \right)$. Tìm $m$ để $A,B,C$ thẳng hàng.

Lời giải

$A,B,C$ thẳng hàng $ \Leftrightarrow \frac{{3 – m}}{{m – 5}} = \frac{{3 – 2m}}{{2m – 1}}$

$ \Leftrightarrow \left( {3 – m} \right)\left( {2m – 1} \right) = \left( {3 – 2m} \right)\left( {m – 5} \right) \Leftrightarrow m = 2$

Bài 3. Trong hệ tọa độ $Oxy$, cho $A\left( {2;1} \right);B\left( {6; – 1} \right)$. Tìm điểm $M$ trên $Ox$ sao cho $A,B,M$ thẳng hàng.

Lời giải

$M \in Ox \Rightarrow M\left( {x;0} \right)$

$\overrightarrow {AB} = \left( {4; – 2} \right),\overrightarrow {AM} = \left( {x – 2; – 1} \right)$

Để $A,B,M$ thẳng hàng $ \Rightarrow \frac{{x – 2}}{4} = \frac{1}{2} \Rightarrow x = 4$

Bài 4. Trong hệ tọa độ $Oxy$, cho $\vec u = 2\vec i – \vec j$ và $\vec v = \vec i + x\vec j$. Tìm $x$ sao cho $\vec u$ và $\vec v$ cùng phương.

Lời giải

Ta có $\vec u = \left( {2; – 1} \right)$ và $\vec v = \left( {1;x} \right)$.

Do $\vec u$ và $\vec v$ cùng phương nên $\frac{1}{2} = \frac{x}{{ – 1}} \Leftrightarrow x = – \frac{1}{2}$.

Bài 5. Cho 4 điểm $M\left( {1; – 2} \right),N\left( {0;3} \right),P\left( { – 3;4} \right),Q\left( { – 1;8} \right)$. Ba điểm nào trong 4 điểm đã cho là thẳng hàng?

Lời giải

Ta có $\overrightarrow {MN} = \left( { – 1;5} \right),\overrightarrow {MP} = \left( { – 4;6} \right),\overrightarrow {MQ} = \left( { – 2;10} \right),\overrightarrow {NP} = \left( { – 3;1} \right),\overrightarrow {NQ} = \left( { – 1;5} \right)$.

Suy ra $\overrightarrow {MN} = \overrightarrow {NQ} $ hay $M,N,Q$ thẳng hàng.

Vậy $M,N,Q$ thẳng hàng.

Bài 6. Trong mặt phẳng $Oxy$, cho $\vec a = \left( {2;1} \right);\vec b = \left( {3;4} \right);\vec c\left( {7;2} \right)$. Tìm $m,n$ để $\vec c = m\vec a + n\vec b$.

Ta có $\vec c = m\vec a + n\vec b \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{2m + 3n = 7} \\
{m + 4n = 2}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{m = \frac{{22}}{5}} \\
{n = – \frac{3}{5}}
\end{array}} \right.} \right.$

DẠNG 3: MỘT SỐ BÀI TOÁN CÓ LIÊN QUAN

Bài 1. Trên mặt phẳng tọa độ $Oxy$, cho $A\left( {1;1} \right),B\left( {2; – 2} \right),M \in Oy$ và $MA = MB$. Tìm tọa độ điểm $M$.

Lời giải

Do $M \in Oy$, đặt $M\left( {0;y} \right)$ suy ra $\overrightarrow {MA} = \left( {1;1 – y} \right),\overrightarrow {MB} = \left( {2; – 2 – y} \right)$.

Vì $MA = MB \Rightarrow {1^2} + {(1 – y)^2} = {2^2} + {(2 + y)^2} \Leftrightarrow y = – 1$. Vậy $M\left( {0; – 1} \right)$.

Bài 2. Trong mặt phẳng tọa độ $Oxy$ cho hai điểm $A\left( {1;2} \right);B\left( { – 1;1} \right)$. Điểm $M$ thuộc trục $Oy$ thỏa mãn tam giác $MAB$ cân tại $M$. Tính độ dài đoạn $OM$

Lời giải

Điểm $M$ thuộc trục $Oy \Rightarrow M\left( {0;y} \right)$.

Ta có tam giác $MAB$ cân tại $M$

$ \Leftrightarrow MA = MB \Leftrightarrow \sqrt {{1^2} + {{(2 – y)}^2}} = \sqrt {{{( – 1)}^2} + {{(1 – y)}^2}} \Leftrightarrow 4 – 4y = 1 – 2y \Leftrightarrow y = \frac{3}{2}$.

Vậy $OM = \frac{3}{2}$.

Bài 3. Trong hệ tọa độ $Oxy$, cho $\vartriangle ABC$ có $A\left( {3;4} \right),B\left( {2;1} \right),C\left( { – 1; – 2} \right)$. Tìm điểm $M$ có tung độ dương trên đường thẳng $BC$ sao cho ${S_{ABC}} = 3{S_{ABM}}$.

Lời giải

Gọi $M\left( {x;y} \right)$. Ta có: ${S_{ABC}} = 3{S_{ABM}} \Leftrightarrow BC = 3BM \Rightarrow \overrightarrow {BC} = \pm 3\overrightarrow {BM} $

$\overrightarrow {BM} = \left( {x – 2;y – 1} \right);\overrightarrow {BC} = \left( { – 3;3} \right)$

• TH1: $\overrightarrow {BC} = 3\overrightarrow {BM} \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{x = 1} \\
{y = 0}
\end{array}} \right.$ (loại)

• TH2: $\overrightarrow {BC} = – 3\overrightarrow {BM} \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{x = 3} \\
{y = 2}
\end{array}} \right.$ (nhận) $ \Rightarrow M\left( {3;2} \right)$

Bài 4. Trong mặt phẳng tọa độ $Oxy$ cho các điểm $A\left( {1; – 17} \right);B\left( { – 11; – 25} \right)$. Tìm tọa độ điểm $C$ thuộc tia $BA$ sao cho $BC = \sqrt {13} $.

Lời giải

Giả sử $C\left( {{x_C};{y_C}} \right)$. Theo bài ra ta có $C$ thuộc tia $BA$ nên $\overrightarrow {BC} ;\overrightarrow {BA} $ cùng hướng.

Với $\overrightarrow {BC} = \left( {{x_C} + 11;{y_C} + 25} \right);\overrightarrow {BA} = \left( {12;8} \right)$ ta có: $\overrightarrow {BC} = k\overrightarrow {BA} (k > 0)$

$ \Leftrightarrow \frac{{{x_C} + 11}}{{12}} = \frac{{{y_C} + 25}}{8} = k \Leftrightarrow 8{x_C} – 12{y_C} – 212 = 0 \Leftrightarrow {y_C} = \frac{{8{x_C} – 212}}{{12}} \Leftrightarrow {y_C} = \frac{{2{x_C} – 53}}{3}$

+) $BC = \sqrt {13} \Leftrightarrow \sqrt {{{\left( {{x_C} + 11} \right)}^2} + {{\left( {{y_C} + 25} \right)}^2}} = \sqrt {13} \Leftrightarrow {\left( {{x_C} + 11} \right)^2} + {\left( {{y_C} + 25} \right)^2} = 13$

Thế (1) vào (2) ta được:

${\left( {{x_C} + 11} \right)^2} + {\left( {\frac{{2{x_C} – 53}}{3} + 25} \right)^2} = 13$

$ \Leftrightarrow {\left( {{x_C} + 11} \right)^2} + {\left( {\frac{{2{x_C} + 22}}{3}} \right)^2} = 13$

$ \Leftrightarrow \frac{{13}}{9}{\left( {{x_C} + 11} \right)^2} = 13$

$ \Leftrightarrow {\left( {{x_C} + 11} \right)^2} = 9 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{{x_C} = – 14} \\
{{x_C} = – 8}
\end{array}} \right.$

Với ${x_C} = – 14$ thế vào (1) ta được: ${y_C} = \frac{{2 \cdot \left( { – 14} \right) – 53}}{3} = – 27$.

Khi đó $k = \frac{{ – 14 + 11}}{{12}} = \frac{{ – 3}}{{12}} = \frac{{ – 1}}{4} < 0$.

Với ${x_C} = – 8$ thế vào (1) ta được: ${y_C} = \frac{{2 \cdot \left( { – 8} \right) – 53}}{3} = – 23$.

Khi đó $k = \frac{{ – 8 + 11}}{{12}} = \frac{3}{{12}} = \frac{1}{4} > 0$.

Vậy $C\left( { – 8; – 23} \right)$.

Bài 5. Trong hệ tọa độ $Oxy$, cho ba điểm $A\left( {1;0} \right),B\left( {0,3} \right),C\left( { – 3; – 5} \right)$. Tìm điểm $M$ thuộc trục $Ox$ sao cho $T = \left| {2\overrightarrow {MA} – 3\overrightarrow {MB} + 2\overrightarrow {MC} } \right|$ nhỏ nhất.

Lời giải

Gọi $I\left( {x;y} \right)$ thỏa mãn: $2\overrightarrow {IA} – 3\overrightarrow {IB} + 2\overrightarrow {IC} = 0$

$ \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{2\left( {1 – x} \right) – 3\left( { – x} \right) + 2\left( { – 3 – x} \right) = 0} \\
{2\left( { – y} \right) – 3\left( {3 – y} \right) + 2\left( { – 5 – y} \right) = 0}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x = 4} \\
{y = \frac{{19}}{3}}
\end{array}} \right.} \right.$

Ta có $T = \left| {2\left( {\overrightarrow {MI} + \overrightarrow {IA} } \right) – 3\left( {\overrightarrow {MI} – \overrightarrow {IB} } \right) + 2\left( {\overrightarrow {MI} + \overrightarrow {IC} } \right)\left| = \right|\overrightarrow {MI} } \right| = MI$

Vì $I$ cố định và $M \in Ox \Rightarrow T$ nhỏ nhất khi $M$ là hình chiếu cảu $I$ trên trục $Ox \Rightarrow M\left( {4;0} \right)$

Bài 6. Trong hệ tọa độ $Oxy$, cho điểm $A\left( {1;3} \right)$ và $B\left( {4,7} \right)$. Tìm điểm $M$ trên trục $Oy$ sao cho $MA + MB$ là nhỏ nhất.

Lời giải

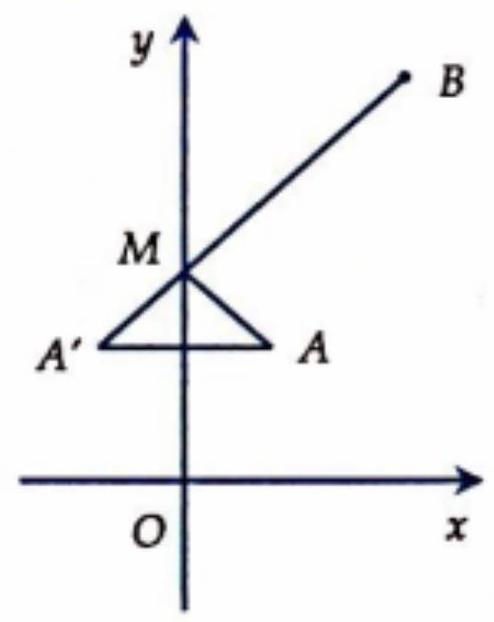
Ta có $A,B$ nằm cùng phía với trục $Oy$

Gọi $A’$ đối xứng với $A$ qua $Oy \Rightarrow A’\left( { – 1;3} \right)$

Giả sử: $M\left( {0;y} \right)$. Ta có $MA + MB = MA’ + MB \geqslant A’B$

$ \Rightarrow MA + MB$ nhỏ nhất khi $A’,M,B$ thẳng hàng

$\overrightarrow {A’B} = \left( {5;4} \right),\overrightarrow {A’M} = \left( {1;y – 3} \right)$

$ \Rightarrow \frac{1}{5} = \frac{{y – 3}}{4} \Leftrightarrow y = \frac{{19}}{5} \Rightarrow M\left( {0;\frac{{19}}{5}} \right)$

Bài 7. Trong hệ tọa độ $Oxy$, cho hai điểm $A\left( {2; – 3} \right),B\left( {3; – 4} \right)$. Tìm tọa độ điểm $M$ trên trục hoành sao cho chu vi tam giác $AMB$ nhỏ nhất.

Lời giải

Cách 1: Do $M$ trên trục hoành $ \Rightarrow M\left( {x;0} \right),\overrightarrow {AB} = \left( {1; – 1} \right) \Rightarrow AB = \sqrt 2 $.

$\overrightarrow {AM} = \left( {x – 2;3} \right),\overrightarrow {BM} = \left( {x – 3;4} \right)$

Ta có chu vi tam giác $AMB:{P_{ABM}} = \sqrt 2 + \sqrt {{{(x – 2)}^2} + {3^2}} + \sqrt {{{(x – 3)}^2} + {4^2}} $

$ = \sqrt 2 + \sqrt {{{(x – 2)}^2} + {3^2}} + \sqrt {{{(3 – x)}^2} + {4^2}} \geqslant \sqrt 2 + \sqrt {{{(x – 2 + 3 – x)}^2} + {{(3 + 4)}^2}} $

$ \Leftrightarrow {P_{ABM}} \geqslant 6\sqrt 2 $. Dấu bằng xảy ra khi $\frac{{x – 2}}{{3 – x}} = \frac{3}{4} \Leftrightarrow x = \frac{{17}}{7} \Rightarrow M\left( {\frac{{17}}{7};0} \right)$.

Cách 2: Lấy đối xứng $A$ qua $Ox$ ta được $A’\left( {2;3} \right)$. Ta có $MA + MB = MA’ + MB \geqslant A’B$.

Dấu bằng xảy ra khi $M$ trùng với giao điểm của $A’B$ với $Ox$.