70 Câu Trắc Nghiệm Bài Tích Của Một VecTơ Với Một Số Giải Chi Tiết

70 câu trắc nghiệm bài Tích của một vectơ với một số giải chi tiết được soạn dưới dạng file word và PDF gồm 8 trang. Các bạn xem và tải về ở dưới.

DẠNG 1: ĐẲNG THỨC VECTƠ CHỨA TÍCH CỦA VECTƠ VỚI MỘT SỐ

Câu 1. Khẳng định nào sai?
A. $1 \cdot \vec a = \vec a$
B. $k\vec a$ và $\vec a$ cùng hướng khi $k > 0$
C. $k\vec a$ và $\vec a$ cùng hướng khi $k < 0$
D. Hai vectơ $\vec a$ và $\vec b \ne \vec 0$ cùng phương khi có một số $k$ để $\vec a = k\vec b$

Lời giải

Chọn C

(Dựa vào định nghĩa tích của một số với một vectơ)

Câu 2. Cho tam giác $ABC$. Gọi I là trung điểm của $BC$. Khẳng định nào sau đây đúng

A. $\overrightarrow {{\text{BI}}} = \overrightarrow {{\text{IC}}} $
B. $3\overrightarrow {{\text{BI}}} = 2\overrightarrow {{\text{IC}}} $
C. $\overrightarrow {{\text{BI}}}  = \overrightarrow {2{\text{IC}}} $
D. $\overrightarrow {2{\text{BI}}}  = \overrightarrow {{\text{IC}}} $

Lời giải

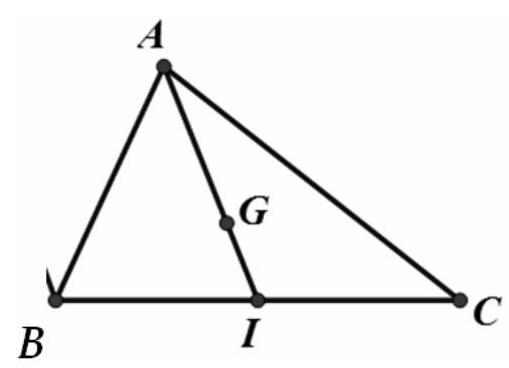
Chọn A

Vì I là trung điểm của ${\text{BC}}$ nên ${\text{BI}} = {\text{CI}}$ và $\overrightarrow {{\text{BI}}} $ cùng hướng với $\overrightarrow {{\text{IC}}} $ do đó hai vectơ $\overrightarrow {{\text{BI}}} ,\overrightarrow {{\text{IC}}} $ bằng nhau hay $\overrightarrow {{\text{BI}}}  = \overrightarrow {{\text{IC}}} $.

Câu 3. Cho tam giác $ABC$. Gọi $M$ và $N$ lần lượt là trung điểm của $AB$ và $AC$. Trong các mệnh đề sau, tìm mệnh đề sai?
A. $\overrightarrow {AB} = 2\overrightarrow {AM} $
B. $\overrightarrow {AC} = 2\overrightarrow {CN} $
C. $\overrightarrow {BC} = – 2\overrightarrow {NM} $
D. $\overrightarrow {CN} = – \frac{1}{2}\overrightarrow {AC} $

Lời giải

Chọn B

Câu 4. Cho $\vec a \ne \vec 0$ và điểm $O$. Gọi $M,N$ lần lượt là hai điểm thỏa mãn $\overrightarrow {OM} = 3\vec a$ và $\overrightarrow {ON} = – 4\vec a$. Khi đó:
A. $\overrightarrow {MN} = 7\vec a$
B. $\overrightarrow {MN} = – 5\vec a$
C. $\overrightarrow {MN} = – 7\vec a$
D. $\overrightarrow {MN} = – 5\vec a$

Lời giải

Chọn C

Ta có: $\overrightarrow {MN} = \overrightarrow {ON} – \overrightarrow {OM} = – 4\vec a – 3\vec a = – 7\vec a$.

Câu 5. Cho ngũ giác $ABCDE$. Gọi $M,N,P,Q$ lần lượt là trung điểm các cạnh $AB,BC,CD,DE$. Gọi $I$ và $J$ lần lượt là trung điểm các đoạn $MP$ và $NQ$. Khẳng định nào sau đây đúng?
A. $\overrightarrow {IJ} = \frac{1}{2}\overrightarrow {AE} $
B. $\overrightarrow {IJ} = \frac{1}{3}\overrightarrow {AE} $
C. $\overrightarrow {IJ} = \frac{1}{4}\overrightarrow {AE} $
D. $\overrightarrow {IJ} = \frac{1}{5}\overrightarrow {AE} $

Lời giải

Chọn C

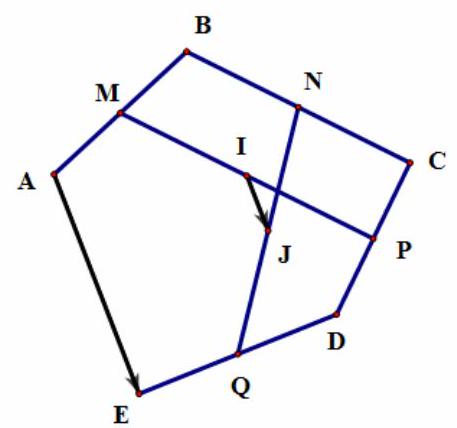
Ta có: $2\overrightarrow {IJ} = \overrightarrow {IQ} + \overrightarrow {IN} = \overrightarrow {IM} + \overrightarrow {MQ} + \overrightarrow {IP} + \overrightarrow {PN} = \overrightarrow {MQ} + \overrightarrow {PN} $

$\left\{ {\begin{array}{*{20}{l}}
{\overrightarrow {MQ} = \overrightarrow {MA} + \overrightarrow {AE} + \overrightarrow {EQ} } \\
{\overrightarrow {MQ} = \overrightarrow {MB} + \overrightarrow {BD} + \overrightarrow {DQ} }
\end{array}} \right.$

$ \Rightarrow 2\overrightarrow {MQ} = \overrightarrow {AE} + \overrightarrow {BD} $$ \Leftrightarrow \overrightarrow {MQ} = \frac{1}{2}\left( {\overrightarrow {AE} + \overrightarrow {BD} } \right).\overrightarrow {PN} = – \frac{1}{2}\overrightarrow {BD} $

Suy ra: $2\overrightarrow {IJ} = \frac{1}{2}\left( {\overrightarrow {AE} + \overrightarrow {BD} } \right) – \frac{1}{2}\overrightarrow {BD} = \frac{1}{2}\overrightarrow {AE} \Rightarrow \overrightarrow {IJ} = \frac{1}{4}\overrightarrow {AE} $.

Câu 6. Ba trung tuyến $AM,BN,CP$ của tam giác $ABC$ dồng quy tại $G$. Hỏi vectơ $\overrightarrow {AM} + \overrightarrow {BN} + \overrightarrow {CP} $ bằng vectơ nào?
A. $\frac{3}{2}\left( {\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {CG} } \right)$
B. $3\left( {\overrightarrow {MG} + \overrightarrow {NG} + \overrightarrow {GP} } \right)$
C. $\frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {AC} } \right)$
D. $\vec 0$

Lời giải

Chọn D

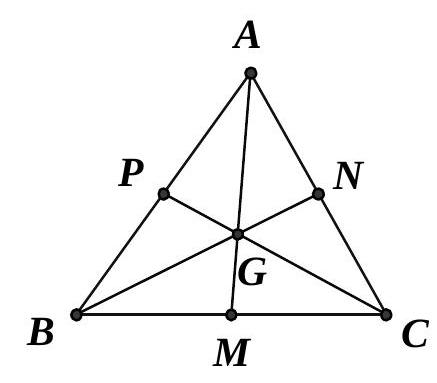
Ta có: $\overrightarrow {AM} + \overrightarrow {BN} + \overrightarrow {CP} = \frac{3}{2}\overrightarrow {AG} + \frac{3}{2}\overrightarrow {BG} + \frac{3}{2}\overrightarrow {CG} = \frac{3}{2}\left( {\overrightarrow {AG} + \overrightarrow {BG} + \overrightarrow {CG} } \right) = \vec 0$.

Câu 7. Cho $I$ là trung điểm của đoạn thẳng $AB$. Với điểm $M$ bất kỳ, ta luôn có:
A. $\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow {MI} $
B. $\overrightarrow {MA} + \overrightarrow {MB} = 2\overrightarrow {MI} $
C. $\overrightarrow {MA} + \overrightarrow {MB} = 3\overrightarrow {MI} $
D. $\overrightarrow {MA} + \overrightarrow {MB} = \frac{1}{2}\overrightarrow {MI} $

Lời giải

Chọn B

Áp dụng tính chất trung điểm của đoạn thẳng: Với điểm $M$ bất kỳ, ta luôn có $\overrightarrow {MA} + \overrightarrow {MB} = 2\overrightarrow {MI} $

Câu 8. Cho $G$ là trọng tâm của tam giác $ABC$. Với mọi điểm $M$, ta luôn có:
A. $\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow {MG} $
B. $\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 2\overrightarrow {MG} $
C. $\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} $
D. $\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 4\overrightarrow {MG} $

Lời giải

Chon C

Áp dụng tính chất trọng tâm của tam giác: Với mọi điểm $M$, ta luôn có $\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} $.

Câu 9. Cho $\vartriangle ABC$ có $G$ là trọng tâm, $I$ là trung điểm $BC$. Đẳng thức nào đúng?
A. $\overrightarrow {GA} = 2\overrightarrow {GI} $
B. $\overrightarrow {IG} = – \frac{1}{3}\overrightarrow {IA} $
C. $\overrightarrow {GB} + \overrightarrow {GC} = 2\overrightarrow {GI} $
D. $\overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow {GA} $

Lời giải

Chọn C

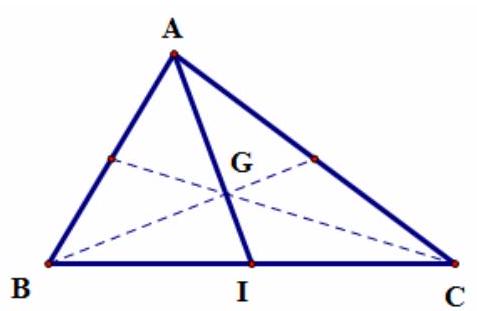
Áp dụng tính chất trung điểm của đoạn thẳng, ta có: $\overrightarrow {GB} + \overrightarrow {GC} = 2\overrightarrow {GI} $.

Câu 10. Cho hình vuông $ABCD$ có tâm là $O$. Trong các mệnh đề sau, tìm mệnh đề sai?
A. $\overrightarrow {AB} + \overrightarrow {AD} = 2\overrightarrow {AO} $
B. $\overrightarrow {AD} + \overrightarrow {DO} = – \frac{1}{2}\overrightarrow {CA} $
C. $\overrightarrow {OA} + \overrightarrow {OB} = \frac{1}{2}\overrightarrow {CB} $
D. $\overrightarrow {AC} + \overrightarrow {DB} = 4\overrightarrow {AB} $

Lời giải

Chọn D

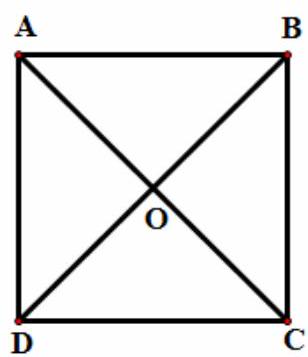
$\overrightarrow {AC} + \overrightarrow {DB} = \overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {DC} + \overrightarrow {CB} = \overrightarrow {AB} + \overrightarrow {DC} = 2\overrightarrow {AB} $

Câu 11. Cho tứ giác $ABCD$. Gọi $M,N$ lần lượt là trung điểm của $AB$ và $CD$. Khi đó $\overrightarrow {AC} + \overrightarrow {BD} $ bằng:
A. $\overrightarrow {MN} $
B. $2\overrightarrow {MN} $
C. $3\overrightarrow {MN} $

Lời giải

Chọn B

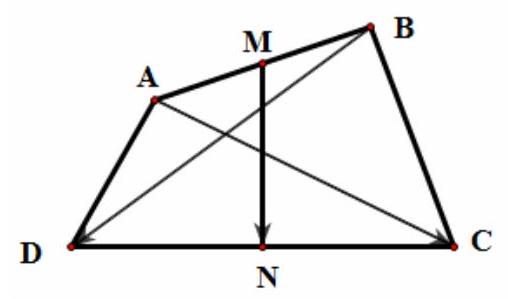
Ta có: $ + \left\{ {\begin{array}{*{20}{l}}
{\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AC} + \overrightarrow {CN} } \\
{\overrightarrow {MN} = \overrightarrow {MB} + \overrightarrow {BD} + \overrightarrow {DN} }
\end{array} \Rightarrow 2\overrightarrow {MN} = \overrightarrow {AC} + \overrightarrow {BD} } \right.$.

Câu 12. Cho hình bình hành $ABCD$ tâm $O$ và điểm $M$ bất kì. Khẳng định nào sau đây đúng?
A. $\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = \overrightarrow {MO} $
B. $\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = 2\overrightarrow {MO} $
C. $\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = 3\overrightarrow {MO} $
D. $\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = 4\overrightarrow {MO} $

Lời giải

Chọn D

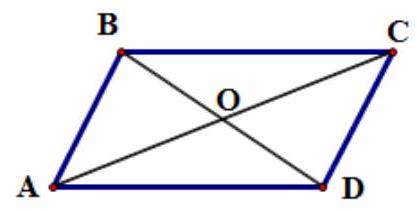
Ta có: $\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = \left( {\overrightarrow {MA} + \overrightarrow {MC} } \right) + \left( {\overrightarrow {MB} + \overrightarrow {MD} } \right) = 2\overrightarrow {MO} + 2\overrightarrow {MO} = 4\overrightarrow {MO} $

Câu 13. Cho tứ giác $ABCD$. Gọi $G$ là trọng tâm của tam giác $ABD,I$ là điểm trên $GC$ sao cho $IC = 3IG$. Với mọi điểm $M$ ta luôn có $\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} $ bằng:
A. $2\overrightarrow {MI} $
B. $3\overrightarrow {MI} $
C. $4\overrightarrow {MI} $
D. $5\overrightarrow {MI} $

Lời giải

Chọn C

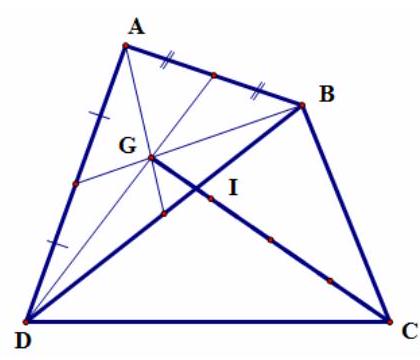
Ta có: $3\overrightarrow {IG} = – \overrightarrow {IC} $.

Do $G$ là trọng tâm của tam giác $ABD$ nên

$\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {ID} = 3\overrightarrow {IG} \Leftrightarrow \overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {ID} = – \overrightarrow {IC} \Leftrightarrow \overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {ID} = \vec 0$

Khi đó:

$\begin{array}{*{20}{r}}
{}&{\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = \overrightarrow {MI} + \overrightarrow {IA} + \overrightarrow {MI} + \overrightarrow {IB} + \overrightarrow {MI} + \overrightarrow {IC} + \overrightarrow {MI} + \overrightarrow {ID} } \\
{}&{\; = 4\overrightarrow {MI} + \left( {\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} + \overrightarrow {ID} } \right) = 4\overrightarrow {MI} + \vec 0 = 4\overrightarrow {MI} }
\end{array}$

Câu 14. Cho $\vartriangle ABC$ với $H,O,G$ lần lượt là trực tâm, tâm đường tròn ngoại tiếp trọng tâm. Hệ thức nào sau đây là đúng?
A. $\overrightarrow {OH} = \frac{3}{2}\overrightarrow {OG} $
B. $\overrightarrow {HO} = 3\overrightarrow {OG} $
C. $\overrightarrow {OG} = \frac{1}{2}\overrightarrow {GH} $
D. $2\overrightarrow {GO} = – 3\overrightarrow {OH} $

Lời giải

Chọn C.

Ta có $\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \vec 0 \Rightarrow \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 3\overrightarrow {OG} $

Gọi $I$ là trung điểm $BC,A’$ đối xứng với $A$ qua $O$.

Dễ thấy $HBA’C$ là hình bình hành

$ \Leftrightarrow \overrightarrow {HB} + \overrightarrow {HC} = \overrightarrow {HA’} \Leftrightarrow \overrightarrow {HA} + \overrightarrow {HB} + \overrightarrow {HC} = \overrightarrow {HA} + \overrightarrow {HA’} = 2\overrightarrow {HO} $

$ \Leftrightarrow 3\overrightarrow {HO} + \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 2\overrightarrow {HO} \Leftrightarrow \overrightarrow {OH} = \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} $

Từ (1) và (2) $ \Rightarrow \overrightarrow {OH} = 3\overrightarrow {OG} \Leftrightarrow \overrightarrow {OG} + \overrightarrow {GH} = 3\overrightarrow {OG} \Leftrightarrow \overrightarrow {GH} = 2\overrightarrow {OG} \Leftrightarrow \overrightarrow {OG} = \frac{1}{2}\overrightarrow {GH} $.

Câu 15. Cho $\vartriangle ABC$ và một điểm $M$ tùy ý. Chọn hệ thức đúng?
A. $2\overrightarrow {MA} + \overrightarrow {MB} – 3\overrightarrow {MC} = \overrightarrow {AC} + 2\overrightarrow {BC} $
B. $2\overrightarrow {MA} + \overrightarrow {MB} – 3\overrightarrow {MC} = 2\overrightarrow {AC} + \overrightarrow {BC} $
C. $2\overrightarrow {MA} + \overrightarrow {MB} – 3\overrightarrow {MC} = 2\overrightarrow {CA} + \overrightarrow {CB} $
D. $2\overrightarrow {MA} + \overrightarrow {MB} – 3\overrightarrow {MC} = 2\overrightarrow {CB} – \overrightarrow {CA} $

Lời giải

Chọn C.

$\begin{array}{*{20}{r}}
{}&{2\overrightarrow {MA} + \overrightarrow {MB} – 3\overrightarrow {MC} } \\
{}&{\; = 2\overrightarrow {MC} + 2\overrightarrow {CA} + \overrightarrow {MC} + \overrightarrow {CB} – 3\overrightarrow {MC} } \\
{}&{\; = 2\overrightarrow {CA} + \overrightarrow {CB} }
\end{array}$

Câu 16. Cho hình chữ nhật $ABCD,I,K$ lần lượt là trung điểm của $BC$ và $CD$. Chọn đẳng thức đúng.
A. $\overrightarrow {AI} + \overrightarrow {AK} = 2\overrightarrow {AC} $
B. $\overrightarrow {AI} + \overrightarrow {AK} = \overrightarrow {AB} + \overrightarrow {AD} $
C. $\overrightarrow {AI} + \overrightarrow {AK} = \overrightarrow {IK} $
D. $\overrightarrow {AI} + \overrightarrow {AK} = \frac{3}{2}\overrightarrow {AC} $

Lời giải

Chọn D.

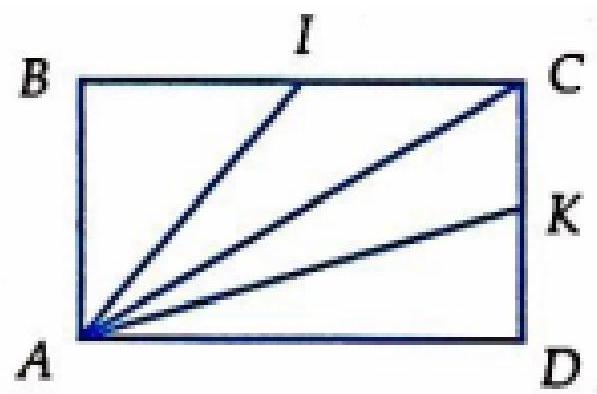
$\overrightarrow {AI} + \overrightarrow {AK} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) + \frac{1}{2}\left( {\overrightarrow {AD} + \overrightarrow {AC} } \right) = \overrightarrow {AC} + \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AD} } \right) = \frac{3}{2}\overrightarrow {AC} $

Câu 17. Cho tam giác $ABC$, có $AM$ là trung tuyến; $I$ là trung điểm của $AM$. Ta có:
A. $\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} = \vec 0$.
B. $\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} = \vec 0$.
C. $2\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} = 4\overrightarrow {IA} $.
D. $2\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} = \vec 0$.

Lời giải

Chọn D.

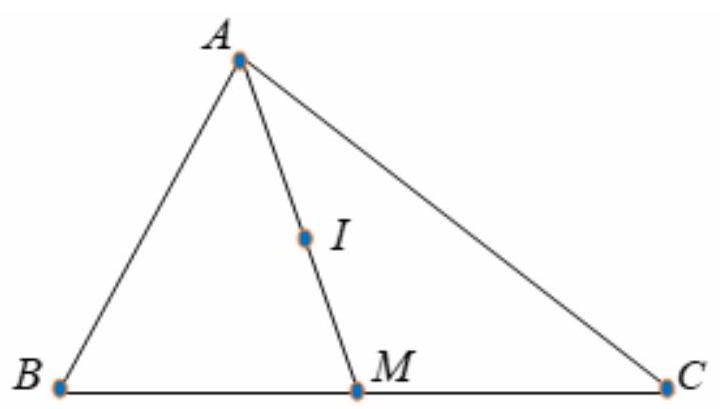
Theo tính chất hình bình hành ta có: $\overrightarrow {IB} + \overrightarrow {IC} = 2\overrightarrow {IM} $

$ \Rightarrow 2\overrightarrow {IA} + \overrightarrow {IB} + \overrightarrow {IC} = 2\overrightarrow {IA} + 2\overrightarrow {IM} = 2\left( {\overrightarrow {IA} + \overrightarrow {IM} } \right) = \vec 0$

Câu 18. Cho tứ giác $ABCD$. $I,J$ lần lượt là trung điểm của $AB$ và $DC$. $G$ là trung điểm của $IJ$. Xét các mệnh đề:

(I) $\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = 4\overrightarrow {AG} $

(II) $\overrightarrow {IA} + \overrightarrow {IC} = 2\overrightarrow {IG} $

(III) $\overrightarrow {JB} + \overrightarrow {ID} = \overrightarrow {JI} $

Mệnh đề sai là:
A. (I) và (II)
B. (II) và (III)
C. Chỉ (I)
D. Tất cả đều sai

Lời giải

Chọn B.

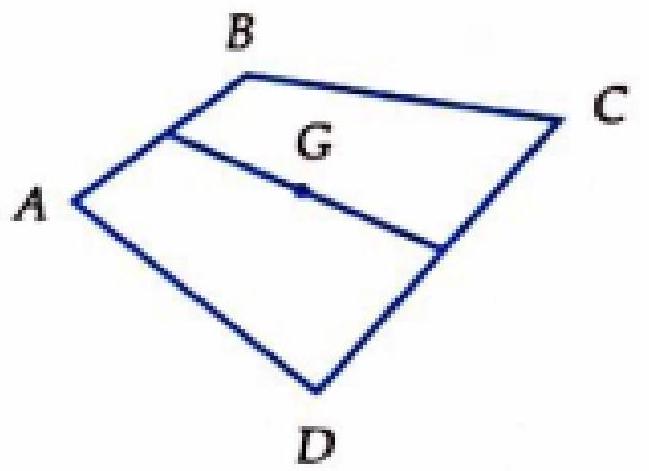
$\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} $

$ = \overrightarrow {AG} + \overrightarrow {GB} + \left( {\overrightarrow {AG} + \overrightarrow {GC} } \right) + \left( {\overrightarrow {AG} + \overrightarrow {GD} } \right)$

$ = 3\overrightarrow {AG} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} $

$ = 4\overrightarrow {GA} + \left( {\overrightarrow {GA} + \overrightarrow {GB} } \right) + \left( {\overrightarrow {GC} + \overrightarrow {GD} } \right)$

$ = 4\overrightarrow {AG} + 2I + 2\overrightarrow {GJ} = 4\overrightarrow {AG} $

(II) và (III) sai vì $G$ không phải là trung điểm của $AC$ và $BD$.

Câu 19. Cho tam giác đều $ABC$ có tâm $O$. Gọi $I$ là một điểm tùy ý bên trong tam giác $ABC$. Hạ $ID,IE,IF$ tương ứng vuông góc với $BC,CA,AB$. Giả sử $\overrightarrow {ID} + \overrightarrow {IE} + \overrightarrow {IF} = \frac{a}{b}\overrightarrow {IO} $ (với $\frac{a}{b}$ là phân số tối giản). Khi đó $a + b$ bằng:
A. 5
B. 4 C. 6
D. 7

Lời giải

Chọn A

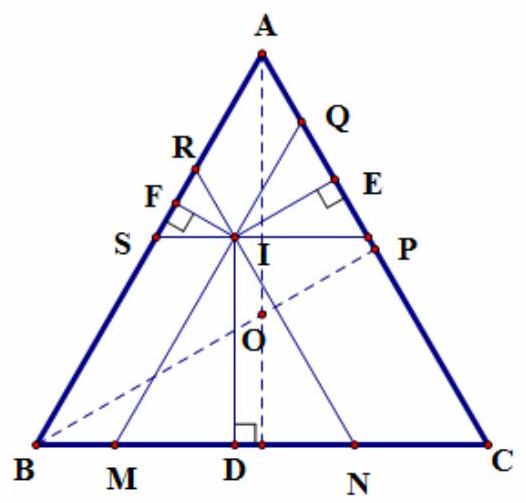
Qua điểm $I$ dựng các đoạn $MQ//AB,PS//BC,NR//CA$.

Vì $ABC$ là tam giác đều nên các tam giác $IMN,IPQ,IRS$ cũng là tam giác đều.

Suy ra $D,E,F$ lần lượt là trung điểm của $MN,PQ,RS$.

Khi đó:

Câu 20. ${^*}$ Cho $\vartriangle ABC$ với $BC = a,AC = b,AB = c.I$ là tâm đường tròn nội tiếp $\vartriangle ABC$, đường tròn nội tiếp $\left( I \right)$ tiếp xúc với các cạnh $BC,CA,AB$ lần lượt tại $M,N,P$. Đẳng thức nào sau đây là đúng?
A. $a \cdot \overrightarrow {IM} + b \cdot \overrightarrow {IN} + c \cdot \overrightarrow {IP} = \vec 0$
B. $a \cdot \overrightarrow {MA} + b \cdot \overrightarrow {NB} + c \cdot \overrightarrow {PC} = \vec 0$
C. $a \cdot \overrightarrow {AM} + b \cdot \overrightarrow {BN} + c \cdot \overrightarrow {CP} = \vec 0$
D. $a \cdot \overrightarrow {AB} + b \cdot \overrightarrow {BC} + c \cdot \overrightarrow {CA} = \vec 0$

Lời giải

Chọn A.

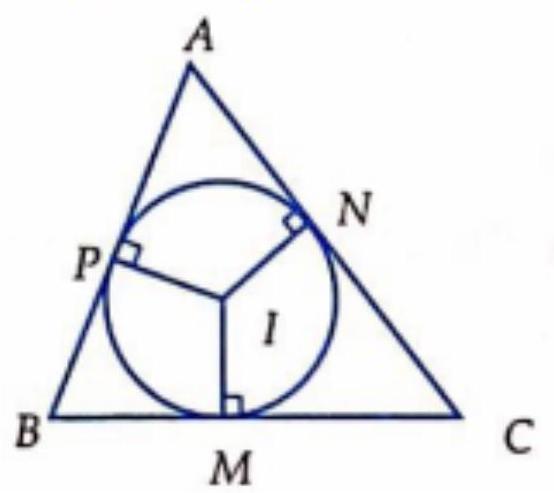
Gọi $p$ là nửa chu vi $\vartriangle ABC$, ta có:

$AP = AN = p – a$

$BM = BP = p – b$

$CN = CM = p – c$

Ta có $\overrightarrow {IM} = \frac{{MB}}{{BC}} \cdot \overrightarrow {IB} + \frac{{MB}}{{BC}} \cdot \overrightarrow {IC} $

$ \Leftrightarrow a\overrightarrow {IM} = \left( {p – c} \right)\overrightarrow {IB} + \left( {p – b} \right)\overrightarrow {IC} \left( 1 \right)$

Tương tự:

$b\overrightarrow {IN} = \left( {p – a} \right)\overrightarrow {IC} + \left( {p – c} \right)\overrightarrow {IA} \left( 2 \right)$

$c\overrightarrow {IP} = \left( {p – b} \right)\overrightarrow {IA} + \left( {p – a} \right)\overrightarrow {IB} \left( 3 \right)$

Cộng từng vế (1), (2), (3) ta được:

$a\overrightarrow {IM} + b\overrightarrow {IN} + c\overrightarrow {IC} $

$ = \left( {2p – b – c} \right)\overrightarrow {IA} + \left( {2p – a – c} \right)\overrightarrow {IB} + \left( {2p – a – b} \right)\overrightarrow {IC} $

$ = a\overrightarrow {IA} + b\overrightarrow {IB} + c\overrightarrow {IC} = \vec 0$

Nhận xét: Áp dụng kết quả nếu $I$ là tâm đường tròn nội tiếp $\vartriangle ABC$ thì $ \Leftrightarrow a\overrightarrow {IA} + b\overrightarrow {BI} + c\overrightarrow {CI} = 0$

DẠNG 2: XÁC ĐỊNH VÀ TÍNH ĐỘ LỚN VECTƠ

• Vẽ hình xác định các vectơ thông qua các quy tắc ba điểm, quy tắc hình bình hành.

• Áp dụng các công thức hình học để tính độ dài vectơ.

• Để tính độ dài $\left| {\vec a \pm \vec b \pm \vec c \pm \vec d} \right|$ thì ta đi rút gọn biểu thức vectơ $\vec a \pm \vec b \pm \vec c \pm \vec d$ rồi tính độ dài.

Câu 21. Tìm giá trị của $m$ sao cho $\vec a = m\vec b$, biết rằng $\vec a,\vec b$ ngược hướng và $\left| {\vec a\left| { = 5,} \right|\vec b} \right| = 15$
A. $m = 3$
B. $m = – \frac{1}{3}$
C. $m = \frac{1}{3}$
D. $m = – 3$

Lời giải

Chọn B

Do $\vec a,\vec b$ ngược hướng nên $m = – \frac{{\left| {\vec a} \right|}}{{\left| {\vec b} \right|}} = – \frac{5}{{15}} = – \frac{1}{3}$.

Câu 22. Cho tam giác $ABC$ đều có cạnh bằng $2a$. Độ dài của $\overrightarrow {AB} + \overrightarrow {AC} $ bằng:
A. $2a$
B. $a\sqrt 3 $
C. $2a\sqrt 3 $
D. $\frac{{a\sqrt 3 }}{2}$

Lời giải

Chọn C

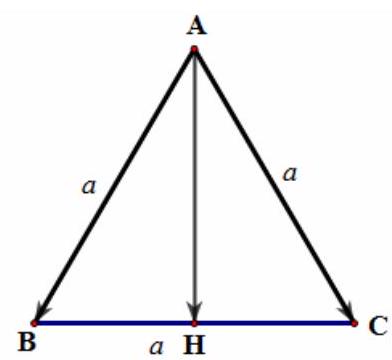
Gọi $H$ là trung điểm của $BC$. Khi đó: $\left| {\overrightarrow {AB} + \overrightarrow {AC} \left| = \right|2 \cdot \overrightarrow {AH} } \right| = 2 \cdot AH = 2 \cdot \frac{{2a\sqrt 3 }}{2} = 2a\sqrt 3 $.

Câu 23. Cho hình thoi $ABCD$ tâm $O$, cạnh $2a$. Góc $\widehat {BAD} = {60^ \circ }$. Tính độ dài vectơ $\overrightarrow {AB} + \overrightarrow {AD} $.
A. $\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = 2a\sqrt 3 $
B. $\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = a\sqrt 3 $
C. $\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = 3a$
D. $\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = 3a\sqrt 3 $

Lời giải

Chọn A

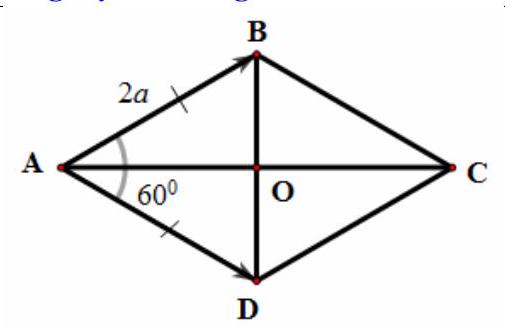
Tam giác $ABD$ cân tại $A$ và có góc $\widehat {BAD} = {60^ \circ }$ nên $\vartriangle ABD$ đều $\left| {\overrightarrow {AB} + \overrightarrow {AD} \left| = \right|\overrightarrow {AC} \left| = \right|2\overrightarrow {AO} } \right| = 2 \cdot AO = 2 \cdot \sqrt {A{B^2} – B{O^2}} = 2 \cdot \sqrt {4{a^2} – {a^2}} = 2a\sqrt 3 $

Câu 24. Cho tam giác $ABC$ vuông cân tại $A$ có $AB = a$. Tính $\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right|$.
A. $\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = a\sqrt 2 $.
B. $\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \frac{{a\sqrt 2 }}{2}$.
C. $\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = 2a$.
D. $\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = a$.

Lời giải

Chọn A.

Gọi $M$ là trung điểm $BC$ thì $\left| {\overrightarrow {AB} + \overrightarrow {AC} \left| = \right|2\overrightarrow {AM} } \right| = 2AM = BC = a\sqrt 2 $.

Câu 25. Cho hình vuông $ABCD$ có cạnh là 3 . Tính độ dài $\left| {\overrightarrow {AC} + \overrightarrow {BD} } \right|$ :
A. 6
B. $6\sqrt 2 $
C. 12
D. 0

Lời giải

Chọn A.

$\begin{array}{*{20}{r}}
{\left| {\overrightarrow {AC} + \overrightarrow {BD} } \right|}&{\; = \left| {2\overrightarrow {AO} + 2\overrightarrow {OD} } \right|} \\
{}&{\; = 2\left| {\overrightarrow {AD} } \right| = 6}
\end{array}$

$\left| {\overrightarrow {AC} + \overrightarrow {BD} } \right| = \left| {2\overrightarrow {AO} + 2\overrightarrow {OD} } \right|$$ = 2\left| {\overrightarrow {AD} } \right| = 6$

Câu 26. Cho tam giác đều $ABC$ cạnh $2a$ có $G$ là trọng tâm. Khi đó $\left| {\overrightarrow {AB} – \overrightarrow {GC} } \right|$ là
A. $\frac{{a\sqrt 3 }}{3}$.
B. $\frac{{2a\sqrt 3 }}{3}$.
C. $\frac{{4a\sqrt 3 }}{3}$.
D. $\frac{{2a}}{3}$.

Lời giải

Chọn C.

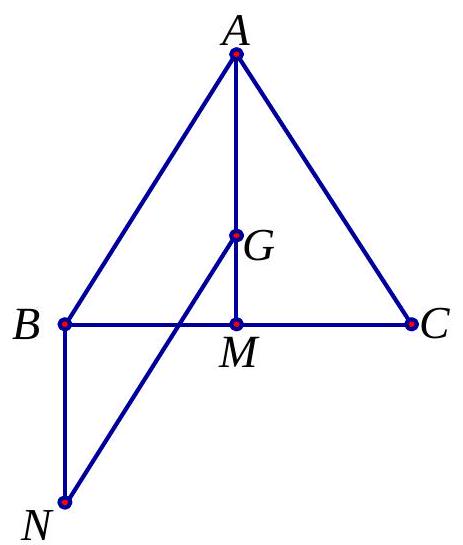
Gọi $M$ là trung điểm $BC$, dựng điểm $N$ sao cho $\overrightarrow {BN} = \overrightarrow {AG} $. Ta có : $\left| {\overrightarrow {AB} – \overrightarrow {GC} \left| = \right|\overrightarrow {GB} – \overrightarrow {GA} – \overrightarrow {GC} \left| = \right|\overrightarrow {GB} – \left( {\overrightarrow {GA} + \overrightarrow {GC} } \right)\left| = \right|2\overrightarrow {GB} } \right| = 2 \cdot GB = 2 \cdot \frac{2}{3} \cdot \frac{{2a\sqrt 3 }}{2} = \frac{{4a\sqrt 3 }}{3}$

Câu 27. Cho hình thang $ABCD$ có đáy $AB = a,CD = 2a$. Gọi $M,N$ lần lượt là trung điểm $AD$ và $BC$. Tính độ dài của véctơ $\overrightarrow {MN} + \overrightarrow {BD} + \overrightarrow {CA} $.
A. $\frac{{5a}}{2}$.
B. $\frac{{7a}}{2}$.
C. $\frac{{3a}}{2}$.
D. $\frac{a}{2}$.

Lời giải

Chọn C.

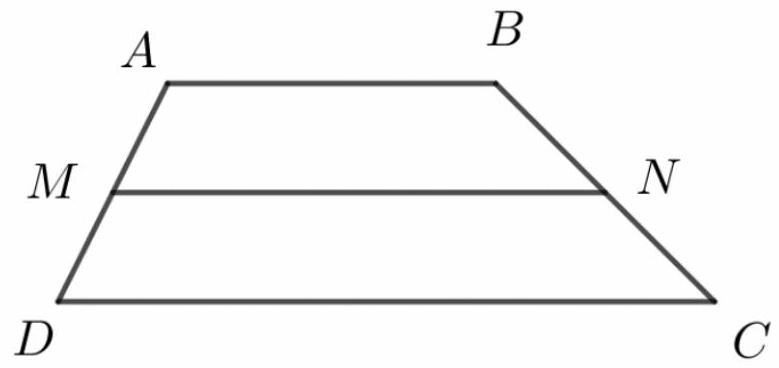
Ta có $M,N$ là trung điểm của $AD$ và $BC$ nên $\overrightarrow {MD} + \overrightarrow {MA} = \vec 0$ và $\overrightarrow {BN} + \overrightarrow {CN} = \vec 0$.

Khi đó: $\left| {\overrightarrow {MN} + \overrightarrow {BD} + \overrightarrow {CA} \left| = \right|\overrightarrow {MN} + \overrightarrow {BN} + \overrightarrow {NM} + \overrightarrow {MD} + \overrightarrow {CN} + \overrightarrow {NM} + \overrightarrow {MA} } \right|$

$ = \left| {\overrightarrow {MN} + 2\overrightarrow {NM} \left| = \right|\overrightarrow {NM} } \right| = NM = \frac{1}{2}\left( {AB + CD} \right) = \frac{{3a}}{2}.$

Câu 28. Cho hình vuông $ABCD$ cạnh $a$. Tính độ dài vectơ $\vec u = 4\overrightarrow {MA} – 3\overrightarrow {MB} + \overrightarrow {MC} – 2\overrightarrow {MD} $.
A. $\left| {\vec u} \right| = a\sqrt 5 $
B. $\left| {\vec u} \right| = \frac{{a\sqrt 5 }}{2}$
C. $\left| {\vec u} \right| = 3a\sqrt 5 $
D. $\left| {\vec u} \right| = 2a\sqrt 5 $

Lời giải

Chọn A.

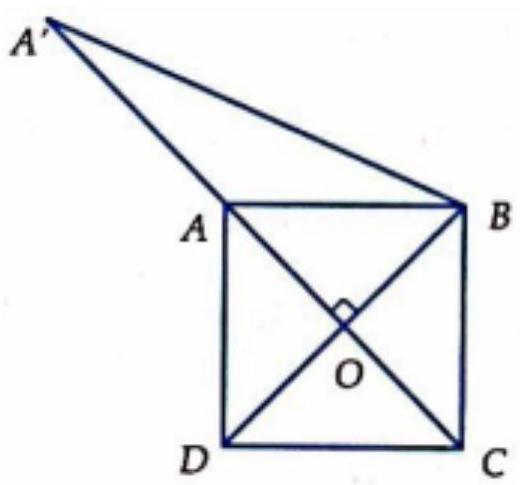
$\vec u = 4\left( {\overrightarrow {MO} + \overrightarrow {OA} } \right) – 3\left( {\overrightarrow {MO} + \overrightarrow {OB} } \right) + \left( {\overrightarrow {MO} + \overrightarrow {OC} } \right) – 2\left( {\overrightarrow {MO} + \overrightarrow {OD} } \right) = 3\overrightarrow {OA} – \overrightarrow {OB} $

Trên $OA$ lấy $A’$ sao cho $OA’ = 3OA$

$ \Rightarrow \vec u = \overrightarrow {OA’} – \overrightarrow {OB’} $

$ \Rightarrow BA’ = \sqrt {O{B^2} + O{A^2}} = a\sqrt 5 $

Câu 29. Cho tam giác $OAB$ vuông cân tại $O$ với $OA = OB = a$. Độ dài của véc tơ $\vec u = \frac{{21}}{4}\overrightarrow {OA} – \frac{5}{2}\overrightarrow {OB} $ là:
A. $\frac{{a\sqrt {140} }}{4}$
B. $\frac{{a\sqrt {321} }}{4}$
C. $\frac{{a\sqrt {520} }}{4}$
D. $\frac{{a\sqrt {541} }}{4}$

Lời giải

Chọn D

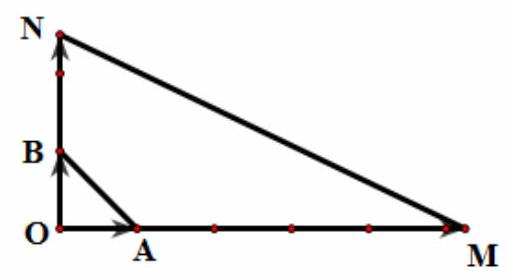
Dựng điểm $M,N$ sao cho: $\overrightarrow {OM} = \frac{{21}}{4}\overrightarrow {OA} ,\overrightarrow {ON} = \frac{5}{2}\overrightarrow {OB} $.

Khi đó: $\left| {\vec u\left| = \right|\overrightarrow {OM} – \overrightarrow {ON} \left| = \right|\overrightarrow {NM} } \right| = MN = \sqrt {O{M^2} + O{N^2}} = \sqrt {{{\left( {\frac{{21a}}{4}} \right)}^2} + {{\left( {\frac{{5a}}{2}} \right)}^2}} = \frac{{a\sqrt {541} }}{4}$.

Câu 30. Cho 2 vectơ $\vec a$ và $\vec b$ tạo với nhau góc ${60^ \circ }$. Biết $\left| {\vec a} \right| = 6$; $\left| {\vec b} \right| = 3$. Tính $\left| {\vec a + \vec b\left| + \right|\vec a – \vec b} \right|$
A. $3\left( {\sqrt 7 + \sqrt 5 } \right)$
B. $3\left( {\sqrt 7 + \sqrt 3 } \right)$
C. $6\left( {\sqrt 5 + 3} \right)$
D. $\frac{1}{2}\left( {2\sqrt 3 + \sqrt {51} } \right)$

Lời giải

Dựng $\overrightarrow {OA} = \vec a;\overrightarrow {OB} = \vec b$

Dựng hình bình hành $OACB \Rightarrow \vec a + \vec b = \overrightarrow {OC} ;\vec a – \vec b = \overrightarrow {BA} $

$ \Rightarrow \vartriangle OAB$ vuông tại $B \Rightarrow IB = \frac{{AB}}{2} = \frac{{3\sqrt 3 }}{2}$

$OI = \sqrt {O{B^2} + I{B^2}} = \frac{{\sqrt {63} }}{2} \Rightarrow OC = \sqrt {63} \Rightarrow \left| {\vec a + \vec b\left| + \right|\vec a – \vec b} \right| = \sqrt {63} + 3\sqrt 3 $

DẠNG 3: BIỂU THỊ MỘT VECTƠ THEO HAI VECTƠ KHÔNG CÙNG PHƯƠNG

Để phân tích một vectơ theo hai vectơ không cùng phương, ta thường sử dụng:

• Qui tắc ba điểm để phân tích các vectơ.

• Các hệ thức thường dùng như: hệ thức trung điểm, hệ thức trọng tâm tam giác.

• Tính chất của các hình (tam giác đều, tam giác vuông, hình vuông, hình chữ nhật …).

Câu 31. Cho tam giác $ABC$ vuông cân tại $A$, vectơ $\vec u = 3\overrightarrow {AB} – 4\overrightarrow {AC} $ đưuọc vẽ đúng ở hình nào dưới đây?

A.

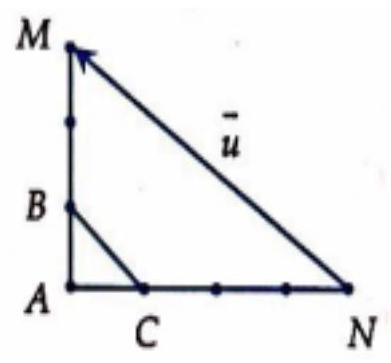
B.

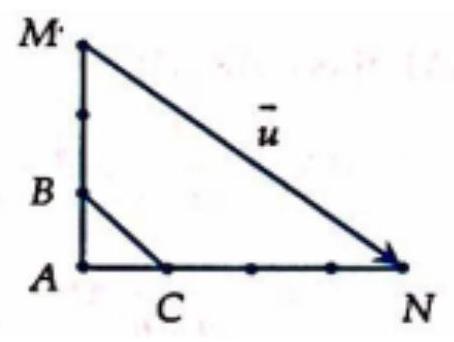
C.

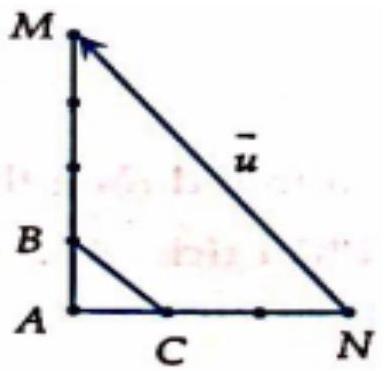
D.

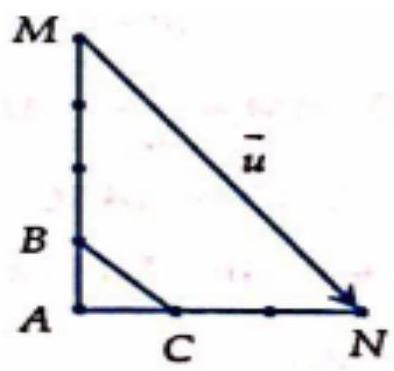
Lời giải

Chọn A.

Câu 32. Cho $AK$ và $BM$ là hai trung tuyến của $\vartriangle ABC$. Hãy phân tích vectơ $\overrightarrow {AB} $ theo hai vectơ $\overrightarrow {AK} $ và $\overrightarrow {BM} $.
A. $\overrightarrow {AB} = \frac{2}{3}\left( {\overrightarrow {AK} – \overrightarrow {BM} } \right)$
B. $\overrightarrow {AB} = \frac{1}{3}\left( {\overrightarrow {AK} – \overrightarrow {BM} } \right)$
C. $\overrightarrow {AB} = \frac{3}{2}\left( {\overrightarrow {AK} – \overrightarrow {BM} } \right)$
D. $\overrightarrow {AB} = \frac{2}{3}\left( {\overrightarrow {AK} + \overrightarrow {BM} } \right)$

Lời giải

Chọn A.

Cách 1:

Ta có: $\overrightarrow {AB} = \overrightarrow {AK} + \overrightarrow {KB} = \overrightarrow {AK} + \overrightarrow {KM} + \overrightarrow {MB} = \overrightarrow {AK} – \frac{1}{2}\overrightarrow {AB} – \overrightarrow {BM} $ (vì $KM = \frac{1}{2}AB$ )

$ \Leftrightarrow \overrightarrow {AB} + \frac{1}{2}\overrightarrow {AB} = \overrightarrow {AK} – \overrightarrow {BM} \Leftrightarrow \frac{3}{2}\overrightarrow {AB} = \overrightarrow {AK} – \overrightarrow {BM} \Leftrightarrow \overrightarrow {AB} = \frac{2}{3}\left( {\overrightarrow {AK} – \overrightarrow {BM} } \right)$

Cách 2: Giả sử có cặp số $m,n$ sao cho $\overrightarrow {AB} = m\overrightarrow {AK} + n\overrightarrow {BM} $, với $G = AK \cap BM$

Ta có $\overrightarrow {AB} = \overrightarrow {AG} + \overrightarrow {GB} ,\overrightarrow {AK} = \frac{3}{2}\overrightarrow {AG} ,\overrightarrow {BM} = \frac{3}{2}\overrightarrow {BG} $

$ \Rightarrow \overrightarrow {AG} + \overrightarrow {GB} = \frac{3}{2}m\overrightarrow {AG} – \frac{3}{2}n\overrightarrow {GB} \Leftrightarrow \left( {\frac{3}{2}m – 1} \right)\overrightarrow {AG} = \left( { – \frac{3}{2}n – 1} \right)\overrightarrow {BG} $

Do $\overrightarrow {AG} ,\overrightarrow {BG} $ không cùng phương $ \Rightarrow \left( {{\;^*}} \right) \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{\frac{3}{2}m – 1 = 0} \\
{ – \frac{2}{2}n – 1 = 0}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{m = \frac{2}{3}} \\
{n = – \frac{2}{3}}
\end{array}} \right.} \right.$

$ \Rightarrow \overrightarrow {AB} = \frac{2}{3}\left( {\overrightarrow {AK} – \overrightarrow {BM} } \right)$.

Câu 33. Cho hình bình hành $ABCD$ có $N$ là trung điểm $AB$ và $G$ là trọng tâm $\vartriangle ABC$. Phân tích $\overrightarrow {GA} $ theo $\overrightarrow {BD} $ và $\overrightarrow {NC} $
A. $\overrightarrow {GA} = – \frac{1}{3}\overrightarrow {BD} + \frac{2}{3}\overrightarrow {NC} $.
B. $\overrightarrow {GA} = \frac{1}{3}\overrightarrow {BD} – \frac{4}{3}\overrightarrow {NC} $.
C. $\overrightarrow {GA} = \frac{1}{3}\overrightarrow {BD} + \frac{2}{3}\overrightarrow {NC} $.
D. $\overrightarrow {GA} = \frac{1}{3}\overrightarrow {BD} – \frac{2}{3}\overrightarrow {NC} $.

Lời giải

Chọn D.

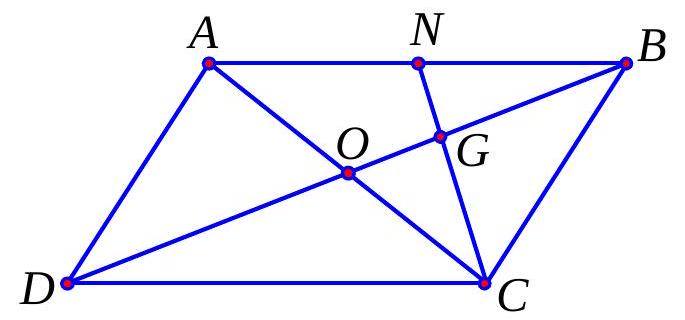
Vì $G$ là trọng tâm $\vartriangle ABC$ nên

$\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \vec 0 \Leftrightarrow \overrightarrow {GA} = – \left( {\overrightarrow {GB} + \overrightarrow {GC} } \right)$

Suy ra $\overrightarrow {GA} = – \left( { – \frac{1}{3}\overrightarrow {BD} + \frac{2}{3}\overrightarrow {NC} } \right) = \frac{1}{3}\overrightarrow {BD} – \frac{2}{3}\overrightarrow {NC} $.

Câu 34. Cho $\vartriangle ABC$ và $I$ thỏa mãn $\overrightarrow {IA} = 3\overrightarrow {IB} $. Phân tích $\overrightarrow {CI} $ theo $\overrightarrow {CA} $ và $\overrightarrow {CB} $.
A. $\overrightarrow {CI} = \frac{1}{2}\left( {\overrightarrow {CA} – 3\overrightarrow {CB} } \right)$.
B. $\overrightarrow {CI} = \overrightarrow {CA} – 3\overrightarrow {CB} $.
C. $\overrightarrow {CI} = \frac{1}{2}\left( {3\overrightarrow {CB} – \overrightarrow {CA} } \right)$.
D. $\overrightarrow {CI} = 3\overrightarrow {CB} – \overrightarrow {CA} $.

Lời giải

Chọn C.

Ta có: $\overrightarrow {CI} = \overrightarrow {CA} + \overrightarrow {AI} $

$ \Leftrightarrow \overrightarrow {CI} = \overrightarrow {CA} – 3\overrightarrow {IB} $

$ \Leftrightarrow \overrightarrow {CI} = \overrightarrow {CA} – 3\left( {\overrightarrow {IC} + \overrightarrow {CB} } \right)$

$ \Leftrightarrow \overrightarrow {CI} = \overrightarrow {CA} + 3\overrightarrow {CI} – 3\overrightarrow {CB} $

$ \Leftrightarrow \overrightarrow {CI} = – \frac{1}{2}\left( {\overrightarrow {CA} – 3\overrightarrow {CB} } \right)$

$ \Leftrightarrow \overrightarrow {CI} = \frac{1}{2}\left( {3\overrightarrow {CB} – \overrightarrow {CA} } \right)$

Câu 35. Cho hình bình hành $ABCD$. Gọi $M,N$ là các điểm nằm trên các cạnh $AB$ và $CD$ sao cho $AM = \frac{1}{3}AB,CN = \frac{1}{2}CD$. Gọi $G$ là trọng tâm của $\vartriangle BMN$. Hãy phân tích $\overrightarrow {AG} $ theo hai vectơ $\overrightarrow {AB} = \vec a,\overrightarrow {AC} = \vec b$.
A. $\overrightarrow {AG} = \frac{1}{{18}}\vec a + \frac{5}{3}\vec b$
B. $\overrightarrow {AG} = \frac{1}{{18}}\vec a + \frac{1}{5}\vec b$
C. $\overrightarrow {AG} = \frac{5}{{18}}\vec a + \frac{1}{3}\vec b$
D. $\overrightarrow {AG} = \frac{5}{{18}}\vec a – \frac{1}{3}\vec b$

Lời giải

Chọn C.

Ta có $\overrightarrow {AM} + \overrightarrow {AN} + \overrightarrow {AB} = 3\overrightarrow {AG} $ mà $\overrightarrow {AM} = \frac{1}{3}\overrightarrow {AB} $

$\begin{array}{*{20}{r}}
{}&{\overrightarrow {AN} = \frac{1}{2}\left( {\overrightarrow {AC} + \overrightarrow {AD} } \right) = \frac{1}{2}\left( {\overrightarrow {AC} + \overrightarrow {AC} – \overrightarrow {AB} } \right) = – \frac{1}{2}\vec a + \vec b} \\
{}&{\; \Rightarrow 3\overrightarrow {AG} = \frac{1}{3}\overrightarrow {AB} – \frac{1}{2}\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AB} = \frac{5}{6}\overrightarrow {AB} + \overrightarrow {AC} } \\
{}&{\; \Leftrightarrow \overrightarrow {AG} = \frac{5}{{18}}\vec a + \frac{1}{3}\vec b.}
\end{array}$

Câu 36. Cho $\vartriangle ABC$. Gọi $I$ là điểm trên cạnh $BC$ sao cho $2CI = 3BI$ và $J$ là điểm trên tia đối của $BC$ sao cho $5JB = 2JC$. Tính $\overrightarrow {AI} ,\overrightarrow {AJ} $ theo $\vec a = \overrightarrow {AB} ,\vec b = \overrightarrow {AC} $.
A. $\overrightarrow {AI} = \frac{3}{5}\vec a + \frac{2}{5}\vec b,\overrightarrow {AJ} = \frac{5}{3}\vec a – \frac{2}{3}\vec b$
B. $\overrightarrow {AI} = \frac{3}{5}\vec a – \frac{2}{5}\vec b,\overrightarrow {AJ} = \frac{5}{3}\overrightarrow {a – \frac{2}{3}\vec b} $
C. $\overrightarrow {AI} = \frac{2}{5}\vec a + \frac{3}{5}\vec b,\overrightarrow {AJ} = \frac{5}{3}\vec a – \frac{2}{3}\vec b$
D. $\overrightarrow {AI} = \frac{3}{5}\vec a + \frac{2}{5}\vec b,\overrightarrow {AJ} = \frac{5}{3}\vec a + \frac{2}{3}\vec b$

Lời giải

Chọn A.

Ta có: $2\overrightarrow {IC} = – 3\overrightarrow {IB} \Leftrightarrow 2\left( {\overrightarrow {AC} – \overrightarrow {AI} } \right) = – 3\left( {\overrightarrow {AB} – \overrightarrow {AI} } \right)$

$ \Leftrightarrow 5\overrightarrow {AI} = 3\overrightarrow {AB} + 2\overrightarrow {AC} \Leftrightarrow \overrightarrow {AI} = \frac{3}{5}\overrightarrow {AB} + \frac{2}{5}\overrightarrow {AC} .$

Ta lại có: $5\overrightarrow {JB} = 2\overrightarrow {JC} \Leftrightarrow 5\left( {\overrightarrow {AB} – \overrightarrow {AJ} } \right) = 2\left( {\overrightarrow {AC} – \overrightarrow {AJ} } \right)$

$ \Leftrightarrow 3\overrightarrow {AJ} = 5\overrightarrow {AB} – 2\overrightarrow {AC} \Leftrightarrow \overrightarrow {AJ} = \frac{5}{3}\overrightarrow {AB} – \frac{2}{3}\overrightarrow {AC} $

Câu 37. Cho hình bình hành $ABCD$ có $E,N$ lần lượt là trung điểm của $BC,AE$. Tìm các số $p$ và $q$ sao cho $\overrightarrow {DN} = p\overrightarrow {AB} + q\overrightarrow {AC} $.
A. $p = \frac{5}{4};q = \frac{3}{4}$
B. $p = – \frac{4}{3};q = \frac{2}{3}$
C. $p = – \frac{4}{3};q = – \frac{2}{3}$
D. $p = \frac{5}{4};q = – \frac{3}{4}$

Lời giải

Chọn D.

$\overrightarrow {DN} = \overrightarrow {DA} + \overrightarrow {AN} = \overrightarrow {CB} + \frac{1}{2}\overrightarrow {AE} $

$ = \overrightarrow {AB} – \overrightarrow {AC} + \frac{1}{4}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)$

$ = \frac{5}{4}\overrightarrow {AB} – \frac{3}{4}\overrightarrow {AC} $

Vậy $p = \frac{5}{4},q = – \frac{3}{4}$

Câu 38. Cho hình chữ nhật $ABCD$ tâm $O$. Gọi $M,N$ lần lượt là trung điểm của $OA$ và $CD$. Biết $\overrightarrow {MN} = a \cdot \overrightarrow {AB} + b \cdot \overrightarrow {AD} $. Tính $a + b$.
A. $a + b = 1$.
B. $a + b = \frac{1}{2}$.
C. $a + b = \frac{3}{4}$.
D. $a + b = \frac{1}{4}$.

Lời giải

Chọn A.

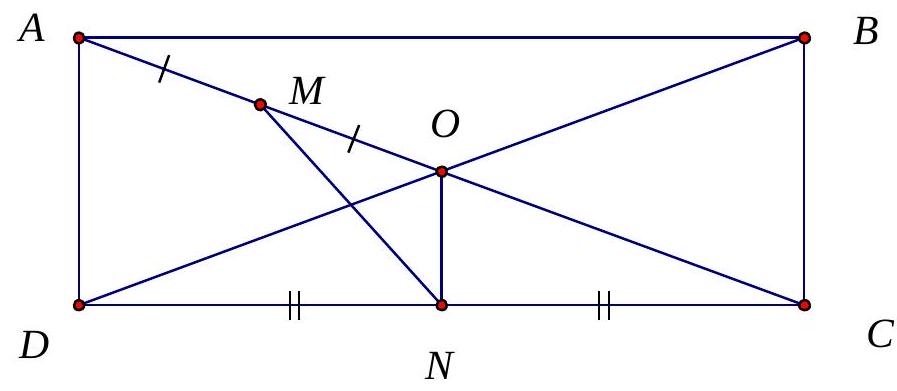
$\overrightarrow {MN} = \overrightarrow {MO} + \overrightarrow {ON} = \frac{1}{4}\overrightarrow {AC} + \frac{1}{2}\overrightarrow {AD} = \frac{1}{4}\left( {\overrightarrow {AB} + \overrightarrow {BC} } \right) + \frac{1}{2}\overrightarrow {AD} = \frac{1}{4}\left( {\overrightarrow {AB} + \overrightarrow {AD} } \right) + \frac{1}{2}\overrightarrow {AD} = \frac{1}{4}\overrightarrow {AB} + \frac{3}{4}\overrightarrow {AD} $

$ \Rightarrow a = \frac{1}{4};b = \frac{3}{4}$. Vậy $a + b = 1$.

Câu 39. Cho tứ giác $ABCD$, trên cạnh $AB,CD$ lấy lần lượt các điểm $M,N$ sao cho $3\overrightarrow {AM} = 2\overrightarrow {AB} $ và $3\overrightarrow {DN} = 2\overrightarrow {DC} $. Tính vectơ $\overrightarrow {MN} $ theo hai vectơ $\overrightarrow {AD} ,\overrightarrow {BC} $.
A. $\overrightarrow {MN} = \frac{1}{3}\overrightarrow {AD} + \frac{1}{3}\overrightarrow {BC} $.
B. $\overrightarrow {MN} = \frac{1}{3}\overrightarrow {AD} – \frac{2}{3}\overrightarrow {BC} $.
C. $\overrightarrow {MN} = \frac{1}{3}\overrightarrow {AD} + \frac{2}{3}\overrightarrow {BC} $.
D. $\overrightarrow {MN} = \frac{2}{3}\overrightarrow {AD} + \frac{1}{3}\overrightarrow {BC} $.

Lời giải

Chọn C.

Ta có $\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AD} + \overrightarrow {DN} = \frac{2}{3}\overrightarrow {BA} + \overrightarrow {AD} + \frac{2}{3}\overrightarrow {DC} $

$ = \frac{2}{3}\left( {\overrightarrow {BC} + \overrightarrow {CA} } \right) + \overrightarrow {AD} + \frac{2}{3}\left( {\overrightarrow {DA} + \overrightarrow {AC} } \right) = \frac{2}{3}\overrightarrow {BC} + \overrightarrow {AD} – \frac{2}{3}\overrightarrow {AD} = \frac{1}{3}\overrightarrow {AD} + \frac{2}{3}\overrightarrow {BC} .\;$

Câu 40. Trên đường thẳng chứa cạnh $BC$ của tam giác $ABC$ lấy một điểm $M$ sao cho $\overrightarrow {MB} = 3\overrightarrow {MC} $. Khi đó đẳng thức nào sau đây đúng?
A. $\overrightarrow {AM} = – \frac{1}{2}\overrightarrow {AB} + \frac{3}{2}\overrightarrow {AC} $
B. $\overrightarrow {AM} = 2\overrightarrow {AB} + \overrightarrow {AC} $
C. $\overrightarrow {AM} = \overrightarrow {AB} – \overrightarrow {AC} $
D. $\overrightarrow {AM} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)$

Lời giải

Chọn A

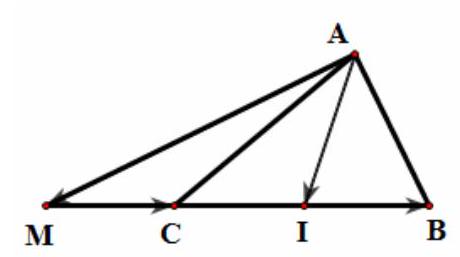
Gọi $I$ là trung điểm của $BC$. Khi đó $C$ là trung điểm của $MI$. Ta có:

$\overrightarrow {AM} + \overrightarrow {AI} = 2\overrightarrow {AC} \Leftrightarrow \overrightarrow {AM} = – \overrightarrow {AI} + 2\overrightarrow {AC} = – \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) + 2\overrightarrow {AC} = – \frac{1}{2}\overrightarrow {AB} + \frac{3}{2}\overrightarrow {AC} .$

Câu 41. Cho tam giác $ABC$ biết $AB = 8,AC = 9,BC = 11$. Gọi $M$ là trung điểm $BC$ và $N$ là điểm trên đoạn $AC$ sao cho $AN = x(0 < x < 9)$. Hệ thức nào sau đây đúng?
A. $\overrightarrow {MN} = \left( {\frac{1}{2} – \frac{x}{9}} \right)\overrightarrow {AC} + \frac{1}{2}\overrightarrow {AB} $
B. $\overrightarrow {MN} = \left( {\frac{x}{9} – \frac{1}{2}} \right)\overrightarrow {CA} + \frac{1}{2}\overrightarrow {BA} $
C. $\overrightarrow {MN} = \left( {\frac{x}{9} + \frac{1}{2}} \right)\overrightarrow {AC} – \frac{1}{2}\overrightarrow {AB} $
D. $\overrightarrow {MN} = \left( {\frac{x}{9} – \frac{1}{2}} \right)\overrightarrow {AC} – \frac{1}{2}\overrightarrow {AB} $

Lời giải

Chọn D

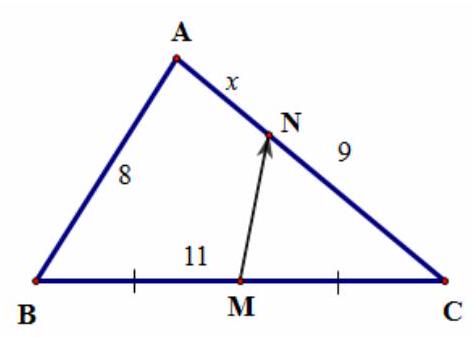
Ta có: $\overrightarrow {MN} = \overrightarrow {AN} – \overrightarrow {AM} = \frac{x}{9}\overrightarrow {AC} – \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) = \left( {\frac{x}{9} – \frac{1}{2}} \right)\overrightarrow {AC} – \frac{1}{2}\overrightarrow {AB} $.

Câu 42. Cho tam giác $ABC$. Gọi $G$ là trọng tâm và $H$ là điểm đối xứng với $B$ qua $G$. Trong các khẳng định sau, khẳng định nào đúng?
A. $\overrightarrow {AH} = \frac{2}{3}\overrightarrow {AC} – \frac{1}{3}\overrightarrow {AB} $
B. $\overrightarrow {AH} = \frac{1}{3}\overrightarrow {AC} – \frac{1}{3}\overrightarrow {AB} $
C. $\overrightarrow {AH} = \frac{2}{3}\overrightarrow {AC} + \frac{1}{3}\overrightarrow {AB} $
D. $\overrightarrow {AH} = \frac{2}{3}\overrightarrow {AB} – \frac{1}{3}\overrightarrow {AC} $

Lời giải

Chọn A

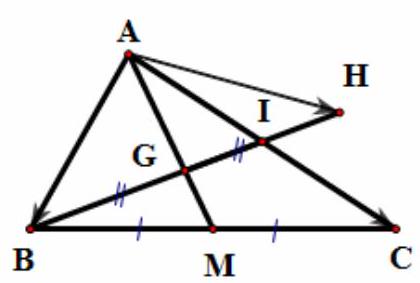
Gọi $M,I$ lần lượt là trung điểm của $BC$ và $AC$.

Ta thấy $AHCG$ là hình bình hành nên

$\overrightarrow {AH} + \overrightarrow {AG} = \overrightarrow {AC} \Leftrightarrow \overrightarrow {AH} + \frac{2}{3}\overrightarrow {AM} = \overrightarrow {AC} \Leftrightarrow \overrightarrow {AH} + \frac{2}{3} \cdot \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) = \overrightarrow {AC} $

$ \Leftrightarrow \overrightarrow {AH} = \overrightarrow {AC} – \frac{1}{3}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) \Leftrightarrow \overrightarrow {AH} = \frac{2}{3}\overrightarrow {AC} – \frac{1}{3}\overrightarrow {AB} $

Câu 43. Cho tam giác $ABC$. Gọi $M$ là trung điểm của $AB,N$ là điểm thuộc $AC$ sao cho $\overrightarrow {CN} = 2\overrightarrow {NA} $. K là trung điểm của $MN$. Mệnh đề nào sau đây là đúng?
A. $\overrightarrow {AK} = \frac{1}{4}\overrightarrow {AB} + \frac{1}{6}\overrightarrow {AC} $.
B. $\overrightarrow {AK} = \frac{1}{2}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} $.
C. $\overrightarrow {AK} = \frac{1}{4}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} $.
D. $\overrightarrow {AK} = \frac{1}{2}\overrightarrow {AB} + \frac{2}{3}\overrightarrow {AC} $.

Lời giải

Chọn A

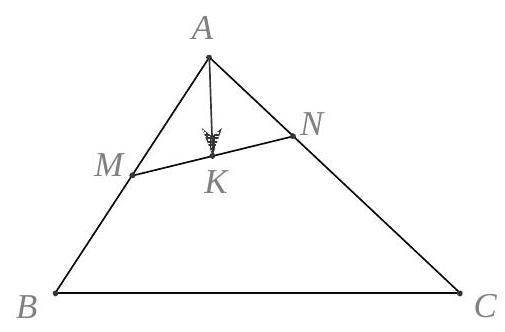
Ta có $M$ là trung điểm $AB$ nên $\overrightarrow {AM} = \frac{1}{2}\overrightarrow {AB} ;\overrightarrow {CN} = 2\overrightarrow {NA} \Rightarrow \overrightarrow {AN} = \frac{1}{3}\overrightarrow {AC} $.

Do đó $\overrightarrow {AK} = \frac{1}{2}\left( {\overrightarrow {AM} + \overrightarrow {AN} } \right) = \frac{1}{4}\overrightarrow {AB} + \frac{1}{6}\overrightarrow {AC} $.

Câu 44. Cho tứ giác $ABCD,O$ là giao điểm của hai đường chéo $AC$ và $BD$. Gọi $G$ theo thứ tự là trọng tâm của tam giác $OAB$ và $OCD$. Khi đó $\overrightarrow {GG’} $ bằng:
A. $\frac{1}{2}\left( {\overrightarrow {AC} + \overrightarrow {BD} } \right)$.
B. $\frac{2}{3}\left( {\overrightarrow {AC} + \overrightarrow {BD} } \right)$.
C. $3\left( {\overrightarrow {AC} + \overrightarrow {BD} } \right)$.
D. $\frac{1}{3}\left( {\overrightarrow {AC} + \overrightarrow {BD} } \right)$.

Lời giải

Chọn D

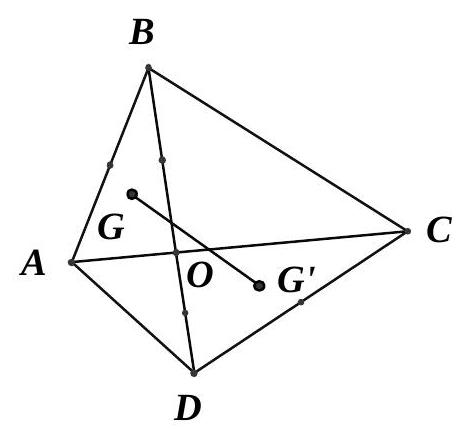
Vì $G’$ là trọng tâm của tam giác $OCD$ nên $\overrightarrow {GG’} = \frac{1}{3}\left( {\overrightarrow {GO} + \overrightarrow {GC} + \overrightarrow {GD} } \right)$.

Vì $G$ là trọng tâm của tam giác $OAB$ nên: $\overrightarrow {GO} + \overrightarrow {GA} + \overrightarrow {GB} = \vec 0 \Rightarrow \overrightarrow {GO} = – \overrightarrow {GA} – \overrightarrow {GB} $ (2)

Từ (1) và (2) suy ra: $\overrightarrow {GG’} = \frac{1}{3}\left( { – \overrightarrow {GA} – \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} } \right) = \frac{1}{3}\left( {\overrightarrow {AC} + \overrightarrow {BD} } \right)$.

Câu 45. Cho tam giác $ABC$ với phân giác trong $AD$. Biết $AB = 5,BC = 6,CA = 7$. Khi đó $\overrightarrow {AD} $ bằng:
A. $\frac{5}{{12}}\overrightarrow {AB} + \frac{7}{{12}}\overrightarrow {AC} $.
B. $\frac{7}{{12}}\overrightarrow {AB} – \frac{5}{{12}}\overrightarrow {AC} $.
C. $\frac{7}{{12}}\overrightarrow {AB} + \frac{5}{{12}}\overrightarrow {AC} $.
D. $\frac{5}{{12}}\overrightarrow {AB} – \frac{7}{{12}}\overrightarrow {AC} $.

Lời giải

Chọn C

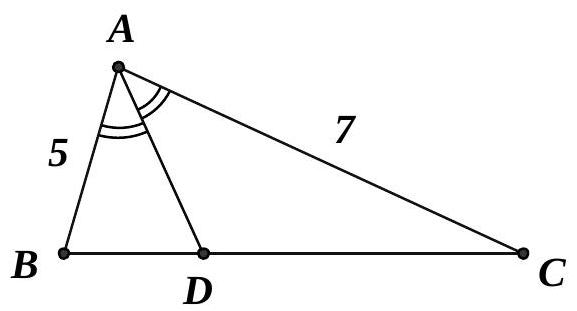
Vì $AD$ là phân giác trong của tam giác $ABC$ nên:

$\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} = \frac{5}{7} \Rightarrow \overrightarrow {BD} = \frac{5}{7}\overrightarrow {DC} $

$ \Leftrightarrow \overrightarrow {AD} – \overrightarrow {AB} = \frac{5}{7}\left( {\overrightarrow {AC} – \overrightarrow {AD} } \right)$

$ \Leftrightarrow \overrightarrow {AD} = \frac{7}{{12}}\overrightarrow {AB} + \frac{5}{{12}}\overrightarrow {AC} $.

Câu 46. Cho tam giác $ABC$. Gọi $M$ là trung điểm của $AB$ và $N$ là một điểm trên cạnh $AC$ sao cho $NC = 2NA$. Gọi $K$ là trung điểm của $MN$. Khi đó:
A. $\overrightarrow {AK} = \frac{1}{6}\overrightarrow {AB} + \frac{1}{4}\overrightarrow {AC} $
B. $\overrightarrow {AK} = \frac{1}{4}\overrightarrow {AB} – \frac{1}{6}\overrightarrow {AC} $
C. $\overrightarrow {AK} = \frac{1}{4}\overrightarrow {AB} + \frac{1}{6}\overrightarrow {AC} $
D. $\overrightarrow {AK} = \frac{1}{6}\overrightarrow {AB} – \frac{1}{4}\overrightarrow {AC} $

Lời giải

Chọn C

Câu 47. Cho tam giác $ABC,N$ là điểm xác định bởi $\overrightarrow {CN} = \frac{1}{2}\overrightarrow {BC} ,G$ là trọng tâm tam giác $ABC$. Hệ thức tính $\overrightarrow {AC} $ theo $\overrightarrow {AG} ,\overrightarrow {AN} $ là:
A. $\overrightarrow {AC} = \frac{2}{3}\overrightarrow {AG} + \frac{1}{2}\overrightarrow {AN} $
B. $\overrightarrow {AC} = \frac{4}{3}\overrightarrow {AG} – \frac{1}{2}\overrightarrow {AN} $
C. $\overrightarrow {AC} = \frac{3}{4}\overrightarrow {AG} + \frac{1}{2}\overrightarrow {AN} $
D. $\overrightarrow {AC} = \frac{3}{4}\overrightarrow {AG} – \frac{1}{2}\overrightarrow {AN} $

Lời giải

Chọn C

Câu 48. Cho tam giác $ABC$. Gọi $M$ là điểm trên cạnh $BC$ sao cho $MB = 2MC$. Khi đó:
A. $\overrightarrow {AM} = \frac{1}{3}\overrightarrow {AB} + \frac{2}{3}\overrightarrow {AC} $.
B. $\overrightarrow {AM} = \frac{2}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} $.
C. $\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {AC} $.
D. $\overrightarrow {AM} = \frac{2}{5}\overrightarrow {AB} + \frac{3}{5}\overrightarrow {AC} $.

Lời giải

Chọn A.

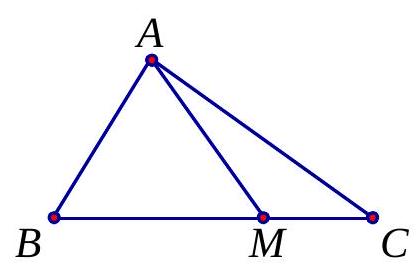
Cách 1: Ta có $\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {BM} = \overrightarrow {AB} + \frac{2}{3}\overrightarrow {BC} = \overrightarrow {AB} + \frac{2}{3}\left( {\overrightarrow {AC} – \overrightarrow {AB} } \right) = \frac{1}{3}\overrightarrow {AB} + \frac{2}{3}\overrightarrow {AC} $.

Cách 2: Ta có $MB = 2MC \Leftrightarrow \overrightarrow {MB} = – 2\overrightarrow {MC} $ (vì $\overrightarrow {MB} $ và $\overrightarrow {MC} $ ngược hướng)

$ \Leftrightarrow \overrightarrow {AB} – \overrightarrow {AM} = – 2\left( {\overrightarrow {AC} – \overrightarrow {AM} } \right) \Leftrightarrow \overrightarrow {AM} = \frac{1}{3}\overrightarrow {AB} + \frac{2}{3}\overrightarrow {AC} $.

Câu 49. Cho tam giác $ABC$. Gọi $M$ là điểm được xác định: $4\overrightarrow {BM} – 3\overrightarrow {BC} = \vec 0$. Khi đó vectơ $\overrightarrow {AM} $ bằng
A. $\overrightarrow {AB} + \overrightarrow {AC} $.
B. $\frac{1}{2}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} $.
C. $\overrightarrow {\frac{1}{3}AB} + \frac{2}{3}\overrightarrow {AC} $.
D. $\frac{1}{4}\overrightarrow {AB} + \frac{3}{4}\overrightarrow {AC} $.

Lời giải

Chọn D.

Ta có: $4\overrightarrow {BM} – 3\overrightarrow {BC} = \vec 0 \Leftrightarrow 4\left( {\overrightarrow {AM} – \overrightarrow {AB} } \right) – 3\left( {\overrightarrow {AC} – \overrightarrow {AB} } \right) = \vec 0$

$ \Leftrightarrow 4\overrightarrow {AM} – 4\overrightarrow {AB} – 3\overrightarrow {AC} + 3\overrightarrow {AB} = \vec 0 \Leftrightarrow \overrightarrow {AM} = \frac{1}{4}\overrightarrow {AB} + \frac{3}{4}\overrightarrow {AC} $.

Câu 50. Cho tam giác $ABC$ có $I,D$ lần lượt là trung điểm $AB,CI$. Đẳng thức nào sau đây đúng?
A. $\overrightarrow {BD} = \frac{1}{2}\overrightarrow {AB} – \frac{3}{4}\overrightarrow {AC} $.
B. $\overrightarrow {BD} = – \frac{3}{4}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AC} $.
C. $\overrightarrow {BD} = – \frac{1}{4}\overrightarrow {AB} + \frac{3}{2}\overrightarrow {AC} $.
D. $\overrightarrow {BD} = – \frac{3}{4}\overrightarrow {AB} – \frac{1}{2}\overrightarrow {AC} $.

Lời giải

Chọn B.

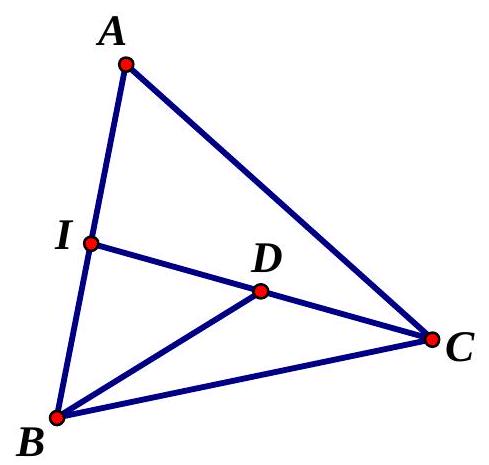
Vì $I,D$ lần lượt là trung điểm $AB,CI$ nên ta có

$\overrightarrow {BD} = \frac{1}{2}\left( {\overrightarrow {BI} + \overrightarrow {BC} } \right) = \frac{1}{2}\left( {\frac{1}{2}\overrightarrow {BA} + \overrightarrow {BA} + \overrightarrow {AC} } \right) = – \frac{3}{4}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AC} $

Câu 51. Cho tam giác $ABC$. Gọi $I,J$ là hai điểm xác định bởi $\overrightarrow {IA} = 2\overrightarrow {IB} ,3\overrightarrow {JA} + 2\overrightarrow {JC} = \vec 0$. Hệ thức nào đúng?
A. $\overrightarrow {IJ} = \frac{5}{2}\overrightarrow {AC} – 2\overrightarrow {AB} $.
B. $\overrightarrow {IJ} = \frac{5}{2}\overrightarrow {AB} – 2\overrightarrow {AC} $.
C. $\overrightarrow {IJ} = \frac{2}{5}\overrightarrow {AB} – 2\overrightarrow {AC} $.
D. $\overrightarrow {IJ} = \frac{2}{5}\overrightarrow {AC} – 2\overrightarrow {AB} $.

Lời giải

Chọn D.

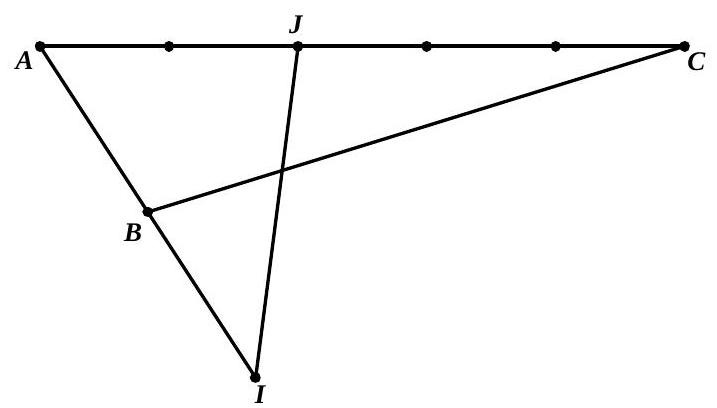
Ta có: $\overrightarrow {IJ} = \overrightarrow {IA} + \overrightarrow {AJ} = – 2\overrightarrow {AB} + \frac{2}{5}\overrightarrow {AC} = \frac{2}{5}\overrightarrow {AC} – 2\overrightarrow {AB} $.

Câu 52. Cho $\vartriangle ABC$. Diểm $M$ nằm trên đường thẳng $BC$ sao cho $\overrightarrow {MB} = k\overrightarrow {MC} \left( {k \ne 1} \right)$. Phân tích $\overrightarrow {AM} $ theo $\overrightarrow {AB} ,\overrightarrow {AC} $.
A. $\overrightarrow {AM} = \frac{{\overrightarrow {AB} + k\overrightarrow {AC} }}{{1 – k}}$
B. $\overrightarrow {AM} = \frac{{\overrightarrow {AB} – k\overrightarrow {AC} }}{{1 + k}}$
C. $\overrightarrow {AM} = \frac{{\overrightarrow {AB} – k\overrightarrow {AC} }}{{1 – k}}$
D. $\overrightarrow {AM} = \frac{{\overrightarrow {AB} + k\overrightarrow {AC} }}{{1 – k}}$

Lời giải

Chọn C.

$\begin{array}{*{20}{r}}
{}&{\overrightarrow {MB} = k\overrightarrow {MC} } \\
{}&{\; \Leftrightarrow \overrightarrow {AB} – \overrightarrow {AM} = k\left( {\overrightarrow {AC} – \overrightarrow {AM} } \right)} \\
{}&{\; \Leftrightarrow \overrightarrow {AM} = \frac{{\overrightarrow {AB} – k\overrightarrow {AC} }}{{1 – k}}}
\end{array}$

Câu 53. Cho $\vartriangle OAB$ với $M,N$ lần lượt là trung điểm của $OA,OB$. Tìm số $m,n$ thích hợp để $\overrightarrow {NA} = m\overrightarrow {OA} + n\overrightarrow {OB} $
A. $m = – 1,n = \frac{1}{2}$
B. $m = 1,n = – \frac{1}{2}$
C. $m = 1,n = \frac{1}{2}$
D. $m = – 1,n = – \frac{1}{2}$

Lời giải

Chọn B.

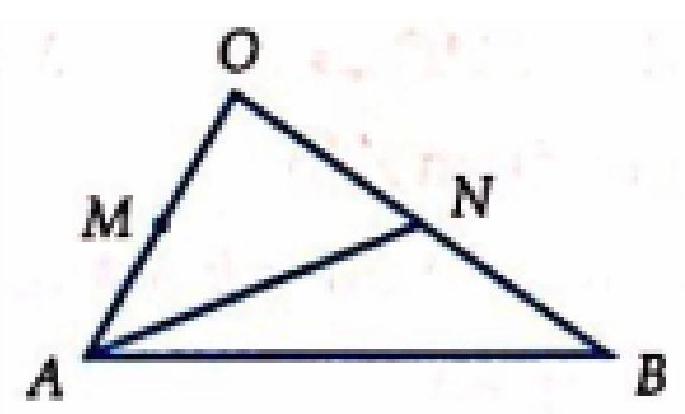
$\overrightarrow {NA} = \overrightarrow {OA} – \overrightarrow {ON} = \overrightarrow {OA} – \frac{1}{2}\overrightarrow {OB} $

Câu 54. Một đường thẳng cắt các cạnh $DA,DC$ và đường chép $DB$ của hình bình hành $ABCD$ lần lượt tại các điểm $E,F$ và $M$. Biết rẳng $\overrightarrow {DE} = m\overrightarrow {DA} ,\overrightarrow {DF} = n\overrightarrow {DC} (m,n > 0)$. Hãy biểu diễn $\overrightarrow {DM} $ qua $\overrightarrow {DB} $ và $m,n$.
A. $\overrightarrow {DM} = \frac{{m \cdot n}}{{m + n}}\overrightarrow {DB} $
B. $\overrightarrow {DM} = \frac{m}{{m + n}}\overrightarrow {DB} $
C. $\overrightarrow {DM} = \frac{n}{{m + n}}\overrightarrow {DB} $
D. $\overrightarrow {DM} = \frac{{m \cdot n}}{{m – n}}\overrightarrow {DB} $

Lời giải

Chọn A.

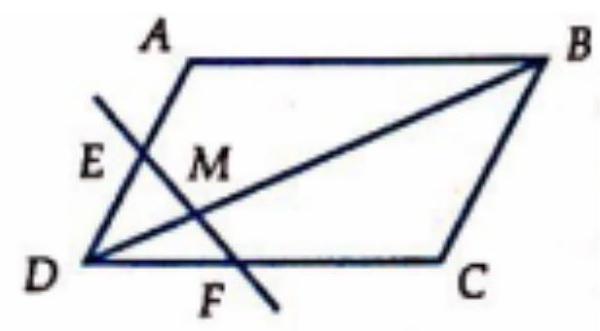
Đặt $\overrightarrow {DM} = x\overrightarrow {DB} ,\overrightarrow {EM} = y\overrightarrow {FM} $

$ \Rightarrow \overrightarrow {DM} = x\overrightarrow {DA} + x\overrightarrow {DC} $

Nên: $\overrightarrow {EM} = \overrightarrow {DM} – \overrightarrow {DE} = x\overrightarrow {DA} + x\overrightarrow {DC} – m\overrightarrow {DA} = \left( {x – m} \right)\overrightarrow {DA} + x\overrightarrow {DC} $

Ta có: $\overrightarrow {EM} = y\overrightarrow {FM} \Leftrightarrow \left( {x – m} \right)\overrightarrow {DA} + x\overrightarrow {DC} – xy\overrightarrow {DA} + y\left( {x – m} \right)\overrightarrow {DC} $

Do $DA$ và $DC$ không cùng phương nên: $\left\{ {\begin{array}{*{20}{l}}
{x – m = xy} \\
{x = y\left( {x – n} \right)}
\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x = \frac{{m \cdot n}}{{m + n}}} \\
{y = – \frac{m}{n}}
\end{array} \Leftrightarrow \overrightarrow {DM} = \frac{{m \cdot n}}{{m + n}}\overrightarrow {DB} } \right.} \right.$

Câu 55. Cho tam giác $ABC$, hai điểm $M,N$ thỏa mãn hệ thức $\overrightarrow {MA} + \overrightarrow {MB} – \overrightarrow {MC} = \vec 0$ và $2\overrightarrow {NA} + \overrightarrow {NB} + \overrightarrow {NC} = \vec 0$. Tìm hai số $p,q$ sao cho $\overrightarrow {MN} = p\overrightarrow {AB} + q\overrightarrow {AC} $.
A. $p = q = – \frac{3}{4}$
B. $p = 2,q = 0$
C. $p = – \frac{1}{2},q = – \frac{1}{2}$
D. $p = – \frac{3}{4},q = \frac{5}{4}$

Lời giải

Chọn D.

Từ giả thiết: $\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow {MC} $

$ \Rightarrow M$ là đỉnh thứ tư của hình bình hành $ACBM$.

Từ giả thiết: $2\overrightarrow {NA} + \overrightarrow {NB} + \overrightarrow {NC} = \vec 0 \Leftrightarrow 2\overrightarrow {NA} + 2\overrightarrow {NK} = \vec 0$

$N$ là trung điểm $AK$, với $K$ là trung điểm $BC$.

Ta có:

$\overrightarrow {MN} = \overrightarrow {MA} + \overrightarrow {AN} = \overrightarrow {BC} + \frac{1}{2}\overrightarrow {AK} = \overrightarrow {AC} – \overrightarrow {AB} + \frac{1}{4}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) = – \frac{3}{4}\overrightarrow {AB} + \frac{5}{4}\overrightarrow {AC} $

$ \Rightarrow p = – \frac{3}{4},q = \frac{5}{4}$

DẠNG 4: CHỨNG MINH BA ĐIỂM THẲNG HÀNG-CHỨNG MINH HAI ĐƯỜNG THẲNG SONG SONG-CHỨNG MINH HAI ĐIỂM TRÙNG NHAU

Để chứng minh ba điểm $A,B,C$ thẳng hàng ta chứng minh ba điểm đó thoả mãn đẳng thức

$ + \overrightarrow {AB} = k\overrightarrow {AC} ,k \ne 0$

$ + \overrightarrow {MC} = \alpha \cdot \overrightarrow {MA} + \left( {1 – \alpha } \right) \cdot \overrightarrow {MB} $ với $\forall M,\alpha \in \mathbb{R}$

• Để chứng minh $AB//CD$ ta chứng minh: $\overrightarrow {AB} = k\overrightarrow {CD} ,k \ne 0$

• Để chứng minh hai điểm $M,N$ trùng nhau ta chứng minh chúng thoả mãn đẳng thức

$\overrightarrow {{\text{OM}}}  = \overrightarrow {{\text{ON}}} $, với ${\text{O}}$ là một điểm nào đó hoặc $\overrightarrow {{\text{MN}}}  = \vec 0$.

Câu 56. Cho ba điểm $A,B,C$ phân biệt. Điều kiện cần và đủ để ba điểm thẳng hàng là:
A. $AB = AC$
B. $\exists k \ne 0:\overrightarrow {AB} = k \cdot \overrightarrow {AC} $
C. $\overrightarrow {AC} – \overrightarrow {AB} = \overrightarrow {BC} $
D. $\overrightarrow {MA} + \overrightarrow {MB} = 3\overrightarrow {MC} ,\forall $

điểm $M$

Lời giải

Chọn B

Câu 57. Cho $\vartriangle ABC$. Đặt $\vec a = \overrightarrow {BC} ,\vec b = \overrightarrow {AC} $. Các cặp vectơ nào sau đây cùng phương?
A. $2\vec a + \vec b,\vec a + 2\vec b$
B. $\vec a – 2\vec b,2\vec a – \vec b$
C. $5\vec a + \vec b, – 10\vec a – 2\vec b$
D. $\vec a + \vec b,\vec a – \vec b$

Lời giải

Chọn C

Ta có: $ – 10\vec a – 2\vec b = – 2.\left( {5\vec a + \vec b} \right) \Rightarrow 5\vec a + \vec b$ và $ – 10\vec a – 2\vec b$ cùng phương.

Câu 58. Cho hai vectơ $\vec a$ và $\vec b$ không cùng phương. Hai vectơ nào sau đây cùng phương?
A. $ – 3\vec a + \vec b$ và $ – \frac{1}{2}\vec a + 6\vec b$
B. $ – \frac{1}{2}\vec a – \vec b$ và $2\vec a + \vec b$
C. $\frac{1}{2}\vec a – \vec b$ và $ – \frac{1}{2}\vec a + \vec b$
D. $\frac{1}{2}\vec a + \vec b$ và $\vec a – 2\vec b$

Lời giải

Chọn C

Câu 59. Cho hai vectơ $\vec a$ và $\vec b$ không cùng phương. Hai vectơ nào sau đây là cùng phương?
A. $\vec u = 2\vec a + 3\vec b$ và $\vec v = \frac{1}{2}\vec a – 3\vec b$
B. $\vec u = \frac{3}{5}\vec a + 3\vec b$ và $\vec v = 2\vec a – \frac{3}{5}\vec b$
C. $\vec u = \frac{2}{3}\vec a + 3\vec b$ và $\vec v = 2\vec a – 9\vec b$
D. $\vec u = 2\vec a – \frac{3}{2}\vec b$ và $\vec v = – \frac{1}{3}\vec a + \frac{1}{4}\vec b$

Lời giải

Chọn D

Câu 60. Biết rằng hai vec tơ $\vec a$ và $\vec b$ không cùng phương nhưng hai vec tơ $3\vec a – 2\vec b$ và $\left( {x + 1} \right)\vec a + 4\vec b$ cùng phương. Khi đó giá trị của $x$ là:
A. -7
B. 7

C. 5
D. 6

Lời giải

Chọn A

Điều kiện để hai vec tơ $3\vec a – 2\vec b$ và $\left( {x + 1} \right)\vec a + 4\vec b$ cùng phương là: $\frac{{x + 1}}{3} = \frac{4}{{ – 2}} \Leftrightarrow x = – 7$.

Câu 61. Cho tam giác $ABC$. Hai điểm $M,N$ được xác định bởi các hệ thức $\overrightarrow {BC} + \overrightarrow {MA} = \vec 0$, $\overrightarrow {AB} – \overrightarrow {NA} – 3\overrightarrow {AC} = \vec 0$. Trong các khẳng định sau, khẳng định nào đúng?
A. $MN \bot AC$
B. $MN//AC$
C. $M$ nằm trên đường thẳng $AC$
D. Hai đường thẳng $MN$ và $AC$ trùng nhau

Lời giải

Chọn B

Ta có: $\overrightarrow {BC} + \overrightarrow {MA} = \vec 0 \Rightarrow \overrightarrow {AM} = \overrightarrow {BC} \Rightarrow M$ là điểm thứ tư của hình bình hành $ABCM$ nên $M \notin AC$ (1) Cộng vế theo vế hai đẳng thức $\overrightarrow {BC} + \overrightarrow {MA} = \vec 0,\overrightarrow {AB} – \overrightarrow {NA} – 3\overrightarrow {AC} = \vec 0$, ta được:

$\overrightarrow {BC} + \overrightarrow {MA} + \overrightarrow {AB} – \overrightarrow {NA} – 3\overrightarrow {AC} = \vec 0$

$ \Leftrightarrow \left( {\overrightarrow {MA} + \overrightarrow {AN} } \right) + \left( {\overrightarrow {AB} + \overrightarrow {BC} } \right) – 3\overrightarrow {AC} = \vec 0$

$ \Leftrightarrow \overrightarrow {MN} + \overrightarrow {AC} – 3\overrightarrow {AC} \Leftrightarrow \overrightarrow {MN} = 2\overrightarrow {AC} \Rightarrow \overrightarrow {MN} $cùng phương với $\overrightarrow {AC} $(2)

Từ (1) và (2) suy ra $MN//AC$.

Câu 62. Cho $\vartriangle ABC$. Lấy các điểm $M,N,P$ sao cho $\overrightarrow {MB} = 3\overrightarrow {MC} ,\overrightarrow {NA} + 3\overrightarrow {NC} = \vec 0,\overrightarrow {PA} + \overrightarrow {PB} = \vec 0$. Đẳng thức nào sau đây là điều kiện cần và đủ để $M,N,P$ thẳng hàng.
A. $\overrightarrow {MP} = – 2\overrightarrow {MN} $
B. $\overrightarrow {MP} = 3\overrightarrow {MN} $
C. $\overrightarrow {MP} = 2\overrightarrow {MN} $
D. $\overrightarrow {MP} = – 3\overrightarrow {MN} $

Lời giải

Chọn C.

$\overrightarrow {AP} = \frac{1}{2}\overrightarrow {AB} ;\overrightarrow {AN} = \frac{3}{4}\overrightarrow {AC} $

$\overrightarrow {MB} = 3\overrightarrow {MC} \Rightarrow \overrightarrow {AM} = \frac{3}{2}\overrightarrow {AC} – \frac{1}{2}\overrightarrow {AB} $

Do đó

$\overrightarrow {MP} = \overrightarrow {AP} – \overrightarrow {AM} = \overrightarrow {AB} – \frac{3}{2}\overrightarrow {AC} \left( 1 \right)$

$\overrightarrow {MN} = \overrightarrow {AN} – \overrightarrow {AM} = \frac{1}{2}\overrightarrow {AB} – \frac{3}{4}\overrightarrow {AC} \left( 2 \right)$

Từ (1), (2) $ \Rightarrow \overrightarrow {MP} = 2\overrightarrow {MN} \Rightarrow M,N,P$ thẳng hàng.

Câu 63. Cho $\vartriangle ABC$ có trung tuyến $AM$. Gọi $I$ là trung điểm $AM$ và $K$ là điểm trên $AC$ sao cho $AK = \frac{1}{3}AC$. Đẳng thức nào sau đây là điều kiện cần và đủ để ba điểm $B,I,K$ thẳng hàng.
A. $\overrightarrow {BK} = \frac{2}{3}\overrightarrow {BI} $
B. $\overrightarrow {BK} = \frac{4}{3}\overrightarrow {BI} $
C. $\overrightarrow {BK} = 2\overrightarrow {BI} $
D. $\overrightarrow {BK} = \frac{3}{2}\overrightarrow {BI} $

Lời giải

Chọn B.

Ta có: $2\overrightarrow {BI} = \overrightarrow {BA} + \overrightarrow {BM} = \overrightarrow {BA} + \frac{1}{2}\overrightarrow {BC} $

$ \Leftrightarrow 4\overrightarrow {BI} = 2\overrightarrow {BA} + \overrightarrow {BC} $

$\overrightarrow {BK} = \overrightarrow {BA} + \overrightarrow {AK} = \overrightarrow {BA} + \frac{1}{3}\overrightarrow {AC} $

$ = \overrightarrow {BA} + \frac{1}{3}\left( {\overrightarrow {BC} – \overrightarrow {BA} } \right) = \frac{2}{3}\overrightarrow {BA} + \frac{1}{3}\overrightarrow {BC} $

$ \Leftrightarrow 3\overrightarrow {BK} = 2\overrightarrow {BA} + \overrightarrow {BC} $

Từ (1) và (2) $ \Leftrightarrow \overrightarrow {BK} = \frac{4}{3}\overrightarrow {BI} \Leftrightarrow B,I,K$ thẳng hàng.

Câu 64. Cho $\vartriangle ABC$ có trung tuyến $AD$.Xét các điểm $M,\;N,\;P\;$ cho bởi $\overrightarrow {AM} = \frac{1}{2}\overrightarrow {AB} ,\overrightarrow {AN} = \frac{1}{4}\overrightarrow {AC} ,\overrightarrow {AP} = m\overrightarrow {AD} $. Tìm $m$ để $M,N,P$ thẳng hàng.
A. $m = \frac{1}{6}$
B. $m = \frac{1}{3}$
C. $m = \frac{1}{4}$
D. $m = \frac{2}{3}$

Lời giải

Chọn B.

Gọi $E$ là trung điểm $AC$ $ \Rightarrow \overrightarrow {AN} = \frac{1}{2}\overrightarrow {AE} \Rightarrow MN//BE$

$ \Rightarrow G$ là trọng tâm $\vartriangle ABE$

$ \Rightarrow \overrightarrow {AG} = \frac{2}{3}\overrightarrow {AD} $ nên $M,N,P$ thẳng hàng

$ \Rightarrow P$ là trung điểm $AG$.

Vậy $\overrightarrow {AP} = \frac{1}{2}\overrightarrow {AG} = \frac{1}{3}\overrightarrow {AD} $

Câu 65. Cho ngũ giác $ABCDE$. Gọi $M,N,P,Q$ lần lượt là trung điểm của cạnh $AB,BC,CD,DE$. Gọi $I$, $J$ lần lượt là trung điểm của các đoạn $MP$ và $NQ$. Đẳng thức nào sau đây là điều kiện cần và đủ để $IJ//AE$ ?
A. $\overrightarrow {IJ} = \frac{3}{4}\overrightarrow {AE} $
B. $\overrightarrow {IJ} = \frac{5}{4}\overrightarrow {AE} $
C. $\overrightarrow {IJ} = \frac{1}{4}\overrightarrow {AE} $
D. $\overrightarrow {IJ} = \frac{1}{3}\overrightarrow {AE} $

Lời giải

Chọn C.

$\overrightarrow {IQ} + \overrightarrow {IN} = 2\overrightarrow {IJ} $

$ \Leftrightarrow \overrightarrow {IM} + \overrightarrow {MQ} + \overrightarrow {IP} + \overrightarrow {PN} = 2\overrightarrow {IJ} $

$ \Leftrightarrow \overrightarrow {MQ} + \overrightarrow {PN} = 2\overrightarrow {IJ} $

$ \Leftrightarrow \frac{1}{2}\left( {\overrightarrow {AE} + \overrightarrow {BD} } \right) – \frac{1}{2}\overrightarrow {BD} = 2\overrightarrow {IJ} $

$ \Leftrightarrow \frac{1}{4}\overrightarrow {AE} = \overrightarrow {IJ} $

Câu 66. Cho $\vartriangle ABC$. Các điểm $I,J$ thỏa mãn hệ thức $\overrightarrow {AI} = \frac{1}{3}\overrightarrow {AB} ,\overrightarrow {AI} = 3\overrightarrow {AC} $. Đẳng thức nào sau đây là điều kiện cần và đủ để $IC//BJ$ ?
A. $\overrightarrow {CI} = – \frac{2}{3}\overrightarrow {BJ} $
B. $\overrightarrow {CI} = 3\overrightarrow {BJ} $
C. $\overrightarrow {CI} = – \frac{1}{3}\overrightarrow {BJ} $
D. $\overrightarrow {CI} = \frac{1}{3}\overrightarrow {BJ} $

Lời giải

Chọn C.

$\overrightarrow {AI} = \frac{1}{3}\overrightarrow {AB} $

$ \Leftrightarrow \overrightarrow {AC} + \overrightarrow {CI} = \frac{1}{3}\left( {\overrightarrow {AC} + \overrightarrow {CB} } \right)$

$ \Leftrightarrow \overrightarrow {CI} = – \frac{1}{3}\left( {2\overrightarrow {AC} + \overrightarrow {BC} } \right)\left( 1 \right)$

$\overrightarrow {AJ} = 3\overrightarrow {AC} \Leftrightarrow \overrightarrow {AB} + \overrightarrow {BJ} = 3\overrightarrow {AB} + \overrightarrow {BC} $

$ \Leftrightarrow \overrightarrow {BJ} = 2\overrightarrow {AB} + \overrightarrow {BC} = 2\overrightarrow {AC} + \overrightarrow {BC} \left( 2 \right)$

Từ (1) và (2) $ \Rightarrow \overrightarrow {CI} = – \frac{1}{3}\overrightarrow {BJ} $

Câu 67. Cho $\vartriangle ABC$. Hai điểm $M,N$ được xác định bởi hệ thức $\overrightarrow {BC} + \overrightarrow {MA} = \vec 0,\overrightarrow {AB} – \overrightarrow {NA} – 3\overrightarrow {AC} = \vec 0$. Đẳng thức nào sau đây là điều kiện cần và đủ để $MN//AC$.
A. $\overrightarrow {MN} = 2\overrightarrow {AC} $
B. $\overrightarrow {MN} = \frac{1}{2}\overrightarrow {AC} $
C. $\overrightarrow {MN} = – 3\overrightarrow {AC} $
D. $\overrightarrow {MN} = \frac{1}{3}\overrightarrow {AC} $

Lời giải

Chọn A.

Ta có: $\overrightarrow {BC} + \overrightarrow {MA} = \vec 0$ và $\overrightarrow {AB} – \overrightarrow {NA} – 3\overrightarrow {AC} = \vec 0$

$ \Rightarrow \overrightarrow {BC} + \overrightarrow {MA} + \overrightarrow {AB} – \overrightarrow {NA} – 3\overrightarrow {AC} = \vec 0$

$ \Leftrightarrow \overrightarrow {AC} + \overrightarrow {MN} – 3\overrightarrow {AC} = \vec 0 \Leftrightarrow \overrightarrow {MN} = 2\overrightarrow {AC} $

Ta có: $\overrightarrow {BC} + \overrightarrow {MA} = \vec 0 \Leftrightarrow \overrightarrow {BC} = \overrightarrow {AM} \Rightarrow ABCM$ là hình bình hành hay $M \notin AC$

$ \Rightarrow MN//AC \Rightarrow $ Chọn đáp án A.

Câu 68. Cho tứ giác $ABCD$. Gọi $I,J$ lần lượt là trọng tâm của $\vartriangle ADC$ và $\vartriangle BCD$. Đẳng thức nào là điều kiện cần và đủ để $IJ//AB$.
A. $\overrightarrow {IJ} = \frac{1}{3}\overrightarrow {AB} $
B. $\overrightarrow {IJ} = \frac{2}{3} \cdot \overrightarrow {AB} $
C. $\overrightarrow {IJ} = \frac{1}{2}\overrightarrow {AB} $
D. $\overrightarrow {IJ} = \frac{1}{4}\overrightarrow {AB} $.

Lời giải

Chọn A.

Gọi $M$ là trung điểm .

Ta có: $\overrightarrow {MI} = \frac{1}{3}\overrightarrow {MA} ,\overrightarrow {MJ} = \frac{1}{3}\overrightarrow {MB} $

$ \Rightarrow \overrightarrow {MJ} – \overrightarrow {MI} = \frac{1}{3}\left( {\overrightarrow {MB} – \overrightarrow {MA} } \right) \Leftrightarrow \overrightarrow {IJ} = \frac{1}{3}\overrightarrow {AB} $

Câu 69. Cho $\vartriangle ABC$. Trên các cạnh $AB,BC$ lấy các điểm $M,N$ sao cho $AM = \frac{2}{5}MB,\frac{{BN}}{{NC}} = \frac{1}{3}$. Gọi $I$ là giao điểm của $AN$ và $CM$. Tính tỉ số $\frac{{AI}}{{AN}}$ và $\frac{{CI}}{{IM}}$.
A. $\frac{{AI}}{{AN}} = \frac{3}{7};\frac{{CI}}{{IM}} = \frac{{21}}{2}$
B. $\frac{{AI}}{{AN}} = \frac{4}{{11}};\frac{{CI}}{{IM}} = \frac{7}{2}$
C. $\frac{{AI}}{{AN}} = \frac{8}{{23}};\frac{{CI}}{{IM}} = \frac{7}{4}$
D. $\frac{{AI}}{{AN}} = \frac{8}{{23}};\frac{{CI}}{{IM}} = \frac{{21}}{2}$

Lời giải

Chọn D.

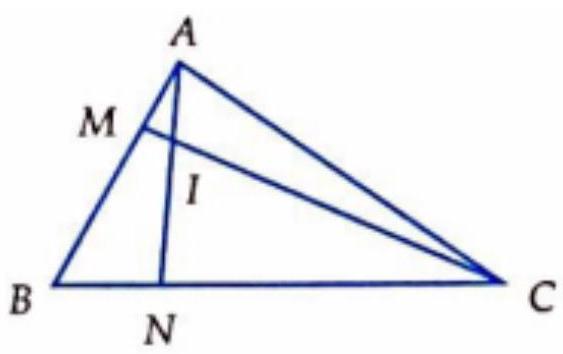
Đặt $\overrightarrow {AI} = x\overrightarrow {AN} ,\overrightarrow {CI} = y\overrightarrow {CM} $

Ta có: $\overrightarrow {AI} = x\left( {\overrightarrow {AB} + \overrightarrow {BN} } \right)$

$ = x\overrightarrow {AB} + \frac{x}{4}\overrightarrow {AC} $

$ = \frac{{3x}}{4}\overrightarrow {AB} + \frac{x}{4}\overrightarrow {AC} = \frac{{21x}}{8}\overrightarrow {AM} + \frac{x}{4}\overrightarrow {AC} $

Vì $M,C,I$ thẳng hàng $ \Rightarrow \frac{{21x}}{8} + \frac{x}{4} = 1 \Leftrightarrow x = \frac{8}{{23}}$

Tương tự ta chưa tìm được $\frac{{IC}}{{IM}} = \frac{{21}}{2}$

Câu 70. Cho $\vartriangle ABC$ và trung tuyến $AM$. Một đường thẳng song song với $AB$ cắt các đoạn thẳng $AM,AC$ và $BC$ lần lượt tại $D,E$, và $F$. Một điểm $G$ nằm trên cạnh $AB$ sao cho $FG$ song song với $AC$. Tính $\frac{{ED}}{{GB}}$.
A. $\frac{1}{2}$
B. $\frac{1}{3}$
C. $\frac{1}{4}$
D. 1

Lời giải

Chọn D.

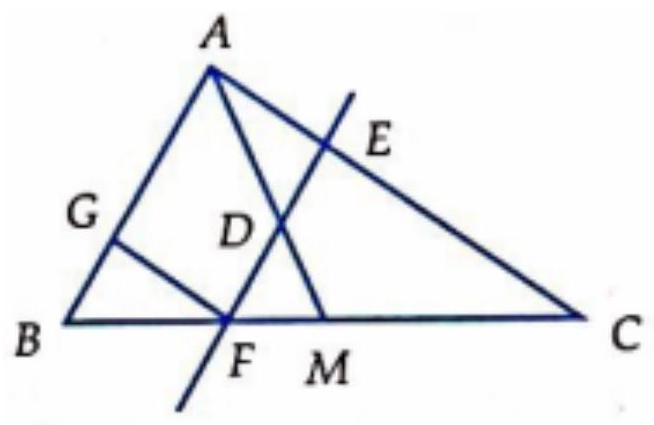
Ta đặt: $\overrightarrow {CA} = \vec a,\overrightarrow {CB} = \vec b$

Khi đó $\overrightarrow {CM} = \frac{b}{2}\overrightarrow {CE} = k\overrightarrow {CA} = k\vec a$

Vì $E$ nằm ngoài $AC$ nên có số $k$ sao cho: $\overrightarrow {CE} = k\overrightarrow {CA} = k\vec a$ với $0 < k < 1$.

Khi đó $\overrightarrow {CF} = k \cdot \overrightarrow {CB} = k\vec b$.

Điểm $D$ nằm trên $AM$ và $EF$ nên có số $x$ này:

$\overrightarrow {CD} = x\overrightarrow {CA} + \left( {1 – x} \right)\overrightarrow {CM} = y\overrightarrow {CE} + \left( {1 – y} \right)\left( {\overrightarrow {CF} } \right)$

Hay $x\vec a + \frac{{1 – x}}{2}\vec b = ky\vec a + k\left( {1 – y} \right)\vec b$

Vì $\vec a,\vec b$ không cùng phương nên: $x = ky$ và $\frac{{1 – x}}{2} = k\left( {1 – y} \right)$

Suy ra $x = 2k – 1$ do đó $\overrightarrow {CD} = \left( {2k – 1} \right)\vec a + \left( {1 – k} \right)\vec b$

$\overrightarrow {AB} + \overrightarrow {GB} = k\overrightarrow {AB} $

$ \Rightarrow \left( {1 – k} \right)\overrightarrow {AB} = \overrightarrow {GB} \Rightarrow \frac{{ED}}{{GB}} = 1$