Các Dạng Toán Bài Tổng Hiệu Hai VecTơ Giải Chi Tiết

Các dạng toán bài Tổng hiệu hai vectơ giải chi tiết được soạn dưới dạng file word và PDF gồm 4 trang. Các bạn xem và tải về ở dưới.

DẠNG 1: CÁC PHÉP TOÁN LIÊN QUAN ĐẾN TỔNG VÀ HIỆU CÁC VECTƠ

Bài 1: Cho tam giác $ABC$. Chứng minh rằng $\overrightarrow {{\mathbf{AB}}} + \overrightarrow {{\mathbf{BC}}} + \overrightarrow {{\mathbf{CA}}} = \overrightarrow {\mathbf{0}} $.

Lời giải

Ta có:

$VT = \overrightarrow {{\mathbf{AB}}} + \overrightarrow {{\mathbf{BC}}} + \overrightarrow {{\mathbf{CA}}} = \left( {\overrightarrow {{\mathbf{AB}}} + \overrightarrow {{\mathbf{BC}}} } \right) + \overrightarrow {{\mathbf{CA}}} = \overrightarrow {AC} + \overrightarrow {{\mathbf{CA}}} = \overrightarrow 0 = VP$

Bài 2. Cho hình bình hành $ABCD$.

a) Xác định các vectơ $\overrightarrow {CB} + \overrightarrow {CD} ,\overrightarrow {AC} + \overrightarrow {DA} $.

b) Gọi $M$ và $N$ lần lượt là trung điểm của $BC$ và $AD$.

• Tính $\overrightarrow {NC} + \overrightarrow {MC} $

• Tính $\overrightarrow {AM} + \overrightarrow {CD} $

Lời giải

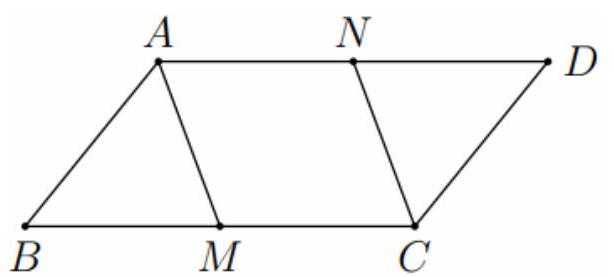
a) $\overrightarrow {CB} + \overrightarrow {CD} = \overrightarrow {CA} $ và $\overrightarrow {AC} + \overrightarrow {DA} = \overrightarrow {DA} + \overrightarrow {AC} = \overrightarrow {DC} $.

b)

Vì $\overrightarrow {MC} = \overrightarrow {AN} $ nên ta có $\overrightarrow {NC} + \overrightarrow {MC} = \overrightarrow {NC} + \overrightarrow {AN} = \overrightarrow {AN} + \overrightarrow {NC} = \overrightarrow {AC} $.

Vì $\overrightarrow {CD} = \overrightarrow {BA} $ nên ta có $\overrightarrow {AM} + \overrightarrow {CD} = \overrightarrow {AM} + \overrightarrow {BA} = \overrightarrow {BA} + \overrightarrow {AM} = \overrightarrow {BM} $.

Bài 3. Cho bốn điểm bất kỳ $A,B,C,D$. Hãy chứng minh rằng

a) $\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DA} = \vec 0$.

b) $\overrightarrow {AC} – \overrightarrow {AD} = \overrightarrow {BC} – \overrightarrow {BD} $

Lời giải

a) Ta có $\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DA} = \left( {\overrightarrow {AB} + \overrightarrow {BC} } \right) + \left( {\overrightarrow {CD} + \overrightarrow {DA} } \right) = \overrightarrow {AC} + \overrightarrow {CA} = \vec 0$.

b) Ta có $\left\{ {\begin{array}{*{20}{l}}
{\overrightarrow {AC} – \overrightarrow {AD} = \overrightarrow {DC} } \\
{\overrightarrow {BC} – \overrightarrow {BD} = \overrightarrow {DC} }
\end{array}} \right.$ nên $\overrightarrow {AC} – \overrightarrow {AD} = \overrightarrow {BC} – \overrightarrow {BD} $.

Bài 4. Cho năm điểm $A,B,C,D,E$. Chứng minh rằng

a) $\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {EA} = \overrightarrow {CB} + \overrightarrow {ED} $

b) $\overrightarrow {AC} + \overrightarrow {CD} – \overrightarrow {EC} = \overrightarrow {AE} – \overrightarrow {DB} + \overrightarrow {CB} $

Lời giải

a) Biến đổi vế trái ta có

$VP = \left( {\overrightarrow {AC} + \overrightarrow {CB} } \right) + \overrightarrow {CD} + \left( {\overrightarrow {ED} + \overrightarrow {DA} } \right)$

$ = \left( {\overrightarrow {CB} + \overrightarrow {ED} } \right) + \left( {\overrightarrow {AC} + \overrightarrow {CD} } \right) + \overrightarrow {DA} $

$\; = \left( {\overrightarrow {CB} + \overrightarrow {ED} } \right) + \overrightarrow {AD} + \overrightarrow {DA} $

$ = \overrightarrow {CB} + \overrightarrow {ED} = VP$

b) Cách 1:

$\overrightarrow {AC} + \overrightarrow {CD} – \overrightarrow {EC} = \overrightarrow {AE} – \overrightarrow {DB} + \overrightarrow {CB} $

$ \Leftrightarrow \left( {\overrightarrow {AC} – \overrightarrow {AE} } \right) + \left( {\overrightarrow {CD} – \overrightarrow {CB} } \right) – \overrightarrow {EC} + \overrightarrow {DB} = \vec 0$

$ \Leftrightarrow \overrightarrow {EC} + \overrightarrow {BD} – \overrightarrow {EC} + \overrightarrow {DB} = \vec 0$

$ \Leftrightarrow \overrightarrow {BD} + \overrightarrow {DB} = \vec 0$ (đúng)

Cách 2:

$VT = \overrightarrow {AC} + \overrightarrow {CD} – \overrightarrow {EC} = \left( {\overrightarrow {AE} + \overrightarrow {EC} } \right) + \left( {\overrightarrow {CB} + \overrightarrow {BD} } \right) – \left( {\overrightarrow {EB} + \overrightarrow {BC} } \right)$

$ = \overrightarrow {AE} + \overrightarrow {EC} + \overrightarrow {CB} + \overrightarrow {BD} – \overrightarrow {EB} – \overrightarrow {BC} $

$ = \left( {\overrightarrow {AE} + \overrightarrow {BD} + \overrightarrow {CB} } \right) + \left( {\overrightarrow {EC} – \overrightarrow {EB} – \overrightarrow {BC} } \right)$

$ = \left( {\overrightarrow {AE} + \overrightarrow {BD} + \overrightarrow {CB} } \right) + \left( {\overrightarrow {BC} – \overrightarrow {BC} } \right)$

$ = \left( {\overrightarrow {AE} + \overrightarrow {BD} + \overrightarrow {CB} } \right) + \overrightarrow 0 $

$ = \overrightarrow {AE} – \overrightarrow {DB} + \overrightarrow {CB} = VP$

Bài 5. Cho tam giác $ABC$. Gọi $M,N,P$ lần lượt là trung điểm của $BC,CA,AB$. Chứng minh rằng:

a) $\overrightarrow {BM} + \overrightarrow {CN} + \overrightarrow {AP} = \vec 0$

b) $\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OM} + \overrightarrow {ON} + \overrightarrow {OP} $, với $O$ là điểm bất kì.

Lời giải

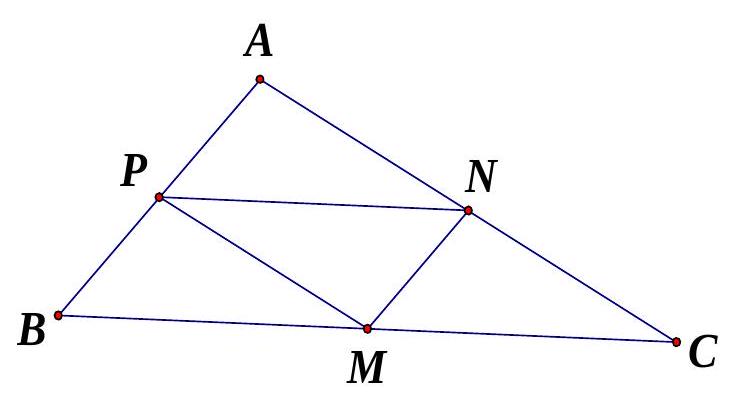
a) Vì $PN,MN$ là đường trung bình của tam giác $ABC$ nên $PN//BM,MN//BP$ suy ra tứ giác $BMNP$ là hình bình hành $ \Rightarrow \overrightarrow {BM} = \overrightarrow {PN} $.

$N$ là trung điểm của $AC \Rightarrow \overrightarrow {CN} = \overrightarrow {NA} $.

Do đó theo quy tắc ba điểm ta có

$\overrightarrow {BM} + \overrightarrow {CN} + \overrightarrow {AP} = \left( {\overrightarrow {PN} + \overrightarrow {NA} } \right) + \overrightarrow {AP} = \overrightarrow {PA} + \overrightarrow {AP} = \vec 0$

b) Theo quy tắc ba điểm ta có

$\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \left( {\overrightarrow {OP} + \overrightarrow {PA} } \right) + \left( {\overrightarrow {OM} + \overrightarrow {MB} } \right) + \left( {\overrightarrow {ON} + \overrightarrow {NC} } \right)$

$ = \left( {\overrightarrow {OM} + \overrightarrow {ON} + \overrightarrow {OP} } \right) + \overrightarrow {PA} + \overrightarrow {MB} + \overrightarrow {NC} $

$\; = \left( {\overrightarrow {OM} + \overrightarrow {ON} + \overrightarrow {OP} } \right) – \left( {\overrightarrow {BM} + \overrightarrow {CN} + \overrightarrow {AP} } \right)$

Theo câu a) $\overrightarrow {BM} + \overrightarrow {CN} + \overrightarrow {AP} = \vec 0$ ta suy ra $\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = \overrightarrow {OM} + \overrightarrow {ON} + \overrightarrow {OP} $.

Bài 6. Cho tam giác $ABC$. Bên ngoài của tam giác vẽ các hình bình hành $ABIJ,BCPQ,CARS$. Chứng minh rằng $\overrightarrow {RJ} + \overrightarrow {IQ} + \overrightarrow {PS} = \vec 0$.

Lời giải

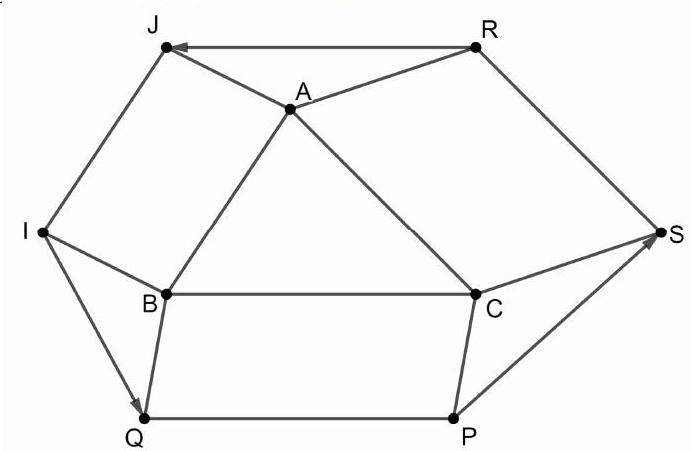
Ta có: $\overrightarrow {RJ} = \overrightarrow {RA} + \overrightarrow {AJ} $

$\overrightarrow {IQ} = \overrightarrow {IB} + \overrightarrow {BQ} ,\overrightarrow {PS} = \overrightarrow {PC} + \overrightarrow {CS} $

Suy ra, $\overrightarrow {RJ} + \overrightarrow {IQ} + \overrightarrow {PS} $$\; = \left( {\overrightarrow {RA} + \overrightarrow {AJ} } \right) + \left( {\overrightarrow {IB} + \overrightarrow {BQ} } \right) + \left( {\overrightarrow {PC} + \overrightarrow {CS} } \right)$

$ = \left( {\overrightarrow {RA} + \overrightarrow {CS} } \right) + \left( {\overrightarrow {AJ} + \overrightarrow {IB} } \right) + \left( {\overrightarrow {BQ} + \overrightarrow {PC} } \right)$

$ = \left( {\overrightarrow {SC} + \overrightarrow {CS} } \right) + \left( {\overrightarrow {BI} + \overrightarrow {IB} } \right) + \left( {\overrightarrow {CP} + \overrightarrow {PC} } \right)$

$ = \overrightarrow {SS} + \overrightarrow {BB} + \overrightarrow {CC} $

$ = \vec 0$

Vậy $\overrightarrow {RJ} + \overrightarrow {IQ} + \overrightarrow {PS} = \vec 0$.

Bài 7. Cho tứ giác lồi $ABCD$ có $I,J$ lần lượt là trung điểm hai cạnh $AD,BC$ và $G$ là trung điểm $IJ$. Gọi $P$ là điểm đối xứng của $G$ qua $I,Q$ là điểm đối xứng của $G$ qua $J$. Chứng minh các đẳng thức vecto sau:

a) $\overrightarrow {GA} + \overrightarrow {GD} = \overrightarrow {GP} ;\overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow {GQ} $.

b) $\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \vec 0$.

Lời giải

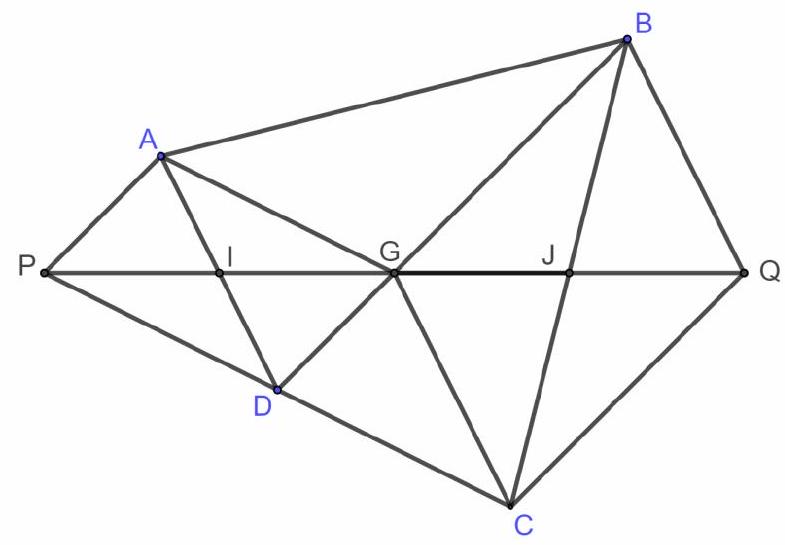
a) Hai tứ giác $AGDP$ và $BGCQ$ có hai đường chéo giao nhau tại trung điểm mỗi đường nên chúng là các hình bình hành.

Theo quy tắc hình bình hành ta có:

$\overrightarrow {GA} + \overrightarrow {GD} = \overrightarrow {GP} $ (đpcm).

$\overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow {GQ} ($ đpcm).

b) Theo cách dựng hình từ đề bài ta thấy $G$ là trung điểm $PQ$ nên $\overrightarrow {GP} + \overrightarrow {GQ} = \vec 0$. Biến đổi biểu thức vectơ đề cho và dựa vào kết quả câu a:

$\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \left( {\overrightarrow {GA} + \overrightarrow {GD} } \right) + \left( {\overrightarrow {GB} + \overrightarrow {GC} } \right) = \overrightarrow {GP} + \overrightarrow {GQ} = \vec 0$

Bài 8. Cho $n$ điểm phân biệt trên mặt phẳng. Bạn An kí hiệu chúng là ${A_1},{A_2}, \ldots ,{A_n}$. Bạn Bình kí hiệu chúng là ${B_1},{B_2}, \ldots ,{B_n}\left( {{A_1}\not \equiv {B_n}} \right)$. Chứng minh rằng: $\overrightarrow {{A_1}{B_1}} + \overrightarrow {{A_2}{B_2}} + \ldots + \overrightarrow {{A_n}{B_n}} = \vec 0$.

Lời giải

Lấy điểm $O$ bất kì. Khi đó

$\overrightarrow {{A_1}{B_1}} + \overrightarrow {{A_2}{B_2}} + \ldots + \overrightarrow {{A_n}{B_n}} = \left( {\overrightarrow {O{B_1}} + \overrightarrow {O{B_2}} + \ldots + \overrightarrow {O{B_n}} } \right) – \left( {\overrightarrow {O{A_1}} + \overrightarrow {O{A_2}} + \ldots + \overrightarrow {O{A_n}} } \right)$

Vì $\left\{ {{B_1},{B_2}, \ldots ,{B_n}} \right\} = \left\{ {{A_1},{A_2}, \ldots ,{A_n}} \right\}$ nên

$\overrightarrow {O{B_1}} + \overrightarrow {O{B_2}} + \ldots + \overrightarrow {O{B_n}} = \overrightarrow {O{A_1}} + \overrightarrow {O{A_2}} + \ldots + \overrightarrow {O{A_n}} $

Do đó $\overrightarrow {{A_1}{B_1}} + \overrightarrow {{A_2}{B_2}} + \ldots + \overrightarrow {{A_n}{B_n}} = \vec 0$.

DẠNG 2: TÍNH ĐỘ DÀI CỦA VEC TƠ

Bài 1. Cho hình vuông $ABCD$ có cạnh bằng $a$. Tính $\left| {\overrightarrow {AD} + \overrightarrow {AB} } \right|$.

Lời giải

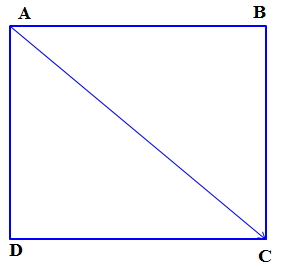
Theo quy tắc đường chéo hình bình hành, ta có $\left| {\overrightarrow {AD} + \overrightarrow {AB} \left| = \right|\overrightarrow {AC} } \right| = AC = AB\sqrt 2 = a\sqrt 2 $.

Bài 2. Cho tam giác $ABC$ đều cạnh $a$. Tính $\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right|$.

Lời giải

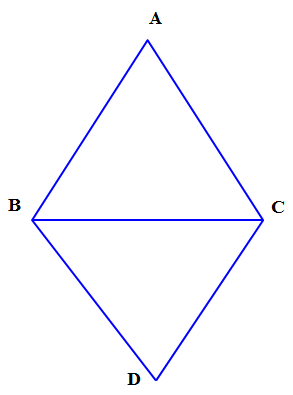
Gọi $D$ là điểm sao cho $ABDC$ là hình bình hành.

Ta có $AB = AC$ nên $ABDC$ là hình thoi.

Gọi $O$ là tâm hình thoi $ABDC$.

Ta có:

$\left| {\overrightarrow {AB}  + \overrightarrow {AC} } \right| = \left| {\overrightarrow {AD} } \right| = AD = 2AO = a\sqrt 3 $.

Bài 3. Gọi $G$ là trọng tâm tam giác vuông $ABC$, với cạnh huyền $BC = 12$. Tính độ dài của vectơ $\overrightarrow {GB} + \overrightarrow {GC} $.

Lời giải

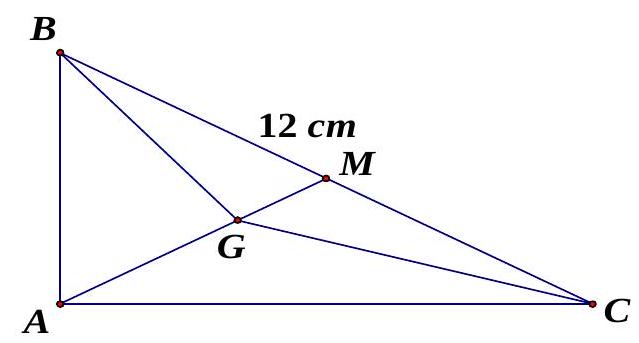
Gọi $M$ là trung điểm $BC$

Ta có $AM = \frac{1}{2}BC = 6;AG = \frac{2}{3}AM = 4$.

Mặc khác $\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \vec 0 \Rightarrow \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow {AG} $

Suy ra $\left| {\overrightarrow {GB} + \overrightarrow {GC} \left| = \right|\overrightarrow {AG} } \right| = AG = 4$.

DẠNG 3: ỨNG DỤNG THỰC TIỄN

Bài 1. Có hai lực ${\vec F_1},{\vec F_2}$ cùng tác động vào một vật đứng tại điểm $O$, biết hai lực ${\vec F_1},{\vec F_2}$ đều có cường độ là $50\left( {\;N} \right)$ và chúng hợp với nhau một góc ${60^ \circ }$. Hỏi vật đó phải chịu một lực tổng hợp có cường độ bằng bao nhiêu?

Lời giải

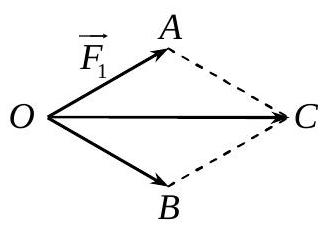
Giả sử ${\vec F_1} = \overrightarrow {OA} ,\overrightarrow {{F_2}} = \overrightarrow {OB} $.

Theo quy tắc hình bình hành, suy ra ${\vec F_1} + \overrightarrow {{F_2}} = \overrightarrow {OC} $, như hình vẽ.

Ta có $\widehat {AOB} = {60^ \circ },OA = OB = 50$, nên tam giác $OAB$ đều, suy ra $OC = 50\sqrt 3 $.

Vậy $\left| {\overrightarrow {{F_1}} + \overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {OC} } \right| = 50\sqrt 3 \left( {\;N} \right)$.

Bài 2. Hình 4.19 biểu diễn hai lực ${\vec F_1},{\vec F_2}$ cùng tác động lên một vật, cho $\left| {{{\vec F}_1}} \right| = 3N,\left| {\overrightarrow {{F_2}} } \right| = 2N$. Tính độ lớn của hợp lực $\overrightarrow {{F_1}} + \overrightarrow {{F_2}} $.

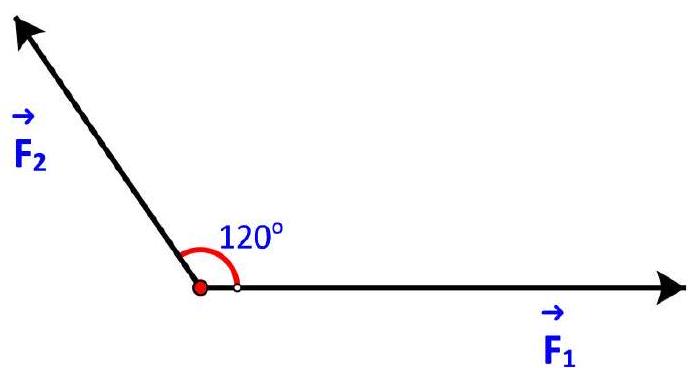
Lời giải

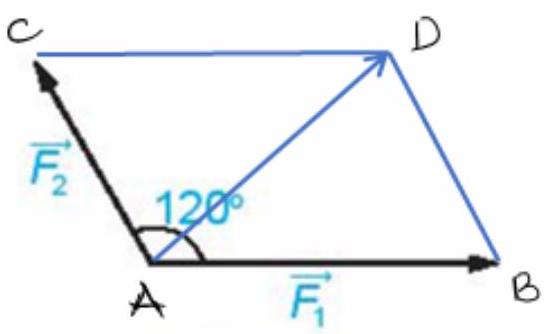
Gọi $\overrightarrow {AB} = {\vec F_1},\overrightarrow {AC} = {\vec F_2}$

Ta có ${\vec F_1} + \overrightarrow {{F_2}} = \overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD} = \vec F$

Xét tam giác $ABD$

$\begin{array}{*{20}{r}}
{AD}&{\; = \sqrt {B{A^2} + B{D^2} – 2BA \cdot BD \cdot cos{{60}^0}} } \\
{}&{\; = \sqrt {9 + 4 – 2 \cdot 3 \cdot 2 \cdot \frac{1}{2}} = \sqrt 7 .}
\end{array}$

Vậy $\left| {\vec F} \right| = \sqrt 7 N$.

Bài 3. Chất điểm $A$ chịu tác động của ba lực $\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} $ như Hình 4.30 và ở trạng thái cân bằng (tức là $\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \vec 0$ ). Tính độ lớn của các lực $\overrightarrow {{F_2}} ,\overrightarrow {{F_3}} $, biết ${\vec F_1}$ có độ lớn là $20\;N$.

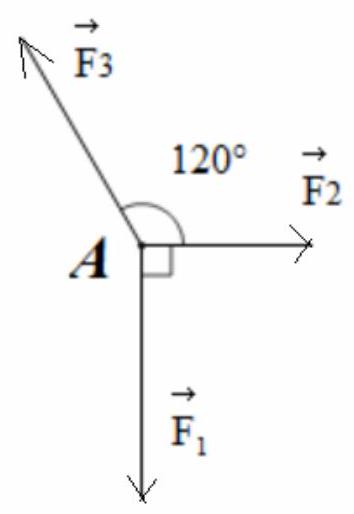
Lời giải

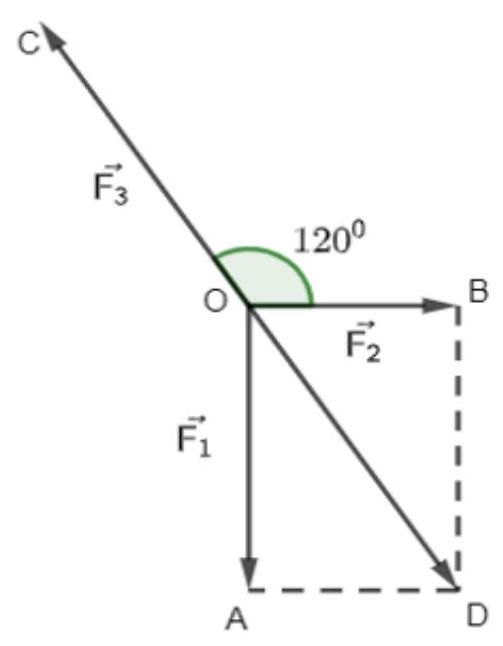
$\overrightarrow {{F_1}} + \overrightarrow {{F_2}} = \overrightarrow {{F_4}} $

$\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \vec 0 \Leftrightarrow \overrightarrow {{F_4}} = – \overrightarrow {{F_3}} \Rightarrow \left| { – \overrightarrow {{F_3}} } \right| = \left| {\overrightarrow {{F_4}} } \right|$

Ta có: $\left| {\overrightarrow {{F_2}} } \right| = \left| {\overrightarrow {{F_1}} } \right| \cdot tan{30^ \circ } = \frac{{20\sqrt 3 }}{3};\left| {\overrightarrow {{F_4}} } \right| = \frac{{\left| {\overrightarrow {{F_1}} } \right|}}{{cos{{30}^ \circ }}} = \frac{{40\sqrt 3 }}{3}$;

Vậy $\left| {\overrightarrow {{F_2}} } \right| = \frac{{20\sqrt 3 }}{3}\;N,\left| {\overrightarrow {{F_3}} } \right| = \frac{{40\sqrt 3 }}{3}\;N$.

Bài 4. Hai con tàu xuất phát cùng lúc từ bờ bên này để sang bờ bên kia của dòng sông với vận tốc riêng không đổi và có độ lớn bằng nhau. Hai tàu luôn được giữ lái sao cho chúng tạo với bờ cùng một góc nhọn nhưng một tàu hướng xuống hạ lưu, một tàu hướng lên thượng nguồn ( hình vẽ). Vận tốc dòng nước là đáng kể, các yếu tố bên ngoài khác không ảnh hưởng đến vận tốc của các tàu. Hỏi tàu nào sang bờ bên kia trước?

Lời giải

Gọi tàu thứ nhất là tàu hướng xuống hạ lưu có vận tốc thực tế là $\overrightarrow {{v_1}} = \overrightarrow {{v_r}} + \overrightarrow {{v_n}} $

tàu thứ hai là tàu hướng lên thượng nguồn có vận tốc thực tế là $\overrightarrow {{v_2}} = \overrightarrow {{v_r}} – \overrightarrow {{v_n}} $

Ta thấy $\overrightarrow {{v_1}} > \overrightarrow {{v_2}} $ nên tàu thứ nhất sẽ sang bờ bên kia trước.